Matematika»Logika

Logika

Sarrera

I. Logika formala

Logika formala arrazoibideen barne zuzenketa da. Arrazoibide esaten zaiona proposizioez edo perpausez osaturiko katea bat da, eta katea horretan perpausetako bat, beste perpaus batzuk, premisak alegia, ontzat ematen direlako, haien ondorio izango da.Arrazoibideen oinarriak perpausak dira, beraz, eta egitura logikoek perpausetan dute abiapuntua. Perpaus bat enuntziatu baten, tasun baten edo gertaera baten egiaztapena da. Logikan, egia nahiz gezur izan daitekeen edozein baieztapen har daiteke perpausatzat. Perpausak dira, esaterako :- Gaur euria ari du.- Autoek zarata ateratzen dute.- Aberatsa banintz yatea erosiko nuke eta itsasora aterako nintzateke . Itsasora ateratzen naizenean zorabiatu egiten naiz. Zorabiatzea ez da ona nire osasunerako. Beraz, aberatsa banintz osasun txarra izango nuke.Logika elementala edo bakuna bi balioko logika bat da. Alegia, perpaus batek bi balio bakarrik har ditzake, egia izan ala gezurra izan. Baieztapen bat, adibidez "gaur bero egiten du", egia ala gezurra izan daiteke soilik. Ez da onartzen "bai, baina fresko samar egiten du" esatea, edo eguraldi epela dagoela esatea. Bi aukera posible bakarrak bero ala ez bero dira.Logikak arrazoibidea du aztergai, eta ez ondorioaren baliozkotasuna edo lortu den ondorioaren eta errealitatearen arteko egokitasuna.

Arrazoibide oker batek, okerra izan arren, ondorio zuzenak izan ditzake, eta litekeena da, halaber, arrazoibide zuzen batetik ondorio faltsuak ateratzea premisen egiatasuna ez bada ziurra.Adibidea : "Aulkiek lau hanka dituzte, zakurrak ez dira aulkiak, beraz zakurrek lau hanka dituzte". Arrazoibide baliogabea da, baina ondorioa zuzena da."Ilargian zuhaitzak daude. Zuhaitzak badaude sua egin daiteke, beraz ilargian sua egin daiteke." Arrazoibidea baliozkoa da, baina ondorioa faltsua.Balio logikoak, egia izan ala gezurra izan, perpaus osoari egoki dakizkioke, perpausa osorik kontuan hartuta, perpausaren barne egiturari erreparatu gabe. Kasu horretan, perpaus bakunak perpaus elkartuak sortzeko nola konbinatzen diren aztertzen du logikak, eta baita perpaus elkartua osatzen duten perpaus bakunen balioaren arabera zein den perpaus berriaren balio logikoa. Logikaren parte horri perpausen logika deritzo. Baina beste kasu batzuetan perpausaren barne logika da aztertu nahi dena, subjektuak eta predikatuak hartzen duten balioaren arabera perpausak duen logika hain zuzen ; horri predikatuen logika esaten zaio.

I I. Perpausen logika

Perpausak izan daitezke : bakunak, edo elementalak, ala elkartuak, edo konplexuak. Perpaus elkartuak perpaus bakunak eragileen bidez elkarri lotuz lortzen dira. Perpaus bakunak letra xehez adierazten dira: p, q, r...Perpaus bat egiazkoa izan daiteke -V edo 1 adierazten da-, edo faltsua -F edo O adierazten da-. Perpaus bakun batek, oro har, bi balio har ditzake. Beti egiazko balioa hartzen duten perpausei tautologia esaten zaie. Eta, aldiz, beti faltsua den perpausa bat kontraesana edo antilogia da. Perpaus batek batzuetan egia balioa eta besteetan faltsua balioa har ditzakeenean, kontingentzia deitzen zaio.Eragile logikoak bi perpaus bakunetatik abiaturik perpaus elkartu bat lortzeko bidea ematen duten lokailuak dira, salbu eta ukapenaren kasuan, ukapenak perpaus bakarrean soilik baitu eragina.

Eragile primarioak ukapena, konjuntzioa eta disjuntzioa dira.

Horietatik abiaturik inplikazioa eta baliokidetasuna atera daitezke.

Bi perpaus bakunen artean era daitezkeen beste konbinazio batzuk baztertzea eta bateraezintasuna dira.Eragile bat zehaztuta geldituko da, baldin eta hura osatzen duten perpaus bakunen balio bakoitzarentzat perpaus elkartuak zein balio hartuko dituen ezaguna bada. Zenbait perpausen balio logikoak alderatzeko balio taulak erabiltzen dira; lehenengo ilaran perpaus bakunak ezartzen dira, edo elkartuak, eta zutabeetan, berriz, perpausek har ditzaketen balioak. Perpaus bakarra dagoenean, hauek dira aukera bakarrak :Bi perpaus direnean, lau aukera daude :

II.I. Ukapena

Ukapena perpaus bakar batez osaturiko eragiketa da. p perpausaren ukapena egia da p faltsua denean, eta faltsua da p egia denean. pperpausa adierazten duen letraren gainean marra bat jarriz ematen da aditzera (p). Eta bere balio taula ondokoa da :p perpausak liburua gorria da" baldin badio, p liburua ez da gorria" izango da.Tasunak : ukapen bikoitzaren legea. Perpaus baten ukapenaren ukapena jatorrizko perpausa bera da :Adibidea: liburua ez da ez gorria" perpausa eta "gorria da" perpausak berdinak dira.Logikan, balio logiko berberak hartzen dituzten bi perpaus aditzera emateko baliokidetasunaren ikurra,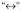, erabiltzen da, berdintasun ikurraren (=) ordez.

II.II. Disjuntzioa :

p eta q perpausen disjuntzio esaten zaio,, bi perpaus horieta- ko bat egia denean egiazkoa den perpausari. p edo q irakurtzen da.

Disjuntzioari dagokion balio taula hau da :Adibidea : "euria ari du edo eguzkia dago" perpausa egia da, baldin eta euria ari badu eta eguzkia badago, eta faltsua da, lainotuta badago edo euririk ari ez badu eta eguzkirik ez badago. Disjuntzioa, logikan, ez da baztertzailea, alegia aldi berean euria ari badu eta eguzkia badago ere perpausa egia izango da.Lege elkarkorra:Trukakortasunaren legea :Eragiketa honetatik egin daitezkeen dedukzioak:Dedukzio bat aditzera emateko, lehenengo atalean egiazkotzat hartzen diren perpausak idazten dira, alegia arrazoibidearen premisak, idazten dira, komen bidez bereizita. Ondoren Ia zeinua idazten da, eta atzetik ondorioak.Disjuntzioaren bidez arrazoibide errazak bakarrik egin daitezke :Batuketa :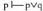Adibidez, "gaur euria ari du" perpausetik "gaur euria ari du edo eguzkia dago" ondoriozta daiteke.Disjuntziozko silogismoa :

II.IIII. Konjuntzioa :

p eta q perpausen konjuntzio esaten zaio,, adierazten da eta p eta q irakurtzen- biak, p eta q, egia direnean soilik egia den perpausari. Kasu honi dagokion balio taula hau da :Sarritan, subjektua edo predikatua komuna dutenean ez da errepikatzen konjuntzioa erredaktatzean : "etxea handia da" eta "etxea hotza da" perpausek "etxea handia eta hotza da" perpausa ematen dute.Tasunak :Lege elkarkorra :Trukakortasunaren legea :Konjuntzio eta disjuntzio legeak dira :Banaketa legeak :Adibidea : balio logiko bera dute "autoa gorria da eta bi edo lau ate ditu" eta "autoa gorria da eta lau ate ditu edo gorria da eta bi ate ditu" perpausek.

Morganen legeak :Adibidez : "ez da handia eta gorria" eta "ez da handia edo ez da gorria" bat datoz.Dedukzio legeak.Sinplifikazioa :Baldin eta "handia eta gorria" bada, "gorria da" betetzen da zehazki.Konjuntzioa :

II.IV Inplikazioa :

p perpausak q inplikatzen du,adierazten da, eta proposizio hori egia izango da baldin eta p egia denean q ere egia bada. Hau da balio taula: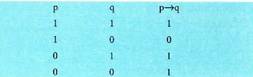Inplikazioa irakurtzeko beste modu bat ere bada : baldin eta p orduan q, edo p gertatzen bada, orduan q gertatzen da, edo p baldintza nahikoa da q-rentzat. p perpausa q gertatzeko baldintza nahikoa dela idaztekojartzen da.Tasunak: inplikazioa ez da ez elkarkorra eta ez trukakorra, baina ondoko lege hau betetzen du :Hortaz, inplikazioa ukapenaren eta disjuntzioaren bidez ere lordaiteke.Kontrajartze Legea: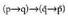"Euria egiten badu lurra bustitzen da" perpausak "lurra bustita ez badago ez du euririk egin" perpausa inplikatzen du.Esportazio Legea:"Baldin eta bero egiten badu eta eguzkia badago, orduan hondartzara noa" eta "baldin eta bero egiten badu beraz eguzkia badago hondartzara noa" perpausak elkarren baliokideak dira.Dedukzio legeak inplikazioarekin :Modu PonensAdibidea : "euria egiten badu lurra bustitzen da" eta "euria ari du" perpausetatik "lurra bustitzen da" ondorioztatzen da.Modu TollensAdibidea : "euria egiten badu lurra bustitzen da" eta "lurra ez dago bustita" perpausetatik "ez du euririk egin" ateratzen da dedukzioz.Silogismo hipotetikoa

II.V. Baliokidetasuna :

p, q perpausak emanik, baliokideak direla esaten da etaidazten dira, baldin eta aldiko balio logiko berberak hartzen badituzte, alegia biak aldi berean egia ala gezurra badira. Era berean, esaten da p egia dela baldin eta soilik baldin q egia bada, edo p q-rentzako baldintza beharrezko eta nahikoa bada. Kasu honi dagokion balio taula: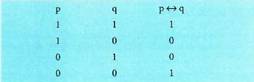Baliokidetasun legeak :Bi perpaus elkarren baliokide direla frogatzeko egia eta gezurra balioak kasu berberetan hartzen dituztela erakustea aski da. Adibidez, baliokidetasunaren azken legea frogatzeko :

II.VI. Baztertzea eta bateraezintasuna:

p eta q perpausen baztertze esaten zaio pWq adierazten da, eta p edo q baina ez biak irakurtzen ondoko balio taula duen perpausari :Bateraezintasuna : p eta q perpausak emanik, p eta q-ren bateraezintasun deitzen zaio,, p eta q biak egia ez direnean egia den perpausari. Bere balio taula hau da :

II.VII. Tautologia eta kontraesanak :

Beti egiazko balioa hartzen duten perpausek tautologia izena dute, eta beti gezurrezko balioa hartzen dutenak kontraesanak. Tautologia adierazteko T ikurra erabiltzen bada eta kontraesana adierazteko F erabiltzen bada, zera ondorioztatzen da :- Tautologiak dira :- Kontraesanak dira :Tautologien eta kontraesanen tasunak dira :

3. Predikatuen logika

Perpaus sinple batek subjektu bat eta predikatu bat ditu. Termino hauek finkoak izan daitezke, edo banakoez osaturiko multzo baten baitako edozein elementu, zehaztu gabeko elementu bat. Lehenengo kasuak konstanteak dira, eta bigarrenak aldakorrak.Adibidez "Ana bilbotarra da" perpausak subjektu finko bat du.

Aldiz, "X bilbotarra da" kasuan subjektua aldakorra da. Osagai aldakor bat gutxienez duten perpausez osaturiko adierazpenari perpaus funtzio deitzen zaio. Aldagaiaren ordez konstante bat jartzen bazaio funtzioari argumentu bat ematen zaiola esaten da. Kasu horretan, funtzioak egiazko balioa hartuko du argumentuak perpausa egia bihurtzen badu, eta balio faltsua, konstanteak balio hori ematen badio perpausari.Badira hitz batzuk, adjektibo zehaztu gabeak oro har, perpaus funtzioari egiatasuna ematen diotenak. Hitz hauei kuantifikatzaile deitzen zaie.Kuantifikatzaile unibertsala : kuantifikatzaile unibertsala egia da, funtzioak kuantifikatzaile hori definitzen den balio multzo guztirako balio duenean.adierazten da, etaguztirako irakurtzen da, x-ek aldagia adierazten du eta A aldagaiak balioak hartzen dituen multzoa da. Kuantifikatzaile unibertsala duen perpaus batek forma hau du :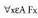A multzoko elementu guztietarako perpaus funtzioa egiaztatzen da, non F den perpaus funtzioa, eta Fx den aldagaiak x balioa duenean funtzioak hartzen duen balioa. Adibidez "zaldi guztiek dute isatsa" perpausak esan nahi du zaldien A multzoko edozein x elementuk, x-ek isatsa du F perpaus funtzioaren subjektu gisa jartzen bada, egiazko balioa ematen duela.Kuantifikatzaile existentziala egia da gutxienez A multzoko elementu batek F perpaus funtzioa betetzen duenean. Horrela idazten da:Eta irakurtzen da : "Bada A-ko x-en bat F betetzen duena", edo x-en batek F betetzen du".Adibidea : "aurten egunen batean loteria tokatuko zait" egia da, baldin eta urtean zehar egunen batean tokatzen bazait loteria. Egia da, halaber, bi egunetan tokatzen bazait loteria, edo urteko egun guztietan tokatzen bazait ere. Urteko egun bakar batean ere tokatzen ez bazait soilik izango da faltsua.Kuantifikatzaile unibertsal baten ukapenak kuantifikatzaile existentziala ematen du, eta alderantziz :Adibidez : ez bada betetzen "zaldi guztiek isatsa dute", hori gertatzeko arrazoia da "zaldiren batek ez du isatsik". Egia ez bada "egunen batean loteria tokatuko zait", horren arrazoia da "ez zait egun bakar batean ere loteria tokatuko".Perpausen logikako legeak kuantifikatzaileekin :