Matematika»Analisiak

Integral mugatua

Aurreko gaian, integrala eta barruti baten azalera edo arearen kalkulua erlazionatzen ziren. Baina, ez definizioan, ez jatorrizkoen kalkuluan, ez zen erlazio hori azaltzen. Integral mugagabea, arearen kalkuluarekin erlazionatu gabe, deribazioaren alderantzizko eragiketa bezala azaltzen zen. Integralaren eta area baten kalkuluaren arteko lotura argituko da gai honetan.Trapezio lerro-nahasiaren area kalkulatuz hasten da gaia, hau da, alde bat zuzenkia izateko ordez kurba jarrai bat duen trapezio baten area kalkulatuz. Area hori kalkulatzeko laukizuzen bitarteko hurbilketa prozedura erabiltzen da ; prozedura hori orokortzea, integral mugatuaren definiziorako baliagarri izango da. Horrela zehaztutako integrala, y = f(x) funtzio batek, x = a eta x = b abzisak eta abzisaardatzaren grafikoak mugatutako barrutiaren area orientatua da.

Definizio hau, hasiera batean integral mugagabearen definizioarekin zerikusirik ez duena, eta hura, estu lotuta daude kalkulu integralaren oinarrizko teorema deritzanari esker. Teorema honek dioenez, f(x) funtzioaren grafikoak, OX ardatzak, x = a abzisa finkoak eta beste edozein x abzisak mugatutako barrutiak ematen duen funtzioa, f(x)-en jatorrizko bat da. Teorema horretatik abiatuz Barrow-ren erregela frogatzen da. Erregela honi esker, f(x) funtzio baten jatorrizko funtzioa ezagutzen bada, y = f(x) funtzioak a eta b abzisen artean duen integral mugatuaren balioa kalkula daiteke.

Integral mugatua eta area erlazionatuta daudenez, muga kurboak dituen edozein barruti lauren area kalkulatzea, adierazpen grafikotzat barruti hori mugatzen duen lerroa duen funtzioaren jatorrizko bat bilatzean datza.Gai honen azken zatian, area eta bolumen ariketa ebatziko dira.

Geometrian edo fisikan dituen beste aplikazio batzuk, hala nola lerro baten luzeraren kalkulua, edo higikari baten desplazamendua, edo indar aldakor batek egiten duen lana, gaia ez luzatzearren, alde batera utzi dira. Integralaren aplikazio hauen adibide asko fisika liburuetan aurki daitezke.

I. Trapezio lerro-nahasi baten azalera

Izan bedi y = f(x), [a,b] tartean jarraia eta positiboa den funtzio bat. f(x) funtzioaren grafikoak, eta x = a, x = b, eta y = 0 ekuazioen zuzenak, trapezio lerro-nahasi deritzan planoko barruti itxi bat mugatzen dute.Alde bat makurra duen trapezio baten area kalkulatu nahi da.

Area hori, y = f(x) funtzioaren grafikoaren, eta a eta b balioen araberakoa izango da. f(x), a eta b balioen mende dagoen area baten balioa horrela idazten da : A(f,a,b). Area horren balioa kalkulatzeko,elkarren ondoan jarritako laukizuzenen bidez hurbilduko da barrutia.

Laukizuzen batzuk trapezioan inskribatuak egongo dira, eta besteak trapezioari zirkunskribatuak.Aurkitu nahi den A(f,a,b) area inskribaturiko laukizuzen guztien areen batura baino handiagoa izango da, eta zirkunskribaturiko laukizuzen guztien areen batura baino txikiagoa. Zenbat eta laukizuzen gehiago hartu, orduan eta txikiagoa izango da laukizuzen horien oinarria, baina orduan eta hurbilago egongo dira batura horiek A(f,a,b) baliotik.

[a,b] zuzenki baten partiketa

[a,b] zuzenki baten partiketa,zenbaki errealen azpimultzo ordenatu eta finitu bat da, non honako hau betetzen den :P partiketak, zuzenki hauek mugatzen ditu [a,b] tartean :

DIRAC-en DELTA FUNTZIOA

Integralaren definizio zehaztasuna, eta definizio hori hedatu beharra, gero eta irregularrago diren funtzioekin erabilgarria izan dadin, ez da bakarrik matematikarien kezka. Fisikariek, mundua deskribatzeko, integralak erabiltzen dituzte sarri, eta fisikarien ondorio dira integrazioaren hedatze batzuk. Mende honetan, mekanika kuantikoak, eta oinarrizko zatikien ikasketak bereziki, proposatu dituzte integrazioaren hedatze horietako batzuk. Dirac-en delta funtzioa eta bere integrala, fisikaren beharraz egindako hedatze horien erakusgarri bat besterik ez da.Mekanika kuantikoan, zatiki baten posizioa jakin nahi denean, ziurgabetasun printzipioak(x,y,z,t) uhin funtzio deritzan funtzio bat ematera behartzen du. Partikula P(x,yz) puntuan t unean aurkitzearen probabilitatearekin dago erlazionatuta uhin funtzio hori.uhin funtzioko elektroi bat aurkitzeko probabilitatea, adibidez, espazio-denbora diferentzial batean, hau da:Uhin funtzio honek probabilitateko dentsitate-funtzio baten papera betetzen du, eta aurreko adierazpeneko x, y, z eta t guztientzat integralak 1 balio behar du, horixe baita gertaera ziurraren probabilitatea ; izan ere, tokiren batean eta uneren batean egongo da elektroia.Gerta daiteke, Heisenberg-en ziurgabetasunaren printzipioa gorabehera, elektroiaren posizioari buruz dena jakitea, eta ezer ez haren lastertasunaz . Orduan, hau da galdera : zein da posizioaz dena eta mugimenduaz ezer ez dakigun elektroi horren uhin-funtzioa? Dakigun tokia ez den beste toki batean aurkitzeko probabilitatea zero da, eta dakigun tokian bertan aurkitzeko probabilitatea berriz 1. Baina orduan bere probabilitate dentsitatea, puntu batean ezik beste denetan zero balio duen funtzio bat, eta espazio osoan bere integralak bat balio duena, izan beharko luke :Funtzio horrek, mota honetakoa izan beharko luke :

Goi eta behe-baturak

Funtzio jarrai baten integral mugatuaren definizioa lortzeko, Weierstrassek emandako teorema hau erabiltzen da :"[a,b] tarte itxi batean definitutako fjarraia den edozein funtziok, tarteko punturen batean balio maximo bat eta balio minimo bat erdiesten ditu"[a,b] tartean f funtzioaren balio maximoa adierazteko M erabiltzen da, eta minimoa adierazteko m.[a,b] tarteanerakoedozein P partiketa emanik, 0 nabaria denez, f funtzioa [a,b] tarteanjarraia bada,azpitartetan ere jarraia izango da.Beraz, f funtzioak azpitarte hauetariko bakoitzean maximo bat eta minimo bat izango ditu. 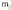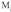Honela izendatzen dira :, f funtzioaren minimoainserted text, f funtzioaren maximoatartean.Hurrengo zenbaki errealari, P partiketara lotutako f-ren goi-batura esaten zaio, eta SM(f,P)-ren bidez izendatzen da :Edo laburtuz :Batura hau, f funtzioaren grafikoaren gainean, hau da, zirkunskribaturik, dauden laukizuzenei dagokien area da. Trapezio lerronahasiaren areari gehiegitzaz egindako hurbilketa bat da.Hurrengo zenbaki errealari berriz, P partiketara lotutako f-ren behe-batura esaten zaio, eta Sm(f,P)-ren bidez izendatzen da :Edo laburtuz :Batura hau, f funtzioaren grafikoaren azpian, hau da, inskribaturik, dauden laukizuzenei dagokien area da. Trapezio lerro-nahasiaren areari gutxiegitzaz egindako hurbilketa da.

A(f,a,b) barrutiaren area

[a,b] -ren partiketa segida bat bada,direlarik, hau betetzen dute goi eta behe-baturek :Lehenengo segida gorakorra denez, eta edozein SM-k goi-bornatua dagoenez, eta bigarren segida beherakorra denez eta Sm-k bornatua, orduan,tarte guztien luzerak zerorantz jotzen badu, beraien arteko diferentziak ere zerorantz jotzen duela egiaztatzen da ; hau da :Definizioz, bi segida hauen limite komuna, f funtzioak eta a eta b puntuak mugatutako trapezio lerro-nahasiaren area da.Zoritxarrez, tarte bateko partiketa denak ez dira beti batzuk besteen barnekoak, beraz ezin da beraien artean,

I I. Itegral mugatua

Integral mugatua, goi eta behe-baturen limite gisa.

Trapezio lerro-nahasi baten area kalkulatzeko erabili den ideia intuitiboa, orokortu egiten da ondoren [a,b] tarte batean jarraia den eta balio positiboak eta negatiboak har ditzakeen funtzioaren inte- gral mugatuaren kontzeptua definitzeko.Goi eta behe-baturak era berean definitzen dira, baina oraingohonetan ez dute orokorrean behintzat arearik adierazten ; izan ere, azpitarte batzuetan balio negatiboak ere har ditzake funtzioak.Hemen azalduko ez bada ere froga daiteke, ezen, baldin eta f, [a,b] tartean jarraia den funtzioa bat bada, [a,b]-renedozein partiketarentzat, goi-baturak eta behe-baturak balio batera hurbiltzen direla, hau betetzen dutenean :a)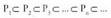b)partiketak mugatzen dituen, tarte guztien luzerek zerorantz jotzen dute n-krantz jotzen duenean.Kasu honetan, hurrengo bi limiteak existitzen dira eta berdinak dira :Limite komun honi [a,b] tartean f funtzioaren integral mugatua esaten zaio, eta horrela izendatzen da :

Azpitarte bakoitzeko bitarteko puntu bat erabiliz mugaturiko integrala, edo Riemann-en integrala.

Izan bitez f [a,b] tartean jarraia den funtzio bat, eta[a,b] tartearen partiketa bat.azpitarte bakoitzeko barnekopuntu bana hartzen bada, honako hau lortzen da :delarik.Beraz :eta hortik hau lortzen da:Horrela, partiketaren azpitarte bakoitzeko maximo eta minimoak erabili gabe, funtzio jarrai baten integral mugatua kalkulatzeko beste era bat lortzen da.

Integal baten zeinua

Funtzioak [a,b] tartean hartzen dituen balioen araberakoa da integral mugartu baten zeinua. Hiru aukera daude:

I I I. Integral mugatuaren propietateak

Ondoren, integral mugatuaren propietate garrantzitsuenak azalduko dira. Definizioaren ondoriozkoak dira. [a,b] tartean funtzioa positiboa den kasuan, interpretazio geometrikoak hobeto ulertzeko balio du.1. c, [a,b] bitarteko puntu bat bada, orduan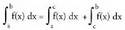f funtzioa positiboa bada [a,b] tartean, integral mugatuak barrutien areak izango dira, eta orduan, aurreko berdintza horrela adierazten da :2. a = b bada, orduan3. Integrazio mugak elkar-trukatzen baditugu, integralaren zeinua aldatu egiten da :4. Bi funtzioren baturaren edo kenduraren integralaf eta g, [a,b] tartean definitutako bi funtzio badira, orduan5. Zenbaki erreal eta funtzio baten arteko biderkaduraren integralaf, [a,b] tartean definitutako funtzio bat bada, eta k zenbaki erreal bat bada, orduan

I V. Batezbesteko balioaren teorema

Teorema honi esker, funtzioak jarraiak direnean kalkulu integralaren oinarrizko teorema froga dezakegu, eta azken honetatik abiatuz Barrow-ren erregela.tartean jarraia bada, bitarte horretako c puntu bat b existitzen da, nonden.Hurrengo irudiak teorema honen esanahi geometrikoa azaltzen digu.Izan bitez M eta m, f funtzioak [a,b] tartean hartzen dituen balio maximoa eta minimoa. Integralaren definizioa dela eta :Desberdintza hau (b - a)-z zatituz, hau lortzen da :Jarraia delako, f funtzioak m balio minimoa eta M balio maximoaren artean dauden balio guztiak hartzen ditu ; beraz, existituko da [a,b] bitarteko c puntu bat, nonhau da :Teorema honen esanahi geometrikoa hau da :abBA trapezio lerro-nahasiaren area, b - a oinarria eta f(c) alturaduen laukizuzen baten arearen berdina da, c, [a,b] bitarteko puntubat delarik.f(c) balioari funtzioaren batezbesteko altura edo batezbesteko balioa esaten zaio.• Adibideadela jakinda, kalkulatu c-ren balioa batezbestekobalioaren teorema aplikatuz.

V. Kalkulu integralaren oinarrizko teorema

a) Funtzio integrala

[a,b] tartean integragarri den f funtzio bat emanda, integral definitu hau existitzen da tarteko x guztientzat :f funtzioa eta integrazioko behe-muga finkoak badira, x integrazioko goi-mugaren arabera dagoen zenbaki erreal bat bezala har daiteke integral mugatu hau. Horrela, F funtzio bat lortzen da. F funtzio hau [a,b] tartean definitua dago, eta horrela azaltzen da :F funtzioari funtzio integral esaten zaio.* x = a bada, orduan* [a,b] tartean f(x)>0 bada, etabada, orduanF funtzio integralak, [a,b] tarteko c bakoitzarentzat, barrutiaren area ematen du.

b) Kalkulu integralaren oinarrizko teorema

Teorema honek F(x) funtzio integralarekin erlazionatzen du f(x) funtzio integrakizuna, eta funtzio integralaren deribatua, F(x), eta f(x) funtzio integrakizuna berdinak direla frogatzen du.F funtzio integrala f-ren jatorrizko bat dela frogatuko dugu :deribatuaren definizioaF-ren definizioa dela mediointegral mugatuaren batukortasuna dela mediobatezbesteko balioaren teorema dela medioeragiketak eginez

c) Barrow-ren erregela

f funtzioa [a,b] tartean jarraia bada, eta G, f-ren jatorrizko batbada, orduanHain zuzen, izan bedi-ren jatorrizko funtzio integrala.

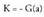Orduan, G ere f-ren jatorrizko delako(K = konstantea) (*)izango da ; izan ere, tarte bereko funtzio baten bi jatorrizkoren arteko aldea konstante bat da. K zenbakia erraz kalkula daiteke ; izan ere x = a deneanbaina F(a) = 0 denez,Balio hau (*) espresioan ordezkatuz hau lortzen da :Erlazio hau [a,b] tarteko balio guztiek betetzen dute ; x = b balioak beteko du bereziki, beraz :G(b) - G(a) diferentzia horrela izendatzen da :• Adibideak

- Ariketak

1. Kalkulatu :

VI. Barruti baten area

Hasteko, funtzio baten grafikoak eta x = a, x = b eta y = o zuzenek mugatutako barrutien areak kalkulatuko dira, elkarrengandik bereiztuko direlarik barruti osoa OX ardatzaren gainetik, barruti osoa OX ardatzaren azpitik, edo zati bat gainetik eta bestea azpitik dutenak. Ondoren, bi kurbak mugatutako barrutien area ikusiko da, eta, kasuren batean, bi kurbak eta x = a, x = b edo y = 0 zuzenak edo zuzenek mugatutako barrutiaren area.Barruti baten area kalkulatzen hasi aurretik, komenigarria da f(x) funtzioaren grafikoa irudikatzea, horrela zein kasuri dagokion jakin baitaiteke.

1. Kurba batek eta hiru zuzenek mugatutako barrutiaren area

a) [a,b] tartean funtzioa positiboa da.Izan bedi f, [a,b] tartean jarraia den funtzio bat, non tarteko edozein x-rentzat,den. x = a, x = b, y = 0 eta funtzioaren grafikoak barruti bat mugatzen dute planoan. Barruti horren area kalkulatzen saiatuko gara.Aurreko atalean ikusi dugunez, barrutiaren area trapezio lerronahasiaren area da, a eta b-ren artean definituriko integral mugatuak emana :• Adibideak 1. Bila ezazuekuazioa duen parabolak, OX ardatzak, x = 4 zuzenak eta x = 8 zuzenak mugatutako barrutiaren area.

Barrutia abAB trapezio lerro-nahasia da, non AB arkua, [4,8] tartean f(x) funtzioaren grafikoaren zatia den.2. Bila ezazufuntzioaren grafikoak, OX ardatzak eta x = 0 eta x = 1 zuzenak mugatzen duten gainazalaren area.3. Bila y = sin x funtzioak, OX ardatzak eta x = 0 etazuzenak mugatzen duten barrutiaren area.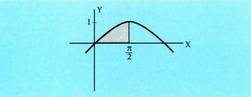b) [a,b] tartean funtzioa negatiboa da.Oraingo honetan, izan bedi f, [a,b] tartean jarraia den funtzio bat, non tarteko edozein x-rentzatden. x = a, x = b, y = 0 eta funtzioaren grafikoak abzisa-ardatzaren azpian dagoen barruti bat mugatzen dute planoan.B barruti horren area trapezio lerro-nahasiaren berdina da, baina oraingo honetan ez da horrela kalkulatzen :f(x) funtzioa negatiboa da, eta, hortaz, integral mugatua ere negatiboa da. Area berriz positiboa da beti, eta, horren ondorioz, bere balioa integralaren zeinua aldatuz ateratzen dena izango da.Balio hau, berez, integral mugatuaren balio absolutua da.• Adibideak1. Bila ezazu barrutiaren area.ekuazioa duen parabolak, OX ardatzak eta x = -2 eta x = 2 zuzenak mugatzen dutenIzan ere, barruti osoa OX ardatzaren azpian dago.2. Bila OX ardatzak,funtzioaren grafikoak eta x = 1 zuzenak mugatzen duten barrutiaren area.Barrutia OX ardatzaren azpian dago, eta kurbak ardatz hori x = 2 puntuan ebakitzen du. Hau izango da eskatutako area :c) [a,bl-ren azpitarte batzuetan funtzioa positiboa da, eta negatiboa besteetan.[a,b] integrazio-tartean f(x) funtzio jarraiaren zeinua konstantea ez denean, bere grafikoak eta OX ardatzak barruti bat baino gehiago mugatzen dute : B1, B2, B3,... hurrengo irudian azaltzen den bezalaxe :Kasu honetan B = B 1 + B2 + B3 barrutiaren area ez da a eta b-ren arteko integral mugatua. Hemen, barruti bakoitzaren area bere aldetik kalkulatu ondoren, batu egin behar dira. Irudian, dagokion integral mugatuaren zeinua jarri da barruti bakoitzean.• Adibideak :1. Bila ezazu y = cos x funtzioaren grafikoak, eta OX ardatzaktartean mugatutako area.Barrutia hiru zatitan banatu behar da ; bi positiboak diraeta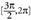eta hirugarrena negatiboa da. Beraz, hau izango da area:2. Bila ezazuekuazioa duen kurbak eta OX ardatzakmugatutako area.eginez, funtzioak OX ardatza x = 0, x = 1 eta x = -1 puntuetan ebakitzen duela ikusten da.-1 eta O-ren arteko barrutia positiboa da, eta 0 eta +1-en artekoa negatiboa, beraz :

2. Bi kurbek mugatutako barrutiaren area

Bi kurba elkarren ebakitzaileak izango dira edo ez dira izango. Ez badira, x = a eta x = b zuzenak izango dira alboko mugak, eta bide batez, integralaren mugak ere izango dira. Bi kurbak tartearen barruan elkar ebakitzen badute, hasteko, ebaki puntu horiek aurkitu behar dira ; izan ere, puntu horietan egon daitezke integralaren zeinu aldaketa posibleak.Ahal bada, barrutia irudikatu behar da, irudian ikusiko baita ebaki punturik baduen edo ebaki puntu horiek mugatzen dituzten azpitarteetan area batu edo kendu egin behar den.a) Bi funtzioak positiboak dira [a,b] tartean eta ez dute elkar ebakitzen .Kasu honetan, irudian ikusten den bezalaxe, barrutiaren area funtzioek zehazten dituzten bi trapezio lerro-nahasien arteko kenduraren berdina da.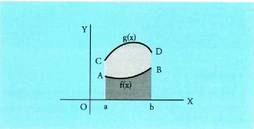b) Bi funtzioak negatiboak dira [a,b] tartean, eta ez dute elkar ebakitzenKasu honetan, aurreko formula baliagarria da ; izan ere, translazio bat eginez, aurreko kasu berean gaude.f + c eta g + c funtzioak f eta g-tik abiatuz lortzen dira hurrenez hurren, funtzio horiek u(0,c) bektore zuzentzailearen arabera OY ardatzarekiko paraleloki lekualdatuz.f + c eta g + c funtzioen grafikoek eta x = a eta x = b zuzenek mugatutako B' barrutia, B barrutiaren berdina da.c > 0 behar bezain handia hautatuz, [a,b] tartean f + c eta g + c funtzioak positiboak izatea lor dezakegu. Beraz,c) Bi funtzioek elkar ebakitzen duteFuntzioak elkar ebakitzen badute, ebaki puntuen arteko azpitarteak aztertzen dira. Beraietan, funtzioek aurreko ataletan ikusitako baldintzak betetzen dituzte.Hau izango da irudiko area:• Adibideak :1. Bilaetaeta y =parabolak mugatutako barrutiaren areaAldameneko irudian bi funtzioen grafikoek mugatzen duten barrutia irudikatu da.Ebaki puntuak: O(0,0), A(1,1)2. Bila ezazueta y = x4 kurbek mugatzen duten barrutiaren areaEbaki puntuak dira ekuazio sistema honen soluzioak :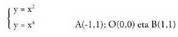Beraz :3. Bila ezazu y = xz eta y = -x + 6 kurbak eta OX ardatzak definitutako barrutiaren areaeta y = -x + 6 kurbak eta OX ardatzak definitutako barrutiaren areaHauek dira kurben arteko ebaki puntuak :Eta beste hauek dira kurba eta OX ardatzaren arteko ebaki puntuak : (0,0) eta (6,0).etabarrutien batura izango da area

- Ariketak

2.funtzioak emanik,a) Bila itzazu bi grafikoen arteko ebaki puntuak.b) Kalkula ezazu grafikoek definitzen duten barrutiaren area3.funtzioa emanda,a) Bila ezazu bere asintota, eta egin kurbaren zirriborroab) Bila ezazu f-ren grafikoak, OX ardatzak eta x = 1 zuzenak definitzen duten barrutiaren area.4.funtzioa emanda,a) Bila itzazu bere asintotak, eta egin kurbaren zirriborroab) Bila ezazu f-ren grafikoak, bere asintota horizontalak eta x = 2 zuzenak definitzen duten barrutiaren area.5.etafuntzioak emanik, bila itzazu f eta g funtzioen grafikoen arteko ebaki puntuak, eta ebaki puntu horien arteko barrutien area.6. Bila ezazuparabolak eta x + y + 1 = 0 zuzenak mugatzen duten barrutiaren area.7. Bila ezazuparabolak, x = 3 abzisa puntuan dagokion zuzen ukitzaileak eta koordenatu ardatzek mugatzen duten barrutiaren area.8. Bila ezazuhiperbolak eta x = 1 eta x = 3 abzisapuntuak lotzen dituen kordak mugatzen duten barrutiarenarea.9. Bila ezazu

VII. Biraketa - gorputz baten bolumena

Izan bedi y = f(x) funtzioa,delarik. Funtzioak, OX ardatzak eta x =a eta x = b zuzenek mugatzen duten barrutia birarazten bada OX ardatzaren inguruan, biraketa gorputz bat sortzen da.

Gorputz horren bolumena zenbatekoa den jakin nahi da.Biraketa gorputza xerraka zatitzen bada, gutxi gorabehera zilindro bat izango da xerra bakoitza. Zilindro baten bolumena oinarriaren area bider altura da ; beraz, irudian nabarmendu den xerraren bolumenaizango da, biraketa gorputzean inskribaturiko zilindro bat delaio. Beraz, biraketa gorputzaren bolumena hau izango da gutxi gorabehera :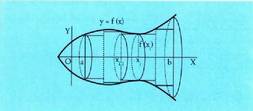Limitera pasatuz hau lortzen da :Kurba sortzailearen ekuazioa jakinda, biraketa gorputzaren bolumena ere jakin dezakegu formula honekin.x ordenatu egoki baten arabera epaien areak ezagutzen direnean, edozein gorputzera orokortu daite bolumena lortzeko adierazpen hau. Funtzioa A(x) bada, eta x aldagaia a-tik b-ra badoa, hau izango da bolumena :Formula hau Cavalieriren teoremaren beste adierazpen bat besterik ez da. Horrela zioen teorema horrek : "Gorputz geometriko bat baino gehiago oinarriarekiko paralelo diren plano batzuen bidez ebakitzen badira, eta plano horiek gorputzetan sortzen dituzten epaiak berdinak badira, orduan gorputz horiek bolumen bera dute."• Adibideak :1. Bila ezazuparabolak, x = 0-tik x = 4-rainoko tartean, OX ardatzaren inguruan biratuz, sortzen duen gorputzaren bolumena.Hau izango da sortzen duen bolumena :2. Kono zuzenaren bolumenaren formula ondorioztatu.3. Bila ezazu r erradioa duen esfera baten bolumenaren formula.Izan bediardatzaren inguruan biratuko den zirkunferentzia. Orduan,4. Bila ezazu elipse bat bere ardatz nagusiaren inguruan biratzean sortzen den elipsoidearen bolumena.Elipsearen ekuazioa :bakanduz :Beraz,

- Ariketak

10. Bila ezazu elipse bat bere bigarren ardatzaren inguruan biratzean sortzen den elipsoidearen bolumena.11. Bila ezazu x = 0 eta

Ebazpenak