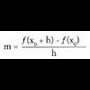Matematika»Analisiak
Funtzio baten deribatua
I. Sarrera historikoa
Newtonek eta Leibnizek zeinek bere aldetik garatu zituzten kalkulu
infinitesimalaren oinarrizko ideiak, eta ordu arte ebatzi ezin
izan ziren problemak erraz ebatzi ahal izan ziren, haiek asmatutako
metodo berriak erabiliz.Kalkulu integrala eta kalkulu diferentziala bateratzea izan zen
haien lorpenik handiena.Kalkulu diferentzialaren ideia nagusia deribatuaren kontzeptua
da. Integralaren antzera, geometria arazo batek sorrarazi zuen deribatua
: kurba baten puntu batean zuzen ukitzailea kalkulatu beharrak,
alegia.Deribatuaren kontzeptua oso berandu azaldu zen matematikaren
historian, XVII. mendean, Pierre Fermat matematikaria funtzio
batzuen maximoak eta minimoak aztertzen hasi zenean.Fermatek hau ikusi zuen : ukitzaileak puntu batean duen norabideak
adierazten du kurbak puntu horretan duen norabidea, eta kurbak
maximoa edo minimoa azaltzen duen puntuetan ukitzailea
horizontala da ; beraz, muturrak aztertzeko, ukitzaile horizontalak
aztertu behar dira.
I I. Higikari baten lastertasunaren arazoa
Demagun jaurtigai bat goraka jaurtikitzen dela 45 m/s-ko lastertasunaz. Marruskadura kontuan hartzen ez bada, grabitateak bakarrik izango du eragina. Hori dela eta, jaurtigai horren lastertasuna gero eta txikiagoa izango da, harik eta zerora iristen den arte ; orduan jaurtigai hori erortzen hasiko da ; f(t) baldin bada t segundutan hartzen duen altura,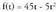 da, esperientzia fisikoen arabera.f(t) = 0 egiten da t = 0 eta t = 9 denean. Jaurtigaia 9 segundura erori da lurrera, beraz
da, esperientzia fisikoen arabera.f(t) = 0 egiten da t = 0 eta t = 9 denean. Jaurtigaia 9 segundura erori da lurrera, beraz Jaurtigaiaren lastertasuna une bakoitzean zein den jakiteko, t
unearen "unean uneko lastertasuna" definitu behar da. Lehenengo,
batez besteko lastertasuna kalkulatu behar da t-tik t + h-ra dagoen
bitartean :
Jaurtigaiaren lastertasuna une bakoitzean zein den jakiteko, t
unearen "unean uneko lastertasuna" definitu behar da. Lehenengo,
batez besteko lastertasuna kalkulatu behar da t-tik t + h-ra dagoen
bitartean : eta t finkatuz, batez besteko lastertasunarekin zer gertatzen den
ikusten da, h-ren balioak O-runtz hurbiltzen direnean.
eta t finkatuz, batez besteko lastertasunarekin zer gertatzen den
ikusten da, h-ren balioak O-runtz hurbiltzen direnean.
Kalkula dezagun unean uneko lastertasuna t=3 denean.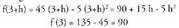 Batez besteko lastertasuna (3, 3 + h) tartean :
Batez besteko lastertasuna (3, 3 + h) tartean : .
.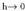 -rantz doanean, bataz besteko lastertasuna 15 m/s-ra hurbiltzen da. Balio horri aldi bateko lastertasuna deitzen zaio, t= 3 s. denean.Beraz :
-rantz doanean, bataz besteko lastertasuna 15 m/s-ra hurbiltzen da. Balio horri aldi bateko lastertasuna deitzen zaio, t= 3 s. denean.Beraz :
I I I. Kurba baten ukitzaileak puntu batean duen malda.
 Demagun y = f(x) funtzioaren kurba (2.a irudia).Har ditzagun kurba horren bi puntu,
Demagun y = f(x) funtzioaren kurba (2.a irudia).Har ditzagun kurba horren bi puntu, eta
eta ; kurbarekin ebakitzailea den
; kurbarekin ebakitzailea den zuzenaren hau da malda :
zuzenaren hau da malda : .
. -ri h deitzen badiogu ;
-ri h deitzen badiogu ; Beraz,
Beraz, ebakitzailearen malda honela idatz daiteke :
ebakitzailearen malda honela idatz daiteke :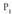 puntua
puntua -rantz hurbiltzen den neurrian,
-rantz hurbiltzen den neurrian,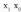 -rantz hurbiltzen da eta
-rantz hurbiltzen da eta -rantz jotzen du.2b irudian ikusten den bezala,
-rantz jotzen du.2b irudian ikusten den bezala, zuzen ebakitzaileak t zuzenera hurbiltzen dira, hots,
zuzen ebakitzaileak t zuzenera hurbiltzen dira, hots,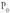 puntuan haren ukitzailea den zuzenera.Beraz, ebakitzaileen maldek ukitzailearen maldaruntz jotzen dute
puntuan haren ukitzailea den zuzenera.Beraz, ebakitzaileen maldek ukitzailearen maldaruntz jotzen dute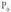 puntuan.
puntuan.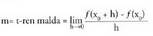 Kurbaren malda
Kurbaren malda puntuan, puntu horretan kurbak duen ukitzailearen malda da.Hemen azaltzen den formula unean uneko lastertasuna kalkulatzeko lortu denaren antzekoa da. Horrela f(x) funtzioaren deribatuaren definiziora garamatza
puntuan, puntu horretan kurbak duen ukitzailearen malda da.Hemen azaltzen den formula unean uneko lastertasuna kalkulatzeko lortu denaren antzekoa da. Horrela f(x) funtzioaren deribatuaren definiziora garamatza
IV. Deribatuaren definizioa funtzio baten puntu batean.
Demagun y= f(x) funtzioa eta x ardatzaren puntu bat.
x ardatzaren puntu bat. puntua hartzen badugu,
puntua hartzen badugu, -tik oso gertu dagoena (h zenbakia infinitoki txikia da),
-tik oso gertu dagoena (h zenbakia infinitoki txikia da), -runtz doan neurrian,
-runtz doan neurrian,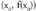 eta
eta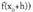 lotzen dituen zuzen ebakitzaileak, kurbak
lotzen dituen zuzen ebakitzaileak, kurbak puntuan duen ukitzailearekin bat egiteko joera du.
puntuan duen ukitzailearekin bat egiteko joera du. ebakitzaileak
ebakitzaileak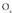 ardatzarekin eratzen duen angelua baldin bada, eta
ardatzarekin eratzen duen angelua baldin bada, eta ukitzaileak
ukitzaileak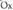 ardatzarekin eratzen duen angelua baldin bada,
ardatzarekin eratzen duen angelua baldin bada,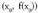 eta
eta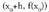 eta
eta erpinak dituen hiruki zuzenean hau egiaztatzen da :
erpinak dituen hiruki zuzenean hau egiaztatzen da : -rantz doanean eta ebakitzailea ukitzailearen zuzenki batekin bat egiten duela kontuan hartuz,
-rantz doanean eta ebakitzailea ukitzailearen zuzenki batekin bat egiten duela kontuan hartuz, -rantz jotzen du, hau da,
-rantz jotzen du, hau da, puntuan kurbak duen ukitzailearenmaldarantz.Matematikoki honela adierazten da :
puntuan kurbak duen ukitzailearenmaldarantz.Matematikoki honela adierazten da :
Funtzio baten deribatua puntu batean
y= f (x) funtzioa emanik, f-ren deribatua puntuan ondoren definitzen den limiteari deitzen zaio, limite hori existitzen bada eta finitoa (zenbaki bat) bada :
puntuan ondoren definitzen den limiteari deitzen zaio, limite hori existitzen bada eta finitoa (zenbaki bat) bada :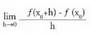 eta
eta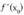 edo
edo adierazten da.
adierazten da. Limite hau existitzen denean (eta finitoa denean), f(x) funtzioa
Limite hau existitzen denean (eta finitoa denean), f(x) funtzioa
Deribatuaren esanahia :
 denez gero, funtzio baten deribatua
denez gero, funtzio baten deribatua puntuan, kurbak
puntuan, kurbak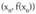 puntuan duen ukitzailearen malda da.• Adibideak1) Kalkula ezazu f(x) = 5x-2 funtzioaren deribatua x=1 abzisa
duen puntuan.Emaitza :
puntuan duen ukitzailearen malda da.• Adibideak1) Kalkula ezazu f(x) = 5x-2 funtzioaren deribatua x=1 abzisa
duen puntuan.Emaitza : -en balioa da eskatzen dena.
-en balioa da eskatzen dena.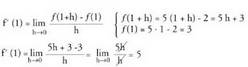 Beraz,
Beraz,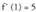 da.2) Kalkula ezazu
da.2) Kalkula ezazu funtzioaren deribatua x=2 denean.Emaitza :
funtzioaren deribatua x=2 denean.Emaitza :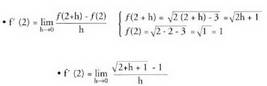 (zenbakitzailea eta izendatzailea zenbakitzailearen konjokatuaz biderkatuz :
(zenbakitzailea eta izendatzailea zenbakitzailearen konjokatuaz biderkatuz :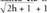 )
) Beraz,
Beraz, 3) Kalkula ezazu
3) Kalkula ezazu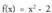 funtzioaren zuzen ukitzailearen ekuazioa abzisa 3 den puntuan.Emaitzax=3 bada ;
funtzioaren zuzen ukitzailearen ekuazioa abzisa 3 den puntuan.Emaitzax=3 bada ; Ukitzailea P (3,7) puntuan bilatu behar da. Zuzen ukitzailearen malda
Ukitzailea P (3,7) puntuan bilatu behar da. Zuzen ukitzailearen malda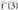 da, beraz, zuzenaren ekuazioa :
da, beraz, zuzenaren ekuazioa :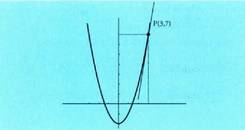 Beraz,
Beraz,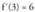 da.Beraz, f'(3) = 6 da.
da.Beraz, f'(3) = 6 da.
Ukitzailearen ekuazioa : y-7 = 6(x-3) da.. -7 = 6x-18
6x-y-11 = 0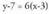 da.
da.
V. Funtzio baten deribagarritasuna puntu batean.
f(x) funtzioa "a" puntuan deribagarria izan dadin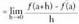 existitu behar du, eta horretarako
existitu behar du, eta horretarako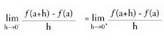 • AdibideaAzter ezazu
• AdibideaAzter ezazu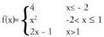 funtzioaren deribagarritasuna
funtzioaren deribagarritasuna eta
eta puntuetan.Emaitza :a)
puntuetan.Emaitza :a) -n deribagarritasuna• h < 0 denean f (-2 + h) = 4, -2 + h < 2 delako
-n deribagarritasuna• h < 0 denean f (-2 + h) = 4, -2 + h < 2 delako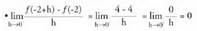 • h > 0 denean
• h > 0 denean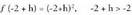 delako
delako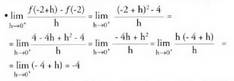 Beraz, eskuin limitea -4 da eta ukitzailearen malda eskubitik -4
da.Aldeetako limiteak desberdinak direnez, ez da existitzen
Beraz, eskuin limitea -4 da eta ukitzailearen malda eskubitik -4
da.Aldeetako limiteak desberdinak direnez, ez da existitzen eta f(x) ez da deribagarria
eta f(x) ez da deribagarria abzisa duen puntuan.b)
abzisa duen puntuan.b) -n deribagarritasuna.• h < 0 denean
-n deribagarritasuna.• h < 0 denean delako
delako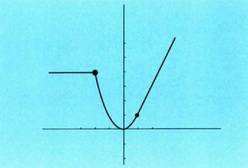 Beraz, ezker limitea x= 1 abzisa duen puntuan 2 da.• h > 0 denean f (1 +h) = 2(1+h) - 1 = 2h + 1, 1 + h > 1 delako
Beraz, ezker limitea x= 1 abzisa duen puntuan 2 da.• h > 0 denean f (1 +h) = 2(1+h) - 1 = 2h + 1, 1 + h > 1 delako Beraz, eskuin limitea x=1 abzisa duen puntuan 2 da.Aldeetako limiteak berdinak direnez, funtzioa deribagarria da x=1 denean eta
Beraz, eskuin limitea x=1 abzisa duen puntuan 2 da.Aldeetako limiteak berdinak direnez, funtzioa deribagarria da x=1 denean eta
VI. Funtzio deribatua.
f (x) funtzioa, (a,b) tarte irekian definitua, deribagarria bada tarte horretarako puntu guztietan, hau da, -rentzat
-rentzat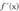 existitzen bada, funtzio berri bat defini daiteke, "funtzio deribatua" deitua.
existitzen bada, funtzio berri bat defini daiteke, "funtzio deribatua" deitua. • Adibidea
• Adibidea Beraz,
Beraz,
VII. Jarraitasunaren eta deribagarritasunaren h arteko erlazioa.
Funtzio bat deribagarria bada puntu batean, puntu horretan
jarraia da derrigor.(Alderantziz ez da beti betetzen).Frogapena :Demagun y=f(x) funtzioa deribagarria dela , puntuan. Funtzioa jarraia dela ikusteko
, puntuan. Funtzioa jarraia dela ikusteko dela frogatu behar da, edo horren baliokidea dena:
dela frogatu behar da, edo horren baliokidea dena: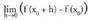 Baina :
Baina : Limiteak hartuz
Limiteak hartuz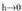 -rantz hurbiltzen denean :
-rantz hurbiltzen denean :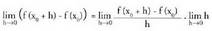 f(x) deribagarria denez :
f(x) deribagarria denez :
VIII. Deribatuak kalkulatzeko arauak.
Funtzio polinomiko baten deribatua kalkulatu nahi dugu, hasteko.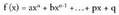 Horretarako, hau ikasi behar da lehenengo :1) f (x) = k ; funtzio konstantearen deribatua.2)
Horretarako, hau ikasi behar da lehenengo :1) f (x) = k ; funtzio konstantearen deribatua.2)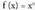 ,
, funtzioaren deribatua.3)
funtzioaren deribatua.3)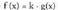 (k konstante) funtzioaren deribatua.4) Bi funtzioen baturaren deribatua.
(k konstante) funtzioaren deribatua.4) Bi funtzioen baturaren deribatua.
1) Funtzio konstantearen deribatua: f(x) = k
f(x) = k bada, f(x+h) = k izango da baita ere.Beraz,
2) f (x) = x´´ funtzioaren deribatua (fn -rentzat)
Lehenengo, f(x+h) kalkulatuko dugu :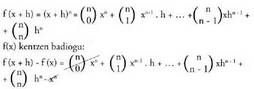 Beraz,
Beraz, (beste batugai guztiak 0 egiten baitira limitea kalkulatzerakoan).
(beste batugai guztiak 0 egiten baitira limitea kalkulatzerakoan). Arau hau n zenbaki arrunta denean bakarrik frogatu da, baina edozein berreketa funtziorentzat ere balio du arau horrek,
Arau hau n zenbaki arrunta denean bakarrik frogatu da, baina edozein berreketa funtziorentzat ere balio du arau horrek,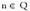 izanik.• Adibideak
izanik.• Adibideak
3) Konstante baten eta funtzio baten biderkaduraren deribatua.
4) Bi funtzioen baturaren deribatua.
 Lau arau horiek ikasi eta gero, edozein funtzio polinomikoren
deribatua kalkula daiteke.
Lau arau horiek ikasi eta gero, edozein funtzio polinomikoren
deribatua kalkula daiteke.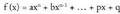 funtzioaren deribatua hau da :
funtzioaren deribatua hau da :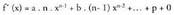 • Adibidea:Demagun:
• Adibidea:Demagun: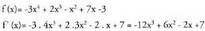 Era berean
Era berean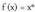 ,
,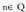 funtzioaren deribatuaren ondorioak aplikatuz, funtzio hauen deribatuak kalkula daitezke.
funtzioaren deribatuaren ondorioak aplikatuz, funtzio hauen deribatuak kalkula daitezke.
• Adibidea:
5) Funtzioen biderkaduraren deribatua
 Frogapena :
Frogapena :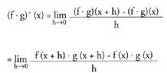 (Zenbakitzailean batzen eta kentzen badugu
(Zenbakitzailean batzen eta kentzen badugu , emaitza hau lortuko da)
, emaitza hau lortuko da)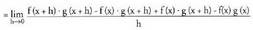 (Lehenengo bi batugaietan g (x+h) biderkagai komuna atereaz,
eta f(x) atereaz azkeneko bietan) :
(Lehenengo bi batugaietan g (x+h) biderkagai komuna atereaz,
eta f(x) atereaz azkeneko bietan) :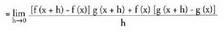 (funtzioen baturaren eta biderkaduraren limiteen ezaugarriak
erabiliz)
(funtzioen baturaren eta biderkaduraren limiteen ezaugarriak
erabiliz) (Horixe nahi baitzen frogatu).• Adibidea :
Kalkula ezazu
(Horixe nahi baitzen frogatu).• Adibidea :
Kalkula ezazu funtzioaren deribatua.
funtzioaren deribatua.
- Ariketak
1. Kalkula itzazu funtzio hauen deribatuak
IX. Alderantzizko funtzioaren deribatua
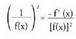 Frogapena:
Frogapena: • Adibidea Deriba ezazu
• Adibidea Deriba ezazu
X. Bi funtzioen zatiduraren deribatua
 Frogapena :
Frogapena :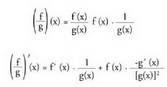 (izendatzaile komunera bihurtuz).
(izendatzaile komunera bihurtuz). (hain zuzen ere frogatu nahi zena).• Adibidea
Deriba ezazu
(hain zuzen ere frogatu nahi zena).• Adibidea
Deriba ezazu
- Ariketak
2. Deriba itzazu :
XI. Funtzio konposatuaren deribatua.
Katearen araua.
Normalean erabiltzen diren funtzioak, funtzio konposatutzat har daitezke. Esate baterako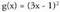 funtzioa beste bi funtzioen konposaketa da :
funtzioa beste bi funtzioen konposaketa da :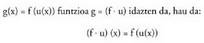 Funtzio honen deribatua kalkulatuko dugu.
Funtzio honen deribatua kalkulatuko dugu. (biderkaduraren limitea limiteen biderkadura denez, eta n(x) jarraia denez
(biderkaduraren limitea limiteen biderkadura denez, eta n(x) jarraia denez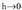 -rantz doanean
-rantz doanean Hori da katearen arau izenez ezagutzen dena ; arau hori hiru funtzioz
edo gehiagoz osaturiko funtzio konposatuetara heda daiteke.
Hori da katearen arau izenez ezagutzen dena ; arau hori hiru funtzioz
edo gehiagoz osaturiko funtzio konposatuetara heda daiteke. • Adibidea
• Adibidea
XII. Funtzio trigonometrikoen deribatua
Arau hauek frogatuko ditugu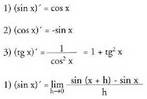 (Sinuen kendura biderkadura bihurtzeko formula trigonometrikoa
erabiliz).
(Sinuen kendura biderkadura bihurtzeko formula trigonometrikoa
erabiliz). Irudian ikus daiteke
Irudian ikus daiteke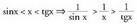 Sin x-ez biderkatuz
Sin x-ez biderkatuz .
. -rantz jotzen duenean :
-rantz jotzen duenean :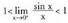 Beraz,
Beraz, 2)
2) kalkulatzeko,
kalkulatzeko, dela kontuan hartu behar da, eta katearen araua aplikatu behar da funtzio konposatuetan.
dela kontuan hartu behar da, eta katearen araua aplikatu behar da funtzio konposatuetan. (hain zuzen ere frogatu nahi zena)3)
(hain zuzen ere frogatu nahi zena)3) denez, zatidura baten deribatua kalkulatzeko formula
denez, zatidura baten deribatua kalkulatzeko formula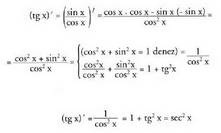 • Adibideak :
Deriba itzazu :
• Adibideak :
Deriba itzazu : Emaitza:
Emaitza:
XIII. Funtzio logaritmikoen deribatuak
a) Logaritmo nepertarraren funtzioaren deribatua. Frogapena :
Frogapena : (h nahikoa txikia izanik x+h>0 izan dadin)
(h nahikoa txikia izanik x+h>0 izan dadin) (logaritmoen ezaugarriak erabiliz)
(logaritmoen ezaugarriak erabiliz)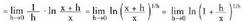 (logaritmo baten limitea, limitearen logaritmoa denez).
(logaritmo baten limitea, limitearen logaritmoa denez).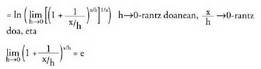 Beraz,
Beraz,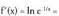 (hain zuzen ere frogatu nahi zena).b) Funtzio logaritmikoaren deribatua oinarria "a" izanik.
(hain zuzen ere frogatu nahi zena).b) Funtzio logaritmikoaren deribatua oinarria "a" izanik.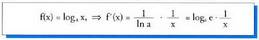 Frogapena :Logaritmoaren oinarri aldaketaren formula aplikatuz
Frogapena :Logaritmoaren oinarri aldaketaren formula aplikatuz • Adibideak:Deriba itzazu :
• Adibideak:Deriba itzazu :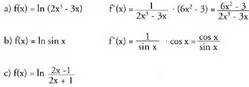 Deribatu baino lehen, logaritmoen ezaugarri hau aplikatzea
komeni da :
Deribatu baino lehen, logaritmoen ezaugarri hau aplikatzea
komeni da : Deribatuz :
Deribatuz : Deribatuz :
Deribatuz :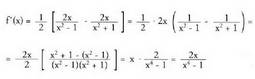 Oharra : Hemen katearen araua erabili dugu, y =1n u (x) funtzioari
aplikatua :
Oharra : Hemen katearen araua erabili dugu, y =1n u (x) funtzioari
aplikatua :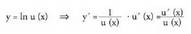 Laburtuz :
Laburtuz :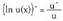
X I V. Funtzio exponentzialen deribatua
a) funtzioaren deribatua
funtzioaren deribatua da.Frogapena :
da.Frogapena : (baldintzaren bi ataletan logaritmo nepertarrak hartuz).
(baldintzaren bi ataletan logaritmo nepertarrak hartuz). (Berdintzaren bi ataletan x-ekiko deribatzen bada).
(Berdintzaren bi ataletan x-ekiko deribatzen bada).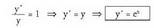 (hain zuzen ere frogatu nahi zena).. )
(hain zuzen ere frogatu nahi zena).. )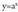 funtzioaren deribatua
funtzioaren deribatua da.Frogapena :
da.Frogapena :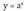 (aurreko kasuan bezala, logaritmo nepertarrak hartuz berdintzaren bi ataletan).
(aurreko kasuan bezala, logaritmo nepertarrak hartuz berdintzaren bi ataletan).
XV Deribazio inplizitoa
Demagun konika baten ekuazioa hau dela :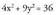 x-ekiko deribatuz :
x-ekiko deribatuz :
XVI. Funtzio trigonometrikoen funtzio alderantzizkoen deribatuak.
a) y = arc sin x funtzioaren deribatua da. Funtzio horiek ikasterakoan ikusi zen bezala, y = sin x funtzioak alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala funtzioa injektiboa izan dadin :
da. Funtzio horiek ikasterakoan ikusi zen bezala, y = sin x funtzioak alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala funtzioa injektiboa izan dadin : Deribazio inplizitoa erabiliz :
Deribazio inplizitoa erabiliz :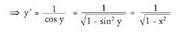 Beraz,
Beraz, b) y = arc cos x funtzioaren deribatua
b) y = arc cos x funtzioaren deribatua da.Kosinu funtzioak alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala injektiboa izan dadin :
da.Kosinu funtzioak alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala injektiboa izan dadin : -ra hain zuzen ere.
-ra hain zuzen ere.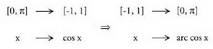 y = arc cos x baldin bada
y = arc cos x baldin bada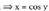 Deribazio inplizitoa erabiliz :
Deribazio inplizitoa erabiliz :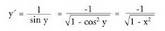 Beraz,
Beraz, c) y = arc tg x funtzioaren deribatua
c) y = arc tg x funtzioaren deribatua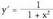 da. Tangentefuntzio horrek alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala funtzioa injektiboa izan dadin. Hori gertatzen da
da. Tangentefuntzio horrek alderantzizko funtzioa izan dezan, haren izate eremua mugatu behar da, hala funtzioa injektiboa izan dadin. Hori gertatzen da funtzioan.Beraz,
funtzioan.Beraz,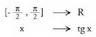 funtzioan, hau definitzen da :
funtzioan, hau definitzen da : Horren deribatua kalkua dezagun.y = arc tgx x= tg yDeribazio inplizitoa erabiliz :
Horren deribatua kalkua dezagun.y = arc tgx x= tg yDeribazio inplizitoa erabiliz : • Adibideak :a) y = arc sin 2x
• Adibideak :a) y = arc sin 2x D)
D)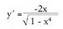 c)
c)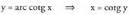 .
.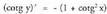 beraz, x= cotg y deribatzerakoan, inplizitoki :
beraz, x= cotg y deribatzerakoan, inplizitoki : d) y = arc sec x x =sec y.Badakigu
d) y = arc sec x x =sec y.Badakigu Beraz, x = sec y inplizitoki deribatzerakoan :
Beraz, x = sec y inplizitoki deribatzerakoan :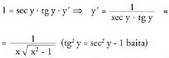 Beraz,
Beraz,
Deribatu taula
- Ariketak
4. Logaritmoen ezaugarriez baliatuz, kalkula itzazu funtzio
hauen deribatuak. 5. y = arc sec x funtzioaren deribatua kalkulatzeko erabili
dugun metodoaz, kalkula ezazu y = arc cosc x funtzioaren
deribatua6. Deriba itzazu :
5. y = arc sec x funtzioaren deribatua kalkulatzeko erabili
dugun metodoaz, kalkula ezazu y = arc cosc x funtzioaren
deribatua6. Deriba itzazu :
XVII. Ondoz ondoko deribatuak.
Ordena goreneko deribatuak
Funtzio bat emanda, f(x), eta funtzio hori (a, b) tartean definituz
gero.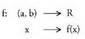 f deribagarria baldin bada,
f deribagarria baldin bada, -rentzat funtzio berri bat defini daitekeela ikusi dugu.
-rentzat funtzio berri bat defini daitekeela ikusi dugu. funtzio deribatua izenekoa.Demagun
funtzio deribatua izenekoa.Demagun deribagarria dela
deribagarria dela , hau da,
, hau da,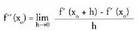 existitzen da.Deribatu horri f-ren bigarren deribatua
existitzen da.Deribatu horri f-ren bigarren deribatua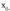 -n esaten zaio, eta
-n esaten zaio, eta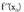 adierazten da.Baina
adierazten da.Baina deribagarria baldin bada
deribagarria baldin bada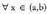 -rentzat,
-rentzat, defini daiteke, eta bigarren funtzio deribatua deitzen da :
defini daiteke, eta bigarren funtzio deribatua deitzen da : Era horretara ondoz-ondoko deribatuak defini daitezke :
Era horretara ondoz-ondoko deribatuak defini daitezke :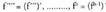 .
. funtzio horiei, n > 2 delarik, existitzen badira, ordena goreneko deribatuak deitzen zaie.1. adibidea
funtzio horiei, n > 2 delarik, existitzen badira, ordena goreneko deribatuak deitzen zaie.1. adibidea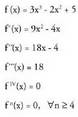 2. adibidea
2. adibidea Idatz genezake :
Idatz genezake :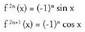 3. adibidea
3. adibidea
- Ariketa
7. Bila itzazu funtzio hauen ondoz ondoko deribatuak.
XVIII. Funtzio baten diferentziala
Demagun y = f(x) funtzioa. Abzisatzat x duen puntu bat hartuz
gero, gehikuntza txiki bat egiten zaio x+h abzisa duen puntua lortzeko
.Abzisatzat x duen puntutik kurbaren ukitzailea marrazten da, eta x + h-tik ordenatu, ardatzarekiko paraleloa den zuzen bat marrazten da, kurba eta ukitzailea ebaki arte. baldin bada ukitzaileak OX ardatzarekin eratzen duen arngelua :
baldin bada ukitzaileak OX ardatzarekin eratzen duen arngelua :
Funtzio baten diferentziala puntu batean.
y=f(x) funtzioaren diferentziala x puntuan, dy edo df(x) adierazten da, eta honela definitzen da :
Definizio horren ondorioak.
• Funtzio baten diferentziala puntu batean bi aldagaien mende
dago : x puntuaren eta hartu den h gehikuntzaren mende.•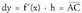 denez, funtzio baten diferentziala puntu batean, abzisatzat x duen puntua h-z gehitzerakoan ukitzailearen ordenatuak duen gehikuntza da.y = f(x) = x funtzioa hartzen badugu,
denez, funtzio baten diferentziala puntu batean, abzisatzat x duen puntua h-z gehitzerakoan ukitzailearen ordenatuak duen gehikuntza da.y = f(x) = x funtzioa hartzen badugu, Horrela, dx = h da, eta
Horrela, dx = h da, eta idatz daiteke.Beraz :
idatz daiteke.Beraz :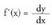 .
. denez, limitearen ideiatik,h infinitoki txikia denean
denez, limitearen ideiatik,h infinitoki txikia denean ondorioztatzenda, eta h=dx denez,
ondorioztatzenda, eta h=dx denez,
Ariketen ebazpenak