Matematika»Analisiak

Limiteak eta funtzioen jarraitasuna

I. Funtzio baten limitea puntu batean

Puntu bateko funtzio baten limiteari buruzko ideia intuitiboa

inserted textpuntuan,-tik oso hurbil dauden puntuentzat, f(x) funtzioak hartzen duen L balioa da;adieratzen da.Limitea hartzerakoan-rantz doanean,-n definituta ez egoteak ez du garrantzirik, ezta difinituta baldin badago-n zein balio hartzen duen jakiteak ere. Garrantzia duen gauza bakarra-ren inguruan nola definituta dagoen jakitea da. Adibidez, irudian f funtzioak nahiz eta-n beste balio bat hartzen duen, kurbatik kanpo,egiaztatzen da, izan ere,-rantz hurbiltzen denean, f(x) l-rantz hurbiltzen baita.

Aldeetako limiteak

• y=f(x) funtzio baten ezker limiteapuntuan, funtzioak-tik ezkerretara oso gertu dauden puntuentzat hartzen duen balioa da. Honela adierazten da:y= f(x) funtzio baten eskuin limiteapuntuan, funtzioak-tik gertu dauden puntuentzat hartzen duen balioa da.Honela idazten da :

Funtzio baten limitearen eta aldeetako limiteen arteko erlazioa

y=f(x) funtzioaren limiteapuntuan existitzen da, baldin eta soilik baldin aldeetako limiteak existitzen badira eta berdinak badira.

- Limiteen hurbilketazko kalkulua.

f(x) funtzioa L-rantz hurbiltzen bada-rantz hubiltzen denean,zenbakien segida bat hartzen bada-rantz jotzen duena,balioak ere L-rantz egingo du.Horretan oinarrituz limitearen balioa hurbilketa bidez kalkula daiteke,-rantz jotzen duen, segida baten funtzioaren balioak kalkulatuz.• Adibidea: Bide f(x) funtzioa era honetan definituta :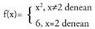Zein da f(x)-en limitea x-ek 2-rantz jotzen duenean.

Ebazpena:kalkulatzeko, 2-tik gertu dauden puntuentzat balio taula bat egin daiteke.-rantz doanean bai eskuinetik bai ezkerretik funtzioak 4-rantz jotzen du. Beraz :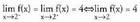

Puntu bateko funtzio baten limitearen definizioa f(x) funtzioak L-rantz konbergitzen du

puntuan, edo f(x)-en limiteapuntuan L da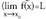idazten da)-tik oso gertudauden balioei funtzioaren bidez L-tik oso gertu dauden balioak egokitzen zaizkienean.Aurreko definizioa gehiago zehatz daiteke :Funtzio batek f(x) L-rantz konbergitzen du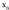puntuan, edo limitetzat L dupuntuan, baldin eta e erradioa duen L-ren inguruneororentzat, E(L,e) = (L-e, L+e), d erradioa duen-ren ingurune bat lim existitzen bada,, halakoa non Einguruneko edozein x-e irudia f(x), E(L, e) ingurunean baitago.Edo bestela :Funtzio batek f(x) L-rantz konbergitzen dupuntuan edo limitetzat L duen, puntuan, baldin eta edozein e-rentat, e > 0 izanik, d > 0 existitzen bada, nonbaita.

- Ariketak

1. Kalkula ezazu2. Kalkula ezazu kalkulagailuarekin

I I. Limite infinituak. Norabide asintotikoak

Funtzio batek +o-rantz dibergitzen duela esaten da, x x ~rantz doanean, baldin eta f(x)-en balioak arbitrarioki handitzen badira 0 x x o -rantz hurbiltzen denean.-rantz dibergitzen duela esaten da,-rantz doanean, baldin eta f(x)-en balioak arbitrarioki handitzen badira-rantz hurbiltzen denean.Era berean, funtzio batek-rantz dibergitzen duela esaten da,-rantz doanean, baldin eta f(x)-en balioak oso txikiak egiten badira-ra hurbiltzen denean.Honela idazten da :Kasu honetan,zuzena funtzioaren asintota bat dela esaten da.• Adibidea:Bedifuntzioa.

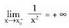Funtzio horren limiteapuntuan aztertzeko, 0-tik oso hurbil dauden puntuen irudien balioak aztertu behar dira. Grafikoa aztertuz ondorio hauek atera daitezke :• 0-tik oso gertu dauden puntuetan 0 baino txikiagoak izanik, funtzioak gero eta balio handiagoak hartzen ditu. Honek zera esan nahi du :0-tik oso gertu dauden puntuetan 0 baino handiagoak izanik, funtzioak geroz eta balio handiagoak hartzen ditu.Horrek, zera esan nahi du :

Funtzio baten limitea x-+oo-rantz edo x-->-oo-rantz doanean

x arbitrarioki handia edo txikia egiten denean, f(x) konbergentea ala dibergentea izan daiteke. Konbergentea baldin bada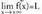; kasu honetan y=L zuzena kurbaren asintota bat da. Dibergentea baldin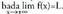• Adibideak: 1. Bedifuntzioa.Funtzioaren grafikoa begiratuz, x-ek zenbat eta balio handiagoak hartu, f(x)1-rantz gehiago hurbiltzen dela ikusten da. Beraz :Era berean, x-ek zenbat eta balio txikiagoak hartu funtzioa 1- rantz gehiago hurbiltzen da. Beraz :Adibide horretan beraz,funtzioa konbergentea da,-rantz doanean edota-rantz doanean.

2. Bedi f(x) = x+7 funtzioa.Grafikoan garbi ikusten da-rantz doanean f(x)-ek ere-rantz egiten duela. Hau da, x-ek zenbat eta balio handiagoa hartu funtzioari dagokion balioa ere handiagoa dela. Beraz :g(x) = -(x+7) funtzioaren limiteak infinituan aztertzen badira :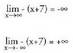Hau da, x-en balioak handitzen direnean,funtzioaren balioak txikiagotuz doaz,. Eta x-en balioak txikitzen direnean,funtzioaren balioak handiagotuz doaz,. Bi adibide horietan, f(x) eta g(x) funtzioak dibergenteak dira,eta

I I I. Funtzioen limiteen kalkulua

Bitez f eta g funtzioak,eta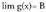dituztenak.- Funtzioen baturaren limiteaBi funtzio konbergenteen baturaren limitea limiteen batura da.- Funtzioen kenduren limiteaBi funtzio konbergenteren kenduraren limitea, limiteen kendura da.- Funtzioen biderkaduraren limiteaBi funtzio konbergenteren biderkaduraren limitea, limiteen biderkadura da.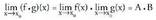- Funtzioen zatiduraren limiteaBi funtzio konbergenteren zatiduraren limitea limiteen zatidura da, baldin eta izendatzailea nulua ez bada.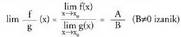• Adibidea :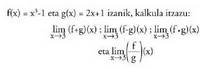Ebazpena :Limiteen eta eragiketen artean dagoen erlazio hori baliagarria da-rantz edota-rantz doan limiteetan ere.• Adibidea :Ebazpena:

Funtzio polinomikoen limiteen kalkulua :

Funtzio polinomiko bat,adierazten den funtzioa da. Honelako funtzioen limitearen kalkulua azter tzeko bi kasu bereizi behar dira :A. Funtzio polinomiko baten limitea, puntu finituan. Funtzio polinomiko baten limiteapuntuan funtzioakhartzen duen balioa da.B. Funtzio polinomiko baten limitea infinituan. Funtzio polinomiko baten limitea infinituan,alada, polinomioaren maila handiena duen gaiaren koefizientearen ikurraren arabera. Koefizientea positiboa bada limiteaizango da ; koefizientea negatiboa bada limiteaizango da., apositiboa bada.negatiboa bada.• Adibideak:1)2), maila handiena duen gaiaren koefizientea x negatiboa delako (-4)3)

Funtzio arrazionalen limiteen kalkulua

Funtzio arrazional bat

A. Funtzio arrazional baten limitea Xo puntu finituan

Funtzio arrazional bat bi polinomioen zatidura denez, bere limitea kalkulatzeko bi funtzioen zatiduraren limitea kalkulatzeko erregela berbera aplika daiteke.

A. 1. Izendatzailearen limitea O-ren desberdina izatea.

A.2. Izendatzailearen limitea 0 izatea.

Izendatzailea-n anulatzen bada gerta daiteke zenbakitzailea anulatzea edo ez anulatzea

A.2.1 Zenbakitzailearen limitea ere 0 da izatea.

Kasu horretanindeterminazioa lortzen da. Indeterminazio hori ekiditeko nahikoa dadiren ikustea. Hala bada,P(x) eta Q(x) polinomioen erro bat da, etazatidura sinplifika daiteke.Behin sinplifikatu denean, P(x) eta Q(x)

A.2.2. Zenbakitzailearen limitea zero ez izatea.

Zatiduraren limitea kalkulatzerakoan,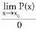indeterminazioa ateratzen da.

Indeterminazio hori ekiditeko,funtzioaren aldeetako limiteak kalkulatu behar dirapuntuan. Eskuineko limitea eta ezkerreko limitea berdinak badira, funtzioaren limiteaalaizango da. Aldeetako limiteak desberdinak badira, funtzioak ez du limiterik.• Adibideak:1. Kalkula ezazufuntzioaren limitea-rantz doanean.2. Kalkula ezazu-rantz doaneanfuntzioaren limitea.indeterminazioa.3. Kalkula ezazufuntzioaren limitea-rantz doanean.indeterminazioa.• Zenbakitzailea eta izendatzailea sinplifikatzen dira :4. 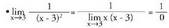Kalkula ezazu :.indeterminazioa.• Indeterminazioa kentzeko alboko limiteak aztertzen dirapuntuan.• Aldeetako limiteak berdinak direnez gero,(1. irudia)5. Kalkula ezazufuntzioaren limitea,-rantz doanean.Aldeetako limiteak desberdinak direnez gerofuntzioakez du limiterik-rantz doanean.

B. Funtzio arrazional baten limitea infinituan

doanean, funtzioen limiteen kalkulurako erregelak eta segiden limiteak kalkulatzeko erregela berdinak dira. Funtzio arrazional baten limitea-rantz doanean, zenbakitzailearen eta izendatzailearen maila hadiena duten gaien koefizienteen arteko zatidura da.Limite horren balioa n eta m balioen araberakoa da : • Zenbakitzailearen maila izendatzailearen maila baino handiagoa bada (n>m), limiteaizango da,etakoefizienteen ikurren arabera. 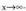Biak berdinak badira limiteaizango da, eta desberdinak badiraizango da limitea.• Zenbakitzailearen eta izendatzailearen mailak berdinak badira (n=m), limiteazatidura izango da.• Zenbakitzailearen maila izendatzailearen maila baino txikiagoa bada (nfuntzioaren limitea-rantz doanean.2) Kalkula ezazufuntzioaren limitea-rantz doanean.Zenbakitzailearen maila izendatzailearena baino handiagoa da eta maila garaiena duen gaien koefizienteak ikur desberdina dute, beraz:3) Kalkula ezazu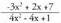Zenbakitzailearen maila eta izendatzailearen maila berdinak dira, beraz :4) Kalkula ezazu :Zenbakitzailearen maila izendatzailearena baino txikiagoa da, beraz:

Funtzio irrazionalen limiteen kalkulua.

Funtzio bat irrazionala da aldagai askea erro ikurraren barruan azaltzen denean. Esaterako,

A. Funtzio irrazional baten limitearen kalkulua x 0 puntu finituan.

Orokorrean, limite hauek funtzio arrazionalen limiteak bezala kalkulatzen dira.Limitea kalkulatzerakoan indeterminazioa azaltzen bada, hori ekiditeko, konjokatzearen bidez biderkatzen dira zenbakitzailea eta izendatzailea.• Adibideak :1) Kalkula ezazuEz da existitzen2) Kalkula ezazu.Indeterminazioa• Indeterminazioa ekiditeko zenbakitzailearen konjokatuaren bidez,biderkatu eta zatitu egiten da.

B. Funtzio irrazional baten limitearen kalkulua infinituan.

B.1. oo/oo indeterminazioa duten limiteak.

Funtzio irrazional baten limitea kalkulatzerakoanindeterminazioa sortzen bada, funtzio arrazionalen limiteak kalkulatzerakoansortzen denean bezala egiten da ; erregela berbera aplikatuz.• Adibideak:1) Kalkula ezazu• Aipatutako erregela erabiliz :Zenbakitzailearen maila : 3Izendatzailearen maila :Beraz,2) Kalkula ezazu :• Zenbakitzailearen eta izendatzailearen limiteak kalkulatuzindeterminazioa• Mailak aztertuz :Zenbakitzailearen maila : 1Izendatzailearen maila :baitaBeraz,3) Kalkula ezazu.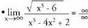IndeterminazioaBeraz,* Frogapena nahiko luzea denez gero, ez da hemen azalduko; baina komenigarria da garbi uztea

B.2. oo-oo indeterminazioa duten limiteak

Funtzio irrazional baten limitea kalkulatzerakoan,indeterminazioa sortzen bada, hori ekiditeko, funtzioa biderkatu eta zatitu egiten da bere konjokatuaren bidez.• Adibideak :1) Kalkula ezazufuntzioaren limitea-rantz doanean•Indeterminazioa.

• Biderkatu eta zatitu egiten da bere konjokatuaren bidez:2) Kalkula ezazu•Indeterminazioa.• Funtzioa biderkatu eta konjokatuaz zatitzen da3) Kalkula ezazu :•Indeterminazioa.• Biderkatu eta funtzio konjokatuaz zatitzen da,

- Ariketak

I V. Jarraitasuna

Funtzio jarraia puntu batean

f funtzio bat jarraia dapuntuan funtzioaren limitea existitzen denean puntu horretan eta bere balioak funtzioakpuntuan hartzen duen balioarekin bat badatoz.f jarraia dapuntuanFuntzio bat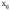puntuan jarraia izan dadin hiru baldintza hauek bete behar dira :1. Funtzioaren limitea existitea-rantz doanean2. Funtzioa definituta egotea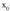-n, hau da,existitzea.3. Aurreko bi balioak berdinak izatea :Hiru baldintza horietakoren bat betetzen ez bada, funtzioa ez da jarraia-n; funtzioa etena da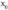

Funtzio jarraia tarte batean

Funtzio bat jarraia da tarte batean tarte horretako puntu guztietan jarraia denean.

Funtzio baten etenguneen azterketa

1) Ikus ezazuEbazpena :• Funtzioapuntuan etena dela frogatzeko, 3 baldintzetatik zein betetzen ez den ikusi behar da.Kasu honetan lehenengoa da, ez delako existitzen funtzioaren limiterik-rantz doanean ; aldeetako limiteak ez dute bat egiten.Beraz, funtzioa etena da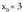puntuan.2) Azter ezazuEbazpena:• Funtzioaren limitea-rantz doanean existitzen da eta 1 balio du ; bi aldeetako limiteak berdinak dira :• x = 3 denean, f(3) = 3 - 2 = 1 •Beraz, funtzioa jarraia dadenean.3)Ebazpena• Funtzioaren limitea existitzen da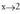-rantz doanean, bi aldeetako limiteak berdinak baitira.• Funtzioa definituta dago x=2 denean eta bere balioa 4 du.• Baina hirugarren baldintza ez da betetzen.Beraz, funtzioa etena da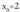

Funtzio jarraien eragiketak

BatuketaPuntu bateko bi funtzio jarraien batura, funtzio jarrai bat da puntu horretan.FrogapenaBitez f eta g bi funtzio,puntuan jarraiak direnak. Horrek zera esan nahi du :f + g funtzioapuntuan jarraia dela frogatzeko,ikusi behar da.Funtzioen limiteen ezaugarri bat aplikatuz :Frogapen horipuntuko n funtzio jarrai baterako baliagarria da.BiderkaketaPuntu bateko bi funtzio jarrairen biderkadura puntu horretako beste funtzio jarrai bat da.Zatiketa

Funtzioen konposaketa

F funtzioa, puntuan jarraia bada eta g funtzioapuntuan jarraia bada, g , f funtzioa konposatua jarraia da

Funtzio jarraien ezaugarria

Funtzio batpuntuan jarraia bada, orduan konbergentea da-n, hau da, funtzioaren limitea existitzen da-rantz doanean.

V. Oinarrizko funtzio batzuen jarraitasuna

Funtzio konstantea

f(x) = k funtzio konstantea jarraia da puntu guztietan

Berreketa funtzioa

Berreketa funtzioajarraia da puntu guztietan, salbu n<0 eta x=0 denean ; izan ere, izendatzaile nulua duen funtzio arrazional bat ateratzen da eta ezin izan daiteke jarraia.

Funtzio polinomikoa

funtzioa puntu guztietan jarraia da, puntu guztietan jarraiak diren funtzioen batura delako.

Funtzio arrazionala

Funtzio exponentziala

funtzioa, a > 0 izanik, puntu guztieetan jarraia da.

Funtzio logaritmikoa

funtzioa, a > 1 izanik, bere izate-eremuko puntu guztietanjarraia da.

Funtzio trigonometrikoak

f(x) = sin x eta g(x) = cos x funtzioak jarraiak dira R osoan.h(x) = tg x funtzioa,

Funtzio baten jarraitasun puntuen edo etenguneen azterketa

1) Zein puntutan eteten da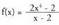funtzioa? Ebazpena :Funtzioa puntu guztietan jarraia da, izendatzailea anulatzen den puntuetan izan ezik, horietan funtzioa definitu gabe dagoelako ; hots, x=2 denean.Beraz, funtzioa puntu guztietan jarraia da, x=2 denean izan ezik, orduan funtzioa etena baita.2) Azter ezazu funtzioa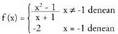x = -1 denean jarraia da?• f(-1) = -2•(kasu horretan funtzioa -1-en ezkerretara eta -1-en eskuinetara berdin dago definituta, beraz, aldeetako limiteak berdinak dira).f(-1)= lim f(x) = - 2 ; berz, x=-1 puntuan jarraia da.3)Funtzio hau Dirichleten funtzioa da.Edozein zenbaki erreal c hartuz gero, x c-rantz hurbiltzen denean x-ek balio arrazionalak eta irrazionalak hartzen ditu. Hori gertatzean f(x) saltoka dabil 1 eta O-ren artean, 1 zenbaki finko baterantz ezin hurbilduz. Beraz,

- Ariketak

5. Esan ezazu ondoko funtzioak jarraiak diren ala ez esaten den puntuetan.

VI. Etenguneen sailkapena

funtzio batpuntuan etena izan dadin (edo ez jarraia) hauetako baldintzaren bat bete behar da :a)ez da existitzen alaez da existitzen?b) Aldetako limiteak existitzen dira bainac)existitzen da, baina

Eten ebitagarria

Funtzio batekpuntuan etengune ebitagarria du baldin etaexistitzen bada, baina bere balioa ez badator bat funtzioak puntu horretan hartzen duen balioarekin.etengune ebitagarria daEtengune hori ebita daiteke funtzioari puntu horretan, hots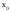puntuan, limitearen balioa emanez.Era horretan,-ri funtzioaren egiazko balioa esaten zaiopuntuan, eta balio horrek egiten du funtzio hori funtzio jarrai

Eten ebitaezina

Funtzio batekpuntuan etengune ebitaezina du funtzioaren limitea puntu horretan existitzen ez denean ; hau da, aldeetako limiteren bat existitzen ez denean edota aldeetako bi limiteak existitzen direnean baina balio desberdinak hartzen dituztenean.• AdibideakEbazpena : • x+4 funtzioa jarraia da puntu guztietan.

• f(x) jarraia da puntu guztietan, x=2 denean izan ezik, f(2)=2 baita.• f(2) = 6 egiten bada, limitearen balioa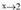-rantz doanean, etengunea ebitatzen da eta f(x) = x+4 funtzioa jarraia da puntu guztietan.Funtzioaren egiazko balioa x=2 puntuan 6 da.2) Azter eta sailka itzazufuntzioaren etenguneak.Ebazpena• Funtzioa jarraia da puntu guztietan, izendatzailea 0 egiten den puntuetan izan ezik : x=3• Ikus dezagunpuntuan dagoen etena ebitagarria ala ebitaezina den.Limitea existitzen da eta bere balioa 6 da ; beraz,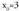puntuan dagoen etena ebitagarria da. Funtzioaren egiazko balioa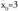puntuan 6 da.f(3)-ri 6 balioa ematen dioguFuntzioa jarraia da bere puntu guztietan

- Ariketak

6. Sailka itzazu etenguneak

Ariketen emaitzak