Matematika»Analisiak
Funtzio transzendenteak
I. Funtzio esponentziala
Ondoko funtzioarioinarriko funtzio esponentzial esaten zaio :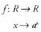 non a > 0 eta
non a > 0 eta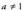 .
.
. eran ere adieraz daiteke.Adibideak
eran ere adieraz daiteke.Adibideak eta
eta funtzioen grafikoak osatzen dira.
funtzioen grafikoak osatzen dira. funtzioarentzat balio taula hau eratzen dugu :
funtzioarentzat balio taula hau eratzen dugu : Eta
Eta funtzioarentzat, berriz, beste balio taula hau :
funtzioarentzat, berriz, beste balio taula hau : Ondoren batari zein besteari dagozkien grafikoak egiten dira.
Ondoren batari zein besteari dagozkien grafikoak egiten dira.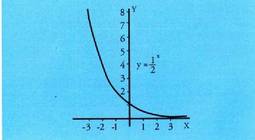
Deskribapen orokorra
Eremua = R(0,1) puntutik igarotzen diraAsintota horizontal bat dute; y = 0 , ekuazioa dagokion
, ekuazioa dagokion ardatza dute, eta ibilbidea
ardatza dute, eta ibilbidea da.Bien arteko desberdintasuna da
da.Bien arteko desberdintasuna da funtzioan berrekizuna a > 1dela eta
funtzioan berrekizuna a > 1dela eta funtzioan berriz, 0 eta 1 artean dagoela, alegia0 < a < 1 dela.a > 1 deneanFuntzioa hertsiki gorakorra da
funtzioan berriz, 0 eta 1 artean dagoela, alegia0 < a < 1 dela.a > 1 deneanFuntzioa hertsiki gorakorra da o < a < 1 deneanFuntzioa hertsiki beherakorra da
o < a < 1 deneanFuntzioa hertsiki beherakorra da
- Ariketak
1. Egin eta
eta
Berreketa arteko eragiketen ezaugarriak hauek dira :
Ekuazio esponentzialak
Ekuazio esponentzial esponente edo berretzailean x ezezaguna
duten ekuazioei esaten zaie. Ekuazio horiek ebazteko zein arau erabili
jakiteko, ondoko sailkapenaren arabera sailkatzen dira ekuazio
hauek :1) Ekuazioan agertzen diren zenbaki eta berreketa guztiek berrekizun bera dutenak (edo berrekizun beraren bidez adieraz daitezkeenak), eta biderkadura edo zatidura eragiketak bakarrik agertzen direnak (alegia ez batuketarik eta ez kenketarik dutenak).
- Adibideak ,adibide horiek ebazteko :Biderkagai edo zatitzaile guztiak berrekizun bereko berreketa gisa erazten dira.Berreketa arteko eragiketak egiten dira, ekuazioaren atal bakoitza
berreketa bakarrera murrizteko.Baldin eta berrekizun bera duten bi berreketa berdinak badira, esponenteek
ere berdinak behar dute izan.Ebazpenaka) Hemen bi atalek berrekizun bera dute, 2 berrekizuna alegia :
,adibide horiek ebazteko :Biderkagai edo zatitzaile guztiak berrekizun bereko berreketa gisa erazten dira.Berreketa arteko eragiketak egiten dira, ekuazioaren atal bakoitza
berreketa bakarrera murrizteko.Baldin eta berrekizun bera duten bi berreketa berdinak badira, esponenteek
ere berdinak behar dute izan.Ebazpenaka) Hemen bi atalek berrekizun bera dute, 2 berrekizuna alegia : . Bi berreketa berdinak izan daitezen esponenteek ere berdinak behar dute izan.
. Bi berreketa berdinak izan daitezen esponenteek ere berdinak behar dute izan.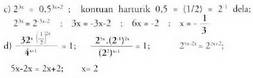 2) Ekuazioaren x berrerzaileko berreketak ere berrekizun beraren
bidez adieraz daitezkeenak, haina ekuazioaren barruan batuketa
edo kenketa eragiketak agertzen diranak.• Adibideak
2) Ekuazioaren x berrerzaileko berreketak ere berrekizun beraren
bidez adieraz daitezkeenak, haina ekuazioaren barruan batuketa
edo kenketa eragiketak agertzen diranak.• Adibideak Era honetako ekuazioak ebazteko
Era honetako ekuazioak ebazteko aldagai aldaketa egin behar da lehenik. Horretarako batugai guztietan
aldagai aldaketa egin behar da lehenik. Horretarako batugai guztietan biderkagaia ordezkatu behar da. Azal dezagun goiko adibideak erabiliz.Ebazpena
biderkagaia ordezkatu behar da. Azal dezagun goiko adibideak erabiliz.Ebazpena 3) Oraingoz ezin ebatz daitezkeen ekuazioak
3) Oraingoz ezin ebatz daitezkeen ekuazioak motako ekuazio esponentzialak ebazteko, b emaitza a-ren esponente osoko berreketa bat ez den kasuetan, logaritmoak erabili behar dira. Hala ere, kalkulagailua erabiliz soluzioaren nahiko hurbileko emaitzak lor dairezke. Adibidez, eman dezagun
motako ekuazio esponentzialak ebazteko, b emaitza a-ren esponente osoko berreketa bat ez den kasuetan, logaritmoak erabili behar dira. Hala ere, kalkulagailua erabiliz soluzioaren nahiko hurbileko emaitzak lor dairezke. Adibidez, eman dezagun ekuazioa ebatzi behar dela.EbazpenaErraz froga daiteke 7 < x < 8 dela, eta
ekuazioa ebatzi behar dela.EbazpenaErraz froga daiteke 7 < x < 8 dela, eta dela. Ebatzi behar den ekuazioaren emaitza 1 28tik hurbilago dagoenen 256tik baino, 7,2 eta 7,1 berretzaileekin egingo dugu kalkulua :
dela. Ebatzi behar den ekuazioaren emaitza 1 28tik hurbilago dagoenen 256tik baino, 7,2 eta 7,1 berretzaileekin egingo dugu kalkulua : eta
eta denez bi emaitza horietan 143tik hurbilenekoa, 7,16 erabiliko dugu hurrena, eta
denez bi emaitza horietan 143tik hurbilenekoa, 7,16 erabiliko dugu hurrena, eta lortuko dugu horrela : emaitza hori ontzat eman daiteke, eta x = 7,16 dela esan dezakegu.Era honetako ekuazioak hurbilketa kalkulurik egin gabe ebatzi ahal izateko
lortuko dugu horrela : emaitza hori ontzat eman daiteke, eta x = 7,16 dela esan dezakegu.Era honetako ekuazioak hurbilketa kalkulurik egin gabe ebatzi ahal izateko
- Ariketak
2. Ebatzi ondoko ekuazio hauek:
- Ariketak
3. Ebatzi ondoko ekuazioak hurbilketa kalkuluak eginez:
Funtzio esponentzialen aplikazioak
Hazkuntza esponentziala askotan gertatu ohi da gure eguneroko
bizitzan ; biztanleriaren hazkundea, animaliena edo landareena,
desintegratzen den gai erradiaktibo batena, edo ekonomian, interes
elkartuan jarritako kapital baten hazkundean etab. Era horretako
kasuak aztertuko dira, orain, zehatz-mehatz.• Adibideaka) 8 milioi pezetako kapital bat urteko %7ko interes elkartuan jarriz gero (alegia, urtean behar ematen dituen interesak urte bakoitzaren amaieran kapitalari eransten bazaizkio, interes gehiago eman dezaten), zenbat diru izango da 10 urteren buruan?EbazpenaUrte bakoitzaren hasieran zegoen kapitala bider 1,07 egingo da urteko, beraz, t urteren ondoren lorturiko kapitala izango da, eta t = 10 bada, C = 15737211 puntuko emaitza lortuko dugu.b) Gai erradiaktiboak desintegratu eta beste gai batzutan bestelakotzen
dira; gai bakoitzak desintegrazio epe bat izaten du, bere
ezaugarrien arabera. Eman dezagun gai erradiaktibo bat bost
urtez behin erdira murrizten dela desintegrazioaren bidez (alegia,
bost urteko desintegrazio epea duela). Kalkulatu t urteren
buruan geratuko den kopurua lortzeko bidea ematen duen
adierazpena.Ebazpena
izango da, eta t = 10 bada, C = 15737211 puntuko emaitza lortuko dugu.b) Gai erradiaktiboak desintegratu eta beste gai batzutan bestelakotzen
dira; gai bakoitzak desintegrazio epe bat izaten du, bere
ezaugarrien arabera. Eman dezagun gai erradiaktibo bat bost
urtez behin erdira murrizten dela desintegrazioaren bidez (alegia,
bost urteko desintegrazio epea duela). Kalkulatu t urteren
buruan geratuko den kopurua lortzeko bidea ematen duen
adierazpena.Ebazpena hasierako kopurua dela kontuan harturik, baldin eta
hasierako kopurua dela kontuan harturik, baldin eta bada, orduan, lehenengo urtearen buruan geldituko den kopurua
bada, orduan, lehenengo urtearen buruan geldituko den kopurua izango da, eta t urteren buruan geldituko dena, berriz,
izango da, eta t urteren buruan geldituko dena, berriz, c) Bakteria hazitegi batean bakteriak 3 orduz behin ugaltzen dira,
zatiketa bidez. Hasieran 500 bakteria bazeuden, orduko zenbat
bider ugaltzen da bakteria kopurua? Eta ordu laurdeneko?
Zenbat bakteria egongo da 24 orduren buruan?EbazpenaHiru orduz behin bakteria kopurua bikoiztu egiten bada, orduko
c) Bakteria hazitegi batean bakteriak 3 orduz behin ugaltzen dira,
zatiketa bidez. Hasieran 500 bakteria bazeuden, orduko zenbat
bider ugaltzen da bakteria kopurua? Eta ordu laurdeneko?
Zenbat bakteria egongo da 24 orduren buruan?EbazpenaHiru orduz behin bakteria kopurua bikoiztu egiten bada, orduko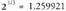 bider ugalduko da eta ordu laurdeneko
bider ugalduko da eta ordu laurdeneko bider ; horrela, 24 orduren buruan geldituko den bakteria kopurua N=
bider ; horrela, 24 orduren buruan geldituko den bakteria kopurua N=
- Ariketak
4. Diruaren balio galerari inflazio esaten zaio ; hau da, baldin
eta salgai batek 100 pezeta balio bazuen hasieran
eta 104ko balioa izango badu urtebeteren buruan,
inflazioa %4koa izan dela esaten da. Urteko %4ko
inflazio konstantea aurrikusten bada,a) zein formulak emango du aukera salgai jakin baten p prezioa t urteren buruan zenbatekoa izango den kalkulatzeko, gaur egungo
I I. Logaritmoak. Logaritmo funtzioak
Sarrera
XVI. mendearen amaieran salerosketaren eta bankaren bilakaerak
kalkuluarekin zerikusia zuten problemak sortu zituen, eta kalkulu
konplexuak eskatzen zituzten, halaber, itsasketa edo astronomiako
problemek; problema horiei soluzioa ematen ahalegindu ziren garai
hartako matematiko ospetsuak, eta kalkulu horiek errazago egin
ahal izateko kalkulu teknikak sortu zituzten.Teknika horien oinarrian ideia bat dago : errazagoa dela batuketa
egitea biderkaketa egitea baino, eta berrekizun bera duten berreketak
biderkatzeko berretzaileak batu behar direla. Ideia hori babiloniarren
garaian zabaldu zen, izan ere antzinako babiloniar oholtxoetan
badira batzuk zenbaki jakin baten ondoz ondoko berreketak
agertzen dituztenak, gaur egun antilogaritmo deitzen zaien taulen
antzera. Arkimedesek ere aipatzen du, zenbaki erraldoiei buruzko
lan batean, handik zenbait mendera logaritmoak asmatzeko bidea
eman zuen hatsapena (berreketen biderkaduraren eta berretzaileen
batuketaren arteko erlazioa).Geroago, Ibn-Yunus arabiar matematikariak (1008) 2 cos x cos y
= cos (x+y) + cos (x-y) formula azaldu zuen. Formula hori da biderkaketak
batuketa bihurtzeko erabiltzen diren lau formula trigonometrikoetako
bat, Europan prostofeiresis (grekeraz batuketak eta
kenketak izendatzeko terminoa) izeneko metodoa erabiliz logaritmoak
aurkitu aurretik biderkaketak batuketa bihurtzeko erabili
izan zena.Logaritmo terminoa John Napierrek asmatu zuen, logos (arrazoia)
eta artihmos (zenbakia) grekerazko terminoak elkartuz ; 1614an
logaritmoei buruzko lehen tratatua idatzi zuen : Mirifici
logarithmorum canonis descriptio ("Logaritmoen lege zoragarriaren
deskribapena").Napier ez zen matematikaria bizibidez ; baroi eskoziar aberats
bat zen, baina bere ondasunak administratzeaz gainera idatziak eta
gogoetak argitaratu zituen hainbat gairi buruz (matematika,
teologia...).Matematiketan zenbakizko kalkulua eta trigonometria izan
zituen aztergai. Berak asmatu zituen biderkadurak egiteko erabili
ohi ziren hagatxoak, Napierren hagatxo deituak, eta parte zirkularrei
buruzko erregela bat eman zuen, Napierren erregela, esferen trigonometriako
formulak ikasteko erregela mnemoteknikoa.Logaritmoak aztertzen 20 urte igaro zituela zioen ; beraz, 1594 inguruan hasi zen gutxi gorabehera. Zenbaki jakin baten ondoz ondoko berreketen azterketa egin zuen, eta Tycho Brahe daniar astronomoak biderkaketak batuketa bihurtzeko erabiltzen zituen prostafeiresi metodoen berri izan zuen Joan Craigen bidez. Metodo horrek eman zion Napierri lanean jarraitzeko kemena, eta azkenik, 1614an eman zuen argitara bere lana ; lan horretan agertzen den logaritmoaren definizioa gaur egun erabiltzen denaren oso bestelakoa da, eta ez du logaritmoen oinarriaren ideia agertzen, baina haren definizioak 1/e oinarriko logaritmoetara garamatza ; bestalde, Napierren logaritmoetan biderkadura baten logaritmoa ez da biderkagaien logaritmoen baturaren berdina gaur egun bezala, izan ere, haren ustez L(N,)=L, eta L(N z )=L z bazen, orduan
Logaritmoa
Definizioa
 x-en a oinarriko logaritmoa, x lortzeko a zein m zenbakira berretu
behar den adierazten duen logaritmoa da.Oinarria 10 denean logaritmo hamartar esaten zaio eta "log"
laburduraz izendatzen da, eta oinarria e zenbakia denean berriz,
logaritmo nepertar deritzo eta "In" izendatzen da.• Adibideak
x-en a oinarriko logaritmoa, x lortzeko a zein m zenbakira berretu
behar den adierazten duen logaritmoa da.Oinarria 10 denean logaritmo hamartar esaten zaio eta "log"
laburduraz izendatzen da, eta oinarria e zenbakia denean berriz,
logaritmo nepertar deritzo eta "In" izendatzen da.• Adibideak Logaritmoaren a oinarria beti positiboa, a > 0, dela kontuan harturik,
zera atera daiteke ondorio :• Zenbaki negatiboek ez dute logaritmorik,
Logaritmoaren a oinarria beti positiboa, a > 0, dela kontuan harturik,
zera atera daiteke ondorio :• Zenbaki negatiboek ez dute logaritmorik,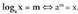 , baldin eta
, baldin eta Horrez gainera,
Horrez gainera, dela egiaztatzen da ; izan ere, baldin eta
dela egiaztatzen da ; izan ere, baldin eta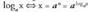 • Adibideak
Kalkulatu :
• Adibideak
Kalkulatu : Ebazpena
Ebazpena
- Ariketak
6. Kalkulatu : 7. Sinplifikatu :
7. Sinplifikatu :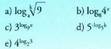 8. Kalkulatu x-en balioak ondoko berdintzak bete daitezen :
8. Kalkulatu x-en balioak ondoko berdintzak bete daitezen :
Logaritmoen ezaugarriak
 Ezaugarrien frogaBitez
Ezaugarrien frogaBitez 1. froga
1. froga 2. froga
2. froga 3. froga
3. froga 4. froga
4. froga • Adibideaa) Idatzi log
• Adibideaa) Idatzi log adierazpena logaritmo batuketa, diferentzia edo anizkoitz eran.Ebazpena
adierazpena logaritmo batuketa, diferentzia edo anizkoitz eran.Ebazpena b) Kalkulatu A, bigarren ataleko logaritmoak logaritmo bakar
batean bilduz.
b) Kalkulatu A, bigarren ataleko logaritmoak logaritmo bakar
batean bilduz.
- Ariketak
9. Kalkulatu logaritmo batuketa, diferentzia eta anizkoitz eran. 10. Bildu logaritmo bakar batean 2. atala eta eman A-ren
adierazpena.
10. Bildu logaritmo bakar batean 2. atala eta eman A-ren
adierazpena.
Logaritmoen oinarri aldaketa
Zenbaki positibo baten edozein oinarriko logaritmoen kalkulua egin daiteke, baldin eta oinarri positiboak badira, adibidez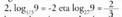 Horrez gainera posible da zenbaki baten logaritmoan b oinarra a oinarrira aldatzea formula honen bidez :
Horrez gainera posible da zenbaki baten logaritmoan b oinarra a oinarrira aldatzea formula honen bidez : Froga
Bedi
Froga
Bedi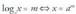 2. berdintzaren bi ataletan b oinarriko logaritmoak harturik
2. berdintzaren bi ataletan b oinarriko logaritmoak harturik lortzen dugu ; m askatuz m =
lortzen dugu ; m askatuz m = gelditzen da, eta m-ren ordez bere balioa jarriaz :
gelditzen da, eta m-ren ordez bere balioa jarriaz :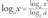 frogatu nahi zen bezala.• Kontuan izanik kalkulagailuaz logaritmo hamartarrak ( 10 oinarrikoak) eta nepertarrak (e oinarrikoak) soilik kalkula daitezkeela, formula honen abantaila nagusia a oinarriko logaritmoa logaritmo hamartarraren edo nepertarraren bidez adierazi ahal izatea da. Kasu horietarako, aldaketa hauek egin behar zaizkio formulari :
frogatu nahi zen bezala.• Kontuan izanik kalkulagailuaz logaritmo hamartarrak ( 10 oinarrikoak) eta nepertarrak (e oinarrikoak) soilik kalkula daitezkeela, formula honen abantaila nagusia a oinarriko logaritmoa logaritmo hamartarraren edo nepertarraren bidez adierazi ahal izatea da. Kasu horietarako, aldaketa hauek egin behar zaizkio formulari : • Logaritmo nepertarren eta logaritmo hamartarren arteko erlazioa
honela adierazten da :
• Logaritmo nepertarren eta logaritmo hamartarren arteko erlazioa
honela adierazten da :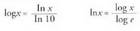 •
• eta
eta arteko erlazioa formula beretik ateratzen da :
arteko erlazioa formula beretik ateratzen da : Beraz,
Beraz, Eta formula horren bidez aurki daiteke
Eta formula horren bidez aurki daiteke eta
eta arteko erlazioa ere:
arteko erlazioa ere:
Logaritmo funtzioa
 funtzioa funtzio esponentzialaren alderantzizko funtzioa da, izan ere bigarren berdintzan x eta y ordezkatuz gero
funtzioa funtzio esponentzialaren alderantzizko funtzioa da, izan ere bigarren berdintzan x eta y ordezkatuz gero ateratzen da.
ateratzen da.
y = log ax funtzioaren grafikoaren ezaugarriak dira :
a) Eremua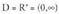 da.b) P(1,0) puntutik igarotzen da, izan ere
da.b) P(1,0) puntutik igarotzen da, izan ere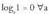 c)
c)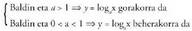 x = 0 denean asintota bertikal bat dago, izan ere
x = 0 denean asintota bertikal bat dago, izan ere bada.
bada. Alderantzizko funtzioak aztertzean ikusi den bezala, era horretako
funtzioen grafikoak simetrikoak dira 1. eta 3. koadranteetako
erdikariari buruz.Aztertu ondoko funtzioak (eremua, ardatzekiko ebakitze puntuak,
asintota) eta egin bakoitzari dagokion grafikoa.
Alderantzizko funtzioak aztertzean ikusi den bezala, era horretako
funtzioen grafikoak simetrikoak dira 1. eta 3. koadranteetako
erdikariari buruz.Aztertu ondoko funtzioak (eremua, ardatzekiko ebakitze puntuak,
asintota) eta egin bakoitzari dagokion grafikoa. Ebazpena
Ebazpena x ardatzarekiko ebakitze puntua
x ardatzarekiko ebakitze puntua beraz ebakitze puntua P(5, 0) da.
beraz ebakitze puntua P(5, 0) da.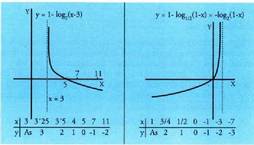 Ez du ardatza ebakitzen, izan ere x > 3Asintota bertikalax = 3, izan ere
Ez du ardatza ebakitzen, izan ere x > 3Asintota bertikalax = 3, izan ere Oinarri aldaketa aztertu denean ikusitakoaren arabera, funtzio hau
Oinarri aldaketa aztertu denean ikusitakoaren arabera, funtzio hau da.
da.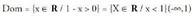 Ardatzekiko ebakitze puntuak :y ardatzarekiko, x = 0 denean
Ardatzekiko ebakitze puntuak :y ardatzarekiko, x = 0 denean x ardatzarekiko,
x ardatzarekiko, hau da, puntu bera, P(O, 0)Asintota bertikala x=1 zuzena da, izan ere
hau da, puntu bera, P(O, 0)Asintota bertikala x=1 zuzena da, izan ere
Logaritmo ekuazioak eta ekuazio sistemak
x ezezaguna logaritmo baten barnean agertzen dutenak dira.Era honetako ekuazioak ebazteko logaritmoak kendu behar dira,
alegia logaritmoak ekuazio polinomiko bihurtu behar dira, ondoren
ekuazioa aljebrari buruzko atalean ikasitako metodoen bidez
ebazteko. Horretarako ekuazioaren atal bakoitzeko logaritmoak
logaritmo bakarrean biltzen dira, logaritmoen ezaugarriez baliaturik,
eta tankera honetako berdintza bat lortzen da :log A = log B, eta hortik A = B ; ekuazio polinomikoa edo (kasuren
batean) esponentziala izan ohi da oro har.• Adibideak1. Bedi log (2x-7) = 2-logx ekuazioa.Ekuazio horretan agertzen direnak 10 oinarriko logaritmoak
direnez, 2 = log100 egiten da, eta balio hori ekuazioan ordezkatuz
log (2x-7) = log 100 - log x gelditzen da.Ondoren logaritmo bakarrean biltzen dira ekuazioaren bigarren
ataleko logaritmoak :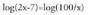 Logaritmo funtzioa funtzio injektiboa denez, 2x-7 = 100/x lortzen da, eta bi osagaiak bider
Logaritmo funtzioa funtzio injektiboa denez, 2x-7 = 100/x lortzen da, eta bi osagaiak bider eginez,
eginez, gelditzen da, beraz soluzioak
gelditzen da, beraz soluzioak dira.Baina -4 soluzioa ez da onargarria, R barnean ez baitago zenbaki
negatiboko logaritmorik. Beraz soluzio bakarra dago : x = 25/2Horren antzeko beste bide bat bada ekuazio hau ebazteko :2-ren ordez log 100 jarri beharrean, logaritmo guztiak atal batean
biltzen dira, eta bestean, berriz, logaritmorik gabeko zenbakiak jar
tzen dira :
dira.Baina -4 soluzioa ez da onargarria, R barnean ez baitago zenbaki
negatiboko logaritmorik. Beraz soluzio bakarra dago : x = 25/2Horren antzeko beste bide bat bada ekuazio hau ebazteko :2-ren ordez log 100 jarri beharrean, logaritmo guztiak atal batean
biltzen dira, eta bestean, berriz, logaritmorik gabeko zenbakiak jar
tzen dira : Lehen ataleko logaritmoak logaritmo bakar batean biltzen dira
gero :
Lehen ataleko logaritmoak logaritmo bakar batean biltzen dira
gero : Eta logaritmoaren definizioari jarraituz :
Eta logaritmoaren definizioari jarraituz : , hau da,
, hau da, , aurreko bidea erabiliz lortu dugun ekuazio berbera.2. Bedi ondoko ekuazio sistema :
, aurreko bidea erabiliz lortu dugun ekuazio berbera.2. Bedi ondoko ekuazio sistema : Adibide honetan bigarren ekuazioan bakarrik agertzen dira logaritmoak
. Aurreko adibidean bezala, lehenengo ataleko logaritmoak
logaritmo bakar batean biltzen dira :
Adibide honetan bigarren ekuazioan bakarrik agertzen dira logaritmoak
. Aurreko adibidean bezala, lehenengo ataleko logaritmoak
logaritmo bakar batean biltzen dira :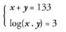 eta logaritmoaren definizioa aplikatuz, 2. mailako ekuazio sistema
bat lortzen da :
eta logaritmoaren definizioa aplikatuz, 2. mailako ekuazio sistema
bat lortzen da : Sistema horren soluzioak x = 125, y = 8 dira.3. Logaritmoen bidez ebazten diren ekuazio esponentzialak :Zenbait ekuazio esponentzial ebazterakoan
Sistema horren soluzioak x = 125, y = 8 dira.3. Logaritmoen bidez ebazten diren ekuazio esponentzialak :Zenbait ekuazio esponentzial ebazterakoan motako berdintza bat lortzen da, eta berdintza hori ebazteko bi ataletan logaritmoak jartzen dira, logaritmo hamartarrak (10 oinarrikoak) zein logaritmo nepertarrak (e oinarrikoak).
motako berdintza bat lortzen da, eta berdintza hori ebazteko bi ataletan logaritmoak jartzen dira, logaritmo hamartarrak (10 oinarrikoak) zein logaritmo nepertarrak (e oinarrikoak). Berreketa baten logaritmoaren ezaugarria aplikatuz :
Berreketa baten logaritmoaren ezaugarria aplikatuz : 4. Bedi
4. Bedi ekuazio esponentziala.Ekuazio esponentzialei buruzko atalean ikusi denez, ekuazio hori ebazteko
ekuazio esponentziala.Ekuazio esponentzialei buruzko atalean ikusi denez, ekuazio hori ebazteko aldagai aldaketa egiten da, eta horrela 2. mailako ekuazio bat lortzen da z-rentzat:
aldagai aldaketa egiten da, eta horrela 2. mailako ekuazio bat lortzen da z-rentzat: Ekuazio horren soluzioak dira :
Ekuazio horren soluzioak dira : Aldagai aldaketa deseginez gero, -2 = 3x gelditzen da bigarren
emaitzarako, eta berdintza hori ezinezkoa denez, ez da soluzio bat.5 = 3x emaitza 3. adibidearen arabera ebazten da : bi ataletan logaritmoak
hartzen dira, log5 = log3x, eta berreketa logaritmoaren propietatea
aplikatuz, log5 = x log3 lortzen da. Soluzioa :
Aldagai aldaketa deseginez gero, -2 = 3x gelditzen da bigarren
emaitzarako, eta berdintza hori ezinezkoa denez, ez da soluzio bat.5 = 3x emaitza 3. adibidearen arabera ebazten da : bi ataletan logaritmoak
hartzen dira, log5 = log3x, eta berreketa logaritmoaren propietatea
aplikatuz, log5 = x log3 lortzen da. Soluzioa :
- Ariketak
11. Ebatzi ondoko ekuazio hauek :
I I I. Funtzio trigonometrikoak
x aldagaia trigonometria arrazoi baten baitan ageri dutenak dira.
Era honetako funtzioak ikertzeko ezinbestekoa da trigonometriari
buruzko atala aurretik aztertu izana.Has gaitezen y = sin x, y = cos x eta y = tg x funtzioekin.Zirkunferentzia goniometriko bat hartuko dugu oinarri, hau da,
erradiotzat banakoa duena eta zentrotzat koordenatu jatorria.x radianeko angelua aurkeztean, angeluaren lehen aldea x-aren ardatz positiboan jartzen da, eta bigarrena zirkunferentzia P puntuan ebakitzen duela. Trigonometriari buruzko atalean ikusi zen bezala, puntu horren koordenatuak P(cos x, sin x) izango dira. Irudian,
Sinu funtzioa
Baldin x edozein zenbaki erreal bada, eta x radianeko neurria
duen angeluaren sinua sin x bada, sinu funtzio deritzo EremuaEdozein
EremuaEdozein -rentzat bada P puntu bat ordenatutzat x-en sinua duena. Sinu funtzioa R guztirako dago definitua.Ibilbideasin x-en balioak-1 eta 1 artean daude, biak barne.PeriodikotasunaBigarren aldeak zirkunferentzia goniometrikoa p puntuan ebaki tzen dutela dituzten angelu guztiek
-rentzat bada P puntu bat ordenatutzat x-en sinua duena. Sinu funtzioa R guztirako dago definitua.Ibilbideasin x-en balioak-1 eta 1 artean daude, biak barne.PeriodikotasunaBigarren aldeak zirkunferentzia goniometrikoa p puntuan ebaki tzen dutela dituzten angelu guztiek radianeko diferentzia dute, eta sinu bera dagokie guztiei, beraz, zera egiaztatzen da :
radianeko diferentzia dute, eta sinu bera dagokie guztiei, beraz, zera egiaztatzen da : , eta horren arabera sinu funtzioa periodikoa da
, eta horren arabera sinu funtzioa periodikoa da periodoan. Zehazki aztertuko ditugu y = sin u(x), y = cos u(x) eta y = tg u(x). Azterketa hau, ordea, u(x) lehen mailako funtzioa-den kasuetara mugatua izango da.
periodoan. Zehazki aztertuko ditugu y = sin u(x), y = cos u(x) eta y = tg u(x). Azterketa hau, ordea, u(x) lehen mailako funtzioa-den kasuetara mugatua izango da. tarteari dagokion balio taula eta grafikoa :
tarteari dagokion balio taula eta grafikoa :
Kosinu funtzioa
Baldin x edozein zenbaki erreal bada, eta x radianeko neurria
duen angeluaren kosinua cos x bada, kosinu funtzio deritzo EremuaEdozein
EremuaEdozein -rentzat bada P puntu bat ordenatutzat x-en kosinua duena. Kosinu funtzioa R guztirako dago definitua.Ibilbideacos x-en balioak -1 eta 1 artean, biak barne, daude.PeriodikotasunaBigarren aldea zirkunferentzia goniometrikoa p puntuan ebaki tzen dutela duten angelu guztiek
-rentzat bada P puntu bat ordenatutzat x-en kosinua duena. Kosinu funtzioa R guztirako dago definitua.Ibilbideacos x-en balioak -1 eta 1 artean, biak barne, daude.PeriodikotasunaBigarren aldea zirkunferentzia goniometrikoa p puntuan ebaki tzen dutela duten angelu guztiek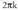 radianeko diferentzia dute, eta kosinu bera dagokie guztiei, beraz, zera egiaztatzen da :
radianeko diferentzia dute, eta kosinu bera dagokie guztiei, beraz, zera egiaztatzen da : , eta horren arabera kosinu funtzioa periodikoa da
, eta horren arabera kosinu funtzioa periodikoa da periodoan. Hona hemen
periodoan. Hona hemen tarteari dagozkion balio taula eta grafikoa :
tarteari dagozkion balio taula eta grafikoa :
Tangente funtzioa
Baldin x edozein zenbaki erreal bada, eta x radianeko neurria
duen angeluaren tangentea tg x bada, tangente funtzio deritzo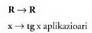 Azalpen honetan sinua, kosinua eta tangentea elkarri lotzen dizkion erlazioa hartzen da oinarri :
Azalpen honetan sinua, kosinua eta tangentea elkarri lotzen dizkion erlazioa hartzen da oinarri : Eremuax-en tangentea ez dago definitua kosinua ezerezten duten x-en balioentzat, alegia,
Eremuax-en tangentea ez dago definitua kosinua ezerezten duten x-en balioentzat, alegia, denean. Beraz,
denean. Beraz, IbilbideaTangenteak R barneko edozein balio har dezake.PeriodikotasunaZirkunferentzia goniometrikoan adierazitako x angelu baten tangentea BT segmentuak emana da, ikusi dugunez. Segmentu hori T- n zirkunferentziaren ukitzaile den zuzenaren gainean dago, eta B puntua, berriz, angeluaren muturrak edo angeluaren luzapenak zuzen ukitzaile hori ebakitzen duen puntua da. Beraz,
IbilbideaTangenteak R barneko edozein balio har dezake.PeriodikotasunaZirkunferentzia goniometrikoan adierazitako x angelu baten tangentea BT segmentuak emana da, ikusi dugunez. Segmentu hori T- n zirkunferentziaren ukitzaile den zuzenaren gainean dago, eta B puntua, berriz, angeluaren muturrak edo angeluaren luzapenak zuzen ukitzaile hori ebakitzen duen puntua da. Beraz, angeluek x angeluak ematen duen B puntu bera emango dute eta tangente bera izango dute, alegia,
angeluek x angeluak ematen duen B puntu bera emango dute eta tangente bera izango dute, alegia, . Hortik atera daiteke tangente funtzioak
. Hortik atera daiteke tangente funtzioak periodikotasuna duela.AsintotakTangenteak asintota bertikalak ditu bere eremuaz kanpoko puntu guztietan ; izan ere, puntu horietan kosinua ezerezten denez, eta sinua 0 ez beste zenbaki bat denez, tangenteak
periodikotasuna duela.AsintotakTangenteak asintota bertikalak ditu bere eremuaz kanpoko puntu guztietan ; izan ere, puntu horietan kosinua ezerezten denez, eta sinua 0 ez beste zenbaki bat denez, tangenteak jotzen du.Hona hemen
jotzen du.Hona hemen tarteari dagozkion balio taula eta grafikoa :Asintota bertikalak
tarteari dagozkion balio taula eta grafikoa :Asintota bertikalak Funtzio trigonometrikoen azterketa ondoko funtzioetara zabalduko
dugu orain : y = sin u(x), y = cos u(x), y = ig u(x), u(x) lehen
mailako funtzioa delarik.Eremua• y= sin u(x), y = cos u(x) funtzioek, oro har, zenbaki errealen R
multzoa dute eremutzat.• y = tg x funtzioaren eremua da :
Funtzio trigonometrikoen azterketa ondoko funtzioetara zabalduko
dugu orain : y = sin u(x), y = cos u(x), y = ig u(x), u(x) lehen
mailako funtzioa delarik.Eremua• y= sin u(x), y = cos u(x) funtzioek, oro har, zenbaki errealen R
multzoa dute eremutzat.• y = tg x funtzioaren eremua da :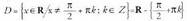 Ikus dezagun nola kalkulatzen den y = tg u(x) motako beste fun
tzio batzuen eremua.• Adibidea
Ikus dezagun nola kalkulatzen den y = tg u(x) motako beste fun
tzio batzuen eremua.• Adibidea izanik, funtzioa ez dago definitua
izanik, funtzioa ez dago definitua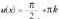 betetzen den puntuetan, eta beraz
betetzen den puntuetan, eta beraz giaztatzen duten x-en balioak kalkulatzen dira, hau da,
giaztatzen duten x-en balioak kalkulatzen dira, hau da, k, eta zati 2 eginez,
k, eta zati 2 eginez, k ateratzen dugu. Beraz, D=
k ateratzen dugu. Beraz, D= Periodikotasunay = f(x) funtzioak T periodikotasuna duela esaten da baldin eta
soilik baldin f(x+T) = f(x) betetzen bada.• y = sin x funtzioak
Periodikotasunay = f(x) funtzioak T periodikotasuna duela esaten da baldin eta
soilik baldin f(x+T) = f(x) betetzen bada.• y = sin x funtzioak periodoa du.• y = cos x funtzioak ere
periodoa du.• y = cos x funtzioak ere periodoa du.• y = tg x funtzioak
periodoa du.• y = tg x funtzioak periodoa du.Hau da :
periodoa du.Hau da : y = sin u(x), y = cos u(x) tankerako funtzioen periodoa kalkulatzeko
y = sin u(x), y = cos u(x) tankerako funtzioen periodoa kalkulatzeko ekuazioa ebatzi behar da.• Adibidea
ekuazioa ebatzi behar da.• Adibidea funtzioaren periodoa kalkulatzen dugu, kontuan harturik
funtzioaren periodoa kalkulatzen dugu, kontuan harturik ; eta hortik ateratzen da
; eta hortik ateratzen da Oro har, sinu edo kosinu funtzioetan u(x) 1. mailako u(x) = ax+b funtzioa denean, funtzio horren periodoa
Oro har, sinu edo kosinu funtzioetan u(x) 1. mailako u(x) = ax+b funtzioa denean, funtzio horren periodoa da, y = sin (ax+b) y = cos (ax+b) denean.Horrela, y = 2 sin (x/2) fmitzioaren periodoa
da, y = sin (ax+b) y = cos (ax+b) denean.Horrela, y = 2 sin (x/2) fmitzioaren periodoa da.• f(x) = tg u(x) motako funtzio baten periodoa kalkulatzeko
u(x+T) = u(x)+n ekuazioa ebazten da.• AdibideaBedi
da.• f(x) = tg u(x) motako funtzio baten periodoa kalkulatzeko
u(x+T) = u(x)+n ekuazioa ebazten da.• AdibideaBedi funtzioa, non
funtzioa, non Beraz, T = 2.Oro har, tangente funtzio batean, u(x) lehen mailako u(x) = ax+b denean, periodoa
Beraz, T = 2.Oro har, tangente funtzio batean, u(x) lehen mailako u(x) = ax+b denean, periodoa
- Ariketak
12. Aurkitu
- Ariketak
13. Aurkitu ondoko funtzioen periodoak :
Asintotak
y = sin u(x) eta y = cos u (x) funtzioak, u(x) lehen mailakoa denean,
ez dute asintotarik.y = tg x funtzioaren asintotak zuzenak direla ikusi dugu.Beraz, y = tg u(x) funtzioaren asintotak aurkitzeko ondoko ekuazio
hau ebatzi beharra dago :
zuzenak direla ikusi dugu.Beraz, y = tg u(x) funtzioaren asintotak aurkitzeko ondoko ekuazio
hau ebatzi beharra dago : • AdibideaAurkitu
• AdibideaAurkitu funtzioaren asintotak.Ebazpena
funtzioaren asintotak.Ebazpena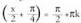 ekuazioa ebazten da :
ekuazioa ebazten da : tartea soilik hartzen badugu, asintota bakarra x =
tartea soilik hartzen badugu, asintota bakarra x = da.• Adibideaka) y = sin 2x funtzioa emanik, kalkulatu periodoa, egin funtzio horri
da.• Adibideaka) y = sin 2x funtzioa emanik, kalkulatu periodoa, egin funtzio horri tartean dagokion grafikoa, eta aurkitu y = 1 /2 zuzenarekin dituen ebakitze puntuen koordenatuak.Ebazpena
tartean dagokion grafikoa, eta aurkitu y = 1 /2 zuzenarekin dituen ebakitze puntuen koordenatuak.Ebazpena b)
b) funtzioa emanik, kalkulatu periodoa eta eremua, aurkitu asintotei ekuazioa, ebatz
funtzioa emanik, kalkulatu periodoa eta eremua, aurkitu asintotei ekuazioa, ebatz ekuazioa, eta egin
ekuazioa, eta egin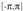 tarteari dagokion grafikoa.Ebazpena
tarteari dagokion grafikoa.Ebazpena
- Ariketak
14. Kalkulatu ondoko funtzio hauen eremua : 15. Kalkulatu ondoko asintota hauek :
15. Kalkulatu ondoko asintota hauek : 16. f(x) = 2sin x funtzioa harturik,
16. f(x) = 2sin x funtzioa harturik, tartean :a) Aurkitu periodoa eta egin funtzioaren grafikoa.b) Adierazi ardatz berberetan g(x) = 1 funtzioa.c) Ebatzi grafikoki f(x) = g(x) ekuazioa, eta frogatu ondoko
ekuazioaren ebazpenaren bidez:2 sin x = 1d) Ebatzi grafikoki 2 sinx < 1 inekuazioa.17. f(x) = cos 2x funtzioa harturik,
tartean :a) Aurkitu periodoa eta egin funtzioaren grafikoa.b) Adierazi ardatz berberetan g(x) = 1 funtzioa.c) Ebatzi grafikoki f(x) = g(x) ekuazioa, eta frogatu ondoko
ekuazioaren ebazpenaren bidez:2 sin x = 1d) Ebatzi grafikoki 2 sinx < 1 inekuazioa.17. f(x) = cos 2x funtzioa harturik,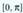 tartean :a) Aurkitu periodoa eta egin funtzioaren grafikoa.b) Adierazi ardatz berberetan g(x) = -1/2 funtzioa.c) Ebatzi grafikoki f(x) = g(x) ekuazioa, eta frogatu ondoko
ekuazio honen ebazpenaren bidez :
tartean :a) Aurkitu periodoa eta egin funtzioaren grafikoa.b) Adierazi ardatz berberetan g(x) = -1/2 funtzioa.c) Ebatzi grafikoki f(x) = g(x) ekuazioa, eta frogatu ondoko
ekuazio honen ebazpenaren bidez : d) Ebatzi grafikoki cos 2x < - 1 /2 inekuazioa.e) Aurreko grafikoa oinarri harturik, adierazi
d) Ebatzi grafikoki cos 2x < - 1 /2 inekuazioa.e) Aurreko grafikoa oinarri harturik, adierazi
Alderantzizko funtzio trigonometrikoak
a) arc sin x funtzioay = sin x funtzioaren alderantzizko funtzioa da sinuaren balio bakoitzari sinuaren balio hori bera duen angelua egokitzen diona ; kontuan harturik sinu bereko infinitu angelu daudela, alderantzizko funtziorik izan dadin sinu funtzioaren eremua funtzio hori bijektiboa den eremura murriztu behar da. Hau da, tartera.
tartera. b) arc cos x funtzioay = cos x funtzioaren alderantzizko funtzioa da kosinuaren balio bakoitzari kosinuaren balio hori bera duen angelua egokitzen diona; kontuan harturik kosinu bereko infinitu angelu daudela, alderantzizko funtziorik izan dadin kosinu funtzioaren eremua funtzio hori bijektiboa den eremura murriztu behar da. Hau da,
b) arc cos x funtzioay = cos x funtzioaren alderantzizko funtzioa da kosinuaren balio bakoitzari kosinuaren balio hori bera duen angelua egokitzen diona; kontuan harturik kosinu bereko infinitu angelu daudela, alderantzizko funtziorik izan dadin kosinu funtzioaren eremua funtzio hori bijektiboa den eremura murriztu behar da. Hau da, tartera.
tartera. arc tg x funtzioa
y = tg x funtzioa injektiboa da
arc tg x funtzioa
y = tg x funtzioa injektiboa da tartean, beraz, bere eremua tarte horretara mugatuz geldituko da definiturik bere tangentefuntzioa eta alderantzizko tangente funtzioa : arc tg x
tartean, beraz, bere eremua tarte horretara mugatuz geldituko da definiturik bere tangentefuntzioa eta alderantzizko tangente funtzioa : arc tg x
Emaitzak