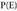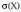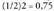Matematika»Probabilitatea
Probabilitatea
`Kausa oso txiki batek, guretzat ezin sumatuzkoa denak, guk nahitaez ikusi behar dugun ondorio bat eragiten du, eta orduan ondorio hori zoriari zor zaiola esaten dugu. Ondo jakinez gero izadiaren legeak zeintzuk diren eta zein egoeratan zegoen unibertsoa hasierako unean, orduan hutsik egin gabe iragar daiteke zein egoeratan egongo den unibertso hori bera geroztikako une jakin batean. Baina, izadiaren legeek batere sekreturik ez balute ere guretzat, hala ere gutxi gorabehera baizik ezingo genuke jakin hasierako egoera hura zein zen. Horri esker geroztikako egoera hori gutxi gorabeherako zehaztasun berberaz aurrikus badaiteke, hori aski izaten da, eta esaten dugu gertaera hori iragarria izan dela, lege jakin batzuek arautua dela, alegia ; gerta daiteke hasierako baldintza haietan alde txikiak egotea, eta alde txiki horiek alde handiak sortzea geroztikako gertaeretan ; hasierako hipotesi horretako hutsegite txiki batek hutsegite handi bat eragingo luke azken hipotesian. Iragarpena ezinezkoa da beraz, eta ustekabeko gertaera esaten zaio horri. " Poincare, Zientzia eta metodoa (1903).
Zoria eta Probabilitatea
Saiakuntza zientifiko batzuetan, emaitza aurrikusi egin daiteke
hasierako egoeraz zenbait datu ezaguturik. Beste kasu batzuetan,
ordea, hasierako egoera ongi ezagutu arren, ezin izaten da emaitza
zein izango den aurrez esan. Azken kasu hauetan, saiakuntza zorizkoa
dela edo emaitzak zoriaren arabera lortzen direla esaten da.
Zoriaren mende dauden egoera hauek aztertzen saiatzen den
matematikaren alorrari probabilitatea deitzen zaio. Egia esan,
zorizko fenomenoen eta fenomeno deterministen arteko muga
zehaztea ez da gauza erraza. Mekanikaren alorreko saiakuntzetan
ere, esaterako, nahiz eta hobeki kontrolatuta dauden, azaltzen dira
zoriari dagozkion errore txikiak. Zorizko prozesuetan, probabilitatearen
azterketan ikusiko dugunez, lege jakin batzuk betetzen dira.Hasteko, probabilitatearen bidez zoriaren mende dagoen saiakuntza
batek, adibidez dado edo karta jokoan, atera ditzakeen
emaitzak zehaztu daitezke, eta ondoren, emaitza horien artean gertagarrienak
zeintzuk diren aurkitu. Estatistikak, egin den saiakuntzako
datuak bilduz, "a posteriori" den zorizko fenomeno bat ikasten
du. Probabilitatea berriz, saiakuntza egin aurretik saiatzen da
gerta daitezkeen emaitzen berri eta emaitza horietako bakoitza
betetzeko dagoen zailtasun edo erraztasunaren berri ematen. Datu
hauek landuz, zoriz lortutako emaitza hauekin zerikusia duten beste
aldagai batzuk ezagutu daitezke, hala nola joko batean lor daitezkeen
irabaziak, biztanle kopuruak izan dezakeen hazkundea, etab.Probabilitatea zoriaren neurri bat ere bada, baina horrez gainera,
matematikaren alor bat da. Eta matematikaren beste edozein alor
bezala, ezin dakizkioke matematikakoak ez diren beste hipotesi
batzuk gehitu gabe errealitate fisikoari edo giza-errealitateari zuzenean
aplikatu. Probabilitatea zientzia zehatza da, bere aplikazioak,
ordea, ez. Probabilitatearen teoria bezalako zientzia batean aurrera
egiteko saiakuntzaren emaitzetik abiatuta suposizioak egin behar
dira. Adibidez, bi dado simetriko jaurtitzen badira, daduetako
puntuen batura 3 izatea 2 izatea baino errazagoa edo gertagarriagoa
dela dio probabilitateak. Baina bi dado simetrikoak direla esatea
dado horien ezaugarri fisikoetan edo saiakuntzan oinarritutako
hipotesi bat da. Halaber, dadoak "faltsuak" direla uste izatea eta "bi
bateko" ateratzea gertagarriagoa dela esatea ere, probabilitatearekin
bat etorriko litzateke.Zorizko joko edo saiakuntza batean gerta daitezkeen emaitza
posible guztiak ezagutu ondoren, emaitza bakoitza gertatzeko
erraztasuna edo emaitza bakoitzaren gertagarritasuna aditzera
emango duen zenbaki bat -hau da probabilitatea- bilatu behar da.
Korrespondentzia hau bilatzeko, pisua, forma edo egoera geometrikoak
har daitezke kontuan. Saiakuntza bera askotan egin bada,
maiztasun erlatiboak probabilitaren berdinak dira ia-ia. Dena dela,
eta hau horrela izan arren, jokalari askok bere senari edo bide irrazionalei
jarraituz egiten dituzte apustuak.Batzuetan zorizko saiakuntza bat izateko ordez prozesu bat izaten
da, hala nola egunaren buruan leihatila batean sor daitezkeenilarak, maila jakin bateko ikasleen altuera banatzeko era, edo
enpresa batean egin behar diren betebeharrak burutzeko behar den
denbora. Zorizko saiakuntza hauek egin ondoren lortzen diren
emaitzak ikasterakoan emaitza horiek lege binomial edo lege normal
bati jarraitzen diotela esatea ez da ziurta daitekeen emaitza bat,
lanerako erabil daitekeen hipotesi bat baizik. Izan ere, probabilitatearen
adar batek saiakuntza batzuk egiten hasterakoan erabili
ziren hipotesiak aztertzen ditu, hain zuzen ere saiakuntzetan lortu
diren emaitzetatik abiatuta hipotesi horiek fidagarriak diren ala ez
aztertzen du. Dena dela, saiakuntza mordo bat eginak ez gaitu
hipotesiak onartzera edo baztertzera behartzen. Dado bat ehun
aldiz jaurti ondoren "seia" inoiz atera ez bada, dadoa faltsua denik
ezingo dugu ziurtatu, seguruenik faltsua izango dela soilik esan
dezakegu.Probabilitatea egoera askotan erabiltzen da. Hasteko zoriaren
mende dauden jokoetan, hau da, zorteak zerikusi handia duen
jokoetan. Aplikazio asko ditu gizarte eta giza zientzietan eta ekonomian
ere. Eta fisikan esaterako, probabilitatearen teorian oinarrituak
dira termodinamika edo mekanika kuantikoa.Probabilitatea ezagutzen ez ditugun edo hain korapilatsuak izanik
beste era batera ikastea ezinezkoak zaizkigun fenomenoak lantzeko
era bat soilik den jakitea, edo zoria gauzen izaeraren zati bat
izanik mundua azaltzeko probabilitatea nahitaezkoa den ala ez, ez
da hemen aztertuko. Mende askotan uste izan zen dado bat jaurti
aurretik eta hainbat kalkulu eginez ezagutu egin zitekeela zein zenbaki
aterako zen, baldin eta ezagunak balira dado baten jaurtiketan
parte hartzen duten xehetasunak, alegia, pisua, forma, jaurtitzen
den indarra, airearen erresistentzia, erortzen den gainaldearen
marruskadura eta pisua eta forma ezaguneko kubo bati dagozkion
mekanika klasikoko legeak. Halaber, ontziaren forma, molekula
arteko talkaren legeak eta gasa eratzen duten milioika molekulen
hasierako egoera ezagutuz, gas baten molekula guztien bilakaera
ezagutu zitekeela uste izan zen. Baina gaur egun, zientzialari askorentzat,
zoria munduaren zati bat da. Era berean, zoria izadiaren
zati bat dela dioen ideian oinarritua da mekanika kuantikoa ere,
eta oinarrizko partikula baten posizioa eta abiadura ezin direla ezagutu
baieztatzen du, eta posizioa edo higidura kantitatearen probabilitate
funtzioak erabiltzen. Mundu determinista bat ezinezkoa
dela uste duten zientzialarien ondoan, badira beste batzuk, esaterako
Einstein, esaten dutenak "jaungoikoak ez du munduarekin
dadotara jokatzen", eta orain probabilitateen teoria erabiliz ikasten
diren fisika edo beste zientzietako fenomenoan lege deterministak
gizadiak ezagutuko dituela uste dutenak.Beraz, zoria eremu askotan azaltzen da gaur egun, baina antzina
jokoen ikasketan soilik agertzen zen. Hori dela eta lehenengo gai
honetako adibide gehienek jokoekin zerikusia izango dute.
Hurrengo ataletan estatistikarekin zerikusia duten aplikazioak, edo
erroreen teoria, eta hipotesi batean konfidantza tarteak aurkitzeko
era edo emaitza baten estimazioa aztertuko dira.
Probabilitatearen historia
Zoria oso aspalditik da ezaguna, baina zoriaren azterketa matematikoa
berri samarra da.Arkeologia aztarnategi askotan zenbait zibilizaziok jokorako eta zoriak
parte hartzen zuen aztikerietarako erabiltzen zituzten dadoak eta tortoloxak
aurkitu dira. Zoriak zerikusia zuen joko edo aztikeria erritoak egiten
zituzten antzinako egiptoarrek, grekoek eta erromatarrek. Aurkitu den
dadorik zaharrena K.a. 3.000. urtekoa da.Garai hartako jokalariek, oraingo jokalariek bezalaxe, intuiziozko
ideiaren bat izango zuten gertaera bat betetzea erraza edo nekeza zen jakiteko
. Izan ere, aurkitutako dado batzuk emaitza baten alde alboratuta
daudela ikusi da, eta beste batzuk, irregularrak izan arren, sei aldeak probabilitate
bereko edo ekiprobable egin arte landu ziren. Baina jokoetan
erabiltzen zituzten probabilitate ideia hauek ez zituzten baliatu teoria
matematiko bat osatzeko.Berpizkunde hasieran ezaguera matematiko guztiak deterministak
ziren. Geometria ezaguera jakin eta ziurra zen, eta probabilitatea, berriz,
seguruak ez ziren ezaguerak azaltzeko erabiltzen zen. Bestalde, etorkizuna
asmatzeko ahalmena jainkoen dohaina zen, eta zoria kontrolatu nahi izatea
fedegabetasunaren azalpentzat hartua zen.Berpizkundean hasi ziren zorizko jokoak ikuspegi matematikotik lantzen.
Lehenengo egile eta berritzaile garrantzitsua G. Cardano (1501-1576)
mediku, matematikari eta jokalaria izan zen. Liber de Ludo Aleae liburua
idatzi zuen, eta dado, tortolox eta karta jokoez gainera, bere bizitzan zehar
jokoan izandako esperientziak kontatzen zituen. Galileok (1564-1642) ere
zerbait idatzi zuen dado jokoei buruz, Toscanako printzearen eskariei
erantzun nahian. Baina probabilitatea, gaur egun ezagutzen den eran
behintzat, Fermat (1601-1665) eta Pascal (1623-1662) matematikarien
idazkiekin sortu zen. Bi matematikari frantses hauek zorizko jokoei buruz
eta apustuetako diru banaketekin zerikusia zuten problemekin osatutakogutun sorta bat idatzi zioten elkarri. Fermatek probabilitate bera zuten
emaitzak bilatzen zituen, eta Pascalek jokalariek irabazteko probabilitate
bera izan zezaten jokoaren bilakaerak nolakoa behar zuen izan aztertzen
zuen. Ez zuten gaur egungo probabilitatearen ideia erabiltzen, emaitza
baten eta beste baten probabilitatearen arteko arrazoia baizik. Hau da,
dado bat jaurtitzerakoan 6 ateratzeko probabilitatea seiren bat denik ez
dute esaten, aldiz 6 bat ateratzearen eta ez ateratzearen erlazioa 1 5-en kontra
dela esaten dute.
Huygens (1629-1695) matematikariak Fermaten eta Pascalen ideiak
garatu zituen eta itxaropen matematikoaren ideia azaldu zuen. Geroxeago
Jacques Bernouilli (1654-1705) matematikariak probabilitateari buruzko
lehen tratatu garrantzitsua idatzi zuen : Ars Conjenctandi (1713an argitara
emana). Bertan agertzen dira lehenengo aldiz probabilitatea gertaera
baten maiztasunarekin loturik, edo "a posteriori" probabilitatea, eta simetriaz
ezarritako probabilitatea, edo "a priori" probabilitatea.
XVIII. mendean zehar, Moivre, Bayes eta Condorcet egileek probabilitatearen
alderdi berriak landu edo probabilitatea alor berrietara, adibidez
ekonomiara, zabaldu zuten. Baina probabilitatean egindako aurreramenduak
laburbiltzen dituen eta emaitza berriak eskaintzen dituen hurrengo
tratatu garrantzitsua 1812. urtean Laplace (1749-1827) matematikariak
argitaratutako Theorie analytique des probabilites da. Bertan egilearen izena
daraman probabilitatearen oinarrizko definizioarekin batera probabilitateen
batura eta biderkadura arauak azaltzen dira. Bayes eta Buffon matematikariek
ordu arte lortutako emaitzak ere biltzen ditu, eta probabilitateen
kalkuluari integrazioa aplikatzen dio. Erroreen teoriari dagozkion problemak
ebazteko probabilitatea erabiltzen du. Lan zabala eta emaitza aberatsekikoa
izan zen, baina azpimarratzekoa du zehaztasun falta ere.
XIX. mendean, Gaussek, erroreen teoria hobetu eta banaketa normalaren
dentsitate funtzioa -Gaussen kanpaia- ezagutarazi zuen.
Tchebychef errusiarrak eta Poisson frantziarrak teoria hauek hobetu
zituzten. XIX. mendearen bigarren erditik aurrera probabilitatea biologia
lantzeko erabili zen. Lan hauetan jardun zuten, besteen artean, Galton,
Student, eta Pearson matematikari ingelesek. Halaber, probabilitatea fisikan
eta bereziki termodinamikan erabiltzen hasi zen.
XIX. mendean aurreramendu handiak egin ziren probabilitatean eta
garrantzi handia hartu zuen, eta horrek probabilitatearen oinarri matematiko
sendo baten beharra areagotu zuen. Integrazioaren teoriak, Lebesgue
eta Borelen ideiekin, neurriaren teoriaren oinarriak ezarri zituen. Teoria
honetan oinarriturik Kolmogorov errusiarrak gaur egun onartzen den probabilitatearen
definizio axiomatikoa eman zuen 1933. urtean.
I. Lagin espazioa. Gertaerak. Gertaeren aljebra
Probabilitatei buruzko problema bat ebaztean, aztergai dugun
zorizko saiakuntzak dituen emaitza posible guztien multzoa ezagutu
behar dugu hasteko. Horretarako, lagin espazio delakoa definitu
behar da.Zorizko saiakuntza baten lagin espazioa saiakuntza hori burutzerakoan
lor daitezkeen emaitza guztien multzoa da.• Adibideak:1. Txanpon bat jaurtitzerakoan «aldea» edo «ifrentzua» atera daiteke
. Horiek dira «txanpon bat jaurti» zorizko saiakuntzako lagin
espazioa (E) eratzen duten elementuak : E = {A,+}.2. Dado bat jaurtitzean bada, la, edo 2a, edo 3a, edo 4a, edo
5a, edo 6a aupegiak gora begira daudela gera daiteke dadoa
. Beraz, saiakuntza honen lagin espazioa da : E = {1, 2, 3, 4,
5, G}.3. Zorizko saiakuntza batean dado jaurtiketan 6a atera dadin
dadoa zenbat aldiz jaurti behar den eskatzen da. Seia lehenengo
jaurtialdian, edo bigarren jaurtialdian, edo hirugarrenean aterako
da, edo agian askotan jaurti beharko da dadoa. Beraz, lagin espazioa
1 etik hasita zenbaki arrunten multzoa izango da : E = 11, 2, 3,
4, 5, 6,....}.4. Zorizko saiakuntza batean gezi bat itu edo diana batera jaurti
eta geziak jotzen duen tokitik dianaren erdi-erdiraino dagoen distantzia
zein den eskatzen da. Emaitza edozein zenbaki erreal positibo
izan daiteke, baina nahi izanez gero, E = [0,a] idatzi daiteke,
non a arkuaren irispide gorenaren eta jaurtitzailea dagoen tokitik
dianara dagoen distantziaren arteko batura baino handiagoa den
zenbaki bat den.Beraz, lehenengo bien moduko adibidetan langin espazioko elementu
kopurua finitua, hirugarrena bezalakoetan infinitu zenbakigarria
eta laugarrena bezalakoetan infinitu jarraitua izan daiteke.
Lehenengo hirurenak lagin espazio diskretuak eta laugarrenarena
lagin espazio jarraitua dela esaten da.Zorizko saiakuntza bateko gertaera bat lagin espazioko edozein
azpimultzo da. Zorizko saiakuntza bat egiterakoan, gertaera jakin
bati dagokion emaitza bat ateratzen denean, gertaera hori egiaztatu
dela diogu, eta ateratzen ez bada, ez dela egiaztatu esango dugu.• Adibideak :1. Txanpon bat jaurtitzerakoan, lau gertaera posible ditugu :
«aldea»
2.. tera, «ifrentzua» atera, «aldea edo ifrentzia» atera, eta «ez
aldea eta ez ifrentzua» atera.
Dado bat jaurtitzean atera daitezkeen gertaera posibleenkopurua askoz handiagoa da. Bat 3a ateratzea izango da, {3} ; beste
bat 3 baino txikiagoa ateratzea, {1, 2} ; beste bat zenbaki bikoitia
ateratzea, {2, 4, 6} ; eta beste bat 1, 2, 3, 5 ateratzea, {1, 2, 3, 5} ateratzea. Gerta daiteke, halaber, {1, 2, 3, 4, 5, 6} ateratzea. Dado bat jaurtitzerakoan, guztira, gertaera ditugu.
gertaera ditugu.
Aurreko bien moduko adibideetan, hau da, lagin espazioa finitua denean. E lagin espazioak n elementu baditu, gertaera posibleak E-ren azpimultzo posible guztiak dira, eta beren kopurua
azpimultzo posible guztiak dira, eta beren kopurua da [multzoak n elementu dituenez, n-naka harturiko 2 propietateren ("barnekoa ez izan") errepikatuzko aldakuntzak dira].Lagin espazioko elementuak oinarrizko gertaerak dira. Adibidez,
txanpon bat dugunean {A} eta {+} dira oinarrizko gertaerak.Zorizko saiakuntza batean elementurik ez duen multzoa da ezinezko gertaera, beraz, multzo huts gisa
da [multzoak n elementu dituenez, n-naka harturiko 2 propietateren ("barnekoa ez izan") errepikatuzko aldakuntzak dira].Lagin espazioko elementuak oinarrizko gertaerak dira. Adibidez,
txanpon bat dugunean {A} eta {+} dira oinarrizko gertaerak.Zorizko saiakuntza batean elementurik ez duen multzoa da ezinezko gertaera, beraz, multzo huts gisa adierazten da.
adierazten da.
Saiakuntzan atera daitekeen emaitzarik ez duenez, gertaera hau ez da inoiz egiaztatzen. Gertaera seguru edo gertaera ziurra E lagin espazioa bera da, espazio hori gertaera gisa harturik. Izan ere, zorizko saiakuntzako emaitza posible guztiak hartzen dituenez, beti egiaztatzen da.
Gertaera arteko eragiketak. Gertaeren artean, multzo artean bezalaxe, bilketa, ebaketa eta diferentzia defini daitezke. Gertaera arteko eragiketak azaltzeko, multzo arteko eragiketak azaltzeko erabiltzen diren Vennen diagramak erabiliko dira.
A eta B gertaeren bilketa, gertaera berri bat da. A-n, B-n edo bietan egiaztatzen diren oinarrizko gertaeren bidez eratua.
gertaera berri bat da. A-n, B-n edo bietan egiaztatzen diren oinarrizko gertaeren bidez eratua.
Adibidez, dado bat jaurtitzerakoan gertaeretako bat bikoitia ateratzea da, A= {2,4,6}; beste bat 3 baino txikiagoa ateratzea da, B={1,2} eta A eta B ren bildura,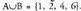 . Diagrama bidez adierazita:
. Diagrama bidez adierazita: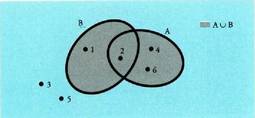 A eta B gertaeren ebaketa,
A eta B gertaeren ebaketa, , beste gertaera berri bat da, A- n eta B-n bietan aldi berean egiaztatzen diren oinarrizko gertaeren bidez eratua. Diagrama bidez adierazita :Aurreko adibidea kontuan harturik:
, beste gertaera berri bat da, A- n eta B-n bietan aldi berean egiaztatzen diren oinarrizko gertaeren bidez eratua. Diagrama bidez adierazita :Aurreko adibidea kontuan harturik: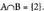 . Diagrama bidez adierazita :
. Diagrama bidez adierazita : A eta B gertaeren diferentzia, A-B, B-n ez daude A-ko oinarrizko gertaeren bidez eraturiko gertaera berri bat da.
A eta B gertaeren diferentzia, A-B, B-n ez daude A-ko oinarrizko gertaeren bidez eraturiko gertaera berri bat da.
Aurreko adibidea kontuan harturik: A-B={4,6}. Diagrama bidez adierazita. A gertaera baten aurkako gertaera. A egiaztatzen ez denean egiaztatzen den eta A egiaztatzen denean egiaztatzen ez den gertaera da. A-ren aurkako gertaera E-A gertaerarekin bat dator, eta A´-ren bidez adierazten da.
A gertaera baten aurkako gertaera. A egiaztatzen ez denean egiaztatzen den eta A egiaztatzen denean egiaztatzen ez den gertaera da. A-ren aurkako gertaera E-A gertaerarekin bat dator, eta A´-ren bidez adierazten da.
Aurreko adibidea kontuan harturik: A´ = {1,3,5} eta B´={3,4,5,6}.Gertaera arteko eragiketen propietateak :Gertaeren bilketak eta ebaketak, eragiketa gisa harturik, trukakortasunaren
legea, elkarketa legea eta banaketa legea betetzen
dituzte, multzo arteko eragiketek bezalaxe :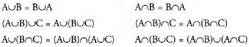 Gertaera baten aurkakoaren aurkakoa hasierako gertaera bera da,
eta Morgan-en legeak betetzen ditu:
Gertaera baten aurkakoaren aurkakoa hasierako gertaera bera da,
eta Morgan-en legeak betetzen ditu:
- Ariketak
1. Idatz ezazu "hiru txanpon jaurti" saiakuntzari dagokion lagin espazioa.2. Zenbat gertaera ditu hiru dago jaurti saiakuntzak?3. Bi txanpon airera jaurtitzen dira. Idatz itzazu gertaera hauek: «alde bat» atera; «bi alde» atera; «alderik ez» atera.4. "Espainiar karta sorta batetik karta bat atera" saiakuntza egiten da. Idatz itzazu gertaera hauek: a) urrea atera; b) erregea atera; c) urrea atera eta erregea atera gertaeren ebaketa ; d) urrea atera eta erregea atera gertaeren bilketa.
Montecarloko iruzurra
Probabilitatearen eta maiztasun erlatiboaren arteko erlazioa dela eta, zenbait jokalarik uste dute aurreko emaitzek ondorengo emaitzetan eragina dutela. Adibidez txanpon bat ehun aldiz jaurti ondoren, ehun alditan, jarraian, aldea atera bada, hurrengo jaurtialdian ifrentzua ateratzea berriro aldea ateratzea baino gertagarriagoa dela uste dute. Bere arrazonamendua hau da : "aldeare eta ifrentzuaren maiztasuna beraien probabilitatea bezala 1/2 denez, aldea askotan atera denez, gauzak berdintzeko, orain askotan aterako da ifrentzua".
Montecarloko iruzurra deitutako arrazonamendu honek ez du kontuan hartzen limite bat ezin dela kopuru finitu batetik abiatuta ezarri.
Milioi bat aldiz segidan aldea atera arren, limiteak 112 izaten jarrai dezake, izan ere, teorian behintzat, oraindik infinitu saiakuntza ditugu egiteko eta hauekin alderatuz, milioi bat ezer gutxi da.
Are gehiago, kopuru handien legeak, baldintza orokorretan, emaitza posibleen maiztasun erlatiboak egonkortu egiten direla ziurtatzeaz gainera, maiztasunabsolutuak probabilitatea eta saiakuntza kopuruen arteko biderkaduraren
arabera espero den maiztasun absolutuetatik gero eta gehiago urruntzen
direla ere ziurtatzen du. Alegia alde eta ifrentzu kopuruen arteko aldea
gero eta handiagoa da. Baina diferentzia hori saiakuntza kopuru osoa baino
mantsoago handitzen da, beraz maiztasun erlatiboa egonkortu egiten da.Aldea ifrentzua baino askoz aldi gehiagotan ateratzen denean agian
txanpona alboratua eta faltsua dela eta oinarrizko bi gertaerak ez dutela
probabilitate bera da atera dezakegun ondorio bakarra. Hori horrela
balitz, berriro aldea ateratzearen alde egin beharko genuke apustu. Baina,
txanpona alboratua dagoenik ere ezin da ziurtatu. Konfiantza handiko
hipotesia izan arren, fisikan bilatu beharko litzateke ziurtasuna, adibidez
grabitate-zentroan, eta ez estatistikan.
II. Probabilitatea
Zorizko saiakuntza batean, gertaera batek ateratzeko duen erraztasuna
adieraziko duen zenbakia gertaera horren probabilitatea
dela esaten da. Askotan egin den saiakuntza bat bada, gertaera
baten maiztasun erlatiboa hartzen da gertaera horren probabilitatetzat.
Hitzarmen hau kopuru handien legea deritzanaren ondorio
bat da, izan ere, zenbat eta saiakuntza gehiago egin orduan eta
egonkorragoak dira maiztasun erlatiboak. Bide hau jarraituz, gertaera
baten P(S) probabilitatea n saiakuntza egin ondoren f(S) gertaera
horrek duen maiztasun absolututik abiaturik lortuko litzateke,
limite baten bidez : Beste metodo bat emaitza posibleen artean dagoen simetria edo
baliokidetasuna oinarri hartzea da. Baina bi kasuek egoera jakin
bat dutenez abiapuntu, ez dute probabilitatearen definizioa orokortzeko
ziurtasunik ematen.Bestalde, probabilitateak lehenxeago ikusi ditugun gertaera arteko
eragiketeen osagarri izan behar du ; hau da, probabilitateen
batura gertaeren bilketarekin eta ebaketarekin erlazionatzen dituen
zenbait propietate beharko ditu bete.Maiztasun erlatiboaren ideiari jarraituz propietate jakin batzuk
izan ditzan, ondoko definizio axiomatiko hau hartu da :Probabilitatea
Beste metodo bat emaitza posibleen artean dagoen simetria edo
baliokidetasuna oinarri hartzea da. Baina bi kasuek egoera jakin
bat dutenez abiapuntu, ez dute probabilitatearen definizioa orokortzeko
ziurtasunik ematen.Bestalde, probabilitateak lehenxeago ikusi ditugun gertaera arteko
eragiketeen osagarri izan behar du ; hau da, probabilitateen
batura gertaeren bilketarekin eta ebaketarekin erlazionatzen dituen
zenbait propietate beharko ditu bete.Maiztasun erlatiboaren ideiari jarraituz propietate jakin batzuk
izan ditzan, ondoko definizio axiomatiko hau hartu da :Probabilitatea gertaera multzoaren eta [0,1] tarte errealaren arteko aplikazio bat da, eta zera betetzen du :
gertaera multzoaren eta [0,1] tarte errealaren arteko aplikazio bat da, eta zera betetzen du : , non E gertaera segurua den
, non E gertaera segurua den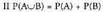 da, baldin eta
da, baldin eta
Probabilitatearen definizioaren ondorioak :
1.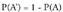 da. Izan ere,
da. Izan ere, da, eta gertaera bat eta bere aurkakoa beti bateraezinak dira.2.
da, eta gertaera bat eta bere aurkakoa beti bateraezinak dira.2. . Izan ere
. Izan ere gertaera ziurraren aurkakoa da, eta
gertaera ziurraren aurkakoa da, eta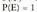 da.3. Baldin eta
da.3. Baldin eta bada
bada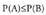 izango da, izan ere
izango da, izan ere da.4.Baldin eta
da.4.Baldin eta gertaerak bateraezinak badira,
gertaerak bateraezinak badira, Bigarren axioma orokortuz.5. Baldin eta A eta B bi gertaera bateraezin ez badira, orduan
Bigarren axioma orokortuz.5. Baldin eta A eta B bi gertaera bateraezin ez badira, orduan da.Izan ere,
da.Izan ere,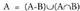 eta
eta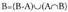 dira, non A-B eta B-A elkarren artean eta AnB-rekin bateraezinak diren.
dira, non A-B eta B-A elkarren artean eta AnB-rekin bateraezinak diren.
Gainera 6. Lagin espazio finitu bat oinarrizko gertaeren bilketa gisa onar daiteke. Kasu horretan, oinarrizko gertaera guztiei dagozkien probabilitate guztien batura 1 da.
6. Lagin espazio finitu bat oinarrizko gertaeren bilketa gisa onar daiteke. Kasu horretan, oinarrizko gertaera guztiei dagozkien probabilitate guztien batura 1 da.
Baldin eta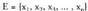 bada, orduan
bada, orduan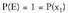
III. Laplaceren erregela
Simetria bidez, estatistika bidez edo beste bideren bat erabiliz,
narrizko gertaera guztiek probabilitate bera dutela edo gertaera
zztiak ekiprobableak direla, hau da P(x 1 ) = P(x 2 ) = P(x3 ) =... =
;x„) dela ziurta daitekeenean, xi guztien ordez x 1 jar daiteke : P(E)
P(x 1 ) + P(x 1 ) + P(x 1 ) +... + P(x l ) = n P(x 1 ) = 1 P
P dela ziurta daitekeenean,
dela ziurta daitekeenean, guztien ordez
guztien ordez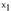 jar daiteke:
jar daiteke: Horren arabera,
Horren arabera, izango da. Eta gauza bera gertatuko da edozein
izango da. Eta gauza bera gertatuko da edozein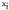 -rekin. Beraz, lagin espazioa finitua bada eta gertaerak ekiprobableak badira, edozein i-rentzat
-rekin. Beraz, lagin espazioa finitua bada eta gertaerak ekiprobableak badira, edozein i-rentzat izango da.Ondorio hau 4. propietatearekin elkartuz, Laplaceren erregela
rtzen da. Horrela dio Laplaceren legeak :
izango da.Ondorio hau 4. propietatearekin elkartuz, Laplaceren erregela
rtzen da. Horrela dio Laplaceren legeak :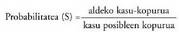 Formula hau sarritan erabiltzen da probabilitatean, eta bereziki
koarekin zerikusia duten problemetan.• Adibideak:40 karta dituen sorta bateko karta guztiak behar bezala eginda daude eta probabilitate bera dute. Bila ezazu :a) Karta bat ateratzerakoan, karta hori bateko urrea izatearen probabilitatea.Laplaceren erregela erabiliz, 40 karta posibletik bakarra da aldeko karta, beraz:P (bateko urrea) =
Formula hau sarritan erabiltzen da probabilitatean, eta bereziki
koarekin zerikusia duten problemetan.• Adibideak:40 karta dituen sorta bateko karta guztiak behar bezala eginda daude eta probabilitate bera dute. Bila ezazu :a) Karta bat ateratzerakoan, karta hori bateko urrea izatearen probabilitatea.Laplaceren erregela erabiliz, 40 karta posibletik bakarra da aldeko karta, beraz:P (bateko urrea) = b) Karta bat ateratzerakoan, karta hori urrea izatearen probabilitatea.Laplaceren erregela erabiliz, 40 karta posibletik 10 dira aldeko, beraz:
b) Karta bat ateratzerakoan, karta hori urrea izatearen probabilitatea.Laplaceren erregela erabiliz, 40 karta posibletik 10 dira aldeko, beraz: c) Karta bat ateratzerakoan, karta hori batekoa izatearen probabilitatea
.Laplaceren erregela erabiliz, 40 karta posibletatik 4 dira aldekoak,
beraz :P(batekoa) =
c) Karta bat ateratzerakoan, karta hori batekoa izatearen probabilitatea
.Laplaceren erregela erabiliz, 40 karta posibletatik 4 dira aldekoak,
beraz :P(batekoa) =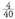 d) Karta bat ateratzerakoan, karta hori batekoa ez izatearen probabilitatea
.Bateko bat ez ateratzea, bateko bat ateratzearen aurkakoa da,
beraz, lehenengo propietatea erabiliz :
d) Karta bat ateratzerakoan, karta hori batekoa ez izatearen probabilitatea
.Bateko bat ez ateratzea, bateko bat ateratzearen aurkakoa da,
beraz, lehenengo propietatea erabiliz :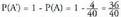 Bateko ez diren 36 karta dira, beraz, Laplaceren erregela erabiliz,
Bateko ez diren 36 karta dira, beraz, Laplaceren erregela erabiliz, da batekoa ez ateratzea gertaeraren probabilitatea.e) Karta bat ateratzerakoan, karta hori batekoa edo bikoa izatearen
probabilitatea.4 bateko eta 4 biko ditugu, beraz Laplaceren erregelaren arabera
da batekoa ez ateratzea gertaeraren probabilitatea.e) Karta bat ateratzerakoan, karta hori batekoa edo bikoa izatearen
probabilitatea.4 bateko eta 4 biko ditugu, beraz Laplaceren erregelaren arabera .
.
Edo bestela, bateko edo biko gertaera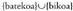 da, eta gainera
da, eta gainera da.Beraz,
da.Beraz,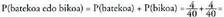 karta hori batekoa edo urrea izatearen probabilitatea.Urrea edo batekoa gertaera
karta hori batekoa edo urrea izatearen probabilitatea.Urrea edo batekoa gertaera gertaeraren berdina da.Baina
gertaeraren berdina da.Baina eta bigarren axioma erabili ezin denez, 5. propietatea erabiliko da :
eta bigarren axioma erabili ezin denez, 5. propietatea erabiliko da : Edo bestela, 10 urre eta beste hiru bateko ditugu, bateko urrea urreen sailaren barruan dagoelako. Beraz, guztira 40 kasu posibletik 13 gertaera aldeko ditugu, hori dela eta :
Edo bestela, 10 urre eta beste hiru bateko ditugu, bateko urrea urreen sailaren barruan dagoelako. Beraz, guztira 40 kasu posibletik 13 gertaera aldeko ditugu, hori dela eta : Laplaceren erregela erabili ahal izateko, ongi ezagutu behar da lagin espazioa, eta gainera oinarrizko gertaera guztiek probabilitate bera dutela ziurtatu behar da. Bi baldintza hauek elkarri lotuta daude, eta zehazten ez badira erroreak sor daitezke.• Adibideak :1. Bi txanpon berdin jaurtitzen dira. Bila itzazu gertaera hauen
probabilitateak : a) bi alde ateratzea, b) alde bat eta ifrentzu bat ateratzea,
eta c) bi ifrentzu ateratzea.Bi txanponak berdinak izan arren, oinarrizko gertaerak ekiprobableak
izatea nahi bada, bere lagin espazioa {AA, A+, +A, ++} da,
eta ez {2 alde, alde 1 eta ifrentzu 1, 2 ifrentzu}, izan ere «alde bat
eta ifrentzu bat» gertaera bi eratara lor daiteke (lehenengo txanponean
aldea eta bigarrenean ifrentzua atereaz, edo lehenengoan
ifrentzua eta bigarrenean aldea atereaz). Bereizi ezin badira ere bi
txanpon ditugu.Beraz, probabilitateak hauek izango dira :
Laplaceren erregela erabili ahal izateko, ongi ezagutu behar da lagin espazioa, eta gainera oinarrizko gertaera guztiek probabilitate bera dutela ziurtatu behar da. Bi baldintza hauek elkarri lotuta daude, eta zehazten ez badira erroreak sor daitezke.• Adibideak :1. Bi txanpon berdin jaurtitzen dira. Bila itzazu gertaera hauen
probabilitateak : a) bi alde ateratzea, b) alde bat eta ifrentzu bat ateratzea,
eta c) bi ifrentzu ateratzea.Bi txanponak berdinak izan arren, oinarrizko gertaerak ekiprobableak
izatea nahi bada, bere lagin espazioa {AA, A+, +A, ++} da,
eta ez {2 alde, alde 1 eta ifrentzu 1, 2 ifrentzu}, izan ere «alde bat
eta ifrentzu bat» gertaera bi eratara lor daiteke (lehenengo txanponean
aldea eta bigarrenean ifrentzua atereaz, edo lehenengoan
ifrentzua eta bigarrenean aldea atereaz). Bereizi ezin badira ere bi
txanpon ditugu.Beraz, probabilitateak hauek izango dira : ; P(alde bat eta ifrentzu bat) =
; P(alde bat eta ifrentzu bat) = 2. Orain kaleko joko bat azalduko dugu: kolorez izan ezik gainerako
guztian berdinak diren hiru txartel ditugu. Txartel baten bi
aldeak zuriak dira, bigarrenak berriz alde bat zuria eta bestea gorria
du, eta hirugarrenak gorriak ditu bi aldeak. Txartel bat aukeratzenda zoriz eta mahai gainean ipintzen da, txartelaren alde bateko
kolorea ikus daitekeela. Eman dezagun ikusten den aldea gorria
dela. Apustua egiten duenak dio : "Ikusten den aldea gorria denez,
txartela gorria-gorria edo gorria-zuria izan daiteke ; nik gorriagorriaren
alde egingo dut apustu". Froga ezazu joko hau ez dela
zuzena.Azaltzen diren gertaerak ez dira txartel gorria-gorria, gorria-zuria edo zuria-zuria ateratzea, baizik eta txartel bat atera eta alde bat gora begira jartzea. Hori horrela izanik, aukeratzen dugun txartelaren eta ikusten den aldearen arabera 6 egoera desberdin ditugu. Sei horietatik aldea zuria duten 3ak bazter ditzakegu kasu honetan, zoriz atera dugun txartelak gorria baitu goialdea. Gelditzen zaizkigun hiruak hauek dira : gorria-gorria, alde bietako bat goialdean dela, gorria-gorria beste aldea goialdean dela, eta gorria-zuria, alde gorria goialdean daukala. Beraz ikusten ez den aldea gorria izatearen probabilitatea
2. Orain kaleko joko bat azalduko dugu: kolorez izan ezik gainerako
guztian berdinak diren hiru txartel ditugu. Txartel baten bi
aldeak zuriak dira, bigarrenak berriz alde bat zuria eta bestea gorria
du, eta hirugarrenak gorriak ditu bi aldeak. Txartel bat aukeratzenda zoriz eta mahai gainean ipintzen da, txartelaren alde bateko
kolorea ikus daitekeela. Eman dezagun ikusten den aldea gorria
dela. Apustua egiten duenak dio : "Ikusten den aldea gorria denez,
txartela gorria-gorria edo gorria-zuria izan daiteke ; nik gorriagorriaren
alde egingo dut apustu". Froga ezazu joko hau ez dela
zuzena.Azaltzen diren gertaerak ez dira txartel gorria-gorria, gorria-zuria edo zuria-zuria ateratzea, baizik eta txartel bat atera eta alde bat gora begira jartzea. Hori horrela izanik, aukeratzen dugun txartelaren eta ikusten den aldearen arabera 6 egoera desberdin ditugu. Sei horietatik aldea zuria duten 3ak bazter ditzakegu kasu honetan, zoriz atera dugun txartelak gorria baitu goialdea. Gelditzen zaizkigun hiruak hauek dira : gorria-gorria, alde bietako bat goialdean dela, gorria-gorria beste aldea goialdean dela, eta gorria-zuria, alde gorria goialdean daukala. Beraz ikusten ez den aldea gorria izatearen probabilitatea da, eta ikusten ez den aldea zuria izatearen probabilitatea
da, eta ikusten ez den aldea zuria izatearen probabilitatea
Konbinatoria erabiliz ebatzitako adibideak:
1. Zenbatekoa da 10 txanpon jaurtitzerakoan 2 alde ateratzearen
probabilitatea?Zenbat kasu desberdin ditugun jakiteko, hamar txanponak ordenatuta
daudela pentsatuko dugu eta txanpon bakoitzean aldea edo
ifrentzu atera daitekeela gogoan hartuko dugu. Alde kopurua eta
ifrentzu kopurua desberdinak badira, edo hauek txanpon desberdinetan
ateratzen badira, emaitzak desberdinak izango dira. Aldea
edo ifrentzua txanpon batean baino gehiagotan errepikatuko da,
eta ikusi dugun bezala ordenak bere garrantzia du, beraz lOnaka
harturiko 2 elementuren errepikatuzko aldakuntzak dira, VR2,1o ,
hau da 2'°=1024.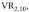 hau da
hau da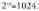 Aldeko kasu denek 2 alde izan behar dituzte. Beraz, aldea duten bi txanponak dira kasu bat bestetik bereizten dutenak. Beraz, konbinazioak izango dira :
Aldeko kasu denek 2 alde izan behar dituzte. Beraz, aldea duten bi txanponak dira kasu bat bestetik bereizten dutenak. Beraz, konbinazioak izango dira : . Laplaceren erregela jarraituz,
. Laplaceren erregela jarraituz, izango da probabilitatea.2. Idazkari batek lau bezerorentzat lau gutun idazten ditu, elkarren
desberdinak lauak, eta dagozkien gutunazalak prestatzen ditu.
izango da probabilitatea.2. Idazkari batek lau bezerorentzat lau gutun idazten ditu, elkarren
desberdinak lauak, eta dagozkien gutunazalak prestatzen ditu.
Hurrengo egunean ez ditu idazkariak bidaltzen, beste lankide
batek baizik, eta helbideari begiratu gabe gutunazal banatan sartzen
ditu gutun bakoitza. Zenbatekoa da bezero bakoitzak beretzat
idatzitako gutuna jasotzeko duen probabilitatea?Lau gutun eta lau gutunazal direnez, gutun eta gutunazalen arteko parekatze kasu posibleak bat datoz gutunek izan ditzaketen ordena posbileen kopuruarekin, kontuan harturik gutunazalak edozein ordenatan daudela. Ordenak garrantzia duenez eta gutun guztiak gutunazal banatan sartzen direnez, 4 elementuren permutazioek emango dizkigute kasu posible guztiak ; hau da, Aldeko kasua bakarra da, hau da gutunak eta gutunazalak zein
berearekin parekatzen direnean.Beraz, probabilitatea :
Aldeko kasua bakarra da, hau da gutunak eta gutunazalak zein
berearekin parekatzen direnean.Beraz, probabilitatea : .
.
3. Karta sorta batetik lau karta ateratzen dira hurrenez hurren.
Zenbatekoa da bateko bat, errege bat, zaldun bat eta txota bat (ordena honetan) ateratzearen probabilitatea?Kasu posibleak 40 elementuren artean 4 hartu eta hauek ordenatzeko dauden aukera guztiak izango dira, baina errepikatzen ez direnez, aldakuntzak izango dira : 4 bateko, 4 errege, 4 zaldun eta 4 txota ditugula kontuan izanik,
aldeko kasuak hauek izango dira :
4 bateko, 4 errege, 4 zaldun eta 4 txota ditugula kontuan izanik,
aldeko kasuak hauek izango dira : Probabilitatea hau izango da :
Probabilitatea hau izango da :
- Ariketak
5. Poltsa batean kolorez ezik bestelako guztian berdinak diren 3 puxtarri zuri, 2 gorri eta 3 urdin ditugu. Bila itzazu puxtarri bat ateratzerakoan, puxtarri hori : a) urdina izatearen probabilitatea ; b) gorria izatearen probabilitatea ; c) zuria ez izatearen probabilitatea.6. Hiru txanpon jaurtitzen dira. Bila ezazu zenbatekoa den : a) alde bat eta bi ifrentzu ateratzearen probabilitatea ; b) hiru ifrentzu ateratzearen probabilitatea ; c) gutxienez ifrentzu bat ateratzearen probabilitatea ; d) ifrentzu baino alde gehiago ateratzearen probabilitatea.7. Bi dado jaurtitzen dira. Bila ezazu zenbatekoa den: a) bi seiko ateratzearen probabilitatea ; b) seikorik ez ateratzearen probabilitatea ; c) gutxienez seiko bat ateratzearen probabilitatea; d) batura 5 ateratzearen probabilitatea ; e) batura 7 ateratzearen probabilitatea; f) batura 12 ateratzearen probabilitatea; g) batura 14 ateratzearen probabilitatea.8. Poltsa batean letik hasi eta 10eraino zenbakiturik dauden hamar puxtarri ditugu. Pertsona batek puxtarri bat hartu, zenbakia ikusi eta poltsan sartzen du berriro. Puxtarriak ongi nahastu ondoren beste pertsona batek puxtarri bat ateratzen du. Zenbatekoa da: a) bi puxtarriek zenbaki bera izatearen probabilitatea; b) bi puxtarriak bakoitiak izatearen probabilitatea ; c) bi puxtarrien zenbakien batura 10 izatearen probabilitatea. Lehenengo puxtarria ateratzen duenak poltsara itzuliko ez balu, zenbatekoak lirateke aurreko hiru galderei dagozkien probabilitateak?9. Toscanako Dukeak Galileori jarritako ariketa : hiru dado jaurtitzerakoan, sei batuketa desberdinen bidez lor daiteke 10 batura (1+3+6, edo 2+2+6, edo 1+4+5, edo 2+3+5, edo 2+4+4, edo 3+3+4), eta beste sei era desberdinetan 9 batura (1+2+6, edo 1+3+5, edo 1+4+4, edo 2+2+5, edo 2+3+4, edo 3+3+3). Baina 10 batura lortzea 9 batura baino errazago ateratzen dela ikusten da. Zergatik?10. Mereko zaldunak Pascali jarri zion lehenengo ariketa : zer da errazagoa, dado bat lau aldiz jaurtiz gutxienez 6ko bat ateratzea edo bi dado 24 aldiz jaurtiz gutxienez bi seiko ateratzea?
IV Baldintzazko probabilitatea
Batzuetan, zorizko saiakuntza baten probabilitate ikasketa egiteko
lagin espazio osoa hartu ordez lagin espazio horren zati bat
hartzen da. Hau, interesgarria izan daiteke batez ere saiakuntza
bi zatitan bana daitekeenean, baina beste kasu batzuetan ere egiten
da.Eman dezagun, adibidez, alboratua dagoen dado baten alde
bakoitzari dagokion probabilitatea ezaguna dugula : "Dado bat jaurti" zorizko saiakuntzan bi gertaera hartuko ditugu
kontuan : A, hau da bikoitia ateratzea, A = {2, 4, 6} ; eta B, 2 eta
5-en artean egotea, 2 eta 5 barne direlarik, B={2, 3, 4, 5}. A-ren
probabilitatea P(A) = 0,15 + 0,20 + 0,17 = 0,5 da. Eta B-ren probabilitatea
P(B) = 0,15 + 0,20 + 0,18 + 0,15 = 0,68 da.• baldintzaren mendeko A-ren probabilitatea B-ko zenbakiak bakarrik (2, 3, 4 eta 5) kontuan harturik dadoa jaurtitzean zenbaki bikoitia ateratzearen probabilitatea da. P(
"Dado bat jaurti" zorizko saiakuntzan bi gertaera hartuko ditugu
kontuan : A, hau da bikoitia ateratzea, A = {2, 4, 6} ; eta B, 2 eta
5-en artean egotea, 2 eta 5 barne direlarik, B={2, 3, 4, 5}. A-ren
probabilitatea P(A) = 0,15 + 0,20 + 0,17 = 0,5 da. Eta B-ren probabilitatea
P(B) = 0,15 + 0,20 + 0,18 + 0,15 = 0,68 da.• baldintzaren mendeko A-ren probabilitatea B-ko zenbakiak bakarrik (2, 3, 4 eta 5) kontuan harturik dadoa jaurtitzean zenbaki bikoitia ateratzearen probabilitatea da. P( ) idazten da. B-n dauden A-ko elementuak 2 eta 4 dira, eta P(B) = 0,68 da. Orduan,
) idazten da. B-n dauden A-ko elementuak 2 eta 4 dira, eta P(B) = 0,68 da. Orduan,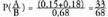 .
B gertaera baten mendeko A gertaera baten probabilitatearen definizio orokorra da:
.
B gertaera baten mendeko A gertaera baten probabilitatearen definizio orokorra da: Eta A gertaera B gertaerari buruz askea edo independentea dela esaten da baldin eta
Eta A gertaera B gertaerari buruz askea edo independentea dela esaten da baldin eta betetzen bada.Aurreko adibidearen arabera :
betetzen bada.Aurreko adibidearen arabera :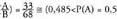 Baina dado baten alde guztiek probabilitate bera dutenean, P (bikoitia) = 0,5 da ;
Baina dado baten alde guztiek probabilitate bera dutenean, P (bikoitia) = 0,5 da ;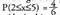 da, eta
da, eta Beraz,
Beraz, Alegia, bi gertaerak independenteak dira.• gertaera baten mendeko probabilitatea benetako probabilitatea
da, non B gertaera ziur edo segurua den. Hain zuzen, bete
beharreko axioma guztiak betetzen ditu B gertaerak baldintzaturiko
probabilitateak.1.
Alegia, bi gertaerak independenteak dira.• gertaera baten mendeko probabilitatea benetako probabilitatea
da, non B gertaera ziur edo segurua den. Hain zuzen, bete
beharreko axioma guztiak betetzen ditu B gertaerak baldintzaturiko
probabilitateak.1.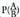 probabilitatea 0 eta 1 balioen artean dago,
probabilitatea 0 eta 1 balioen artean dago, delako eta biak positiboak direlako.2.
delako eta biak positiboak direlako.2.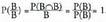 . Beraz, B gertaera segurua da.3. C eta D bateraezinak badira,
. Beraz, B gertaera segurua da.3. C eta D bateraezinak badira, izango da.Hain zuzen, bilketarekiko ebaketaren banatze propietatea erabiliz :
izango da.Hain zuzen, bilketarekiko ebaketaren banatze propietatea erabiliz : inserted text
inserted text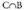 eta
eta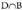 ere bateraezinak dira, eta P-ren hasierako probabilitateari bigarren axioma aplikatuz :
ere bateraezinak dira, eta P-ren hasierako probabilitateari bigarren axioma aplikatuz : Beraz,
Beraz,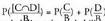 da, eta B gertaerak baldintzatutako probabilitateak probabilitate matematiko baten axioma guztiak betetzen ditu.Propietateak : Definizioa beste era honetara idatz daiteke :
da, eta B gertaerak baldintzatutako probabilitateak probabilitate matematiko baten axioma guztiak betetzen ditu.Propietateak : Definizioa beste era honetara idatz daiteke : A gertaera B gertaerarekiko independentea bada, orduan :
A gertaera B gertaerarekiko independentea bada, orduan : A gertaera B gertaerarekiko independentea bada, orduan B gertaera A gertaerarekiko independentea da. Hain zuzen, Baldin eta
A gertaera B gertaerarekiko independentea bada, orduan B gertaera A gertaerarekiko independentea da. Hain zuzen, Baldin eta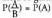 bada,
bada, izango da.Eta horrela:
izango da.Eta horrela: Beraz, Bgertaera A gertaerarekiko independentea da.Baldintzazko probabilitatea hiru edo gertaera gehiago direnean
ere betetzen da. Halakoetan zera egiaztatzen da :
Beraz, Bgertaera A gertaerarekiko independentea da.Baldintzazko probabilitatea hiru edo gertaera gehiago direnean
ere betetzen da. Halakoetan zera egiaztatzen da :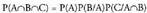 Gertaera independenteak badira:
Gertaera independenteak badira: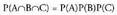 Adibide bat erabiliz argituko dugu hau. Iaz matrikulatutako
100.000 automobilek izandako istripuak aztertu dira. Automobil
hauek A, B eta C markakoak dira, eta marka bakoitzak ondoko
taulan adierazten den istripu kopurua izan du :
Adibide bat erabiliz argituko dugu hau. Iaz matrikulatutako
100.000 automobilek izandako istripuak aztertu dira. Automobil
hauek A, B eta C markakoak dira, eta marka bakoitzak ondoko
taulan adierazten den istripu kopurua izan du : Aztertutako automobil guztien artean bat aukeratzen da zoriz. a)
Zenbatekoa da A markakoa, B markakoa, edo C markakoa izatearen
probabilitatea? b) Zein markakoa da seguruena?Maiztasun erlatiboak probabilitate gisa har daitezkeenez, zenbatekoa
da P(A), P(A/Is), P(IsEz/A) eta zer esanahi du bakoitzak?Problema ebazteko, guztizkoen zutabea eta errenkada erantsiko
zaizkio taulari :
Aztertutako automobil guztien artean bat aukeratzen da zoriz. a)
Zenbatekoa da A markakoa, B markakoa, edo C markakoa izatearen
probabilitatea? b) Zein markakoa da seguruena?Maiztasun erlatiboak probabilitate gisa har daitezkeenez, zenbatekoa
da P(A), P(A/Is), P(IsEz/A) eta zer esanahi du bakoitzak?Problema ebazteko, guztizkoen zutabea eta errenkada erantsiko
zaizkio taulari : Beraz
Beraz Markarik seguruena zein den jakiteko, marka bakoitzak zenbat istripu izan dituen aztertu behar da, istripua izatearen probabilitateak kalkulatuz.
Markarik seguruena zein den jakiteko, marka bakoitzak zenbat istripu izan dituen aztertu behar da, istripua izatearen probabilitateak kalkulatuz. Probabilitaterik txikiena C markarena denez, C da markarik
seguruena.P(A) = 0,5 berdintzak zoriaren arabera hartutako automobila A
markakoa izatearen probabilitatea 0,5 dela esan nahi du.
Probabilitaterik txikiena C markarena denez, C da markarik
seguruena.P(A) = 0,5 berdintzak zoriaren arabera hartutako automobila A
markakoa izatearen probabilitatea 0,5 dela esan nahi du.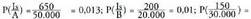 berdintzak istripua izan duten automobilen artean bat zoriz hartzen bada, automobil hori A markakoa izatearen probabilitatea 0,65 dela esan nahi du.
berdintzak istripua izan duten automobilen artean bat zoriz hartzen bada, automobil hori A markakoa izatearen probabilitatea 0,65 dela esan nahi du.
V. Probabilitatea, saiakuntza elkartua denean
Egoera askotan, ariketaren zailtasuna murriztu egiten da saiakuntza
bakar baten moduan hartu ordez bi edo saiakuntza desberdin
gehiagoz osaturiko saiakuntza gisa hartzen bada. Halakoetan,
zorizko saiakuntzaren probabilitatea, emaitza partzialen probabilitatetan
bana daiteke. Oro har, saiakuntza batean, zati bati dagokion
probabilitatea kalkulatzerakoan, aurretik izandako emaitzak
kontuan hartu behar dira, probabilitate horren kalkuluan eraginaizan dezaketelako, baina hala eta guztiz ere, errazagoa izaten da
saiakuntza elkartu gisa hartzea."Hiru txanpon jaurti" saiakuntzaren ordez, "Txanpon bat hiru aldiz jaurti" saiakuntza elkartua har daiteke. Kasu honetan gainera, bigarren edo hirugarren jaurtialdian ateratzen den emaitzak ez du zerikusirik izango aurretik atera denarekin ; hau da, hiru jaurtialdiak independenteak balira bezala har daitezke. Hiru alde ateratzearen probabilitatea jakin nahi bada, lehenengo jaurtialdian aldea ateratzearen probabilitatea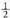 da, eta berdina beste bi jaurtialdietan ere, beraz :
da, eta berdina beste bi jaurtialdietan ere, beraz : Ariketa hau Laplaceren erregela erabiliz landu izan bagenu, gauza bera aterako litzake, izan ere, kasu posibleak
Ariketa hau Laplaceren erregela erabiliz landu izan bagenu, gauza bera aterako litzake, izan ere, kasu posibleak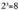 izango genituzke eta aldeko kasu bakarra, beraz
izango genituzke eta aldeko kasu bakarra, beraz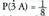 .
.
Saiakuntza elkartu baten oinarrizko saiakuntzak beraien artean independenteak ez direnean ere, saiakuntza horren deskonposaketak kalkuluak erraz ditzake, baina gogoan izan behar da bigarren zatitik aurrera lortzen diren probabilitateek aurrekoak kontuan hartu behar dituztela.40 karta dituen karta sorta batetik bi karta ateratzen dira, eta biak urreak izatearen probabilitatea zenbatekoa den jakin nahi da. Horretarako, hasteko karta bat aterako dugu, eta gero beste bat ; hau da, saiakuntza bitan banatuko dugu. Kasu honetan, bigarren ateraldiari dagokion probabilitatea lehenengo ateraldian lortutako probabilitatearen mende dago ; izan ere, bigarren ateraldia egiterakoan lehenengoan atera dugun karta ezingo dugu kontuan hartu. Lehenengo karta urrea izatearen probabilitatea da. Baina lehenengoa urrea bada, orain karta sortan guztira 39 karta ditugu eta hauetatik 9 dira urre. Orduan, probabilitatea hau izango da :
da. Baina lehenengoa urrea bada, orain karta sortan guztira 39 karta ditugu eta hauetatik 9 dira urre. Orduan, probabilitatea hau izango da : Ariketa hau ere Laplaceren erregela erabiliz egin daiteke. 40 kartako sorta batetik bi karta ateratzeko dauden era desberdin guztiak izango dira kasu posibleak. Aldi berean ateratzen direnez, ordenak ez du axola, beraz, binaka harturiko 40 elementuren konbinazioak izango dira; hau da:
Ariketa hau ere Laplaceren erregela erabiliz egin daiteke. 40 kartako sorta batetik bi karta ateratzeko dauden era desberdin guztiak izango dira kasu posibleak. Aldi berean ateratzen direnez, ordenak ez du axola, beraz, binaka harturiko 40 elementuren konbinazioak izango dira; hau da: . Aldeko kasuak lortzeko, 10urretik 2 aukeratu behar ditugu. Eta orain ere ordenak ez du axola ; beraz, binaka harturiko 10 elementuren konbinazioa izango da ; hau da:
. Aldeko kasuak lortzeko, 10urretik 2 aukeratu behar ditugu. Eta orain ere ordenak ez du axola ; beraz, binaka harturiko 10 elementuren konbinazioa izango da ; hau da: . Hori horrela izanik, probabilitatea ondo- (2. 1) ten aditzera ematen dena izango da :
. Hori horrela izanik, probabilitatea ondo- (2. 1) ten aditzera ematen dena izango da :
Zuhaitz diagramak
Probabilitate ariketa bat saiakuntza elkartu gisa hartzen denean, zuhaitz diagramek problemaren ebazpena erraz dezakete. Hasteko, saiakuntzaren lehenengo deskonposaketari dagokio balio bakoitza adar batean jarriko dugu. Adar hauetako bakoitzetik, saiakuntzaren bigarren deskonposaketak dituen balio bezainbeste adar berri aterako dira, eta horrela saiakuntza erabat deskonposatu arte. Ondoren, adar bakoitzari zein probabilitate dagokio idatziko dugu, horretarako balioaren aurreko emaitzak,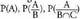 etab., kontuan harturik.
etab., kontuan harturik.
• Adibideak :1. UDARA hitzaren bi letra zoriaren arabera hartuz, zenbatekoa da UR ateratzearen probabilitatea? Gertaera horren probabilitatea UR hitzari dagokion adarretako
emaitzen biderkadura eginez lortzen da; kasu honetan : (1/5)(1/4).
Gertaera horren probabilitatea UR hitzari dagokion adarretako
emaitzen biderkadura eginez lortzen da; kasu honetan : (1/5)(1/4).
Adibide honetan eta honen antzekoetan, azken emaitzarekin zerikusirik
ez duten adarrak osa gabe utz daitezke.2. Poltsa batean 3 puxtarri zuri, 3 puxtarri gorri eta 4 puxtarri
urdin daude. Elkarren segidan hiru puxtarri ateratzen dira. Bila
ezazu zenbatekoa den lehenengoa gorria, bigarrena zuria eta hirugarrena
urdina ateratzearen probabilitatea.Horretarako zuhaitz diagrama egingo dugu : Dagokien adarretako emaitzen arteko biderkadura e mez lortuko dugu probabilitatea. Oraingo honetan:
Dagokien adarretako emaitzen arteko biderkadura e mez lortuko dugu probabilitatea. Oraingo honetan:
- Ariketak
11. Bi kutxa ditugu. Batean, A kutxan, 2 puxtarri gorri
eta 3 puxtarri berde daude, eta bestean, B kutxan, 4
puxtarri gorri eta 2 berde. A kutxatik puxtarri bat
hartu eta B-n sartzen da. B kutxan dauden puxtarriak
nahastu eta puxtarri bat ateratzen da. Zenbatekoa da
puxtarri hori gorria izatearen probabilitatea?12. PACCIOLIren problema (1494) : Joko zuzen edo
bidezko batean bi jokalarik parte hartzen dute,
bakoi-tzak 4 txanpon jarririk. 6 partida irabazten
dituen jokalariak txanpon guztiak irabaziko ditu. 5 eta
3 doazenean jokoa bertan behera utzi behar izan dute.
Nola banatu behar dituzte txanponak? Pacciolik
batentzat 5 eta bestearentzat 3 izan behar zutela zioen.
Froga ezazu banaketa hori okerra dela, eta mende bat
geroago Pascalek Mereko zaldunari azaldu zion bezala,
jokalari batentzat 7 eta bestearentzat 1 izan behar zuela.13. Joko honen beste aldaera bat da Fermatek, gutun
bidez, 1654ko irailaren 25ean Pasacali ebatzi zion
hau : Hiru jokalari ari dira jokoan. Jokoa n partida irabazten
dituenak garaituko du. A jokalariari n partidak
irabazteko partida bakarra eta B eta C-ri bina partida
falta zaizkienean, jokoa bertan behera utzi behar izan
dute. Nola banatu behar dute jarritako dirua?14. Tortoloxen jokoa oso ezaguna izan zen Grezia eta
Erroman. Lau tortolox botatzen ziren eta gora begira gelditzen
ziren alderdien arabera jokaldia hobea edo okerragoa
izaten zen. Jokaldirik onena lau tortoloxek alde
desberdin bana gora begira zutela gelditzea izaten zen.
"Venusen ukaldia" izenarekin ezagutzen zen, eta beste
emaitza guztiek baino gehiago balio zuen. Tortoloxaren
alde zabala gora begira gelditzearen probabilitatea 5 eta
alde estuen probabilitatea 10 dela jakinik, zenbatekoa da
"Venusen ukaldia" ateratzeko probabilitatea?
VI. Guztizko probabilitatea
E lagin espazio batean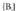 partizio bat, hau da bateraezinak diren segida sail bat, hau da
partizio bat, hau da bateraezinak diren segida sail bat, hau da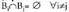 definitzen bada eta j guztien bildura E bada,
definitzen bada eta j guztien bildura E bada,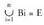 orduan edozein A gertaerak baldintza hauek beteko ditu :
orduan edozein A gertaerak baldintza hauek beteko ditu : Eta horren ondorioz, gertaera horren probabilitatea honela kalkula
daiteke :
Eta horren ondorioz, gertaera horren probabilitatea honela kalkula
daiteke :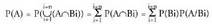 Berdintza honi guztizko probabilitatearen teorema deitzen zaio.
Berdintza honi guztizko probabilitatearen teorema deitzen zaio. • Adibideak:1. Eman dezagun bihar egingo duen eguraldia gaur egiten duenaren
araberakoa dela. Gaur euria egiten badu, bihar euria egitearen
probabilitatea 0,7 da, eta gaur ateri badago, bihar euria egitearen
probabilitatea 0,55 da. a) Gaur euria egitearen probabilitatea
0,6 bada, zenbatekoa da bihar euria egitearen probabilitatea? b)
Gaur ateri badago, zenbatekoa da etzi euria egitearen probabilitatea?Euria egin (Eu) eta ateri egon (At) partizio bat da, eta gertaera
horiei dagozkien probabilitateak ezagunak dira. Zuhaitz diagramak
erabiliko ditugu bi gertaera horien probabilitateak aurkitzeko :
• Adibideak:1. Eman dezagun bihar egingo duen eguraldia gaur egiten duenaren
araberakoa dela. Gaur euria egiten badu, bihar euria egitearen
probabilitatea 0,7 da, eta gaur ateri badago, bihar euria egitearen
probabilitatea 0,55 da. a) Gaur euria egitearen probabilitatea
0,6 bada, zenbatekoa da bihar euria egitearen probabilitatea? b)
Gaur ateri badago, zenbatekoa da etzi euria egitearen probabilitatea?Euria egin (Eu) eta ateri egon (At) partizio bat da, eta gertaera
horiei dagozkien probabilitateak ezagunak dira. Zuhaitz diagramak
erabiliko ditugu bi gertaera horien probabilitateak aurkitzeko :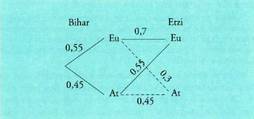 Eu-ra doazen adarrak kontuan hartu behar dira.
Eu-ra doazen adarrak kontuan hartu behar dira. 2. Auto bat goizean lehenengo ahaleginean martxan jartzeak ala
ez nagusiak autoa garajean sartu ala kalean utzi izanarekin zerikusia
du. Gauean garajean gordeta egon bada, lehenengoan martxan
jartzearen probabilitatea 0,8 da, eta nagusiak gau guztian kalean
utzi badu, berriz, lehenengoan martxan jartzearen probabilitatea,
0,15 da. Badakigu, bestalde, nagusiak garajean sartzearen probabilitatea
0,9 dela. Nagusiak gauean autoa garajean ala kalean utzi
duen ez badakigu, zenbatekoa da autoa lehenengo ahaleginean
martxan jartzearen probabilitatea?
2. Auto bat goizean lehenengo ahaleginean martxan jartzeak ala
ez nagusiak autoa garajean sartu ala kalean utzi izanarekin zerikusia
du. Gauean garajean gordeta egon bada, lehenengoan martxan
jartzearen probabilitatea 0,8 da, eta nagusiak gau guztian kalean
utzi badu, berriz, lehenengoan martxan jartzearen probabilitatea,
0,15 da. Badakigu, bestalde, nagusiak garajean sartzearen probabilitatea
0,9 dela. Nagusiak gauean autoa garajean ala kalean utzi
duen ez badakigu, zenbatekoa da autoa lehenengo ahaleginean
martxan jartzearen probabilitatea? Zuhaitz diagrama egingo dugu :
Zuhaitz diagrama egingo dugu : Beraz, eskatutako probabilitatea hau izango da :
Beraz, eskatutako probabilitatea hau izango da :
- Ariketak
15. Pertsona bat goizean garaiz jaikitzeak aurreko gauean iratzargailua
jarri ala ez jartzearekin zerikusia du. Pertsona
batek %90etan iratzargailua jartzen du, eta %loetan ez.
Iratzargailua jartzen duen %95etan garaiz jaikitzen da,
baina iratzargailua jartzen ez duen %65etan lo gelditzen
da. Zenbatekoa da garaiz jaikitzearen portzentaia?16. Ikasle batek getako klasea galtzeko duen probabilitatea
0,4koa da eta 10etako klasea galtzeko duen probabilitatea
0,35ekoa da. 9etako klasea galtzen duen %75etan
loetako klasea ere galtzen du. a) Zenbatekoa da bi klaseak
galtzeko duen probabilitatea? b) Zenbatekoa da
loetako klasea bakarrik galtzeko duen probabilitatea?17. Tiratzaile batek helburua edo diana lortzeko duen
probabilitatea 1/3 da. a) 7 jaurtialdi egiten baditu,
zenbatekoa da bere helburua gutxienez bi aldiz lortzeko
duen probabilitatea? b) Zenbat jaurtialdi egin
behar ditu bere helburua gutxienez behin lortzeko
probabilitatea 0,9 baino handiagoa izan dadin?18. Urre, kopa, ezpata eta bastoiez osaturiko karta sorta
batean palo edo sail bakoitzari dagokion txota, zaldun,
errege eta batekoekin 16 kartako sorta bat osatu dugu.a) Elkarren segidan hiru karta ateratzen dira.i) Zenbatekoa da hiru kartak sail berekoak izatearen
probabilitatea?ii) Zenbatekoa da ateratako bi karta prezeski sail
berekoak izatearen probabilitatea?b) Oraingo honetan karta bat atera ondoren, berriro
sortako gainerako kartekin batera jartzen da.i) Hiru karta ateratzen dira. Zenbatekoa da hiru kartak
kopakoak izatearen probabilitatea?ii) n ateratze saio egiten dira (n osoa>1). Zenbatekoa da
gutxienez kopako bat ateratzearen Pn probabilitatea?
Pn>0,99 izateko, zenbatekoa behar du izan n-ek?
VII. BAYESen TEOREMA
Batzuetan, lagin espazioaren partizio bat eratzen duten B ; gertaera multzo batek baldintzaturiko A gertaera baten probabilitateak ezagutuz, A gertatu delarik B ; jakin bat gertatzearen probabilitatea zenbatekoa den jakin nahi da. Hau da, probabilitateak ezagutzen dira, eta
probabilitateak ezagutzen dira, eta ezagutu nahi da.
ezagutu nahi da.
Hori lortzeko, badakigu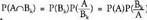 betetzen dela.Beraz,
betetzen dela.Beraz,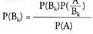 Baina
Baina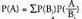 betetzen denez,
betetzen denez, izago da.Berdintza honi Bayesen teorema esaten zaio. Bayes (1702-1761)
matematikari ingelesa izan zen hain zuzen, era honetako problemak
aztertzen hasi zen lehena. Ondorio batek kausa posible bat baino
gehiago duenean, eta ondorio jakin hori gertatu delarik, horren
kausa zehatza zein izan den jakin nahi denean erabiltzen da teorema
hau. Horregatik deitzen zaio kausen probabilitatearen teorema ere.• Adibideak:1. Gaixotasun baten diagnosia egiteko erabiltzen den proba
batek positiboa ematen du gaixotasun hori duten pertsonen
%95etan eta gaixotasun hori ez dutenen %8tan. Estatistika ikasketek
diotenez biztanleen %7ak du gaixotasun hori.. ) Pertsona bati proba egin diote eta emaitza positiboa eman du,
baina pertsona hori baikorra denez, diagnostikoa okerra dela uste
du. Zenbatekoa da diagnostikoa okerra izatearen probabilitatea?b) Beste pertsona bati ere proba bera egin diote eta negatiboa eman
du, baina pertsona hori ezkorra denez, diagnostikoa okerra dela eta
gaixo dagoela uste du. Zenbatekoa da asmatzeko duen probabilitatea?c) Zenbatekoa da proba honen asmatze portzentaia? ; hau da, biztanle guztiei froga egin eta froga honen emaitzen arabera zenbati esaten dio gaixo dagoela benetan hala izanik eta zenbati esaten zaio ez duela gaixotasun hori diagnosia zuzen eginik? Gaixo egoteari G eta gaixo ez egoteari G' deituko diogu, eta proban emaitza positiboa emateari S eta ez emateari S' deituko diogu.
izago da.Berdintza honi Bayesen teorema esaten zaio. Bayes (1702-1761)
matematikari ingelesa izan zen hain zuzen, era honetako problemak
aztertzen hasi zen lehena. Ondorio batek kausa posible bat baino
gehiago duenean, eta ondorio jakin hori gertatu delarik, horren
kausa zehatza zein izan den jakin nahi denean erabiltzen da teorema
hau. Horregatik deitzen zaio kausen probabilitatearen teorema ere.• Adibideak:1. Gaixotasun baten diagnosia egiteko erabiltzen den proba
batek positiboa ematen du gaixotasun hori duten pertsonen
%95etan eta gaixotasun hori ez dutenen %8tan. Estatistika ikasketek
diotenez biztanleen %7ak du gaixotasun hori.. ) Pertsona bati proba egin diote eta emaitza positiboa eman du,
baina pertsona hori baikorra denez, diagnostikoa okerra dela uste
du. Zenbatekoa da diagnostikoa okerra izatearen probabilitatea?b) Beste pertsona bati ere proba bera egin diote eta negatiboa eman
du, baina pertsona hori ezkorra denez, diagnostikoa okerra dela eta
gaixo dagoela uste du. Zenbatekoa da asmatzeko duen probabilitatea?c) Zenbatekoa da proba honen asmatze portzentaia? ; hau da, biztanle guztiei froga egin eta froga honen emaitzen arabera zenbati esaten dio gaixo dagoela benetan hala izanik eta zenbati esaten zaio ez duela gaixotasun hori diagnosia zuzen eginik? Gaixo egoteari G eta gaixo ez egoteari G' deituko diogu, eta proban emaitza positiboa emateari S eta ez emateari S' deituko diogu.
Eskuartean ditugun datuak hauek dira :Gauzak errazteko zuhaitz diagrama egingo dugu : Lehenengo galderak era eskatzen du :
Lehenengo galderak era eskatzen du : Eta hiru ten galderak
Eta hiru ten galderak 2. Unibertsitate batean jasotako estatistikek diotenez, irakasgai
bateko klasetara ikasleen %50a bakarrik joaten da. Azken azterketen
arabera ikasleen %70ak gainditu du ikasturtea. Gainditu duten
ikasleen %60a ia klase guztietara joaten zen. Klasera joaten zirenen
artean, zenbatekoa da gainditu dutenen portzentaia?G = gainditu eta K = klasera joan dela esango dugu. P(G) = 0,7 ; P(K) = 0,5 etaZuhaitz diagrama egingo dugu :
2. Unibertsitate batean jasotako estatistikek diotenez, irakasgai
bateko klasetara ikasleen %50a bakarrik joaten da. Azken azterketen
arabera ikasleen %70ak gainditu du ikasturtea. Gainditu duten
ikasleen %60a ia klase guztietara joaten zen. Klasera joaten zirenen
artean, zenbatekoa da gainditu dutenen portzentaia?G = gainditu eta K = klasera joan dela esango dugu. P(G) = 0,7 ; P(K) = 0,5 etaZuhaitz diagrama egingo dugu :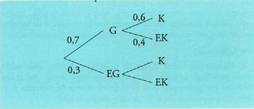 Beraz,
Beraz,
- Ariketak
19. X jauna bulegora berandu iristen denean nagusiak errieta egiten dio, hurrengo egunean garaiz iristearen probabilitatea 3/4 da. Baina X jauna egun batean garaiz iristen bada, axolagabetu egiten da, eta hurrengo egunean berandu iristearen probabilitatea 1/3 da.Asteburu zoriontsu baten ondorengo astelehenean, X jauna berandu iristen da. Bila itzazu ondorengo kasuei dagozkien probabilitateak :a) Asteartean eta asteazkenean garaiz iristea.b) Asteazkenean berandu iristea.c) Asteazkenean berandu iristen dela jakinik, asteartean berandu iristea.20. Tuberkulosia detektatzeko erabiltzen den Rongten testak errore hauek ematen ditu :- Gaixo dauden pertsonen % lOa ez du detektatzen.- Osasuntsu dauden %2a gaixo dagoela esaten du.Tuberkulosiaren aurkako tratamenduan dauden pertsonak Rongten testa eginez kontrolatzen dituzte urtero. Urtetako lanaren ondorioz, urtero tuberkulosia hartzen dutenen kopurua biztanleriaren %0,07a dela jakin ahal izan da.a) Test horren arabera pertsona bat tuberkulosiak jota dagoela esateko probabilitatea, gutxi gora behera, %2koa dela frogatu.b) Kalkula ezazu testak gaixo dagoela esan duen pertsona bat benetan gaixo egotearen probabilitatea.c) Kalkula ezazu testak osasuntsu dagoela esan duen pertsona bat benetan gaixo egotearen probabilitatea.21. T ikasle talde batean %60 dira emakumezkoak eta %40 gizonezkoak. Emakumeen %30a eta gizonen %25a ez da alemaneraz mintzatzen.a) T taldeko pertsona bat hautatzen da zoriz. Kalkula ezazu pertsona hori alemaneraz ez mintzatzeko dagoen probabilitatea.b) T taldeko pertsona bat hautatzen da zoriz, eta ez da alemaneraz mintzatzen. Kalkula ezazu pertsona hori emakumea izatearen probabilitatea.22. Hiru kutxatan zenbait puxtarri ditugu, horrela :- A kutxan 3 puxtarri gorri eta 5 puxtarri beltz daude.- B kutxan 2 puxtarri gorri eta puxtarri beltz bat dago.- C kutxan 2 puxtarri gorri eta 3 puxtarri beltz daude.Kutxa bat hautatzen da zoriz. Atera dugun puxtarria gorria bada, zenbatekoa da puxtarri hori A kutxakoa izatearen probabilitatea?23. Bi kutxa ditugu, A kutxa eta B kutxa. A kutxan 8 pieza daude lokabe ; hauetatik 3, akastunak. B kutxan, berriz, 5 pieza lokabe daude ; hauetatik 2, akastunak . Kutxa bakoitzetik pieza bana ateratzen da.a) Zenbatekoa da atera diren bi piezak akatsik gabeak izatearen probabilitatea?b) Zenbatekoa da atera diren bi piezetatik bat akastuna eta bestea akatsik gabea izatearen probabilitatea?c) Piezetariko bat akastuna eta bestea akatsik gabea bada, zenbatekoa da pieza akastuna A kutxakoa izatearen probabilitatea?24. Abenduko gau batean, mendiko errepide batean, tenperatura zero azpitikoa izatearen probabilitatea 1/5 da. Izotza egin duen gau batean istripu bat izatearen probabilitatea 1/40, da; aldiz izotzik ez denean istripu bat izatearen probabilitatea 1/200 da. Kalkula itzazu ondorengo probabilitateak:a) Abenduko gau batean izotza egin eta istripua egotea.b) Abenduko edozein gautan istripu bat egotea.c) Istripua izan den abenduko gau batean izotza egin izana.25. Ikasle asko dituen unibertsitate batean egindako saiakuntzen bidez jakin da ikasleen %25a barazkijalea dela. Barazkijaleen artean %58ak betaurrekoak erabili behar ditu, eta gainerakoen artean %62ak erabili behar ditu betaurrekoak.a) Bila ezazu zenbatekoa den, unibertsitate horretan, zoriaren arabera hautatutako ikasle batek betaurrekoak erabili behar izatearen probabilitatea.b) Zoriaren arabera hautatu den ikasleak betaurrekoak erabili behar ditu. Bila zenbatekoa den ikasle hori barazkijalea izatearen probabilitatea.
Ebazpenak:
1. .
.
2. Nahiz dadoak bereizezinak, koloretakoak edo desberdinak izan, gertaera korpurua 216 da.3. Alde bat = {A+,+A} ; Bi alde = {AA} ; Alderik ez ={++}4. Urrea atera ={Url, Ur2, Ur3, Ur4, Ur5, Ur6, Ur7, Ur10, Url l, Ur12} (oinarrizko
10 gertaera).Erregea atera = {Errege urrea (Ur12), errege kopa (Ko12), errege
ezpata (Ez12), errege bastoia (Eg12)} (oinarrizko 4 gertaera).
Nahiz dadoak bereizezinak, koloretakoak edo desberdinak izan, gertaera korpurua 216 da.3. Alde bat = {A+,+A} ; Bi alde = {AA} ; Alderik ez ={++}4. Urrea atera ={Url, Ur2, Ur3, Ur4, Ur5, Ur6, Ur7, Ur10, Url l, Ur12} (oinarrizko
10 gertaera).Erregea atera = {Errege urrea (Ur12), errege kopa (Ko12), errege
ezpata (Ez12), errege bastoia (Eg12)} (oinarrizko 4 gertaera). (oinarrizko 13 gertaera ; errege urreak ez du bi aldiz azaldu behar).
(oinarrizko 13 gertaera ; errege urreak ez du bi aldiz azaldu behar).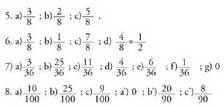 9. Hiru dado ditugunez, kasu posibleak 6' = 216 dira. 10 batura
ez da 6 eratan lortzen, 27 eratan baizik, izan ere 1,3 eta 6 zenbakien
arteko batuketak egiteko erak dira 1+3+6 edo 1+6+3 edo
3+6+1 edo 3+1+6 etab. Gauza bera gertatzen da 2+2+6 eta besteekin
; guztira 27 era desberdin daude. Batura 9 denean, ordea, 25 era
desberdin ateratzen dira. Beraz batura 10 ateratzea batura 9 ateratzea
baino gertagarriagoa da.10. Lau jaurtialditan gutxienez seiko bat ateratzearen probabilitatea hau da:
9. Hiru dado ditugunez, kasu posibleak 6' = 216 dira. 10 batura
ez da 6 eratan lortzen, 27 eratan baizik, izan ere 1,3 eta 6 zenbakien
arteko batuketak egiteko erak dira 1+3+6 edo 1+6+3 edo
3+6+1 edo 3+1+6 etab. Gauza bera gertatzen da 2+2+6 eta besteekin
; guztira 27 era desberdin daude. Batura 9 denean, ordea, 25 era
desberdin ateratzen dira. Beraz batura 10 ateratzea batura 9 ateratzea
baino gertagarriagoa da.10. Lau jaurtialditan gutxienez seiko bat ateratzearen probabilitatea hau da: . Hogeitalau jaurtialditan gutxienez seiko bikoitza ateratzearen probabilitatea, berriz, hau da :
. Hogeitalau jaurtialditan gutxienez seiko bikoitza ateratzearen probabilitatea, berriz, hau da :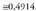 . Beraz, gertagarriagoa da lehenengoa.
. Beraz, gertagarriagoa da lehenengoa. 12. Izan ere, irabazteko probabilitateak
12. Izan ere, irabazteko probabilitateak eta
eta dira.Ebazpenak : 13. Bidezko banaketa, banaketa horren probabilitateekin bat datorrena da; hau da
dira.Ebazpenak : 13. Bidezko banaketa, banaketa horren probabilitateekin bat datorrena da; hau da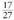 A-rentzat, eta
A-rentzat, eta B eta C-rentzat.
B eta C-rentzat.
Zorizko aldagai diskretua.
Banaketa binomiala
Zorizko saiakuntza batean zenbakiak, gauzak, ezaugarriak edo
pertsonak izan daitezke oinarrizko gertaerak. Zenbakizko emaitzak
dituen zorizko saiakuntza bati batez besteko balio bat eta barreiadura
neurri bat dagozkio, saiakuntza estatistikoetan bezalaxe.
Baina kasu honetan, ez dira izango estatistika batean lortutako
balioen laburpena egiteko parametroak, baizik eta zorizko saiakuntza
batean itxaro diren balioak.Saiakuntza batean itxarondako emaitzak zenbakizkoak ez direnean
ere, emaitzetatik zenbait kantitate atera daitezke, saiakuntza egiten
duenarentzat probabilitatea kalkulatzen den gertaera bezainbateko
garrantzia dutenak. Honen adibide dira, esaterako, diru
apustuak. Halakoetan emaitza jakin bat ateratzearen probabilitateak,
adibidez bateko bat ateratzearenak, ez du garrantzi handiegirik
izango bere horretan, baina garrantzi handia hartzen du bateko hori
ateratzearen probabilitateak dirua irabaztearen ala galtzearen probabilitatearekin
zerikusia duenean. Termodinamika, meteorologia
edo ekonomiarekin zerikusia duten probabilitatearen aplikazioetan
emaitza posibleak zenbakizkoak izaten dira, eta halakoetan,
garrantzizkoena, itxarondako balioa eta emaitzen barreiadura ezagutzea
izaten da. Beste batzuetan gertatu ohi da saiakuntzaren
emaitza zenbakizkoa izan arren, emaitza horretatik lortzen diren
beste batzuk izatea benetan garrantzitsuak. Beraz, edozein motako
zorizko saiakuntza batean elkarri loturiko bi problema azalduko
zaizkigu: alde batetik zorizko saiakuntza baten emaitzetatik abiatuta
zenbakizko aldagai bat definitzea, eta bestetik aldagai horren probabilitate
banaketaren parametroak aurkitzea.Atal honetan zorizko aldagai funtzioa aztertuko da lehenik.
Zorizko aldagai funtzioak zorizko saiakuntza bateko emaitzak zenbakizko
balioekin erlazionatzeko bidea ematen du. Horrela definitutako
aldagai bati dagozkion probabilitate banaketek balio horietarako
itxaroten den batez bestekoa eta desbideratze tipikoa
bilatzeko balio dute; baina badira sarriago azaltzen direlako arreta
berezia eskatzen duten banaketa batzuk ere. Ikasgai honetan banaketa
binomiala eta Poissonen banaketa ikusiko dira.
I. Zorizko aldagaia
Hiru txanpon jaurtitzerakoan, txanpon bakoitzean aldea edo
ifrentzua aterako da. Emaitza posible guztiek eratzen duten lagin
espazioa hau izango da : Guztira 8 elementu daude. Alde gehien ateratzen dituenak irabazten
badu jokoa, oinarrizko emaitza bakoitzari zenbaki bat ematen zaio :
Guztira 8 elementu daude. Alde gehien ateratzen dituenak irabazten
badu jokoa, oinarrizko emaitza bakoitzari zenbaki bat ematen zaio : Horrela, "zoriz hiru txanpon jaurti" saiakuntzatik abiatuta zorizko
aldagai bat definitu da. Saiakuntza berean beste zorizko aldagai
batzuk defini genitzakeen ; hala nola ifrentzu kopurua, edo alde eta
ifrentzu arteko diferentzia, edo zorizko saiakuntza honetan emaitza
bakoitzari zenbaki bat emateko dauden eratatik beste edozein.Oro har, E lagin espazioa duen edozein zorizko saiakuntza emanik,
E eta zenbaki errealen arteko edozein aplikaziori deitzen zaio X
zorizko aldagaia.
Horrela, "zoriz hiru txanpon jaurti" saiakuntzatik abiatuta zorizko
aldagai bat definitu da. Saiakuntza berean beste zorizko aldagai
batzuk defini genitzakeen ; hala nola ifrentzu kopurua, edo alde eta
ifrentzu arteko diferentzia, edo zorizko saiakuntza honetan emaitza
bakoitzari zenbaki bat emateko dauden eratatik beste edozein.Oro har, E lagin espazioa duen edozein zorizko saiakuntza emanik,
E eta zenbaki errealen arteko edozein aplikaziori deitzen zaio X
zorizko aldagaia.
II. Probabilitate funtzioa Bi dado jaurti eta emaitzen batura
Joko batean hiru txanpon botatzen badira eta ateratzen den
alde kopurua kontatzen bada, kontuan hartu behar diren probabilitateak
alde kopuruen zorizko aldagaiaren balioei dagozkienak
dira. Eman dezagun oinarrizko gertaera guztiak gertatzeko probabilitate
bera dagoela, hau da gertaera ekiprobableak direla guztiak
; kasu horretan probabilitate hauek dagozkie gertaera bakoitzari
: Aldagaiaren balioen eta probabilitatearen arteko korrespondentzia
hau beste funtzio bat da. Funtzio honi hiru txanpon jaurtitzean
ateratzen diren alde kopurua zorizko aldagaiaren probabilitate funtzioa
edo probabilitate legea deitzen zaio.X aldagai diskretu baten probabilitate funtzioa deitzen zaio
Aldagaiaren balioen eta probabilitatearen arteko korrespondentzia
hau beste funtzio bat da. Funtzio honi hiru txanpon jaurtitzean
ateratzen diren alde kopurua zorizko aldagaiaren probabilitate funtzioa
edo probabilitate legea deitzen zaio.X aldagai diskretu baten probabilitate funtzioa deitzen zaio ; zorizko aldagaiaren balio bakoitzari, aldagaiak balio hori izateko duen probabilitatea elkartzen dion f aplikazioari :
; zorizko aldagaiaren balio bakoitzari, aldagaiak balio hori izateko duen probabilitatea elkartzen dion f aplikazioari :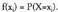 Balio bakoitzari dagokion probabilitate funtzioaren irudia kalkulatzeko,
balio horri dagozkion oinarrizko gertaeren probabilitaten
batuketa egiten da. Balio gutxi direnean balio taula baten bidez
azaltzen da funtzioa."Hiru txanpon jaurtitzean ateratako alde kopurua kontatu " adibidean :
Balio bakoitzari dagokion probabilitate funtzioaren irudia kalkulatzeko,
balio horri dagozkion oinarrizko gertaeren probabilitaten
batuketa egiten da. Balio gutxi direnean balio taula baten bidez
azaltzen da funtzioa."Hiru txanpon jaurtitzean ateratako alde kopurua kontatu " adibidean : "bi dado jaurti eta emaitzen batura" aldagaiari, berriz, ondoko taula dagokio :
"bi dado jaurti eta emaitzen batura" aldagaiari, berriz, ondoko taula dagokio : Eta aurreko ataleko 2. adibideari, loteriarenari, dagokion taula:
Eta aurreko ataleko 2. adibideari, loteriarenari, dagokion taula: "Dado bat jaurti eta 6ko bat atera arte jaurtitzen jarraitu" saiakuntzan ezin da taularik egin, infinitu balio har ditzakeelako.
"Dado bat jaurti eta 6ko bat atera arte jaurtitzen jarraitu" saiakuntzan ezin da taularik egin, infinitu balio har ditzakeelako.
Horren ordez, eta espresio aljebraiko baten bitartez ematen da aditzera funtzioa, i zorizko aldagaiaren balio bakoitzarentzat ondoko probabilitatea ematen duen espresioaren bidez : Hain zuzen, eskatutako 6a, lehenengo aldiz i. jaurtialdian ateratzen da [bere probabilitatea 1/6 da], aurreko i-1 jaurtialdietan beste zenbaki bat atera delarik [bere probabilitatea
Hain zuzen, eskatutako 6a, lehenengo aldiz i. jaurtialdian ateratzen da [bere probabilitatea 1/6 da], aurreko i-1 jaurtialdietan beste zenbaki bat atera delarik [bere probabilitatea . Gertaera hauek elkarren
artean independenteak direnez, probabilitatea
. Gertaera hauek elkarren
artean independenteak direnez, probabilitatea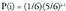 da.Ikasleen garaiera aipatzen zuen adibidean, eta zorizko aldagaia
jarraitua den kasu guztietan, aldagaiaren balio bakoitzari ezin zaio
probabilitate jakin bat ezarri ; hori dela eta, zorizko aldagai jarraituak
beste era batera definitzen dira. Baina definizio hori hurrengo
gaian ikasiko da.Zorizko aldagai diskretuen probabilitate funtzioak, aldagai estatistiko
diskretuak bezalaxe, barra diagramen bidez irudikatzen dira.
da.Ikasleen garaiera aipatzen zuen adibidean, eta zorizko aldagaia
jarraitua den kasu guztietan, aldagaiaren balio bakoitzari ezin zaio
probabilitate jakin bat ezarri ; hori dela eta, zorizko aldagai jarraituak
beste era batera definitzen dira. Baina definizio hori hurrengo
gaian ikasiko da.Zorizko aldagai diskretuen probabilitate funtzioak, aldagai estatistiko
diskretuak bezalaxe, barra diagramen bidez irudikatzen dira.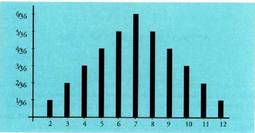 Propietateak :Aldagaiaren edozein balioren probabilitateak positiboak edo
nuluak dira, eta beraien arteko baturak bat balio du. n balio desberdin
ditugunean, zera egiaztatzen da :
Propietateak :Aldagaiaren edozein balioren probabilitateak positiboak edo
nuluak dira, eta beraien arteko baturak bat balio du. n balio desberdin
ditugunean, zera egiaztatzen da : Zorizko aldagai diskretua infinitua denean, baturak jarrai bat
osatzen du, baina batura horrek ere bat balioa behar du izan :
Zorizko aldagai diskretua infinitua denean, baturak jarrai bat
osatzen du, baina batura horrek ere bat balioa behar du izan :
- Ariketak
l. Lau pertsonentzako lau pakete ditugu (pakete bana bakoitzarentzat) . Bakoitzari dagokion paketea eman ordez, zoriaren arabera banatzen dira. Izan bedi X dagokion paketea jasotzen duen pertsona kopurua adierazten duen zorizko aldagaia. Zein da X-en probabilitate funtzioa?
III. Banaketa funtzioa
Zorizko aldagai baten balio batekiko banaketa funtzioak balio
hori edo txikiagoa ateratzearen probabilitatea ematen du. Aldagai
estatistikoetako maiztasun metatuen parekoa da. Baliagarria izaten
da, balio bakoitzaren probabilitatea txikia denean, eta bereziki taldetan
bildutako balioen probabilitatea jakin nahi denean.X zorizko aldagai diskretu baten F banaketa funtzioa esaten zaio ; balio bakoitzari
; balio bakoitzari -ren balio bereko probabilitatea edo balio hori baino probabilitate txikiagoa elkartzen dion funtzioari :
-ren balio bereko probabilitatea edo balio hori baino probabilitate txikiagoa elkartzen dion funtzioari : "Hiru txanpon jaurtitzean ateratzen den alde kopurua kontatu"
adibidean :
"Hiru txanpon jaurtitzean ateratzen den alde kopurua kontatu"
adibidean : "Bi dado jaurti eta emaitzen batura kalkulatu" saiakuntzan :
"Bi dado jaurti eta emaitzen batura kalkulatu" saiakuntzan : Loteriaren saiakuntzan ezin da funtzio hau erabili, baina bai "6
bat atera arte dadoa jaurti" saiakuntzan. Kasu honetan, banaketa
funtzioen bidez aise aurki daitezke «lehenengo 6a lortzeko bost
jaurtialdi baino gehiago behar izatearen probabilitatea» edo «lehenengo
6a hirugarren eta seigarren jaurtialdien artean lortzearen probabilitatea»
. Ariketa honetan, zorizko aldagaiak infinitu balio hartzen
ditu, baina balio guztien probabilitatea txikia da eta balio
bakoitzari dagokion probabilitatearen eta gainerako balioei dagokien
probabilitateen arteko aldea ez da handia. Probabilitate funtzioaren
taulako lehenengo balioak hartu eta probabilitateak laugarren
hamarrenean, hau da hamarmilarenean biribilduz, ondoko
taula lortzen da :
Loteriaren saiakuntzan ezin da funtzio hau erabili, baina bai "6
bat atera arte dadoa jaurti" saiakuntzan. Kasu honetan, banaketa
funtzioen bidez aise aurki daitezke «lehenengo 6a lortzeko bost
jaurtialdi baino gehiago behar izatearen probabilitatea» edo «lehenengo
6a hirugarren eta seigarren jaurtialdien artean lortzearen probabilitatea»
. Ariketa honetan, zorizko aldagaiak infinitu balio hartzen
ditu, baina balio guztien probabilitatea txikia da eta balio
bakoitzari dagokion probabilitatearen eta gainerako balioei dagokien
probabilitateen arteko aldea ez da handia. Probabilitate funtzioaren
taulako lehenengo balioak hartu eta probabilitateak laugarren
hamarrenean, hau da hamarmilarenean biribilduz, ondoko
taula lortzen da : Eta taula honi dagokion banaketa funtzioa :
Eta taula honi dagokion banaketa funtzioa : Banaketa funtzioa ezagutu ondoren, lehenengo 6a lortzeko bost jaurtialdi baino gehiago behar izatearen probabilitatea jakiteko ondoko eragiketa egin beharko da :
Banaketa funtzioa ezagutu ondoren, lehenengo 6a lortzeko bost jaurtialdi baino gehiago behar izatearen probabilitatea jakiteko ondoko eragiketa egin beharko da : . Eta lehenengo 6a hirugarren eta seigarren jaurtialdien artean, biak barne, lortzearen probabilitatea jakiteko, berriz :
. Eta lehenengo 6a hirugarren eta seigarren jaurtialdien artean, biak barne, lortzearen probabilitatea jakiteko, berriz :
F(x) banaketa funtzioaren propietateak
1. F(x) funtzioa beti positiboa eta gorakorra da.2. Zorizko aldagai diskretuaren lehenengo balioa baino lehenagoko banaketa funtzioa zero da ; aldagaia finitua bada, azken balioaren ondorengo banaketa funtzioa konstantea da, eta 1 balioa izango du.3. F(x) funtzioa konstantea da zorizko aldagaiaren bi balioen artean, beraz funtzio mailakatua da.Propietate hauen ondorioz, banaketa funtzioen grafikoak funtzio mailakatuak dira.
- Ariketak
2. Ongi orekatutako txanpon bat lau aldiz jaurtitzen da. Izan bedi X lortutako alde kopurua.a) Kalkula ezazu probabilitate banaketa edo probabilitate legea. Irudika ezazu lege horri dagokion barra diagrama.b) Bila ezazu banaketa funtzioa.3. Bi dado perfektu jaurtitzen dira. Izan bedi X lortzen diren bi zenbakien artean txikiena adierazten duen zorizko aldagaia. Kalkula ezazu probabilitate banaketa . Bila ezazu banaketa funtzioa eta funtzio honi dagokion diagrama irudikatu.
IV. Zorizko aldagai diskretu baten batez bestekoa eta desbideratze tipikoa
Zorizko aldagaietan, aldagai estatistikoetan bezalaxe, zentralizazio
parametro bat definitzen da, batez bestekoa, balio bakar baten
bidez adierazten duena aldagaiak hartzen duen balio multzo osoa.
Horrez gainera bariantza eta desbideratze tipikoa ere definitzen
dira, baina bi hauek, aurrekoa ez bezala, barreiadura parametroak
dira, eta emaitzak bilduta ala sakabanatuta dauden adierazten dute.Zorizko aldagai diskretu finitu baten batez bestekoa edo itxaropen matematikoa aldagai horren ; balio bakoitzaren eta balio bakoitzari dagokion pi probabilitatearen arteko biderkadura guztien batura da, non i 1-etik n-raino doan. Batez bestekoa edo itxaropen matematikoa adierazteko
; balio bakoitzaren eta balio bakoitzari dagokion pi probabilitatearen arteko biderkadura guztien batura da, non i 1-etik n-raino doan. Batez bestekoa edo itxaropen matematikoa adierazteko , E(x) edo X erabiltzen da :
, E(x) edo X erabiltzen da :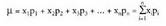 Aldagai estatistikoei dagokien batez besteko aritmetikoarenbaliokidea da. Baina estatistikan, batez bestekoak atera diren balioen
batez bestekoa adierazten duen bezala, probabilitatearen alorrean
ateratzea espero den balioen batez bestekoari dagokio, eta hori
dela eta itxaroen p edo eserantza p matematiko ere deitzen zaio.a Adibideak:1. Dado bat jaurtitzerakoan lor daitezkeen balioak 1, 2, 3, 4, 5 eta 6 dira, eta bakoitzaren probabilitatea 1/6 da. Batez bestekoa, beraz, ,hau da :
Aldagai estatistikoei dagokien batez besteko aritmetikoarenbaliokidea da. Baina estatistikan, batez bestekoak atera diren balioen
batez bestekoa adierazten duen bezala, probabilitatearen alorrean
ateratzea espero den balioen batez bestekoari dagokio, eta hori
dela eta itxaroen p edo eserantza p matematiko ere deitzen zaio.a Adibideak:1. Dado bat jaurtitzerakoan lor daitezkeen balioak 1, 2, 3, 4, 5 eta 6 dira, eta bakoitzaren probabilitatea 1/6 da. Batez bestekoa, beraz, ,hau da : 2. Hiru txanpon jaurti eta ateratzen den alde kopurua kontuan
sartzen bada, saiakuntza horren batez bestekoa hau da :
2. Hiru txanpon jaurti eta ateratzen den alde kopurua kontuan
sartzen bada, saiakuntza horren batez bestekoa hau da : 3. Bi dado jaurti eta ateratzen diren zenbakien batura kontuan
sartzen bada, berriz, batez bestekoa hau da :
3. Bi dado jaurti eta ateratzen diren zenbakien batura kontuan
sartzen bada, berriz, batez bestekoa hau da : 4. Lehenengo gaiko bigarren adibidean aipatu den loteriaren
tasuan, irabazien batez bestekoa hau da :
4. Lehenengo gaiko bigarren adibidean aipatu den loteriaren
tasuan, irabazien batez bestekoa hau da :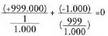 Zorizko aldagai diskretu infinitu baten batez bestekoa kalkulatu
iahi izanez gero, zailtasunak handiagoak izan daitezke, aldagai finiua
definitzen duen baturak jarrai bat osatzen duelako eta horrek
:onbergentzia arazoak sor ditzakeelako :
Zorizko aldagai diskretu infinitu baten batez bestekoa kalkulatu
iahi izanez gero, zailtasunak handiagoak izan daitezke, aldagai finiua
definitzen duen baturak jarrai bat osatzen duelako eta horrek
:onbergentzia arazoak sor ditzakeelako : • Adibidea :1. 6 atera arte dado bat jaurti eta 6koa lortzeko behar izan diren
aurtialdiak kontatzen badira, batez bestekoa hau izango da :
• Adibidea :1. 6 atera arte dado bat jaurti eta 6koa lortzeko behar izan diren
aurtialdiak kontatzen badira, batez bestekoa hau izango da : Aurreko berdintzari azken berdintza kentzen badiogu :
Aurreko berdintzari azken berdintza kentzen badiogu :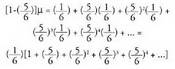 Kortxete artean azaltzen den zaria,
Kortxete artean azaltzen den zaria, arrazoia duen progresio geometriko indeterminatu edo infinitua a, beraz bere batura hau da:
arrazoia duen progresio geometriko indeterminatu edo infinitua a, beraz bere batura hau da: Hori dela eta
Hori dela eta Hau da
Hau da
Bariantza eta desbideratze tipikoa
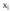 x; balioak bere pi probabilitateekin (i, letik n-ra doa) hartu eta
x; balioak bere pi probabilitateekin (i, letik n-ra doa) hartu eta batez bestekoa duen X zorizko aldagai diskretu baten bariantza, ondorengo eragiketa honen emaitza da :
batez bestekoa duen X zorizko aldagai diskretu baten bariantza, ondorengo eragiketa honen emaitza da :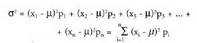 Bariantza adierazteko
Bariantza adierazteko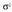 zeinua erabiltzen da.Zorizko aldagai baten desbideratze tipikoa bere bariantzaren erro
karratua da, eta s adierazten da.• Adibidea:Dado bat jaurtitzerakoan lor daitezkeen balioak 1, 2, 3, 4, 5 eta 6
dira, bakoitzaren probabilitatea 1/6 da, eta batez bestekoa 3,5 da,
bariantza eta desbideratze tipikoak ondoren adierazten direnak
izango dira :
zeinua erabiltzen da.Zorizko aldagai baten desbideratze tipikoa bere bariantzaren erro
karratua da, eta s adierazten da.• Adibidea:Dado bat jaurtitzerakoan lor daitezkeen balioak 1, 2, 3, 4, 5 eta 6
dira, bakoitzaren probabilitatea 1/6 da, eta batez bestekoa 3,5 da,
bariantza eta desbideratze tipikoak ondoren adierazten direnak
izango dira : "bi dado jaurti eta ateratzen diren zenbakiak batu" saiakuntza
kontuan hartzen bada, batez bestekoa 7 da, eta bariantza eta desbideratze
tipikoak hauek izango dira :
"bi dado jaurti eta ateratzen diren zenbakiak batu" saiakuntza
kontuan hartzen bada, batez bestekoa 7 da, eta bariantza eta desbideratze
tipikoak hauek izango dira : Lehenengo galderako loteriaren adibidean batez bestekoa 0 zela
ikusi zen. Bere bariantza eta desbideratze tipikoak hauek izango dira :
Lehenengo galderako loteriaren adibidean batez bestekoa 0 zela
ikusi zen. Bere bariantza eta desbideratze tipikoak hauek izango dira : Emandako bariantzaren formulan azaltzen den binomiotik abiaturik:
Emandako bariantzaren formulan azaltzen den binomiotik abiaturik: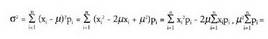 Kontuan harturik probabilitateen bat dela, eta bigarren gaiko batukaria denez batez bestekoa, bariantzaren formula berri bat lortzen dugu, kalkuluak egiteko errazagoa:
Kontuan harturik probabilitateen bat dela, eta bigarren gaiko batukaria denez batez bestekoa, bariantzaren formula berri bat lortzen dugu, kalkuluak egiteko errazagoa:
- Ariketak
4. Kutxa batean 8 gai ditugu, hauetatik 3 akastunak.
Zoriaren arabera, kutxatik bi gai ateratzen dira. Kalkula
ezazu ateratako gai akastunen kopuruari dagokion
itxaropen matematikoa.5. Bi dado perfektu ditugu. Lehenengoaren aldeetan 1, 2, 3,
4, 5 eta 6 jartzen du, eta bigarrenaren aldeetan 1, 1, 1, 2,
2, 3. Bi dadoak jaurtitzen dira, eta lortutako bi zenbakien
arteko biderkadura X zorizko aldagaia da. Bila itzazu X-
en batez bestekoa, bariantza eta desbideratze tipikoa.6. Zorizko aldagai batek 1, 2, 3, 4, 5, 6 balioak hartzen ditu, eta balio hauen probablitateak 0, l ; 0,2 ; 0, l ; 0,3 ; 0,1 ; eta 0,2 dira. Kalkulatu E(X) edo eta V(X) edo
eta V(X) edo 7. Ongi orekatutako txanpon bat lau aldiz jaurtitzen da.a) Izan bedi X zorizko aldagaia, 2. ariketan aztertu den
lortutako alde kopurua. Kalkulatu X-en batez bestekoa,
bariantza eta desbideratze tipikoa.b) Y zorizko aldagaiak, txanpona lau aldiz jaurtitzerakoan
elkarren segidan ateratzen den alde kopururik handiena
adierazten du. Kalkulatu Y-ren probabilitate
funtzioa edo legea, batez bestekoa, bariantza eta desbideratze
tipikoa.8. Alboratua dagoen txanpon bat alde bat edo bost
ifrentzu atera arte jaurtitzen da. Txanpona horrela
alboratua dago : p(aldea) = 1/3 eta p(ifrentzua) = 2/3.
7. Ongi orekatutako txanpon bat lau aldiz jaurtitzen da.a) Izan bedi X zorizko aldagaia, 2. ariketan aztertu den
lortutako alde kopurua. Kalkulatu X-en batez bestekoa,
bariantza eta desbideratze tipikoa.b) Y zorizko aldagaiak, txanpona lau aldiz jaurtitzerakoan
elkarren segidan ateratzen den alde kopururik handiena
adierazten du. Kalkulatu Y-ren probabilitate
funtzioa edo legea, batez bestekoa, bariantza eta desbideratze
tipikoa.8. Alboratua dagoen txanpon bat alde bat edo bost
ifrentzu atera arte jaurtitzen da. Txanpona horrela
alboratua dago : p(aldea) = 1/3 eta p(ifrentzua) = 2/3.
Kalkula ezazu jaurtiketa kopuruari dagokion itxaropen
matematikoa.9. Bi dado perfektu jaurtitzen dira. Izan bedi X lortzen
diren bi zenbakien artean txikiena adierazten duen
zorizko aldagaia (3. ariketan ikusi den bezala) Kalkula
itzazu X-en batez bestekoa, bariantza eta desbideratze
tipikoa.10. Azterketa batera bost hautagai aurkezten dira. Azterketa hori hautagaien %40ak gainditzen du. Izan bedi X azterketa hori gainditzen duen hautagai kopurua.
Kalkula itzazu X-en probabilitate funtzioa edo legea, E(X), V(X),
V. Tchebychefen desberdintza
Zorizko aldagai baten batez bestekoa eta desbideratze tipikoa nola definitu diren kontuan izanik, balio gehienak batez bestekotik hurbil egongo direla esan daiteke. Nahiz zorizko saiakuntza batean nahiz bestelakoetan, emaitza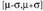 tartean edo
tartean edo tartean egotearen probabilitateak oso handia izan behar luke. Tchebychefen desberdintzak horixe frogatzen du, baldintza orokorretan, probabilitate horrentzat gutxieneko borne bat ematen duela.Hori frogatzeko bariantza hartzen da oinarri :
tartean egotearen probabilitateak oso handia izan behar luke. Tchebychefen desberdintzak horixe frogatzen du, baldintza orokorretan, probabilitate horrentzat gutxieneko borne bat ematen duela.Hori frogatzeko bariantza hartzen da oinarri : .
. tartean gutxienez daude emaitzen proportzioa jakin nahi bada :
tartean gutxienez daude emaitzen proportzioa jakin nahi bada : Hiru batugaiak positiboak dira. Bigarrena kentzen badugu,
horrela geldituko litzateke :
Hiru batugaiak positiboak dira. Bigarrena kentzen badugu,
horrela geldituko litzateke :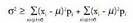 Bi batukarietan
Bi batukarietan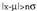 dela egiaztatzen da, beraz,
dela egiaztatzen da, beraz, -ren ordez
-ren ordez jarriko balitz, horrela geldituko litzateke :
jarriko balitz, horrela geldituko litzateke : Baina parentesi artean dauden probabilitateen batura, aztergari denaren aurkako gertaeraren probabilitatea da ; hau da,
Baina parentesi artean dauden probabilitateen batura, aztergari denaren aurkako gertaeraren probabilitatea da ; hau da, da.
da.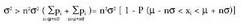 .
. sinplifikatuz, eta probabilitatea bakartuz, hau lortzen da :
sinplifikatuz, eta probabilitatea bakartuz, hau lortzen da : Desberdintza hau Tchebychefen desberdintza izenaz ezagutzen da. Aldagai arruntenetan borne hau erraz gainditzen da. Hurrengo gaian ikusiko den bezala, banaketa normalean,
Desberdintza hau Tchebychefen desberdintza izenaz ezagutzen da. Aldagai arruntenetan borne hau erraz gainditzen da. Hurrengo gaian ikusiko den bezala, banaketa normalean,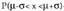 -ren balioa, gutxi gora behera, 0,6826 da, eta Tchebychefen desberdintzak
ez du ezer ziurtatzen.
-ren balioa, gutxi gora behera, 0,6826 da, eta Tchebychefen desberdintzak
ez du ezer ziurtatzen.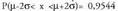 inserted text
inserted text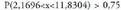 inserted text
inserted text
Bidezko jokoak: itxaropen matematikoa
Joko bat bidezkoa edo ekitatiboa da irabazteko zailtasuna lor daitekeen
sariaren mailakoa denean. Traineru apustuetan aritzen diren askok A trainerua
B trainerua baino lau aldiz hobea bada, ziur aski A traineruak irabaziko
duen arren, B traineruaren alde apustua egitea hobe dela uste dute, batez ere
irabaz daitekeena galduko litzatekeenaren laukoitza bada. Zoriaren araberako
joko askotako partehartzaileek ideia horren arabera jarduten dute : "irabaztea
zaila izan arren, irabazten bada jasoko den saria, seguruenik, galduko
dena baino askoz ere handiagoa izango da". Matematikoki honela adieraziko
litzateke ideia hau: bidezko joko batean itxaropen matematikoak zero
izan behar du. Adibidez, lehen ikasitako loteriaren jokoan, zenbaki bakar bat
zegoen saritua, baina itxaropen matematikoa zero zela eta, sariaren tamainak
saria lortzeko zegoen zailtasuna berdintzen zuen.Joko bat aldekoa da itxaropen matematikoa positiboa denean, hau da,
irabaztea espero daitekeenean, eta kontrakoa itxaropen matematikoa
negatiboa denean. Kalkulu hauek guztiak egiten direnean, irabazitako
dirua positibotzat eta galdutakoa edo txartela erosterakoan ordaindutakoa
negatibotzat hartu behar dira.Zorte onak edo txarrak sor ditzakeen gorabeherak alde batera utzita,
kalkulu honek, joko bat jokatzen hasi aurretik dirua irabaz daitekeen ala ez
esango digu kalkulu honek.• Adibideak:1. A eta B jokalariek dado bat jaurtitzen dute. Zenbaki txikiena ateratzen
duenak 1.000 pta. emango dizkio zenbaki handiena atera duenari
batek atera duenaren eta besteak atera duenaren artean dagoen puntu
bakoitzeko. Joko hau bidezkoa edo ekitatiboa al da?Bai, bidezkoa da. Irabazi aldagaiaren banaketa hau da : eta batez bestekoa :
eta batez bestekoa : Beraz bidezkoa edo ekitatiboa da.2. ONCEk egiten duen zozketa bakoitzean 100.000 zenbaki sartzen
dira, eta zenbaki bakoitzak 100 serie edo kupoi ditu. Kupoi bakoitza 100
pezetatan saltzen bada, eta jokoa bidezkoa izatea nahi bada, zenbat eman
beharko lukete saritan : a) «zenbakia asmatu» sari bakarra egongo balitz, eta
b) »¢zenbakia eta seriea asmatu» gertaerak jasoko balu saria.a) Guztira 100.000 zenbaki ditugu eta bakarra da aldekoa; beraz:
Beraz bidezkoa edo ekitatiboa da.2. ONCEk egiten duen zozketa bakoitzean 100.000 zenbaki sartzen
dira, eta zenbaki bakoitzak 100 serie edo kupoi ditu. Kupoi bakoitza 100
pezetatan saltzen bada, eta jokoa bidezkoa izatea nahi bada, zenbat eman
beharko lukete saritan : a) «zenbakia asmatu» sari bakarra egongo balitz, eta
b) »¢zenbakia eta seriea asmatu» gertaerak jasoko balu saria.a) Guztira 100.000 zenbaki ditugu eta bakarra da aldekoa; beraz: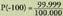 eta
eta Jokoa bidezkoa izateko :.
Jokoa bidezkoa izateko :. honi kupoia erosteko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Beraz jokoabidezkoa izateko hamar milioi pezetako saria eman behar luteke.b) Salgai jartzen den kupoi kopurua 100.100.000 = 10.000.000 da.
honi kupoia erosteko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Beraz jokoabidezkoa izateko hamar milioi pezetako saria eman behar luteke.b) Salgai jartzen den kupoi kopurua 100.100.000 = 10.000.000 da.
Irabazle bakarra zenbakia eta seriea asmatzen dituena bada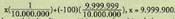 , honi kupoia eros- 0 000 090 )' teko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Beraz, jokoabidezkoa izateko mila milioi pezetako saria eman behar lukete.3. Loto edo "Loteria primitiva" delakoak letik 49ra zenbakituriko 6
zenbakitan 6 marra behar dira. Txartel bakoitzak 100 pezeta baliodituela suposatzen da. Jokoa bidezkoa edo ekitatiboa izateko, zenbatekoa
izan behar du sariak,a) Saria sei zenbakiak asmatzen dituenei bakarrik ematen bazaie?b) 5 asmatzen dutenen artean eta Eak asmatzen dituztenen artean diru
kopuru bera banatzen bada?a) Kasu posibleak
, honi kupoia eros- 0 000 090 )' teko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Beraz, jokoabidezkoa izateko mila milioi pezetako saria eman behar lukete.3. Loto edo "Loteria primitiva" delakoak letik 49ra zenbakituriko 6
zenbakitan 6 marra behar dira. Txartel bakoitzak 100 pezeta baliodituela suposatzen da. Jokoa bidezkoa edo ekitatiboa izateko, zenbatekoa
izan behar du sariak,a) Saria sei zenbakiak asmatzen dituenei bakarrik ematen bazaie?b) 5 asmatzen dutenen artean eta Eak asmatzen dituztenen artean diru
kopuru bera banatzen bada?a) Kasu posibleak dira. Txartel bakarra jokatzen bada aldeko kasua bakarra da:
dira. Txartel bakarra jokatzen bada aldeko kasua bakarra da: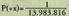 Beste denak aurkakoak dira :
Beste denak aurkakoak dira : Jokoa bidezkoa izateko :
Jokoa bidezkoa izateko :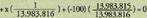 izan behar du; beraz x=1.398.381.500. Honi txartela erosteko ordaindu ditugun 100pezetak gehitu behar zaizkio. Jokoa bidezkoa izango da, saria 1.398.381.600 pezetatakoab) Sei zenbakiak asmatzeko aukera bakarra dugu, baina 5 zenbaki asmatzeko 6.43=258 (6, atera diren sei zenbakietarik edozein oker jar daitekeelako eta 43 oker dagoen horren ordez gelditzen den edozein jarri daitekeelako) aukera desberdin ditugu. Seirak asmatu dituenak x irabazten badu, bostak asmatu dituztenek ere x irabaziko dute ; hau da hauetariko bakoitzak x/258 irabaziko du.Jokoa bidezkoa izateko :
izan behar du; beraz x=1.398.381.500. Honi txartela erosteko ordaindu ditugun 100pezetak gehitu behar zaizkio. Jokoa bidezkoa izango da, saria 1.398.381.600 pezetatakoab) Sei zenbakiak asmatzeko aukera bakarra dugu, baina 5 zenbaki asmatzeko 6.43=258 (6, atera diren sei zenbakietarik edozein oker jar daitekeelako eta 43 oker dagoen horren ordez gelditzen den edozein jarri daitekeelako) aukera desberdin ditugu. Seirak asmatu dituenak x irabazten badu, bostak asmatu dituztenek ere x irabaziko dute ; hau da hauetariko bakoitzak x/258 irabaziko du.Jokoa bidezkoa izateko : izan behar du; beraz x=699.177.850 eta bost asmatu dutenentzat
izan behar du; beraz x=699.177.850 eta bost asmatu dutenentzat izango litzateke. Honi txartela erosteko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Jokoa bidezkoa izangoda, sariak 699.177.950 eta 2.710.091,7 pezetatakoak direnean.4. "Chuck-a-luck" iparrameriketako feria joko bat da. Joko honetan
letik 6ra bitarteko zenbaki baten alde apustu egiten da bankuaren aurka.
izango litzateke. Honi txartela erosteko ordaindu ditugun 100 pezetak gehitu behar zaizkio. Jokoa bidezkoa izangoda, sariak 699.177.950 eta 2.710.091,7 pezetatakoak direnean.4. "Chuck-a-luck" iparrameriketako feria joko bat da. Joko honetan
letik 6ra bitarteko zenbaki baten alde apustu egiten da bankuaren aurka.
Bankuak hiru dado jaurtitzen ditu. Apusturako hautatu dugun zenbakia
behin azaltzen bada, hasieran jarritakoa eta beste hainbeste ematen du
bankuak. Bi aldiz ateratzen bada apustuan jarritakoari honen bikoitza
gehitzen dio. Eta hiru aldiz ateratzen bada apustuan jarritakoa eta honen
hirukoitza itzultzen du bankuak. Zenbatekoa da irabazteko itxaropena?Eman dezagun 3 zenbakiaren alde 100 pezeta jokatu ditugula. Hiruhiruko ateratzearen probabilitatea da, bi hiruko ateratzearen probabilitatea
da, bi hiruko ateratzearen probabilitatea , eta hiruko bat ateratzearen probabilitatea
, eta hiruko bat ateratzearen probabilitatea . Hirukorik ez ateratzearen probabilitatea
. Hirukorik ez ateratzearen probabilitatea da. Beraz, jokalariak duen irabaztekoitxaropena hau izango da :
da. Beraz, jokalariak duen irabaztekoitxaropena hau izango da : Beraz, jokoa ez da bidezkoa. Bankua daukanak irabazteko aukera gehiago ditu, eta beraren aurka jokatzen duenak galtzeko batez besteko itxaropena %7,87koa da.Legeak onartzen dituen joko gehienak ez dira bidezkoak. Espainian
loteriako diruaren %30a eta kinieletako diruaren %45a ez dira saritan
banatzen. Kiniela edo zaldi lasterketetako apustuetan, Frantziako tierce
delakoetan adibidez, ongi informatuta dagoen jokalari batek beste jokalari
batek baino apustu gehiago asma ditzake, eta irabazien galera hori probabilitateen
hobekuntzarekin berdin dezake. Baina horretarako gaizki
informatuta dauden apustulari dezentek parte hartu behar dute.
Beraz, jokoa ez da bidezkoa. Bankua daukanak irabazteko aukera gehiago ditu, eta beraren aurka jokatzen duenak galtzeko batez besteko itxaropena %7,87koa da.Legeak onartzen dituen joko gehienak ez dira bidezkoak. Espainian
loteriako diruaren %30a eta kinieletako diruaren %45a ez dira saritan
banatzen. Kiniela edo zaldi lasterketetako apustuetan, Frantziako tierce
delakoetan adibidez, ongi informatuta dagoen jokalari batek beste jokalari
batek baino apustu gehiago asma ditzake, eta irabazien galera hori probabilitateen
hobekuntzarekin berdin dezake. Baina horretarako gaizki
informatuta dauden apustulari dezentek parte hartu behar dute.
VI. Banaketa binomiala
Zorizko aldagai batek emaitza edo balio gutxi dituenean, zuzenean
kalkula daiteke aldagai honi dagokion probabilitate funtzioa,
taula baten edo barra diagrama baten bidez. Kasu gehienetan, zorizko
aldagaiaren balio bakoitzari dagokion probabilitatea ematen
duen adierazpen aljebraiko baten bidez ematen da. Esapide hauek
zorizko aldagaiak bete behar dituen hipotesi batzuetatik lortzen
dira. Azterketa sakonagoa merezi dute horietan ohikoenak, alegia
zorizko aldagai diskretuen banaketa binomialak eta zorizko aldagai
jarraituen banaketa normalak.Banaketa binomiala, edo Bernoulliren banaketa, zorizko n oinarrizko
saiakuntzez osaturiko saiakuntza batean asmatze kopurua
zenbatekoa den jakin nahi den kasuari dagokion banaketa da. Banaketa
batek, binomiala izateko, zera bete behar du :1. Oinarrizko esperientzia bakoitzak bi aukera bakarrik izan ditzake
: asmatu (arrakasta) A edo huts egin (porrota) (H), eta aukera
horien probabilitateak dira :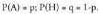 2. Saiakuntza n aldiz egiten da, eta zorizko saiakuntza asmatze
kopurua edo arrakasta deritzana izango da.3. Saiakuntza bakoitzeko arrakasta edo porrotaren probabilitateak
aurreko saiakuntzakoekin ez du zerikusirik izan behar. Hau da, p
eta q balioak konstante mantenduko dira n saiakuntzetan.Bi banaketa binomial desberdinak dira saiakuntza errepikatzen
den n aldi kopurua edo oinarrizko saiakuntza bakoitzeko p probabilitatea
desberdinak direnean. Hauek dira banaketa binomiala
zehazten duten parametroak, eta hori dela eta, banaketa hau izendatzeko
B(n, p) idazten da.• Adibideak:1. Txanpon bat bost aldiz jaurtitzen da, eta 3 alde ateratzearen
probabilitatea ezagutu nahi da. Saiakuntza honetan bi aukera bakarrik
daude, aldea edo ifrentzua atera, eta beraz lehenengo baldintza
betetzen du. Ateratzen den alde kopurua eskatzen duenez, bigarren
baldintza betetzen du. Txanponen jaurtialdi guztiak elkarren independenteak
direnez, hirugarren baldintza ere betetzen du, beraz B
(5, 1/2) banaketa binomial bat da.2. Europako biztanleriaren %50 emakumezkoez osatua da.
2. Saiakuntza n aldiz egiten da, eta zorizko saiakuntza asmatze
kopurua edo arrakasta deritzana izango da.3. Saiakuntza bakoitzeko arrakasta edo porrotaren probabilitateak
aurreko saiakuntzakoekin ez du zerikusirik izan behar. Hau da, p
eta q balioak konstante mantenduko dira n saiakuntzetan.Bi banaketa binomial desberdinak dira saiakuntza errepikatzen
den n aldi kopurua edo oinarrizko saiakuntza bakoitzeko p probabilitatea
desberdinak direnean. Hauek dira banaketa binomiala
zehazten duten parametroak, eta hori dela eta, banaketa hau izendatzeko
B(n, p) idazten da.• Adibideak:1. Txanpon bat bost aldiz jaurtitzen da, eta 3 alde ateratzearen
probabilitatea ezagutu nahi da. Saiakuntza honetan bi aukera bakarrik
daude, aldea edo ifrentzua atera, eta beraz lehenengo baldintza
betetzen du. Ateratzen den alde kopurua eskatzen duenez, bigarren
baldintza betetzen du. Txanponen jaurtialdi guztiak elkarren independenteak
direnez, hirugarren baldintza ere betetzen du, beraz B
(5, 1/2) banaketa binomial bat da.2. Europako biztanleriaren %50 emakumezkoez osatua da.
Zoriaren arabera 6 pertsona hautatzen dira eta horietariko 2 emakume
izatearen probabilitatea ezagutu nahi da. Saiakuntza honetan
aldiko hautatzen den pertsonaren sexua zein den zehazten da. Saiakuntza
bakoitzean bi aukera bakarrik ditugu emakumea izan ala ez
izan. Aldagaia emakume kopurua da. Eta probabilitatea finkoa da :
0,5. Beraz hau ere B (6 ; 0,5) banaketa binomial bat da.3. Aurrekoaren antzekoa izan arren banaketa binomiala ez den
adibide bat azalduko da orain :Hamar pertsonek osatzen duten talde batean erdiak emakumeak
dira eta beste erdiak gizonak. Bila ezazu talde horretatik zoriaren
arabera hautatutako sei kideren artean bi emakume bakarrik izatearen
probabilitatea.Kasu honetan ez da hirugarren baldintza betetzen. Izan ere, taldea
10 pertsonek bakarrik osatzen dutenez, lehenengoa emakumea izatearen
probabilitatea 5/10 da, baina lehenengoa emakumea izanik
bigarrena emakumea izatearen probabilitatea 4/9 da. Aurreko adibidean
honek ez zuen zerikusirik, izan ere hartu den populazioa
hain handia zenez, elementu bat gutxiago kontuan hartzeak ez zuen
emaitza aldatzen.Banaketa binomial baten probabilitate funtzioaIkus dezagun banaketa binomial baten adibidea : 6 txintxeta berdin
jaurtitzen dira. Txintxeta hauek buruz (B) edo puntaz (P) geldi
daitezke, gertaera bakoitzaren probabilitateak P(B) = 0,6 eta P(P) =
0,4 dira, eta puntaz zenbat gelditzen diren jakin nahi da. B(6 ; 0,4)
banaketa binomial bat da.4 puntaz eta 2 buruz gelditzearen probabilitatea zenbatekoa den
jakiteko, lehenengo lauak puntaz eta azken biak buruz gelditu direla
pentsatuko dugu. Gertaera honen probabilitatea hau da : Baina hau ez da 4 puntaz eta 2 buruz gelditzeko era bakarra ; PPBBPP edo PBPPBP aukerak ere badira. 6 txintxetatik lau puntaz gelditzeko era desberdin guztiak, launaka harturiko sei elementuren konbinazioak, hau da
Baina hau ez da 4 puntaz eta 2 buruz gelditzeko era bakarra ; PPBBPP edo PBPPBP aukerak ere badira. 6 txintxetatik lau puntaz gelditzeko era desberdin guztiak, launaka harturiko sei elementuren konbinazioak, hau da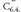 kalkulatuz lortzen dira. Beraz,
kalkulatuz lortzen dira. Beraz,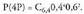 Oro har, B(n, p) banaketa binomial batean, metodo bera erabiliz k
arrakasta lortzeko formula hau erabiliko dugu :
Oro har, B(n, p) banaketa binomial batean, metodo bera erabiliz k
arrakasta lortzeko formula hau erabiliko dugu : Hau da saiakuntza binomial bati dagokion probabilitate funtzioa
. Banaketa funtzioa, berriz, aurretik lortutako emaitzak batuz
lortzen da :
Hau da saiakuntza binomial bati dagokion probabilitate funtzioa
. Banaketa funtzioa, berriz, aurretik lortutako emaitzak batuz
lortzen da :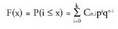
Banaketa binomial baten batez bestekoa eta desbideratze tipikoa
Ariketaren enuntziatua edozein dela ere, banaketa binomial
guztietan probabilitatearen banaketa funtzioa berdina izateak
aukera ematen du batez bestekoa eta desbideratze tipikoa kalkulatzean
n eta p-ren balioen mende bakarrik dauden formulak erabiltzeko
.B(n, p) banaketa binomialaren batez bestekoa hau da : Bariantza kalkulatzeko :
Bariantza kalkulatzeko : Eta hortik,
Eta hortik, eginez eta batukaritik kopuru konstanteak atereaz :
eginez eta batukaritik kopuru konstanteak atereaz : Azken batukariak, probabilitate guztien batura denez, 1 balio du.
Azken batukariak, probabilitate guztien batura denez, 1 balio du.
Bigarrena, batez bestekoaren definizioa da. Eta lehenengoarentzat,
x=k-ren probabilitatea ateratzeko dagokion formula erabiliz eta
konbinazio zenbakia sinplifikatuz, zera lortzen da : Eta
Eta denez, gehiago sinplifika daiteke :
denez, gehiago sinplifika daiteke : Beraz desbideratze tipikoa
Beraz desbideratze tipikoa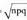 izango da.• Adibideak:1. Txanpon bat 10 aldiz jaurtitzen da. Zenbatekoa da 5 alde ateratzearen
probabilitatea? Zenbat balio dute batez bestekoak eta desbideratze
tipikoak?Banaketa binomial bat da ; izan ere, bi aukera, aldea edo ifrentzua,
bakarrik daude. Jaurtialdi bateko emaitzak ez du zerikusirik hurrengo
jaurtialdiko emaitzarekin. Eta zorizko aldagaia, ateratzen den
alde kopurua da. n = 10 eta p = 0,5 denez, banaketa binomiala
B(10 ; 0,5) da.
izango da.• Adibideak:1. Txanpon bat 10 aldiz jaurtitzen da. Zenbatekoa da 5 alde ateratzearen
probabilitatea? Zenbat balio dute batez bestekoak eta desbideratze
tipikoak?Banaketa binomial bat da ; izan ere, bi aukera, aldea edo ifrentzua,
bakarrik daude. Jaurtialdi bateko emaitzak ez du zerikusirik hurrengo
jaurtialdiko emaitzarekin. Eta zorizko aldagaia, ateratzen den
alde kopurua da. n = 10 eta p = 0,5 denez, banaketa binomiala
B(10 ; 0,5) da.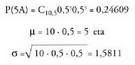 2. Test batean 10 galdera daude, eta galdera bakoitzak 4 aukera
ditu, horietatik bakarra zuzena. Pertsona batek zoriaren araberaerantzuten du.a) Zenbatekoa da 5 galderak asmatzearen probabilitatea?b) Zenbatekoa da galdera guztiak asmatzearen probabilitatea?c) Zein da, ezer jakin gabe erantzuten duenaren asmatze kopuruaren
batez bestekoa? Zein desbideratze tipikoa?d) Tchebychefen desberdintza erabiliz, eman itzazu ezer ez dakitenek
emandako erantzunen %75 baino gehiago biltzen dituen tarteari
dagozkion bi mugak.B(10 ; 0,25) banaketa binomiala da.
2. Test batean 10 galdera daude, eta galdera bakoitzak 4 aukera
ditu, horietatik bakarra zuzena. Pertsona batek zoriaren araberaerantzuten du.a) Zenbatekoa da 5 galderak asmatzearen probabilitatea?b) Zenbatekoa da galdera guztiak asmatzearen probabilitatea?c) Zein da, ezer jakin gabe erantzuten duenaren asmatze kopuruaren
batez bestekoa? Zein desbideratze tipikoa?d) Tchebychefen desberdintza erabiliz, eman itzazu ezer ez dakitenek
emandako erantzunen %75 baino gehiago biltzen dituen tarteari
dagozkion bi mugak.B(10 ; 0,25) banaketa binomiala da.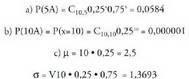 d) Tchebychefen desberdintza erabiliz
d) Tchebychefen desberdintza erabiliz ateratzen da, beraz eskatutako %75a 0 eta 5,23 noten artean egongo da.3. Pertsona bat eta bere ama urteko egun berean, urte bisiestoak
kontuan hartu gabe, jaio izanaren probabilitatea 1/365 da. Milioi
bat biztanleko biztanleria batean zenbat kasu izango dira, batez
beste? Zein da banaketa honen desbideratze tipikoa?
ateratzen da, beraz eskatutako %75a 0 eta 5,23 noten artean egongo da.3. Pertsona bat eta bere ama urteko egun berean, urte bisiestoak
kontuan hartu gabe, jaio izanaren probabilitatea 1/365 da. Milioi
bat biztanleko biztanleria batean zenbat kasu izango dira, batez
beste? Zein da banaketa honen desbideratze tipikoa? Adibide honetan ikusten denez, hurbilketarik egin gabe ariketa
hauek askatzeko posibilitatea n-ren balioaren mende dago. Balio
hau oso handia denean probabilitatea kalkulatzea oso zaila da,
baina batez bestekoa eta desbideratze tipikoa kalkulatzea oso erraza
da.• Adibidea :Garbigailu fabrika bateko produktuen % 1 ak akatsak ditu. 10
garbigailu hartzen badira, zenbatekoa da horietako 4 akastun izatearen
probabilitatea?Egunero 50 garbigailu egiten badira, zenbatekoa da akastunak bi
baino gutxiago izatearen probabilitatea?Urtero 1.000 garbigailu egiten badira, zenbatekoa da akastunak 5
baino gehiago eta 10 baino gutxiago izatearen probabilitatea?Zenbatekoa da urtero espero den garbigailu akastunen batez besteko
balioa? Zenbatekoa bere desbideratze tipikoa?
Adibide honetan ikusten denez, hurbilketarik egin gabe ariketa
hauek askatzeko posibilitatea n-ren balioaren mende dago. Balio
hau oso handia denean probabilitatea kalkulatzea oso zaila da,
baina batez bestekoa eta desbideratze tipikoa kalkulatzea oso erraza
da.• Adibidea :Garbigailu fabrika bateko produktuen % 1 ak akatsak ditu. 10
garbigailu hartzen badira, zenbatekoa da horietako 4 akastun izatearen
probabilitatea?Egunero 50 garbigailu egiten badira, zenbatekoa da akastunak bi
baino gutxiago izatearen probabilitatea?Urtero 1.000 garbigailu egiten badira, zenbatekoa da akastunak 5
baino gehiago eta 10 baino gutxiago izatearen probabilitatea?Zenbatekoa da urtero espero den garbigailu akastunen batez besteko
balioa? Zenbatekoa bere desbideratze tipikoa?
n eta k-ren balio desberdinetarako banaketa binomialaren probabilitate balioak.
- Ariketak
11. Gaitasun test batean sei galdera azaltzen dira, eta galdera
bakoitzerako hiru erantzun posible daude. Hiru
erantzun posible horietatik, bakarra da zuzena.ai) Zenbatekoa da jarritako lehenengo galdera zuzen
erantzutearen probabilitatea?aii) Zenbatekoa da jarritako galderetatik bat bakarrik
zuzen erantzutearen probabilitatea?aiii) Zenbatekoa da jarritako sei galderetatik lau
zuzen erantzutearen probabilitatea?aiv) Zenbatekoa da jarritako sei galderak zuzen erantzutearen
probabilitatea?av) Zenbatekoa da bosgarren galdera zuzen erantzun,
eta erantzun hori zuzen erantzuten duen
bigarrena izatearen probabilitatea?avi) Lehenengo biak ongi erantzun direla jakinik,
zenbatekoa da hiru galdera zuzen erantzutearen
probabilitatea?b) Gutxienez lau erantzun zuzen emanda hautagaiak
testa gainditzen du. Zenbatekoa da hautagaiek
testa gainditzeko duten probabilitatea?c) Hautagaiak zuzen emandako erantzun kopurua X
zorizko aldagaiak adierazten badu, kalkulatu X-
en itxaropen matematikoa eta bariantza.12. Joko bat irabaztearen probabilitatea 0,8 da. 12 aldiz
elkarren segidan jokatzen bada, zenbatekoa da 12-tik 7-
tan irabaztearen probabilitatea? Kalkulatu itxaropen
matematikoa eta desbideratze tipikoa.13. Hazi bat ernamuintzearen probabilitatea 0,98 da.
Lorazain batek dituen 400 lorontzietako bakoitzean
hazi bana jartzen du. Kalkula ezazu zenbat lorontzitako
hazia ernamuintzea espero den eta zenbatekoa
den desbideratze tipikoa.14. Futbolari batek penalti bat jaurtitzerakoan gola sartzeko
duen probabilitatea p = 0,70 da.ai) Zenbatekoa da jaurtitzen dituen 5 penaltietatik 3
gol sartzearen probabilitatea?aii) Zenbatekoa da jaurtitzen dituen 5 penaltietatik
gutxienez 3 gol sartzearen probabilitatea?aiii) Zenbatekoa da jaurtitzen dituen 5 penaltietatik
2, 4 eta 5. jaurtialdietan bakarrik gol sartzearen
probabilitatea?b) Zenbatekoa da gutxienez 0,95eko probabilitatearekin
gutxienez gol bat sartzeko egin behar duen
jaurtialdi kopururik txikiena?c) Beste jokalari batek (B), jaurtitako hiru penaltietatik
gutxienez batean gola sartzeko du 0,90eko probabilitatea
du. Zenbatekoa da jokalari honek jaurtialdi
bakar batean gola sartzeko duen probabilitatea?15. Iker eta Jokinek 5 partiduko tenis lehiaketa batean
parte hartzen dute. Elkarren aurka jokatzen dutenean,
Ikerrek irabazteko duen probabilitatea 3/5 da.a) Zenbatekoa da, Ikerrek zehazki hiru partidu irabazteko
duen probabilitatea?Beste batean ere Iker eta Jokinek beste lehiaketa batean
parte hartzen dute. Lehiaketa hiru partidu irabazten
dituenak irabaziko du.Oraingo honetan ere, Ikerrek partidua irabazteko probabilitatea
3/5 bada,b) Zenbatekoa da hiru partidu jokatu ondoren Ikerrek
lehiaketa irabazteko duen probabilitatea?c) Zenbatekoa da lau partidu jokatu ondoren Ikerrek
lehiaketa irabazteko duen probabilitatea?d) Zenbatekoa da Ikerrek lehiaketa irabazteko duen
probabilitatea?16. Loteria batean 20 txartel saltzen dira. Hauetatik 3 txartelek
saria dute. Pertsona batek 10 txartel erosten ditu.a) Kalkula ezazu, erosi dituen hamar txartel horien artean,
zenbatekoak diren hurrengo gertaeren probabilitateak
:i) Txartel saridun bakar bat izatearena.ii) Gutxienez txartel saridun bat izatearena.b) Saria duten hiru txartel horietako batekin 100 franko
irabazten dira, eta beste biekin 50na franko.
Erositako 10 txarteleko sorta bati lortutako irabazia
elkartzen dion X zorizko aldagaia kontuan harturik,
bila X-en probabilitate legea eta kalkulatu E(X)
batez bestekoa eta 6(X) desbideratze tipikoa.17. Joko bat irabazteko probabilitatea 0,75 da. Joko hori
7 aldiz jokatzen da. Kalkula ezazu, jokoa 5 aldiz irabazteko
dagoen probabilitatea. Zein da banaketa lege
honen irabaztea itxaron ditzakedan joko kopuruaren
itxaropen matematikoa?18. Lantegi batean industriarako pieza elektronikoak egiten
dira, eta egiten diren piezen %7 akastuna dela
ikusten da. Kalkula ezazu 10 pieza dituen kaxa batean
gutxienez bat akastuna izatearen probabilitatea.19. Berrehun pertsonek galdera bati erantzuten diote, erantzunak
zuzenak (Z) edo okerrak (O) izan daitezkela.
Erantzun okerra ematearen probabilitatea, aldi bakoitzean,
0,25 da. Erantzunak elkarren independenteak
direla suposatuz, bila erantzuna zuzena emango duela
espero den pertsona kopuruari dagokion probabilitate
funtzioa eta kalkulatu bere itxaropen matematikoa.
VII. Poissonen banaketa
Poissonen banaketa, aplikazio praktiko asko dituen probabilitate
diskretuko beste banaketa bat da. Zorizko aldagaia diskretu infinitua
da, nahiz eta aintzat hartzeko probabilitateak balio txikiei
dagozkienak izan, eta zorizko aldagaia infiniturantz doanean probabilitateak
zerorantz jo. Praktikan, kontuan hartzeko probabilitateak
dituzten balioak finituak dira.Denbora tarte finko batean gertaera bat zenbat aldiz betetzen den
kontatzea den zorizko saiakuntza, baldintza jakin batzuk beteaz,
Poissonen banaketaren adibide bat da. Bete behar dituen baldintzak
hauek dira :
- Denbora banako bakoitzeko, gertaera bat betetzearen probabilitateak
konstantea izan behar du.
- Aldi berean, ezin dira gertaera baten bi egoera gertatu.- Une jakin batean gertaera jakin bat gertatu izanak ez du zerikusirik
lehenago gertatu izan edo ez izanarekin.Egoera honen adibide gisa, zirkulazio gutxi duen errepide batetik
ordu jakin batean, adibidez goizeko bostetatik seietara, pasatzen
den auto kopurua har daiteke. Edo, ordu jakin batean, adibidez goizeko
hamarretatik hamaiketara, bulego batean sartzen den jende
kopurua, bezero asko ez dituenean. Adibide hauek ez dira baliagarriak
iharduera txikiko eta handiko aldiak batera hartuko balira edo
pertsonak eta autoak taldeka pasatzeko joera balute.. saiakuntza kopurua oso handia eta arrakasta lortzeko p probabilitatea
oso txikia denean banaketa binomialaren hurbilketa gisa
ere erabili daiteke Poissonen banaketa. Limitean, hau da, saiakuntza
kopurua infiniturantz doanean, banaketa binomiala Poissonen
banaketa bihurtzen da.Adibidez : Torloju fabrika batean urtero hamar milioi pieza egiten
badira, eta torloju bat akastuna izatearen probabilitatea %0,001
bada, zenbatekoa da torloju akastunen kopurua 50 eta 150 bitartekoa
izatearen probabilitatea? Ezinezkoa ez bada ere, 150naka harturiko
hamar milioiren konbinazioak kalkulatzea oso astuna da, horregatik
hobe da Poissonen banaketa erabiliz hurbilketa bat egitea.. infiniturantz doanean banaketa binomialeko probabilitate funtzioaren
limiteak Poissonen banaketako probabilitate funtzioaren
formula lortzeko balio du. Binomialetik Poissonenera dagoen urratsa
egitean kontuan hartzen da arrakasta kopuruen batez bestekoak
bere horretan irauten duela, hau da i=np finko dagoela. Datu
honekin, Poissonen banaketa erabat finkaturik gelditzen da. eginez, arrakastarik ez lortzearen probabilitatea hau izango da :
eginez, arrakastarik ez lortzearen probabilitatea hau izango da : Aldagaiaren ondoz ondoko bi baliori dagokien banaketa binomialeko probabilitate funtzioaren formulak alderatuz, eta ondoren ahal dena sinplifikatuz, erlazio hau lortzen da :
Aldagaiaren ondoz ondoko bi baliori dagokien banaketa binomialeko probabilitate funtzioaren formulak alderatuz, eta ondoren ahal dena sinplifikatuz, erlazio hau lortzen da : Bi espresio hauetan limiteak aplikatuz n oo-rantz doanean, hau ateratzen da :
Bi espresio hauetan limiteak aplikatuz n oo-rantz doanean, hau ateratzen da :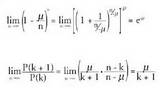 Hau da, limitean
Hau da, limitean Bi berdintza hauetatik abiatu eta errekurrentzia metodoa erabiliz
Poissonen banaketako probabilitate funtzioa lor daiteke :
Bi berdintza hauetatik abiatu eta errekurrentzia metodoa erabiliz
Poissonen banaketako probabilitate funtzioa lor daiteke :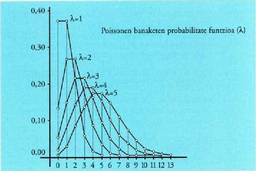 Banaketa binomiala erabiliz lortzen diren emaitzak, Poissonen
banaketara hurbilketa eginez lortzen diren emaitzen antzekoak direla
ikusteko, hurrengo adibideko emaitzak alderatuko ditugu :20 pieza ditugu, eta akastunak izatearen probabilitatea %4 da.
Banaketa binomiala erabiliz lortzen diren emaitzak, Poissonen
banaketara hurbilketa eginez lortzen diren emaitzen antzekoak direla
ikusteko, hurrengo adibideko emaitzak alderatuko ditugu :20 pieza ditugu, eta akastunak izatearen probabilitatea %4 da.
Aztertutako piezetatik bat, bi, etab. pieza akastun izatearen probabilitatea lortuko da, alde batetik B(20 ; 0,04) banaketa binomiala erabiliz, eta bestetik Poisson(0,8) banaketa erabiliz, izan ere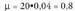 da.
da. Ondorio bera atera daiteke bien barra diagramak alderatzen badira ere.
Ondorio bera atera daiteke bien barra diagramak alderatzen badira ere. Poissonen banaketa baten batez bestekoa p dela eta bere bariantzarekin bat datorrela, hau da
Poissonen banaketa baten batez bestekoa p dela eta bere bariantzarekin bat datorrela, hau da
Poissonen banaketen probabilitate funtzioa
- Ariketak
20. Pertsona bat makinaz idazten ari da, eta idazten dituen
1.000 karaktereko 3 akats egiten ditu batez beste. Gutxi
gora behera 1.000na karaktere dituen hiru orrialde idatzi
behar baditu, kalkula ezazu, banaketa binomiala eta
Poissonen hurbilketa erabiliz, zenbatekoa den orrialde
bakar bat zuzendu behar izatearen probabilitatea.2 1. Biltzar batean 1.000 pertsona bildu dira, kalkula ezazu
zenbatekoa den bi biltzarkideren urtemuga abenduaren
31n izatearen probabilitatea. Zenbatekoa da bat
etortze edo kointzidentzia kopururik probableena?22. Ordu batzuetan ehungailu batek egiten duen lana
aztertu da, eta anezkaren 10.000 pasa aldiko sortutako
hausturak kontatu eta ondoko taula osatu da
VIII. Beste banaketa batzuk
Banaketa binomiala eta Poissonen banaketaz gainera, gai honetan
beste bi banaketa diskretu ikusiko ditugu : uniformea eta geometrikoa
. Ikas daitezkeen beste asko daude, baina bi hauek dira hemen
aztertuko diren azkenak.Dado bat jaurti eta ateratzen den zenbakia idaztea, banaketa diskretu uniformearen adibide bat da. 6 balio daude, letik 6ra, eta denek probabilitate bera dute :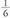 Oro har, balioak l etik n-ra baldin badoaz, probabilitatearen legea
Oro har, balioak l etik n-ra baldin badoaz, probabilitatearen legea da.letik n-ra bitarteko balioak hartzen dituen banaketa diskretuuniforme batean, batez bestekoa
da.letik n-ra bitarteko balioak hartzen dituen banaketa diskretuuniforme batean, batez bestekoa da, eta bariantza
da, eta bariantza 6 bat atera arte dado bat jaurti eta egin diren jaurtialdiak kontatzea,
banaketa diskretu geometriko bat da. Edozein banaketa geometrikori
dagokion
6 bat atera arte dado bat jaurti eta egin diren jaurtialdiak kontatzea,
banaketa diskretu geometriko bat da. Edozein banaketa geometrikori
dagokion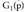 probabilitate funtzioa
probabilitate funtzioa da.
da.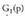 probabilitate funtzioaren batez bestekoa
probabilitate funtzioaren batez bestekoa da eta berebariantza
da eta berebariantza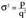 da.
da.
Bestalde, badago k = l etik hasteko ordez k = 0tik hasten den banaketa geometrikoa. Banaketa honen adibide gisa har daitke
ondokoa: jokalari batek dato bat jaurtitzen du ; 6 ateratzen badu
1.000 pta. irabaziko ditu, bestela jokoa bertan behera geldituko da.
banaketa geometrikoa. Banaketa honen adibide gisa har daitke
ondokoa: jokalari batek dato bat jaurtitzen du ; 6 ateratzen badu
1.000 pta. irabaziko ditu, bestela jokoa bertan behera geldituko da.
Adibide honetako zorizko aldagaia, jokalariak joko honekin irabazten
dituen milaka pezetak dira. Hau izango litzateke bere probabilitate
funtzioa : Oro har, k milakoen probabilitatea hau da.
Oro har, k milakoen probabilitatea hau da. Era honetako banaketa diskretu infinituak adierazteko G o (p) erabiltzen da, eta banaketa funtzioa
Era honetako banaketa diskretu infinituak adierazteko G o (p) erabiltzen da, eta banaketa funtzioa da.Batez bestekoa
da.Batez bestekoa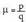 da, eta bariantza
da, eta bariantza
Formularioa
Ebazpideak
Zenbaki irrazionalen balioak hamarmilarenera eta ehunmilarenera biribildu dira. 10. Probabilitate funtzioa ;
10. Probabilitate funtzioa ; Ariketa hau errazago ebatzi daiteke B(5 ; 0,4) banaketa binomial
bat dela kontuan hartuz gero.
Ariketa hau errazago ebatzi daiteke B(5 ; 0,4) banaketa binomial
bat dela kontuan hartuz gero.
Zorizko aldagai jarraituak.
Banaketa Normala
I. Zorizko aldagai jarraituak
Zorizko aldagai diskretuek aldez aurretik ezagunak diren balioetatik
kopuru finito bat (edo infinito zenbagarria) besterik ezin dezakete
hartu. Atal honetan tarte bateko balio guztiak, baita edozein
balio erreal ere, har dezaketen zorizko aldagaiak kontuan hartuko
dira. Halakoak, zorizko aldagai jarriak dira.Biztanleria bateko elementu bakoitza bere altuerarekin elkartzen
duen aldagaia, makina batek egindako pieza bakoitza bere pisuarekin
elkartzen duena, edo autobus-geltoki jakin batean autobusa
hartzen duten pertsona bakoitzak autobusa hartzeko itxaron behar
duten denborarekin elkartzen duen aldagaia, zorizko aldagai jarraituaren
adibideak dira.Zorizko aldagai diskretuaren eta jarraituaren arteko desberdintasuna,
horiek definitzen dituzten bi funtzioetako irudi-multzo desberdinetan
dago. Desberdintasun horiek direla eta, zorizko aldagai
jarraituari dagokion probabilitate trataera, zorizko aldagai diskretuari
dagokionarengandik oso desberdina da. Zorizko aldagaia
jarraitua denean, ezin da aldagaiaren balio posible bakoitzari bere
probabilitatea elkartzen dion X-en probabilitate legea definitu ; izan
ere, aldagaiak balio infinito desberdin ditu, eta bakoitzari dagokion
probabilitatea, oro har, nulua izango da. Gainera, horrela izango ez
balitz, probabilitate guztien baturak, normalean, infinito emango
luke. Adibidez, [a,b] tartean definitutako banaketa uniforme bat
hartzen bada, non tarteko zenbaki guztiek probabilitate bera dutela
uste den, zenbaki bakoitzari dagokion probabilitatea kalkulatzeko
Laplaceren legea erabiltzeko aukera izanez gero, hori zero izango litzateke
; izan ere, aldeko kasua bakarra izango litzateke eta kasu posibleak
infinitoak. Edo biztanleria bateko altueren adibidea kontuan
hartuz gero, zoriaren arabera hautatutako pertsona batek 1,73
metro neurtzeko probabilitatea zenbatekoa den jakin nahi bada,
probabilitate hori zero da. 1,732 neurtzeko probabilitatea oraindik
txikiagoa izango zen. Eta metro bat eta 732050 mikra neurtzearen
probabilitatea ez litzateke kontuan hartzeko modukoa izango i3
metroko (hau da 1,732050807... metroko) altuera izateari dagokion
probabilitateak nulua izan beharko luke. Berez, lehenengo
kasuetan, altuera biribilduz, 1,73 ematean probabilitatea bilatzen
da; hau da, altuera [1,725, 1,735] tartean egotea bilatzen da, edo
altuera 1,732 denean, [1,7315, 1,7325] tartean egotea bilatzen da,
eta abar.Ariketa hori ebazteko era uler dadin, aurreko adibidean bezala
tarteetan taldekatzen den aldagai jarraitu bat hartzen da. Baina
balio zehatz bat ikasi ordez, zorizko aldagai jarraitua diskretu bezala
lantzerakoan lortzen diren histogramen aldakuntza aztertuko da.• Adibidez :Kimika arloko enpresa bateko kontrol-sailak produktu bateko
botilen edukien bolumena 210 zentimetro kubikokoa den jakin
nahi du. Horretarako 1.000 botila hartzen dituzte eta horien bolumena
zentimetro kubikotan neurtzen dute. Banaketa hau lortzen
dute : Emaitza hauei dagokien histograma hau da :
Emaitza hauei dagokien histograma hau da :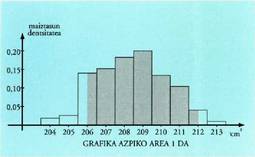 Lauki zuzen guztien azaleren batura bat da. Maiztasun guztiak
positiboak dira, eta zentimetro batzuetako zabalera duen tarte bateko
maiztasuna zenbatekoa den jakin nahi denean, tartean dauden
balioen maitasunak edo dagozkien lauki zuzenen azalerak batuko
dira. Adibide gisa, azpimarratutako zatiaren azalera eta botilen
bolumena [206, 211 ] tartekoa izateko probabilitatea bera da.Zentimetro kuboak neurtzen dituen tresna bat erabilti ordez,
zentimetro kubo laurdenak neurtzen dituen bat erabiliz gero, baliotaula
berriak aurreko taulak baino lau aldiz emaitza gehiago izango
lituzke, eta emaitza bakoitzari dagokion maiztasun erlatiboa txikiagoa
izango litzateke. Honek histograma hau emango luke :
Lauki zuzen guztien azaleren batura bat da. Maiztasun guztiak
positiboak dira, eta zentimetro batzuetako zabalera duen tarte bateko
maiztasuna zenbatekoa den jakin nahi denean, tartean dauden
balioen maitasunak edo dagozkien lauki zuzenen azalerak batuko
dira. Adibide gisa, azpimarratutako zatiaren azalera eta botilen
bolumena [206, 211 ] tartekoa izateko probabilitatea bera da.Zentimetro kuboak neurtzen dituen tresna bat erabilti ordez,
zentimetro kubo laurdenak neurtzen dituen bat erabiliz gero, baliotaula
berriak aurreko taulak baino lau aldiz emaitza gehiago izango
lituzke, eta emaitza bakoitzari dagokion maiztasun erlatiboa txikiagoa
izango litzateke. Honek histograma hau emango luke : Probabilitatearen eta histogramako goialdeko lerroaren azpian
dagoen azaleraren arteko erlazioa ez da aldatuko.Zentimetro kubotan neurtzeko ordez milimetro kubotan neurtzen
bada, eta lagineko botila-kopurua gehitzen bada, eta eskalak
aldatzen ez badira, dagokion histogramako eskilara-mailak ia ez dira
igarriko eta kurba baten antza izango du. Baina kurba hori beti
ardatz horizontalaren gainetik egongo da, beti positiboa da, eta
kurba eta ardatz horizontalaren arteko azalera osoak bat balio du.
Probabilitatearen eta histogramako goialdeko lerroaren azpian
dagoen azaleraren arteko erlazioa ez da aldatuko.Zentimetro kubotan neurtzeko ordez milimetro kubotan neurtzen
bada, eta lagineko botila-kopurua gehitzen bada, eta eskalak
aldatzen ez badira, dagokion histogramako eskilara-mailak ia ez dira
igarriko eta kurba baten antza izango du. Baina kurba hori beti
ardatz horizontalaren gainetik egongo da, beti positiboa da, eta
kurba eta ardatz horizontalaren arteko azalera osoak bat balio du.
Tarte bateko probabilitatea, tarteko mugen artean eta kurbaren
azpian dagoen azalera kalkulatuz lortzen da. Tarteen zabalerak zerorantz
egiten badu, batura hori integral batean bihurtuko da.
II. Zorizko aldagai jarraitu baten dentsitate-funtzioa
X zorizko aldagai jarraitu bat emanik, f funtzio erreal bat, zorizko
aldagaiaren dentsitate-funtzioa da ondokoa betetzen duenean :1. x-en edozein baliotarako, f(x) ez-negatiboa da.2. X, [x,x+h] tartean egotearen probabilitatea, tarte horretan
f(x)-eri dagokion kurbaren azpiko azalera da.3. Kurbaren azpiko azalera osoak 1 balio du.Definizio hau erabiliz, aldagaiaren balioa [x l ,xZ ] tartean egotearen
probabilitatea, integral honen bidez kalkulatzen da :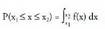 Zorizko aldagaien balioak a eta b-ren artean badaude, hirugarren
baldintza honako honen baliokidea da :
Zorizko aldagaien balioak a eta b-ren artean badaude, hirugarren
baldintza honako honen baliokidea da : Zorizko aldagaia zenbaki erreal guztientzat definituta badago,
integral hau beste honetan bihurtzen da :
Zorizko aldagaia zenbaki erreal guztientzat definituta badago,
integral hau beste honetan bihurtzen da : Definizio honen ondorio logiko bezala, aldagaiaren balio zehatz
baten probabilitatea nulua dela esan dezakegu.• Adibidea:Emandako tarte batean, adibidez [1,51 tartean, banaketa uniformea duen zorizko aldagai baten dentsitate-funtzioa definitu nahi da. Banaketa uniformea delako probabilitateak konstantea izanbeharko du. Hau da, dentsitate-funtzioa y = k izango da. k-ren
balioa zein den jakiteko :
Definizio honen ondorio logiko bezala, aldagaiaren balio zehatz
baten probabilitatea nulua dela esan dezakegu.• Adibidea:Emandako tarte batean, adibidez [1,51 tartean, banaketa uniformea duen zorizko aldagai baten dentsitate-funtzioa definitu nahi da. Banaketa uniformea delako probabilitateak konstantea izanbeharko du. Hau da, dentsitate-funtzioa y = k izango da. k-ren
balioa zein den jakiteko : Kasu honetan dentsitate-funtzioa hau izango da :
Kasu honetan dentsitate-funtzioa hau izango da :
III. Banaketa-funtzioa
Zorizko aldagai jarraituetan tarte bati dagokion probabilitatea,
Barrow-en erregela erabiliz, integral mugagabe baten goiko muturreko
balioa eta beheko muturreko balioaren arteko diferentzia
bezala lortzen da. Kasu honetan, aldagai baten balio bakoitzarentzako
balio hori edo balio txikiagoen probabilitatea ematen duen
banaketa-funtzioa oso erabilgarria izango da ; izan ere, horrela, probabilitateak
zuzenean lortu daitezke.[a,b] tartean definitutako X zorizko aldagai jarraituaren F banaketa-funtzioa
honela definitzen da :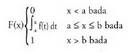 Zorizko aldagaiaren dentsitate-funtzioak honako itxura hau baldin
badu:
Zorizko aldagaiaren dentsitate-funtzioak honako itxura hau baldin
badu: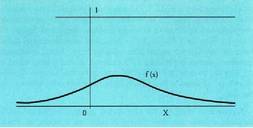 Banaketa-funtzioa hau izango da :
Banaketa-funtzioa hau izango da : Aldagaiak zenbaki erreal guztientzat balioak hartzen dituenean,
berriz, definizioa hau izango da :
Aldagaiak zenbaki erreal guztientzat balioak hartzen dituenean,
berriz, definizioa hau izango da : Propietateak :Definiziotik ondorio hauek atera daitezke :1. Banaketa-funtzioaren deribatua dentsitate-funtzioa da :F'(x) = f(x)2. F(x) gorakorra da ; hau da :
Propietateak :Definiziotik ondorio hauek atera daitezke :1. Banaketa-funtzioaren deribatua dentsitate-funtzioa da :F'(x) = f(x)2. F(x) gorakorra da ; hau da : bada, orduan
bada, orduan da.
da.
3.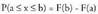 • Adibidea :Bilatu edozein [a,b] tartean definitutako zorizko aldagai jarraitu
uniforme baten banaketa-funtzioa.Oro har, banaketa uniforme bati dagokion dentsitate-funtzioa
hau da :
• Adibidea :Bilatu edozein [a,b] tartean definitutako zorizko aldagai jarraitu
uniforme baten banaketa-funtzioa.Oro har, banaketa uniforme bati dagokion dentsitate-funtzioa
hau da : Azken hau integratuz lortzen den banaketa-funtzioa hau da:
Azken hau integratuz lortzen den banaketa-funtzioa hau da:
- Ariketak
1. Zorizko aldagai jarraitu baten dentsitate-funtzioa
ondokoa da: a) Bila bere banaketa-funtzioa.b) Bila zenbatekoa den lortutako balioa 1/2 eta 1 balioen
artekoa izatearen probabilitatea.2. Zorizko aldagai jarraitu baten banaketa-funtzioa
hurrengoa da :
a) Bila bere banaketa-funtzioa.b) Bila zenbatekoa den lortutako balioa 1/2 eta 1 balioen
artekoa izatearen probabilitatea.2. Zorizko aldagai jarraitu baten banaketa-funtzioa
hurrengoa da :
IV. Zorizko aldagai jarraitu baten parametroak
Zorizko aldagai jarraituentzat, diskretuentzat bezalaxe, batez bestekoa
bezalako zentralazizaio parametroa eta bariantza edo desbidatze
tipikoa bezalako barreiadura parametroak defini daitezke.Balioak [a,b] tartean hartu, eta f(x) dentsitate-funtzioa duen
zorizko aldagai jarraitu baten Batez bestekoa edo Itxaropen Matematikoa,
honako integral honen emaitza da : Aldagai jarraituentzat emandako definizioa hau, aldagai diskretuentzat
emandako batez bestekoaren definizioaren baliokidea da.• Adibidea :Bilatu [1,5] tartean definitutako funtzio uniformearen batez bestekoa
.Dentsitate-funtzioa hau da :
Aldagai jarraituentzat emandako definizioa hau, aldagai diskretuentzat
emandako batez bestekoaren definizioaren baliokidea da.• Adibidea :Bilatu [1,5] tartean definitutako funtzio uniformearen batez bestekoa
.Dentsitate-funtzioa hau da : Balioak [a,b] tartean hartu, eta f(x) dentsitate-funtzioa duen
zorizko aldagai jarraitu baten d' bariantza hau da :
Balioak [a,b] tartean hartu, eta f(x) dentsitate-funtzioa duen
zorizko aldagai jarraitu baten d' bariantza hau da : Edo sinplifikatuz :
Edo sinplifikatuz :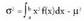 Zorizko aldagai jarraitu baten desbideratze tipikoa bariantzaren erro karratua da eta
Zorizko aldagai jarraitu baten desbideratze tipikoa bariantzaren erro karratua da eta -ren bidez adierazten da.• Adibidea:[a,b] tartean definitu, eta U(a,b)-ren bidez adierazitako banaketa
jarraitu uniforme bat emanik, bila bere batez bestekoa eta bere desbideratze
tipikoa.Banaketa uniforme bati dagokion dentsitate-funtzioa hau da :
-ren bidez adierazten da.• Adibidea:[a,b] tartean definitu, eta U(a,b)-ren bidez adierazitako banaketa
jarraitu uniforme bat emanik, bila bere batez bestekoa eta bere desbideratze
tipikoa.Banaketa uniforme bati dagokion dentsitate-funtzioa hau da : Beraz batezbestekoa hau izango da :
Beraz batezbestekoa hau izango da : Desbidazio tipikoa kalkulatu aurretik bariantza kalkulatuko
dugu :
Desbidazio tipikoa kalkulatu aurretik bariantza kalkulatuko
dugu : Sinplifikatuz hau gelditzen da:
Sinplifikatuz hau gelditzen da: Beraz desbidazio tipikoaren balioa hau izango da :
Beraz desbidazio tipikoaren balioa hau izango da :
- Ariketak
3. Zorizko aldagai batek balio erreal positiboak hartzen ditu, eta bere dentsitate-funtzioa da, batez besteko bezala 1 duen banaketa esponentziala.a) Dentsitate-funtzioak bete behar dituen baldintzak
betetzen dituela egiaztatu.b) Bilatu F(X) banaketa-funtzioa.c) Bilatu batez bestekoa.d) Bere mediana bere batez bestekoa baino txikiagoa dela
egiaztatu.e) Bilatu bariantza.4. X zorizko aldagai jarraitu bati dagokion banaketa-funtzioa
hau da :
da, batez besteko bezala 1 duen banaketa esponentziala.a) Dentsitate-funtzioak bete behar dituen baldintzak
betetzen dituela egiaztatu.b) Bilatu F(X) banaketa-funtzioa.c) Bilatu batez bestekoa.d) Bere mediana bere batez bestekoa baino txikiagoa dela
egiaztatu.e) Bilatu bariantza.4. X zorizko aldagai jarraitu bati dagokion banaketa-funtzioa
hau da :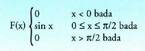
V. Zorizko alda aien artean eragiketak ditugunean, batez bestekoa eta bariantza kalkulatzeko era
Y zorizko aldagaia, ezaguna den beste X zorizko aldagai baten
konbinazio lineala bezala definituta dagoenean, hau da, a eta b zenbaki
errealak direlarik, Y = aX + b denean, batez bestekoaren definiziotik
ondorio hau atera daiteke : Mendekotasuna lineala izan ordez, beste edozein h(X) erakoa
bada, ezin esan daiteke E(h(X)) eta h(E(X)) berdinak direnik.Z aldagaia, elkarren artean linealki askeak edo independenteakdiren X eta Y zorizko bi aldagaien batura bada, (Z = X + Y bada),E(Z) = E(X) + E(Y) dela egiaztatzen da.X eta Y linealki independenteak ez direnean, E(Z) = E(X) + E(Y)
dela ezin ziurta daiteke.Era berean, zorizko aldagai baten bariantza adierazteko V(X) erabiltzen
bada, eta Y=aX+b bada, bariantzaren definizioa erabilita hau
lortzen da :
Mendekotasuna lineala izan ordez, beste edozein h(X) erakoa
bada, ezin esan daiteke E(h(X)) eta h(E(X)) berdinak direnik.Z aldagaia, elkarren artean linealki askeak edo independenteakdiren X eta Y zorizko bi aldagaien batura bada, (Z = X + Y bada),E(Z) = E(X) + E(Y) dela egiaztatzen da.X eta Y linealki independenteak ez direnean, E(Z) = E(X) + E(Y)
dela ezin ziurta daiteke.Era berean, zorizko aldagai baten bariantza adierazteko V(X) erabiltzen
bada, eta Y=aX+b bada, bariantzaren definizioa erabilita hau
lortzen da : X eta Y aldagaiak independenteak badira, eta Z = X + Y bada,
V(X+Y) = V(X) + V(Y) beteko da.Beti ere, dagozkien batez bestekoak eta bariantzak existitzen
direnean.• Adibidea:
X eta Y aldagaiak independenteak badira, eta Z = X + Y bada,
V(X+Y) = V(X) + V(Y) beteko da.Beti ere, dagozkien batez bestekoak eta bariantzak existitzen
direnean.• Adibidea: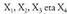 zorizko aldagai jarraituak independenteak badira, eta dagozkien batez bestekoak :
zorizko aldagai jarraituak independenteak badira, eta dagozkien batez bestekoak : eta
eta badira eta dagozkien bariantzak :
badira eta dagozkien bariantzak : eta
eta badira, bilatu
badira, bilatu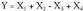 aldagaiaren batez bestekoa eta bariantza.Independenteak direlako :
aldagaiaren batez bestekoa eta bariantza.Independenteak direlako : .
.
VI. Banaketa normala
Banaketa normala, zorizko aldagai jarraituen artean askotan ematen
den banaketa legea da. Normalaren antzeko banaketak lortzen
dira gizakien, animalien edo landareen garaierak, pisuak edo luzerak
lantzen direnean. Iritzi edo produktu baten kontsumoari dagozkien
inkestak ere banaketa normalaren antzekoak dira. Makina
batek egiten dituen piezen luzeren aldakuntzak, edo beste makina
batek betetzen duen likido-kopurua, edo saiakuntza zientifiko batean
egiten diren nahigabeko erroreak ere banaketa normalaren antzekoak
dira. Azterketa bat gainditzen duen pertsona-kopurua, edo
talde baten adimen-kozientea eta, oro har, emaitzak alderdi askoren
mende daudenean, balioen banaketak lege hau jarraituko duela
pentsa daiteke.
Banaketa normal bati dagokion dentsitate-funtzioa hau da : Formula honetan
Formula honetan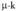 zorizko aldagai honen batezbestekoa eta 6-k zorizko aldagai honen desbideratze tipikoa adierazten dute. Banaketa normalaren ezaugarriak batez bestekoa eta desbideratze tipikoa direnez, banaketa normala adierazteko
zorizko aldagai honen batezbestekoa eta 6-k zorizko aldagai honen desbideratze tipikoa adierazten dute. Banaketa normalaren ezaugarriak batez bestekoa eta desbideratze tipikoa direnez, banaketa normala adierazteko erabiltzen da.
erabiltzen da.
Funtzio honen grafikoa espresio algebraikoa baino ezagunagoa da, kanpai itxura baitu.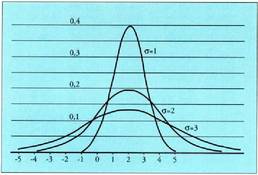 Funtzio hau eta bere grafikoa, neurketa bat egiterakoan egiten
diren nahigabeko erroreak nola banatzen diren ikasteko proposatu
zituen Gauss-ek. Horregatik, Gauss-en kanpaia esaten zaio.Banaketa-funtzioen propietate orokorrak betetzeaz gain, funtzio
honek beste hauek betetzen ditu :1. Bere mendeko-eremua zenbaki errealen multzoa da.2.
Funtzio hau eta bere grafikoa, neurketa bat egiterakoan egiten
diren nahigabeko erroreak nola banatzen diren ikasteko proposatu
zituen Gauss-ek. Horregatik, Gauss-en kanpaia esaten zaio.Banaketa-funtzioen propietate orokorrak betetzeaz gain, funtzio
honek beste hauek betetzen ditu :1. Bere mendeko-eremua zenbaki errealen multzoa da.2. zuzenarekiko simetrikoa da.
zuzenarekiko simetrikoa da.
3. puntua maximoa da.
puntua maximoa da.
4. Bi inflexio-puntu ditu eta
eta absizetan.
absizetan.
5.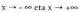 -rantz doanean, OX ardatza asintota horizontala da.Aldagai normal baten banaketa-funtzioa hau da :
-rantz doanean, OX ardatza asintota horizontala da.Aldagai normal baten banaketa-funtzioa hau da : Zoritxarrez,
Zoritxarrez,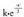 erako funtzioen jatorrizko funtzioak ez dira funtzio elementalak, eta hori horrela izanik, banaketa-funtzioko balioak denbora laburrean zein diren jakiteko taulak erabili behar dira. f(x) funtzioaren balioak
erako funtzioen jatorrizko funtzioak ez dira funtzio elementalak, eta hori horrela izanik, banaketa-funtzioko balioak denbora laburrean zein diren jakiteko taulak erabili behar dira. f(x) funtzioaren balioak eta
eta balioen arabera aldatzen dira.
balioen arabera aldatzen dira.
µ-ren balioa handiago edo txikiago denaren arabera, kanpaia eskuinerago edo ezkerrerago egongo da. -en balioa zenbat eta handiagoa izan, orduan eta zorrotzagoa izango da kanpaiaren muturra, eta balioa zenbat eta txikiagoa izan, orduan eta zapalagoa izango da kanpaia.
-en balioa zenbat eta handiagoa izan, orduan eta zorrotzagoa izango da kanpaiaren muturra, eta balioa zenbat eta txikiagoa izan, orduan eta zapalagoa izango da kanpaia. Hori dela eta, banaketari dagozkion tauletan
Hori dela eta, banaketari dagozkion tauletan eta
eta
Banaketa normala 1 Banaketa-funtzioaren taula
Banaketa normala 2 Banaketa-funtzioaren taula
Taulen erabilera
Bi taula erabiltzen dira, bata x-en balio positiboentzat eta bestea
x-en balio negatiboentzat. Liburu batzuetan balio positiboen taula
bakarrik azaltzen da, balio negatiboen kalkulurako funtzioaren
simetria erabiltzen delarik : Liburu honetan azaltzen diren tauletako lehenengo zutabean, x
aldagaiaren balioa hamarren batez azaltzen da. Ehunena zutabeen
gainean dagoen lerroan irakurri behar da. Adibidez, x = -2,13ri
dagokiona kalkulatzeko, -2,1 lerroko laugarren zutabea aukeratuko
dugu, zutabe horrek gainean hiruko bat duelako. -2,13 balioari
dagokion banaketa-funtzioa, -2,1 lerroa eta hiru zenbakia daraman
zutabea gurutzatzen diren tokian azaltzen den zenbakia da :
Liburu honetan azaltzen diren tauletako lehenengo zutabean, x
aldagaiaren balioa hamarren batez azaltzen da. Ehunena zutabeen
gainean dagoen lerroan irakurri behar da. Adibidez, x = -2,13ri
dagokiona kalkulatzeko, -2,1 lerroko laugarren zutabea aukeratuko
dugu, zutabe horrek gainean hiruko bat duelako. -2,13 balioari
dagokion banaketa-funtzioa, -2,1 lerroa eta hiru zenbakia daraman
zutabea gurutzatzen diren tokian azaltzen den zenbakia da : N(0,1) aldagai batekiko taula hauekin, tarte bat emanik bere probabilitatea
kalkulatu daiteke, edo probabilitatea emanik bere tartea
kalkulatu daiteke.A. Probabilitatea kalkulatu1. Kalkula ezazu zenbatekoa den x, x 0 balio bat baino txikiagoa izateko probabilitatea :
N(0,1) aldagai batekiko taula hauekin, tarte bat emanik bere probabilitatea
kalkulatu daiteke, edo probabilitatea emanik bere tartea
kalkulatu daiteke.A. Probabilitatea kalkulatu1. Kalkula ezazu zenbatekoa den x, x 0 balio bat baino txikiagoa izateko probabilitatea :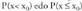 izan ere, ezinezko gertaera ez izan arren,
izan ere, ezinezko gertaera ez izan arren, da.Adibidez, P(x<2,43) zuzenean kalkulatzen da tauletan ; izan ere
F(2,43) = P(x<2,43) = 0,99245
da.Adibidez, P(x<2,43) zuzenean kalkulatzen da tauletan ; izan ere
F(2,43) = P(x<2,43) = 0,99245 2. Kalkula ezazu zenbatekoa den
2. Kalkula ezazu zenbatekoa den balio bat baino handiagoa, -do handiagoa edo berdina izateko probabilitatea :
balio bat baino handiagoa, -do handiagoa edo berdina izateko probabilitatea :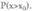 Adibidez, P(x>0,74) kalkulatzeko P(x>0,74) + P(x<0,74) + P(x=0,74)
= 1 berdintza erabiltzen da, P(x=0,74) = 0 dela kontuan izanik.
Adibidez, P(x>0,74) kalkulatzeko P(x>0,74) + P(x<0,74) + P(x=0,74)
= 1 berdintza erabiltzen da, P(x=0,74) = 0 dela kontuan izanik. 3. Kalkula ezazu zenbatekoa den x aldagaia x
3. Kalkula ezazu zenbatekoa den x aldagaia x eta
eta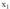 balioen artekoa
izatearen probabilitatea :
balioen artekoa
izatearen probabilitatea :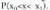 Horretarako berdintza
hau erabiltzen da :
Horretarako berdintza
hau erabiltzen da :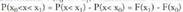 Adibidez,
Adibidez, Taulak erabiliz, bi hamarren dituzten aldagaiaren balioei dagozkien
probabilitateak lortu daitezke. Balioek hiru hamarren edo
gehiago dituztenean, banaketa-funtzioa bilatzeko zenbakia bi
hamarrenen bidez biribil daiteke, edo zehatzago egin nahi izanez
gero, hurbilen dituen bi balioen arteko interpolazio lineala egin daiteke
. Milarenak kalkulatzeko, lehenbizi, kalkulatzen da gainetik eta
azpitik hurbilen dauden bi hamarren dituzten balioen probabilitateen
arteko kenketa. Kendura hori 1 Oez zatitzen da eta milarenez
biderkatzen. Balio baten banaketa-funtzioa bilatu nahi denean,
balio hori positiboa bada, azpitik dagoen balioaren probabilitateari
gehituko zaio. Balio baten banaketa-funtzioa bilatu nahi denean,
balio hori negatiboa bada, gainetik dagoen balioaren probabilitateari
kenduko zaio. Horren bidez, biribiltzea baino hobea den hurbilketa
lineal bat lortzen da, zehatza ez bada ere.Adibidez, P(x<1,746) kalkulatu nahi bada,
Taulak erabiliz, bi hamarren dituzten aldagaiaren balioei dagozkien
probabilitateak lortu daitezke. Balioek hiru hamarren edo
gehiago dituztenean, banaketa-funtzioa bilatzeko zenbakia bi
hamarrenen bidez biribil daiteke, edo zehatzago egin nahi izanez
gero, hurbilen dituen bi balioen arteko interpolazio lineala egin daiteke
. Milarenak kalkulatzeko, lehenbizi, kalkulatzen da gainetik eta
azpitik hurbilen dauden bi hamarren dituzten balioen probabilitateen
arteko kenketa. Kendura hori 1 Oez zatitzen da eta milarenez
biderkatzen. Balio baten banaketa-funtzioa bilatu nahi denean,
balio hori positiboa bada, azpitik dagoen balioaren probabilitateari
gehituko zaio. Balio baten banaketa-funtzioa bilatu nahi denean,
balio hori negatiboa bada, gainetik dagoen balioaren probabilitateari
kenduko zaio. Horren bidez, biribiltzea baino hobea den hurbilketa
lineal bat lortzen da, zehatza ez bada ere.Adibidez, P(x<1,746) kalkulatu nahi bada, biribildu eta
biribildu eta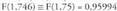 egin daiteke.Baina balio zehatzagoa lortu nahi bada, F(1,74) = 0,95907, eta
F(1,75) = 0,95994 hartuko dira. Ondoren horien arteko kenketa
kalkulatuko dugu : F(1,75) - F(1,74) = 0,95994 - 0,95907 =
0,00087. Hamarrez zatituta 0,000087 lortzen da, eta seiz biderkatuta
0,000522 ateratzen da ; biribilduta 0,00052 atertzen da.
egin daiteke.Baina balio zehatzagoa lortu nahi bada, F(1,74) = 0,95907, eta
F(1,75) = 0,95994 hartuko dira. Ondoren horien arteko kenketa
kalkulatuko dugu : F(1,75) - F(1,74) = 0,95994 - 0,95907 =
0,00087. Hamarrez zatituta 0,000087 lortzen da, eta seiz biderkatuta
0,000522 ateratzen da ; biribilduta 0,00052 atertzen da.
Azkenik F(1,74)-ri dagokion balioari gehituz, F(1,746) _
0,95959 da.B. Probabilitatea emanik, aurkitu aldagaiaren balioa
1. dela badakigu eta
dela badakigu eta zenbat den jakin nahi da.Probabilitatea 0,5 baino txikiago denez, zenbaki negatibo bati dagokio. 0,05938 zenbakia negatiboen taulan bilatuz, -1,5 lerroa eta 6ari dagokion zutabea elkartzen diren tokian dagoela ikusten da ; beraz
zenbat den jakin nahi da.Probabilitatea 0,5 baino txikiago denez, zenbaki negatibo bati dagokio. 0,05938 zenbakia negatiboen taulan bilatuz, -1,5 lerroa eta 6ari dagokion zutabea elkartzen diren tokian dagoela ikusten da ; beraz da.Probabilitatea 0,5 baino txikiago denez, zenbaki negatibo bati dagokio. 0,05938 zenbakia negatiboen taulan bilatuz, -1,5 lerroa eta 6ari dagokion zutabea elkartzen diren tokian dagoela ikusten da ; beraz2.
da.Probabilitatea 0,5 baino txikiago denez, zenbaki negatibo bati dagokio. 0,05938 zenbakia negatiboen taulan bilatuz, -1,5 lerroa eta 6ari dagokion zutabea elkartzen diren tokian dagoela ikusten da ; beraz2. da. Bilatu
da. Bilatu Tauletan begiratzen badugu, F(0,67) = 0,74857 eta F(0,68) _ 0,75175 dela ikusi dezakegu. Halakoetan, nahi izanez gero,
Tauletan begiratzen badugu, F(0,67) = 0,74857 eta F(0,68) _ 0,75175 dela ikusi dezakegu. Halakoetan, nahi izanez gero,
- Ariketak
5. N(0,1) banaketa normal batekiko Z zorizko aldagai
bat emanik, kalkula itzazu probabilitate hauek : 6. Bilatu hurrengo adibideetan kurba normalaren azpian
eta abzisen artean dauden azalerak :
6. Bilatu hurrengo adibideetan kurba normalaren azpian
eta abzisen artean dauden azalerak :
VII. Aldagaiaren tipifikazioa
Taula hauek ez dira erabilgarriak izaten edozein banaketa normalerako, batez bestekoaren balioa 0 ez denean, edo
batez bestekoaren balioa 0 ez denean, edo desbideratze tipikoaren balioa 1 ez denean. Baina aldagai aldaketa erraz bat egitea nahikoa da, taula hauek erabiliz probabilitateak irakurtzeko. Aldaketa horri, aldagaiaren tipifikazioa esaten zaio.Adibide gisa, gizon askoren altuerek banaketa normal bat jarraitzen dute, batez bestekoa
desbideratze tipikoaren balioa 1 ez denean. Baina aldagai aldaketa erraz bat egitea nahikoa da, taula hauek erabiliz probabilitateak irakurtzeko. Aldaketa horri, aldagaiaren tipifikazioa esaten zaio.Adibide gisa, gizon askoren altuerek banaketa normal bat jarraitzen dute, batez bestekoa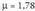 eta desbideratze tipikoa
eta desbideratze tipikoa direlarik. Zoriaren arabera elementu bat hartzen bada : a) bilatu zenbatekoa den 1,70 baino gehiago neurtzearen probabilitatea, eta b) bilatu zenbatekoa den 1,95 baino gutxiago neurtzearen probabilitatea.Batez bestekoa 0 duen aldagai bat izateko, aldagai bezala x-1,78
hartzen da, eta desbideratze tipikoak 1 izan behar duenez, 0,14-z
zatitzen da. Hau da, aldagai laguntzaile bezala z = (x-1,78)/0,14
hartzen da. Orduan :
direlarik. Zoriaren arabera elementu bat hartzen bada : a) bilatu zenbatekoa den 1,70 baino gehiago neurtzearen probabilitatea, eta b) bilatu zenbatekoa den 1,95 baino gutxiago neurtzearen probabilitatea.Batez bestekoa 0 duen aldagai bat izateko, aldagai bezala x-1,78
hartzen da, eta desbideratze tipikoak 1 izan behar duenez, 0,14-z
zatitzen da. Hau da, aldagai laguntzaile bezala z = (x-1,78)/0,14
hartzen da. Orduan : Oro har, tipifikatutako aldagaia z bada,
Oro har, tipifikatutako aldagaia z bada, normaleko x aldagai arruntetik, N(0,1) normaleko z aldagaira dagoen urratsa horrela ematen da:
normaleko x aldagai arruntetik, N(0,1) normaleko z aldagaira dagoen urratsa horrela ematen da: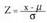 Aldaketa hauen justifikazioa horrela azaltzen da : X aldagaiak
Aldaketa hauen justifikazioa horrela azaltzen da : X aldagaiak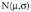 normala jarraitzen badu,
normala jarraitzen badu,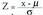 aldagaiak N(0,1) normala jarraituko du, izan ere orokorrean Y = aX+b bada eta
aldagaiak N(0,1) normala jarraituko du, izan ere orokorrean Y = aX+b bada eta bada, orduan
bada, orduan da.• Adibidea :Eskolaurreko haurren altueren batez bestekoak banaketa normala jarraitzen du, batez bestekoa
da.• Adibidea :Eskolaurreko haurren altueren batez bestekoak banaketa normala jarraitzen du, batez bestekoa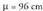 eta desbideratze tipikoa
eta desbideratze tipikoa direlarik. Kalkulatu hurrengo gertaeren probabilitateak :
direlarik. Kalkulatu hurrengo gertaeren probabilitateak : a) Aldagaia batez bestekoa baino txikiagoa edo handiagoa izatearen
probabilitateak 0,5 izan behar du. Tauletan F(0) = 0,5 dela ikus
daiteke.Hurrengo hiru galderei erantzuteko
a) Aldagaia batez bestekoa baino txikiagoa edo handiagoa izatearen
probabilitateak 0,5 izan behar du. Tauletan F(0) = 0,5 dela ikus
daiteke.Hurrengo hiru galderei erantzuteko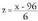 aldaketa egin behar da.
aldaketa egin behar da.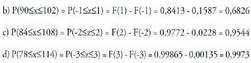 Batez bestekoarekiko diferentzia
Batez bestekoarekiko diferentzia eta abar... duen balioekiko probabilitateen banaketak ez du zerikusirik
eta abar... duen balioekiko probabilitateen banaketak ez du zerikusirik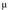 eta
eta balioekin.
balioekin. eta abarren probabilitateak, aurreko adibidean lortutakoak dira beti. Portzentaien laburpena hurrengo grafiko honetan azaltzen da :
eta abarren probabilitateak, aurreko adibidean lortutakoak dira beti. Portzentaien laburpena hurrengo grafiko honetan azaltzen da :
- Ariketak
7. Pertsona multzo baten pisuak N(72,8) normalaren
arabera banatzen dira. Bilatu pertsona batek :a) 80 kg. baino gehiago pisatzearen probabilitatea.b) 60 kg. baino gutxiago pisatzearen probabilitatea.c) 70 eta 75 kg.-ren arteko pisua edukitzearen probabilitatea
.8. Irakasle bat azterketa bat zuzentzen ari da, eta emaitzak
N(6,8 ; 1,35) normal legea jarraitzen dutela konturatzen da.
Azterketa egin duten % 10ari «bikain», % 15ari «oso ongi»
eta %30ari «gutxiegi» jartzeko asmoa dauka. Ze notatik
aurrera jarriko du bikain, oso ongi edo gutxiegi?9. Txokolate-barra batek 100 gramo pisatzen ditu, baina
egia esan, pisua ez da erabat zehatza eta N(101,1 ; 3,8) normalaren
arabera banatzen da.a) Txokolate fabrikak, txokolate-barrak, gutxienez 95
gramo pisatzen dituela ziurtatu behar du. Zenbatekoa
da, zoriz hartutako barrak, baldintzak ez betetzearen
probabilitatea?b) Tresnerian moldaketa batzuk egin dira eta orain,
N(99,3 ; 2,6) banaketa normala jarraitzen du. Oraingo
honetan, edozein barrak, jarritako gutxineneko pisuaren
baldintza betetzea, errazagoa al da?10. 70 km/h lastertasun mugatua duen errepide batean,
autoen lastertasuna N(74 ; 11,8) banaketa normalera hurbiltzen
dela konturatu da polizia.a) 75 km/h lastertasuna gainditzen dutenei isuna jartzea
erabaki dute. Zenbateko probabalitatea du zoriz hautatutako
auto batek isuna jasotzeko?b) 85 km/h lastertasuna gainditzen dutenei hamar aldiz
handiagoa den isuna jartzen badiete, zenbatekoa da,
zoriz hautatutako kotxe batek, isun gogorra jasotzeko
probabilitatea?c) 100 km/,h lastertasuna gainditzen duten gidariei gida
baimena kentzen diete. Zenbatekoa da, zoriz hautatutako
gidari batek, gida baimenik gabe gelditzeko duen
probabilitatea?d) Isunen ondoren, gidariek abiadura gutxitu egiten dute
eta orain N(71,3 ; 7,6) banaketa normala jarraitzen du.
Hori dela eta, agintariek erabaki dute lastertasun
muga baino bizkorrago doazen kotxeen % 1 Oari jartzea
bakarrik isuna. Isunen mugak zein lastertasunean
egon beharko du?11. Donostiako Kontxako uraren tenperaturak uztailean,
gradu zentigradotan eta goizeko 1 letan, N(21 ; 3,2) banaketa
normala jarraitzen duela esan daiteke. F = (9/5)C + 32
dela jakinik, eman batez bestekoa eta desbideratze tipikoa
Farenheit gradutan.
VIII. Asimetria eta zapalketa
Banaketa normala simetrikoa da, baina Poissonena adibidez ez.
Zorizko banaketa baten simetria neurtzeko hirugarren ordenako momentua deritzana erabiltzen da ; hau da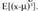 . Zorizko aldagai baten bigarren ordenako momentua bariantzak ematen du, eta lehenengo ordenakoa, berriz, batez bestekoak. Erabilitako unitateek informazioa aldatu ez dezaten, hirugarren ordenako momentua
. Zorizko aldagai baten bigarren ordenako momentua bariantzak ematen du, eta lehenengo ordenakoa, berriz, batez bestekoak. Erabilitako unitateek informazioa aldatu ez dezaten, hirugarren ordenako momentua zatitzen da. Asimetria koefizientea edo alborapena hau da :
zatitzen da. Asimetria koefizientea edo alborapena hau da : Banaketak simetrikoak direnean, alborapena zero da. Banaketauniforme eta normalak asimetria zero dute. Poissonen banaketak
Banaketak simetrikoak direnean, alborapena zero da. Banaketauniforme eta normalak asimetria zero dute. Poissonen banaketak asimetria koefizientea du, eta
asimetria koefizientea du, eta funtzio esponentzialaren asimetria koefizienteak 2 balio du.Batzuetan, komenigarria izaten da jakitea normalera hurbiltzen
den banaketa normala baino zapaldua dagoen ala ez. Horretarako
zapaltasun-koefizientea edo kurtosia erabiltzen da. Balio hori lortzeko,
laugarren ordenako momentua desbideratze tipikoaren laugarren
berreduraz zatitzen da.
funtzio esponentzialaren asimetria koefizienteak 2 balio du.Batzuetan, komenigarria izaten da jakitea normalera hurbiltzen
den banaketa normala baino zapaldua dagoen ala ez. Horretarako
zapaltasun-koefizientea edo kurtosia erabiltzen da. Balio hori lortzeko,
laugarren ordenako momentua desbideratze tipikoaren laugarren
berreduraz zatitzen da. Banaketa normala denean, koefiziente honek 3 balio du. Banaketa normala baino zapalduagoa denean kurtosiaren balioa 3 baino txikiagoa izaten da, eta zorrotzagoa denean kurtosiaren balioa 3 baino handiagoa izaten da. Poissonen banaketaren zapaltasun-koefizientearen balioa
Banaketa normala denean, koefiziente honek 3 balio du. Banaketa normala baino zapalduagoa denean kurtosiaren balioa 3 baino txikiagoa izaten da, eta zorrotzagoa denean kurtosiaren balioa 3 baino handiagoa izaten da. Poissonen banaketaren zapaltasun-koefizientearen balioa
Limitearen Teorema Zentrala
Zorizko aldagai jarraituen ikasketan banaketa normalak duen garrantzia azaltzen du limitearen teorema zentralak. Edozein banaketatan batez bestekoa bada, eta desbideratze tipikoa
bada, eta desbideratze tipikoa bada,
bada, , n emaitzeko lagin bat hartzen da. Lagin horretako x batez bestekoa kalkulatzen da. Ñ batez besteko hori zorizko aldagaia bezala har daiteke. Laginaren emaitzakopurua infinitorantz doanean,
, n emaitzeko lagin bat hartzen da. Lagin horretako x batez bestekoa kalkulatzen da. Ñ batez besteko hori zorizko aldagaia bezala har daiteke. Laginaren emaitzakopurua infinitorantz doanean, zorizko aldagaiak jarraitzen duen banaketa normalera hurbiltzen da. Zehazki, n infinitorantz doanean,
zorizko aldagaiak jarraitzen duen banaketa normalera hurbiltzen da. Zehazki, n infinitorantz doanean,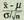 aldagaiak N(0,1) banaketa normal murriztua jarraitzen du.Abiapuntu bezala hartzen den banaketa uniformea edo esponentzialaizan daiteke , n elementuko lagineko batez bestekoak
aldagaiak N(0,1) banaketa normal murriztua jarraitzen du.Abiapuntu bezala hartzen den banaketa uniformea edo esponentzialaizan daiteke , n elementuko lagineko batez bestekoak
Formulak
IX. Banaketa normala, banaketa binomialaren hurbilketa bezala
B(n,p) banaketa binomial bat,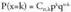 (k, 0 eta n arteko balioak hartzen ditu) probabilitate-funtzioa duen banaketa diskretu bat da. Bere batez bestekoa
(k, 0 eta n arteko balioak hartzen ditu) probabilitate-funtzioa duen banaketa diskretu bat da. Bere batez bestekoa eta bariantza
eta bariantza delarik, erraz kalkula daitezke. Balio baten edo, n txikia denean,
balio batzuen probabilitatearen kalkuluak ez dauka inolako zailtasunik,
baina n saiakuntza kopurua handitzen denean oso zaila bihur
daiteke. n handia eta p oso txikia direnean, Poissonen banaketak
hurbilketa ona eskaini dezake, zorizko aldagai diskretuen gaian
ikusi den bezalaxe. Baldintzak orokorragoak direnean, banaketa
binomiala banaketa normalaren bidez hurbildu daiteke, B(n,p)
banaketa binomialaren ordez batez besteko eta desbideratze tipiko
bera duen
delarik, erraz kalkula daitezke. Balio baten edo, n txikia denean,
balio batzuen probabilitatearen kalkuluak ez dauka inolako zailtasunik,
baina n saiakuntza kopurua handitzen denean oso zaila bihur
daiteke. n handia eta p oso txikia direnean, Poissonen banaketak
hurbilketa ona eskaini dezake, zorizko aldagai diskretuen gaian
ikusi den bezalaxe. Baldintzak orokorragoak direnean, banaketa
binomiala banaketa normalaren bidez hurbildu daiteke, B(n,p)
banaketa binomialaren ordez batez besteko eta desbideratze tipiko
bera duen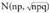 banaketa normala hartuz.Hurbilketa honen baliagarritasuna, B(n ; 0,2) n=10, 20, 30 eta 50
denean lortzen diren maiztasun-poligonoak alderatuz ikus daiteke.
banaketa normala hartuz.Hurbilketa honen baliagarritasuna, B(n ; 0,2) n=10, 20, 30 eta 50
denean lortzen diren maiztasun-poligonoak alderatuz ikus daiteke.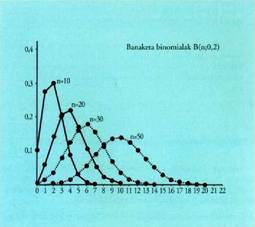 n hazten doan eran, p finko batekiko hurbilketa hobetzen doala
ikus daiteke. Era berean n finko mantentzen bada, 0,5etik hurbilen
dauden p probabilitatearen balioak dira normalera gehien hurbiltzen
den banaketa eskaintzen dutenak. Banaketa binomial bati jarri
behar zaizkion baldintzak normal baten bidez lortu nahi den hurbilketa
onargarria izateko, bilatu nahi den zehaztasunaren mendedaude. Oro har, npq>9 izatea eskatzen da, baina np>3 eta np>3 ere
erabiltzen da.Tarteko kasu bat hartuko dugu : B(16 ; 0,5). Kasu honetan np = nq = 8>3 da, baina npq = 4<9 da, eta bestalde, banaketa binomial honetan
n hazten doan eran, p finko batekiko hurbilketa hobetzen doala
ikus daiteke. Era berean n finko mantentzen bada, 0,5etik hurbilen
dauden p probabilitatearen balioak dira normalera gehien hurbiltzen
den banaketa eskaintzen dutenak. Banaketa binomial bati jarri
behar zaizkion baldintzak normal baten bidez lortu nahi den hurbilketa
onargarria izateko, bilatu nahi den zehaztasunaren mendedaude. Oro har, npq>9 izatea eskatzen da, baina np>3 eta np>3 ere
erabiltzen da.Tarteko kasu bat hartuko dugu : B(16 ; 0,5). Kasu honetan np = nq = 8>3 da, baina npq = 4<9 da, eta bestalde, banaketa binomial honetan eta
eta da. B(16 ; 0,5) banaketa binomiala eta N(8 ; 2) banaketa normalaren funtzioen balioak alderatuz, hau lortuko genuke :
da. B(16 ; 0,5) banaketa binomiala eta N(8 ; 2) banaketa normalaren funtzioen balioak alderatuz, hau lortuko genuke :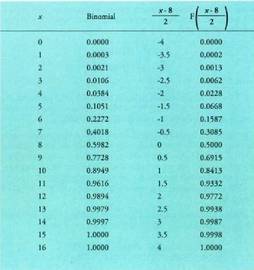 Balioak hurbil samar daudela ikus daiteke, baina edozein x baliorentzat,
normaleko F(x) funtzioa binomialeko funtzioa baino txikiagoa
da beti. Sistematikoa den diferentzia hau, banaketa binomiala
diskretua eta banaketa normala jarraitua delako sortzen da ;
hau da, bi balio hartzen baditugu, adibidez 6 eta 6,5, normalaren
probabilitate-banaketan aldaketa bat nabarmentzen da, baina binomialaren
probabilitate-banaketan, 7 zenbaki osora iritsi arte ez da
aldaketarik nabarmenduko.Banaketa binomialean aldagaiak zazpi balioa hartzeari dagokion
probabilitatea kalkulatu nahi bada :
Balioak hurbil samar daudela ikus daiteke, baina edozein x baliorentzat,
normaleko F(x) funtzioa binomialeko funtzioa baino txikiagoa
da beti. Sistematikoa den diferentzia hau, banaketa binomiala
diskretua eta banaketa normala jarraitua delako sortzen da ;
hau da, bi balio hartzen baditugu, adibidez 6 eta 6,5, normalaren
probabilitate-banaketan aldaketa bat nabarmentzen da, baina binomialaren
probabilitate-banaketan, 7 zenbaki osora iritsi arte ez da
aldaketarik nabarmenduko.Banaketa binomialean aldagaiak zazpi balioa hartzeari dagokion
probabilitatea kalkulatu nahi bada :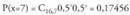 N(8,2) banaketa normalean, berriz, edozein banaketa jarraituan
balio diskretuekin gertatzen denez, P(x=7) = 0 izango da.Probabilitatea bilatzeko ordez,
N(8,2) banaketa normalean, berriz, edozein banaketa jarraituan
balio diskretuekin gertatzen denez, P(x=7) = 0 izango da.Probabilitatea bilatzeko ordez, denean, x-en
denean, x-en balioa ezagutu nahi bada, banaketa normalarekin
balioa ezagutu nahi bada, banaketa normalarekin denez, x = 7,2 lortuko litzateke ; baina binomialarekin ez genuke balio zehatzik lortuko, 7 eta 8-ren artean egon beharko lukeela soilik. Dena dela, aldagaia osoa denez ezin du 7,2 balioa hartu ; halakotan, emaitza biribilduz, soluzio bezala 7 emango litzateke.
denez, x = 7,2 lortuko litzateke ; baina binomialarekin ez genuke balio zehatzik lortuko, 7 eta 8-ren artean egon beharko lukeela soilik. Dena dela, aldagaia osoa denez ezin du 7,2 balioa hartu ; halakotan, emaitza biribilduz, soluzio bezala 7 emango litzateke.
Horrela egin behar da (6,5, 7,5) tarteko edozein baliorekin.
Alderantziz, aldagai binomialeko 7 balioarentzat aldagai normaleko (6,5, 7,5) tartea hartu behar da. Beraz, arrazonamendu hau kontuan hartuz, banaketa normal hurbilduarekin P(x=7) kalkulatzeko horrela egin behar da :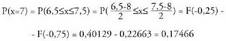 Zuzenean kalkulatutako probabilitatearen eta banaketa normalaren
hurbilketa erabiliz lortu den probabilitatearen arteko diferentzia
milaren batekoa da.Aldaketa hau kontuan hartu behar da banaketa binomial bat
banaketa normal baten bidez hurbiltzerakoan. Beharrezkoa den
doitze honi jarraitasun-zuzenketa esaten zaio, eta aldagaia binomiala
x-en bidez, eta aldagai normala y-ren bidez adierazten badira,
horrela azaltzen da :
Zuzenean kalkulatutako probabilitatearen eta banaketa normalaren
hurbilketa erabiliz lortu den probabilitatearen arteko diferentzia
milaren batekoa da.Aldaketa hau kontuan hartu behar da banaketa binomial bat
banaketa normal baten bidez hurbiltzerakoan. Beharrezkoa den
doitze honi jarraitasun-zuzenketa esaten zaio, eta aldagaia binomiala
x-en bidez, eta aldagai normala y-ren bidez adierazten badira,
horrela azaltzen da : • Adibidea:1. Ongi orekatuta dagoen txanpon bat 1.000 aldiz jaurtitzen da,
eta aldea ateratzeko aukera 450 eta 500 artean egotearen probabilitatea
zenbatekoa den jakin nahi da. [P(450(x(500)]B(1000 ; 0,5) banaketa binomial bat da, baina binomialaren probabilitate-funtzioa erabiliz kalkulatzen oso zaila da. Kasu honetan
• Adibidea:1. Ongi orekatuta dagoen txanpon bat 1.000 aldiz jaurtitzen da,
eta aldea ateratzeko aukera 450 eta 500 artean egotearen probabilitatea
zenbatekoa den jakin nahi da. [P(450(x(500)]B(1000 ; 0,5) banaketa binomial bat da, baina binomialaren probabilitate-funtzioa erabiliz kalkulatzen oso zaila da. Kasu honetan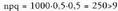 denez, normalarekin egindako hurbilketak emaitza ona eman behar du. Hurbilketa egiten den normalak batez besteko bera du :
denez, normalarekin egindako hurbilketak emaitza ona eman behar du. Hurbilketa egiten den normalak batez besteko bera du :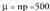 eta bariantza
eta bariantza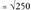 denez, desbideratze tipikoa
denez, desbideratze tipikoa izango da.Aldagai binomiala adierazteko x, hurbildutako aldagai normalerako
y eta murriztutako aldagai normalerako z erabiliz gero :
izango da.Aldagai binomiala adierazteko x, hurbildutako aldagai normalerako
y eta murriztutako aldagai normalerako z erabiliz gero : 2. Dado bat 500 aldiz jaurtitzen da, eta 6 emaitza 70 eta 120 artean egotearen probabilitatea zenbatekoa den jakin nahi da, muturrak baztertuta.
2. Dado bat 500 aldiz jaurtitzen da, eta 6 emaitza 70 eta 120 artean egotearen probabilitatea zenbatekoa den jakin nahi da, muturrak baztertuta.
Aldagaia denez, hurbilketa ona izango da. Hurbileko banaketa normalaren batez bestekoa
denez, hurbilketa ona izango da. Hurbileko banaketa normalaren batez bestekoa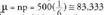 izango da, bariantza
izango da, bariantza eta desbidazio tipikoa
eta desbidazio tipikoa izango da.
Aldagai binomiala adierazteko x, hurbildutako aldagai normalerako
y eta murriztutako aldagai normalerako z erabiliz gero :
izango da.
Aldagai binomiala adierazteko x, hurbildutako aldagai normalerako
y eta murriztutako aldagai normalerako z erabiliz gero :
- Ariketak
12. Zenbait milioi pertsonek osatzen duten biztanleria batean %30ak begiak urdinak ditu. Biztanleria horretatik 250 pertsona zoriaren arabera hautatzen dira. Bila zenbatekoa den begi urdinen x pertsona-kopurua 75 eta 100 bitartean egotearen probabilitatea, bi horiek barne.13. Iruñeko gizonen %8ak eta emakumeen %lk moto gidabaimena (M.G.) dute.a) Iruñeko 1.000 gizoneko lagin batean, bila 60 baino gehiago eta 90 baino gutxiago M.G.dun izatearen probabilitatea .b) 1.000 emakumeko lagin batean, bila M.G.dunak 20 eta 30, biak barne, bitartean izatearen probabilitatea.14. Ikasle asko dituen unibertsitate bateko ikasleen %24a barazkijalea dela onartzen da. Unibertsitate horretako 2. 100 ikaslek osatutako lagin bat hartzen da. Kalkula ezazu, horietatik gutxienez 540 eta gehienez 610 barazkijale izatearen probabilitatea.15. A markako film bobinak egiten dituen fabrikatzaile batek dionez, bobina bat akastuna ez izatearen probabilitatea 0,99 da. Denda batean 1.000 bobina daude. Kalkula ezazu denda horretan dauden bobina akastunen kopurua 3 eta 22 bitartean, muturrak barne, egotearen probabilitatea.16. Ikerketa batek jakinarazi duenez, helduen %3ak daltonismoa du. Zoriz aukeratutako lagin bat hartzen da 1.000 helduek osatua. Kalkula ezazu zenbatekoa den, lagin horretako gutxienez 15 pertsona daltoniko izatearen probabilitatea .
Poissonen banaketaren hurbilketa normalaren bidez
Poissonen banaketa ere normala erabiliz hurbil daiteke. Kasu honetan, Poissonen banaketaren asimetria dela-eta, hurbilketak okerragoak dira ; baina limitearen teorema zentrala dela-eta, hurbilketa hori posible da. Hurbilketa ona da denean.Binomialean bezala, aldagai diskretu baten hurbilketa aldagai
jarraitu baten bidez egiten denez, jarraitasun-zuzenketa egin behar
da; hau da aldagai diskretua x eta aldagai jarraitua y bada :
denean.Binomialean bezala, aldagai diskretu baten hurbilketa aldagai
jarraitu baten bidez egiten denez, jarraitasun-zuzenketa egin behar
da; hau da aldagai diskretua x eta aldagai jarraitua y bada : Hurbilketa oso ona ez den adibide bat hartuz : Poisson(16) banaketa N(16,4) banaketarekin konparatuz gero, banaketa-funtzioen balioak hauek dira:
Hurbilketa oso ona ez den adibide bat hartuz : Poisson(16) banaketa N(16,4) banaketarekin konparatuz gero, banaketa-funtzioen balioak hauek dira:
X Hipotesi-testa
Zorizko aldagaietan landutako ezagutzak estatistikara egokitzen
saiatuko gara atal honetan. Saio estatistiko batean lortu diren
datuak ikusirik, horren emaitzak ezaguna den banaketa batetara
hurbiltzen direla pentsatu da. Hipotesi hori zuzena den ala ez egiaztatzen
da hipotesi-testen bidez. Inkesta batean jasotako datuak
baieztapenaren bat egiteko nahikoak diren jakitea da estimazioaren
bidez aztertzen dena. Hipotesi-testarekin hasiz :- Hipotesi bat biztanleria estatistiko bati dagokion baieztapena da. Baieztapen hori zuzena ala okerra izan daiteke.- Hipotesi baten testa egitea hau da : ikertzen ari garen biztanleriko
lagin bat aztertu eta hipotesia onartu edo baztertzen duen erabakitzea
.Beraz, hipotesi-test bat biztanlerio lagin batek hipotesia onartu edo baztertzen duen erabakitzeko balio duen arau edo erregela bat da.
Oro har, bi hipotesi proposatzen dira :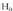 eta
eta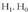 hipotesi nulua
esaten zaion hipotesi nagusia da.
hipotesi nulua
esaten zaion hipotesi nagusia da. berriz, ordezko hipotesia da, eta
oro har,
berriz, ordezko hipotesia da, eta
oro har, hipotesiaren ezeztapena da, baina beti ez da horrela izaten.Bi hipotesietako bat zuzena izango balitz bezala lan egingo da beti.• Adibidea:
Jonek dionez, txanpon bat Laplaceren txanpona da (aldea ateratzeko
probabilitatea
hipotesiaren ezeztapena da, baina beti ez da horrela izaten.Bi hipotesietako bat zuzena izango balitz bezala lan egingo da beti.• Adibidea:
Jonek dionez, txanpon bat Laplaceren txanpona da (aldea ateratzeko
probabilitatea da). Mikelek ordea, adea ifrentzua baino
sarriago ateratzen dela dio. Txanponaren testa egin eta arrazoia bietariko
bati eman behar zaio (ezin esan daiteke biak oker daudenik).
da). Mikelek ordea, adea ifrentzua baino
sarriago ateratzen dela dio. Txanponaren testa egin eta arrazoia bietariko
bati eman behar zaio (ezin esan daiteke biak oker daudenik).
Izan bedi p aldea ateratzearen probabilitatea. Jonen hipotesian idazten da, baina Mikelen hipotesian
idazten da, baina Mikelen hipotesian idatzi beharko da.
idatzi beharko da.
Testa txanpona 100 aldiz jaurtiz egiten da eta 60 aldiz aldea atera da.
Txanpona Laplacerena dela onartu al daiteke?Adibide honetan kontuan hartu behar diren hipotesiak hauek
dira:- : txanpona Laplacerena da ; hau da, aldea ateratzearen p probabilitatea
: txanpona Laplacerena da ; hau da, aldea ateratzearen p probabilitatea da.-
da.- : Txanpona ez da Laplacerena, eta aldea ateratzearen probabilitatea handiagoa da, beraz
: Txanpona ez da Laplacerena, eta aldea ateratzearen probabilitatea handiagoa da, beraz da.
da.
Kasu honetan hipotesia
hipotesia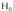 hipotesiaren ezeztapena ez bada ere, hipotesi horren kontrakoa da.Kalkuluak egiteko banaketa binomialaren hurbilketa egiten da normala erabiliz.
hipotesiaren ezeztapena ez bada ere, hipotesi horren kontrakoa da.Kalkuluak egiteko banaketa binomialaren hurbilketa egiten da normala erabiliz. kontuan hartuz :
kontuan hartuz :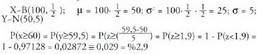 Probabilitatea oso txikia denez, txanpona Laplacerena zela esaten zuen
Probabilitatea oso txikia denez, txanpona Laplacerena zela esaten zuen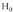 hipotesia baztertu egiten da, eta
hipotesia baztertu egiten da, eta hipotesia onartzen da, beraz
hipotesia onartzen da, beraz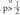 da. Noski, ondorioa oker egon daiteke.Hipotesietako bat berdintza baten bidez azaltzen denean eta bestea desberdintza baten bidez, berdintzaren bidez azaltzen denari
da. Noski, ondorioa oker egon daiteke.Hipotesietako bat berdintza baten bidez azaltzen denean eta bestea desberdintza baten bidez, berdintzaren bidez azaltzen denari
Adierazkortasun mailak
Aurreko adibideko hipotesian, hau da txanpona Laplacerena
hipotesian, hau da txanpona Laplacerena dela kontuan hartut , txa ona 100 aldiz jaurtiz ero aldea 60 edo gehiagotan ateratzearen probabilitatea %2,9 atera da.
dela kontuan hartut , txa ona 100 aldiz jaurtiz ero aldea 60 edo gehiagotan ateratzearen probabilitatea %2,9 atera da.
Balio hori, hipotesia onartzeko txikiegia dela uste da.Oro har, hipotesi bat zuzentzat hartzerakoan, landutako gertaeraren
probabilitatea "adierazkortasun maila" esaten zaion balioa baino
txikiagoa dela ikusten denean, hipotesi hori baztertu egiten da.Aztertzen den ariketaren izaeraren arabera, %5a edo % 1 a hartzen
da adierazkortasun maila bezala.Aurreko adibidean hipotesia baztertu egin da atera den emaitza,
%2,9, aiderazkortasun maila bezala hartu den %5a baino txikiagoa
delako ; baina adierazkortasun maila bezala %la hartu izan balitz,
ezingo genuke baztertu.- Adibideak:1. Eritasun larri bat A sendagaia erabiliz senda daiteke, sendatzeko duen probabilitatea %68koa delarik. Sendatze portzentai hori B sendagai baten bidez gainditu nahi da. Egia den frogatzeko 200 gaixori B sendagai hori eman zaie eta 150 sendatu dira. Ziur egon al gaitezke sendagai berria zaharra baino hobea dela? Sendakuntzen %75 portzentai berria, ez ote da kasualitatez izan?. Beste era batera esanda, sendagai berria ez dugu uste zaharra baino hobea denik : H o hipotesia, B eta A sendagaiek sendatzeko duten gaitasuna berdina dela suposatuz, 200 gaixo sendagai horrekin tratatu ondoren 150 edo sendaketa gehiago lortzea oso gertagarria al da, edo ez da ia batere gertagarria?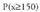 kalkulatu behar da n = 200, p = 0,68 parametroak dituen banaketa binomial batean. Bestalde,
kalkulatu behar da n = 200, p = 0,68 parametroak dituen banaketa binomial batean. Bestalde,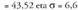 da.npq = 43,5 denez, banaketa binomialaren hurbilketa bat lortu
daiteke normalaren bidez :
da.npq = 43,5 denez, banaketa binomialaren hurbilketa bat lortu
daiteke normalaren bidez : P(x?150) < %5 denez, eta adierazkortasun maila bezala 0,05 = %5a onartuz, B eta A sendagaien sendatzeko gaitasun berdina zutela zioen HO hipotesia baztertu dezakegu ; beraz, B sendagaia A sendagaia baino hobea dela onartuko da:
P(x?150) < %5 denez, eta adierazkortasun maila bezala 0,05 = %5a onartuz, B eta A sendagaien sendatzeko gaitasun berdina zutela zioen HO hipotesia baztertu dezakegu ; beraz, B sendagaia A sendagaia baino hobea dela onartuko da: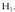 2. Egiaztatu denez, behatu den sendatze kopurua eta adierazkortasun
maila bezala %5a hartuz B sendagai kasuen %68an eraginkorra
dela dion hipotesia ez dira bateragarriak. Eta kasuen %69an eraginkorra
dela dioen hipotesiarekin bateragarria ote da? Eta
%70arekin?Aurreko adibidean egindako berbera eginez, ondoko taula hau
lortzen da :
2. Egiaztatu denez, behatu den sendatze kopurua eta adierazkortasun
maila bezala %5a hartuz B sendagai kasuen %68an eraginkorra
dela dion hipotesia ez dira bateragarriak. Eta kasuen %69an eraginkorra
dela dioen hipotesiarekin bateragarria ote da? Eta
%70arekin?Aurreko adibidean egindako berbera eginez, ondoko taula hau
lortzen da :
Alde bakarreko testa eta alde biko testa
Aurreko adibidean bi hipotesi hartu dira kontuan : B sendagaiak
A sendagaiak adina sendatzen zuela, eta hipotesi horren kontrakoa
den beste hau: B sendagaiak duen sendatzeko ahalmena A sendagaiak
duena baino handiagoa da.Lehenengo hipotesia betetzen dela suposatu da eta probabilitatearen kalkuluak, hau da X zorizko aldagaiak 150aren eskuinean dagoen balio bat hartzeko probabilitatearen kalkuluak erabaki du zein hautatu. X zorizko aldagaia bakarrik balio baten eskuinaldera edo bakarrik ezkerraldera egotearen probabilitatea kalkulatzen diren test mota hauek, alde bakarreko testak dira.Beste ariketa batzuetan balio banaren eskuinaldeko eta ezkerraldeko
probabilitateak kalkulatu behar izaten dira ; alde biko testak
dira.• Adibidea :Txanpon bat 0,05eko adierazkortasun mailarekin Laplacerena
den ikusteko, ikas ezazu hipotesi-test bat egiteko erabaki araua,
txanpon baten 144 jaurtialdiko lagin baten kasuan.Izan bedi X saiakuntza egiten denean lortu den alde-kopurua.
probabilitatearen kalkuluak, hau da X zorizko aldagaiak 150aren eskuinean dagoen balio bat hartzeko probabilitatearen kalkuluak erabaki du zein hautatu. X zorizko aldagaia bakarrik balio baten eskuinaldera edo bakarrik ezkerraldera egotearen probabilitatea kalkulatzen diren test mota hauek, alde bakarreko testak dira.Beste ariketa batzuetan balio banaren eskuinaldeko eta ezkerraldeko
probabilitateak kalkulatu behar izaten dira ; alde biko testak
dira.• Adibidea :Txanpon bat 0,05eko adierazkortasun mailarekin Laplacerena
den ikusteko, ikas ezazu hipotesi-test bat egiteko erabaki araua,
txanpon baten 144 jaurtialdiko lagin baten kasuan.Izan bedi X saiakuntza egiten denean lortu den alde-kopurua.
Txanpona Laplacerena bada B(144,1/2) legea jarraituko du, eta dela lortzen da. Beraz normala erabiliz hurbilketa egokia egin daiteke.
dela lortzen da. Beraz normala erabiliz hurbilketa egokia egin daiteke.
Izan bedi Y aldagaia tipifikatutako aldagaia.N(O,1) banaketari dagokion taulari esker, hau baiezta daiteke :
tipifikatutako aldagaia.N(O,1) banaketari dagokion taulari esker, hau baiezta daiteke : y aldagaia bakartuta :
y aldagaia bakartuta : Lortutako alde kopurua 60 eta 80-ren artean badago, biak kanpo,
txanpona Laplacerena dela dioen hipotesia onartuko da; bestela,
baztertu egingo da.Zona kritiko esaten zaio hipotesia bazterrarazi dituzten balioak
dauden x-en tarteei. Kasu honetan :
Lortutako alde kopurua 60 eta 80-ren artean badago, biak kanpo,
txanpona Laplacerena dela dioen hipotesia onartuko da; bestela,
baztertu egingo da.Zona kritiko esaten zaio hipotesia bazterrarazi dituzten balioak
dauden x-en tarteei. Kasu honetan :
- Ariketak
17. Kirol bat egitearen emaitzek ez du beti "kirola osasuna da" dioen ideia egiaztatzen. Zenbait estatistikak diotenez, futbola egiten dutenen artean dagoen istripu portzentaia %22ra iristen da. Denboraldi batean igeriketa egiten duten 400 pertsonen artean sortu diren istripuak kontuan hartu dira, 36 istripu gertatu direlarik. Igeriketa futbola bezain arriskutsua al da?
Lehen motako errorea eta bigarren motako errorea
Aurreko adibideetan A eta B bi egoera ikasi dira (bi sendagai, Laplaceren txanpon bat benetako txanpon batekin), eta biak alderatzerakoan B egoera A egoeraren berdina dela suposatu da, hau da, aldaketarik ez dagoela. Ezer aldatu ez dela azaltzen duen hipotesi horri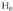 hipotesi nulua esaten zaio.Hipotesi nulua baztertzeko asmoarekin egiten da, hala, aldaketarik
egotekotan, kontrako hipotesia onartuko baita.
hipotesi nulua esaten zaio.Hipotesi nulua baztertzeko asmoarekin egiten da, hala, aldaketarik
egotekotan, kontrako hipotesia onartuko baita.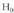 baztertzen den ala ez erabakitzeko,
baztertzen den ala ez erabakitzeko, adierazkortasun maila finkatu behar da, eta aldagaiaren
adierazkortasun maila finkatu behar da, eta aldagaiaren balioa emango duen testa egin.
balioa emango duen testa egin.
Adierazkortasun mailak, X zorizko aldagaiarekiko K zona kritiko bat finkatzen du. Estatistikatik lortzen den balioaren arabera, hau gerta daiteke :-
balioaren arabera, hau gerta daiteke :- zuzena dela suposatzen da, eta
zuzena dela suposatzen da, eta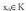 dela gertatzen da, orduan
dela gertatzen da, orduan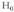 baztertu egingo dugu.-
baztertu egingo dugu.- zuzena dela suposatzen da, eta
zuzena dela suposatzen da, eta dela gertatzen da, orduan ez dugu
dela gertatzen da, orduan ez dugu baztertuko.Halako egoeratan bi errore mota egin daitezke :- Lehen mailako errorea :
baztertuko.Halako egoeratan bi errore mota egin daitezke :- Lehen mailako errorea : zuzena izan eta baztertzen denean.- Bigarren mailako errorea :
zuzena izan eta baztertzen denean.- Bigarren mailako errorea : okerra izan eta onartzen denean.Lehen mailako errore bat egitearen probabilitatea
okerra izan eta onartzen denean.Lehen mailako errore bat egitearen probabilitatea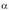 adierazkortasun mailaren berdina da. Izan bedi
adierazkortasun mailaren berdina da. Izan bedi bigarren mailako errore bat egitearen probabilitatea. Errore mota hau kalkulatzea zailagoa da.Erabaki arauak beti
bigarren mailako errore bat egitearen probabilitatea. Errore mota hau kalkulatzea zailagoa da.Erabaki arauak beti onartuko balu
onartuko balu eta
eta izango litzateke. Aldiz
izango litzateke. Aldiz beti baztertuko balu
beti baztertuko balu eta
eta izango litzateke
izango litzateke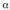 eta
eta biak txikiak izatea izango litzateke egokiena, baina bietako bat txikitzeko erabaki araua aldatzen denean, bestea handitu egiten da. Praktikan,
biak txikiak izatea izango litzateke egokiena, baina bietako bat txikitzeko erabaki araua aldatzen denean, bestea handitu egiten da. Praktikan, -rentzat ustez txikia den balio bat finkatukoda (oro har 0,05 edo 0,01) eta
-rentzat ustez txikia den balio bat finkatukoda (oro har 0,05 edo 0,01) eta alde batera uzten da. Hautatutako
alde batera uzten da. Hautatutako -ren balioa "testaren adierazkortasun maila" da, eta baldintzazko probabilitate bat bezala har daiteke :
-ren balioa "testaren adierazkortasun maila" da, eta baldintzazko probabilitate bat bezala har daiteke : baztertu/
baztertu/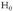
Balio kritikoak
Testaren adierazkortasun mailak %5era edo % 1 era finkatuta
daudenez, z aldagaiaren muga balioak finkoak dira.1. Alde biko testaren kasuana) Adierazkortasun maila 0,05 denean-1,96 eta 1,96 balioak garrantzitsuak izan dira alde biko testari
zegokion lehenengo adibidean, izan ere :F(1,96) = 0,975 ; F(-1,96) = 0,025. Beraz F(1,96) - F(-1,96) = 0,95b) Adierazkortasun maila 0,01 deneanKasu honetan -2,576 eta 2,576 balioak erabili beharko dira, izan
ere :F(2,576) = 0,995 ; F(-2,576) = o,oos.Beraz F(2,576) - F(-2,576) = 0,992. Alde bakarreko testaren kasuana) Adierazkortasun maila 0,05 deneanKasu honetan 1,645 edo -1,645 balioak erabiliko dira x oso handia
denean edo x oso txikia denean hipotesia baztertzeko, izan ere :0,95 = F(1,645) = P(z<1,645)0,05 = F(-1,645) = P(z> -1,645) = 1 - P(z<-I,G45) ;Beraz : P(z>-1,645) = 1 - 0,05 = 0,95b) Adierazkortasun maila 0,0 1 deneanHemen 2,326 eta -2,326 balioak erabiliko dira, izan ere :F(2,326) = 0,99 = F(-2,326) = 0,01
F(-2,326) = 0,01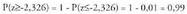 Balio hauek F funtzioko taularen azpialdean azaltzen dira.
Balio hauek F funtzioko taularen azpialdean azaltzen dira.
XI. Estimazioa
Batzuetan ez da aurretiko hipotesiarik izaten. Halakoetan probabilitatea
estimatzeko azterketa bat egiten da. Azterketa hori ez da
hipotesia onartzeko edo baztertzeko egiten.• Adibidea:Fabrika batean egindako pieza bat akastuna izatearen p probabilitatea
zenbatekoa den jakin nahi da. Fabrika horretako 200 piezatako
lagin bat hartzen da eta 20 pieza akastun aurkitzen dira. Zer
esan daiteke eskatutako probabilitateari buruz?Izan bedi X, 200 piezek osatutako edozein lagineko pieza akastunen kopurua, pieza bat akastuna izatearen probabilitatea p dela suposatuz. X, B(200, p) banaketa binomialeko zorizko aldagai bat da.
Logikoena p = 20/200 = 0,1 pentsatzea da. Kasu honetan beraz, hurbilketa ona lor daiteke lege normala erabiliz. Ariketa honetan p probabilitatea estimatu nahi denez, normalarekiko hurbilketa "jarraitasun-zuzenketa"z kezkatu gabeegiten da, hau da, X aldagaiak
beraz, hurbilketa ona lor daiteke lege normala erabiliz. Ariketa honetan p probabilitatea estimatu nahi denez, normalarekiko hurbilketa "jarraitasun-zuzenketa"z kezkatu gabeegiten da, hau da, X aldagaiak legea jarraitzen duela suposatzen da. Hau idatzi daiteke :
legea jarraitzen duela suposatzen da. Hau idatzi daiteke : P(-1,9G<_ X-200p < 0,95
J200pq
200pq - 18 hartuz, hau lortzen da :
P(-1,9G<_ X-200p < 0,95
J200pq
200pq - 18 hartuz, hau lortzen da :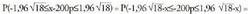 dena -200ekin zatituz
dena -200ekin zatituz Horren arabera lagin posibleen %95etan "p" balioa
Horren arabera lagin posibleen %95etan "p" balioa tartekoa izango da.Lagin atean lortu den X balioarentzat, hau da x 20 balioarentzat tartea
hau izango da
tartekoa izango da.Lagin atean lortu den X balioarentzat, hau da x 20 balioarentzat tartea
hau izango da %95eko probabilitatearekin, "p" lortutako tartea izango da.Tarte horri p-rekiko konfidantza tartea esaten zaio, konfidantza
maila %95ekoa delarik.Tarteko muturretan atera zaizkigun 0,058 eta 0,142 balioei konfidantza-mugak
esaten zaie.Azken atal horren eta hipotesi testei buruz azaldutakoaren artean
dagoen lotura estua ikusteko, hurrengo ariketa hau ikusi daiteke :Aditu batek dioenez pieza akastunen proportzioa %l0ekoa da.
%95eko probabilitatearekin, "p" lortutako tartea izango da.Tarte horri p-rekiko konfidantza tartea esaten zaio, konfidantza
maila %95ekoa delarik.Tarteko muturretan atera zaizkigun 0,058 eta 0,142 balioei konfidantza-mugak
esaten zaie.Azken atal horren eta hipotesi testei buruz azaldutakoaren artean
dagoen lotura estua ikusteko, hurrengo ariketa hau ikusi daiteke :Aditu batek dioenez pieza akastunen proportzioa %l0ekoa da.
Adituak arrazoia duen ala ez jakiteko 200 pieza aztertuko dira. Alde
biko test bat egiaztatzen bada, zein izango da erabaki araua? hipotesi nulua : p = 0, 1. Adierazkortasun maila %sekoa dela eman dezagun. Hipotesia onartu egin behar da tarte kritikoaren barruan ez badago, hau da banaketa honen balio kritikoak aurkitu behar dira.
hipotesi nulua : p = 0, 1. Adierazkortasun maila %sekoa dela eman dezagun. Hipotesia onartu egin behar da tarte kritikoaren barruan ez badago, hau da banaketa honen balio kritikoak aurkitu behar dira.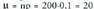 eta
eta denez,
denez, banaketa erabiliz kalkulatu daitezke. z-ren balio kritikoak
banaketa erabiliz kalkulatu daitezke. z-ren balio kritikoak denean -1,96 eta 1,96 dira.
denean -1,96 eta 1,96 dira.
.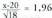 izango da. x despejatuz
izango da. x despejatuz eta
eta izango da. x despejatuz
izango da. x despejatuz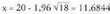 Adituaren baieztapena baztertuko da x>28 edo
Adituaren baieztapena baztertuko da x>28 edo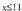 bada.200 pieza aztertzerakoan 20 pieza akastun aurkitu direla dioen
zorizko saiakuntza batetik abiatuz probabilitatearen konfidantza
tartea (%95era) ezagutu nahi bada, kalkulu berdinak egin beharko
dira, baina azalpenak aldatu egingo lirateke. x-en balioak lortu
ondoren konfidantza tartea hau dela esango da :
bada.200 pieza aztertzerakoan 20 pieza akastun aurkitu direla dioen
zorizko saiakuntza batetik abiatuz probabilitatearen konfidantza
tartea (%95era) ezagutu nahi bada, kalkulu berdinak egin beharko
dira, baina azalpenak aldatu egingo lirateke. x-en balioak lortu
ondoren konfidantza tartea hau dela esango da : Hau da :
Hau da :
Kasu orokorra
n lagun dituen lagin batean, horietako k lagunek propietate bat
dutela ikusten da.Propietate hori duten lagunen proportzioa estimatu nahi da. hartzen da, orduan
hartzen da, orduan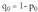 izango da, eta
izango da, eta bada, normala erabiliz egiten da hurbilketa. %95eko konfidantza maila batekin, propietate hori duten "p" lagunen proportzioa hurrengo tartean dagoela baiezta daiteke:
bada, normala erabiliz egiten da hurbilketa. %95eko konfidantza maila batekin, propietate hori duten "p" lagunen proportzioa hurrengo tartean dagoela baiezta daiteke:
- Ariketak
18. Zenbait milioi lagunek osatutako biztanle multzo
batetik 3001aguneko lagin bat hautatzen da. Lagin honetako
45 lagunen begien kolorea berdea da. Zein balioren artean
egongo da begiak kolore berdekoak dituzten pertsonen
portzentaia, errore arriskua %5a baino txikiagoa izatea nahi
bada?19. 50 hazietako lagin bateko 14 hazi ez dira ernamuindu.
Bilatu hazien ernamuintze probabilitatearekiko %95eko
konfidantza tartea.20. Fabrikatzaile batek dioenez, egiten dituen bonbilen
artetik akastunak %15a dira gehienez ere. Fabrika horretako
400 bonbilako lagin bat hartzen da(i) %5eko adierazkortasun mailarekin, zenbatgarren
bonbila akastunetik aurrera baztertu behar da fabrikatzaileak
dioen hipotesia zuzena dela?(ii) Lagineko 400 bonbiletatik 65 akastunak dira. Zein
balioen artean estimatzen da dagoela akastunen proportzioa,
errore probabilitatea % l a baino txikiagoa
bada?21. Gaixotasun bat duten 500 pertsonek A sendagai bat
hartzen dute gaixotasun hori gainditzeko. 360 sendatzen
dira. Zein balioen artean egongo da sendatze proportzioa,
errore probabilitatea %la baino txikiagoa bada?22. Enpresa batean, egunean 500 tresna egiten dira. Tresna
bakoitza 4 zatitan egiten da, horretarako elkarren artean
loturarik ez duten 4 makina erabiltzen direlarik.Makina horietako bakoitzak egiten dituen piezen %2,6a
akastuna dela egiaztatu da. Tresna bat kalitate onekoa dela
esaten da lau makinek ematen dituzten lau piezak kalitate
onekoak direnean.A) Zenbatekoa da tresna bat kalitate onekoa izateko probabilitatea?B) (i) Zein formula erabili behar da, egun batean egindako
tresnetatik zehatz-mehatz k tresna akastunak
direla esango digun probabilitatea kalkulatzeko?(ii) Gaussen Normalaren legea erabiliz, kalkula itzazu
hurrengo galderen probabilitateen hurbileko
balioak :a) Egun batean, zehatz-mehatz 40 tresna akastun egin
dira.b) Egun batean egindako tresna akastunen kopurua
40 eta 60ren artean dago.C) Egunaren bukaeran erosle bat azaltzen da. Oraindik
60 tresna salgai daude, horietatik 10 akastunak direlarik.
Erosleak, zoriz aukeratuta, tresna horietako 20
erosten baditu, zenbatekoa da, horietatik 4 akastunak
izatearen probabilitatea?23. C fabrikatzaileak dio bere fabrikan egiten diren bonbilen
% 1 5a akastuna dela. Fabrikatzaileak dioena baiezteko,
300 bonbilek osatutako lagin bat hartzen da, adierazkortasun
maila %sekoa delarik. 300 bonbileko laginean, zenbatgarren
bonbila akastunetik aurrera baztertuko da fabrikatzailearen
hipotesia?24. A fabrikatzaile batek bidalitako 2.000 bonbilak osatutako
lagin bat jaso da, horietatik 80 kalitate txarrekoak direlarik
. Bila kalitate txarreko bonbilen proportzioarentzat
konfidantza tarte bat, nahi den konfidantza maila %95ekoa
bada.25. C fabrikatzaileak dioenez, bere fabrikan egiten diren
bonbilen %15a kalitate txarrekoa da. Baieztapen hau test
baten bidez egiaztatu behar da. Fabrikatzailearen hipotesia
onartuko da, 100 bonbilaz osatutako lagin batean kalitate
txarreko 20 bonbila baino gutxiago aurkitzen badira.(i) Zein izango da hipotesi hau okertzat baztertzeko probabilitaterik
handiena?(ii) Zein izango da hipotesi hau onartzeko probabilitatea,
bonbilen %20a, benetan, kalitate txarrekoa bada?26. Denda batean A fabrikatzaileak bidalita 2.000 bonbila
jaso dira, bonbila horien produkzioko %4ak akatsak
dituelarik. Izan bedi X multzo honetan kalitate txarreko
bonbila kopurua.(i) Tchebycheffen desberdintza erabiliz, bila X-entzat
%90erako konfidantza tarte bat, tarte hori X itxaropen
matematikoak erdiratua dagoelarik.(ii) Banaketa normala erabiliz aurreko galdera kalkulatu
eta bi emaitzak alderatu.
Ebazpenak
Pierre de Fermat
(1601-1665)Pierre de Fermat matematikari handia Beaumont
de Lomagnen jaio zen, Frantziako Tolosako
eskualdean, 1601ean. Aita merkatari aberatsa
zuen, ama berriz abokatu eta epaile familiakoa.
Pierre de Fermat Tolosan hasi zen ikasten, Bordelera
igaro zen gero, eta 1631 n Zuzenbideko lizentziatura
eskuratu zuen Orleansen. Tolosara itzulita,
lanpostu bat lortu zuen eskualdeko
parlamentuan, bigarren lehengusu batekin ezkondu
zen eta bost seme-alaba izan zituzten. Zaharrenak
aitaren abokatu karrera bera egin zuen, artxidiakonoa
izan zen bigarrena, alaba zaharrena
ezkondu egin zen, eta bi alaba gazteenak komentuan
sartu ziren.Ez zen nabarmendu Fermat abokatu lanetan.
Pixkana-pixkana gora egin zuen eskualdeko parlamentuan
eta Tolosako epaitegietan, baina gehiago
antzinatasunagatik merituengatik baino. Ondasun
handien jabe izatera iritsi ez bazen ere, lanaren
bidez eta zentzuko inbertsioak egin baitzituen,
herentzia aski zabala utzi zien seme-alabei. Castrets-en
hil zen, 1665eko urtarrilaren 12an.Aspaldi ahaztua legoke Tolosako burgesia onaren
aitzindari baten bizimodu arazo eta gatzik gabe
hori, matematikaren hain zale izan ez balitz. Zaletasun
horrek XVII. mendearen lehen erdiko egile
orijinal eta interesgarrienetako bat izatera eraman
zuen. Newtonen eta Leibnizen kalkuluaren aitzindaria
izan zen, probabilitateen hasle eta goi mailako
matematika modernoaren sortzaile. Hori guztia
dela-eta, Amateurren Printzea deitzen zaio Pierre
Fermati.Ez zuen atsegin bere aurkikuntzak argitaratzea,
eta ez zuen Parisa joan izan nahi beste matematikariekin
harremanetan jartzera. Gutunezko harremanak
izan zituen, zuzenean nahiz Marin Mersenneren
bidez, edota haren ondorengo Carcaviren
bidez, hark egiten baitzituen, Zientzien Akademien
sorreraren aurretik, frantses eta europar zientzialarien
arteko bitartekari lanak. Fermatek Descartes,
Pascal, Wallis eta Huygens eta beste askorekin izan
zituen harremanak. Lan gehienak seme zaharrenak
argitaratu zizkion, zeinak 1670ean 111. mendeko
Diofanto greziar matematikariaren Aritmetika
berrargitaratu baitzuen, Fermaten iruzkin eta oharrekin,
DiophantiAlexandriniArithmetieorum libri
sex izenburuz ; gero, 1679an, seme zaharren horretxek
Uaria Opera argitaratu zuen, aitaren idatzien
parte handi batekin batera.Oraindik Bordelen zela, antzinako Greziako
matematikarien liburu galduak berregiteko ahaleginetan
hasi zen Fermat, hala adibidez Euklides,
Arkimedes edota Apoloniorenak. Haren metodoak
ez ziren horretan ohi zirenak, Francois Vietek
XVII. mende hasieran proposatu zituenak baizik ;
aljebraren prozedurak geometrian erabiltzearen
aldeko zen Viete. Fermatek leku geometrikoak
ekuazio bidez aztertu zituen, eta kurba bat zehazteko,
kurba horrek puntu eta ardatz finko bati buruz
zuen posizioa ematen zuen. Prozedura hori Descartesenaren
baliokidea da, bestelako idazkera bat
erabiltzen zuen arren, eta beste era batera garatzen.Metodo bat proposatu zuen maximoen eta minimoen
arazoak ebazteko. Gauza zen kurbaren balioa
x puntu maximo batean eta x+e puntu hurbileko
batean konparatzea, bi balioak berdindu, sinplifikatu,
eta e-ko terminoak kendu. Izan, ez zen berez
metodo infinitesimala, funtzioaren balioak maximoan
eta puntu hurbil batean duen sasi berdintasunean
oinarritzen zen, eta horrela adierazpenaren
termino finitoak ezaba zitzakeen, berak "adequalitas"
zeritzanak. Areak aurkitzeko batura geometriko
mugagabeen ezaugarriak erabili zituen, eta zenbaki
osoen berreduren baturen ezaugarriak. Fermatek
lortu zuen aurkitzea adierazpen polinomikoa duten
kurbek mugaturiko esparruen area.Probabilitate modernoaren abiapuntutzat hartzen
dira Fermatek eta Pascalek elkarri idatzi zizkioten
gutunak. Probabilitatean, Fermat konbinatoriaren
metodoak aplikatzearen aldeko izan zen, aldeko
kasuak eta kasu posibleak ezagutu ahal izateko.Fermatek goi mailako aritmetikan izan zituen
emaitzarik onenak, zenbakien teorian alegia.
Zoritxarrez, XVII. mendean, matematikari gutxi
ziren alor horretan interesatuak, eta Fermatek ez
zituen idatzi aurkitu zituen teorema askoren frogabideak
. Era horretan, Fermaten teorema txikia
deritzana, "p primoa baldin bada eta a p-z zatigarri
ez den zenbaki osoa, orduan aP -1 -1 zatigarria
da p-z", Eulerrek frogatu zuen 1736an. Badirudi
Fermaten azken teoremaren frogantza, "ezin aurki
daiteke x, y, z zenbaki osorik, xn + yn = z n denik n
> 2 bada", bukatua dagoela edozein n-ren kasuan,
1993 ezkero. Teorema hori Fermatek n = 3 eta n =
4 kasuetan frogatu zuen, eta esan zuen nola egiten
zen frogabidea "beheratze mugagabearen" bitartez,
beheranzko indukzio moduko baten bidez
alegia. Gauza aski sinesgarria dirudi akatsak aurkitu
zituela lehen frogabidean, baina, jakin, Diofantoren
Aritmetika-ri egin zizkion oharretan zioena
besterik ez dakigu : "liburu honen bazterrak txikiegiak
dira (froga hori) idatzi ahal izateko".