Matematika»Konbinatoria
Konbinatoria

Sarrera
Konbinatoria multzo finito baten elementuak hautatzeko edota ordenatzeko dauden era desberdinak aztertzen dituen matematikaren alorra da. Elementuak hautatzeko eta ordenatzeko arau jakin batzuk daude, eta batez ere, arau horiei jarraituz osa daitekeen taldeen kopurua du aztergai konbinatoriak. Taldeak osatzeko kontuan hartu behar izaten diren baldintza ohikoenek talde bakoitzean elementu guztiak ala batzuk bakarrik hartzen diren, elementuak errepika daitezkeen ala ez, eta elementuen ordenak eragina duen ala ez adierazten dute.Ezar daitezkeen baldintzak hainbat motakoak izan daitezkeenez, ordea, konbinatoriako problemak era askotakoak izan daitezke. Problema arruntenak konbinazioak, aldakuntzak eta errepikatu gabeko ala errepikatuzko permutazioak dira. Sarri askotan problema bat ebazteko, problema hori kasu ezagunetara eramaten duten problema txikiagoetan deskonposatu behar izaten da. Orokorrean, konbinatorian jarraitu behar den metodologia ez da analisian bezain uniformea, problemak ebazteko era desberdinak egon daitezkeelako. Hau dela eta, konbinatorian bereziki aplika daitezkeen kontzeptu batzuk berrikustea komenigarria da.
Konbinatoriaren jatorria
Konbinatoria modernoak Pascal eta Leibnitzen idatzietan du jatorria,
beraz, alor nahikoa berria da. Haien aurreko garaietan ez zen aurreramendu
handirik egin alor honi dagokionez mendebalean ; ekialdeko zibilizazioetan,
Indian eta Txinan egin ziren aurrerapen nagusiak XVII. mendea
bitarrean.Konbinatoriaren lehenengo urratsak aritmetikako problemekin erlazionaturik
daude, erroak ateratzearekin adibidez, edo aljebrarekin, binomioen
berredurarekin, esaterako. Horrez gainera konbinatoriako gaiak
agertzen ziren erlijioan edo igarmenean ere : txinatar karratu magikoetan,
juduen Cabalan edo Ramon Llull Beatoren eskema konbinatorioetan,
hain zuzen ere.Aldaketen liburua, edo I Ching, aintzinako ezagupide txinatarren bilduma
bat da, K.a. VII. mendetik aurrera argitara emana. Liburu honetan
bi elementutatik abiatuta -Yang eta Yin- hirunakako edo seinakako zenbat
talde desberdin osa daitezkeen aztertzen da. Bere helburua zoriz hartutako
hiru edo sei ikur erabiliz etorkizuna asmatzea da. Yang edo Yinekin osa daitezkeen segidak ezagutzea konbinatoriako problema bat da,
eta igarmenari lotuta dagoenez, Txinan interes handia sortu zuen gure
aroa baino lehenagotik.Bestalde, Indian, dirudienez K.a. VI. mendeko medikuntzako idatzietan
agertzen dira lehen aldiz konbinatoriako arazoak ; oinarrizkoak diren
sei zapore erabiliz, zenbat zapore desberdin lor daitezkeen azaltzen saiatzen
dira besteak beste. K.a. 11. mendean Pingala liburuak silaba luze edo
motzen kopuru jakin batetik abiaturik poesian zenbat erritmo desberdin
eman daitezkeen aztertzen du (sei silabekin zortzi aukera desberdin hain
zuzen). Gure aroko VI. mendean badirudi Indian ezagunak zirela konbinazio
kopurua kalkulatzeko formulak. Bhaskararen Lilivati liburuan, XII.. endean gutxi gora behera, konbinazioen hainbat problema ebazten
dira.Konbinatoriako problema bezala har daiteke, halaber, Txinan aintzinatik
aztertua izan zen karratu magikoen problema ere, nahiz eta problema
horrek ez duen aplikazio asko eta hori dela eta ez den hemen aztertuko
. Karratu magiko bat 1 -etik n--ra zenbaki multzo bat da, n lerro eta n
zutabetan ordenatua halako eran non lerro bakoitzean dauden elementuen
batura berdina baita.Adibidez 9 zenbakiekin K.a. I. mendean txinatar idatzietan azaltzen
den karratua kalkula daiteke.XIII. mendean Yang Huik 9x9 ordenako karratu magiko bat eman
zuen. Arestian, XVIII. mendearen bukaeran, Euler suitzarrak karratu
magikoak aztertu zituen, eta XX. mendean, haren ustea zuzena zela frogatu
da : ez dago 6x6 karratu latino ortogonalik, hau da, 6x6 karratu batean
graduazio eta errejimentu desberdinetako sei ofizial nolanahi ordenatuta
ere, ez da lortuko lerro eta zutabe bakoitza graduazio eta erregimentu
desberdineko ofizialez osatzea. Hala ere, 1Ox10 karratu magikoak ezinezkoak
direla ere uste izan zuen, eta uste hori ez da zuzena. Gaur egun,
hainbat eta hainbat kasu frogatu behar direla-eta ebazten zailak ziren elementu
finitoen problemen kalkulua asko erraztu da ordenagailuei esker.Badirudi, txinatarrek eta indiarrek aztertu zutela, halaber, triangelu
aritmetikoa. Triangelu aritmetikoa Pascal edo Tartagliaren triangelua izenez
ere ezagutzen da, edota koefiziente binomialen triangelu izenez.Mendebalean, Ramon Llullek (Palma de Mallorca 1232-1315) konbinatoria
ezagutzeko interesa sortu zuen. Zuzenak diren proposizioak lortzeko
metodo unibertsal bat proposatu zuen, hitz idatziak gurpiletan,
triangeluetan edo laukietan nahastuz. Nahasketa hauekin era guztietako
egiak -kristau erlijioarenak barne- frogatzea zuen helburu, eta bere metodoa
erabiliz, musulmanak kristautasunera limurtzea. Bere ideiak ArsMagna liburuan eta beste obra askotan bildu zituen. Konbinatoriaren
alorrean prozedura deskribatzaileak erabili zituen prozedura matematikoak
baino areago ; beraz, ez zuen aurreramendu handirik ekarri. Nolanahi
ere, Erdi Aroan eta Berpizkundean eragin handia izan zuen ; besteak
beste, Llull izan zen olerkiak katalanez idatzi zituen lehenengoetakoa.
Aipagarria du "Llibre d'amic i d'amant " olerki liburua.Juduen artean Cabalari azaltzen dira konbinatoriako problemak, Erdi
Aroan eta Berpizkundean zenbakiak, hizkiak eta betiko salbaziorako
bideak nahastuz.Azkenik, XVIIL mendean zehar finkatu ziren konbinatoria sistematikoki
tratatzeko oinarriak, probabilitateen kalkulu problemak, koefiziente
binomikoak eta logikako problemen oinarriak aztertuz eta ebatziz.
Horrela, Pascalen "Triangle Aritmetique" (1654) eta Leibnitzen
"Dissertatio de Arte Combinatoria" (1666) liburuak gaur egungo konbinatoriaren
abiapuntutza hartuak dira.
I. Metodologia
Konbinatoriako problemak ebazteko era baliagarri orokor bat ez
badago ere, badaude hainbat metodo, kasu askotan baliagarriak
izan daitezkeenak. Hasteko, badira bi bide beti saiatu beharrekoak :- Problema sinplifikatu. Enuntziatuak esaten badu baldintza
jakin batzuetan 50 pertsonen artean 20 hautatu behar direla,
horren baliokide izango den problema bat planteatu behar da zenbaki
errazagoez (txikiagoez) baliaturik ; alegia, 5 pertsonen artean 2
hautatu. Era honetan errazagoa izango da zerrendak eta eskemak
egitea, emaitzak behatzea eta orokorrean aplika daitezkeen legeak
ateratzea.- Problemaren terminoak sinplifikatu. Agirresarobe, Barkaiztegi,
Urretabizkaia eta Zuazabeitia abizenak dituzten lau pertsona ordenatu
behar badira, izen horiek A, B, U eta Z letrez izendatzeak, edo
era horretako sinplifikazioak egiteak, problema errazten du.
Bukaeran berriro abizen osoak eman daitezke, beharrezkoa izanez
gero.Sinplifikazio hauek ondoren aipatzen diren bideak erabiliz kalkuluak
egiteko aukera ematen dute :- Zuhaitz diagramak. Probleman azal daitezkeen kasu guztiak
ezagutzeko aukera ematen dute.Adibidez: hiru seme-alaba dituen sendi batean, seme-alabak
sexuaren arabera ordenatuz gero, zenbat kasu desberdin izan daitezkeen
jakin nahi da ; alegia, mutila, mutila, mutila izango litzateke
kasu bat, mutila, mutila, neska beste kasu bat, etab. Adinaren
arabera nagusia, erdikoa eta txikia badira, eta sexuaren arabera o
(mutila) eta a (neska) izendatzen baditugu, honela osatuko litzateke
zuhaitz diagrama :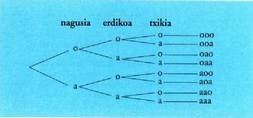 8 kasu posible daude beraz. Nagusitik txikienera ordenatuta : :
(mutila, mutila, mutila), (mutila, neska, mutila) , etab.- Zerrendak. Ez dira zuhaitzak bezain erabilgarriak baina problema
batzuetan lagungarriak izan daitezke. Zerrendak erabiltzerakoan
elementuen artean ordena jakin bat markatzea komenigarria
da, alegia, txikienetik handienera zenbakiak badira, edo alfabetoaren
arabera hizkiak badira :Adibidez, 1, 2, 3, 4 zifrez bi zifrako zenbat zenbaki osa daitezkeen
jakin nahi da. Txikienetik handienera : 11, 12, 13, 14, 21, 22,
23, 24, 31, 32, 33, 34, 41, 42, 43, 44 izango lirateke.- Diagrama kartesiarra. Bi multzotako elementuak parekatu
behar direnean izan daiteke erabilgarria.Adibidez, 3 mutil eta 4 neska daude. Dantza egiteko zenbat
bikote desberdin egin daitezke?Neskak
8 kasu posible daude beraz. Nagusitik txikienera ordenatuta : :
(mutila, mutila, mutila), (mutila, neska, mutila) , etab.- Zerrendak. Ez dira zuhaitzak bezain erabilgarriak baina problema
batzuetan lagungarriak izan daitezke. Zerrendak erabiltzerakoan
elementuen artean ordena jakin bat markatzea komenigarria
da, alegia, txikienetik handienera zenbakiak badira, edo alfabetoaren
arabera hizkiak badira :Adibidez, 1, 2, 3, 4 zifrez bi zifrako zenbat zenbaki osa daitezkeen
jakin nahi da. Txikienetik handienera : 11, 12, 13, 14, 21, 22,
23, 24, 31, 32, 33, 34, 41, 42, 43, 44 izango lirateke.- Diagrama kartesiarra. Bi multzotako elementuak parekatu
behar direnean izan daiteke erabilgarria.Adibidez, 3 mutil eta 4 neska daude. Dantza egiteko zenbat
bikote desberdin egin daitezke?Neskak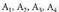 eta mutilak
eta mutilak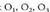 izendatzen baditugu :
izendatzen baditugu :
I I. Multzoen bilketa eta biderkadura kartesiarra
Multzo baten elementuen kopuruari edo kardinalei dagozkien bi
propietate daude konbinatorian aplikazio ugari dutenak :- Baldin eta multzoa bi multzo disjunturen bilketaren bidez sortua
bada, bilketaren elementu kopurua bi multzoen elementu
kopuruen arteko batura izango da. Adibidez, baserri batean behiak
eta oiloak badaude, animalia kopurua behi kopurua gehi oilo
kopurua izango da. Propietate hau bi multzoek elementu amankomunik
ez dutenean bakarrik betetzen da. Izan ere, lau pertsonari
abestea gustatzen bazaie eta hiruri dantza egitea gustatzen bazaie,
litekeena da lau pertsona bakarrik izatea orotara eta horietako bati
dantza egitea ez gustatzea, eta litekeena da, halaber, zazpi pertsona
izatea eta hauen artean dantza egitea eta abestea, biak, gustatzen
zaionik inor ez egotea.- Bi multzoren arteko biderkadura kartesiarraren elementu
kopurua bi multzoen elementu kopuruen arteko biderkadura izango
da. Multzo bateko elementu bat eta beste multzo bateko beste
elementu bat hartuz, osa daitezkeen bikoteen kopurua bi multzoen
elementu kopuruen arteko biderkadura da. Aurreko adibidea,
diagrama kartesiarrarena, da adibidez biderkadura kartesiarraren
adibide bat.Metodo orokor hauek konbinatoriako hainbat problema ebazten laguntzen dute ; baina zailtasun nagusia kasu orokorra deskonposatzerakoan sortzen diren problema txikiak ebazten datza.
Esaterako, gosaltzeko kafe hutsa ala kafesnea, edota tea limoiaz ala tea esneaz har badaitezke, guztira eskaintzen diren aukerak 2 + 3 = 5 dira ; beste askotan ordea, ez da hain erraz egiten problema bateko kasu posibleen kalkulua. Biderkadura kartesiarraren adibide bat izan daiteke : ekipo batek 4 margoko kamisetak eta hiru margoko galtzak ditu aukeratzeko. Zenbat uniforme desberdin jantzi ditzakete jokalariek? Uniforme bakoitza bikote ordenatu bat da, beraz, guztira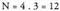
- Ariketak
1.- Jatetxe batean eguneroko menuan 1. platerarako 4 aukera dituzte, 2. platerarako 3 aukera eta postrerako 5 aukera. Zenbat menu desberdin osa daitezke?2.- Bost alkandora, 3 galtza pare eta 3 zapata pare badituzu, zenbat jantzi desberdin osa ditzakezu?3.- Herrialde batean autoen matrikula osatzeko alfabetoko lehenengo hogei letren artean hautatutako hizki bat jartzen da eta gero 1000-ren artean hautatutako zenbaki bat. Zenbat matrikula desberdin atera daitezke?4.- Antzinako problema bat : zazpi atso Erromarantz doaz, zazpina mandorekin, mando bakoitzak zazpina zaku daramatza, zaku bakoitzean zazpina ogitzar daude, ogitzar bakoitzak zazpina aizto ditu eta aizto bakoitzak zazpina leka. Zenbat gauza daude guztira? (Fibonacci Liber Abaci, Italia XIII. mendea)
I I I. Errepikatuzko aldakuntzak
k-naka harturiko n elementuen errepikatuzko aldakuntzak n elementu
horietatik k elementuak hartu eta ordenean jarriaz, bainaelementuak errepikatzen direla, osa daitezkeen taldeak dira.
Adibidez : AEO elementuak ditugula, binaka hizki hartuaz ondoko
errepikatuzko aldakuntzak lortuko dira :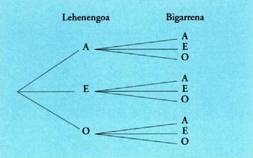 Beraz, AA, AE, AO, EA, EE, EO, OA, OE, 00 dira. Hau da,
k elementuz osatutako multzoak dira, non 1. elementua edo 2.a
edo k.a, n horietako edozein izan daitekeen. Beraz, aurreko puntuan
ikusitako biderkadura kartesiarraren kasu berezi bat da, non
multzo berbera k aldiz errepikatzen den. Multzo kopurua kalkulatzeko
nahikoa litzateke hemen ere biderkadura egitea. Adibidez,
10 korrikalarik 3 lasterketa egiten badituzte, lasterketetako irabazleen
zerrenda osatzeko zenbat era daude?Lehenengo lasterketa 10 korrikalarien artean edozeinek irabaz
dezake, bigarrena berriz ere 10-en artean edozeinek ; 1. lasterketa
irabazi duenak, 2.a ere irabaz dezake ; eta gauza bera 3. lasterketan.Beraz :
Beraz, AA, AE, AO, EA, EE, EO, OA, OE, 00 dira. Hau da,
k elementuz osatutako multzoak dira, non 1. elementua edo 2.a
edo k.a, n horietako edozein izan daitekeen. Beraz, aurreko puntuan
ikusitako biderkadura kartesiarraren kasu berezi bat da, non
multzo berbera k aldiz errepikatzen den. Multzo kopurua kalkulatzeko
nahikoa litzateke hemen ere biderkadura egitea. Adibidez,
10 korrikalarik 3 lasterketa egiten badituzte, lasterketetako irabazleen
zerrenda osatzeko zenbat era daude?Lehenengo lasterketa 10 korrikalarien artean edozeinek irabaz
dezake, bigarrena berriz ere 10-en artean edozeinek ; 1. lasterketa
irabazi duenak, 2.a ere irabaz dezake ; eta gauza bera 3. lasterketan.Beraz :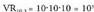 Hau da, 3-rekin biderkatzen da multzoan dagoen elementu
kopurua. Beraz, bat dator biderkadura kartesiarrarekin.Orokorrean multzoak n elementu baditu eta aldakuntzak osatzeko
k elementu hartzen badira, gerta litezkeen kasu guztiak formula
honen bidez aterako ditugu :
Hau da, 3-rekin biderkatzen da multzoan dagoen elementu
kopurua. Beraz, bat dator biderkadura kartesiarrarekin.Orokorrean multzoak n elementu baditu eta aldakuntzak osatzeko
k elementu hartzen badira, gerta litezkeen kasu guztiak formula
honen bidez aterako ditugu :
- Ariketak
5.- Ordenagailu batean "bit" izenekoa da oinarrizko informazio banakoa; bitak bi aukera bakarrik onartzen ditu : 0 eta 1. Informazio hauek 8 bit-ek osatutako byte izeneko talde ordenatuetan sailkatzen dira. Esaterako 01010010 edo 10001011. Zenbat byte desberdin lor daitezke?6.- Zenbat auto matrikula desberdin lor daitezke 25 hizkien artean 3 hizki eta ohiko 10 zifren artean (0 9) 5 zifra hartzen dituen herrialde batean? (Matrikuletan zifrak eta letrak errepika daitezke).7.- Kiniela bat egitean, kiniela osatzen duten 15 partiduen aurrean ,l, X edo 2 jartzen da; 1, etxean jokatzen duen taldeak irabaziko duela pentsatzen bada, X, berdindu egingo dutela pentsatzen bada eta 2, kanpokoak irabaziko duela pentsatzen denean. Zenbat kiniela desberdin egin daitezke?
IV. Ohiko aldakuntzak
k-naka harturiko n elementuen aldakuntza esaten zaie k-nako
elementu sailekin osa daitezkeen talde bakoitzari, talde guztietan k
elementu desberdinek parte hartzen dutela, eta talde guztien arteko
desberdintasuna elementuren bat edo elementuen ordena dela.Aldakuntza kopurua adierazten da gazteleraz ("variaciones"),
adierazten da gazteleraz ("variaciones"),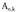 frantsesez ("arrangements"). Liburu batzuetan
frantsesez ("arrangements"). Liburu batzuetan edo
edo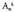 azaltzen da. Kalkulagailuetan eta ingelesezko liburuetan
azaltzen da. Kalkulagailuetan eta ingelesezko liburuetan Adibidez, 3 margoko banderak egin nahi dira oihal gorria, berdea,
urdina eta txuria erabiliz. Margoak beti zerrenda horizontaletan
jarriaz, zenbat bandera desbedin egin daitezke hiruna margokoak?
Adibidez, 3 margoko banderak egin nahi dira oihal gorria, berdea,
urdina eta txuria erabiliz. Margoak beti zerrenda horizontaletan
jarriaz, zenbat bandera desbedin egin daitezke hiruna margokoak? Lehenengo zerrenda 4 kolore horietako edozeinetakoa izan daiteke,
erdikoa gelditzen diren 3 margoetatik batekoa izango da eta
3. zerrenda oraindik erabili ez diren beste bi margoetako batekoa.
Lehenengo zerrenda 4 kolore horietako edozeinetakoa izan daiteke,
erdikoa gelditzen diren 3 margoetatik batekoa izango da eta
3. zerrenda oraindik erabili ez diren beste bi margoetako batekoa.
Beraz, guztira : Orokorrean, n margo kopurua bada eta k zerrenda kopurua, 1.. errenda osatzeko n era izango dira, 2. zerrenda osatzeko n-1 era,
3. zerrenda osatzeko n-2 era eta azkenik, k. zerrenda osatzeko n -
(k - 1) era desberdin izango dira, aurreko zerrendak osatzeko erabilitako
margo kopurua k-1 izango baita. Hau da :
Orokorrean, n margo kopurua bada eta k zerrenda kopurua, 1.. errenda osatzeko n era izango dira, 2. zerrenda osatzeko n-1 era,
3. zerrenda osatzeko n-2 era eta azkenik, k. zerrenda osatzeko n -
(k - 1) era desberdin izango dira, aurreko zerrendak osatzeko erabilitako
margo kopurua k-1 izango baita. Hau da :
- Ariketak
8.- 40 karta dituen karta sorta batetik, karta bana ematen zaie lau jokalariri. Zenbat karta joku desberdin osa daitezke lau jokalarien kartez?9.- 30 ikasle dituen ikasgela batean ordezkaria eta ordezkari-laguntzailea aukeratu behar dira. Zenbat era desberdinetan egin daiteke aukeraketa?10.- 3 opari desberdin banatzen dira 5 neska-mutilen artean. Zenbat era desberdinetan egin daiteke banaketa, inork ezin badu opari bat baino gehiago hartu?11.- Hamar korrikalarik lasterketa bateko azken proban parte hartzen dute. Lehenengo iristen diren hiruei urrezko domina, zilarrezkoa eta brontzezkoa emango zaizkie hurrenez-hurren. Zenbat eratan bana daitezke dominak?
V. Permutazioak
n elementuren permutazioak n elementu horiekin sor daitezkeen talde desberdin guztiak dira. Multzo baten permutazioetan multzo horretako elementu guztiak sartzen dira beti eta bi permutazioen arteko diferentzia elementuen ordenean datza soilik. n- naka harturiko n elementuen aldakuntza bakoitzean n elementuak sartuko dira eta bi aldakuntzen arteko diferentzia elementuen ordenean bakarrik ikusiko da, beraz, n-naka harturiko n elementuen aldakuntzak eta n elementuen permutazioak berdinak dira.
Beraz, n elementuen permutazioak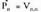 izango dira.n elementuren permutazio kopurua n elementuen aldakuntza
kopuruaren kasu berezi bat da, non biderkagaiek beherako baloreak
hartzen dituzten, n-tik hasi eta 1-era iritsi arte. Esaterako, OGI
hitzaren hizkiak zenbat eratan ordenatu daitezkeen jakin nahi
bada, ondorengo zuhaitz diagrama egin daiteke :
izango dira.n elementuren permutazio kopurua n elementuen aldakuntza
kopuruaren kasu berezi bat da, non biderkagaiek beherako baloreak
hartzen dituzten, n-tik hasi eta 1-era iritsi arte. Esaterako, OGI
hitzaren hizkiak zenbat eratan ordenatu daitezkeen jakin nahi
bada, ondorengo zuhaitz diagrama egin daiteke : Hau da, sei kasu daude : OGI, OIG, GOI, IOG, IGO. Eta multzoak
elementu gehiago balitu, berdin. Hamar pertsonak korritzen
duten lasterketa batean, zenbat sailkapen desberdin era daitezkeen
jakin nahi bada, I.a, 10 korrikalarietatik edozein izan daiteke, 2.. ailka daiteke lehenengo iritsi ez diren gainerako 9 korrikalarietako
edozein, 3.a gelditzen diren 8-ren arteko bat, eta horrela azkena
iritsi arte. Beraz :
Hau da, sei kasu daude : OGI, OIG, GOI, IOG, IGO. Eta multzoak
elementu gehiago balitu, berdin. Hamar pertsonak korritzen
duten lasterketa batean, zenbat sailkapen desberdin era daitezkeen
jakin nahi bada, I.a, 10 korrikalarietatik edozein izan daiteke, 2.. ailka daiteke lehenengo iritsi ez diren gainerako 9 korrikalarietako
edozein, 3.a gelditzen diren 8-ren arteko bat, eta horrela azkena
iritsi arte. Beraz :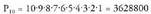 Orokorrean n elementu ordenatu behar badira, goiko prozedura
bera erabiliz :
Orokorrean n elementu ordenatu behar badira, goiko prozedura
bera erabiliz :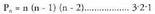 Faktorialan (n - 1) (n - 2) (n - 3) 3-2.1 biderkadurari n faktorial
esaten zaio, eta n! idazten da.• Adibidez:
Faktorialan (n - 1) (n - 2) (n - 3) 3-2.1 biderkadurari n faktorial
esaten zaio, eta n! idazten da.• Adibidez: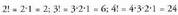 Orokorrean :
Orokorrean :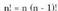 betezen da.0!-entzat definizio honek ez luke balioko, eta hitzarmenez 1
balioa duela onartzen da: 0! = 1Aldakuntzen kopurua :
betezen da.0!-entzat definizio honek ez luke balioko, eta hitzarmenez 1
balioa duela onartzen da: 0! = 1Aldakuntzen kopurua :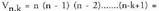
- Ariketak
12.-Kalkula itzazu :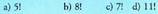 13.-Adierazi faktorial moduan :
13.-Adierazi faktorial moduan :
VI. Errepikatuzko permutazioak
n elementu dituen multzo baten permutazioak errepikatuzkoak
dira permutatzen diren elementu horien artean batzuk berdinak
direnean. Berdinak diren elementuak batzuk besteekin aldatuko
bagenitu, ordenazio berbera lortuko genuke ; beraz, kasu honetan
ordenazio kopurua txikiagoa izango da. Adibidez, zein da ELE hizkien
permutazio kopurua?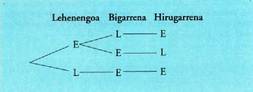 Bakarrik ELE , EEL eta LEE izan daitezke. Hiru elementu desberdin
permutatzerakoan berriz, 6 kasu desberdin lortuko lirateke.Errepikatuzko permutazioak
Bakarrik ELE , EEL eta LEE izan daitezke. Hiru elementu desberdin
permutatzerakoan berriz, 6 kasu desberdin lortuko lirateke.Errepikatuzko permutazioak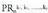 adierazten dira, n permutatzen den elementu kopurua izanik, eta
adierazten dira, n permutatzen den elementu kopurua izanik, eta bidez adierazten dela zenbat aldiz errepikatzen den elementu bakoitza.Adierazpen orokorra lortzeko, ikus dezagun aurrekoa baino adibide zailtxoagoa : zenbat adierazpen lor daitezke NAFARROA hitzaren hizkiak permutatzerakoan? Guztira 8 hizki daude, baina A 3 aldiz azaltzen da, eta R 2 aldiz. Hitza NAFaRroa idatziko balitz permutazio guztiak 8! izango lirateke. Baina bi R-ak ezin direnez bereizi,
bidez adierazten dela zenbat aldiz errepikatzen den elementu bakoitza.Adierazpen orokorra lortzeko, ikus dezagun aurrekoa baino adibide zailtxoagoa : zenbat adierazpen lor daitezke NAFARROA hitzaren hizkiak permutatzerakoan? Guztira 8 hizki daude, baina A 3 aldiz azaltzen da, eta R 2 aldiz. Hitza NAFaRroa idatziko balitz permutazio guztiak 8! izango lirateke. Baina bi R-ak ezin direnez bereizi,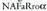 eta
eta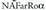 eta desberdintasun bakarra R letra duten gainerako bikoteak berdinak direnez, erdira murrizten da permutazio kopuru posiblea. Baina gauza bera gertatzen da A- rekin, ezin baitira hiru A-k bereizi. Beraz A hizkiak trukatzerakoan lortzen diren kasu guztiak berdinak dira.Beraz, hasierako 8! kasuak, 2! eta 3!-rekin zatitu beharko dira,
zenbat permutazio desberdin lor daitekeen jakiteko.
eta desberdintasun bakarra R letra duten gainerako bikoteak berdinak direnez, erdira murrizten da permutazio kopuru posiblea. Baina gauza bera gertatzen da A- rekin, ezin baitira hiru A-k bereizi. Beraz A hizkiak trukatzerakoan lortzen diren kasu guztiak berdinak dira.Beraz, hasierako 8! kasuak, 2! eta 3!-rekin zatitu beharko dira,
zenbat permutazio desberdin lor daitekeen jakiteko.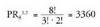 Azalpen hori jarraituz, orokorrean :
Azalpen hori jarraituz, orokorrean :
- Ariketak
17.- Zenbat hitz desberdin, ahozkatu daitezkeenak ala ez, idatz daitezke PINPILINPAUXA hitza osatzen duten hizkiekin?18.- Hamar korrikalariko multzoa gainerako korrikalariei aurrea hartuta iritsi da helmugara, hauetatik 5 dira A ekipokoak, B ekipokoak 3 eta C ekipokoak 2. Helmugan ekipoen ordenari bakarrik erreparatzen badiogu, zenbat ordena desberdin egon daitezke?19.- Ikasgela bateko 20 ikasleak era honetan banatu behar dira : 10-ek fisikako laborategira joan behar dute, 5-ek informatikako klasera eta 5 klaserik gabe gelditzen dira. Zenbat eratan bana daitezke?
VII. Konbinazioak
n elementu dituen multzo bat emanda, k elementu hartuz talde
desberdinak osatu behar dira, kontuan harturik talde desberdinak
direla elementu bat beste taldeekiko desberdina dutenak, hau da,
konbinazioetan ez dela kontuan hartuko ordena.Adibidez, Miren, Jaione, Ander eta Koldoren artetik bik platerak
garbitu behar dituzte eta beste biak libre gelditzen dira. Zenbat eratan
egin daiteke banaketa?M, j, A, K izendatuko ditugu, alfabetikoki : A, j, K, M.Osa daitezkeen bikoteak hauek dira : AJ, AK, AM, JK, JM, KM.
Beste edozein bikote hartzen badugu, hauetako bat izango da, elementu
berberez osatua baina ordena aldatuta.Konbinazio kopurua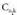 adierazten da; adierazpen horretan n letrak multzoan dauden elementu kopurua adierazten du, eta k letrak aukeratzen diren elementuen kopurua. Horrela, aurreko kasuan :
adierazten da; adierazpen horretan n letrak multzoan dauden elementu kopurua adierazten du, eta k letrak aukeratzen diren elementuen kopurua. Horrela, aurreko kasuan : Ikus dezagun beste adibide bat : Ikasgela batean 15 ikasle daude
eta horietatik 3 hautatu behar dira lasterketa batean parte hartzeko
. Zenbat eratan egin daiteke hautaketa?Hirurak ordena kontuan harturik hautatu beharko balira -lehenengoa,
lehen ordezkoa eta bigarren ordezkoa- aldakuntza problema
bat izango litzateke. Baina kasu honetan ordenak ez du eraginik,
berdin zaigu ABC edo ACB edo BCA. Aldakuntza problema gisa
hartzen badugu, konbinazio bakoitza 3Y aldiz errepikatuko litzateke,
hori baita 3 elementuren artean era daitekeen ordenazio kopurua.Beraz, konbinazioak
Ikus dezagun beste adibide bat : Ikasgela batean 15 ikasle daude
eta horietatik 3 hautatu behar dira lasterketa batean parte hartzeko
. Zenbat eratan egin daiteke hautaketa?Hirurak ordena kontuan harturik hautatu beharko balira -lehenengoa,
lehen ordezkoa eta bigarren ordezkoa- aldakuntza problema
bat izango litzateke. Baina kasu honetan ordenak ez du eraginik,
berdin zaigu ABC edo ACB edo BCA. Aldakuntza problema gisa
hartzen badugu, konbinazio bakoitza 3Y aldiz errepikatuko litzateke,
hori baita 3 elementuren artean era daitekeen ordenazio kopurua.Beraz, konbinazioak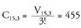 = 455 izango dira.Problema hau ikusteko beste era bat ere badago. Eman dezagun
15 ikasleen artetik hiru direla aukeratuak, A (aukeratuak), eta 12
ez aukeratuak, EA (ez aukeratuak). Era honetan errepikatuzko permutazio
problema bat izango genuke, non A hiru aldiz errepikatzen
den eta EA 12 aldiz. Eta errepikatuzko permutazio kopurua :
= 455 izango dira.Problema hau ikusteko beste era bat ere badago. Eman dezagun
15 ikasleen artetik hiru direla aukeratuak, A (aukeratuak), eta 12
ez aukeratuak, EA (ez aukeratuak). Era honetan errepikatuzko permutazio
problema bat izango genuke, non A hiru aldiz errepikatzen
den eta EA 12 aldiz. Eta errepikatuzko permutazio kopurua : Orokorrean, n elementuren artetik k elementu aukeratu behar
badira :
Orokorrean, n elementuren artetik k elementu aukeratu behar
badira :
- Ariketak
20.- Fabrika baten mantenuaz 10 pertsona arduratzen
dira. Aste bukaeran hiruk lan egin behar dute.
Zenbat eratan aukeratu daitezke?21.- Matematikako irakasleak ostiralero gelan dituen 20 ikasleetatik
bosti galdetzen die. Zenbat eratan egin dezake
galdetu nahi dion ikaslearen aukera? Zenbat kasutan galdetuko
dio Mireni? Zenbat kasutan ez dio galdetuko?22.- Azterketa batek dituen 20 galderetatik 10 aukeratu
behar dira erantzuteko. Zenbat eratan egin daiteke
hautaketa?23.- Antzinako problema bat : eraikitzaile ospatsu batek 8
ateko eraikuntza atsegin, handi eta dotore bat eraiki du
hemengo Lurren jaunarentzat. Aurki itzazu ate baten,
biren, hiruren,... irekiera desberdinak (konbinazioak).- Matematikari, esaidazu zenbat nahastura desberdin egin
daitezkeen zeinek bere zapore berezia (gozoa, mina, heste
lehorgarria, garratza, gazia eta mingotsa) duten sei osagaiz,
osagaiak banaka, binaka, hirunaka etab. hartuaz
(Bhaskararen Lilivatti liburutik, India XIII. mendea).
VIII. Errepikatuzko konbinazioak
Errepikatuzko konbinazio esaten zaien elementu desberdin
dituen multzo bat emanda, elementu horiek k-naka harturik egin
daitezkeen talde desberdinei (ohiko konbinazioetan bezala ordena
kontuan izan gabe), k horien artean elementuak errepika daitezkeela
. Elementu bakoitza gehienez ere k aldiz errepikatuko da, k-
naka harturiko taldeak osatu behar baitira. Adibidez, A eta B hizkiekin
hiruna letrako zenbat talde lor daitezke? Alfabetoaren arabera
ordenaturik : AB Lau aukera bakarrik daude : AAA, AAB, ABB, BBB. Errepikatuzko konbinazioak
Lau aukera bakarrik daude : AAA, AAB, ABB, BBB. Errepikatuzko konbinazioak adierazten dira eta ohiko konbinazioetan n > k izaten bada ere, errepikatuzko konbinazioetan n < k izan daiteke.Ohiko konbinazioetatik errepikatuzko konbinazioetarako pausoa ez da permutazioetan bezain argia. Hona adibide bat : har ditzagun 2, 3, 5, 7 zenbaki lehenak. Zenbat zenbaki desberdin lor daitezke faktore horien artean hirunakako biderkaketak eginaz? Esaterako :
adierazten dira eta ohiko konbinazioetan n > k izaten bada ere, errepikatuzko konbinazioetan n < k izan daiteke.Ohiko konbinazioetatik errepikatuzko konbinazioetarako pausoa ez da permutazioetan bezain argia. Hona adibide bat : har ditzagun 2, 3, 5, 7 zenbaki lehenak. Zenbat zenbaki desberdin lor daitezke faktore horien artean hirunakako biderkaketak eginaz? Esaterako :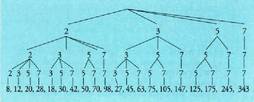 Biderkaduraren emaitza biderkagaien arabera aldatuko da, baina
biderkagaien ordenak ez du eraginik izango emaitzean eta, gainera,
elementuak errepika daitezke, beraz errepikatuzko konbinazioak
dira. Zenbat biderkaketa desberdin egin daitezkeen jakiteko,
zerrenda bat egingo dugu guztiekin. Biderkadura bera bi aldiz ez
agertzeko biderkagaiak txikienetik handienera ordenatuko ditugu
edo txikiena jarriko dugu beti aurretik, eta bestela hurrengo txikiena
(edo berriro txikiena, errepikaturik agertzen bada), etab.
Biderkaduraren emaitza biderkagaien arabera aldatuko da, baina
biderkagaien ordenak ez du eraginik izango emaitzean eta, gainera,
elementuak errepika daitezke, beraz errepikatuzko konbinazioak
dira. Zenbat biderkaketa desberdin egin daitezkeen jakiteko,
zerrenda bat egingo dugu guztiekin. Biderkadura bera bi aldiz ez
agertzeko biderkagaiak txikienetik handienera ordenatuko ditugu
edo txikiena jarriko dugu beti aurretik, eta bestela hurrengo txikiena
(edo berriro txikiena, errepikaturik agertzen bada), etab.
Adibidez: 12 biderkadura biderkaketa egitean lortzen dela
emango dugu eta ez ditugu kontuan harturko
biderkaketa egitean lortzen dela
emango dugu eta ez ditugu kontuan harturko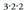 edo
edo biderkaketa, emaitza bera lortuko dugulako. Lehenengo biderkagaia
edozein izan daiteke 2, 3, 5 edo 7. Lehengoa 2-a bada, bigarrena
2-a errepika daiteke,
biderkaketa, emaitza bera lortuko dugulako. Lehenengo biderkagaia
edozein izan daiteke 2, 3, 5 edo 7. Lehengoa 2-a bada, bigarrena
2-a errepika daiteke,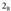 adieraziko dugu, edo bestela 3 edo 5
edo 7 izan daiteke. Lehenengoa 3-a bada, bigarrena 3 izan daiteke
berriz ere edo bestela 5 edo 7. Honela, bigarren biderkagaia lehengo
bera errepikatuta bada
adieraziko dugu, edo bestela 3 edo 5
edo 7 izan daiteke. Lehenengoa 3-a bada, bigarrena 3 izan daiteke
berriz ere edo bestela 5 edo 7. Honela, bigarren biderkagaia lehengo
bera errepikatuta bada azpi-indizea jarriko diogu. Lehenengo
biak 2 eta 2 badira, hirugarrena beste 2 bat izan daiteke -bi aldiz
errepikatuko litzateke eta
azpi-indizea jarriko diogu. Lehenengo
biak 2 eta 2 badira, hirugarrena beste 2 bat izan daiteke -bi aldiz
errepikatuko litzateke eta jarriko genuke-, edo bestela 3 edo 5
edo 7. Lehenengo biak 23 badira, hirugarrena beste 3 bat izan daiteke,
jarriko genuke-, edo bestela 3 edo 5
edo 7. Lehenengo biak 23 badira, hirugarrena beste 3 bat izan daiteke, edo bestela 5 edo 7. Era honetan
edo bestela 5 edo 7. Era honetan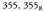 adieraziko
da. Baina
adieraziko
da. Baina edo
edo inserted textjartzerakoan, 2, 3 edo 5 ekidin daiteke
beti, aurreko zenbakiaren berdina baita. Orduan bigarrena lehenengoa
errepikatuta bada azpi-indizea jarri beharrean, L bat jar
daiteke lehenengoa dela adierazteko ; hirugarrena bigarrena errepikatuta
bada B bat jar daiteke bigarrena dela adierazteko, etab. Inoiz
errepikatuko ez dena hirugarrena izango da, hiru toki bakarrik baitaude.
inserted textjartzerakoan, 2, 3 edo 5 ekidin daiteke
beti, aurreko zenbakiaren berdina baita. Orduan bigarrena lehenengoa
errepikatuta bada azpi-indizea jarri beharrean, L bat jar
daiteke lehenengoa dela adierazteko ; hirugarrena bigarrena errepikatuta
bada B bat jar daiteke bigarrena dela adierazteko, etab. Inoiz
errepikatuko ez dena hirugarrena izango da, hiru toki bakarrik baitaude.
Era honetan 223, 2L3 jar daiteke eta 355, 35B. Honela
konbinazio guztiak idatziko genituzke beren elementuetan errepikapenik
egon gabe : 2LB, 222 litzateke, eta 57L, 557 litzateke.
Biderkaketa bat bi aldiz ez kontuan hartzeko 2,3,5 eta 7 zenbakiei
L eta B gehitu beharko genizkieke. Orduan 3-naka harturiko lau
elementuen errepikatuzko konbinazioak ohiko konbinazio problema
bezala har daiteke, non elementu desberdinak 4+3-1 hirunaka
harturik izango diren. Gehitu behar direnen kopurua 3-1 da, zeren
eta ordenatzen baditugu, edozein elementu errepika daiteke azkenengo
lekuan dagoena ezik.Kopurua izango litzateke.Hau zuhaitz diagraman lortutakoarekin bat dator.Orokorrean,
izango litzateke.Hau zuhaitz diagraman lortutakoarekin bat dator.Orokorrean,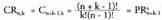
- Ariketak
24.- Fabrika batek kolore desberdinetako arkatzak saltzen ditu
10 arkatzeko paketetan. 5 kolore desberdinetako arkatzak
egiten badituzte, zenbat pakete desberdin egon daitezke?25.- Pertsona batek hiru alkandora erosi behar ditu,
baina lau marka desberdinen artean zalantzak ditu.
Marka bakoitzeko bat baino gehiago eros balezake,
zenbat eratan aukera ditzake markak?26.- Hiru laguni opari bana egin behar diezu. Gehien
gustatzen zaizkizun bost diskoen artean bakoitzari
bana oparitzea erabaki duzu. Dendara erostera zoazenean,
zenbat eskaera desberdin egin ditzakezu bi
lagunei diska berdina oparitzea axola ez bazaizu?
- Ariketa orokorrak
27.- Kalkulatu :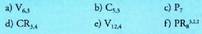
I X. Zenbaki konbinatorioak
k-naka harturiko n elementuen konbinazio zenbakiak matematikaren
alor askotan azaltzen dira. Adibidez, n elementuz osaturiko
multzo batetik elementuak k-naka harturik zenbat azpimultzo osa
daitezkeen aurkitzean, aljebran binomioaren berreketak egitean,
konbinatoria problema askotan edo probabilitatean banaketa
binomiala ikastean.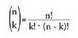 Zenbaki hauen propietateak dira :
1)
n! n!
1 _
_
(n - n)! n! • 0!
Zenbaki hauen propietateak dira :
1)
n! n!
1 _
_
(n - n)! n! • 0! Tartagliaren triangeluan, binomioaren berreketak egitean monomioen
lehenengo koefizientea eta azken koefizientea 1 dira. n elementutatik
n-naka harturiko multzoak osatzeko era bakarra dago,
denak hartuz multzo bat osatzea alegia ; eta elementurik gabeko
azpimultzoak osatu nahi badira, aukera bakarra dago, multzo
hutsa, hain zuzen. Adierazpen hauetan 0! = 1 egitea komenigarra
da, muturretan kasu bereziak ez kontsideratzeko.
Tartagliaren triangeluan, binomioaren berreketak egitean monomioen
lehenengo koefizientea eta azken koefizientea 1 dira. n elementutatik
n-naka harturiko multzoak osatzeko era bakarra dago,
denak hartuz multzo bat osatzea alegia ; eta elementurik gabeko
azpimultzoak osatu nahi badira, aukera bakarra dago, multzo
hutsa, hain zuzen. Adierazpen hauetan 0! = 1 egitea komenigarra
da, muturretan kasu bereziak ez kontsideratzeko.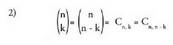 n elementuez osaturiko multzotik elementuak k-naka hartuz osa
daitekeen talde kopurua eta n elementuetatik n-k-naka hartuz osaturikoak
berdina izan behar du, erlazio bijektiboa baitago. Froga
hori aljebra bidez ere egin daiteke, n - (n - k) = k baita.
n elementuez osaturiko multzotik elementuak k-naka hartuz osa
daitekeen talde kopurua eta n elementuetatik n-k-naka hartuz osaturikoak
berdina izan behar du, erlazio bijektiboa baitago. Froga
hori aljebra bidez ere egin daiteke, n - (n - k) = k baita. k-naka harturiko elementuez osa daitezkeen taldeak dira : elementu
finko bat dutenak, gelditzen diren n - 1 elementuetatik k - 1 elementu
hartuz osatutako taldetzat har daitezkeenak, eta elementu jakin
hori baztertzean gelditzen diren n - 1 elementuetatik k elementu atereaz
osaturiko taldeak. Hemen froga aljebraikoa luzeagoa da :(izendatzaile komuna atereaz)
k-naka harturiko elementuez osa daitezkeen taldeak dira : elementu
finko bat dutenak, gelditzen diren n - 1 elementuetatik k - 1 elementu
hartuz osatutako taldetzat har daitezkeenak, eta elementu jakin
hori baztertzean gelditzen diren n - 1 elementuetatik k elementu atereaz
osaturiko taldeak. Hemen froga aljebraikoa luzeagoa da :(izendatzaile komuna atereaz) Zenbaki konbinatorioen aplikazioaren adibideak :Bila ezazu zenbat bide desberdin dauden bidegurutze batera iristeko
n etxe multzo ibili ondoren, kontuan harturik kale guztiak
elkarzutak direla eta ezin dela behin ere atzera egin.
Zenbaki konbinatorioen aplikazioaren adibideak :Bila ezazu zenbat bide desberdin dauden bidegurutze batera iristeko
n etxe multzo ibili ondoren, kontuan harturik kale guztiak
elkarzutak direla eta ezin dela behin ere atzera egin. Bidegurutze bakoitzean ezkerrera edo eskuinera egin aukeratu behar da. Guztira n etxe multzo ibiliko dira; beraz, n hautaketa egin beharko dira. Eskuinera edo ezkerrera jotzen den, bidegurutze batera edo bestera iritsiko da ; beraz, ezkerreko muturretik hirugarren bidegurutzera iristeko bide posibleen kopurua, n bidegurutzetan eskuinera bi aldiz jotzeko posibilitateen kopurua izango da,
Bidegurutze bakoitzean ezkerrera edo eskuinera egin aukeratu behar da. Guztira n etxe multzo ibiliko dira; beraz, n hautaketa egin beharko dira. Eskuinera edo ezkerrera jotzen den, bidegurutze batera edo bestera iritsiko da ; beraz, ezkerreko muturretik hirugarren bidegurutzera iristeko bide posibleen kopurua, n bidegurutzetan eskuinera bi aldiz jotzeko posibilitateen kopurua izango da,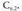 . Laugarren bidegurutzera iristeko, ezkerrera hiru aldiz jo behar da; beraz,
. Laugarren bidegurutzera iristeko, ezkerrera hiru aldiz jo behar da; beraz, ; eskuinalderago dagoen bidegurutzera iristeko beti eskuinera jo beharko da ; beraz,
; eskuinalderago dagoen bidegurutzera iristeko beti eskuinera jo beharko da ; beraz, , beti eskuinera jotzeko aukera bakarra baitago.Beste adibide bat izan daiteke txanpon bat n aldiz boteaz k aurpegi zenbat eratara lor daitezkeen kalkulatzea.
, beti eskuinera jotzeko aukera bakarra baitago.Beste adibide bat izan daiteke txanpon bat n aldiz boteaz k aurpegi zenbat eratara lor daitezkeen kalkulatzea. zenbaki konbinatorioak txanpona n aldiz botatzerakoan k aurpegi lortzeko formak emango dizkigu.Aljebran, berretzaile osoko binomio baten n. berredura monomioen
baturaren bidez ebaztean lortzen dira zenbaki konbinatorioak.
zenbaki konbinatorioak txanpona n aldiz botatzerakoan k aurpegi lortzeko formak emango dizkigu.Aljebran, berretzaile osoko binomio baten n. berredura monomioen
baturaren bidez ebaztean lortzen dira zenbaki konbinatorioak.
Newtonen binomioaren ebazpena izenez ezagutzen da ebazpen hori. zeren eta
zeren eta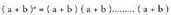 Eta
Eta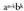 berredura agertuko da biderkatzen diren n parentesietan, a faktorea n-k aldiz eta b faktorea k aldiz hartzeko dauden modu bakoitzeko.Newtonen binomioaren kasu berezi bat a = b = 1 denean azaltzen
da. Era honetan zenbaki konbinatorioen beste propietate interesgarri
bat lortzen da :
berredura agertuko da biderkatzen diren n parentesietan, a faktorea n-k aldiz eta b faktorea k aldiz hartzeko dauden modu bakoitzeko.Newtonen binomioaren kasu berezi bat a = b = 1 denean azaltzen
da. Era honetan zenbaki konbinatorioen beste propietate interesgarri
bat lortzen da :
- Ariketak
38.- Ebatz ezazu berreketa.
berreketa.
39.- Ebatzi :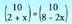
Triangelu aritmetikoa
Zenbaki konbinatorioak edo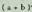 binomioaren berredura aurkitzeko koefizientea triangelu eran antolatu ohi da. Triangelu honi Tartagliaren triangelua edo Pascalen triangelua ere esaten zaio ; 1, 2, 3, 4 etab. elementuen konbinazioak jarriaz lortzen da, halako eran non lerroa elementu kopuru osoarekin bat datorren (n) eta zutabea hautatzen den elementu kopuruarekin.Badago beste era bat zenbaki berberak lortzeko triangelu isoszele bat
osatuz: alboetan batekoak jartzen dira eta erdian goiko lerroko ezkerreko
eta eskuineko bi zenbakien arteko baturaren emaitza.
binomioaren berredura aurkitzeko koefizientea triangelu eran antolatu ohi da. Triangelu honi Tartagliaren triangelua edo Pascalen triangelua ere esaten zaio ; 1, 2, 3, 4 etab. elementuen konbinazioak jarriaz lortzen da, halako eran non lerroa elementu kopuru osoarekin bat datorren (n) eta zutabea hautatzen den elementu kopuruarekin.Badago beste era bat zenbaki berberak lortzeko triangelu isoszele bat
osatuz: alboetan batekoak jartzen dira eta erdian goiko lerroko ezkerreko
eta eskuineko bi zenbakien arteko baturaren emaitza. Triangelu aritmetikoari buruz hemen emandako azalpenak eta ezaugarriak
Pascalek eman zituen ezagutzera 1654. urtean, triangelu aritmetikoari
buruz argitaratu zuen liburuan, baina askoz antzinagotik ere erabilia
zen. Triangelu hori Tartagliak XVI. mendean erabiltzen zuen, eta Peter
Apianek 1527.urtean eta Michael Stiefelek 1544. urtean argitaratu zuten
beren liburuetan.
Triangelu aritmetikoari buruz hemen emandako azalpenak eta ezaugarriak
Pascalek eman zituen ezagutzera 1654. urtean, triangelu aritmetikoari
buruz argitaratu zuen liburuan, baina askoz antzinagotik ere erabilia
zen. Triangelu hori Tartagliak XVI. mendean erabiltzen zuen, eta Peter
Apianek 1527.urtean eta Michael Stiefelek 1544. urtean argitaratu zuten
beren liburuetan. Lehendik ere, 1430. urte inguruan, Al-Kashik argitaratua zen. Baina hauek denak baino lehen Yang-Huik XIII. mendean eta batez ere Chu Shih Chiehk 1303. urtean bere "Ispilu ederra" liburuan, marraztu zuten.
Lehendik ere, 1430. urte inguruan, Al-Kashik argitaratua zen. Baina hauek denak baino lehen Yang-Huik XIII. mendean eta batez ere Chu Shih Chiehk 1303. urtean bere "Ispilu ederra" liburuan, marraztu zuten.
Laburpena
Kalkulagailuaren erabilpena konbinatorian
Kalkulagailu zientifikoek tekla bat edukitzen dute zenbaki baten faktoriala
lortzeko. Tekla horrek "!" ikurra darama, eta teklan adierazita egon
ordez teklaren gainean adierazi ohi den bigarren funtzio bat da. Kasu batzuetan
aldakuntzetarako eta konbinazio ez errepikatuzkoetarako ere
tekla bat izaten da.Faktorial teklarekin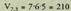 kalkulatu nahi badugu, faktorial tekla erabiliz,
kalkulatu nahi badugu, faktorial tekla erabiliz,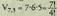 dela kontuan hartuz, prozedura honako hau da :
dela kontuan hartuz, prozedura honako hau da : inserted texteta 210 azalduko zaigu pantailan.Konbinazioak kalkulatzeko, adibidez
inserted texteta 210 azalduko zaigu pantailan.Konbinazioak kalkulatzeko, adibidez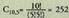 prozedura honako hau da :
prozedura honako hau da : eta pantailan 252 azalduko zaigu.Zenbaki negatibo baten faktoriala edo osoa ez den zenbaki baten faktoriala
kalkulatzerakoan kalkulagailuan errorea emango digu.Aldakuntzak edo permutazioak teklarekin :Aldakuntza teklaren bigarren funtzio bat izaten da eta
eta pantailan 252 azalduko zaigu.Zenbaki negatibo baten faktoriala edo osoa ez den zenbaki baten faktoriala
kalkulatzerakoan kalkulagailuan errorea emango digu.Aldakuntzak edo permutazioak teklarekin :Aldakuntza teklaren bigarren funtzio bat izaten da eta bidez adierazten da (inglesetik dator, aldakuntzetarako "permutations " erabiltzen dute). Tekla honek r-naka harturiko n elementuen aldakuntzak zuzenean ematen ditu.
bidez adierazten da (inglesetik dator, aldakuntzetarako "permutations " erabiltzen dute). Tekla honek r-naka harturiko n elementuen aldakuntzak zuzenean ematen ditu.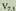 kalkulatzeko adibidez, prozedura honela da :
kalkulatzeko adibidez, prozedura honela da : eta pantailan 210 azalduko zaigu.Funtzio hauetan r > n hartzen bada, kalkulagailuak errorea emango
digu.
eta pantailan 210 azalduko zaigu.Funtzio hauetan r > n hartzen bada, kalkulagailuak errorea emango
digu.
Koenigsberg-eko zubiak
Ikusi diren konbinatoria problemen ebazpena nahikoa erraza da.
Baina beste kasu batzuetan enuntziatua sinplea izan arren, ebazpena
zail samarra izan daiteke. Topologiari buruzko problema batzuk eta
batez ere grafoen teoriari buruzkoak edo puntuen arteko sareenak
konbinatoriako problemak bailiran ebatz daitezke. Enuntziatu klasiko
bat da Koenigsbergko zubien problema deitua, Eulerrek emana.
Emaitzen eranskinerako
Carl Friedrich Gauss
(1777-1855)Gauss-i "Princeps Mathematicorum" esaten zaio,
izan ere, askorentzat, garai eta aro guztietan izan den
gaitasun handieneko matematikaria baita, bai landu
zituen matematika adar desberdinengatik, bai adar
horietan guztietan egin zituen aurkikuntzengatik.Gotingenen jaio zen 1777an, eta alemaniar hiri
horretan berorretan bizi izan zen bizitza osoan. Langile
familia bateko semea zen eta bere aitak askoz ere
nahiago izango zukeen gazte-gaztetatik ikasten hasi
ordez lanean hasi izan balitz. Carl, ordea, haur miragarria
zen eta Brunswick-eko dukearen babesa lortu
zuen ; hark unibertsitateko ikasketak ordaindu zizkion
. 19 urte zituela, zirkuluaren barruan 17 aldeko
poligono erregularra inskribatzeko modua aurkitu
zuen, erregela eta konpasa soil-soilik erabilita. Antzinako
Greziatik ezagutzen zen nola inskribatzen
ziren hirukia, laukia, pentagonoa eta aldeak bi, hiru
edo bosten multiplo zituzten poligonoak. Gauza
jakina zen, bestalde, heptagonoa ezin zitekeela inskribatu
eta susmoa ere bazegoen alde gehiagoko
poligonoak, alde kopuru lehena zutenak, ezin izango
zirela erregela eta konpasaz inskribatu. Gaussek
frogatu zuen zenbaitetan posible zela hori egitea.Gaussen garrantzi handiko lehen lana doktore
tesia izan zen. Tesi hartan teorema bat frogatzensaiatu zen, alegia polinomio ekuazio oro lehen eta
bigarren mailako faktoreetan deskonposa daitekeela,
hau da, polinomio ekuazio orori emaitza erreala
edo konplexua aurki dakiokela. Teorema hori,
ordea, Eulerrek eta Legendrek frogatua zuten ordurako,
baina Gaussek haien frogabideak kritikatu
zituen eta frogabide osoago bat proposatu zuen.
Gaussek geometria metodoak erabili zituen froga
hartarako, baina irtenbide hura ez zuen gustukua
izan, eta beste bi frogabide argitaratu zituen, aljebra
metodoetan oinarrituak batez ere.Ondoren, zenbakien teoria landu zuen. Disquisitiones
Arithmeticae liburua argitaratu zuen, latinez
idatzia-garai hartan, alemaniar unibertsitateetan
horrela zuten ohitura-. Kongruentzien teoria
landu zuen liburu hartan. Teoria hura lantzeko,
modulu izeneko zenbaki oso batez egindako zatiketen
hondarretatik abiatuta lortzen diren zenbakiez
defini daitezkeen eragiketak aztertu zituen.
Elkarrekiko karratuen teorema ere aztertu zuen,
baita Gaussen zenbakiak izenez ezagutzen direnak
ere; zenbaki lehenen propietate berri asko adierazi
zituen.Astronomia eta zenbaki kalkuluak aztertu zituen
eta metodo berriak aurkitu zituen argizarien orbitak
hurbilketa bidez kalkulatzeko. Lan horiei esker
1807an Gotingen-go astronomia behatokiko
zuzendari izendatu zuten. Elektromagnetismo,
mekanika eta geodesia gaietan ere egin zituen lanak.
Froga fisiko batean zoriaren arabera gertatutako
akatsei buruz egin zituen azterlanek y = e ` moduko
funtzioak aztertzera eraman zuten ; funtzio horiek
"Gaussen kanpaia' izenez ezagutzen den kurba dute
grafikotzat eta estatistikako banaketa normalaren
dentsitate funtzioari dagozkie.Bestalde, matematika gaiak lantzen jarraitu zuen,
hala nola, funtzio eliptikoak, zenbaki lehenak edota
geometria. Geometrian, esaterako, geometria ezeuklidearrak
ez zirela elkarren aurkako atera zuen
ondorio, baina ez zen ausartu emaitza haiek argitaratzera,
garai hartan gai haietan lan egiten zuen jendeak
zer esango zuen beldur baitzen. Bolyaik eta
Lobatxevskik geometria ez-euklidearraren azterketan
Gaussen idazlanak argitaratu zituztenean, Gaussek
onartu egin zituen berekiko, baina ez zuen haien
aldeko adierazpenik egin.Gaussek idazki asko argitaratu zituen, baina are gehiago utzi zituen argitaratu gabe. Ikertzaile askok, egindako aurkikuntzaren bat berari aurkezten zizkiotenean, Gaussek ordurako emaitza haiek atereak zituela ikusi ahal izan zuten. Gauss hil ondoren, koadernotxo bat aurkitu zen, haren aurkikuntza eta susmo guztiak idatzita zituena. Ohar horien bidez jakin ahal izan da haren pentsamenduak zer-nolako bilakaera izan zuen eta argitaratu ez zituen aurkikuntza asko egin zituela. Adibidez, zenbaki jakin bat baino txikiagoak diren zenbaki lehenen kopuruaren eta zenbaki horren arteko arrazoia (zatidura), zenbaki horren logaritmoaren alderantzizkoa dela zenbakia mugarik gabe handitzen denean, hau da : Non,
Non,, n baino txikiagoak diren zenbaki lehenen kopurua den. Ez zuen, ordea, frogapen hura idatzi eta ez zen 1896 arte frogatu.Izaeraz itxia eta hitz gutxikoa zen. Bere famili
bizitza berriz, oso zaila egin zitzaion, izan ere, izan
zituen bi emazteek osasun txarra izan baitzuten, eta
gainera, seme-alabekin harreman txarrak izan
zituen eta USAra emigratu zuten. Alaba gazteenarekin
bakarrik konpondu zen ondo eta bere azken
urteetan ere hura izan zuen lagun bere ondoan.
Bakarrik lan egiteko ohitura zuenez gero, harreman
gutxi izan zuen bere garaiko matematikariekin,
nahiz eta haren izen handia denek aitortu. Unibertsitatean
lan egin ordez astronomia behatokian lan
egin zuenez, laguntzaile distiratsu gutxi batzuk baizik
ez zituen izan, baina bere ikerkuntzei esker ez
zien eskola eman behar izan interes handirik gabeko
ikasleei.Hil zorian zegoela, bere hilobian zirkunferentzia
batean inskribatutako 17 aldeko poligono aldekidea
grabatzeko agindua eman zuen, hori izan baitzen
bere bizitzako garrantzizko lehen aurkikuntza,
hain zuzen ere, bere bizitza osoan zehar ospetsu sentiarazi
zuena. Zoritxarrez, alabak ezin izan zuen
aitaren nahia bete, izan ere, harginaren ustez hainbeste
aldeko irudia eta zirkunferentzia nahastu egin
baitziren.
Bernoulli
Familia berean ez dira matematikari handi asko
izaten. Arau horren salbuespena ordea, Bernoulli
familia da, bost belaunalditan matematikari handiak
izan baitziren familia horretan, XVII. mendeko
azken laurdenetik XIX. mendearen hasiera
arte. Beren izenak errepikatu egiten direnez,
bereizteko, I.a, II.a, etab. eransten zaie izenari
errege dinastietan egin ohi den bezala (Jean I.a,
Jean II.a, Daniel I.a, Daniel II.a, etab.).Bernoullitarrak kalvindarrak ziren, flandriarrak
jatorriz. Espainiako erregearen gudarosteakAnberes
hartu zuenean, nahiago izan zuten Basileara
alde egin, protestantea baitzen hura. Dinastiaren
sortzailea, Nicolaus, estatu kontseilari izan zen
Basilean ; seme etab alaba asko izan zituen. Aitak
ez zuen bat bera ere matematikari izateko prestatu
; hala ere, bosgarrenak, Jacques I.ak, aitak artzai
protestante izateko izendatuak, eta hamargarrenak,
Jean I.ak, mediku edota merkatari izatekoa
zenak, matematikari izatea erabaki zuten.Jacquesek bidaiak egin zituen sei urtetan zehar
Frantzian, Herbehereetan eta Ingalaterran barrena.
Ondoren, Basileara itzuli zen matematikan
aritzeko. 1684an, kalkulu infinitesimalaren metodo
berriak aztertu zituen eta berehala ohartu zen
haiek indar handia izango zutela. Eta hala kalkulu
infinitesimalaren defendatzaile sutsu bihurtu zen.
Gainera, Jacques Bernoulli I.a eta jean Bernoulli
I.a Leibnizen metodoen aldeko agertu ziren XVII.. endearen amaieran eta XVIII.aren hasieran
Leibnizen eta Newtonen metodoak zirela eta izan
ziren eztabaidetan.Jacques I.ak, segiden, kalkulu infinitesimalaren eta probabilitateen arloetan lan egin zuen. Berak idatzi zuen Ars Conjenctandi liburua, lehen probabilitate liburutzat hartzen dena. Berak proposatu zion Leibnizi "kalkulu integral" izena kalkulu diferentzialaren alderantzizkoa izendatzeko.
Ekuazio diferentzialen hainbat problema ebatzi zituen ; Bernoulliren ekuazioa deitua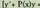 bere anaia Jeanekin eta Newtonekin batera ebatzi zuen.Jean I.ak, ekuazio diferentzialak ebazten lan
egin zuen batez ere eta emaitza kopuru izugarria
argitaratu zuen. Besteren artean, grabitatearen
mende egon eta airearen edota uraren erresistentzia
duela higitzen den gorputz pisudun baten ibilbidea
aurkitzeko problema ebatzi zuen. Irakasle
handia izan zen ; ikasle izan zituen, besteak beste,
1'Hospital-go markesa, gazte zela, eta ondoren
bere seme Daniel I.a eta Euler. Oso haserre erraza
zen eta Leibnizen eta Newtonen jarraitzaileen
artean izan ziren eztabaidetan, berak izandako
esku hartzeak ozpindu egin zituen eztabaidak.Bernoullitarren familia barruko harremanak ez
ziren oso gozoak izan. Jean I.ak uste osoa zuen Jacquesek paternalismoz tratatzen zuela, anaia gazteena
izateagatik-edo. Jeanek, erronka jo zion
anaiari brakistokronaren problema ebazteko, hau
da, pisudun gorputz batek puntu batetik beherago
eta bere parean ez dagoen beste puntu batera
erortzen igarotzen duen denbora minimoa kalkulatzeko.
bere anaia Jeanekin eta Newtonekin batera ebatzi zuen.Jean I.ak, ekuazio diferentzialak ebazten lan
egin zuen batez ere eta emaitza kopuru izugarria
argitaratu zuen. Besteren artean, grabitatearen
mende egon eta airearen edota uraren erresistentzia
duela higitzen den gorputz pisudun baten ibilbidea
aurkitzeko problema ebatzi zuen. Irakasle
handia izan zen ; ikasle izan zituen, besteak beste,
1'Hospital-go markesa, gazte zela, eta ondoren
bere seme Daniel I.a eta Euler. Oso haserre erraza
zen eta Leibnizen eta Newtonen jarraitzaileen
artean izan ziren eztabaidetan, berak izandako
esku hartzeak ozpindu egin zituen eztabaidak.Bernoullitarren familia barruko harremanak ez
ziren oso gozoak izan. Jean I.ak uste osoa zuen Jacquesek paternalismoz tratatzen zuela, anaia gazteena
izateagatik-edo. Jeanek, erronka jo zion
anaiari brakistokronaren problema ebazteko, hau
da, pisudun gorputz batek puntu batetik beherago
eta bere parean ez dagoen beste puntu batera
erortzen igarotzen duen denbora minimoa kalkulatzeko.
Jacquesek zikloide izeneko kurba aurkitu
zuen, eta gainera, frogatu zuen jeanen frogapena
ez zela zuzena. Bestalde, Jean I.ak etxetik kanpora
bidali zuen bere seme Daniel I.a, bera ere aurkeztua
zen l'Academie des Sciences-ek antolatutako
lehiaketa batean saria atera zuelako.Hurrengo belaunaldian lau matematikari izan
ziren, hiru Jean I.aren semeak eta laugarrena,
Nicolaus II.a hain zuzen, Nicolaus La margolariaren
-Jeanen anaiaren- semea. Nicolaus II.a irakasle
izan zen Paduan, Galileok izan zuen katedran.
Hark argitaratu zuen bere osaba Jacques
I.aren probabilitate liburua. Nicolaus III.a eta
Daniel La irakasle izan ziren San Petersburgon.
Lehena gazterik hil zen. Daniel I.a, berriz,
matematikari handia izan zen ; kalkulu infinitesimalaren
eta hidrodinamikaren aplikazioetan
ihardun zuen batez ere. Hari zor zaio "Bernoulliren
printzipio" esaten zaiona. Matematikan,
Daniel I.ak, probabilitate gaiak landu zituen
batez ere, baina funtzio trigonometrikoetan eta
zatiki jarraietan ere aritu zen. San Petersburgon
era Basilean irakasle izan zen. Aita eta osaba ez
bezala, Newtonen teorien aldekoa zen.Dinastiako gainerako kideei dagokienez, Jean
II.a matematika irakasle izan zen Bernan eta fisika
gaietan aritu zen batez ere. Haren seme jean
III.a matematika irakasle izan zen Berlingo Akademian
eta probabilitateez idatzi zuen. Dinastiako
gainerako kideek ez zuten ekarpen nabarmenik
egin matematikaren alorrean.'





















