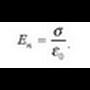Fisika-Kimika»Fisika - Kimika
Elektrika eta Magnetika

1. Gaia: eremu elektrikoa
Indar elektrostatikoari buruzko lehen aurkikuntzak oso aspaldikoak dira. Antzinateko Grezian egin ziren gai honi buruzko lehen ikerketak. Tales Miletokoa (K.a. 640-546) greziar matematikari eta filosofoa ohartu zen anbarrak, igurtziz gero, propietate berezi bat hartzen zuela, igurtziz gero gauza txikiak erakartzeko gaitasuna hartzen zuela hain zuzen. Erakarpen ahalmen hori imanaren erakarpen magnetikoarekin nahastu izan zen sarritan.
Baina lehenengo ikerketak aspaldi egin ziren arren, ez zen gertaera horiei buruzko azalpen garbirik eman XVI. mendea arte. XVI. mendean, Ingalaterrako erreginaren osagile zen William Gilbertek (1540-1603) sistematikoki aztertu zituen efektu elektrikoak eta magnetikoak. Eta anbarraz gainera beste material batzuek ere propietate hura bera zutela frogatu zuen. Adibidez, beirazko ziri bat igurtziaz beirazko ziriak ezaugarri berezi bat hartzen du, elektrizazio deritzona. Elektrizaturiko beirazko ziria, kortxozko esfera baten aurrean jartzean, kortxozko esfera beirari hurbiltzen zaio beiraren elektrizazioagatik. Eta esperientzia hori bera egiten bada elektrizaturiko anbarrezko ziri batekin, beirarekin gertatutako erakarpen fenomeno bera gertatzen da. Gilbertek efektu elektrikoak eta magnetikoak bereizi zituen, eta ondoko terminoak definitu zituen: indar elektrikoa, erakarpen elektrikoa eta polo magnetikoa. (Elektriko hitza grekerazko elektron-etik dator, eta anbar esan nahi du; magnetiko hitza, berriz, Magnesia eskualdetik dator, han topatu baitzen lehenengoz magnetita edo imana). Dirudienez, Gilbert ez zen konturatu aldaratze elektrikoaren efektuaz.
Geroago, Charles François Du Fayk (1698-1739) material elektrikoen artean bi elektrizazio mota desberdin gertatzen direla baieztatu zuen. Kortxozko esfera baten aurrean elektrizaturiko anbarrezko eta beirazko ziriak batera jarriz gero, erakarpena handitu ordez, moteldu edo erabat desagertu egiten zela ohartu zen Du Fay. Horren azalpen gisa, beirak eta anbarrak kontrako efektuak eragiten dituztela esan zuen. Mota honetako esperimentuak eginez aurkitu zuen gai batzuek elkar erakartzen dutela igurtziz gero, eta beste batzuek berriz aldaratu egiten direla. Hau guztia kontuan harturik bi eratako elektrizazioa zegoela berretsi zuen: alde batetik, beirak eta beste materialeek sortzen dutena, eta bestetik, anbarrak eta beste material batzuek sorturikoa.
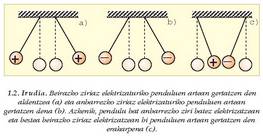
1.1.Irudia. Kortxozko esferan anbarrezko ziri batek duen eragina (a), beirazko ziri batek duena (b) eta biek batera dutena (c).
1729. urtean, Stephen Gray britainiarrak (1696-1736) erakarpen eta aldarapen elektrikoa gorputz batetik beste batera igaro daitezkeela ikusi zuen. Horretarako, bi gorputzek zenbait gauzarekin, batez ere metalekin, konektaturik egon behar zuten. Horrela frogatu zuen propietate elektrikoak gorputz batetik beste batera pasa daitezkeela; hura izan zen korronte elektrikoaren lehenengo aipamena.
1747. urtean, Benjamin Franklinek (1706-1790) bi elektrizazio motei buruzko teoria osatu zuen; teoria horretan zeinuen kontzeptua azaldu zuen. Beirak sortzen duen elektrizazioari positibo deitu zion; eta anbarrak sortutakoari negatibo. Definizio honen aukeraketa, esan beharrik ez dago, guztiz hautazkoa izan zen, izenak alderantziz ere erabil baitzitzakeen nahi izanez gero.
Horiek izan ziren fisikaren alor berri baten, hau da elektrikaren, azterketan eman ziren lehenengo pausoak. Elektrikaren definizio zehatza hau da:
Geldirik dauden karga elektrikoek sorturiko fenomenoak aztergai dituen fisikaren alorra.
Elektrikari buruzko atal honetan, beraz, kargak bere horretan aztertuko dira, geldirik daudela; lastertasunik eta azeleraziorik gabeko kargak eta horiek sorturiko efektuak aztertuko dira.
William Gilbert
(Colchester (Essex), 1540 - 1603) Britainiar fisikari eta sendagilea. Cambridgeko St. John´s College-n egin zituen ikasketak. Londresen hartu zuen bizilekua, eta Isabel eta Jacobo I.aren gorteko sendagile ere izan zen. Errege Sendagile Eskolako lehendakari izendatu zuten 1600ean. Urte hartan bertan, “De Magnete, Magneticisque corporibus, et de Magno Magnete Tellure, Physiologia Nova” idatzi zuen, Ingalaterran argitaratu zen fisikako lehen liburu garrantzitsua. Liburu horretan, batetik, bere teoria baliatu zuen Lurraren magnetismoa azaltzeko, eta bestetik, marruskadura bidezko elektrizazioa azaldu zuen.
Tales Miletokoa
(Mileto, K.a. 640 - K.a. 546) Greziako zazpi jakintsuen artean gailendu zen. Matematikaren sortzailea esaten zaio Egiptoko eta Babiloniako kulturetatik harturiko ezaupide garrantzitsu batzuk eman zituelako geometriaren eta algebraren alorretan. Bere izena duen teoreman triangeluaren angeluen arteko erlazioa ikertu zuen. Astronomia ere landu zuen, eta eguzki eklipse bat iragarri ere zuen zehaztasun handiz K.a. 585 urteko maiatzaren 28rako. Teoria kosmologiko bat aurkeztu zuen, unibertsoa lau elementuz osatua dagoela dioena: ura, sua, airea eta lurra. Filosofian, politikan eta merkataritzan ere ari izan zen.
1.1. Karga elektrikoa
Gorputzen elektrizazioa ez da beti intentsitate berekoa izaten. Elektrizazioaren intentsitatea neurtzeko karga magnitudea erabiltzen da eta, oro har, karga adierazteko q ikurra erabiltzen da. Karga beste magnitude batzuei buruz independentea da, beraz, edozein gorputz edo zatikik gutxienez oinarrizko bi propietate independente ditu: masa eta karga.
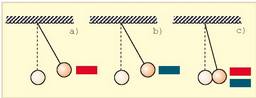
Ikusi den bezala, XVIII. mendean bereizi ziren bi elektrizazio motak, positiboa eta negatiboa. Bereizketa hori frogatzeko kortxozko esfera bana duten bi penduluren adibidea erabil daiteke. Lehenik, elektrizatutako beirazko ziriaz ukitzen dira bi penduluak. Ziriak ukitzen dituelarik, esferak elektrizatu egiten dira eta, jakina, biek mota bereko elektrizazioa izango dute. Penduluak elkarren ondoan ipini bezain laster, bolak elkarrengandik aldentzen dira. Anbarrezko ziri elektrizatuarekin berdin egiten bada, gauza berbera gertatzen da. Baina anbarrezko eta beirazko zirien bitartez elektrizaturiko esfera bana hartzen badira, esferak elkarren ondoan jartzean elkarren arteko erakarpena gertatzen da. (Ikus 1.2. irudia). Horrela, ondorio hau atera daiteke:
Elektrizazio mota berdina duten gorputzek elkar aldaratzen dute, eta alderantziz, elektrizazio mota desberdina dutenek, elkar erakartzen.
Gorputz batek elektrizazio positiboa duela esaten da karga elektriko positiboa duenean, eta elektrizazio negatiboa duela karga elektriko negatiboa duenean. Gorputz baten elektrizazio positiboaren eta negatiboaren mailak berdinak badira (hots, bere karga osoa zero denean), gorputz neutroa dela esaten da. Materiaren ezaugarri hau, karga elektrikoarena, magnitude eskalarra da, praktikak erakusten duenez. Horrela, karga positiboei zeinu positiboa ematen zaie eta negatiboei negatiboa eta sistema baten kar ga osoa zenbatekoa den jakiteko, bere karga guztien batuketa egiten da. Honi kargaren gainezarmenaren printzipioa deritzo.
Kargak, gainera, badu beste ezaugarri bat. Gorputz batek ezin du edozein balioko karga eduki. Gorputz baten kargak oinarrizko beste karga baten anizkoitza izan behar du nahitaez. Ezaugarri honi kargaren kuantizazioa deritzo. Oinarrizko kargari e izena ematen zaio, eta balio hau du, Nazioarteko Banako Sisteman:

Formula horretan, C coulomb banakoa da; coulomb banakoa da Nazioarteko Banako Sisteman karga neurtzeko erabiltzen den banakoa. [OHARRA: hemendik aurrera, elektrikako eta magnetikako gaietan, ekuazio eta adierazpen matematiko guztiak Nazioarteko Banako Sistemaren arabera adieraziko dira].
1909. urtean, Robert Andrews Millikan (1868-1953) fisikari estatubatuarrak esperimentu baten bidez frogatu zuen hau guztia. Esperimentu haren bidez karga kuantizatuta dagoela erakutsi zuen, eta baieztapen hau egin zuen:
Izadian agertzen diren karga guztiak e oinarrizko kargaren anizkoitzak dira. Hau da, karga elektrikoa kuantizaturik dago.
Millikanek bi eroale xafla elkarren paraleloan jarri zituen eta goiko xaflan eginiko zulo batzuetatik olio zipriztinak bota zituen. Olio tanta txikiak xaflaren zuloetatik pasatzean, elektrizitatez kargatzen dira, zuloen paretek igurtzitzen dituztelarik. Xaflen artean eremu elektriko bat ezarriz, olio tanten karga kalkulatu zuen ondoren. Kalkuluetan ateratzen zituen balioak beti ziren oinarrizko karga baten anizkoitzak. Orain arte, ez da azaldu inolako esperimenturik Millikanen aurkikuntza ukatzen duenik, eta horrenbestez, kargaren kuantizazioa funtsezko legetzat hartzen da.
Oinarrizko karga positiboa eta negatiboa neurri berekoak dira. Gainera, e oinarrizko kargari m masa bat dagokio beti. Horrela, oinarrizko zatiki bat osatzen du, adibidez, elektroia, protoia… Hala ere, teoria modernoak ez datoz bat oinarrizkotasunaren ikuspegi honekin. Izan ere, gaur egun unibertsoaren oinarrizko osagaiak beste batzuk direla uste baita.
Bestalde, behin eta berriro esperimentu bidez egiaztatu denez, sistema batean ez da kargarik sortzen, ezta deusezten ere. Denboran zehar kargak bere horretan irauten du. Argi dago, beraz, kargari kontserbazio printzipio bat dagokiola, printzipio hau hain zuzen ere:
Bakarturik dagoen sistema baten karga osoak aldagabe irauten du sistema horretan edozein prozesu gertatzen dela ere.
Printzipio horri kargaren kontserbazio printzipioa deritzo, eta Izadiaren oinarrizko legetzat hartua da.
Robert Andrews Millikan
(Morrison, 1868 - San Marino (Kalifornia), 1953) Illinois-eko Morrison herrian jaio zen. Efektu fotoelektrikoa eta karga elektriko txikia landu zituen. Hori dela eta, 1911an, elektroiaren karga elektrikoa neurtu zuen berak asmatutako esperimentu baten bidez. Aurkikuntza horrengatik, Fisikako Nobel saria eman zioten 1923an. Izpi ultramoreak eta kosmikoak ere aztertu zituen.
1.2. Coulomben legea
Elektrostatikan, puntu bakarreko bi kargaren arteko elkar eragina Coulomben legearen bidez azaltzen da. Charles de Coulombek (1736-1806), ikerketa eta neurketa asko egin ondoren, lege hau proposatu zuen:
Puntu bakarreko karga batek beste baten gainean eragiten duen indarra, bi kargak lotzen dituen lerroan eratzen da. Indar hori, aldaratzailea izango da karga biek zeinu berabaldin badute, eta berriz, erakarlea izango da karga biek elkarren kontrako zeinua izanez gero. Indarra karga bakoitzaren balioaren proportzionala da, eta alderantziz proportzionala kargen arteko distantziaren karratuari buruz.
Coulomben legea bektore ekuazio modura adieraz daiteke.
Eman dezagun,  eta
eta
 puntu
bakarreko kargen balioak direla,
puntu
bakarreko kargen balioak direla,  kargatik
kargatik  kargara
doan bektorearen modulua eta
kargara
doan bektorearen modulua eta  bektore unitarioa, orduan Coulomben legearen adierazpen matematikoa hau da:
bektore unitarioa, orduan Coulomben legearen adierazpen matematikoa hau da:
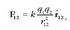
non k konstante bat den. 1.3. irudian, bi kargak eta bektore guztien norabideak agertzen dira.
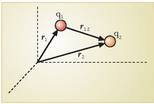
1.3. Irudia. Bi karga eta beraien arteko bektoreak.
 indarrak
indarrak
 kargak
kargak
 kargaren gainean
eragiten duen indarra adierazten du, eta
kargaren gainean
eragiten duen indarra adierazten du, eta 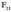 indarrak, berriz,
indarrak, berriz, 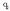 kargak
kargak
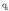 kargaren gainean eragiten duena.
Azken honen adierazpen matematikoa aurrekoaren modukoa da, hau hain zuzen ere:
kargaren gainean eragiten duena.
Azken honen adierazpen matematikoa aurrekoaren modukoa da, hau hain zuzen ere:
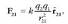
non  kargatik
kargatik
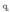 kargara
doan bektorearen bektore unitarioa den
kargara
doan bektorearen bektore unitarioa den 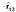 eta
eta 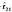 bektore unitarioek
kontrako norabidea dute, eta orduan,
bektore unitarioek
kontrako norabidea dute, eta orduan,  betetzen da. Horrela, Newtonen hirugarren legea, akzio-erreakzio printzipioa
betetzen da. Horrela, Newtonen hirugarren legea, akzio-erreakzio printzipioa
 , betetzen dela frogatuta gelditzen da.
, betetzen dela frogatuta gelditzen da.
 indarraren adierazpen
matematikoa arretaz aztertzen baldin bada, garrantzi handiko ondorioak atera daitezke. Adibidez,
indarraren adierazpen
matematikoa arretaz aztertzen baldin bada, garrantzi handiko ondorioak atera daitezke. Adibidez,
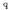 eta
eta
 kargek zeinu berbera
dutenean (positiboa ala negatiboa),
kargek zeinu berbera
dutenean (positiboa ala negatiboa), 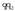 biderkaketa positiboa da, eta
biderkaketa positiboa da, eta 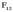 indarraren norabidea eta norazkoa
indarraren norabidea eta norazkoa 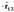 bektorearenak dira. Horrela, bi kargen arteko indarra aldaratzailea da.
Berriz,
bektorearenak dira. Horrela, bi kargen arteko indarra aldaratzailea da.
Berriz,  eta
eta
 kargek kontrako zeinua badaukate,
kargek kontrako zeinua badaukate,
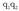 biderkaketa negatiboa da,
eta indarra erakarlea da.
biderkaketa negatiboa da,
eta indarra erakarlea da.
Coulomben legearen adierazpen matematikoan zehaztu gabe gelditzen dira
 .
Hain zuzen ere, k konstantea karga adierazteko aukeratzen diren banakoen mende dago. Fisikan kalkuluak
egiteko Nazioarteko Banako Sistema erabiltzen da, oro har. Horretan, lehen aipatu dugunez, karga neurtzeko
coulomb (C) banakoa erabiltzen da. Banako hori erabiliz,k konstantearen dimentsioak ondoko hauek izango dira:
.
Hain zuzen ere, k konstantea karga adierazteko aukeratzen diren banakoen mende dago. Fisikan kalkuluak
egiteko Nazioarteko Banako Sistema erabiltzen da, oro har. Horretan, lehen aipatu dugunez, karga neurtzeko
coulomb (C) banakoa erabiltzen da. Banako hori erabiliz,k konstantearen dimentsioak ondoko hauek izango dira:
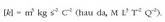
Behin k konstantearen dimentsioak ezagututa, bere balioa aurkitu behar da. Hori esperimentu bidez egiten da,
ekuazioaren gainerako magnitudeen balioak  zein bere aldetik zehazten direla. Horrela, k-ren balioa esperimentalki finkatuta geratzen da:
zein bere aldetik zehazten direla. Horrela, k-ren balioa esperimentalki finkatuta geratzen da:

k konstantearen balioa finkatu eta gero, eta Coulomben legea erabiliz, coulomb karga banakoarentzat definizio hau eman daiteke:
Coulomb bateko puntu bakarreko karga batek, hutsean beste karga berdin batetik metro batera jarrita,
elkarren artean 8’9875 ( 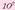 N-eko aldaratze indarra sortzen du.
N-eko aldaratze indarra sortzen du.
Bestalde, aurreko ekuazioen kalkulua erraztearren, k konstantea hutsean honela ere idatz daiteke:
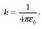
non  konstante bat den, hain zuzen hutsaren permitibitate deritzona. Hutsaren permitibitatearen balioa
k konstantearen balioa erabiliz kalkulatzen da:
konstante bat den, hain zuzen hutsaren permitibitate deritzona. Hutsaren permitibitatearen balioa
k konstantearen balioa erabiliz kalkulatzen da:

Hutsaren permitibitatearen dimentsioak, Nazioarteko Banako Sisteman, hauek dira:

Kargak hutsean ez badaude,  konstantea erabiltzen da
konstantea erabiltzen da  aldagaiaren ordez.
aldagaiaren ordez. 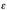 konstanteak ingurunearen permitibitatea adierazten
du, eta bere balioa ingurunearen araberakoa da.
konstanteak ingurunearen permitibitatea adierazten
du, eta bere balioa ingurunearen araberakoa da.
Aldaketa horiek Coulomben legearen adierazpen matematikoan sartuz, horrela geratuko da ekuazioa:
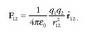
Esan bezala, Coulomben legea elektrostatikan baino ezin da erabili. Hau da, kargek geldirik egon behar dute behatzailearen erreferentzia sistemari buruz, edo hurbilketa batean, argiaren lastertasunarekin alderaturik, oso mantso higitu beharko lirateke. Gainera, Coulomben legea erabat zuzena izan dadin, kargek puntu bakarrekoak izan behar dute.
Coulombek, bihurritze balantzaren bitartez (ikus 1.4. irudia) jakin zuen
 delakoaren goi-indizea 2 dela.
Gaur egungo neurketekin, emaitza hori nahikoa zehatza dela ikusi da. Gainera, Coulomben
legearen adierazpen matematikoak eta eragin grabitatorioarenak distantziarekiko mendekotasun berdina daukate, hau da,
delakoaren goi-indizea 2 dela.
Gaur egungo neurketekin, emaitza hori nahikoa zehatza dela ikusi da. Gainera, Coulomben
legearen adierazpen matematikoak eta eragin grabitatorioarenak distantziarekiko mendekotasun berdina daukate, hau da,
 proportzionalak dira.
proportzionalak dira.

1.4. Irudia. Coulomben bihurritze balantza.
Hona hemen Coulomben indarrak nola eragiten duen ikusteko adibide bat. Eman dezagun,
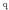 karga baten gainean karga multzo batek -adibidez
karga baten gainean karga multzo batek -adibidez
 eta
eta
 kargek- eragina duela.
Zein izango da
kargek- eragina duela.
Zein izango da 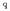 kargak
jasango duen indarra?
kargak
jasango duen indarra?
Gainezarmenaren printzipioa erabiliz,
 kargak jasaten duen indarra
kargak jasaten duen indarra
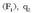 kargak sortzen duen indarraren
kargak sortzen duen indarraren
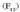 eta
eta
 kargak sortzen duenaren
kargak sortzen duenaren
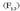 arteko batuketa da.
(Ikus 1.4. irudia). Matematikoki adierazita:
arteko batuketa da.
(Ikus 1.4. irudia). Matematikoki adierazita:

Gainezarmenaren printzipioa erabiltzean, kontuan hartu behar da hipotesi hau:
 eta
eta
 kargen arteko
elkar eraginak ez du inolako aldaketarik jasaten inguruan beste edozein karga egon arren.
kargen arteko
elkar eraginak ez du inolako aldaketarik jasaten inguruan beste edozein karga egon arren.

Orain arte, karga puntu jakin batzuetan kokatuta zegoela hartu da kontuan.
Puntu jakin batean egon ordez espazioko eremu bat hartuko balu
 dq karga txikiek
sorturiko indarren batuketa bektoriala egin beharko litzateke. Horrela Coulomben legearen bertsio
diferentziala lortzen da, ondoren azaltzen dena hain zuzen:
dq karga txikiek
sorturiko indarren batuketa bektoriala egin beharko litzateke. Horrela Coulomben legearen bertsio
diferentziala lortzen da, ondoren azaltzen dena hain zuzen:
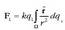
non  integrazio-eremua den, eta
integrazio-eremua den, eta
 dq eta
dq eta
 kargek osatzen duten
norabide aldakorreko zuzenaren bektore unitarioa. (Ikus 1.6. Irudia)
kargek osatzen duten
norabide aldakorreko zuzenaren bektore unitarioa. (Ikus 1.6. Irudia)

Charles Augustin de Coulomb
(Angulême, 1736 - Paris, 1806) Frantzian jaio zen. Ingeniaria izan zen bederatzi urtez frantses gudarostean. 1781ean Frantziako Akademian sartu zen, gudarostean egon zenean idatzi zituen artikulu batzuei esker. Marruskadurari buruzko ikerketengatik da ezaguna. Hark asmatu zuen indar elektrikoak eta magnetikoak neurtzeko bihurritze balantza, eta tresna horri esker aurkitu zituen elektroestatikaren eta magnetismoaren lege esperimental eta teorikoak. Coulomben legea da horien artean aipagarriena. Polarizazio eta momentu magnetiko kontzeptuak asmatu zituen. Frantziako Iraultza bitartean, pisu eta neurri sistema berri bat ikertzen ari izan zen beste batzuekin batera. Nazioarteko sisteman erabiltzen den elektrizitate kopuruak eta karga elektrikoaren banakoak haren izena du, coulomb (C).
1.3. Eremu elektrikoa
Atal honetan, eragin elektrikoa azaltzeko beste tresna matematiko bat definituko da, eremu elektrikoa hain zuzen. Coulomben legearen arabera, karga baten eragina espazio osora hedatzen da. Orduan, espazioko edozein puntutan beste karga bat jarriz gero, espazioko puntu horrek indar baten eragina jasango du. Horren arabera, eremu elektrikoaren definizio hau eman daiteke:
Puntu bateko eremu elektrikoa da puntu horretan legokeen karga unitate positiboak jasango lukeen indar elektrikoa.
Eremu elektrikoa indar elektrikoaren neurketa da, nolabait, eta horregatik, bektore magnitudea da. Beraz, eremu elektrikoak, bektore eremua denez, espazioko puntu bakoitzari bektore bat egokitzen dio. Eremu elektrikoa kalkulu matematikoko artifizio bat besterik ez da. Horrela, errazago egin daitezke kalkuluak, eta gainera zenbait arazo ekiditen dira. Adibidez, eremu kontzeptuarekin urrunetiko eraginaren arazoa ekiditen da. Karga elektriko bat beste baten eraginpean dagoela haietariko bat lekuz aldatzen bada, teorian, leku aldatze horrek sorturiko gorabeherak denbora jakin bat behar du puntu batetik bestera hedatzeko. Indar elektrikoa ez da aldatzen kargaren leku aldaketa gertatu eta une berean. Horren arrazoia erlatibitate bereziaren teoriak azaltzen du. Teoria horrek dioenez, elkar eraginaren barreiadura lastertasunak finitua behar du izan. Hala ere, eremu elektrikoaren kontzeptua erabiliz gero ez da arazo hau sortzen. Espazioko puntu guztietan eremu elektrikoa dago, eta karga lekuz aldatzean, toki jakin bakoitzeko eremu elektrikoaren eragina jasango du.
Eremu elektrikoaren definizioa matematikoki definitzerakoan, oro har, E letra erabiltzen da eremua izendatzeko.
 lekuko karga espazioko
puntu jakin batean baldin badago, puntu horretan dagoen eremu elektrikoa honela adierazten da matematikoki:
lekuko karga espazioko
puntu jakin batean baldin badago, puntu horretan dagoen eremu elektrikoa honela adierazten da matematikoki:

non F,  kargak jasaten dituen indar elektriko guztien bektore batuketa den. Nazioarteko Sisteman,
eremu elektrikoa newton coulomb-eko (N/C) banakoetan neurtzen da.
kargak jasaten dituen indar elektriko guztien bektore batuketa den. Nazioarteko Sisteman,
eremu elektrikoa newton coulomb-eko (N/C) banakoetan neurtzen da.
Aurreko formularen azterketatik ondorio hau ateratzen da:
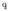 karga positiboa denean E eta F aldagaiek zentzu berbera dute biek. Aldiz,
karga positiboa denean E eta F aldagaiek zentzu berbera dute biek. Aldiz,
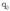 karga negatiboa denean,
E eta F aldagaiek elkarren kontrako zentzua dute.
karga negatiboa denean,
E eta F aldagaiek elkarren kontrako zentzua dute.
Coulomben legearen formula hartzen bada, puntu bakarreko karga batek
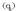 sorturiko E eremu
elektrostatikoa matematikoki honelaxe idazten da:
sorturiko E eremu
elektrostatikoa matematikoki honelaxe idazten da:
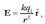
non  bektore unitarioak,
bektore unitarioak, 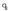 kargatik zein punturen E kalkulatu nahi dugun, puntu hartaranzko norabide erradiala duen.
Adierazpen matematiko hau ondo ikertzen bada, bi ondorio nagusi atera daitezke.
Batetik, eremua erradiala da, hau da, E bektorea
kargatik zein punturen E kalkulatu nahi dugun, puntu hartaranzko norabide erradiala duen.
Adierazpen matematiko hau ondo ikertzen bada, bi ondorio nagusi atera daitezke.
Batetik, eremua erradiala da, hau da, E bektorea
 kargatik igarotzen da beti.
Bestetik, E eremuak simetria esferikoa du. Beste era batera esanda, q 1 kargatik distantzia jakin
berera dauden puntu guztiek (
kargatik igarotzen da beti.
Bestetik, E eremuak simetria esferikoa du. Beste era batera esanda, q 1 kargatik distantzia jakin
berera dauden puntu guztiek (  kargan zentroa duen esfera bat osatzen dutela), E berbera daukate (E, E bektorearen modulua da).
kargan zentroa duen esfera bat osatzen dutela), E berbera daukate (E, E bektorearen modulua da).
Kasu orokorrago batean, puntu bakarreko karga bat baino gehiago izan daitezke, adibidez n karga. Kasu horretan, karga sistema horrek sortzen duen eremu elektrikoa kalkulatzeko gainezarmenaren printzipioa erabiltzen da:
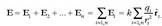
Ekuazio honen bidez erraz kalkula daiteke karga sistema batek puntu batean sortzen duen eremu elektrikoa. Lehenik karga bakoitzak puntu horretan sortzen duen eremu elektrikoa kalkulatzen da. Horretarako gainerako kargen eragina eremu elektrikoan zero dela esango da. Karga guztien eremu elektrikoa kalkulatu ondoren, eremu elektriko guztien bektore batuketa egiten da.
Azkenik, eremu elektrikoa kasurik orokorrenean nola kalkulatzen den azalduko da. Karga banaketa jarraitu bat badago, hau da, karga espazioko eremu batean barreiaturik badago, karga horrek sortzen duen eremu elektrikoa, dq karga txiki guztiek sortzen duten eremu elektrikoen batuketa integrala eginez kalkulatzen da, ondoko formularen bidez:

Azken adierazpen honek aurreko guztiak hartzen ditu bere baitan.
Galvanometroa
Doitasun handiko tresna elektriko hau korronte elektriko ahulen intentsitatea neurtzeko erabiltzen da. Eskuarki erabiltzen diren galvanometroak, J. A. D’Arsonvalek asmaturikoaren antzekoak dira, aldaketa txiki batzuekin. Galvanometroak bi osagai ditu: bobina eta magnetoa. D’Arsonvalen galvanometroa, bobina higikorra eta magneto finkoa zituen lehenengoa izan zen. Bobina finkoa eta magneto higikorra dituzten galvanometroak ere badira.
1.4. Eremu elektrikoaren lerroak
Eremu elektriko baten adierazpen grafikoa egiteko eremu lerroak erabiltzen dira. Eremu lerroak karga positiboetan sortu edo hastendira, eta karga negatiboetan amaitzen dira. Definizioz, E eremu elektrikoaren bektorea puntu bakoitzean puntu horretako eremu lerroarekiko tangentziala da. Eremu lerroei indar lerro ere esaten zaie.
Eremu lerroak irudikatzerakoan espazioko puntu kopurua infinitua dela kontuan hartu behar da. Hortaz, eremu lerro guztiak ezin direnez irudikatu, batzuk besterik ez dira adierazten. Eremu lerroak irudikatzerakoan arau hauek hartzen dira kontuan:
a) Karga batean sortzen edo amaitzen den lerro kopurua karga horren balioaren proportzionala izaten da.
b) Karga batetik sortzen edo han amaitzen diren lerroak elkarren simetrikoak dira.
c) Eremu lerroak lerro jarraituak dira, beraien iturri (karga positiboak) edo hobietan (karga negatiboak) izan ezik. Beraz, lerroak kargetan sortzen edo amaitzen dira beti.
d) Eremu lerroek ezin dute elkar ebaki. Eremu jakin bateko bi lerrok elkar ebakiko balute, E eremu elektrikoak puntu horretan bi norabide edukiko lituzke, eta hori ezinezkoa da.
e) Lerro dentsitatea, eremu elektrikoaren intentsitatearen araberakoa da. Lerro dentsitateak eremu lerroekiko gainalde elkarzut bat zeharkatzen duen lerro kopurua adierazten du. Lerro dentsitate handia duen eremu batean, eremu elektrikoaren intentsitatea handia da, eta lerro dentsitatea txikia den lekuetan, txikia.
Eremu lerroekin batera gainalde ekipotentzialak ere irudikatu ohi dira. Gainalde ekipotentzialak lerroei buruz elkarzutak dira, eta potentzial elektriko berbereko puntuak lotzen dituzte. (Potentzial elektrikoa hurrengo gaian aztertuko da). Ondoko irudietan zenbait eremu lerro (lerro jarraituak) eta gainalde ekipotentzial (lerro ez-jarraituak) azaltzen dira.
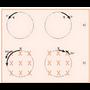
Aztertuko den lehenengo kasuan, 1.8. irudian, karga positibo eta negatibo bakartuei dagozkien eremu lerroak eta gainalde ekipotentzialak agertzen dira; simetria esferikoa dute.
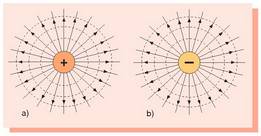
1.8. Irudia. (a) Karga positibo bakartu baten eremu lerroak eta gainalde ekipotentzialak; (b) gauza bera karga negatibo batentzako
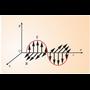
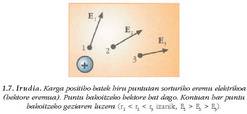
Bigarren kasuan, 1.9. irudian, bi karga positibo (q) berdinei dagozkien eremu lerroak agertzen dira. Kargak distantzia jakin batetaraino (L) urrunduta daude. Ikus daitekeenez, karga bakoitzaren inguruan oso distantzia hurbilean, hau da r « L distantzian, er emu lerroak erradialak dira eta beraien arteko distantzia berdina da. Hala ere, poliki-poliki, kargatik urrundu ahala desbideratu egiten dira. Eta, aldiz, karga batetik besterako distantzia baino urrunago badaude eremu lerroak, hau da r » L betetzen denean, eremu lerroak puntu bakarreko karga baten eremu lerroak bailiran ageri dira.

1.9. Irudia. Bi karga berdinek sorturiko eremu elektrikoaren eremu lerroak eta gainalde ekipotentzialak.
Azkenik, 1.10. irudian bi karga desberdini dagozkien eremu lerroak ageri dira. Aurreko kasuan bezala, kargak elkarretatik L distantziara urrunduta daude. Karga baten karga +q da, eta bestearena -q. Sistema hau nahiko berezia da, eta dipolo elektriko deritzo.
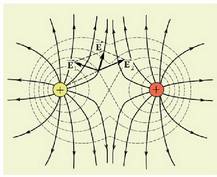
1.10. Irudia. +q eta -q kargak sorturiko eremu elektrikoaren eremu lerroak eta gainalde ekipotentzialak
1.5. Gaussen legea
Jarraian, K. F. Gaussek aurkituriko legea azalduko da. Horretarako, eremu elektriko batek gainalde bat zeharkatzean sortzen duen jarioa aztertzea komeni da lehenik. Jario horri, jario elektriko deritzo.
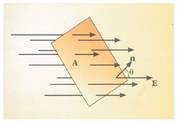
1.11. Irudia. Eremu lerroek A gainaldea nola zeharkatzen duten.
Eman dezagun gainalde lau bat, A area duena (ikus 1.11. irudia), eta E eremu elektriko uniformea, gainalde hura zeharkatzen duena. Jario elektrikoak gainaldeko puntu bakoitzean duen balioa honela kalkulatzen da:

non 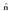 gainaldearekiko
bektore elkarzut unitarioa den, eta A gainaldearen zati horri dagokion area.
Gainaldea laua eta eremu elektriko uniformea izan ezean, jario elektrikoa kalkulatzeko
adierazpen matematiko hau erabili behar da:
gainaldearekiko
bektore elkarzut unitarioa den, eta A gainaldearen zati horri dagokion area.
Gainaldea laua eta eremu elektriko uniformea izan ezean, jario elektrikoa kalkulatzeko
adierazpen matematiko hau erabili behar da:
Horrela, Gaussen legea betetzen dela ikusiko da.

Eman dezagun gainalde itxi bat, 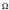 ,
ikus 1.12. irudia, eta haren barnean
,
ikus 1.12. irudia, eta haren barnean  ,
kargak daudela eta (
,
kargak daudela eta ( 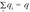 dela karga guztien batura).
dela karga guztien batura).  gainaldea zeharkatzen duen jario elektrikoa (hau da, eremu elektrikoaren jarioa) kalkulatzeko formula hau erabiltzen da:
gainaldea zeharkatzen duen jario elektrikoa (hau da, eremu elektrikoaren jarioa) kalkulatzeko formula hau erabiltzen da:

non E barruko karga guztiek sortzen duten eremu elektriko garbia den, ds gainalde elementu diferentziala,
 gainaldearen bektore elkarzut unitarioa, eta
gainaldearen bektore elkarzut unitarioa, eta
 hutsaren permitibitate elektrikoa.
hutsaren permitibitate elektrikoa.
Beraz, ondorio modura, zera esan daiteke: gorputz baten barruan dagoen karga guztia ezaguna baldin bada, Gaussen legea erabiliz, gorputzaren kanpoko eremu elektrikoa kalkula daiteke; eta alderantziz, eremu elektrikoa ezagututa, karga ezagutu daiteke
Karl Friedrich Gauss
(Brunswick, 1777 - 1855)
Matematikari eta astronomo alemana. Gotingako Unibertsitatean egin zituen ikasketak. Elektromagnetismoaren oinarri matematikoa finkatu zuen W. Weber-ekin batera. Lurreko magnetismoaren legeak formulatu zituen. Estatistika matematikoan erroreen teoria landu zuen. Heliografoa ere asmatu zuen.
1.6. Karga eta eremua eroaleetan
Eroale eta bakartzaileen arteko desberdintasuna aspalditik da ezaguna; eroamen elektrikoa aurkitu aurretik zen ezaguna. XVI. mendean, W. Gilbertek elektrizatuak izateko duten gaitasunaren arabera sailkatu zituen materialak. Elektriza zitezkeenei elektriko deitu zien, eta elektriza ezin zitezkeenei, ez-elektriko. S. Grayk eroamen elektrikoa aurkitu ondoren, C. F. du Fayk material guztiak elektriza zitezkela frogatu zuen. Baina hori gertatzeko, materialek lurretik (edo ikerlaritik) ondo bakartuta egon behar dute, bestela, karga berehala hedatuko da lurrera, materialean zehar.
Kargak garraiatzeko ahalmena asko aldatzen da material batetik beste batera. Material batek kargak garraiatzeko duen ahalmena eroamen elektriko deritzon magnitudearen bidez neurtzen da. Magnitude hori erabiliz, materialak bi multzo nagusitan bereiz daitezke, alde batetik eroaleak, eta bestetik bakartzaileak. Eroale arrunt baten eroamen elektrikoaren magnitude ordena 10 15 aldiz handiagoa da bakartzaile arrunt batena baino. Eroaleen artean ez da magnitude ordenan alde handirik izaten eroamen ahalmen desberdina izan arren.
1.6.1. Karga askea eroaleetan
Eremu elektrostatikoak aztertzeko, oso garrantzitsua da eroaleen ezaugarri bat aztertzea, hain zuzen ere, bere barruan karga elektrikoak higitzeko erraztasunaren ezaugarria aztertzea. Karga elektriko aske hauek atomoekin lotuta ez dauden elektroiak dira. Material eroaleen atomoek, beste guztiek bezala, elektroi kopuru jakin bat dute nukleoari loturik. Elektroi horiek geruzetan banatuta daude. Barneko geruzetako elektroiek kanpokoek baino lotura estuagoa dute nukleoarekin; kanpoko elektroiak nukleotik urrutiago daudenez, eta barneko elektroien aldarapena dela-eta, lotura ahulagoa dute. Prozesu horri estalkuntza deitzen zaio. Metal zati batean material eroaleen atomo asko elkartzen dira, eta elektroiek eta alboko atomoek elkarri eragiten diete. Elkar eragite horri esker

kanpoko elektroi batek edo batzuk nukleoaren eraginpetik ateratzen dira, eta aske geratzen dira, metaletik higitzeko moduan. Elektroi askeen kopurua metal motaren araberakoa da, baina, oro har, atomo bakoitzeko elektroi aske bat egoten da.
Kanpoko eremu elektriko baten eraginari aurre egiteko eroale baten karga askeak eremu hori konpentsatzea bilatuko du. Horrela, karga elektriko askea, elektroiak alegia, metaletik higituko dira, eta oreka bideratuko duen banaketa egoki bat eratuko da hrorela. Banaketa horrek sorturiko eremu elektrikoak, kanpoko eremuaren eragina desagerraraziko du metalaren barruan. Kontuan hartu behar da material barruan eremu elektriko bat egongo balitz, karga askeak indar elektriko bat jasango lukeela, eta horrek karga askeak higituko lituzkeela kanpoko eremua berdintzeko. Horregatik, eroale baten barruan oreka elektrostatikoa egon dadin, eremu elektrikoak hutsa izan behar du beti.
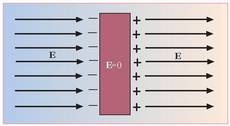
1.13. Irudia. Xafla eroale bat kanpoko eremu elektriko baten eraginpean. Eremu elektrikoa zero da eroalearen barruan.
Xafla eroale bat eremu elektriko baten eraginpean jartzean zer gertatzen den ikusten da 1.13. irudian. Hasieran, elektroi guztiak eroalean zehar barreiaturik daude. Eta xafla atomo neutroz osaturik dagoenez, xaflaren karga garbia zero da. Hala ere, kanpoko eremu elektrikoa aplikatzean, eroale barruan desagertu egiten da, eta ondorioz, eroalearen gainaldean karga dentsitateak sortzen dira. Beraz, kanpoko eremu elektrikoa eroalearen gainaldeetan iraungitzen eta sortzen da. Honen azalpen mikroskopikoa erraza da. Eroalearen karga askea, elektroiak alegia, kanpoko eremu elektrikoaren eraginpean higitu egiten dira. Beraien gainean sorturiko indar elektrikoa eremu elektrikoaren kontrakoa izango da, karga negatiboa dute-eta. Orduan, elektroiak irudiaren ezkerraldera higituko dira. Eskuinean berriz, elektroien faltagatik karga positiboa izango da. Horrela, gainaldeko bi karga dentsitateek eremu elektriko bat sortuko dute bi gainaldeen artean, eta kanpoko eremu elektrikoa desagertu edo ezereztuko da. Prozesu honen bidez oreka lortzeko denbora jakin bat behar da, materialaren eroamen elektrikoaren arabera. Kobrearen kasuan, adibidez, denbora tarte hori 10-16 segundokoa da, ia bat-batean gertatzen da, beraz.
1.6.2. Karga eta eremua eroaleen gainaldeetan
Aurreko atalean ikusitakoaren arabera, bi ondorio nagusi atera daitezke eremu elektrikoek eta kargek eroalearen gainean sortzen dituzten efektuei dagokienez:
a) Eroale batean, eroalearen gainaldean kokatzen da edozein karga garbi.
b) Eroalearen kanpoaldean, gainaldearen alboan, eremu elektrikoaren noranzkoa gainaldearekiko elkarzuta da, eta bere balioa
 ,
eroalearen gainaldeko puntu horretan dentsitatearen lekuan lekuko balioa da gainaldeko karga.
,
eroalearen gainaldeko puntu horretan dentsitatearen lekuan lekuko balioa da gainaldeko karga.
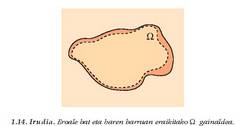
Lehenengo ondorioa Gaussen legearen bidez froga daiteke. Hartu eroale bat, ikus 1.14. irudia, eta bere barruan gainalde bat,
 . Eremu elektrikoa
eroalearen barnealdean hutsa dela kontuan harturik, Gaussen legea aplikatuko da.
. Eremu elektrikoa
eroalearen barnealdean hutsa dela kontuan harturik, Gaussen legea aplikatuko da.
 gainaldeko puntu
guztietan eremu elektrikoa hutsa denez, gainalde horretatik irteten den jario elektriko garbia ere zero da.
Gaussen legearen arabera, jario elektrikoa zero bada, gainalde horren barruan dagoen karga garbia ere zero da.
gainaldeko puntu
guztietan eremu elektrikoa hutsa denez, gainalde horretatik irteten den jario elektriko garbia ere zero da.
Gaussen legearen arabera, jario elektrikoa zero bada, gainalde horren barruan dagoen karga garbia ere zero da.
 gainaldea,
eroalearen gainaldera nahi dugun beste hurbil dezakegu, elkar ukitzen ez duten bitartean, noski.
Horren arabera, eroale baten karga garbia bere gainaldean kokatzen da.
gainaldea,
eroalearen gainaldera nahi dugun beste hurbil dezakegu, elkar ukitzen ez duten bitartean, noski.
Horren arabera, eroale baten karga garbia bere gainaldean kokatzen da.

1.15. Irudia. Kutxa baten itxurako gainaldea, eroale batean
Bigarren baieztapenaren kasuan ere, Gaussen legea erabiliko da egiaztapena egiteko.
Eman dezagun gorputz eroale bat dagoela, eta bere gainaldeko eremu txiki batean
 gainaldeko karga
dentsitate uniformea duela. Eremu txiki hori zilindro moduko batekin ixten da. Zilindro horren aurpegi
zirkularrak paraleloak dira eroalearen gainaldearekiko, eta bakoitzaren area A da. Beste aldetik,
zilindroaren luzera ahal den eta laburrena izan dadin ahalegina egingo da.
Ondorioz, zilindroa zeharkatzen duen jario elektriko garbia,
gainaldeko karga
dentsitate uniformea duela. Eremu txiki hori zilindro moduko batekin ixten da. Zilindro horren aurpegi
zirkularrak paraleloak dira eroalearen gainaldearekiko, eta bakoitzaren area A da. Beste aldetik,
zilindroaren luzera ahal den eta laburrena izan dadin ahalegina egingo da.
Ondorioz, zilindroa zeharkatzen duen jario elektriko garbia,
 , soilik aurpegi zirkularretatik
aterako da, eremu elektrikoa paraleloa baita beste aurpegiekiko. Gainera, eremu elektrikoa eroalearen
barruan zero denez, barruko aurpegiaren osagaia zero da, eta jario elektrikoa soilik eroaletik kanpo
dagoen gainalde zirkularrak bakarrik eratuko du. Beraz, Gaussen legea, zilindroari aplikaturik, horrela adierazten da:
, soilik aurpegi zirkularretatik
aterako da, eremu elektrikoa paraleloa baita beste aurpegiekiko. Gainera, eremu elektrikoa eroalearen
barruan zero denez, barruko aurpegiaren osagaia zero da, eta jario elektrikoa soilik eroaletik kanpo
dagoen gainalde zirkularrak bakarrik eratuko du. Beraz, Gaussen legea, zilindroari aplikaturik, horrela adierazten da:
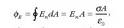
non 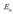 zilindroaren
kanpoko aurpegiako eremu elektrikoa den. Eta eragiketak eginez, gainaldetik hurbil dagoen eremu elektrikoak ondoko balioa du:
zilindroaren
kanpoko aurpegiako eremu elektrikoa den. Eta eragiketak eginez, gainaldetik hurbil dagoen eremu elektrikoak ondoko balioa du:

1.7. Indukzio biderko karga
Badago eroale bat kargatzeko era erraz bat, eroalearen kargen higidura askea erabiliz egin daitekeena. Eman dezagun, esfera eroale bat bakarturik dagoela (Ikus 1.16. a) irudia), eta karga negatiboaduen ziri bat jartzen dela hartatik hurbil. Esferaren elektroiek aldarapen elektriko bat jasaten dute ziriaren karga negatiboaren eraginez, eta urrundu egiten dira. Hau dela eta, esferaren alde batean, ziritik urrutienekoan, karga negatiboa pilatzen da, eta beste aldean, berriz, karga positiboa, elektroien faltagatik. Horrela, esfera polarizatuta geratzen da. Ikusten denez, ziriak esfera ukitu gabe eta ziriaren karga aldatu gabe, esferaren alde biak kargaturik geratzen dira. Fenomeno honi indukzio elektrostatikoa deitzen zaio.

1.16. Irudia. Indukzio bidezko karga esfera eroale batean. a) Esfera bakartua denean. b) Esfera Lurrari lotua denean.
Orain, eman dezagun hasieran polarizaturik zegoen esfera Lurrari lotuta dagoela. Lurrarekiko lotura hori, oro har, lerro paralelo batzuei lotuta dagoen hari batez adierazten da (ikus 1.16. b) irudia). Lurra eroale ahalmen handikoa da, eta bere karga positiboek orekatu egiten dute esferaren karga negatiboa. Horrela, ziria kendu baino lehen Lurrarekiko lotura eteten bada, ziria kentzean, esferak karga positiboa izango du. Esferak karga negatiboa izateko, ziriak karga positiboa izan beharko luke. Prozesu honi, indukzio bidezko elektrizazioa deritzo.
1.8. Puntu bakarreko kargen higidura eremu elektrostatikoetan
Elektrizitatez kargaturiko zatiki bat eremu elektriko baten eraginpean jartzen denean, indar baten eragina jasaten du. Zatikiaren karga q bada eta eremu elektrikoa E bada, orduan zatikiak jasoko duen indarra qE izango da. Beraz, zatikiaren gainean eragiten duen indar bakarra indar elektrikoa baldin bada, Newtonen adierazpena erabiliz, jasaten duen indarra honela idatziko da matematikoki:

non m zatikiaren masa den. Zatikiak jasaten duen azelerazioa hau izango da:
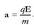
Ekuazio hauek aplikatu ahal izateko, zatikiaren lastertasunak argiarena baino askoz ere txikiagoa izan behar du; bestela, Einsteinen Erlatibitate Bereziaren Teoria aplikatu beharko litzateke. Adibidez, kasu askotan elektroien lastertasuna eremu elektrikoen eraginpean oso handia da, eta orduan aurreko ekuazioak ezin dira erabili.
Beraz, eremu elektrikoa ezaguna bada, azelerazioa neurtuz, zatikiaren karga-masaren zatiketaren balioa kalkula daiteke. Adibidez, eman dezagun eremu elektriko uniforme eta konstante bat dagoela. Lehenik, eremu elektriko uniformea zer den argitu behar da: eremu elektriko uniformeak, definizioz, puntu guztietan intentsitate eta norabide berbera du, eta bere indar lerroak paraleloak dira, elkarrengandik distantzia berera kokatuta daude. Horrelako eremu elektriko batean, zatikiaren hasierako abiadura zero ez bada, bere ibilbidea parabola bat izango da, eremu grabitatorio uniforme eta konstante baten eraginpean bezala. 1897an, J. J. Thomsonek elektroien higidura eremu elektriko uniforme batean erabili zuen, elektroien karga-masa erlazioa kalkulatzeko.
Joseph John Thomson (sir)
(Cheetham Hill, 1856 - Cambridge, 1940)
Britainiar kimikaria. Cambridgeko Trinity College-n egin zituen ikasketak. Cavendish-eko laboratorioa zuzendu zuen. Izpi katodikoak aztertuz elektroia materiaren oinarrizko karga zela aurkitu zuen 1897an. Elektroiaren eta protoiaren masa eta karga elektrikoa finkatu zituen, e/m zatidura neurtuz. Masa espektrografoa ere asmatu zuen. Tresna horrek atomoak pisatzeko balio du, eta horri esker isotopoak aurkitu ziren beranduago. 1906an Fisikako Nobel saria eman zioten.
1.9. Dipolo elektrikoak eremu elektrikoetan
Atomoak eta molekulak neutroak badira ere, barruan zenbait karga dituzte. Horrenbestez, eremu elektriko batean daudenean eremu haren eragina jasaten dute. Kasu batzuetan, molekularen karga negatiboen zentroaren posizioa ez da karga positiboenaren berdina (kargen zentroa, masa zentroa bezala definitzen da, masa jartzen den lekuan karga jarririk). Molekula horiei molekula polar deritze, eta beraien ezaugarriak azaltzeko beste magnitude bat definitzen da: momentu dipolar elektriko permanentea. Hala ere, nahiz eta hasierako unean momentu dipolar elektrikorik ez izan, eremu elektriko baten eraginpean dauden molekula guztietan agertzen da, indar elektrikoak karga positibo eta negatiboen zentroei kontrako norabidean eragiten baitie. Horrela, karga zentroenposizioak urruntzen dira, eta momentu dipolarra sortzen da. Era honetan sorturiko momentu dipolarrari, momentu dipolar elektriko induzitu deritzo.
Momentu dipolar elektrikoa, p, honela definitzen da matematikoki:
zioak urruntzen dira, eta momentu dipolarra sortzen da. Era honetan sorturiko momentu dipolarrari, momentu dipolar elektriko induzitu deritzo.. Momentu dipolar elektrikoa, p, honela definitzen da matematikoki:
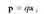
non q karga positibo eta negatiboen balio absolutua den, eta a karga negatiboen zentrotik karga positiboen zentrora doan bektorea.
Molekula dipolar bat eremu elektriko uniforme batean dagoenean, haren gaineko indar garbia zero da, karga negatiboak eta positikiaren boak modulu bera baitute, eta eremu elektrikoa bi kargen zentroeere bai. Hala ere, molekularen gainean indar bikote bat agerela tzen da. Indar bikote horren eraginez, zatikiak biratu egiten du. Eremu elektrikoa uniformea ez bada, eremu elektrikoa desberdina baita karga zentro bakoitzean. Orduan, indar bikoteaz gainera, molekulak indar garbi baten eragina ere jasango du.
1. 17. b ) irudian ageri den dipoloa eremu elektriko uniforme batean, E, dago. Esan bezala, karga zentro bakoitzak indar elektriko baten eragina jasango du, eta horrela:


1.17. Irudia. a) Molekula polarra. b) Dipoloaren gainean agertzen diren indarrak, eremu elektriko uniforme batean jartzean
2. Gaia: potentzial elektrikoa
Karga batek eremu batean sortzen duen elkarrekintza elektrikoa deskribatzeko, eremu elektrikoa azaldu da aurreko gaian. Tresna matematiko hori laguntza handikoa izaten da. Hala ere, zenbaitetan elkarrekintza elektrikoa ondo azaltzeko, beste magnitude berri bat erabili behar da. Magnitude berri hori potentzial elektrikoa da, eta horixe da, hain zuzen, gai honetan aztertuko dena.
2.1. Eremu elektriko kontserbakorra
Eremu elektrikoak ezaugarri berezi bat duela ikusteko, Coulomben legea aztertuko da adibide baten bidez.
Demagun, q karga 0 puntuan geldi dagoela.
Karga horrek eremu elektriko bat sortuko du espazioko puntu guztietan. Beste karga bat hartuz gero,
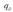 adibidez, eta 1 puntutik 2
puntura eramanez gero kurban zehar, indar elektrikoak
adibidez, eta 1 puntutik 2
puntura eramanez gero kurban zehar, indar elektrikoak
 kargaren gainean
egiten duen lana indarra bider desplazamenduaren bektorea eginez lortzen da. Beraz, ibilbide osoa
modu integralean kalkulatu behar da:
kargaren gainean
egiten duen lana indarra bider desplazamenduaren bektorea eginez lortzen da. Beraz, ibilbide osoa
modu integralean kalkulatu behar da:
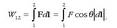

Baina, aurreko ekuazioa sinplifika daiteke. 2.1. irudian ikusten denez,
 da,
hau da, bi kargen arteko distantzia erlatiboaren aldakuntza infinitesimala. F indarra adierazteko
Coulomben legea erabiliz gero, ondoko formula hau lortzen da:
da,
hau da, bi kargen arteko distantzia erlatiboaren aldakuntza infinitesimala. F indarra adierazteko
Coulomben legea erabiliz gero, ondoko formula hau lortzen da:

eta ondorioz esan daiteke: indar elektrikoak egindako lana hasierako eta bukaerako puntuen mende dago eta ez karga eramateko aukeratu den ibilbidearen mende. Ezaugarri hori duen eremu bat ezagutzen dugu jadanik, eremu grabitatorioa alegia. Eremu kontserbakorra esaten zaio horri. Beraz, Coulomb-en legeak eremu kontserbakor bat definitzera eramaten du, eremu elektrikoa hain zuzen.
Karga jakin batek sortutako eremu elektrikoa hartu beharrean, edozein karga-banaketak sortutakoa hartzen bada, gainezarmenarenprintzipioagatik, eremuak ere kontserbakorra izan behar du. Hala ere, aurreko ekuazioaren emaitza ez da hasieratik ezagutzen. Baina, jakin badakigu, egindako lana hasierako eta bukaerako puntuen funtzio bat dela. Funtzio hori, f(1,2) delakoa baldin bada, karga elektrikoa 1 puntutik 2 puntura eramateko egin behar den lana ondoko hau izango da:
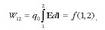
Azken adierazpen horretan eragiketa matematiko batzuk eginez, eta f(1,2) funtzioa bitan bananduz, honela adieraz daiteke:
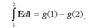
g(2) eta g(2), 1 eta 2 puntuetan, definitu behar den beste funtzio batek hartzen dituen balioak dira. Azkenik, aurreko ekuazioaren kasu berezi bat aztertuko da. 2 puntua 1 bihurtzen bada, hau da, kargak egiten duen ibilbidea itxia bada, garrantzi handiko adierazpen orokor hau lortzen da:

Beraz, karga elektriko batek eremu elektriko konstante batean ibilbide itxia egiten badu, hau da, hasierako puntura itzultzen bada, higidura horrek sortzen duen lana zero izango da.
Eremu elektrikoarekin egin diren kalkuluak, eremu grabitazionalarekin errepika daitezke; desberdintasun bakarra konstanteetan dago.
2.2. Karga puntual batek sortutako potentziala
Jakina denez, jatorrian dagoen q karga puntualak r distantziara sortzen duen eremu elektrikoa ondoko hau da:

non  norabide erradialeko bektore unitarioa den. Eremu elektrikoa eremu kontserbakorra da, eta horregatik,
eremu eskalar bat dagokio. Eremu eskalar hori lortzeko,
norabide erradialeko bektore unitarioa den. Eremu elektrikoa eremu kontserbakorra da, eta horregatik,
eremu eskalar bat dagokio. Eremu eskalar hori lortzeko,
 kargari
aurreko eremu elektrikoan sartzen denean zer gertatzen zaion aztertu behar da.
kargari
aurreko eremu elektrikoan sartzen denean zer gertatzen zaion aztertu behar da.
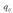 karga puntuala puntu batetik beste batera garraiatzeko zenbat lan egin behar den kalkulatu da jadanik.
Gainera, egindako lana energia potentzial elektrikoaren,
karga puntuala puntu batetik beste batera garraiatzeko zenbat lan egin behar den kalkulatu da jadanik.
Gainera, egindako lana energia potentzial elektrikoaren,
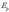 , txikitxea da:
, txikitxea da:

Hala, energia potentzial elektrikoaren adierazpen matematikoa ondoko hau izango da:
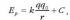
non C integrazio-konstante arbitrario bat den. Konstante horren balioa zehazten da energia potentzial elektrikoaren zeroa zehazten denean. Ikus daitekeenez, r distantzia handitzen denean, energia potentziala txikitu egiten da. Energia potentzialaren balio txikiena, C, r delakoa infiniturantz eramaten lortzen da. Horregatik, normalean C-ri zero balioa ematen zaio, hala, r = denean, energia potentziala zero izango da. Horrela, energia potentzial elektrikoaren adierazpen matematikoa hau izango da:
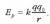
Karga bat puntu batetik bestera eramateko behar den karga-unitateko energiari potentzial-diferentzia esaten zaio, eta
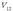 ikurraz adierazten da.
Potentzial-diferentziaren balioa honela lortzen da:
ikurraz adierazten da.
Potentzial-diferentziaren balioa honela lortzen da:
karga bat eramateko egiten den lana zati karga horren balioa, hau da:

Hortik potentzial elektrikoaren definizioa lor daiteke. Puntu zehatz baten V potentzial elektrikoa hau da:
Karga bat infinitutik aipatutako puntu horretara eramateko behar den karga-unitateko energia.
Horren adierazpen matematikoa, aurreko ekuaziotik ateratzen da:
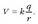
Bai definizioan bai adierazpen matematikoan, potentzial elektrikoa infinituan zero hartzen da. Beraz, potentzial elektrikoari dagokion integrazio-konstantetzat zero hartu da. Hortik abiatuta, argi ikus daiteke energia potentzial elektrikoaren eta potentzialaren arteko lotura:
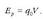
Jakina denez, eremu elektrikoa magnitude bektoriala da, espazioko puntu guztietan bektore bat baitagokio. Potentzial elektrikoa, berriz, eskalarra da, hau da, espazioko puntu guztietan zenbaki bat dagokio. Bestalde, potentzial elektrikoaren zeinua, eremu elektrikoa sortzen duen kargaren araberakoa da. Hau da, karga positiboa denean, potentzial elektrikoa positiboa da, eta karga negatiboa denean, berriz, potentzial elektrikoa negatiboa da.
Energiarekin gertatzen den bezala, potentzial elektrikoan garrantzi handienekoak diferentziak dira. Hau da, potentzialaren balioa puntu batean, hartu den erreferentziaren araberakoa da. Beraz, erreferentzia aldatuz gero, potentzialaren balioa aldatu egiten da puntu horretan. Potentzial-diferentziekin ez da halakorik gertatzen.
Unitateei dagokionez, Nazioarteko Unitate-Sisteman potentzial elektrikoaren unitateari volta (V) esaten zaio, A. G. Volta (1745-1827) fisikari italiarraren omenez:


2.2. Irudia. Karga puntual positiboen eta negatiboen eremu elektrikoa eta gainalde ekipotentzialak. a) karga positiboa eta b) karga negatiboa.
Behin maila honetara iritsita, ezinbestekoa da beste kontzeptu bat definitzea. Kontzeptu horren oinarria potentzial elektrikoa da, eta izena gainalde ekipotentziala du. Kontzeptu horren definizioa hau da:
Potentzial elektrikoa konstantea den gainaldea.
Karga puntualen kasuan (ikus 2.2. irudia), gainalde ekipotentzialak karga erdian duten esfera konzentrikoak dira
2.3. Eremu eta potentzial elektrikoak
Ikusi denez, kargek inguruan sortzen duten eragina aztertzeko bi magnitude erabil daitezke: alde batetik, magnitude bektoriala den E eremu elektrikoa, eta bestetik, magnitude eskalarra den V potentzial elektrikoa. Ondoren, magnitude horiek batak bestearekin zein harreman mota duten aztertuko da.
Horretarako indar kontserbakorren kasua hartuko da, indar grabitatorioa esaterako. Eremu baten indarraren eta energiaren artean erlazioa hau betetzen da:

non grad ( ) eragile matematiko bat den, gradientea hain zuzen ere.
Gradientearen azalpena:
Gradientea eragile matematiko bat da, eta horren eraginez, eremu eskalar bat eremu bektorial bihurtzen da. Horrez gainera, gradienteak aplikatzen zaion magnitudearen aldaketak azaltzen ditu. Demagun hiru dimentsiotako eremu eskalar bat koordenatu kartesiarren bidez adierazten dela, adibidez g(x,y,z). Eremu eskalar horri gradientea aplikatzen bazaio, ondoko hau lortuko da:

non  delakoa g(x,y,z) funtzioaren x-ekiko deribatu partziala den. g funtzioa aldagai bakarrekoa bada,
g(x) adibidez, gauzak asko errazten dira:
delakoa g(x,y,z) funtzioaren x-ekiko deribatu partziala den. g funtzioa aldagai bakarrekoa bada,
g(x) adibidez, gauzak asko errazten dira:
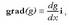
non  deribatu osoa den.
deribatu osoa den.
Indarraren eta energiaren arteko adierazpena eremu elektrikoaren kasuan aztertuz gero, eta
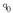 kargaz zatituz gero, hau geratzen da:
kargaz zatituz gero, hau geratzen da:

Baina formula hori, zuzenean, beste hau bilakatzen da:
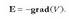
Gradientearen bektorea eta gainalde ekipotentzialak elkarzutak dira. Beraz, puntu bateko eremu elektrikoa puntu horretatik igarotzen den gainazal ekipotentzialaren elkarzuta da.
2.4. Partikula kargadunaren energia eremu elektrikoan
Fisikako problemak ebazteko sistemaren energia guztiak kontutan hartuz gero, asko errazten dira problemak. Hori dela eta, sistema elektrikoen jokaera mekanikoak aztertzen direnean, zenbaitetan, komeni da energiekin lan egitea.
Demagun partikula kargadun
bat eremu elektriko batean higitzen ari dela. Partikula horren energia aztertu nahi baldin bada,
hasiera batean, energiaren hiru osagai kontutan izan behar ditugu.
Hiru osagai horiek ondoko hauek izango dira: energia zinetikoa,
 ,
energia potentzial grabitatorioa,
,
energia potentzial grabitatorioa, 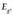 ,
eta azkenik, energia potentzial elektrikoa,
,
eta azkenik, energia potentzial elektrikoa,
 .
Kalkuluak eginez gero, energia grabitatorioaren balioa beste balioen aldean oso txikia dela ikus daiteke.
Beraz,azterketa honetan ez da balio hori kontuan hartuko, arbuiagarria baita.
Eremu elektrikoan higitzen den partikula kargadunaren energia espazioko puntu jakin batean, honako hau da:
.
Kalkuluak eginez gero, energia grabitatorioaren balioa beste balioen aldean oso txikia dela ikus daiteke.
Beraz,azterketa honetan ez da balio hori kontuan hartuko, arbuiagarria baita.
Eremu elektrikoan higitzen den partikula kargadunaren energia espazioko puntu jakin batean, honako hau da:

non q, m eta v partikularen karga, masa eta abiadura diren; V partikulak jasaten duen potentzial elektrikoa da.

2.3. Irudia. Partikula kargadunaren higidura eremu elektrikoan. Vi eta vi, partikulak puntu bakoitzean duen potentzial elektrikoa eta abiadura dira, hurrenez hurren
Partikula kargadunari, 1 puntutik 2 puntura higitzean (ikus 2.3. irudia), potentziala eta abiadura aldatzen zaizkio. Sisteman parte hartzen duen indar bakarra, indar elektrikoa alegia, kontserbakorra denez, partikularen energia kontserbatu egin behar da. Hasierako eta bukaerako puntuen potentzialak V1 eta V2, eta abiadurak v1 eta v2 baldin badira, orduan partikularen energiaren kontserbazioaren teorema honela idatzi beharko da:
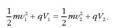
Berdintza zeinuaren alde batera eta bestera, partikulak 1 puntuan eta 2 puntuan dituen energiak adierazten dira.
Indar kontserbakor batek prozesu dinamiko batean egiten duen lana, W, bi puntuenarteko energia zinetikoaren diferentzia da,
 alegia.
Aurreko ekuaziotik abiatuta, hau guztia lor daiteke:
alegia.
Aurreko ekuaziotik abiatuta, hau guztia lor daiteke:

Espero denez, indar kontserbakorrak egindako lana (W) minus energia potentzial elektrikoaren diferentzia da.
Azken ekuazio hori aztertzean, bi kasu garrantzitsu azaltzen dira:
a) Karga positiboko partikulek, q > 0, energia zinetikoa irabazteko,
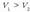 izan behar du. Hau da, karga positiboa duen partikula bat, eremu elektriko batean,
potentzial elektriko txikiagoko eskualdeetara joaten da.
izan behar du. Hau da, karga positiboa duen partikula bat, eremu elektriko batean,
potentzial elektriko txikiagoko eskualdeetara joaten da.
b) Karga negatiboa duten partikulentzat, q < 0, berriz, energia zinetikoa irabazteko
 behar du. Horrela, partikula horiek
potentzial elektriko handiagoko eskualdeetara joaten dira.
behar du. Horrela, partikula horiek
potentzial elektriko handiagoko eskualdeetara joaten dira.
Azken ekuazioan oinarrituta, volta-ren (potentzial elektrikoaren unitatea) beste definizio bat eman daiteke:
Coulomb bateko kargak joule bateko energia irabazteko behar duen potentzial-diferentzia volta da
Voltimetroa
Voltimetroa, bi punturen arteko potentzial-diferentzia neurtzeko erabiltzen den tresna da. Zirkuituko elementu baten potentzial-diferentzia neurtzeko, voltimetroa elementu horren paraleloan jarri behar da. Horrela jarrita, voltimetrotik intentsitate asko desbideratuko ez bada, voltimetroaren barne-erresistentziak elementuarena baino askoz handiagoa izan behar du. Horregatik, voltimetroen barne-erresistentziak handiak izaten dira.
Alessandro Giuseppe Volta
Alessandro Giuseppe Volta
(Como, 1745-1827)
Italiar fisikaria. Eudiometroa egokitu zuen (1776) eta elektrizitateari buruzko ikerketak egin zituen. 1800ean lehenengo bateria asmatu zuen, eta pila elektrikoa deitu zion. Potentzial-diferentziaren banakoari volt izena jarri zitzaion haren omenez.
2.5. Potentzial elektrikoaren kalkulua
Potentzial elektrikoarentzat azaldu den adierazpen bakarra partikula kargatuarena da. Hala ere, oro har, karga bat baino gehiago izaten dira. Kasu horietan, eremu elektrikoa kalkulatzeko egiten den bezala, gainezarmenaren printzipioa erabiltzen da. Hau da, partikula kargadun multzo batek puntu batean sortzen duen potentzial elektrikoa, karga bakoitzak puntu horretan sortzen duen potentzial elektriko guztiak batuz lor daiteke.
2.4. Irudia. Karga multzo batek puntu batean sorturiko potentziala
Adibidez, sistema batean N partikula kargadun badaude, puntu batean partikula horiek sortzen duten potentzial elektrikoa era honetan kalkulatzen da:
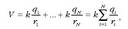
non  partikula bakoitzaren karga den, eta ri partikula kargadun bakoitza dagoen
lekutik potentziala kalkulatzen den lekura dagoendistantzia. Adierazpen horretan, potentzial elektrikoa infinituan zero
balioa ematen zaio.
partikula bakoitzaren karga den, eta ri partikula kargadun bakoitza dagoen
lekutik potentziala kalkulatzen den lekura dagoendistantzia. Adierazpen horretan, potentzial elektrikoa infinituan zero
balioa ematen zaio.
Bestalde, karga-banaketa jarraituak daudenean, antzeko erara jokatu behar izaten da. Baina, kasu horretan, batuketa egin beharrean, karga barreiaturik dagoen eskualdean integrazioa egin behar da. Adibidez, karga-banaketa jarraitu bat gainalde itxi baten barruan barreiaturik baldin badago, edozein puntutako potentzial elektrikoa ondoko adierazpenaren bidez lortu ahal izango da:

non r, dq karga-elementu diferentziala dagoen lekutik potentziala kalkulatzen den puntura dagoen distantzia den. Emaitza hori er e, infinituan potentziala zero denean lortzen da. Horrez gainera, azken adierazpen hori bakarrik erabil daiteke karga-banaketaren tamaina finitua denean. Horrela, karga-banaketaren potentzialak infinituan muga-balio baterantz jotzen du; balio horri zero balioa ematen zaio.
Azkenik, eroaleen kasua aztertuko da. Aurretik ikusi bezala, orekan dagoen eroale batek bere gainaldean sortzen duen eremu elektrikoa gainaldearekiko elkarzuta da. Beraz, eroalearen gainaldea ekipotentziala dela esan daiteke, eremu elektrikoa gainalde ekipotentzialarekiko elkarzuta baita beti. Bestalde, oreka elektroestatikoan dagoen eroale baten eremu elektrikoa konstantea da, eta konstante horren balioa zero da. Eremu elektrikoa egon dadin, potentzialak espazioan duen balioa aldatu behar da. Beraz, er emu elektrikoa zero denez gero, eroalearen barruko eta gainaldeko puntu guztietan potentzialak balio konstantea hartzen du.
Transformadorea
Transformadorea, indukzio elektromagnetikoaz baliatzen den tresna elektriko estatikoa da (ez du parte higikorrik). Tresna honek zirkuitu batetik korronte elektrikoa hartu, eta beste batetik ematen du, voltajea aldatu ondoren (handitu edo txikitu). Transformadoreak korronte alternoarekin egiten du lan, eta ez du aldatzen korrontearen maiztasuna. Bere oinarri fisikoa Faradayren legean datza. Oso errendimentu ona izan ohi du, %99 ingurukoa. Oinarrizko bi osagai ditu: nukleoa, normalean burdinezkoa, eta horren inguruan bi solenoide, bata primarioa deitzen zaiona (N1 birarekin), eta bestea sekundarioa (N2 birarekin). Primarioko tentsioa (V1) eta sekundarioko tentsioa (V2), solenoide bakoitzaren bira-kopuruen proportziokoak dira, ondoko erlazioa ematen dutelarik:

Pila
Erreakzio batean askatzen den energia (kimikoa, eguzkitikoa, nuklearra,...) energia elektriko bihurtzen duen tresna da pila elektrikoa. Pila elektrikoak, L. Galvanik egindako ikerketetan du sorburua (1786). Hala ere, 1793. urtean A. Volta izan zen lehenengo pila egin zuena. Horregatik, pila galvanikoa edo voltaikoa ere deitu izan zaio batzuetan. Kontuan hartu behar da M. Faradayk dinamoa asmatu arte (1831), Voltaren pila baino ez zegoela argi-indarra sortzeko. Pilan erabiltzen den erreakzio kimikoaren arabera sailkatzen dira mota desberdinetako pilak: pila lehorrak, Daniellen pila, eta abar... Azken hamarraldietako garapen zientifikoari esker, pila atomikoek eta eguzki pilek ere aurrerapen handiak egin dituzte, eta pilen autonomia ia infinituraino zabaldu da. Gaur egun, gainera, pila batzuk erabili eta ahitu ondoren, berriro karga daitezke. Bestalde, pilen erabilpena asko hedatu da, tresna elektroniko txikiak zabaltzearekin. Oso pila txikiak gai baitira tresna horiek behar duten indar elektrikoa eskaintzeko.
3. Gaia: kapazitatea eta dielektrikoak
3.1. Kapazitatea
Demagun eroale bakartu bat kargatuta hartzen dela. Eroale horrek sortzen duen potentzial elektrikoa infinituan zero dela jotzen bada, eroalearen karga ( Q ), forma eta tamainaren araberakoa izango da potentziala. Oro har, zenbat eta handiagoa izan eroalea, orduan eta karga gehiago pila dezake potentzial jakin batentzat. Adibidez, eroale esferiko batean edo geruza esferiko batean ( R erradioduna eta Q kargaduna ) potentzial elektrikoa hau izango da:
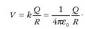
Ekuazio horretan argi ikus daiteke aurretik esandakoa. Potentzial elektriko jakin batentzat zenbat eta handiagoa izan erradioa, orduan eta karga gehiago eduki behar du eroaleak. Behin maila horretara iritsita, beste magnitude berri bat definitu behar da. Magnitude hori eroale bakartu baten karga eta potentzial elektrikoaren arteko zatidura da: eroalearen kapazitatea. Kapazitatearen ikurra C da:
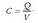
Potentzial elektrikoa kargarekiko proportzionala denez beti, zatidura horrek ez du mendekotasunik, ez V-rekiko, ezta Q-rekiko ere. Kapazitateak, beraz, eroalearen tamainarekiko eta formarekiko du soilik mendekotasuna.
Adibidez, eroale esferikoaren kapazitatea hau da:

beraz, bere erradioarekiko proportzionala da.
Kapazitatearen banakoa faraday da (F), M. Faraday (1791-1867) fisikaria britaiarraren omenez:

3.2. Kondentsadoreak
Zirkuitu elektrikoetan askotan agertzen den osagai kondentsadorea da. Kondentsadorearen definizio arruntenak dio:
Bi eroale dira, bien artean potentzial diferentzia jartzen denean, kopuruz berdinak baina zeinuz kontrakoak diren kargaz kargatuak.
Kondentsadore bat definitzeko erabiltzen den ezaugarria kondentsadore horrek duen kapazitatea da. Kapazitate horri esker, kondentsadorearipotentzial-diferentzia bat jartzean zaionean, bere eroaleetan zenbat karga sortzen den jakin daiteke. Gehien erabiltzen diren kondentsadoreak xafla paralelotakoak eta zilindro kontzentrikokoak dira. Horregatik, aztertuko dira arretaz bi kondentsadore mota horiek.
3.2.1. Xafla paralelotako kondentsadorea

Xafla paralelotako kondentsadoreak bi xafla eroale ditu paraleloan (ikus 3.1. irudia). Xafla horiek elkarrengandik oso hurbil daude, eta bataren eta bestearen arteko distantzia d da. Xafla bakoitzak A gainaldea baldin badu, eta baten karga + Q baldin bada, eta bestearena -Q, orduan, xafla bakoitzaren gainaldeko karga dentsitateak hauek dira:

Xaflen arteko eremu elektrikoa uniformea da ia. Bi xaflen artean eta ertzetatik urrun
dagoen inguruko eremu elektrikoa, bi xafla kargatu infinituek sortutako eremu elektrikoa da ia.
Xafla bakoitzari dagokion eremu elektrikoak  balio hartzen du.
Xafletatik kanpora eremuak anulatu egiten dira; bi xaflen arteko inguruan, berriz, batu egiten dira, eta ondorioz,
eremuak honako balioa hartzen du:
balio hartzen du.
Xafletatik kanpora eremuak anulatu egiten dira; bi xaflen arteko inguruan, berriz, batu egiten dira, eta ondorioz,
eremuak honako balioa hartzen du:

Eremu elektrikoa, Gauss-en legearen bidez ere kalkula daiteke. Lortu den balioa hurbilketa bat baino ez da, xafletako ertzen eragina baztertu egin baita. Hala ere, hurbilketa hori praktikan nahiko ona izaten da. Hori horrela izan dadin, xaflen arteko distantziak xaflen dimentsioak baino txikiagoa izan behar du.
Bestalde, xaflen arteko tartean eremu elektrikoa konstantea eta uniformea denez gero, potentzial elektrikoaren balioa honela lortzen da:
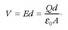
Dena dela, eroale biak ekipotentzialak direla hartu behar da kontuan. Hau da, eroalearen potentziala berdina da puntu guztietan. Azaldu den formula erabiliaz, kondentsadorearen kapazitatea hauxe izango litzateke:
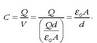
Argi ikusten denez, xafla paralelotako kondentsadorean kapazitatea xaflen gainaldeen arearekiko proportzionala da, eta xaflen arteko distantziarekiko, berriz, alderantziz proportzionala. Hau da, zenbat eta gainalde handiagoko eroaleak eduki, edo zenbat eta distantzia txikiagoa egon eroaleen artean, hainbat eta handiagoa izango da kapazitatea.
Zirkuitu elektrikoetan gehien erabiltzen den kondentsadore mota xafla paralelotako kondentsadorea da. Hori dela eta, zirkuituetanedozein kondentsadore adierazteko erabiltzen den ikurra bi lerro paralelo dira (ikus 3.2. irudia).

3.2. Irudia. Kondentsadorearen ikurra zirkuituetan.
3.2.2. Kondentsadore zilindrikoa
Kondentsadore zilindrikoa ere bi eroalek osatzen dute (ikus 3.3. irudia).
Bata  erradiodun hari eroale edo zilindro eroale txiki bat da.
Bestea
erradiodun hari eroale edo zilindro eroale txiki bat da.
Bestea 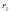 erradiodun zilindro eroale handiago bat, bestearen inguruan dagoena.
Eman dezagun bien luzera (L)
erradiodun zilindro eroale handiago bat, bestearen inguruan dagoena.
Eman dezagun bien luzera (L) 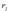 eta
eta  erradioak baino askoz handiagoa dela; ondorioz, ertzen efektuak arbuiagarriak dira.
Bestalde, ontzat hartuko da barruko eroaleak +Q karga duela eta kanpokoak -Q.
erradioak baino askoz handiagoa dela; ondorioz, ertzen efektuak arbuiagarriak dira.
Bestalde, ontzat hartuko da barruko eroaleak +Q karga duela eta kanpokoak -Q.

Horien arteko eremu elektrikoa, bestalde, erraz kalkula daiteke Gauss-en legearen bidez.
Kalkulu horiek egiteko, gainalde bat erabili behar da, gainalde gausstarra alegia. Gainalde hori
 erradiodun eta
erradiodun eta 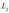 luzeradun
zilindroa izango da (ikus 3.4. a irudia).
luzeradun
zilindroa izango da (ikus 3.4. a irudia).
Gauss-en legearen arabera, aukeratu den gainalde gausstarretik igarotzen den jario elektrikoa hau da:

non q gainalde gausstarraren barruan dagoen karga garbia den. Eroaleen luzerak erradioak baino handiagoak badira, eroaleen ertzen efektuak arbuia daitezke, eta ondorioz, eremu elektrikoa eroaleen ardatzarekiko elkarzuta izango da (ikus 3.4. b, irudia). Eremu elektrikoaren balioa eroaleen gainaldetik ardatzera dagoen distantziaren araberakoa da. Eremu elektrikoa mota horretakoa denez gero, hau da, erradiala denez gero, gainalde gausstarraren gainalde kurbatutik igarotzen den jario elektrikoa baino ez da izango;
zirkunferentzietatik ez da inolako jariorik igaroko.
Gainalde gausstarrean eremu elektrikoaren balioa konstantea,
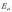 ,
eta gainaldearekiko zuta denez gero, jario elektrikoaren balioa hau izango da:
,
eta gainaldearekiko zuta denez gero, jario elektrikoaren balioa hau izango da:


3.3. Irudia. Kondentsadore zilindrikoaren bi eroaleak
non 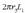 adierazpena gainalde gausstarraren gainalde kurbatuaren azalera den,
eta
adierazpena gainalde gausstarraren gainalde kurbatuaren azalera den,
eta  barruko eroalearen karga luzera unitateko.
barruko eroalearen karga luzera unitateko.
 delakoa honela defini daiteke matematikoki:
delakoa honela defini daiteke matematikoki:

Orduan, aurreko ekuazioetatik eremu elektrikoaren balioa atera daiteke:

 -ren balioa karga lineal
infinituak sortzen duen eremu elektrikoaren berdina da.
-ren balioa karga lineal
infinituak sortzen duen eremu elektrikoaren berdina da.
Bestalde, kapazitatearen balioa kalkulatzeko, bi eroaleen arteko potentzial-diferentzia ezagutu behar da.
Aurreko kasuan bezala hemen ere, bi eroaleak ekipotentzialak direla kontuan hartu behar da.
Hau da, bakoitzak potentzial jakin bat du bere puntu guztietan.
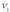 ikurraz barruko eroalearen potentziala adierazten bada, eta
ikurraz barruko eroalearen potentziala adierazten bada, eta
 ikurraz kanpokoa, potentzial-diferentzia hauxe izango da:
ikurraz kanpokoa, potentzial-diferentzia hauxe izango da:
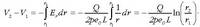
Lortzen den potentzial-diferentziaren balioa negatiboa da. Ondorioz, argi ikus daiteke barruko eroaleak kanpokoak baino potentzial handiago duela, kanpokoak baitu karga positiboa. Horregatik, eremu elektrikoaren eremu-lerroak barruko eroaletik kanpoko eroalera doaz. Hala, potentzial-diferentziaren balioa hau izango da:

Eta orduan, kapazitatea lehen azaldu den adierazpenaren bidez lortzen da:

Kapazitatea zilindroaren luzerarekiko proportzionala da, eta bi eroaleen erradioen arteko diferentziaren mendekoa. Beste era batera esanda, eroaleak zenbat eta luzeago izan edo eroaleen arteko distantzia zenbat eta txikiagoa izan, orduan eta handiagoa izango da kondentsadorearen kapazitatea. Beraz, potentzial-diferentzia jakin batentzat, eroaleak zenbat eta luzeagoak izan, edo bata bestearekiko zenbat eta hurbilago egon, kondentsadoreak hainbat eta karga gehiago pila dezake
3.3. Energia kondentsadoreetan
Kondentsadore bat, bertako eroale batetik bestera karga garraiatuz karga daiteke. Prozesu horretan, garraiatutako kargaren potentzial elektrikoa handitu egiten da. Beraz, edozein kondentsadore kargatzeko lan bat egin behar da. Lan horren zati bat, edo guztia, kargatzeko metodoaren arabera, energia potentzial modura pilatzen da. Demagun C kapazitatea duen kondentsadore bat kargatu nahi dela. Garrantzia duen magnitudea potentzial-diferentzia da. Horregatik, zehaztuko da potentzialak zein lekutan hartzen duen zero balioa. Komeni da potentzialaren zeroa eroale batean egotea, esate baterako, karga negatiboa pilatzen duen eroalean. Hasieran, eroaleak potentzial berean daude, ez dute kargarik, eta ez dago eremu elekb) trikorik horien artean. Q karga eroale batetik bestera garraiatu eta gero, bi eroaleen arteko potentzial-diferentzia hauxe izango da:
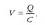
Hala, potentzial zero duen eroalean -Q karga izango da, eta bestean, +Q karga eta V potentziala. Prozesu horretan egindako lanak, garraiatutako karga (Q) bider energia potentziala karga unitateko (V) izan behar du. Bi eroaleen hasierako potentziala zero da; bukaeran, eroale baten potentziala zero da, eta bestearena, berriz, V. Beraz, potentzial-diferentziaren batez bestekoa (1/2) V da. Egin beharreko lana ondoko hau izango da:
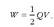
Kondentsadore kargatu baten energia ekuazio hortatik aterako da.
Dena dela, kontuan hartu behar da beste modu desberdinetan ere azal daitekeela:
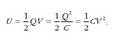
Adierazpen hori edozein kondentsadorentzat erabil daiteke, orokorra da.
3.4. Dielektrikoak
Material dielektrikoen definizio egoki bat hau izan daiteke:
Material dielektrikoak korronte elektrikoa garraiatzeko ahalmena ez duten materialak dira.
Beraz, material dielektriko perfektuak, ez luke edukiko libre korronte elektrikoa garraiatu ahal izango duen karga elektrikorik. Dielektrikoak oso interesgarriak dira kondentsadoreekin erabiltzeko, hainbat arrazoirengatik.
M. Faraday konturatu zen kondentsadorearen bi eroaleen arteko tartean dielektriko bat jartzean kapazitatea handitu egiten dela. Dielektrikoak eroaleen arteko tarte osoa betetzen badu, kodentsadore horren kapazitatea K faktoreaz handitzen da. Faktore hori dielektrikoaren ezaugarria da, eta konstante dielektriko esaten zaio.
Hala ere, adibide batez errazago ulertuko da hori. Demagun C’ kapazitateko kondentsadorea dugula. Kondentsadorea pila batekin lotzean, bi eroaleen artean V’ potentzial-diferentzia sortzen da. Potentzial-diferentzia dela-eta, eroaleek Q’ = C’ V’ karga hartzen dute. Pila kentzen bazaio, eta bi eroaleen arteko ingurua erabat betetzen duen dielektriko bat jartzen bada, potentzial-diferentziak balio berri bat hartzen du, aurrekoa baino txikiagoa:
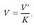
Adierazpen horretan, K dielektrikoaren konstante dilektrikoa da. Hasierako karga eroaleen gainaldean jarraitzen du, prozesuan zehar ez baita aldatu. Beraz, eroalearen kapazitate berria hau izango da:

Dielektrikoa sartzen denean beste aukera bat pila konektaturik edukitzea da. Kasu horretan, hasierako potentzial-diferentziari eusteko, pilak karga gehiago eman beharko du. Horrela eroaleen karga berria honako hau izango da:

Argi ikusten denez, kasu horretan ere kapazitatearen balioa K faktoreaz handitzen da.
Xafla paralelotako kondentsadore batean, potentzial-diferentzia hau da: bi eroaleen arteko eremu elektrikoa bider horien arteko distantzia. Ondorioz, pila deskonektaturik dagoenean, potentzial-diferentzia txikitzen denean eremu elektrikoa ere txikitu egiten da. Hala, dielektrikorik gabeko hasierako eremu elektrikoa E’ baldin bada, eremu elektriko berria hau izango da:

Bestalde, dielektriko batek kondentsadorearen kapazitatea handitzeaz gain, hainbat zeregin betetzen ditu
kondentsadore batean. Zereginetako bat du eroaleak bakartzeko ingurune mekanikoa sortzea. Jakina da,
kondentsadore batean bi eroaleak elkarren oso hurbil egon behar dutela kapazitateak balio handia izan dezan.
Beraz, dielektrikoari esker, eroaleak elkarren oso hurbil egoten dira, baina elkar ukitu gabe.
Bestetik, bi eroaleen arteko potentzial-diferentzia garaia denean, bi eroaleak banatzen dituen ingurunea
eroale bihur daiteke. Hori hala denean, beste baldintzetan higitzen ez den karga, garraiatu egiten da.
Prozesu horri, haustura dielektrikoa esaten zaio. Haustura dielektrikoa gertatu gabe, materialek jasan
dezaketen eremu elektriko handienari zurruntasun dielektrikoa esaten zaio. Esate baterako, baldintza
arruntetan airean haustura dielektrikoa gertatu dadin
 eremu elektrikoa behar da.
Eremu elektriko horretara heltzean, airea ionizatu egiten da, eta ondorioz, korronte elektrikoa garraiatzen du.
Hala, barruan dielektrikoa duen kondentsadore batean haustura dielektrikoa gertatzea zailagoa da; izan ere,
dielektrikoaren zurruntasun dielektrikoa airearena baino garaigoa baita eta potentzial-diferentzia garaiagoak
behar izaten baitira.
eremu elektrikoa behar da.
Eremu elektriko horretara heltzean, airea ionizatu egiten da, eta ondorioz, korronte elektrikoa garraiatzen du.
Hala, barruan dielektrikoa duen kondentsadore batean haustura dielektrikoa gertatzea zailagoa da; izan ere,
dielektrikoaren zurruntasun dielektrikoa airearena baino garaigoa baita eta potentzial-diferentzia garaiagoak
behar izaten baitira.
Dielektrikoen portaera mikroskopiokoa aztertuz gero, askoz ere errazago uler daiteke material horien ezaugarri makroskopikoak. Dielektrikoa osatzen duten molekulak polarrak badira, hau da, momentu dipolarra badute, horien momentu dipolarrak hasieran arbitrarioki orientaturik aurkitzen dira. Ondorioz, molekulen efektu elektrikoak anulatu egiten dira, eta ez dago eremu elektriko garbirik. Momentu dipolarrek, kondentsadore baten bi eroaleen artean sortzen den eremu elektrikoaren eraginpean, indar-bikote bat jasaten dute. Indar-bikote horren eraginez, molekula polarrak eremu elektrikoaren norabidean lerrokatzen dira. Lerrokaduraren magnitudea tenperaturaren eta eremu elektrikoaren indarraren araberakoa da. Molekulen higidura termikoa guztiz zorizkoa da, eta tenperatura garaietan lerrokadura ezeztatzeko joera du. Hala ere, dipoloen lerrokadurak eremu elektriko bat sortzen du dielektrikoaren barruan, kanpoko eremuaren kontrako norabidea duena. Eremu elektriko berri horren eraginez, dielektrikoaren barruan kanpoko eremu elektrikoa ahuldu egiten da.

3.1. Taula. Zenbait material dielektrikoren konstante dielektrikoak, eta zurruntasun dielektrikoak. (*) Material horien osaera kimikoa erraz aldatzen da; horregatik, konstante dielektrikoen balioentzat tarte batzuk azaltzen dira, eta ez balio zehatzak.
Bestalde, dielektrikoa osatzen duten molekulek momentu dipolarra ez badute, kanpoko eremua jartzean momentu induzituak sortuko dira. Beraz, aurreko kasuan bezala, induzitutako momentu horiek, kanpoko eremua ahultzen dute.

3.5. Irudia. E kanpoko eremu elektriko baten eraginpean jartzean, material dielektrikoaren jokabide mikroskopikoa (a), eta makroskopikoa (b). E’ dielektriko barruan gainaldeko kargen ondorioz sortzen den eremu elektrikoa da.
Dielektrikoaren momentu dipolarrak, iraunkorrak edo induzituak,
batez ere kanpoko eremuaren norabidean lerrokaturik badaude,dielektrikoa polarizatuta dagoela esaten da.
Dielektrikoa homogeneoa denean, polarizazioak sortzen duen efektu garbia hau da: xaflen alboan sortzen den
gainaldeko karga bat. Azter dezagun, adibidez, 3.5. irudian ikusten den kasua. Kanpoko E eremu elektrikoa aplikatzean,
momentu dipolarrak nolabait lerrokatzen dira (ikus 3.5. a) irudia). Irudi horretan adierazten diren momentu
dipolarrak, guztiz lerrokaturik daude. Hala ere, hori ez da egoera erreala, lerrokadura ez baita inoiz erabatekoa,
baina prozesua errazago uler dadin jarri dira horrela. Kanpoko eremua jarri aurretik konpentsaturik zeuden kargak,
berrantolatu egin dira. Eta ondorioz, dielektrikoaren bi gainaldeetan kontrako zeinuko bi gainaldeko karga-dentsitate
garbiak azaldu dira,  eta
eta  alegia (ikus 3.5. b) irudia). Bi karga-dentsitate horien artean eremu elektriko
bat dago, E’. Eremu elektriko horrek kanpoko eremuaren kontrako
norabidea du, eta hark baino balio txikiagoa. Beraz, dielektrikoar en
barruan gainezarmenaren printzipioa aplikatuz gero, bi eremu elektrikoen
bektore batuketa egin behar da. Lortzen den eremu elektrikoak
kanpokoaren norabide bera du, baino balio txikiagokoa
da. Horregatik, kanpoko eremu elektrikoa dielektrikoaren barruan
ahultzen dela esaten da.
alegia (ikus 3.5. b) irudia). Bi karga-dentsitate horien artean eremu elektriko
bat dago, E’. Eremu elektriko horrek kanpoko eremuaren kontrako
norabidea du, eta hark baino balio txikiagoa. Beraz, dielektrikoar en
barruan gainezarmenaren printzipioa aplikatuz gero, bi eremu elektrikoen
bektore batuketa egin behar da. Lortzen den eremu elektrikoak
kanpokoaren norabide bera du, baino balio txikiagokoa
da. Horregatik, kanpoko eremu elektrikoa dielektrikoaren barruan
ahultzen dela esaten da.
Eremu elektrikoen eraginpean dauden dielektrikoetan azaltzen den karga mota horri karga lotua esaten zaio. Karga mota hori ez da eroaleen karga mota berekoa; karga lotua ezin da higitu. Baina karga lotuak sortzen duen eremu elektrikoa beste edozein kargak sortzen duenaren antzekoa da. Hala ere, kanpoko eremu elektrikoa desagertzen denean, karga lotuak sorturiko eremu elektrikoa ere desagertu egiten da. Eroaleetan agertzen den kargak, berriz (karga askea deitua), higitzeko gaitasuna du.
Dielektrikoa edo kanpotik aplikatzen den eremu elektrikoa homogeneoa ez bada, karga dentsitatea dielektrikoaren gainaldean agertzeaz gain, eta barruan ere ager daiteke
Kondentsadorea
Kondentsadorearen eginkizuna karga elektriko positiboa eta negatiboa bildu eta bi eroaletan gordetzea da. Kondentsadore elektrikoan bi parte bereizten dira. Alde batetik, bi xafla eroale daude, eta bestetik, material dielektriko bat. Material dielektrikoa bi xafla eroaleen artean kokatzen da. Horrela, bi xaflen artean potentzial diferentzia dagoenean, xafla metaliko bakoitzak bestearen karga kopuru berdina metatzen du, baina kontrako zeinukoa. Kondentsadore baten karga metatzeko ahalmena, magnitude fisiko baten bidez azaltzen da, kapazitate elektrikoaren bitartez, alegia. Eta kapazitate unitateari faraday deitzen zaio. Kondentsadore jakin baten kapazitate elektrikoa, barruan daukan dielektrikoaren araberakoa da. Dielektrikoaren eginkizuna kondentsadorearen kapazitatea handitzea da.
Bikote termoelektrikoa
Gai desberdinetako bi hari eroale seriean soldatzen direnean eratzen den zirkuitua da bikote termoelektrikoa. Bi soldaguneak tenperatura desberdinetan daudenean, zirkuituan indar elektroeragilea sortzen da eta korronte elektriko bat ematen du. Bi metal jakin harturik, korronte elektrikoaren intentsitatea tenperatura-diferentziaren araberakoa izaten da. Hori dela eta, tenperatura neurtzeko erabiltzen dira gehienbat bikote termoelektrikoak. Tenperatura-diferentzia jakin batzuei potentzial-diferentzia jakin batzuk dagozkie, balio hauekin guztiekin taula bat egiten da, eta horri deitzen zaio kalibrazio-taula. Gero, tenperatura neurtu nahi den tokian soldagune bat sartzen da, eta bestea, tenperatura ezaguna duen beste toki batean. Sistema egonkortu eta gero, potentzial-diferentzia neurtzen da, eta kalibrazioaren bitartez, ezagutu ahal izango dugu tenperatura-diferentzia. Bikote termoelektrikoak asko erabiltzen dira leku txikietan tenperatura zehaztasunez neurtzeko, bikoteek oso leku txikia behar bait dute.
4. Gaia: korronte elektrikoa
Elektrizitatea oso gauza arrunta da gaur egun. Oso gogorra egingo litzaiguke egun bat hura gabe. Hor ditugu, adibidez, elektrizitateaz “elikatzen” diren tresnak: irratia, igogailua, ordenagailua… edo beste edozein tresna elektriko. Den-denek dituzte zirkuitu elektrikoak. Argi indarra daraman sarera edo iturriren batera lotzean korronte elektrikoak agertzen dira zirkuitu horietan. Eta hain zuzen, korronte elektriko horiek aztertzea izango da gure helburua gai honetan.
4.1. Korronte elektrikoa
Orain arte ikuspuntu estatiko batetik aztertu dugu elkarrekintza elektrikoa; hura ikuspuntu dinamiko batetik aztertzean oinarrizko kontzeptu bat azaldu beharra dago ezer baino lehen: korronte elektrikoa. Hona korronte elektrikoaren definizio egoki bat:
Gainalde batean zehar karga elektriko baten jarioa dagoenean, gainalde hori korronte elektriko batek zeharkatzen duela esaten da.
Korronte elektriko hitzak kargen higidura edo garraioa adierazi nahi du azken batean; higidura hori eremu elektrikoaren eraginpean sortzen da. Hau da, eroale baten karga askea higitu egiten da kanpotik ezarritako eremu elektriko baten eraginpean. Bestela, eremu elektrikorik gabe, eroalearen karga askearen batez besteko lastertasuna baliogabea da.
Horrela bada, korronte elektrikoa jario bat izanik, norabide jakin bat izango du. Norabide hori karga positiboen norabidearen arabera adierazten da (hala adieraztea onartu baita hitzarmnez); korronte elektrikoaren norabidea karga positiboen higidurarena da, beraz. Nolanahi ere, karga negatiboak —elektroiak— dira higitzen direnak —eroaleen artean behintzat hala da—. Hitzarmen hori aspaldian hartu zen eta bere horretan mantendu da orain arte.
Bestalde, korronte elektriko mota asko daude, eta, hori dela eta, sailkapena egitea komeni izaten da. Oro har, bi korronte mota nagusi bereizten dira: alegia, batetik, korronte jarraia (karga elektrikoa norabide bakar batean doa beti) eta, bestetik, korronte alternoa edo aldizkatzailea (karga elektrikoa norabidez aldatuz joaten da eroalearen mutur batetik bestera, maiztasun jakin baten arabera). 4.1. irudian gisa horretako korronteek denborarekin izaten duten aldaketa adierazten da: 4.1. a) irudia korronte jarrai ez-konstanteari dagokio; korrontearen balioa aldatuz doa denborarekin, aldatzeko irizpide jakinik gabe; 4.1. b) irudia, berriz, korronte jarrai konstanteari dagokio (korrontearen balioa konstantea da, ez da aldatzen denborarekin); eta 4.1. c) irudia korronte jarrai alterno edo aldizkatzaileari dagokio (korrontearen balioa aldian behin aldatzen da, sinu funtzio baten erara). Horra, beraz, dauden korronte mota aipagarrienak. Nolanahi ere, beste mota bateko aldaketak ere izan daitezke.

4.1. Irudia. Arestian aipaturiko hiru korronte moten adierazpen grafikoak. a) Korronte jarrai ez-konstantea. b) Korronte jarrai konstantea. c) Korronte alternoa edo aldizkatzailea.
Gai honetan korronte jarrai konstantea aztertuko da gehienbat, korrontearen atal egonkorra.
Dauden korronte elektriko motak ikusi ondoren, ikus dezagun orain korronte jarraia nola sortzen den. Iturri edo sorgailu mota asko izan ditzake korronte jarraiak; pila eta metagailu elektrikoetan, adibidez, prozesu kimikoen bidez lortzen da potentzial diferentzia, hots, korronte elektrikoa. Dinamoetan, ordea, energia mekanikoa da energia elektriko bihurtzen. Nolanahi ere, korronte jarraia lortzeko bi bide horiez gainera bada beste bat ere, bereziagoa, korronte alternoaren noranzkoa zuzentzea, alegia. Diodo erdieroaleak bezalako balbulei esker noranzko bakarreko korrontea lortzen da, kontrako noranzkoa ezabatuta. Gero, iragazki elektrikoak erabiltzen dira tentsio aldaketa gutxitzeko, eta prozesuaren amaieran lortzen den korrontea erabat leuna eta konstantea da ia.
Korronte elektrikoak, bestalde, gai eroale batean zehar igarotzean, zenbait efektu sortzen ditu. Hiru motatan salka daitezke efektuak:
a) Efektu termikoa: Korronte elektrikoa eroalean zehar igarotzean materiala berotu egiten da.
b) Efektu kimikoa: Isurkari ionizatuak deskonposatu egiten dira korronte elektrikoaren eraginez.
c) Efektu magnetikoa: Eroalearen ondoan ipar orratza jarrita froga daitekeen bezala, korronte elektrikoak eremu magnetikoa sortzen du irauten duen bitartean. Efektu magnetiko horiek fenomeno mekanikoak sortzen dituzte, elkarrekintza magnetikoa aztertzean ikusiko den bezala; besteak beste, motore elektrikoen funtsa dira efektu magnetiko horiek.
Bestelako efektu batzuk ere badira, baina gehien-gehienak goian aipatu diren hiru efektu horien artean sartzen dira. Bonbilaren argia, adibidez, efektu termikoak sortzen duen goritasunaren ondorio besterik ez da; deskarga elektrikoaren zartakoak eragiten dituen efektu fisiologikoak ere efektu termikoen eta kimikoen ondorio dira.
Korronte elektrikoaren zenbatekoa zehazteko, magnitude berezi bat erabiltzen da. Eta hala, eroale batean zehar denbora banako bakoitzeko igarotzen den elektrizitate kopuruari korrontearen intentsitatea esaten zaio. Sinboloa I da, eta hau, berriz, haren matematika adierazpena:
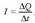
Korrontearen intentsitatea magnitude eskalarra da. Haren banakoari ampere (A) esaten zaio, André Marie Ampère (1775-1836) fisikari frantsesaren ohorez:
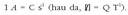
Zenbait zirkuitutan, ordea, ampere banakoa kopuru handiegiea dela eta, miliamperea
 eta are mikroamperea
eta are mikroamperea

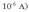 ere erabiltzen dira amperearen ordez. Korrontearen inten176
tsitateak, bestalde, magnitude eskalar bat den arren, noranzkoa du
(karga positiboarenaren araberakoa hau ere), korronte elektrikoak
bezala. Zirkuitu batean, beraz, karga eramale positiboen noranzkoa
izango du intentsitateak.
ere erabiltzen dira amperearen ordez. Korrontearen inten176
tsitateak, bestalde, magnitude eskalar bat den arren, noranzkoa du
(karga positiboarenaren araberakoa hau ere), korronte elektrikoak
bezala. Zirkuitu batean, beraz, karga eramale positiboen noranzkoa
izango du intentsitateak.
4.2. Korronte dentsitatea
Korronte elektrikoa hura sortzen duten partikula edo zatiki kargadunen higiduraren araberakoa da. Hari bateko intentsitatea gainalde finito eta jakin bati dagokio; hau da, intentsitatea gainalde baten ezaugarria da. Gainalde horretan beste magnitude bat ere defini daiteke, gainalde banakoko intentsitatea, korronte dentsitatea, alegia. Korrontearen eta zatiki kargadunen higiduraren araberakoa da korronte dentsitatea.

4.2. Irudia. Hari bateko zatiki kargadunen higidura eremu elektriko baten eraginpean
Eman dezagun hari eroale zilindriko bat dugula; hariaren zeharkako epaia A dela; eta hariko zatiki kargadun mota bakarra q zatikia dela (eta q positiboa dela). Harian korronte elektrikoa izango bada, eremu elektriko bat izan behar da muturren artean. Horrela, eremu elektriko horren eraginez, eremuaren noranzko berean higituko dira kargak, v lastertasunaz. Eman dezagun ere n karga daudela bolumen banakoko. Hala bada, dt denbora tartean zilindroaren vdt tartean dauden kargek bakarrik zeharkatuko dute 1gainaldea. Karga horien balioa nqvAdt izango da. Intentsitatea, beraz, honela adieraz daiteke:
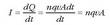
Eta korrontearen epai perpendikularreko gainalde banakoko intentsitatea -hots, korronte dentsitatea- honela adierazten da:
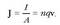
Korronte elektrikoa sortzen duten zatikiek baina, karga eta lastertasun edo dentsitate desberdina dute,
elektrolisiaren kasuan bezala. Halakoetan, zatiki bakoitzeko
 adierazpenak batuz lortzen da
korronte dentsitate osoa:
adierazpenak batuz lortzen da
korronte dentsitate osoa:
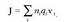
Beraz, A gainalde guztian J konstantea bada, A gainaldea zeharkatzen duen korronte elektrikoaren intentsitatea hau da:

 beraz, A gainaldeari
buruz zut dagoen bektore unitarioa da, eta
beraz, A gainaldeari
buruz zut dagoen bektore unitarioa da, eta  ,
berriz,
,
berriz, 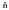 bektorearen paralelo den
korronte dentsitatearen osagaia. Gainaldeko korronte dentsitatea konstantea ez bada, honela kalkula daiteke korronte
elektrikoaren intentsitatea:
bektorearen paralelo den
korronte dentsitatearen osagaia. Gainaldeko korronte dentsitatea konstantea ez bada, honela kalkula daiteke korronte
elektrikoaren intentsitatea:

Hala beraz, gainalde bat zeharkatzen duen korronte dentsitatearen jarioa da intentsitatea.
André Marie Ampère
(Lyon, 1775 - Marseilla, 1836)
Ampère, frantses fisikari eta matematikaria, Lyon inguruan jaio zen. Oso ume bizkorra izan zen, eta txikitatik egon zen matematikara emana. Matematikako irakaslea izan zen Pariseko Eskola Politeknikoan (1809-1828), eta Fisikako irakaslea, Frantziako Unibertsitatean (1826-1836). 1819an H. C. Oersted-ek elektrikaren eta magnetikaren arteko harremanak aurkitu zituen. Lan horiek oinarri harturik, Ampèrek elektromagnetismoa azaltzen duen teoria matematikoa landu zuen, eta elektrodinamismoa deitu zion elektromagnetismoari. Haren ikerketei esker, korronte elektrikoaren intentsitatea neurtu ahal izan zen, imanak erabiliz. Tresna haren gaur egungo bertsioari galbanometroa esaten zaio. Ampèrek eman zion hain zuzen ere izena korronte elektrikoaren intentsitatearen banakoari: anpere (A). Matematikan, bestalde, alor hauetan egin zituen Ampèrek ekarpen garranzitsuenak: bariazioen kalkuluan, probabilitateen kalkuluan, eta deribatu partzialetako ekuazio diferentzialen integrazioan.
4.3. Kargaren jarraitasunaren ekuazioa
Eragin elektrostatikoa aztertzean Naturaren oinarrizko legetzat hartu genuen kargaren kontserbazioaren printzipioa. Azken batean Naturan zatiki kargadunak sortzen direnean beti binaka agertzen dira, eta karga garbia zero da.
Espazioko eskualde batean kargaren balioa handitu edo txikitu egiten bada denboran zehar, eskualde horretan sartu edo eskualde horretatik atera den karga jario batengatik da horrela. Azter dezagun kuantitatiboki gertaera hori.

4.3. Irudia. A gainaldetik ateratzen den korronte dentsitatea.
Eman dezagun A gainalde itxia dugula, eta t denbora bitartean gainalde horren barnean dagoen karga q dela. Horrela, egoera dinamiko batean gainaldean dagoen karga aldatu egingo da denborarekin:
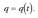
Kanporatzen den intentsitatea da, kargaren kontserbazioaren printzipioaren arabera, denbora banakoko kargaren galera —hots, denbora banakoan gainaldea kanpora zeharkatzen duen karga—. Hori honela adierazten da:
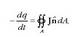
Adierazpen horretan, gainaldean zehar dagoen korronte dentsitatea da J; eta
 , berriz,
puntu bakoitzean gainaldeari buruz zut dagoen bektore bateratua da. Bestalde, honela adierazten da
barneko karga puntu bakoitzeko kargaren dentsitatearen funtzioan:
, berriz,
puntu bakoitzean gainaldeari buruz zut dagoen bektore bateratua da. Bestalde, honela adierazten da
barneko karga puntu bakoitzeko kargaren dentsitatearen funtzioan:
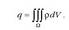
Eta hala, aurreko bi adierazpenak kontuan harturik, honela adierazten da kargaren kontserbazioaren printzipioa:
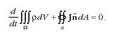
Ekuazio horri jarraitasunaren ekuazioa esaten zaio.
Oharra: egoera dinamikoan barneko karga dentsitatea eta gainaldetik ateratzen den korronte dentsitatea denboraren funtzioak izan behar dute. Hau da:

Dena den, hemendik aurrera, gai honetan korronte egonkorrak —hots, denborarekiko aldatzen ez direnak— aztertuko ditugu soilik. Eta orduan:

izango ditugu.
4.4. Ohmen legea eroaleen kasuan
Korronte elektrikoaren ikuspuntutik begiratuta bi multzotan sailka daitezke materialak: dielektrikoak eta eroaleak.
a) Dielektrikoak: Material hauek ez dute karga askerik. Hau da, elektroiak —zeinek karga aske gisa jokatzen baitute normalean— estuki loturik daude atomoen nukleoekin edo atomoen arteko loturekin. Hori dela eta, material dielektrikoetan ez da korronte iraunkorrik sortzen kanpoko eremu elektriko baten eraginpean, nahiz eta horren pean polarizatzen diren. (Dielektrikoak 3. gaian aztertu dira).
b) Eroaleak: Material hauen kasuan, berriz, karga askeak badira. Eta karga askea eremu elektrikoaren eraginpean badago, korronte elektrikoa sortzen da. Metalak, adibidez, eroaleak dira.
Material eroaleek dituzte, beraz, korronte elektrikoa aztertzeko ezaugarri egokienak.
Eman dezagun metal baten barne egitura aztertzen ari garela. Material metalikoak sare kristalino bat du. Karga positiboak edo nukleoak finko daude hartan, eta haien inguruan elektroi lotuez gainera elektroi askeen hodeia dago. Elektroi askeak alde batetik bestera higitzen dira, karga positiboekin talka eginez. Nahiz eta higidura desordenatu hori lastertasun handian gertatu, batez besteko lastertasuna (bektoriala) baliogabea da, eta, denetara, korronte makroskopiko garbia baliogabea da.
Eroalea eremu elektrikoaren eraginpean jartzean, nolanahiko higidura horri beste higidura ordenatu bat gehitzen zaio, eta horrenlastertasuna elektroiena baino askoz txikiagoa den arren, garrantzi handiagoa du, kargen jario garbia —alegia, korronte elektrikoa— sortzen baitu.
4.4.1. Eroamen eta erresistibitate elektrikoa
Beraz, dirudienez, erlazioren bat badago eremu elektrikoaren intentsitatearen eta korronte elektrikoaren artean, eta erlazio hori metalaren barne egituraren ondorio da.
Hain zuzen ere, erlazio horri Ohmen legea esaten zaio, eta eremu elektrikoaren intentsitatearen eta korrontearen dentsitatearen arteko proportzioa adierazten du:
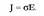
Adierazpen horretako s proportzio faktoreari eroalearen eroamen elektrikoa esaten zaio eta material mota bakoitzaren ezaugarria da. Dimentsionalki honela adierazten da:

Izatez, legea baino gehiago eroaleen propietate bat zehazteko ekuazioa da hori.
Baldintza horietan definituz, gero esperimentu bidez ikusten denez, beste dependentzia batzuez gain,
eroamena tenperaturaren arabera aldatzen da 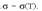
Kargak hainbat material motatan garraia daitezkeenez, oso kontuan hartzekoak izango dira material bakoitzaren tasunak. Eroamena tenperaturaren arabera nola aldatzen den, hiru material mota bereiz daitezke:
a) Eroale metalikoak: Eroamena txikiagoa da tenperatura handitzean.
b) Supereroaleak: Giro tenperaturan metal arruntena bezalakoa da eroamena, baina gaiaren tenperatura kritikoa
(Tc) baino apalagoetan izugarri handitzen da,
 , eta err
esistentzia elektrikoa zero da; aluminioaren kasuan, adibidez, tenperatura kritikoa
, eta err
esistentzia elektrikoa zero da; aluminioaren kasuan, adibidez, tenperatura kritikoa

c) Erdieroaleak: Material hauen eroamena txikiagoa da tenperatura beheratzean, eta oso tenperatura apaletan gai isolatzaileen antzeko portaera dute.
4.4 irudian ikus daiteke argi eta garbi hiru material mota horien portaera.
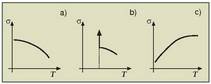
4.4. Irudia. Materialen eroamenaren adierazpen grafikoa. a) Eroale arrunta. b) Supereroalea. c) Erdieroalea.
Materialen eroamen elektrikoaren bidez garrantzi handiko beste magnitude bat definitu ahal da: erresistibitate elektrikoa alegia. Hain zuzen ere, eroamenaren alderantzizko magnitudea da erresistibitatea:
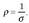
Beraz, eroamenaren banakoak ezagututa, hauek izango dira erresistibitatearenak:

Eroamena eta erresistibitatea lotzen dituen adierazpen matematikotik oso ondorio interesgarriak atera daitezke. Eroale arrunten kasuan, adibidez, tenperatura handitzean eroamena txikitu egiten da, eta erresistibitatea, aldiz, handitu.

4.2. Taula. Materialen erresistibitate elektrikoa T = 20º C denean; hau da, giro tenperaturan.
Eroamen elektrikoa eskalartzat hartu dugula esan beharra dago azkenik. Hurbiltze hori eroale isotropoen kasuan baizik ez da egokia. Eroale anisotropoetan baliabide matematiko ahaltsuagoekin deskribatzen da eroamena
Georg Simon Ohm
(Erlangen, 1787 - Munich, 1854)
Fisikari alemana. Erlangen-go unibertsitatean egin zituen ikasketak. 1825ean hasi zen bere izena duen legea aurkitzeko ahaleginetan. 1827ean deskribatu zuen Ohmen legea. Hura izan zen elektrizitate kopurua eta indar elektroeragilea kontzeptuak erabili zituen lehena. 1829an fisikako irakasle izendatu zuten Municheko Unibertsitatean. 1861ean nazioarteko sistemak bere izena eman zion erresistentzia elektrikoaren banakoari: ohm (O). Akustikaren arloan ere lan egin zuen.
4.4.2. Hari eroale baten erresistentzia elektrikoa
Zirkuituetan erabiltzen diren eroaleek hari itxura dute. Eroale meheen kasuan Ohmen legearen adierazpen bakun batera irits gaitezke kalkulu erraz batzuk eginez.

4.5. Irudia. Hari eroale zilindriko baten epaiak I korronte elektrikoak zeharkaturik.
Eman dezagun epai perpendikularra A duen hari eroale zilindriko bat dugula (4.5. irudia), eta harian zehar I intentsitatea igarotzen dela. Hari horren zati batean (L), 1 gainaldetik 2 gainaldera zuzendurik baldin badago eremu elektrikoa (E), potentziala txikiagoa da

Haritik igarotzen den korronte elektrikoaren intentsitatea korronte dentsitatea bider epai perpendikularraren azalera da. Hala bada, ezagutzen ditugun erlazioen arabera:
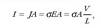
Eta 1 eta 2 puntuen arteko potentzial diferentziak balio hau hartuko du:
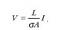
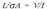 kopuruak 1 eta 2
puntuen arteko erresistentzia elektrikoa ematen digu, eta R ikurraren bidez adierazten da:
kopuruak 1 eta 2
puntuen arteko erresistentzia elektrikoa ematen digu, eta R ikurraren bidez adierazten da:
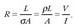
Hortaz, definitu berri den erresistentzia elektrikoa erabiliz honetara laburtzen da potentzial direfentziaren, intentsitatearen eta erresistentziaren arteko erlazioa:

Hau da Ohmen legearen itxurarik arruntena. Azken adierazpen horretan ageri denez, korronte elektrikoaren sortzailea eremu elektrostatikoa baizik ez denean, hari eroalearen muturren arteko potentzial diferentzia erresistentziaren eta intentsitatearen arteko biderkadura da.
Ohmen legea beste era honetara ere adieraz daiteke:
Potentzial diferentziari eta korrontearen intentsitateari buruz guztiz independentea da erresistentzia.
Hemen ohar bat eman behar dugu. Material eroale guztiek ez dute Ohmen legea betetzen. Legea betetzen dutenak eroale ohmikoak direla esaten da, eta betetzen ez dutenak, berriz, eroale ez-ohmikoak.

4.6. Irudia. Material eroale ohmiko eta ez-ohmikoen portaera
Erresistentzia elektrikoa neurtzeko banakoari ohm
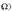 esaten zaio.
G.S. Ohm (1787-1854) fisikari alemaniarraren ohorez esaten zaiohala, hark aurkitu baitzuen elektrizitate korronteei
buruzko oinarrizko legea:
esaten zaio.
G.S. Ohm (1787-1854) fisikari alemaniarraren ohorez esaten zaiohala, hark aurkitu baitzuen elektrizitate korronteei
buruzko oinarrizko legea:
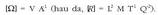
Aurreko adierazpenean ikusten denez, ohma banako eratorria da; erresistentzia handiak adierazteko kiloohm
 eta megaohm
eta megaohm
 banakoak erabiltzen dira.
Zirkuitu elektrikoak eraikitzeko balio finkoko erresistentziak fabrikatzen dira, eta 4.7. irudian ikusten den
ikurra erabiltzen da, berriz, haiek adierazteko.
banakoak erabiltzen dira.
Zirkuitu elektrikoak eraikitzeko balio finkoko erresistentziak fabrikatzen dira, eta 4.7. irudian ikusten den
ikurra erabiltzen da, berriz, haiek adierazteko.
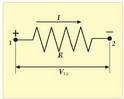
4.7. Irudia. Zirkuitu elektrikoetan erresistentzia adierazteko erabiltzen den ikurra
4.5. Jouleren legea
Material eroale batean korronte elektrikoa igarotzen denean energia elektrikoaren zati bat energia termiko bihurtzen da. Hori erraz ulertzeko metal baten kasua aztertuko dugu.
Arestian ikusi den bezala metal bateko karga askea —hau da, elektroiak— materialean zehar higitzen da. Korronte elektrikoa mantentzeko erabiltzen den eremu elektrikoak sare metalikoan zehar mugiarazten ditu elektroiak. Elektroiek, beraz, talka egiten dute higitzean, bai gaiaren ioi positiboekin bai beraien artean ere. Talka horien ondorioz, eroalean korronte elektriko iraunkorra mantentzean, eremu elektrikoak elektroiei emandako energia zinetikoa talketan galtzen da. Beraz, nahiz eta elektroiek etengabe energia lortzen duten eremu elektrikotik, energia hori berehala galtzen da energia termiko gisa. Galera hori kanpotik ikusita bero modura ageri da. Orain aztertuko da nola galtzen den energia erresistentzia elektrikoetan.

4.8. Irudia. Elektroi batek metalaren ioi positiboekin egiten dituen talken adierazpen grafikoa.
Eman dezagun erresistentzia baten bi muturren artean
 potentzial diferentzia aplikatzen dugula.
Dakigunez, Ohmen legea hau izango da erresistentzian:
potentzial diferentzia aplikatzen dugula.
Dakigunez, Ohmen legea hau izango da erresistentzian:

Hau, zehazki, karga banakoko erresistentzian egiten den lana da. Argi dagoenez, hau da t denbora tartean korronte jarrai konstantez garraiatzen den karga:

Orduan, denbora tarte horretan erresistentzian galtzen den energia karga guztia bider egiten duen lana izango da, hau da:

Emaitza horri Jouleren legea esaten zaio, eta korronte elektrikoak eroaleari emandako energia termikoa adierazten du. Kaloriatan ere ematen da:
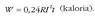
Bestalde, denbora banakoko energia galera, hots, erresistentzian galtzen den potentzia, honela adierazten da:
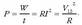
James Prescott Joule
(Salford, 1818 - Sale, 1889)
Britainiar fisikaria. Hasierako ikerketak magnetismoaren alorrean egin zituen, burdinaren imantazioa ardatz harturik. Eroale batetik korronte elektrikoa igarotzen denean sortzen den beroa korrontearen intentsitatearen berreduraren eta eroalearen erresistentziaren proportzionala zela aurkitu zuen 1840an. Lege horri Jouleren legea esaten zaio. Kaloriaren baliokide mekanikoa kalkulatu zuen (1842). 1843an termodinamikaren lehenengo printzipioa eman zuen. Horri esker energia mekanikoaren kontserbazio printzipioa adierazi zuen, eta gas molekulen batez besteko lastertasuna kalkulatu zuen, gasen teoria zinetikoa erabiliz. Nazioarteko sisteman lan, energia eta bero kopuruaren banakoak haren izena du: joule (J).
4.6. Sorgailu elektrikoa
Erresistentzia soila ez den elementu batek —sorgailu elektrikoak— zirkuitu elektrikoetan duen portaera aztertuko dugu atal honetan.
Aurreko atalean ikusi dugunez, Joule efektuagatik korronte elektriko egonkor bat mantendu ahal izateko beharrezkoa zen energia elektrikoko sorgailu bat, alegia, sorgailu elektriko bat.
Energia kimikoa —pilen kasuan adibidez—, mekanikoa —dinamoen kasuan— edo bestelako energia motaren bat energia elektriko bihurtzen duen tresna da sorgailu elektrikoa.
Sorgailuak sortzen duen korronte elektrikoaren potentzia P izanik, eta zirkuituan zehar bidaltzen duen korrontearen intentsitatea I, honela definitzen da sorgailuaren indar elektroeragilea:

Banakoei dagokienez, P wattetan eta I amperetan adierazten direnez, indar elektroeragilea voltetan neurtzen da, potentzial diferentziaren modura.
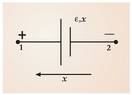
4.9. Irudia. Zirkuitu elektrikoetan korronte jarraiko sorgailua adierazteko erabiltzen den ikurra
4.9. irudian ikusten da nola adierazten den korronte jarraiaren sorgailua zirkuitu elektriko batean. Irudian jarri den r hori sorgailuaren barneko erresistentzia elektrikoa da.

4.10. Irudia. Sorgailua eta erresistentzia dituen zirkuitu bat
4.10. irudian sorgailua eta erresistentzia dituen zirkuitu bat ikus daiteke. Interesgarria izan daiteke hura aztertzea, hango energia balantzea batez ere. Zirkuituari ematen zaion potentzia bakarra sorgailuarena da. Zirkuituan potentzia hori erabiliko duten elementu bakarrak erresistentziak dira, r eta R erresistentziak alegia. Hori guztia kontuan harturik, ekuazio hau ematen du potentziaren kontserbazioak:
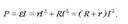
Horrela, zirkuituan dagoen intentsitatearen balioa atera daiteke aurreko ekuaziotik:
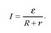
Bestalde, aurreko adierazpenean aldaketa batzuk eginez hau lortzen da:
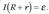 Hortik sorgailuaren muturren arteko potentzial diferentzia lor daiteke:
Hortik sorgailuaren muturren arteko potentzial diferentzia lor daiteke:

Azken adierazpena aztertzen badugu, kasu berezi bat agertzen zaigu. Zirkuitua irekirik dagoenean —hau da, intentsitatea baliogabea denean—, orduan:

Eta hala, zirkuitua ixtean, barne erresistentziaren ondorioz sorgailuaren muturren artean potentzial diferentziak rI balioko beherapena duela esaten da.
Indar elektroeragileari buruzko zenbait ohar egitea komeni da orain. Hasteko, «indar» izenak ez du kasu honetan fisikan ohi duen esanahia, beste bat baizik. Hain zuzen, sorgailuak karga banako bakoitzeko egiten duen lana baita indar elektroeragilea:
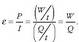
Bestetik, indar elektroeragilea eta potentzial diferentzia banako berberetan adierazten diren arren ez dira gauza bera. Indar elektroeragileak potentzial diferentzia sortzen du sorgailuaren muturren artean, eta horretarako beste energia mota bat erabiltzen da, energia kimikoa (metagailuetan) edo energia mekanikoa (dinamoetan) adibidez
Dinamoa
Dinamo hitza makina dinamoelektrikoaren laburpena da. Tresna hau, energia mekanikoa erabiliz, korronte elektrikoa sortzeko erabiltzen den jeneradorea da. Lehenengo dinamoa, 1831. urtean egin zuen M. Faradayk. Hortik aurrera, dinamoak aldaketa asko izan ditu bere egituran, eta mota desberdinak agertu dira. Dinamo guztiek bi osagai nagusi dituzte: eremu magnetikoa, jario magnetikoa sortzen duena, eta eroale sistema bat (induzitua), eremu magnetikoaren barnean higitzen dena. Eroale sistema, birakorra da, eta higitzean jario magnetikoa aldatzen da bere barnean. Jario magnetikoaren aldaketarekin batera indar elektro-eragile bat sortzen da (Faradayren legea), eta korronte elektrikoa eratzen.
4.7. Hargailu elektrikoa
Energia elektrikoa bero ez beste energia bihurtzen duen tresnari hargailu elektrikoa esaten zaio. Motore elektrikoetan, adibidez, energia mekanikoa sortzen da korronte elektrikoaren eraginez.

4.11. Irudia. Hargailu elektrikoaren ikurra zirkuitu elektrikoetan
Eman dezagun 1 eta 2 puntuen artean potentzial diferentzia konstante bat, V12, dagoela eta bi puntu horietara barne erresistentzia rm duen hargailu elektrikoa lotzen dugula, 1 puntutik 2 puntura I intentsitatea igaroaraziz. Egin dezagun energiaren balantzea.
1 eta 2 puntuen artean sorgailu elektrikoak ematen duen potentzia hau da:
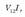
Hargailua, bestalde, energiari dagokionez, elementu pasiboa da; hau da, energia hartzen du. Eta hartzen duen energia hori bi eratara gastatzen du. Batetik, barne erresistentzian galera hau dago denbora banako bakoitzeko:

Bestetik, P potentzia beste energia mota bilakatzen du. Horrela, energiaren kontserbazioa gertatzeko, ekuazio hau bete behar da:

Potentzia, beraz, honela adierazten da:

Motore elektrikoetan, adibidez, energia mekaniko bihurtzen da P.
Honela definitzen den magnitudeari
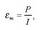
hargailuaren indar kontraelektroeragilea esaten zaio. Magnitude hori hargailuaren ezaugarria da, barne erresistentziarekin batera. Indar elektroeragilea bezala, voltetan neurtzen da. Bestalde, aurreko atalean indar elektroeragileaz egindako oharrak baliagarriak dira indar kontraelektroeragilearentzat ere. Indar kontraelektroeragilea ez da indar bat, hargailuan energia termikoaz gain karga banakoko kontsumitzen den energia baizik. Indar kontraelektroeragilea voltetan neurtzen da, baina ez da potentzial diferentziarekin nahastu behar.
Indar kontraelektroeragilea erabiliz, honela geratzen zaigu hargailuaren muturren arteko potentzial diferentziaren adierazpena:

Hargailuek, azkenik, sorgailu gisa jokatzen dute beren mutur edo borneak alderantziz konektaturik dituztenean
4.8. Ohmen legearen orokortzea
Zirkuitu berean sorgailua, hargailua eta erresistentzia batera agertzen direnean, energiaren balantzea aurreko kasuan bezala egin daiteke.

4.12. Irudia. Sorgailua, hargailua eta erresistentzia duen zirkuitua
Azken finean, sorgailuaren potentzia zirkuituan I intentsitateko korrontea mantentzeko erabiltzen da. Orduan, ondoko ekuazio honek azaltzen digu zertan erabiltzen den sorgailuaren potentzia:

Sorgailuaren barne erresistentzian gastatzen den potentzia
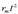 da
da
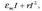 berriz,
hargailuak harturiko potentzia; eta, azkenik,
berriz,
hargailuak harturiko potentzia; eta, azkenik,
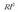 erresistentziari dagokiona.
Aurreko ekuazioa errazago adieraz daiteke
honela:
erresistentziari dagokiona.
Aurreko ekuazioa errazago adieraz daiteke
honela:
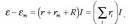
Eta orokortzean, korronte jarraiko zirkuitu berean sorgailu, hargailu eta erresistentzia desberdinak ditugunean, honela geratzen da aurreko ekuazioa:

Hau da, hain zuzen, Ohmen legearen orokortzea zirkuitu bakarraren kasuan
4.9. Banden teoria
Korronte elektrikoa ulertzeko hemen ikusi dugun teoria eroamen elektrikoaren eredu klasikoa da. Eredu klasikoa baliagarria da efektu batzuk —Ohmen legea eroaletan, adibidez— azaltzeko. Hala ere, eredua ez da korronte elektrikoan azaltzen diren efektu guztiak interpretatzeko nahikoa: zergatik dira material batzuk bakartzaileak eta beste batzuk, berriz, eroaleak?
Galdera hori eta beste batzuk erantzun ahal izateko, Quantumen teoriaz baliatu behar gara. Eta Quantumen teoriatik bi ideia nagusi erabili beharko ditugu. Bata, energiaren kuantizazioa da, eta bestea, Pauliren baztertze printzipioa.
Energiaren kuantizazioaren ideia beste honetan oinarritzen da:
Atomo batean dagoen elektroi baten energiak ezin du edozein balio hartu, kuantizaturik baitago.
N. Bohr izan zen ideia horren aitzindaria; 1913. urtean hidrogeno atomoa azaltzeko eredu bat proposatu zuen. Eredu horretan, beste gauza batzuen artean, hidrogeno atomo batean elektroiek har zitzaketen energia balioak eman zituen.
Bestalde, Quantumen teoriaren bigarren ondorioak, Pauliren baztertze printzipioak alegia, honako hau dio:
Egoera kuantiko zehatz batean kontrako spina duten bi elektroi baino ezin dira egon.
Quantumei buruzko bi ideia horiek kontuan hartuz gero gauza asko aldatzen dira korronte elektrikoaren ereduan. Eman dezagun bi atomo berdin elkarrengandik oso aldenduta daudela. Atomo bakoitzak bere baimenduriko energia mailak ditu, berdinak bietan. Atomo bakoitzean energia bereko energia maila bana dago. Atomoak hurbiltzen baditugu, energia maila horien energia aldatu egingo da atomoen arteko eraginagatik. Bi atomoak elkarrengandik oso hurbil baldin badaude, energia mailak ezin dira bereizi. Ezin dezakegu esan maila bat atomo batena dela eta bestea bestarena. Kasu horretan bi atomoek sistema konplexu bat osatzen dute, eta sistema horrela tratatu behar da. Aurretik genituen bi energia maila berdintsuak deskonposatu egin dira eta energia desberdintasun oso txikia duten beste bi energia maila bilakatzen dira.

4.13. Irudia. Bi atomoren energia mailak: a) bakarturik; b) elkarrengandik oso hurbil.
Orain, bi atomo izan beharrean N atomo baldin baditugu, atomo bakartuaren energia maila bat,
N energia maila ia-ia energia antzekodunak, baina desberdinetan banatu egiten da. Metal baten kasuan,
metalaren zati txikitxo batean dagoen atomo kopurua oso handia da, Avogadroren zenbakiaren ingurukoa,
 .
Hori kontuan hartzen badugu, metalaren atomo bakartu baten energia maila bat energia maila
askoko banda batean banatzen da. Banda horretan energia mailen energia balioak elkarrengandik oso
hurbil daude. Hainbeste energia maila daudenez, energia espektruan iaia jarraian kokaturik daude.
Gainera, atomo bakartu energia mailabakoitzeko energia maila banda banandu bat dago. Banda guzti
horiek hurbil, urrun edo solapatuta egon daitezke, atomoaren eta
kristalaren loturaren arabera.
.
Hori kontuan hartzen badugu, metalaren atomo bakartu baten energia maila bat energia maila
askoko banda batean banatzen da. Banda horretan energia mailen energia balioak elkarrengandik oso
hurbil daude. Hainbeste energia maila daudenez, energia espektruan iaia jarraian kokaturik daude.
Gainera, atomo bakartu energia mailabakoitzeko energia maila banda banandu bat dago. Banda guzti
horiek hurbil, urrun edo solapatuta egon daitezke, atomoaren eta
kristalaren loturaren arabera.

4.14. Irudia. Hainbat materialen banda egitura. Alde ilunak elektroiek harturikoak dira. a) eta b) material eroaleak dira; c) bakartzailea; d) erdieroalea
4.14. irudian material batzuen banda egiturak ageri dira. a) eta b) kasuetan material eroaleak ditugu. a) kasuan materialaren elektroiek bandak betetzen dituzte banan-banan. Hau da, atomoen barneko elektroiek beheko bandak betetzen dituzte. Energia handiagoko elektroiek, Pauliren baztertze printzipioa dela eta, ezin dituzte beheko bandak bete, eta libre dauden energia mailak betetzen dituzte. Eroaleari eremu elektriko bat ezartzean, elektroiak dituen azken bandako elektroiak azeleratu egiten dira eta energia irabazten dute. Horrela, banda berberean beteriko mailen gainean egoera energetiko libre asko dagoenez, azken bandako elektroiek energia irabaz dezakete, korronte elektrikoa eramanez. Beterik dauden beste bandek, energia maila guztiak okupaturik dituztenez, ezin izango dute korronte elektrikoa garraiatu, ez baitago aukerarik libre dauden energia mailetara igarotzeko. Hori guztia dela eta, beterik dagoen azken bandari eroamen banda esaten zaio, eta banda horren elektroiei eroamen elektroi. b) metalaren kasuan, berriz, aurreko metalarekin gertatzen den gauza bera gertatzen zaio. Metal horrek, hala ere, bi banda solapaturik ditu. Elektroiei banda batetik bestera igarotzeko aukera ematen die horrek. Orduan, metal horren kasuan eroamen elektroiek energia maila libre gehiago izango dituzte.
Bestalde, c) kasuan, bakartzaile bat dugu. Ikusten denez, elektr oiak dituen azken banda beterik dago, eta hurrengo banda hutsik. Bi bandak banandurik daude, eta elkarren artean energia tarte bat dago. Energia mailarik gabeko energia tarte horri gap esaten zaio, eta bakartzaileetan oso balio handia du. Beraz, eremu elektrikoa jartzean, beterik dagoen azken bandaren elektroiek ezin dute energia irabazi; hau da, ezin dute azeleratu. Izan ere, haien energia mailen gainean, hurbiltasunean, ez baitago energia maila librerik hara igarotzeko. Hurbilen dauden energia maila libreetara igarotzeko energia asko behar da, gapa gainditu behar baita, eta hori ezinezkoa da eremu elektriko soil batekin. Beraz, nahiz eta eremu elektrikoa jarri, korronte elektrikoa ez da sortzen.
Azkenik, d) kasuan erdieroale bat dugu. Erdieroaleek, bakartzaileek bezala, betea dute elektroiak dituen azken banda. Azken banda horren eta hurrengoaren artean gap bat dago. Bakartzaileetatik desberdintzen dituena gaparen balioa da. Erdieroaleetan gapa oso txikia da, eta kitzikapen termikoekin elektroiak banda batetik bestera igaro daitezke. Horrela, eremu elektrikoa jartzean, libre dagoen bandara igaro diren elektroiek korronte elektrikoa garraiatu ahal izango dute. Hau jakinda, uler daiteke orain zergatik erdieroaleek tenperatura igo ahala eroamen elektriko handiagoa duten. Tenperatura igotzean, gero eta elektroi gehiago igaroko baitira beste bandara eta korronte elektrikoa garraitzeko ahalmena handiagoa izango da.
Diodoa
Bi elektrodo (anodoa eta katodoa) dituen tresna elektronikoa da diodoa. Bere ezaugarri nagusia ondoko hau da, korronte elektrikoa noranzko bakar batean baino ez duela uzten pasatzen. Eskuarki diodoa, korronte alternoa korronte jarraitu bihurtzeko erabiltzen da. Garai batean, barrena hustutako bonbiletan elektrodoak jarriz egiten baziren ere, gaur egun, erdieroalez egiten dira. Bonbilak bi elektrodo dituelako hartzen du diodo izena.

Triodoa
Triodoa, hiru elektrodo dituen hodi edo balbula elektronikoa da. Elektrodo bat (katodoa) elektroien iturburua da. Beste elektrodoaren (anodoa) zeregina elektroiak hartzea da. Azken elektrodoa, aurreko bi elektrodoen artean kokatuta egoten da, eta sare baten modukoa da. Elektrodo honen potentziala aldatuz, elektroi jarioa kontrola daiteke. Triodoak eskuarki anplifikadore eta etengailuetan erabiltzen dira.
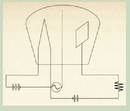
5. Gaia: korronte jarraiko zirkuituak
Gai honetan, korronte jarraiko zirkuituak aztertuko ditugu. Zirkuitu hauetan korronte elektrikoa jarraia izango da; hau da, korrontearen zentzua eta norabidea ez dira denboran zehar aldatuko zirkuituaren puntu guztietan.
Zirkuitu osoari sare elektrikoa esaten zaio. Zirkuituko elementuak bi eratan lot daitezke elkarrekin:
a) Bide berean eta elkarren ondoan bata bestearen atzetik jarririk lotzen direnean seriean daudela esaten da (serie elkarketa); halakoetan, zirkuituaren bi elementuetatik intentsitate berbera iragaten da.
b) Bi punturen arteko bi bide desberdinetan daudenean, berriz, paraleloan daudela esaten da (paralelo elkarketa); kasu honetan potentzial diferentzia berbera dago bi elementuen muturren artean, baina intentsitatea desberdina izango da, bi elementuak berdinak direnean izan ezik.
5.1. Erresistentzia baliokidea
Zirkuituaren elkarketetan erabiltzen diren elementuak erresistentziak badira, multzo osoaren erresistentzia baliokidea lor dezakegu. Erresistentzia multzoaren ordez jarriz, sare elektrikoaren beste elementuak korronte berberaz eta baldintza berberetan iraunarazten dituena da erresistentzia baliokidea.
Serie eta paralelo elkarketako erresistentzia baliokideak kalkulatuko ditugu orain.
a) Serie elkarketa

5.1. Irudia. Erresistentzia multzo bat seriean elkarturik.
Kasu orokorrenean N erresistentzia ditugu seriean elkarturik. Eta guztiak zeharkatzen dituen intentsitatea, I, berbera da guztietan. Erresistenzia bakoitzarekin Ohmen legea erabiliz ekuazio multzo hau agertuko zaigu:

N erresistentziari dagokion potentzial diferentzia da
 Potentzial diferentzia guztiak baturik, a eta b puntuen arteko potentzial diferentzia
Potentzial diferentzia guztiak baturik, a eta b puntuen arteko potentzial diferentzia
 da:
da:
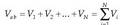
Aurreko ekuazio multzoko erresistentzia guztiak askatuko ditugu, gero, haien batura egiteko. Hala beraz, honako hau da batuketaren adierazpen matematikoa:

Eta batuketa eginez adierazpen honetara heltzen gara:

Hau da, beraz, R erresistentzia baliokidearen adierazpena:

Hots, serie elkarketan, erresistentzien batura da erresistentzia baliokidearen balioa
b) Paralelo elkartea
Elkarketa mota honetan, a eta b puntuen arteko potentzial diferentzia berdina da bide guztietan, Vab da hain zuzen.
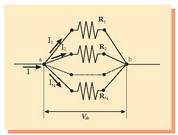
5.2. Irudia. Erresistentzia batzuk paraleloan elkarturik
Bestetik, a puntura heltzen den intentsitatea, I, erresistentzia guztietatik banatzen da. Eta erresistentzia bakoitzari Ohmen legea aplikatuz gero:
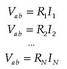
Eta zirkuituan intentsitatearen jarraitasuna bermatu behar denez, honako hau lortzen da:
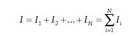
Aurreko ekuazio multzo horretan intentsitateak askatuz eta azken adierazpenean ordezkatuz emaitza hau lortzen da:
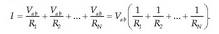
eta orduan 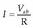 baita definizioz,
sistemaren erresistentzia baliokidea kalkulatzen da, horrela:
baita definizioz,
sistemaren erresistentzia baliokidea kalkulatzen da, horrela:
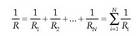
Beraz, paralelo elkarketa batean erresistentzia baliokidearen alderantzizkoa erresistentzien alderantzizkoen arteko batura da.
Adibide gisa erresistentzia baliokidea kalkulatuko dugu N = 2 denean —hau da, bi erresistentzia paraleloan elkarturik ditugunean—:

Material superreroaleak
Superreroamena 1911. urtean aurkitu zen. Urte hartan, H. Kammerlingh Onnes, fisikari holandarra, merkurioak oso tenperatura txikietan zuen portaera ikertzen ari zen. Hala, 4,2 Kelvinetan merkurioaren erresistentzia bat-batean desagertzen zela konturatu zen. Hortik aurrera ikerketak egin dira behin eta berriz eta gauza asko argitu dira. Adibidez, bi motatako superreroaleak daude, kanpotik aplikaturiko eremu magnetikoen aurrean erakusten duten portaeraren arabera. Ikerketak egin ondoren aurkitu dira tenperatura kritikoa handiagoa duten superreoaleak ere. Tenperatura txikiko superreroaleen teoria garatuta dagoen arren, tenperatura handiagokoen azalpen teorikoa oraindik argitu gabe dago. Gaur egun, ikerketa eremu irekia da, beraz. Inguruneko tenperaturako superreroale baten bila dabiltza zientzilariak. Horrelako material batek aldaketa sakonak sortuko lituzke gizartean. Argi dagoenez, horrelako material bat erabilita galera energetikoa zero izango litzateke Joule efektuaren eraginez, eta horrek energia aurrezpen handia ekarriko luke. Bestalde, berorik ez sortzeak zirkuituak elkarrengandik hurbilago kokatzeko bidea emango luke. Superreroamenaren beste tasun batzuek (Meissner efektua,...) ere beste eremu asko zabalduko lituzkete.
Osziloskopioa
Bi atal nagusi bereizten dira tresna honetan. Bata telebista moduko pantaila bat da, eta bestea, seinaleak prozesatzeko zirkuitua. Pantaila horretan, denboran zehar aldatzen diren magnitude fisikoen aldaketak aztertu, erregistratu eta irudika daitezke. Horretarako, magnitude fisikoarekin zerikusia duen sarrerako seinale elektroniko bat behar da. Behin seinale hori jasotzen duenean, osziloskopioak pantailan adieraziko du, behar diren aldaketa elektroniko guztiak egin eta gero. Osziloskopioak eskeintzen dituen eskala desberdinak erabiliz, zehaztasun handiko neurketak egin daitezke. Fisikako laborategietan erabiltzeaz gain, sarritan zirkuitu elektronikoetako seinaleak aztertzeko, eta horren bidez, akatsak somatu eta konpontzeko erabiltzen da.
5.2. Kapazitate baliokidea
Aurreko zirkuituetan erresistentziak erabili dira elkarketetan. Orain, berriz, kondentsadoreak dituzten elkarketak aztertuko ditugu. Erresistentziekin egin dugun bezala, multzo osoaren kapazitate baliokidea lortuko dugu. Kondentsadoreen multzoaren ordez jarriz, sare elektrikoaren beste elementuak korronte berberaz eta baldintza berberetan iraunarazten dituena da kapazitate baliokidea.
Serie eta paralelo elkarketen kapazitate baliokideak kalkulatuko ditugu orain hurrena.
a) Serie elkarketa
5.3. irudian N kondentsadore daude seriean elkarturik. Eman dezagun a eta b puntuen artean Vab potentzial diferentzia dagoela. Orduan, ekuazio hauek betetzen dira kondentsadoreetan:
Ekuazioetan kontuan hartu da kondentsadore guztiek karga berbera pilatzen dutela.
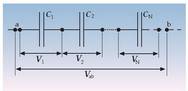
5.3. irudia. Kondentsadore multzo bat seriean elkarturik.
Kontuan hartuta potentzial diferentzia guztien batuketa
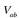 dela:
dela:
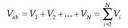
Ekuazio multzotik p,tentzial diferentzia guztiak askatuz eta haien batuketa eginez:
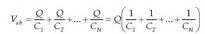
Eta orduan serie elkarketan adierazpen honen bitartez lortuko da kapazitate baliokidearen balioa:

b) Paralelo elkarketa
Kasu honetan N kondentsadoreak potentzial diferentzia berberaren eraginpean daude, Vab hain zuzen. Hori jakinik, honako ekuazio sail hau agertzen zaigu:
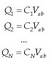
Elkarketa honetan kondentsadore guztiek pilatzen dutenaren batura da sistema osoak pilatzen duen karga guztia:

Orduan, batuketa eginez:
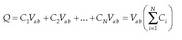

5.4. irudia. Kondentsadore batzuk paraleloan elkarturik
Eta horrela, paralelo elkarketan ondoko adierazpena erabiliz lortuko dugu kapazitate baliokidearen balioa:
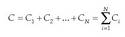
5.3. Kirchhoffen legeak
Osagai asko dituzten zirkuitu korapilotsuen kasuan, eta erresistentziekin batera hargailu eta sorgailuak ditugunean, ezin ditugu erresistentzia baliokideak aurrean azaldu dugun modura kalkulatu. Kasu honetan erabiltzen den metodoa G.R.Kirchhoff (1824-1887 ) ikerlari alemaniarrari zor zaio, eta horregatik Kirchhoffen legeak izenaz zagutzen da.
Legeak azaldu baino lehen, sare elektrikoaren egiturari dagozkion bi osagairen definizioak ikusiko ditugu.
Korapiloa: Sare elektrikoan bi eroale baino gehiago batzen direneko puntua da.
Maila: Sare elektrikoan dagoen edozein ibilbide itxia da.
Definizio hauek ikusi eta gero, prest gaude Kirchhoffen legeak aurkezteko:
1.- Korapiloen legea:
Edozein korapilotarantz doazen intentsitateen arteko batura zero da:
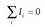
Lege horrek, bistan denez, zirkuituan kargaren kontserbazioa betetzen dela adierazten du. Intentsitateen batura era algebraikoan egin behar da. Eta orduan zeinuak jarri behar zaizkie intentsitateei arau bat jarraituz. Adibidez, korapiloranzko intentsitateak positibotzathartuko ditugu, eta korapilotik ateratzen direnak, berriz, negatibotzat (alderantzizko irizpidea ere erabil daiteke).
2.- Mailen legea:
Edozein mailatan dauden indar elektroeragileen arteko batura maila horretako IR biderkaduren baturen berdina da; hots, potentzial erorketa guztien arteko baturaren berdina:
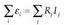
Lege hau, beraz, zirkuituko energiaren kontserbazioari dagokio eta Ohmen legea orokortzearen ondorio zuzena da.
Motore elektrikoa
Motore elektrikoek, indar elektromagnetikoak erabiliz, energia elektrikoa energia mekaniko bihurtzen dute. Estatore edo zirkuitu induzitzaile finko bat dute, eremu magnetikoa sortzen duena. Eremu horren barnean, errotore edo zirkuitu induzitu birakorra dago. Zirkuitu induzituan zehar korronte elektrikoa pasatzean sortzen den eremu magnetikoaren eta induktoreko eremu magnetikoaren arteko elkar eraginez indar-bikote bat sortzen da. Indar-bikote horrek, errotorea birarazten du, energia mekanikoa sortuz. Mota askotako motore elektrikoak daude, baina bi talde nagusitan bana daitezke, hain zuzen, korronte jarraitukoak (seriean kiribildutakoak,…) eta korronte alternokoak (sinkronoak, indukziozkoak,...).
Robert Gustav Kirchhoff
(Königsberg, 1824 - Berlin, 1887)
Fisikari alemana. Elektrizitatearen arloan, Wheatstone-ren zubia hobetu zuen, eta elektrizitatea argiaren lastertasunaz hedatzen dela frogatu zuen. Halaber, oinarrizko legeak eman zituen zirkuitu elektrikoei buruz, Kirchhoffen legeak esaten zaienak. Espektroskopia asmatu zuen; elementu kimiko bakoitzak bere espektroa duela frogatu zuen, eta espektro bidezko analisiaren teoriaren oinarriak jarri zituen R. W. Bunsenekin batera. Horri esker argitu ahal izan zen eguzkiaren espektroan agertzen diren Fraunhoferren marren zergatia. Espektroskopiaren bidez zesioa (1860) eta errubidioa (1861) aurkitu zituen. Gorputz beltzaren kontzeptua ere hark sortu zuen, eta hark eman zituen mekanika estatistikoan eta fisika kuantikoan hain garrantzitsua den kontzeptu horri buruzko legeak.
6. Gaia: eremu magnetikoa
Duela 2.000 urte, antzinako Grezian, Magnesia izeneko eskualde batean aurkitutako harri batzuek burdinezko zatiak erakartzeko gaitasuna zutela ezaguna zen. Gaur egun, horrelako harriei magnetitak deitzen zaie, eta hau dute formula kimikoa: Fe3O4. Hortik hartzen dute izena aipatu dugun gaitasun horrek, hots, magnetismoak, eta magnetismoarekin zerikusirik duen guztia aztertzen duen Zientziaren atalak, Magnetikak alegia. Hori izan zen, beraz, gizakiak magnetismoarekin izan zuen lehenengo harremana. Baina kontu handiz behar dugu hitz egin gai hauei buruz, Historian zehar askotan nahastu baitira elkarrekin efektu elektrikoak eta efektu magnetikoak.
Imanek itsasketan noiztik erabiltzen diren ez da zehazki ezagutzen, aspalditik erabiltzen da, nolanahi ere. Batzuek txinatarrek asmatutzat jotzen dute, beste batzuek asmazio hori arabiarrena dela uste dute. Hala ere, XII. mendean, iparrorratz modura erabiltzen zutela idatzizko aipamenez zihurta daiteke. Bestalde, 1600. urtean, William Gilbert (1540-1603) iparrorratzaren orratza leku jakin batera begira zergatik jartzen den azaltzen saiatu zen. Arrazoia Lurrean aurkitzen da, iman iraunkor handi bat baita.
Elektrika eta Magnetikaren arteko lotura XIX. mendea arte ez zen ezagutu. Garai horretan, 1820. urtean, Hans Christian Oersted (1777- 1851), korronte elektrikoek alboan iparrorratz bat badute, haren gainean eragiten dutela konturatu zen. Urte horretan berorretan, André Marie Ampèrek (1775-1836) korronte elektrikoek burdin puskak erakartzen zituztela ikusi zuen. Eta gainera, korronte elektriko paraleloen artean indar erakarle bat azaltzen dela er e egiaztatu zuen. Beraz, imanen eta korronteen arteko baliokidetasuna frogatuta zegoen. Elektrikaren eta Magnetikaren arteko lotura sakonkiago aztertu zen. Alde batetik, Michael Faradayk (1791-1867) eta Joseph Henryk (1797-1878), eremu magnetiko aldakor batek kontserbakorra ez den eremu elektriko bat sortzen zuela erakutsi zuten.
Bestetik, eremu elektriko aldakor batek, eremu magnetiko bat sortzen duela ere frogatu zen. Horri guztiari, James Clerk Maxwellek (1831-1879) eman zion formulazio matematikoa, zehaztasun handiz. Horrela, elektromagnetismoa teoria bakar batean bilduta utzi zuen.
6.1. Polo magnetikoak eta indar magnetikoa
1269. urtean, Petrus Peregrinus Maricourtek (XIII. mendea) garrantzi handiko aurkikuntza bat egin zuen. Iman esferiko natural baten gainean orratz bat posizio desberdinetan utzi zuen. Orratza meridiano sistema baten arabera lerrokatzen zen beti, meridianoaren ukitzaile gisa, haren zentzuan. Ondorioa garbia zen, norabide guztiak esferaren bi puntutara zihoazen, meridianoen gurutzamendu puntuetarantz. Bi puntu horiei polo izena jarri zien, Lurrarekiko konparazioa eginez. Iman guztiek, itxurak axola ez duela, bi poloak dituztela aspalditik zen ezaguna. Bi polo horiei ipar, I, eta hego, H, izenak eman zitzaizkien.
Lurraren kasua, dagoeneko aipatu duguna, oso berezia da. Iman handi bat izanik, izaera magnetiko hori zergatik duen oraindik ez dago oso garbi. Bere ipar-polo geografikoan, hego-polo magnetikoa du, eta hego-polo geografikoan ipar-polo magnetikoa. Horregatik, Lurraren azalean dauden iman guztien ipar-poloak, Lurraren ipar-polo geografikorantz begira jartzen dira. Hala ere, polo magnetikoen eta geografikoen kokaera ez datoz guztiz bat. Hau da, hego-polo magnetikoa ez dago zehazki ipar-polo geografikoan. Kristobal Kolon (~1451-1506) bere bidaiak egin zituenean jadanik konturatu zen horretaz. Gainera, denboran zehar polo magnetikoak lekuz aldatu egiten direla uste dute gaur egun zientzilariek. Datu modura, esan daiteke ezen 1954. urtean, Galesko Printzearen uharteen (Kanada) ipar-mendebaldean zegoela hego-polo magnetikoa.

6.1. Irudia. Bi imanen arteko indarrak, erakarleak (a) eta aldaratzaileak (b).
Frogatu zenez, iman baten poloetan indar magnetikoa askoz indartsuagoa da. Beste alde batetik, poloek, karga elektrikoek bezala, badute ezaugarri berezi bat. Izen bereko bi poloak elkartzean aldendu egiten dira, eta izen desberdinekoak elkartu, ikus 6.1. irudia. 1750. urtean, John Michellek (1724-1793) imanen poloen elkarrekiko eraginaren azterketa kuantitatiboa egin zuen. Horretarako, bihurritze balantza bat erabili zuen. Eta poloen arteko erakarpena eta aldarapena intentsitate berekoak direla frogatu zuen. Eta orobat indar magnetikoa poloen arteko distantziaren karratuaren alderantzizko proportzionala dela ikusi zuen.
Elektrika kamarekin konparatuz, zenbait zientzilarik karga magnetikoa bilatzen ahalegindu zuten. Baina berehala konturatu ziren ezinezkoa zela hori. Karga magnetikoa, edo monopolo magnetikoa ere deitu dena, ezin da bakartu. Horren froga bat, 6.2. irudian ikusdaiteke. Aztertu dugunez, imanek bi polo dituzte. Polo bat bakar - tzeko, iman bat puskatuz ez da ezer lortzen, agertzen diren iman puska bakoitzak bi poloak baititu berriro.
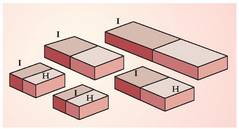
6.2. Irudia. Imana puskatzean, polo magnetiko berriak agertzen dira iman berrietan
Beste alde batetik, zientzilariak berehalaxe konturatu ziren ez dela karga magnetikoaren beharrik, gertaeren azalpenetarako eta iker187 ketarako. Gainera, indar magnetikoak azaltzeko, ezin azalpen egokirik eman daiteke karga edo monopolo magnetikoetan oinarriturik. Orduan, galdetu daiteke ea nola azter daitekeen indar magnetikoa. Hori argitzeko ondoko definizio hau hartu behar da kontuan: Elkar eragin magnetikoa higitzen diren kargek elkarri egiten dioten eragina besterik ez da.
Beraz, eragin magnetikoa aztertzeko, partikulen karga eta lastertasuna ezagutzea aski da. Horrela, ez dugu materiaren ezaugarri berririk zertan sarturik.
Eremu magnetikoaren “iturriei” buruz ez dugu gai honetan ezer berezirik aipatuko, hurrengo gaian aztertuko baititugu zehatzago. Gauza bat aurreratu nahi dugu bakarrik: eremu magnetikoak karga higikorrek sortzen dituztela.
Eragin elektrikoak eta magnetikoak oso lotura estua dute elkarr ekin, karga elektrikoaren bi alderdi desberdin baitira. Azken finean, magnetismoa karga elektrikoaren higiduraren ondorioa da. Horrela, eragin elektrikoa eta magnetikoa batera har daitezke, eta elkarrekin eragin elektromagnetikoa osatzen dute. Eragin elektromagnetikoa ikertzen duen Zientziaren atalari Elektromagnetika esaten zaio.
6.2. Zatiki kargatu higikorren gain eragiten diren indarrak
Zatiki kargatu higikorretan eremu magnetikoak duen eragina aztertzean, behin jatorri grabitatorioa edo elektrostatikoa dutenak kenduta, beste indar bat topatzen dugu askotan. Indar hori indar magnetikoa izaten da. Lehen ere aipatu dugunez, indar magnetiko hori zatikiaren kargaren eta lastertasunaren araberakoa da. Hemen, ondoren, indar magnetikoaren adierazpen matematikoa aurkeztuko dugu:
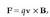
non q zatikiaren karga, v zatikiaren lastertasuna, B eremu magnetikoaren intentsitate-bektorea eta ¥ biderkadura bektoriala diren. Beraz, ikusten denez, indar magnetikoaren norabidea ateratzeko, bi bektoreen arteko biderkadura bektorialaren arauak behar dira jarraitu.
Grabitazioan eta Elektrikan ez bezala, Magnetikan eremu kontzeptua hasiera-hasieratik behar da. Eragin magnetikoa azaltzeko, Fisikaren beste arlo askotan bezala, eremu kontzeptua guztiz baliozkoa da. Beraz, B eremu magnetikoaren intentsitate bektorea, edo izen laburragoaz, eremu magnetikoa, onartu eta erabiliko dugu.
Aurreko adierazpen hori hobeto ulertzeko, eremu magnetikoaren dimentsioak aztertuko ditugu:
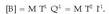
Banako Sistema Internazionalean eremu magnetikoaren banakoa Tesla da, Nikola Tesla (1856-1943) ikerlari kroaziarraren omenez; T da ikurra:

Indar magnetikoaren modulua kalkulatu ahal izateko, biderkadura bektorialaren definizioa erabili behar da. Hori eginda, ondoko hau lor daiteke:
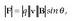
non ? angelua, v lastertasuna eta B eremu magnetikoaren artean dagoen angelua den.
6.3. irudian ikus daiteke, bai karga positiboarentzat bai negatiboarentzat, zein den indar magnetikoaren norabidea. Esan dugunez, indarraren norabidea eta noranzkoa, biderkaketa bektorialaren arauak aplikatuz ateratzen da.

6.3. Irudia. Indar magnetikoaren norabidea karga elektrikoaren arabera. Karga positiboa (a) eta karga negatiboa (b).
Indar magnetikoa eta zatikiaren lastertasunaren bektoreen norabideak kontutan hartzen baldin baditugu, bi ondorio garrantzitsu atera ditzakegu. Alde batetik, indar magnetikoaren bektorea, F alegia, v bektorearen perpendikularra da, hau da, lastertasunaren bektorearen perpendikularra. Beraz, zatikiak pairatzen duen azelerazioa normala da, eta horregatik, lastertasunaren modulua aldagabe mantentzen da. Hala ere, zatikiaren lastertasuna norabidez etengabe aldatuz doa. Beste alde batetik, indar magnetikoak ez du inoiz lanik egiten. Honen azalpena erraza da, indar magnetikoa zatikiaren ibilbidearen perpendikularra da. Horrela, lanaren definizio matematikoa, W, indarra eta ibilbidearen arteko biderkaketa eskalarra eginez lortzen da, honako hau alegia:
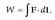
Perpendikularrak direnez, biderkadura zero izango da, eta lana ere berdin. Horregatik, zatikiaren energia aldagabe mantentzen da.
Beste alde batetik, eragin elektromagnetikoan agertzen den indarra, hau da, kargatutako zatiki higikor batek eremu elektromagnetiko batean pairatuko duen indarra, honela adieraziko da:
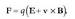
Indar honi Lorentzen indarra esaten zaio, H. A. Lorentz fisikari holandarraren omenez. Ikusten denez, agerturiko indarra, indar elektrikoaren eta magnetikoaren batuketa besterik ez da.
Eremu elektrikoa irudikatzen zen bezala, eremu magnetikoa ere irudikatzeko ohitura dago. Horretarako, lerro batzuk erabiltzen dira, eremu magnetikoaren lerroak deritzenak alegia. Lerro horiek eremu magnetikoaren ukitzaile dira, pasatzen diren puntu guztietan.
Gainera, eremu magnetikoaren modulua, lerroen dentsitatearen bidez adierazten da. Kasu praktiko batean, eremu lerroak ateratzeko, iparrorratz bat erabiltzea komeni da. Bestela, burdinezko limautsak ere erabil daitezke.
6.3. Eremu magnetikoa zeharkatzen duen zatiki kargatuaren higidura
Ikusi dugunez, zatiki kargatu batek, eremu magnetiko batetik higitzean, indar magnetiko baten eragina hartzen du. Indar magnetikoa, eremuaren, lastertasunaren eta kargaren araberakoa izango da. Bestalde, aplikazio zientifikoetan normalean erabili ohi diren eremu magnetikoak uniformeak izaten dira. Hau da, espazioko lekujakin batean, puntu guztietan balio berbera du eremu magnetikoak. Horregatik, gure azterketarako kontutan hartuko dugun eremu magnetikoa uniformea izango da. Horrela, higidura sinpleak azalduko dira.
Eremu magnetiko uniformean agertzen diren higidurak, karga eramaleen lastertasunaren eta aplikaturiko eremu magnetikoaren arteko angeluaren arabera, hiru motatakoak izan daitezke. Hain zuzen, horiek aztertuko ditugu ondoren.
6.3.1. v eta B paraleloak

6.4. Irudia. Zatiki kargatuen higidura, eremu magnetikoaren norabide berean gertatzen denean.
Zatiki kargatuaren lastertasuna eta aplikatzen zaien eremu magnetikoa paraleloak baldin badira, horixe da kasurik errazena. Horrelako ezaugarriak dituen adibide bat 6.4. irudian ikus daiteke. Irudiko edozein zatikik jasaten duen indar magnetikoa, aurretik aztertutako ekuazioa erabiliz atera daiteke. Adibidez, kalkula dezagun v lastertasunaz higitzen den zatikiak jasaten duena, bere karga mota edozein izanik:
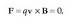
Hau da, lastertasunaren eta eremu magnetikoaren bektoreak norabide berean daudenez, beren arteko biderkadura bektoriala zero da. Beraz, zatikiak pairatzen duen indarra zero da, eta bere azelerazioa ere zero izango da, eta lastertasun konstante batez higituko da. Horren ondorioz, lastertasunaren modulua ez da aldatuko, eta norabidea ere ez. Orduan, zatikiaren lastertasuna eta eremu magnetikoa paraleloak direnean, zatikiaren higidura zuzena eta uniformea izango da
6.3.2. v eta B perpendikularrak

6.5. Irudia. Karga negatiboaren (a) eta positiboaren (b) higidura, lastertasuna eta eremu magnetikoa perpendikularrak direnean.
Eremu magnetikoa eta zatiki kargatuaren lastertasun perpendikularrak direnean, konplikatuxeagoa da kasua. Aurreko kasuan erabili dugun ekuazio bera erabiliz, ondoko hau atera dezakegu:

Lastertasuna eta eremu magnetikoa elkarren perpendikularrak direnez, haien arteko biderkadura bektoriala ez da nulua. Beraz, indar magnetiko bat azalduko da, eta ondorioz, ibilbideari buruz azelerazio normala. Hori dela eta, lastertasunaren norabidea aldatuz joango da, baina, dakigunez, modulua ez. Bestalde, lastertasunaren norabide berriek, hasierako lastertasunak eta azelerazioak, edo indarrak, osatzen duten planoan kokatuta daudenez, eremuaren perpendikularra izango dute. Beraz, zatikiaren ibilbidea eremu magnetikoaren perpendikularra den plano batean gertatzen dela ateratzen da ondorioz. Angelua 90°koa denez, eta lastertasunaren modulua konstantea denez, ondoko emaitza hau ateratzen da:
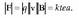
Hau da, agertu den indar magnetikoaren modulua konstantea da.
Bestalde, indar magnetikoa eta lastertasuna elkarren perpendikularrak direnez, azelerazio zentripeto bat pairatuko du zatikiak:

Aurreko bi adierazpenak berdinduz, zatikiaren ibilbidearen kurbatura erradioa atera daiteke:
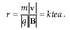
Ikusten denez, kurbatura erradioa konstantea da, eta zatikiaren lastertasunaren eta eremu magnetikoaren mende dago. Horrelako ezaugarria duen higidura lau bakarra dago, higidura zirkularra alegia. Beraz, kasu honetan, zatiki kargatuak higidura zirkular bat izango du. Zirkunferentziaren erradioa, handiagoa izango da lastertasun handiekin, eta txikiagoa eremu magnetiko handiekin.
Higidura zirkularrak ezaugarri bereziak ditu, periodoa, T, maiztasuna,
 , e
ta lastertasun angeluarra,
, e
ta lastertasun angeluarra,  ,
alegia. Aurreko emaitzak erabiliz, magnitude hauentzako ondoko adierazpen hauek atera daitezke:
,
alegia. Aurreko emaitzak erabiliz, magnitude hauentzako ondoko adierazpen hauek atera daitezke:
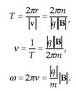
Ikusten denez, hiru magnitudeok ez daude lastertasunaren mende, eremu magnetikoaren mende bakarrik baizik.
6.5. irudian zatiki positiboen eta negatiboaren ibilbideak ageri dira.
a) kasuan, zatiki negatiboaren higidura azaltzen da, b) kasuan, positiboarena. Zatiki negatiboarentzat,
 eta B bektoreen noranzkoak berberak dira, zatiki positiboarentzat, berriz, elkarren aurkakoak dira.
Hori ikusita, lastertasun angeluarra honela adierazten da bektorialki:
eta B bektoreen noranzkoak berberak dira, zatiki positiboarentzat, berriz, elkarren aurkakoak dira.
Hori ikusita, lastertasun angeluarra honela adierazten da bektorialki:
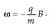
Laburbiltzeko, zatiki kargatuaren lastertasun eta eremu magnetikoa elkarren perpendikularrak direnean, zatikiak higidura zirkularra du
6.3.3 v eta B bektoreen artean edozein angelu

6.6. Irudia. Zatiki kargatuaren higidura helikoidala
Hau da kasu orokorrena, aurreko bi kasuen batura baino ez baita.
Demagun zatikiaren lastertasunaren eta eremu magnetikoaren arteko angelua
 dela.
Orduan, lehenengo urratsa lastertasuna eremuaren norabide paraleloan eta perpendikularrean deskonposatzea izango da:
dela.
Orduan, lehenengo urratsa lastertasuna eremuaren norabide paraleloan eta perpendikularrean deskonposatzea izango da:
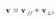
non 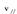 lastertasunak eremu magnetikoaren norabidean duen osagaia, eta
lastertasunak eremu magnetikoaren norabidean duen osagaia, eta
 lastertasunak eremu magnetikoari buruz perpendikular duen osagaia diren. Hauek, matematikoki, honela defini daitezke:
lastertasunak eremu magnetikoari buruz perpendikular duen osagaia diren. Hauek, matematikoki, honela defini daitezke:
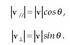
Era horretara egiten den lastertasunaren deskonposaketa, indar magnetikoaren adirezpenean ordezkatzen baldin badugu, indar magnetikoak ere bi osagai izango ditu:

non  ,
besteak beste, aplikatu zaien eremu magnetikoari buruz indar paraleloa eta
indar perpendikularra diren.
,
besteak beste, aplikatu zaien eremu magnetikoari buruz indar paraleloa eta
indar perpendikularra diren.
Indarraren bi osagai hauek, aurreko bi kasuetan agertu diren berberak dira. Beraz, Gainezarmenaren Printzipioan oinarrituta, aipaturiko kasu biak batera hartu behar dira. Eta, kasu honetako ibilbidea helize bat dela ikus dezakegu. Helize honen ardatza eremu magnetikoari buruz paraleloa da, eta erradioa honako hau du:

Aurreko kasuarekin alderatuz, lastertasuna da erradioan aldatu den parametro bakarra. Hemen, hasierako lastertasunaren eremu magnetikoarekiko osagai paraleloa sartu dugu. Beste alde batetik, lastertasun angeluarrak, periodoak eta maiztasunak, lastertasun linealaren mendeko ez direnez, aurreko kasuaren berdinak dira, 6.3.2 atalekoak alegia.
Baina helizea ondo definitzeko, beste parametro bat kalkulatu behar dugu, pausoa alegia. Pausoaren definizioa ondoko hau da:
Zatikiak bira oso bat ematen igarotako denboran ardatzaren norabidean ibili den distantzia.
Beraz, pausoa kalkulatzeko, eremuaren norabidean den lastertasunaren osagaia
 ,
eta bira bakoitzean behar duen denbora,
,
eta bira bakoitzean behar duen denbora, 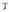 ,
biderkatu behar ditugu:
,
biderkatu behar ditugu:

non  pausoaren ikurra den.
pausoaren ikurra den.
Beraz, orokorrean, helize baten modukoa da eremu magnetiko uniformean zehar doan zatiki kargatuaren ibilbidea. 6.6. irudian, zatiki negatiboa denean agertzen den helizea, a), eta zatiki positiboa denean agertzen dena, b), ikus daitezke
6.4. Korronte elektrikoaren gain eragiten den indar magnetikoa
Azaldu denez (ikus 4. gaia), higituz doan elektroi multzo bat besterik ez da korronte elektrikoa. Hori dela eta, korronte elektrikoak, eremu magnetiko batean dagoenean, haren nolabaiteko eragina jasan behar du. Karga eramaleek jasaten dituzten indar magnetiko guztien batuketa da hari eroalearen gainean agertzen den indarra.

6.7. Irudia. A epaia perpendikularra eta l luzera duen hari eroale baten zatia
6.7. irudian, hari eroale zati bat ageri da. Ikusten denez, hariaren sekzio perpendikularra A da,
eta luzera l. Demagun haritik I intentsitatea igarotzen dela.
Haria, B eremu magnetiko uniformean murgilduta baldin badago, karga eramale bakoitzak jasaten duen indar magnetikoa,
 , ondoko eran azalduko da:
, ondoko eran azalduko da:

non q eta v, besteak beste, karga eramaleen karga eta lastertasuna diren. Behin karga eramale bakoitzak jasaten duen indar magnetikoa aterata, ikertzen ari garen hari zatian dagoen karga eramaleen kopurua kalkulatu behar dugu. Hariaren bolumen unitateko karga eramaleen dentsitatea n baldin bada, karga eramaleen kopurua, hari zatiaren bolumena bider n eginez kalkulatuko da. Hariaren bolumena Al denez, karga eramaleen kopurua nAl izango da. Beraz, karga eramale guztien gainean dagoen indar magnetikoa, ondoko hau da:
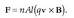
Beraz, aurreko adierazpenak erakusten digu haria horrek eremu magnetiko batean zenbateko indarra jasaten duen. Hala ere, aurreko formula era sinpleago batean ere idaz daiteke. Horretarako,korrontearen intentsitaterako lortutako adierazpen bat erabiliko dugu, 4. gaian lortu genuena alegia:
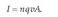
Aurreko bi formulak erabiliz, ondoko adierazpena lortzen da:
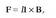
non l bektorearen modulua hariaren luzera den, eta haren norabidea korronte elektrikoaren norabidea, hau da, qv bektorearena.
Ekuazio hori ateratzeko, bi suposaketa egin ditugu: alde batetik, hariaren zatia zuzena dela, eta bestetik, eremu magnetikoa uniformea dela hari osoan. Hala ere, nahiz eta haria eta eremu magnetikoa edozein motatakoak izan, indar magnetikoa ere kalkula daiteke. Horretarako, hariaren oso zati txiki bat hartu behar da, dl alegia, eta haren gainean egiten den indarra kalkulatu, dF. Hariaren zati txiki horri, hari elementu diferentziala deritzo, eta jasaten duen indar magnetikoa honako hau da:
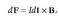
non B hariaren zati diferentzialean dagoen eremu magnetikoaren bektorea den. Aurreko terminologia erabilita, Idl magnitudeari korronte elementua deritzo. Indarraren adierazpen honekin, hariaren gainean eragiten den indar osoa kalkula daiteke. Horretarako, aurreko formulak hari zati guztietan duen balioa kalkulatu behar da, B-ri eta dl-ri dagozkien balioak erabiliz. Gero, hari zati guztiak kontuan hartuz, batuketa, edo integrazioa, egin behar da. Integrazioa egin behar izatekotan, ondoko adierazpenaz baliatu behar gara:
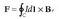
non C delakoak zirkuituaren ibilbidea adierazi nahi duen
Nikola Tesla
(Smiljan, 1856 - New York, 1943)
Kroaziar fisikaria eta sortzailea. 1884an Estatu Batuetako Edison laboratorioetara joan zen lanera. Sortzaile bikaina izan zen, hark landutako tresnen ugariak erakusten duenez: korronte alternoko motorra (1888), transformadorea edo Tesla bobina (1891), haririk gabeko igorpen sistema (1893), eta eremu magnetiko birakorraren printzipioa (1893) Nazioarteko sistemak haren izena jarri zion indukzio magnetikoaren banakoari: tesla (T).
6.5. Indar momentu magnetikoa
Aurretik azaldu dugunez, iman txiki bat eremu magnetiko baten barnean jartzen denean, lerrokatu egiten da. Lerrokaketa horretan, imanaren ipar-polo magnetikoak eremu magnetikoaren norabideeta noranzko bera hartzen du. Magnetizaturik gabeko burdin limautsak badira ere, efektu berbera gertatzen da. Hala ere, hauen kasuan, lehenago limautsak magnetizatu egiten dira eremu magnetikoaren eraginez.

6.8. Irudia. Iman txiki batek eremu magnetiko uniforme batean pairatzen dituen indarrak.
6.8. irudian, eremu magnetiko uniformeari buruz angelu bat, edozein, eratzen duen iman
txiki bat ageri da. Ikusten denez, bi indar agertzen dira. Bata,
 alegia,
ipar-poloaren gainean eragiten du, eremu magnetikoaren norabide eta noranzko berean. Bestea,
alegia,
ipar-poloaren gainean eragiten du, eremu magnetikoaren norabide eta noranzko berean. Bestea,
 hain zuzen,
aurrekoaren berdina da, baina, hego-poloaren gainean eremuaren kontrako noranzkoan eragiten du.
Imanaren poloaren intentsitatea, q', poloan eragiten ari den indar magnetikoa zati indukzio magnetikoaren balioa da:
hain zuzen,
aurrekoaren berdina da, baina, hego-poloaren gainean eremuaren kontrako noranzkoan eragiten du.
Imanaren poloaren intentsitatea, q', poloan eragiten ari den indar magnetikoa zati indukzio magnetikoaren balioa da:
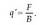
Aurreko ekuazio hau moduluak erabiliz idatzita dago, eta ez bektoreak erabiliz. Bektoreak erabiliz idatzi ahal izateko, poloaren intentsitaterako zeinu-akordio bat hartu behar da. Hitzarmen honetan, ipar-poloa positiboa da, eta hego-poloa negatiboa. Horrela, polo baten gainean eragiten duen indarra honako hau izango da:

Polo magnetikoaren intentsitatearen notazioa, Magnetikako ekuazioek Elektrikakoen antza izan dezaten ari gara erabiltzen.
6.8. irudian ikusten denez, indar-momentu bat dago imanaren gainean. l hego-polotik ipar-polora zuzenduta dagoen bektorea baldin bada, eta bere modulua bi poloen arteko distantzia bada, orduan, indar-momentua honela idazten da:
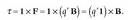
Aurreko formulatik, iman baten momentu magnetikoa, m, definitu ohi da. Horretarako, ondoko formula honetaz baliatzen gara:

Definizio hau, Elektrikako 1. gaian definituriko dipolo elektrikoaren baliokidea da, ikusten denez. Momentu magnetikoaren unitateak ondoko hauek dira:

Beraz, imanaren gainean eragiten duen indar momentua honela geratuko da:

non × ikurrak biderkaketa bektoriala adierazten duen.
Aurreko atalean ikusi dugunez, eremu magnetiko batean korronte elektrikoa zeharkatzen duen hari eroale batek ere indar magnetiko bat pairatzen du. Eremu magnetiko uniformean dagoen zirkuitu elektriko itxi batean indar desberdinak azaltzen dira, eta hor ere momentu magnetikoa defini daiteke. Adibidez, plano batean dagoen espiraren kasuan, ikus 6.9. irudia, bere momentu magnetikoa honako hau du:

non N, espiran hariak ematen dituen birak, I espiratik igarotzen ari den intentsitatea, S espirak ixten duen azalera, eta nˆ azalera horrekiko perpendikularra den bektore unitarioa diren. Espirarekin egiten den moduan, momentu magnetikoa zirkuitu guztientzat defini daiteke. Beste aldetik, edozein zirkuituk ere indar momentua jasoko du eremu magnetikoan. Pairatzen duen indar momentua, zirkuituaren momentu magnetiko eta eremu magnetikoaren arteko biderkaketa bektoriala eginez lortzen da; beraz, imanaren kasuan bezala.
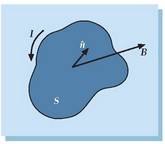
6.9. Irudia. Espira baten gainean azaltzen den momentu magnetikoa
6.6. Hall efektua
Eremu magnetiko batek, korronte elektrikoa eramaten duen eroale baten gainean eragiten duen indarra lehendik kalkulaturik daukagu. Indar magnetiko horrek, eroalearen barruan dauden karga eramaleen gain eragiten du zuzenean. Eta hauek indar magnetikoaren eragina eroaleari transferitzen diote, material eroalearen barnean dauden indarren bidez. Beraz, karga eramaleek kanpoko eremu magnetikoaren eragina pairatzen dute. Efektu honi Hall efektua deritzo.
Eramaleen gainean kanpoko eremu magnetikoak sortzen duen eragina azelerazio batean azaltzen da. Eramaleek daukaten azelerazio berri honen eraginez, beraien higiduretatik desbideratzen dira. Demagun erabiltzen ari garen haria zinta baten modukoa dela. Hau da, bere sekzio perpendikularra errektangulu bat du. Kanpotik aplikaturiko eremu magnetiko uniformea perpendikularki sartzen baldin bada, gainazaleko bi karga dentsitate azalduko dira hariaren bi gainazaletan, ikus 6.10. irudia. Karga eramaleen desbideraketaren eraginez agerturiko bi karga dentsitateek eremu elektriko bat sortzen dute. Eremu elektriko horrek indar magnetikoaren kontrako norabidea duenez, azken hau konpentsatu egiten da. Horrela, egoera egonkor bat azaltzen da. Esan beharra dago zintaren sekzioan luzera zabalera baino askoz handiagoa baldin bada, efektua askoz nabarmenagoa izango dela. Hau da, gainazaletan pilatzen den karga dentsitatea askoz handiagoa izango da.

6.10. Irudia. Hall efektua. Eremu magnetikoa B ikurraz adierazten da, eta orriaren planoan perpendikularki sartzen da.
Beste alde batetik, Hall efektuan oinarrituta, parametro berri bat definitu ohi da, Hall koefizientea alegia. Hall koefizientea esperimentalki neur daiteke. Horretarako, perpendikularki aplikaturiko eremu magnetikoa, B, harian dagoen korronte dentsitatea, J, eta gainazaleko bi karga dentsitateen artean dagoen eremu elektrikoa, E, zehaztu behar dira. Behin horiek zehaztuta, Hall koefizientea kalkulatzeko, ondoko adierazpen matematikoan ordezkatzea aski da:

Beste alde batetik, Hall koefizientearentzat beste adierazpen bat ere bada. Horretan, karga eramaleen dentsitatea eta karga azaltzen da, era honetara:
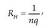
non q karga eramaleen karga elektrikoa den.
Beraz, Hall koefizientearen bitartez, karga eramaleen dentsitatea eta kargaren zeinua esperimentalki zehatz daitezke. Zenbait metalentzako esperimentalki lorturiko Hall koefizientea zati teorikoki kalkulaturikoa ikus daitezke 6.1. taulan. Hall koefizientea teorikoki kalkulatzeko, metalaren balentziazko elektroiak karga eramaletzat jo ditugu.
6.1. taula arretaz aztertzen badugu, gauza bitxiak gertatzen direla konturatuko gara. Metal alkalinoetan, hasierako bostetan, hain zuzen, balio teorikoak eta esperimentalak nahiko ondo egokitzen dira. Gainontzeko metaletan, nahikoa balio desberdinak azaltzen dira. Adibidez, kobrearen kasuan, karga eramaleen dentsitate esperimentala teorikoa baino txikiagoa da. Hala ere, harrigarriena azken hiru kasuetan azaltzen da. Horietan, zeinu negatibo bat agertzen da emaitzetan. Honek, karga eramaleek karga positiboa dutela adierazi nahi digu. Beraz, metal hauetan, elektroiak ez dira karga eramale modura jokatzen dutenak. Desberdintasun hauek guztiak azaltzeko, Mekanika Kuantikoa eta Banden Teoria, Elektrikako 4.9. atala, erabiltzea beharrezkoa suertatzen da.
Azkenik, Hall efektua eremu magnetikoa zehazteko ere erabiltzen da.
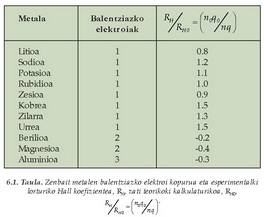
Iparrorratza
Plano horizontal batean iparra erakusten duen tresna da iparrorratza. Bi motatakoak izan daitezke. Batzuk, iparrorratz magnetikoak dira, eta besteak, giroskopikoak, giroskopioaren funtzionamenduan oinarritzen direlako, hain zuzen. Txinatarrek asmatu omen zituzten iparrorratz magnetikoak. Hauek, burdinazko pieza imandu birakorrean oinarritzen dira. Pieza imandu hau Lurraren eremu magnetikoan kokatzen da eta eremuaren iparraldea markatzen du. Gehienetan, haize-arrosa marraztua duen kutxatxo kristaldun batean egoten da kokatua. Iparrorratz magnetikoen erabilpena asko zabaldu zen Erdi Aroan. Mendeetan ez zuen aldaketa handirik izan; hala ere, XIX. mendean zientzilari, ingeniari eta itsasgizonek asko hobetu zuten.
7. Gaia: eremu magnetikoaren iturriak
Aurreko gaian eremu magnetikoak sortzen dituen indarrak eta zenbait efektu aztertu dira. Gai honetan, berriz, eremu magnetikoa nola sortzen den izango da aztergai.
Eremu magnetikoaren sortzaile gisa imanak hartu ziren hasieran. Baina 1820. urtean, H. C. Oerstedek ikusi zuen eroale baten alboan ipar orratz bat jarriz gero, eroalean zehar korronte elektrikoa pasatzean orratza desbideratu egiten dela, eta horrela jakin zen korronte elektrikoek ere sor ditzatekela eremu magnetikoak. Urte hartan bertan, Jean Baptiste Biot (1774-1862) eta Félix Savart (1791- 1841) fisikari frantsesek eroale luze batetik igarotzen den korronteakiman baten gainean eragiten duen indarra neurtu zuten. Neur - keta haren emaitzak korronte elementu bakoitzak sortzen duen eremu magnetikoaren arabera aztertu zituzten. A. M. Ampèrek ikerketa haiek sakondu zituen, eta bi korronte elektrikoren artean zenbait indar eratzen direla frogatu zuen.
Ampèrek iman iraunkorren portaera azaltzeko eredu bat finkatu zuen. Eredu horretan, imanaren barruan korronte elektriko mikroskopikoak daudela esan zuen; korronte elektriko hauek espira mikroskopikoen modukoak dira. Ampèreren eredu hura nahiko egokia da hainbat fenomenoren azalpena egiteko; dena dela, 9. gaian aztertuko da sakonago material magnetikoen portaera.
7.1. Korronte elektrikoak sorturiko eremu magnetikoa
Higitzen diren zatiki kargadunek sortzen dituzte eremu magnetikoak, eta korronte elektrikoa ere higitzen ari den karga multzo bat denez, eremu magnetikoa sortzeko ahalmena du. Baina, korrontearen eta hari dagokion eremuaren arteko lotura zein den ez da aztertzen erraza. J. B. Biot eta F. Savartek egindako ikerketei esker, korronte elektrikoak sortutako eremu magnetikoaren fenomenoa azaltzeko adierazpen matematiko bat lortu zen, Biot-Savarten legea deritzona.
7.1. Irudia. Eroale batetik iragaten den korronte elektrikoak sorturiko eremu magnetikoa. dB bektorea orrian sartzen da P puntuan.
7.1. irudian korronte elektrikoa daraman eroale zati bat agertzen da. Biot-Savarten legeak edozein P puntutan dagoen eremu magnetikoa kalkulatzeko bidea ematen du. Idl eroalearen korronte elementu bat baldin bada, eta P puntua korronte elementu horretatik r distantziara baldin badago, P puntuan dagoen eremu magnetikoak (dB) balio hau du:

non  aldagaia
korronte elementutik P puntura doan bektore unitarioa den, eta × biderkaketa bektorialaren ikurra.
Ekuazio honetako
aldagaia
korronte elementutik P puntura doan bektore unitarioa den, eta × biderkaketa bektorialaren ikurra.
Ekuazio honetako  konstanteari irazkortasun magnetikoa hutsean deritzo, etabalio hau du:
konstanteari irazkortasun magnetikoa hutsean deritzo, etabalio hau du:
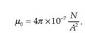
Beraz, irazkortasun magnetiko horren dimentsioak Nazioarteko Banako Sisteman hauek dira:
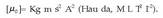
Ampèrek ere bere ikerketetan Biot-Savarten legea aurkitu zuen. Lege hau elektrikako Coulomben
legearen baliokidea da magnetikaren alorrean. Elektrikaren kasuan eremu elektrikoaren iturria karga da;
magnetikan, berriz, eremu magnetikoaren iturria Idl korronte elementua da. Lege horren adierazpen
matematikoaren arabera, eremu magnetikoa distantziaren koadroaren alderantzizko proportzioan txikitzen da,
eremu elektrikoa bezala. Hala ere, eremu elektrikoaren eta eremu magnetikoaren norabideak ez dira berdinak.
Eremu elektrikoa erradiala da, hau da, eremu elektrikoak kargatik eta neurtzen ari garen puntutik igarotzen
den bektorearen norabidea du. Eremu magnetikoa, berriz, norabide erradialarekiko eta korronte
elementuarekiko elkarzuta da. Adibidez, 7.1. irudian, P’ puntuan eremu magnetikoa zero da, rˆ bektore
unitarioa korronte elementuaren norabide berean kokatuta dagoelako

Zirkuitu oso batek puntu jakin batean sortzen duen eremu magnetikoa Biot-Savarten legea erabiliz kalkula daiteke. Horretarako, zirkuituaren korronte elementu guztiek puntu horretan sortzen dituzten eremu magnetikoak kalkulatzen dira. Lorturiko eremu guztien bektore batuketa eginez aterako da zirkuitu osoak puntu horretan sorturiko eremu magnetikoa zein den. Korronte elementuak infinitesimalak baldin badira, eremuaren kalkulua integral honen bidez egin behar da:

non integrazioa C zirkuituaren ibilbidean egiten den. Aurreko beste integral batzuetan gertatu denez, hemen ere barneko funtzioa bektore funtzio bat dela kontuan hartu behar da.
Biot-Savarten legeak maila teorikoan garrantzi handia eduki arren, praktikan ez du erabilgarritasun handirik, integrala ebaztea zailegia gertatzen baita, eite errazeko zirkuituen kasuetan izan ezik. Horren adibide modura, korronte zuzenak eta korronte zirkularrak sorturiko eremuak kalkulatuko dira jarraian.
Elektroimana
Korronte elektrikoa pasatzean, eremu magnetikoa sortzen duen tresna da. 1819an, H. C. Oerstedek aurkitu zuen korronte elektriko batez zeharkaturiko eroale batek eremu magnetikoa sortzen duela bere inguruan. Hori erabilita, Arago fisikari frantziarrak, solenoide batek sortzen zuen eremu magnetikoa aztertu zuen. Geroago, 1823. urtean, Sturgeon fisikari britaniarrak, burdinezko zati bat solenoidearen barruan jarriz gero eremu magnetiko indartsuagoa lortzen zela ikusi zuen. Azkenik, J. Henry estatubatuarrak, elektroimanekin lanean jardun ondoren, 365 kilogramo jasotzea lortu zuen 1827an. Beraz, elektroimana bi partez osatua dago; burdina gozozko nukleoa, alde batetik, eta solenoidea bestetik. Esan dugunez, burdina gozozko zatia solenoidearen barnean kokatzen da. Orduan, solenoidetik korronte elektrikoa pasatzean, eremu magnetikoa sortzen da. Burdinaren eginkizuna, ordea, eremu magnetiko hori indartzea eta bideratzea da. Zenbait laborategitan, elektroimanak erabiliz oso eremu magnetiko altuak lortu ahal izan dira.
Hans Christian Oersted
(Rudkobing, 1777 - Kopenhage, 1851)
Danimarkako fisikaria, Langeland uhartean jaio zen; Kopenhageko unibertsitatean egin zituen ikasketak, eta gero fisikako irakasle izan zen unibertsitate horretan bertan (1806). Korronte elektrikoa hari eroale batetik igarotzen denean alboan duen orratz imandu bat mugiarazten duela aurkitu zuen 1820an. Era horretara konturatu zen korronte elektrikoek eremu magnetiko bat sortzen dutela. Kimikaren alorrean ere lan egin zuen. Adibidez, 1825ean aluminatik aluminioa lortu zuen.
7.1.1. Korronte zuzenak sorturiko eremu magnetikoa

7.2. Irudia. Eroale zuzen batean Biot-Savarten legea aplikatzeko beharrezkoa den geometria.
7.2. irudian, I intentsitateko eroale zuzen bat agertzen da. Hari eroaletik R distantziara dagoen P
puntuan eremu magnetikoa kalkulatu nahi da. Horretarako, x ardatz gisa haria hartu da, eta y
ardatza P puntutik pasatzen dela irudikatu da. Eremu magnetikoaren norabidea P puntuan x ardatzari
elkarzuta da, orritik ateratzen da. Eremu magnetikoaren norabidea
 biderkaketak ematen du.
Gainera, korronte elementu guztiek norabide eta noranzko bereko eremuko osagaiak eratzen dituzte.
Beraz, eremuaren norabidea Ppuntuan orritik ateratzen da perpendikularrean.
Hariaren goialdean dauden puntu guztientzat, eremuaren norabidea berdina da, P puntuarenaren berdina alegia.
Hariaren behealdeko puntuetan, berriz, eremua orrian sartzen da perpendikularrean.
Behin eremuaren norabidea finkatuta, bere modulua kalkulatzea besterik ez da gelditzen.
biderkaketak ematen du.
Gainera, korronte elementu guztiek norabide eta noranzko bereko eremuko osagaiak eratzen dituzte.
Beraz, eremuaren norabidea Ppuntuan orritik ateratzen da perpendikularrean.
Hariaren goialdean dauden puntu guztientzat, eremuaren norabidea berdina da, P puntuarenaren berdina alegia.
Hariaren behealdeko puntuetan, berriz, eremua orrian sartzen da perpendikularrean.
Behin eremuaren norabidea finkatuta, bere modulua kalkulatzea besterik ez da gelditzen.
Bektore biderkaketaren modulua  izanik, Biot-Saarten legea honela gelditzen da:
izanik, Biot-Saarten legea honela gelditzen da:
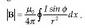
Hariak eta P puntuak sortzen duten geometriaren ezaugarrien bidez, aurreko integrala bi zatitan banatzen da. Lehenengo zatian, x=0 puntutik eskuinera dauden korronte elementuek sorturiko eremu magnetikoaren modulua kalkulatzen da:

Bigarren zatian, berriz, x=0 puntutik ezkerrera dauden korronte elementuei emaitza hau dagokie:
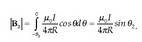
Bi aldeetako balioak batuz, eremu magnetikoaren modulua honela gelditzen da:
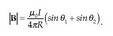
Eroalea infinitua bada,  angeluek 90°-ra joko dute, eta 2 orduan,
angeluek 90°-ra joko dute, eta 2 orduan, 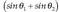 adierazpenak 2 balioa hartuko du. Ordezkaketa eginez, adierazpen hau aterako da:
adierazpenak 2 balioa hartuko du. Ordezkaketa eginez, adierazpen hau aterako da:
Eroale infinituaren egoera idealizatua bada ere, eroalea zuzena denean, bere luzeraren neurria baino hurbilago dauden puntuetako eremu magnetikoa harturik egiten diren hurbilketak nahiko egokiak dira. Kasu horietan, eremu magnetikoa intentsitatearen proportzionala da. Hau da, zenbat eta korronte elektriko handiagoa izan, hainbat handiagoa izango da eremu magnetikoa. Bestalde, eremua hariarekiko distantziaren alderantziz proportzionala da. Beste era batera esanda, haritik zenbat eta gehiago urrundu, or - duan eta txikiagoa izango da eremu magnetikoa.
7.3. irudian, korronte zuzen infinitu baten eremu lerroak ageri dira. Kasu honetan, eremu magnetikoaren lerroak zirkunferentzia zentrokideak dira, eta haria bera dute zentro. Bestalde, zirkunferentzien planoak hariarekiko elkarzutak dira.
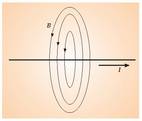
7.3. Irudia. Korronte zuzen infinituak sorturiko eremu magnetikoa.
7.1.2. Korronte zirkularrak sorturiko eremu magnetikoa
Kasu honetan, korronte zirkularrak, edo beste era batera esanda, espira batek, sortzen duen eremu magnetikoa aztertuko da. Eremua lortzeko, kasu honetan aurreko kasuan baino geometria zailagoa erabiliko da. Hala ere, espiraren simetria zilindrikoaren bidez ardatzeko puntuetan eremu magnetikoaren balioa zenbatekoa den kalkula daiteke. Espazioko beste edozein puntutan eremua aztertzen saiatuz gero, integral korapilatsuegia ebatzi beharko litzateke.
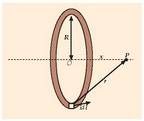
7.4. Irudia. Espiraren korronte elementua eta gainerako parametro geometrikoak
Eman dezagun, I intentsitatea duen espiraren erradioa R dela, eta eremu magnetikoa kalkulatu nahi dela espiraren ardatzean O zentrotik x distantziara dagoen P puntuan. Espiraren behealdean dagoen korronte elementua hartzen bada (ikus 7.4. irudia), korronte elementuaren norabidea orriaren barrura doa. Eremu magnetikoa korronte elementuarekiko eta rˆ bektorearekiko elkarzuta da. Horren ondorioz, eremua orriaren plano berean dago. Espiraren goialdeko korronte elementua kontuan hartzen bada, berak sorturiko eremu magnetikoa ere orrian egongo da. Baina, eremuaren bi osagai hauek batuz, neurri batean orekatu egiten dira, eta eremu magnetikoa x norabidean geratzen da soilik. Eta gauza bera egin daiteke korronte elementu guztiekin. Hori dela eta espiraren ardatzaren edozein puntutako eremua x ardatzaren balio positibotara bideratuta dago.
Behin eremu magnetikoaren norabidea eta norantza finkatuta daudela, korronte elementu batek sorturiko eremuaren modulua Biot- Savarten legearen bitartez kalkulatuko da:

Hala ere, eremu magnetiko honetatik, soilik x ardatzean duen proiekzioa hartuko da kontuan, azken finean, hori izango baita geratuko dena, gainerakoa ezereztu egingo baita. x ardatzeko proiekzioa erabiliz, eta integrazioa espiran eginez, espira osoak bere ardatzean zentrotik x distantziara dagoen puntuan sorturiko eremuaren balioa formula honen bidez lor daiteke:
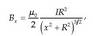
non  den eremu magnetikoaren modulua x ardatzaren norabidean. Espiraren ardatzean neurtzen den eremu
magnetikoa, intentsitatearen proportzionala da. Hau da, espiran zenbat eta intentsitate handiagoa egon,
orduan eta eremu magnetiko handiagoa neurtuko da. Eremuak espiraren erradioarekin eta x distantziarekin
duen lotura kalkulatzea nekezagoa da. Hala ere, erradioa eta x distantzia handitzen diren heinean,
eremu magnetikoa txikitu egiten dela esan daiteke, oro har.
den eremu magnetikoaren modulua x ardatzaren norabidean. Espiraren ardatzean neurtzen den eremu
magnetikoa, intentsitatearen proportzionala da. Hau da, espiran zenbat eta intentsitate handiagoa egon,
orduan eta eremu magnetiko handiagoa neurtuko da. Eremuak espiraren erradioarekin eta x distantziarekin
duen lotura kalkulatzea nekezagoa da. Hala ere, erradioa eta x distantzia handitzen diren heinean,
eremu magnetikoa txikitu egiten dela esan daiteke, oro har.
Aurreko ekuaziotik informazio gehiago ere lor daiteke, ordea. Adibidez, espiraren zentroan dagoen eremu magnetikoa, x=0 eginez lor daitekena, kalkula daiteke:
Azkenik, 7.5. irudian espirak espazio osoan sortzen duen eremuaren lerroak ikus daitezke. 7.5. irudian, espiraren ardatzetik pasatzen den plano bat eta bertan dauden eremu lerroak ageri dira. Espiraren ardatza hartzen duten plano guztien eremu lerroak honen modukoak dira, simetria zilindrikoa dagoelako. Irudian, korronte elektrikoaren noranzkoa bi ikurrekin adierazita dago.Zirkunferentzia eta puntu bat barruan duen ikurrak, korronte elektrikoa orritik perpendikularrean ateratzen dela adierazten du. Zirkunferentzia eta × bat barruan daukanak, korrontea orrian perpendikularrean sartzen dela esan nahi du.
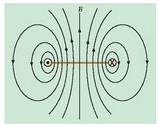
7.5. Irudia. Espira batek bere inguruan sortzen duen eremu magnetikoa
Charles Wheatstone (sir)
(Gloucester, 1802 - Paris, 1875)
Britainiar fisikaria. 1829an kontzertina asmatu zuen. Londreseko King’s College-ko kidea izan zen 1834tik aurrera. Estereoskopioa eta telegrafo elektriko bizkor bat (1837) asmatu zituen. Baina 1843an sortu zuen tresnagatik da batez ere ezaguna. Tresna horrek erresistentzia elektrikoa neurtzeko balio du, eta Wheatstoneren zubia deitu zitzaion. Argiari eta soinuari buruzko ikerketak ere egin zituen (1823-35).
Wheatstoneren zubia
Wheatstoneren zubia, C. Wheatstone fisikari britaniarrak, 1843. urtean aipatu zuen tresna da. Hala ere, dirudienez, 1833. urterako S. H. Christiek tresnaren deskribapena eginda zuen. Tresna honen bidez, ezagutzen ez diren erresistentzia elektrikoen balioa oso azkar eta zehatz neur daiteke. Oso eskema xumea du, nahiz eta itxura desberdinekoak badauden. Hiru erresistentzia ezagun (R1,R2,R4) erabiliz, laugarren baten balioa (Rx) ezagutu daiteke. Horretarako, ezagutzen den erresistentzia bat edo bi (adibidez, R1 eta R2) aldatzen dira, zirkuituaren erdian jartzen den galvanometroan intentsitaterik ez dela pasatzen ikusi arte. Orduan, zirkuituen teoriaren bidez ondoko adierazpena betetzen dela froga daiteke:


7.2. Ampèreren legea
Korrontea daraman hari zuzen luze batean eremu magnetikoaren lerroak zirkunferentzia zentrokideak direla ikusi da. Bestalde, karga dentsitate lineal batek sortzen duen eremu elektrikoa erradiala da, eta baita haren eremu lerroak ere. Beraz, eremu elektrikoaren eta eremu magnetikoaren lerroak ez dira elkarren berdinak.
Hala ere, desberdintasun bakarra ez da lerroei dagokiena. Eremu elektrostatikoan ibilbide
itxi batetik karga bat eramatean egiten den lana beti zero da. Lan horren balioa lortzeko,
ibilbide itxian zehar  biderkaketaren batuketa egin behar da. Eremu elektrikoa iraunkorra denez,
edozein ibilbide itxitan ondoko integrala beti zero da:
biderkaketaren batuketa egin behar da. Eremu elektrikoa iraunkorra denez,
edozein ibilbide itxitan ondoko integrala beti zero da:

Integral horretan C delakoak eremu elektrostatikoan dagoen edozein ibilbide itxi adierazten du. Eremu magnetiko estatiko batean gauza bera egiten saiatuz gero, emaitza nahiko desberdina ateratzen da. Ibilbide itxi batean B · dl biderkaketaren batuketak ez du zertan zero izan behar. Honek, eremu magnetikoa ez dela kontserbakorra adierazten du.
Eremu magnetikoaren ezaugarri hau, Ampèreren legea delakoan azaltzen da:
Edozein ibilbide itxitan zehar eremu magnetikoaren lerroko integrala izango da ibilbide horrek mugaturiko edozein gainalde aldi kopuru bakoitiz igarotzen duen korronte guztiaren intentsitatea bider µ0 faktorea.
Ampèreren legea aplikatu ahal izateko, gainaldea igarotzen duten korronte elektrikoek egonkorrak izan behar dute. Gainera gainaldea aldi kopuru bakoitiz igarotzen duten korronteak bakarrik hartuko dira kontuan. Gainaldea aldi kopuru bikoitiz igarotzen dituztenen kasuan, efektuak orekatu egiten dira, eta ekarpen garbia zero da. Ampèreren legea matematikoki honela adierazten da:

non C delakoak eremu magnetiko estatikoan dagoen ibilbide itxia adierazten duen.
Bestalde, Ampèreren legea aplikatzean, oso kontuan hartu behar dira zeinuak. Eremu magnetikoaren noranzkoa ondo zehazteko, integrazio ibilbidea egiteko noranzko eta korronte intentsitatea ibilbideak mugaturiko gainaldean nola sartzen den kontuan hartu behar da. 7.6. irudian Ampèreren legean erabiltzeko zeinu hitzarmen bat ageri da. Geziekin azaltzen diren zirkunferentzia handiak integrazio ibilbideak dira, eta haien erdian korronte bat dute orritik ateratzen edo orrian sartzen dena. Lehenengo zutabean, × ikurraz adierazten diren korronteak orrian sartzen dira perpendikularrean. Bigarren zutabean, puntuarekin adierazten diren korronteak, berriz, orritik ateratzen dira perpendikularrean. Kasu bakoitzarentzat korronte intentsitateak hartu behar duen zeinua ere azaltzen da. 7.6. irudian ageri diren ibilbide itxiak zirkunferentziak dira, baina, edozein motako eitea eduki dezakete.
7.6. Irudia. Ampèreren legea aplikatzeko hitzarmenez erabil daitezkeen zeinuak
7.3. Zatiki kargadun higikorrek sorturiko eremu magnetikoa
Esan bezala, zatiki kargadunen higidurak sortzen du eremu magnetikoa. Hala ere, orain arte, korronte elektrikoek sorturiko eremu magnetikoak bakarrik aztertu dira. Beraz, oraindik ez da ikusi eremu magnetikoaren eta zatiki higikorren arteko harreman zuzena zertan den.

7.7. Irudia. Higitzen ari den zatiki kargadun baten eremu magnetikoa
Eman dezagun zatiki bat v lastertasunaz higitzen ari dela. Zatiki horrek bera dagoen lekutik r distantziara sortzen duen eremu magnetikoa adierazpen honen bidez kalkula daiteke:

Hemen ere, eremuaren norabidea biderkaketa bektorial batek zehazten du. Zatikiak sorturiko eremuaren norabidea berelastertasunarekiko elkarzuta da. 7.7. irudian ikusten den kasuan, adibidez, zatikiak P puntuan sorturiko eremu magnetikoa orrian perpendikularrean sartzen da.
Elkarrekintza elektrikoa eta magnetikoa oso estu lotuta daudela esan da aurreko gaiaren hasieran. Harreman hori aztertzeko zatiki kargadun bakar baten eremu elektrikoaren adierazpen matematikoa kontuan hartzea komeni da:

Zatikiak sorturiko bi eremuen ekuazioak erabiliz ikusiko da bien arteko lotura. Horrela, adierazpen hau lortzen da:

Bi eremuen arteko erlazioan zatikiaren lastertasuna agertzen da. Ez da harritzekoa hala izatea, lastertasunik gabe ez baitago er emu magnetikorik, ekuazioan azaltzen den bezala. Aipagarria da, orobat, zatikiaren eremu magnetikoa eremu elektrikoarekiko elkarzuta dela
7.4. Solenoideen eremu magnetikoa
Helize baten modura kiribilduta dagoen eroaleari ematen zaio solenoide izena. Bere zeregina, espazioko gune txiki batean indar handiko eremu magnetiko uniformea sortzea da. Elektrikan xafla paraleloekiko kondentsadoreak betetzen duen zeregin bera betetzen du solenoideak magnetikan. Elektrikako 3. gaian ikusi zen bezala, xafla paraleloekiko kondentsadoreak eremu elektriko uniforme bat sortzen du bere xaflen artean.

7.8. Irudia. Solenoide trinko baten eremu lerroak.
Solenoidearen eremu magnetikoa espira berdintsu askok sortzen dituzten eta elkarren gainean jarrita dauden eremu magnetikoez osatua da. Solenoidearen barruan, espiren eremu magnetikoak batu egiten dira, eta kanpoaldean elkar ezabatzen dute, oro har. 7.8. irudian eremu lerroen dentsitatea aztertuz, solenoidearen barruan eremu magnetikoa kanpoan baino askoz indartsuagoa dela ikusten da. Gainera, barrualdean eremu lerroak ardatzarekiko ia paraleloak dira, eta lerro guztien arteko distantzia ia berdina da. Beraz, barruan dagoen eremu magnetikoa indartsua eta ia uniformea da. Kanpoaldean, eremu lerroen dentsitatea askoz txikiagoa da, eta gainera, dibergenteak dira lerroak. Lerroak solenoidearen mutur batetik dibergentzian irteten dira, eta beste muturretik konbergentzian sartzen.

7.9. Irudia. Solenoide mugagabean Ampèreren legea aplikatzeko behar den zirkuitua
Solenoide mugagabearen kasuan, kanpoaldean ez dago eremu magnetikorik. Eremu magnetikoa barnealdean dago.
Ampèreren legea erabiliz kalkula daiteke solenoidearen barrualdean dagoen eremu magnetikoa. Horretarako, 7.9. irudian ikusten den C ibilbide itxia hartuko da oinarri. Solenoidearen kanpoaldean eremu magnetikoa zero denez, ibilbidearen kanpoaldean integrala zero da. Barrualdean ibilbidearen hiru zati daude. Hala ere, haietako bi zero dira. Zati horietan, eremu magnetikoa eta ibilbidea elkarzutak dira eta biderkaketa eskalarra egitean zero ateratzen da. Beraz, integralaren osagai bakarrak ondoko adierazpena ematen du:

Ampèreren legea aplikatzeko, C zirkuituak mugatzen duen gainaldean zehar zenbateko
intentsitatea pasatzen den zehaztu behar da. Solenoidearen l luzeran N bira baldin badaude,
eta zirkuituak solenoidearen b luzera hartzen duenez, zirkuituaren gainaldea zeharkatzen duten bira kopurua
 da.
Solenoidetik I intentsitatea l pasatzen baldin bada, orduan, Ampèreren legea honela geratzen da:
da.
Solenoidetik I intentsitatea l pasatzen baldin bada, orduan, Ampèreren legea honela geratzen da:
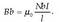
Intentsitaterako balio positiboa hartu da, 7.2. atalean azaldu den zeinu hitzarmenari jarraituz. Aurreko ekuaziotik eremu magnetikoa askatzen baldin bada:
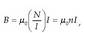
non n aldagaia solenoidearen luzera unitateko bira kopurua den.
Infinitoa izan gabe, edozein solenoideren kanpoaldean eta ardatzean dagoen eremu magnetikoa kalkula daiteke. Aztertu nahi den solenoidetik I intentsitatea igarotzen bada, solenoide horren epai perpendikularra A bada, eta luzera unitateko bira kopurua n bada, eremu magnetikoa honako adierazpenaren bidez azalduko da:
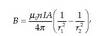
non 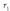 eremua
neurtzen ari garenetik solenoidearen mutur hurbilenera dagoen distantzia den, eta
eremua
neurtzen ari garenetik solenoidearen mutur hurbilenera dagoen distantzia den, eta
 , berriz, mutur urrutienera dagoena.
, berriz, mutur urrutienera dagoena.
7.10. irudian barra itxurako iman baten eremu lerroak ikus daitezke. Solenoidearen eremu lerroekin alderatzen badira(ikus 7.8. irudia), berdin-berdinak direla ikus daiteke. Beraz, solenoide baten eta iman baten portaera nahiko antzekoak direla esan daiteke.
7.10. Irudia. Barra itxurako iman baten eremu lerroak
Karl Ferdinand Braun,
(Fulda, 1850 - New York, 1918)
Alemanian jaio zen, eta Marburgo eta Berlingo unibertsitateetan egin zituen ikasketak. Alemaniako unibertsitate batzuetan lan egin zuen irakasle. I. Mundu Gerran Estatu Batuetara joan zen. Elektrika, magnetismoa, telegrafia eta termodinamika landu zituen batez ere. 1897. urtean, oszilazio elektrikoak aztertzeko izpi katodikoko hodi bat asmatu zuen. Hodi horri osziloskopio katodikoa esan zitzaion. 1898. urtetik aurrera, haririk gabeko telegrafoa aztertu zuen. 1909an Fisikako Nobel saria eman zioten hari eta G. Marconiri.
8. Gaia: indukzio magnetikoa
Aurreko gaietan aztertu denez, korronte elektrikoak eremu magnetiko bat sortzen du. Alderantzizko fenomenoa ere gertatzen dela ikusiko da gai honetan. Aurrera egin baino lehen hobe da ordea historiako jakingai batzuk gogoratzea. 1830eko hamarraldiaren bukaeran, Michael Faraday britainiar fisikariak (1791-1867) aurkikuntza garrantzitsu bat egin zuen. Konturatu zen eremu magnetiko aldakorrek korronte elektrikoak sortzen dituztela. Korronte horiei korronte induzituak esaten zaie. Baina gertaera hori ez zuen Faradayk soilik aurkitu. Zientzialari asko ari zen fisikaren alor hori ikertzen, eta Estatu Batuetako Joseph Henry fisikariak (1797-1878) aurkikuntza bera garai berean egin zuen. Eremu magnetikoak beraz korronte elektrikoa sortzen du.
Gaur egun erabiltzen diren tresna batzuk –dinamoak eta abar– efektu horretaz baliatzen dira korronte elektrikoa sortzeko. Tresna horiek energia elektrikoa sortzen dute energia mekanikotik. Alderantzizko lana egiten duten tresnak ere –motor elektrikoak eta– aurkikuntza horretan daude oinarrituta, eta energia mekanikoa sortzen dute energia elektrikotik.
8.1. Jario magnetikoa
Eremu elektrikoa aztertzerakoan egin zen bezala, eremu magnetikoa aztertzerakoan ere hobe da lehendabizi jario kontzeptua zer den ondo jakitea. Zenbait kasutan, kontzeptu hori erabiltzeak arazo asko saihesten ditu eta.
Gainalde bat igarotzen duen jario magnetikoa,
 , jario
elektrikoa bezalaxe definitzen da. Gainaldearen elementu diferentziala dA baldin bada,
eta B, eremu magnetikoaren bektorea, orduan hau da jario magnetikoaren adierazpen matematikoa:
, jario
elektrikoa bezalaxe definitzen da. Gainaldearen elementu diferentziala dA baldin bada,
eta B, eremu magnetikoaren bektorea, orduan hau da jario magnetikoaren adierazpen matematikoa:

formula horretan  bektore unitarioa da, gainaldeko puntu bakoitzean gainaldeari buruz perpendikularra dena.
bektore unitarioa da, gainaldeko puntu bakoitzean gainaldeari buruz perpendikularra dena.
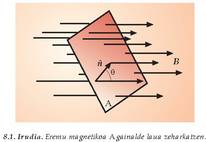
Demagun A gainaldea laua dela (ikus 8.1. irudia). Eremu magnetikoa uniformea baldin bada, hau da, balio eta norabide berbera baldin badu puntu guztietan, lehengo adierazpen hori askoz soilagoa da orduan:

formula horretan  eremu magnetikoak eta
eremu magnetikoak eta 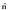 bektore unitarioak sortzen duten angelua da.
bektore unitarioak sortzen duten angelua da.
Jario magnetikoaren banakoak Weber du izena, eta Wb du ikurra. Hauek dira bere dimentsioak eta beste banakoekin duen harremana:

Elektrikako 1. ikasgaian gainalde itxi batean dagoen eremu elektrikoaren jarioa aztertu da. Jario elektrikoa gainaldearen barrutik ateratzen diren eremu lerroen proportzionala da. Alegia, barruan dagoen karga garbiaren proportzionala da jarioa, Gaussen legeak dioen bezala. Baina eremu magnetikoa eta elektrikoa elkarren oso bestelakoak dira. Eremu magnetikoko lerroak jarraituak dira, ez dira ez sortzen eta ez bukatzen. Beraz, eremu lerro kopuru berberak sartu eta atera behar du gainalde itxi batean. Hori dela eta, gainalde itxi bateko jario magnetiko garbia zero da beti:

formula horretan  haren integrazioa egiten ari garen gainalde itxia da. Monopolo magnetikorik ez egoteak sortzen du desberdintasun hori.
Eremu magnetikoaren lerroek ez baitute ez non "sortua", ez non "bukatua".
haren integrazioa egiten ari garen gainalde itxia da. Monopolo magnetikorik ez egoteak sortzen du desberdintasun hori.
Eremu magnetikoaren lerroek ez baitute ez non "sortua", ez non "bukatua".
Zirkuituetan eragina duten indarren eta jario magnetikoaren aldaketen arteko harremana aztertu beharra dago.
Demagun eremu magnetiko baten baitan dagoen zirkuitu bat (ikus 8.2. irudia). Zirkuitu horrek,
korronte elektrikoa daramanez, momentu magnetiko bat du: m. Zirkuituari eragiten zaion indar pareak,
 , eremuaren n
orabidea harrarazten dio zirkuituaren momentu magnetikoari. Norabide horretan du baliorik handiena
zirkuitua zeharkatzen duen jario magnetikoak, baldin eta momentu magnetikoak jario magnetikoaren
noranzko berbera badu. Beraz, oro har, eremu magnetiko uniforme batean edozein zirkuituri eragiten dioten
indarrek jario magnetikoa handitzeko joera izaten dute beti.
, eremuaren n
orabidea harrarazten dio zirkuituaren momentu magnetikoari. Norabide horretan du baliorik handiena
zirkuitua zeharkatzen duen jario magnetikoak, baldin eta momentu magnetikoak jario magnetikoaren
noranzko berbera badu. Beraz, oro har, eremu magnetiko uniforme batean edozein zirkuituri eragiten dioten
indarrek jario magnetikoa handitzeko joera izaten dute beti.

8.2. Irudia. Korronte elektrikoa duen zirkuitu bat kanpoko eremu magnetiko baten barnean
Arestian esandako guztia 8.3. irudian ikus daiteke. Lehenengo irudian iman batek edo solenoide batek sortzen dituen eremu lerroak ageri dira, bigarrenean, berriz, dipolo elektriko batek sorturikoak. Imanaren edo solenoidearen kanpoaldean sortzen den eremu magnetikoaren lerroak eta dipolo elektrikoak sortzen duen eremu elektrikoaren eremu lerroak antzekoak dira. Baina imanaren edo solenoidearen barrenaldean sortzen den eremu magnetikoaren lerroaketa dipoloak sortzen duen eremu elektrikoaren eremu lerroak ez dira antzekoak. Eremu magnetikoan eremu lerroak itxi egiten dira, eta eremu elektrikoan, berriz, kargatzen “hasi” eta “bukatzen” dira.
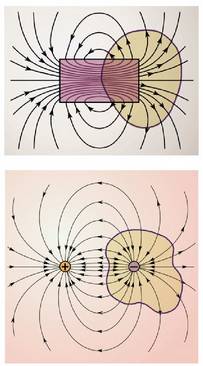
8.2. Faradayren legea
Faradayk eta beste zientzialari batzuek egindako ikerketak erlazio erraz batean laburbiltzen dira.
Erlazio hori definitzeko, demagun zirkuitu itxi bat mugatzen duen gainaldeak jario magnetiko bat duela,
 Jario horretan edozein aldaketa gertatzen bada, indar elektroeragile bat azalduko da zirkuituan.
Fenomeno horri Faradayren legea esaten zaio, eta honela adierazten da matematikoki:
Jario horretan edozein aldaketa gertatzen bada, indar elektroeragile bat azalduko da zirkuituan.
Fenomeno horri Faradayren legea esaten zaio, eta honela adierazten da matematikoki:

formula horretan  indar elektroeragilea da. Indar elektroeragilea zirkuituan agertzen den korronte elektriko
baten bidez neurtzen da (ikus 8.4. irudia).
indar elektroeragilea da. Indar elektroeragilea zirkuituan agertzen den korronte elektriko
baten bidez neurtzen da (ikus 8.4. irudia).
Eremu elektriko ez-elektrostatikoak karga zirkuitu itxiari bira oso bat ematen dionean sortzen duen karga unitateko lana da indar elektroeragilea.
Eremu elektriko elektrostatiko batek zirkuitu itxi batean zehar karga eramaten duenean, haren lana zero da, iraunkorra baita. Indarelektroeragilea pila batek sortzen duenean, eremu ez-elektrostatikoa bi borneen artean egoten da, eta pila barruko kargek dituzten erreakzio elektrokimiko ez-kontserbakorren ondorioa izaten da. Indar elektroeragilea eremu magnetiko aldakor baten ondorioa denean, eremu ez-elektrostatikoa ez dago leku jakin batean, zirkuituko puntu guztietan dago. Eremu elektriko hori bada, izan, eroalerik edo beste materialik ez egon arren.

8.4. Irudia. Jario magnetikoa aldatzeak indar elektroeragile bat sortzen du zirkuituan, eta, beraz, korronte elektrikoa sortzen da.
E eremu elektrikoa ez-elektrostatikoa baldin bada, zirkuituaren ibilbide itxiko
 biderkaketaren
integrazioa izango da eremu horrek karga unitateko egiten duen lana. Beraz, integrala zirkuituaren indar elektroeragilea da:
biderkaketaren
integrazioa izango da eremu horrek karga unitateko egiten duen lana. Beraz, integrala zirkuituaren indar elektroeragilea da:

formula horretan C-k zirkuituaren ibilbidea adierazten du. Zirkuituan zehar dagoen jario magnetikoa era askotara alda daiteke: iman iraunkorrak zirkuitutik hurbildu edo urrundu egin daitezke, zirkuituaren gainaldea aldatu egin daiteke eremu magnetikoa egonkorra denean, zirkuituak jario magnetikoaren iturriarekiko duen kokalekua alda dezake…
Michael Faraday
(Newington Butts, 1791 - Hampton Court, 1867)
Britainiar fisikaria eta kimikaria. Hasierako ikerketetan bentzenoa aurkitu zuen. Korronte elektriko batek iman batean sortzen dituen aldaketei ohartu zitzaien gero. Horrela aurkitu zituen imanek eta korronteek elkarren artean dituzten eraginak. 1831. urtean indukzio elektromagnetikoaren aurkikuntzaren berri eman zuen, eta gertaera hori aurkitu izanari esker, lehen dinamoa sortu zuen. 1834. urtean gatz disoluzioen deskonposatzearen legeak eman zituen, elektrolisiarenak, alegia. Hark erabili zituen lehendabizi anodo eta katodo izenak tresna elektrolitikoan dauden elektrodo positibo eta negatiboa definitzeko. Diamagnetismoa ere aurkitu zuen (1846), eta baita diamagnetismoak kristalaren indarrarekin duen harremana ere (1849). Haren aurkikuntzak oso garrantzitsuak izan ziren, eta bidea erraztu zioten Maxwell-i teoria elektromagnetikoaren formulazio zehatza egiteko. Haren garaian ezagutzen ziren ia gas guztiak isurkari bihurtzea lortu zuen. Kapazitate elektrikoaren banakoak haren izena du: faraday (F).
8.3. Lenzen legea
Indar elektroeragile induzituaren balioa Faradayren legearen bidez jakin daiteke. Baina indar elektroeragilearen eta berari dagokion korronte elektrikoaren norabidea eta noranzkoa zeintzuk diren jakin beharra dago lehenengo. Badago adierazpen orokor bat horretarako. Adierazpen horri Lenzen legea esaten zaio, eta hau dio:
Korronte elektriko induzituaren noranzkoa beti da korronte hori eragin duen aldaketaren kontrakoa.
Horrek argitzen du Faradayren legean agertzen den zeinu negatiboa.
Hemen ez da zehazten indar elektroeragile induzituak sortzen duen aldaketa zein motatakoa den, eremu magnetikoaren aldaketa nola eta zergatik gertatzen den, alegia. Hala ere, ez da jarioaren aldaketa zertan zehazturik, Lenzen legea orokorra baita.
8.4. Higidurazko indar elektroeragilea

8.5. Irudia. Eremu magnetikoan hari eroale baten higidurak karga metatzen du eroalearen muturretan.
Lenzen legea hobeto ulertzeko, higiduraren bitartez sortzen den indar elektroeragilea aztertuko da. Horretarako, 8.5. eta 8.6. irudietan ageri diren sistemak erabiliko dira.
Demagun hari eroale bat erresistentzia bati eta etengailu bati loturiko bi eroale paraleloen gainetik higitzen dela, ikus 8.5. irudia. Irudian ageri den tresna horretan eremu magnetiko bat dago, eta haren norabidea eta noranzkoa orriari buruz elkarzut dago. Tresna horren bidez hobeto ulertuko dira zirkuituetako karga eramaileen gainean dauden indarrak. Harian dauden karga eramaileen zeinua positiboa baldin bada, eta haria eskuinerantz v lastertasunaz higitzen baldin bada, karga eramaileen gainean dagoen indarmagnetikoa, F = q v × B, paraleloa da hariari buruz eta gorantzako noranzkoa du. Etengailua irekita baldin badago, harian zehar banatuko da karga, Hall efektuan gertatzen den moduan. Beraz, karga positiboa hariaren goialdean pilatuko da, eta karga negatiboa, behealdean. Horrelako karga eramaile positiboak hariaren goialdera joango dira, karga banaketak sortu duen indar elektrostatikoak indar magnetikoa konpentsatzen duen arte. Hariaren lastertasuna eta eremu magnetikoa bata besteari buruz elkarzutak direla kontuan hartuta, hau da eremu elektriko horren modulua:

Horren arabera, 8.5. irudiko 2. puntuaren potentziala, 1. puntukoa baino handiagoa da. Bi puntu horien artean dagoen potentzial diferentzia hau da:
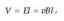
non l bi puntuen arteko distantzia baita, hari eroalearen luzera, alegia.
Erreferentzia sistema aldatuz gero, eta hari eroalea geldirik daukan beste erreferentzia sistema hartuz gero, bi eroale paraleloak eta eremu magnetikoa higikorrak izango dira. Erreferentzia sistema horretan, hari eroaleko kargek ez dute inolako indar magnetikorik izango. Hala ere, hari horretako karga banaketa mantendu egingo da indar ez-iraunkor baten bidez. Hau da, karga banaketak sorturiko indar elektrikoaren kontra egiten duena da indar ez-iraunkorra, eta qvB du balioa. Hala, indar ez-iraunkorrak karga batean egiten duen lana qvBl da l distantzia egiten duenean. Beraz, vBl da karga unitateko lana, edo beste hitzetan esanda, zirkuituaren indar elektroeragilea.
Indar elektroeragile hori Faradayren legearen bidez ere lor daiteke. Horretarako, zirkuituaren etengailuak itxita egon behar du (ikus 8.6. irudia). Hari eroalea ezkerreko muturretik x distantziara baldin badago, zirkuitu horretan dagoen jario magnetikoa hau izango da:

Beraz, denbora unitateko jario magnetikoaren aldaketa hau izango da:

Emaitza berbera da beraz.

8.6. Irudia. Kasu honetan hari eroalearen higidurak korronte elektrikoa sortzen du eremu magnetikoan
Hala bada, zirkuituaren etengailua itxita badago, hari eroalea higitzeak korronte elektrikoa sortuko du. 8.6. irudian agertzen den korronte elektrikoaren noranzkoa Lenzen legearen bidez jakin daiteke. Lenzen legearen arabera, korronte induzituak jario magnetikoaren aldaketaren kontrako noranzkoa izango du. Kasu honetan jario magnetikoa orrian sartzen da, eta handitu egiten da haria higitzean. Korronte induzituak erlojuaren orratzen kontrakoa du noranzkoa. Beraz, korronteak sortzen duen eremu magnetikoa orritik ateratzen da, eta ez dio handitzen uzten jario magnetikoari. Beraz, sistema horrek hasierako egoerara bihurtzeko joera du. Baina sistema horren jario magnetikoa handitzen bada, korronte induzituak txikitu egingo du jarioa. Gerta daiteke baita ere hari eroalea ezkerrerantz higitzea eskuinerantz higitu beharrean, korronte induzituak erlojuaren orratzen noranzko berbera izango du orduan, eta ez dio jario magnetikoari txikitzen utziko.
Zirkuitu hori eremu magnetiko batean baldin badago, eta korronte elektrikoa baldin badu orobat, indar magnetiko bat sortzen zaio gainean. Hari higikorrari eragiten dion indarra du indar horrek osagai nagusia. Korronteak harian barrena gorantz egiten duenez, eta eremu magnetikoa orrian sartzen denez, indar horrek ezkerrerantz egiten du. Eta balio hau du:
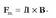
Indar horrek kontra egiten dio hariaren higidurari. Beraz, higidura edo korronte elektrikoa mantendu nahi izanez gero, hariari IlB balioko beste indar batez eragin behar zaio kontrako noranzkoan, eskuinerantz hain zuzen. Horrela, hari horren higiduraren lastertasuna konstantea izango da, eta korronte elektrikoa mantendu egingo da
Jean Bernard Léon Foucault
(Paris, 1819 - 1868)
Frantses fisikaria. Astrofisika eta astronomia izan zituen lan alor nagusiak. Hura izan zen astronomian fisika erabili zuen lehenengotaeko bat. 1851. urtean Lurraren errotazio higidura frogatu zuen bere izena duen penduluaren bidez. Pendulu hori Pariseko Panteoiko kupulan jarri zuen. Giroskopioa ere asmatu zuen 1852. urtean. Eroale metalikoetan eremu magnetiko aldakorrez induzitutako korronte elektrikoak aurkitu zituen, Foucaulten korronteak edo korronte parasitoak esaten zaienak. Argiak airean eta uretan duen lastertasuna ere kalkulatu zuen. Oso zientzialari emankorra izan zen.
8.5. Foucaulten korronteak
Arestian aztertu diren kasuetan, jario magnetikoa aldatzeak sortzen dituen korronte elektrikoak zirkuitu jakin batzuetan daude. Baina jarioa aldatzeak bestelako korronteak sor ditzake eroalearen zati handi batean. Korronte horiei Foucaulten korronteak esaten zaie, Jean Bernard Léon Foucault frantses fisikariak (1819-1868) aurkitu baitzituen. Era horretako korronteak tresna elektriko jakin batzuetan agertzen dira, horien artean transformadoreen nukleoa da ezagunena.

8.7. Irudia. Eroale baten zati bat elektroiman baten poloen artean. Zirkunferentziak elektroimanaren poloak adierazten ditu. X ikurrak eremu magnetikoa orriari buruz elkarzut sartzen dela adierazten du.
8.7. irudiak adierazten duen bezala, eroale baten zati bat elektroiman baten poloen artean baldin badago, eta poloen arteko eremumagnetikoa aldatzen bada, orobat aldatuko da eroalearen barruko edozein zirkuitu itxi zeharkatzen duen jario magnetikoa. Elektroimanaren zirkuituan korronte aldakor bat ssrtzeak jario hori aldaraziko du. Adibidez, C zirkuitu itxiko jario magnetikoa eremu magnetikoaren balioa eta zirkuituaren azalera biderkatuz ateratzen da. Eremu magnetikoa aldatzeak jario magnetikoa ere aldatzea dakar, eta, beraz, indar elektroeragile bat induzituko da zirkuitu horretan zehar. Ibilbide hori eroalea denez, korronte elektrikoa sortuko du, eta haren balioa materialaren erresistentziaren eta indar elektroeragile induzituaren bitartez jakin daiteke. 8.7. irudian ibilbide edo zirkuitu bakarra baizik ez dugu irudikatu, eroalearen zati horretan asko baitira, izan, ibilbideak.
Foucaulten korrontea existitzen dela frogatzeko, badago esperimentu bat egitea. Xafla eroale bat behar da horretarako, indar handiko iman iraunkor baten poloen artean jarria (ikus 8.8. irudia). Eremu magnetikoak C ibilbide itxiak ixten duen gainaldearen zati bat zeharkatzen du, gainontzekoa, berriz, eremu horretatik kanpo dago. Irudian ageri denez, eremu magnetiko hori orriari buruz elkarzut sartzen baldin bada, eta xafla eskuineko aldetik ateratzen bada, gainalde osoko jario magnetikoa gutxitu egingo da. Faradayren eta Lenzen legeen arabera, C ibilbidean korronte induzitu bat sortuko da erlojuen orratzen norabidean. Eremu magnetikoaren eraginpean dagoen zirkuitu honen zatian hiru norabide nagusi ditu korronteak. Beraz, korronte elektrikoak indar magnetiko bakarra pairatuko du, eremu magnetiko batean murgildurik baitago. Arestian aipatu diren hiru norabide horietatik bi konpentsatu egiten dira, eta gorantz doanak baizik ez du sortuko indarra. Ezker aldera joko duen indar magnetiko horrek arestian eman diren legeetan du azalpena. Hala, xafla azkar ateratzen saiatuz gero, aise antzemango zaio indar horien eraginari.

8.8. Irudia. Eroalearen zati bat (Cu, Al,…) ateratzean indar magnetiko batek kontra egiten dio higidura horri
Foucaulten korronteak oso kaltegarriak izaten dira, bero handia sortzen baitute eta ahalmena galarazten baitiote tresnari, Joule efektuaren eraginez. Bero hori disipatzeak ere lanak ematen ditu. Foucaulten korronteen ibilbidea txikitzeko ahaleginak egiten dira, arazorik sor ez dezaten. Bi teknika erabiltzen dira horretarako: lehenengoan, material eroalea xaflatan banatzen da (ikus 8.9. a) irudia); bigarrenean, ebaki batzuk egiten zaizkio materialari (ikus 8.9. b) irudia) korronte induzitua txikiagoa izan dadin horrela, eta horrenbesteko galerarik egin ez dezan.
Foucaulten korronteak oso kaltegarriak badira ere, probetxuzko erabilerak ere badauzkate; garrantzi handia dute indukziozko labeetan eta makina askoren balaztetan.
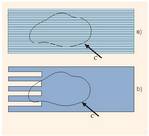
8.9. Irudia. Foucaulten korronteek sortzen dituzten arazoak saihesteko bi teknika: xaflen bidez (a), eta eroalearen zati batean ebakiak eginez (b).
8.6. Induktantzia
Inguruan iman iraunkorrik ez duen zirkuitu bat igarotzen duen jario magnetikoa harremanetan dago bere baitatik igarotzen den korrontearekin eta inguruko zirkuituak zeharkatzen dituzten korronteekin. Harreman hori argitzeko, adibide bat aztertuko dugu.
8.10. Irudia. Elkarrengandik hurbil dauden bi zirkuitu elektriko
Jario magnetikoaren mendekotasuna aztertzeko, 8.10. irudian ageri diren zirkuituak
hartuko dira kontuan. A puntuan dagoen eremu magnetikoa bi zirkuituetako
korronteek sortua da. Eremu hori proportzionala da bi korronteekiko, eta B
iot-Savarten legearen bidez kalkulatzen da. Beraz, 2. zirkuitua zeharkatzen duen jario magnetikoa
kalkulatu nahi izanez gero, 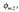 ,
bi osagaien batuketa egin beharko da. Bata proportzionala da
,
bi osagaien batuketa egin beharko da. Bata proportzionala da
 intentsitatearekiko, eta bestea,
intentsitatearekiko, eta bestea,
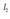 intentsitatearekiko da proportzionala:
intentsitatearekiko da proportzionala:
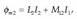
non  eta
eta
 konstanteak baitira.
konstanteak baitira.
 -ri 2. zirkuituaren autoindukzio
koefizientea edo induktantzia esaten zaio, eta 2. zirkuituko egitura geometrikoaren mende dago.
-ri 2. zirkuituaren autoindukzio
koefizientea edo induktantzia esaten zaio, eta 2. zirkuituko egitura geometrikoaren mende dago.
 -ri, berriz,
bi zirkuituen arteko elkarinduktantzia esaten zaio, eta bien artean dagoen antolamendu geometrikoaren
mende dago, distantziaren, orientazioaren, eta horrelakoen mende, alegia. Beste zirkuituaren jario
magnetikoa modu berean kalkulatzen da:
-ri, berriz,
bi zirkuituen arteko elkarinduktantzia esaten zaio, eta bien artean dagoen antolamendu geometrikoaren
mende dago, distantziaren, orientazioaren, eta horrelakoen mende, alegia. Beste zirkuituaren jario
magnetikoa modu berean kalkulatzen da:

non  1. zirkuituko geometriaren mende baizik ez baitago, eta
1. zirkuituko geometriaren mende baizik ez baitago, eta
 berriz, zirkuituen artean
dagoen antolamendu geometrikoaren mende. Hala ez badirudi ere, froga daiteke
berriz, zirkuituen artean
dagoen antolamendu geometrikoaren mende. Hala ez badirudi ere, froga daiteke
 eta
eta
 berdinak direla kasu guztietan,
baina hori ez da hemen frogatuko.
berdinak direla kasu guztietan,
baina hori ez da hemen frogatuko.
Kasu berezi bat aztertuko dugu adibide gisa. Demagun zirkuituak finko daudela, eta korronteak baino ez direla aldatzen. Orduan, Faradayren legearen arabera, hauek izango dira zirkuitu horien indar elektroeragileak:
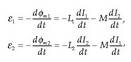
formula horretan elkarinduktantziaren azpi-indizeak kendu dira.
Induktantzia edo autoindukzio koefizientearen banakoak Henry du izena J. Henry (1797-1878) Estatu Batuetako fisikariaren omenez, eta H du ikurra.

Zirkuitu guztiek gutxi-asko induktantzia badute ere, zirkuitu jakin bateko elementu batzuen induktantzia zirkuituarena berarena baino handiagoa izaten da maiz. Elementu horien induktantzia nagusitzen zaio orduan zirkuituaren induktantziari berari. Elementu horiei induktoreak deritze.

8.11. Irudia. Zirkuitu elektrikoetan induktoreak adierazteko erabiltzen den ikurra.
Induktoreak bi eratara elkar daitezke, erresistentziak eta zirkuituetako beste elementuak bezalaxe: seriean edo paraleloan. Demagun induktoreek ez dutela elkarren artean eraginik, orduan bi elkartze mota horien eragin bereko induktantzia aurki daiteke. Horretarako, kontuan hartu behar da induktore guztiek nolabaiteko erresistentzia izaten dutela. Beraz, elkartze horietan erresistentziak ere egoten dira, induktantziez gainera.

8.12. Irudia. Induktore batzuk seriean elkartuta; haien erresistentziak ere ageri dira.
a) Serieko elkarketa
Demagun zirkuitu batean N induktore seriean daudela elkartuta (ikus 8.12. irudia).
Induktore bakoitzaren induktantzia  baldin bada, eta bakoitzaren erresistentzia
baldin bada, eta bakoitzaren erresistentzia
 baldin bada,
korronte elektrikoa igarotzean zirkuituaren muturretan dagoen potentzial diferentzia,
baldin bada,
korronte elektrikoa igarotzean zirkuituaren muturretan dagoen potentzial diferentzia,
 hau da
hau da

non  zirkuituko induktoreen indar elektroeragileak diren. Induktore guztien indar elektroeragileen
adierazpenak ordezkatzen badira aurreko ekuazioan:
zirkuituko induktoreen indar elektroeragileak diren. Induktore guztien indar elektroeragileen
adierazpenak ordezkatzen badira aurreko ekuazioan:

Orduan hau da elkartze horretan eragin bereko induktantzia:

alegia, serieko elkartzean, eragin bereko induktantzia induktore guztien induktantzien batura da, erresistentzien kasuan bezala.
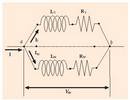
8.13. Irudia. Induktore batzuk paraleloan elkartuta
b) Elkarketa paraleloa
N induktore paraleloan baldin badaude elkartuta haien eragin bereko induktantzia kalkula daiteke. Baina elkartze paraleloan aurreko kasuan baino askoz nekezago atera daiteke eragin bereko induktantzia. Beraz, emaitza baizik ez dugu emango. L baldin badazirkuituaren eragin bereko induktantzia, eta Li, induktoreen induktantziak, emaitza hau da:

Joseph Henry
(Albany, 1797 - Washington, 1878)
Estatu Batuetako fisikaria. Albany-ko akademian egin zituen ikasketak; matematika eta filosofia naturaleko irakasle izendatu zuten unibertsitate horretan bertan. 1830. urtean, lehenengo telegrafo elektromagnetikoa sortu zuen. Autoindukzioa aztertzea izan zen (1832) elektromagnetismoan egin zuen ekarpenik nagusia. Urte hartan bertan New Jersey-ko Eskolara (gaur egun Princeton-eko Unibertsitatea du izena) joan zen irakasle. Gasak isurkaritan disolbatzeari buruzko legea aurkitu zuen, Henry legea esaten zaiona. Nazioarteko sisteman induktantzia banakoak haren izena du: henry (H). S. F. B. Morse-rekin polemika gogor bat izan zuen, zeinek beretzak baitzeukan telegrafo elektrikoaren aurkikuntza.
8.7. Energia magnetikoa
Erresistentzia eta autoinduktantzia duen zirkuitu bati korronte elektrikoa ezartzen zaionean, bateriaren energiak zati bat baizik ez du berotzen, Joule efektuaz endekatzen dena hain zuzen, beste zatia bobinan pilatzen da. Matematikoki honela adierazten da hori:
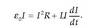
Lehenengo osagaiak, 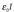 ,
indar elektroeragileak sortzen duen energiarenlastertasuna adierazten du. Bigarren osagaian bi zati daude,
bata,
,
indar elektroeragileak sortzen duen energiarenlastertasuna adierazten du. Bigarren osagaian bi zati daude,
bata,  , energia elektrikoak
erresistentzian bero bihurtzeko behar duen lastertasuna da, eta bestea,
, energia elektrikoak
erresistentzian bero bihurtzeko behar duen lastertasuna da, eta bestea,
 ,
energiak bobinan pilatzeko behar duen lastertasuna.
,
energiak bobinan pilatzeko behar duen lastertasuna.
Zirkuitu zurrun bakar batean pilatutako energia magnetikoa era honetara adierazten da:

non L zirkuituaren autoindukzio koefizientea den, I zirkuitutik igarotzen den intentsitatea,
eta  zirkuitua zeharkatzen duen jario magnetikoa. Ekuazio horrek informazio interesgarria ematen du.
Adibidez, zirkuitua igarotzen duen intentsitatea handitzen baldin bada, zirkuituaren energia magnetikoa ere handitu egiten da.
zirkuitua zeharkatzen duen jario magnetikoa. Ekuazio horrek informazio interesgarria ematen du.
Adibidez, zirkuitua igarotzen duen intentsitatea handitzen baldin bada, zirkuituaren energia magnetikoa ere handitu egiten da.
Hemen frogatuko ez bada ere, azken adierazpen hori orokorra izan daiteke. Demagun N zirkuitu egonkor eta zurrun daudela,
eta bakoitzaren intentsitatea eta jario magnetikoa, besteak beste,
 eta
eta  direla. Hortaz, zirkuitu sisteman pilatzen den energia magnetikoa adierazpen honen bidez kalkulatzen da:
direla. Hortaz, zirkuitu sisteman pilatzen den energia magnetikoa adierazpen honen bidez kalkulatzen da:
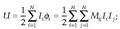
non  zirkuituen elkarren arteko induktantziak eta autoindukzio koefizienteak diren
zirkuituen elkarren arteko induktantziak eta autoindukzio koefizienteak diren

Energia magnetikoa kalkulatzeko aztertu den guztiak orobat balio du zirkuituko elementu guztientzat ere, solenoide, bobina eta, oro har, induktoreentzat, alegia
9. Gaia: magnetismoa materian
Eremu elektrikoak materian duen eragina aztertzean (ikus 3. gaia) dipolo elektrikoek eremu elektrikoaren aurrean duten portaera aztertu dugu. Eremu elektrikoan bi kasu bereizten dira: alegia, batetik, materialaren molekulak polarrak direnekoa, eta, bestetik, polarrak ez direnekoa. Eremu magnetikoak materian duen eragina ikertzean antzeko fenomenoak agertzen direla ikusiko dugu. Nolanahi ere, Magnetikako fenomeno horiek Elektrikakoak baino katramilatsuagoak dira, ikusiko denez.
Bere garaian A.M. Ampère material magnetikoen portaera aztertzen ahalegindu zen. Lehen ere aipatu dugunez (ikus 7. gaiaren sarrera), Ampèrek eredu bat prestatu zuen iman iraunkorrek duten magnetizazioa azaltzeko; imanen barruan korronte elektriko mikroskopikoak zeudela uste izan zuen. Korronte elektriko horiek —Ampèreren korronteak deituak— espira mikroskopiko modukoak zirela pentsatu zuen. Espira bakoitzak, beraz, momentu magnetikoa izan behar zuen elkarturik. Bere ereduan, material ez-magnetikoetan, zorizko orientazioa dute espirek. Eta horren ondorioz, material horietan, momentu magnetikoen efektu garbia zero da. Material magnetikoetan, berriz, lerro multzo bat-edo eratzen dute espirek, eta eremu magnetiko garbia sortzen dute. Egia esateko, Ampèreren eredua nahikoa zuzena da, eremu magnetiko guztiak korronte elektrikoren batek sortuak balira bezala azaltzen delako. Hala ere, Ampèreren korronteak, berak uste zuena baino askoz ere korapilotsuagoak dira. Korronte horiek atomoetan eta molekuletan gertatzen dira, eta ezin dira Mekanika Klasikoaren bitartez azaldu; Quantumen Mekanikara jo behar da horretarako. Liburu honetan bertan, beste atal batean azaltzen den bezala, elektroien higidura behar bezala azalduko bada, Quantumen Mekanika erabili beharra dago derrigor.
9.1. Momentu magnetiko atomikoak eta magnetizazioa
Lehenago aipatu dugunez, atomo eta molekulen momentu magnetikoen azterketa egiteko Quantumen Mekanikaz baliatu behar gara. Elektroiek beraien higidura orbitalagatik eta spinagatik momentu magnetiko bat elkarturik dutela azaltzen du teoria horrek. Horrela, atomoa edo molekula osatzen duen elektroi kopurua eta beraien egoera kontuan hartuz, atomoaren edo molekularen momentu magnetikoa kalkula daiteke. Bestalde, momentu magnetikoaren banakoak A m2 direla gogoratu behar da (ikus 6.5. atala).
Material batean dauden momentu magnetikoek nolabaiteko antolamendua dutenean, momentu magnetiko makroskopiko bat agertzen da materialean. Antolamendua neurtzeko bolumen unitateko momentu magnetikoa edo magnetizazioa definitzen da, M alegia. Magnetizazioa kalkulatzeko momentu magnetikoen batuketa bektoriala egiten da. Hau da horren definizio matematikoa:
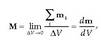
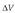 bolumenean dauden momentu atomikoak baitira
bolumenean dauden momentu atomikoak baitira  Magnetizazioa, beraz, materialean diren atomoen momentu magnetikoekin lot daiteke.
Momentu magnetikoaren banakoak kontuan harturik, hauek dira magnetizazioaren banakoak:
Magnetizazioa, beraz, materialean diren atomoen momentu magnetikoekin lot daiteke.
Momentu magnetikoaren banakoak kontuan harturik, hauek dira magnetizazioaren banakoak:

Normalean materiala magnetizaturik ez badago momentu magnetikoen batura zero izaten da. Kanpoko eremu magnetiko bat aplikatzen baldin badiogu, magnetizazioa aplikaturiko eremuaren mendekotasuna izango du. Kasu berezi gisa eman dezagun gai baten atomo edo molekula guztiek noranzko konkretu baterantz lerrokaturik dituztela beraien momentu magnetikoak. Kasu honetan, beraz, bolumen unitateko molekula kopurua (n) bider molekula bakoitzak duen momentu magnetikoa (m) izango da materialaren magnetizazioa:

Hemen, materiala osatzen duten molekula guztiek momentu magnetiko berdina dutela jo dugu.
Bestalde, materialean magnetizazioa asetasun balio batera iritsi da, eta ezinezkoa da balio
handiagorik hartzea. Horregatik,  magnetizazioari asetasun magnetizazioa
esaten zaio.
magnetizazioari asetasun magnetizazioa
esaten zaio.
9.2. Kitzikadura magnetikoa
Material bat magnetizatzen dugunean, kanpoko eremu magnetiko bat aplikatu behar dugu normalean. Hori egiten denean, kanpoko eremu hori eta materialaren magnetizazioak sortzen duena bereizteko, beste magnitude mota bat erabili ohi da. Magnitude hori definitzeko azter dezagun adibide hau.
Eman dezagun luzera banakoko n bira dituen solenoide batetik I intentsitatea igarotzen dela (ikus 9.1. irudia). Solenoideak bere ardatzean sortzen duen eremu magnetikoa edo indukzio magnetikoa hau da (ikus 7.4. atala):

Adierazpen hori zuzena izango bada solenoidearen muturretatik urrun egon behar gara. Muturren efektuak saihestu ahal izateko solenoidea oso luzea dela joko dugu kasu honetan. Praktikan, toroide bat erabil daiteke muturren efektuak guztiz saihesteko.

9.1. Irudia. Solenoidea material magnetiko baten inguruan kiribildua.
Solenoidearen barruko aldean material bat sartzen baldin badugu,
aurretik kalkulatu dugun solenoidearen eremu magnetikoak magnetizazio
bat sortuko du materialean. Horregatik, indukzio magnetikoa
kalkulatzean, kontuan izan beharko da materialaren magnetizazioa.
Materialaren bolumen banakoko magnetizazioa M bada,materialak sortzen duen eremu magnetikoa
 izango da.
Eremu hori aurrekoaren antzera defini daiteke:
izango da.
Eremu hori aurrekoaren antzera defini daiteke:

Beraz, solenoidearen ardatzean dagoen indukzio magnetiko garbia aurreko bien batura da, hots:

Ikusten denez, aurreko adierazpena batura bektoriala da. Kontuan hartzekoa da hori, kanpoko eremuak eta materialaren magnetizazioak kontrako noranzkoa baitute, ikusiko denez, diamagnetikoen kasuan.
Orduan, aplikaturiko eremu magnetikoa eta magnetizaturik dagoen materialak sortzen duen eremua bereizteko beste kontzeptu bat definitu ohi da. Magnitude berriak kitzikadura magnetikoa du izena, eta H ikurra. Azken ekuazioa hartuz, honela definitzen da kitzikadura magnetikoa:
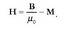
Honela adieraz daiteke eremu magnetiko garbia:

Azken bi ekuazio horiek orokorrak dira. Hau da, nahiz eta kasu jakin batean atera, beste edozein kasutarako
ere balio dute. Bestalde, ekuazioak ikusiz, kitzikadura magnetikoak eta magnetizazioak banako berdinak
dituztela ondoriozta daiteke, ampere metroko 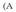
Solenoide luze batek bere ardatzean eragiten duen kitzikadura magnetikoa kalkula daiteke adibide gisa. Eragiketa erraz batzuk eginez, hau lortzen da:
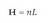
Hermann von Helmholtz,
(Postdam, 1821 - Berlin, 1894)
Fisikari eta fisiologo alemana. Berlinen egin zituen ikasketak, eta Bonn, Heidelberg eta Berlingo Unibertsitateetan izan zen irakasle. Bere garaiko jakintsu handietako bat izan zen. Alor asko landu zituen, eta horietan guztietan ekarpen garrantzitsuak egin zituen. Termodinamikan, 1847. urtean, energiaren iraupenaren hatsapena formulatu zuen. Elektromagnetismoan, berak sortuak dira Helmholtz-en “txirrikak”. Txirrika horiek eremu magnetiko uniforme bat sortzen dute espazioko eremu batean. Energia potentzialaren kontzeptua azaldu zuen. Akustikan, harmonikoak aurkitu zituen. Alor asko landu zituen: oftalmologia, otologia, meteorologia…
9.3. Kitzikaberatasun eta irazkortasun magnetikoak
Zenbait material magnetikotan, kitzikadura magnetikoaren proportzionala da magnetizazioa:

 proportzionaltasun
konstantea da, kitzikaberatasun magnetikoa esaten dena, hain zuzen. Magnetizazioak eta kitzikadura
magnetikoak banako berberak dituztenez, kitzikaberatasun magnetikoa dimentsiorik gabea da.
Kitzikaberatasun magnetikoak, bestalde, material magnetikoaren erantzuna ematen digu kanpoko
eremu magnetiko baten aurrean.
proportzionaltasun
konstantea da, kitzikaberatasun magnetikoa esaten dena, hain zuzen. Magnetizazioak eta kitzikadura
magnetikoak banako berberak dituztenez, kitzikaberatasun magnetikoa dimentsiorik gabea da.
Kitzikaberatasun magnetikoak, bestalde, material magnetikoaren erantzuna ematen digu kanpoko
eremu magnetiko baten aurrean.
Aurretik lortutako ekuazioei kitzikaberatasunaren emaitza aplikatzen baldin badiegu, hau lortzen da:
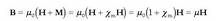
(konstanteari materialaren irazkortasuna esaten zaio. Hau da haren definizio matematikoa:

Irazkortasuna material konkretu batzuen deskripzioan erabiltzen da bereziki. Hurrengo ataletan aztertuko ditugu, eta material diamagnetiko eta paramagnetikoak dira. Oso kitzikaberatasun txikia izaten dute normalean, eta haien irazkortasuna hutsa-edo izaten da.
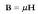 ekuazioa material ferromagnetikoen kasuan ere erabil
daiteke. Hala ere, material horietan zailagoa da ulertzea, magnetizazioa
ez baita kitzikadura magnetikoaren funtzio lineala. Gainera,
aurreko ekuazioaren irazkortasunak kitzikaduraren mendekotasuna
izateaz gainera material ferromagnetikoaren hasierako magnetizazio
egoerarena ere badu.
ekuazioa material ferromagnetikoen kasuan ere erabil
daiteke. Hala ere, material horietan zailagoa da ulertzea, magnetizazioa
ez baita kitzikadura magnetikoaren funtzio lineala. Gainera,
aurreko ekuazioaren irazkortasunak kitzikaduraren mendekotasuna
izateaz gainera material ferromagnetikoaren hasierako magnetizazio
egoerarena ere badu.
9.4. Material magnetikoak
Zer portaera duten, hainbat motatan sailka daitezke material magnetikoak: paramagnetikoak, diamagnetikoak, ferromagnetikoak, antiferromagnetikoak, ferrimagnetikoak, eta abar. Hala ere, liburu honetan material horietarik lehenengo hirurak baino ez ditugu aztertuko, horiek baitira garrantzitsuenak.
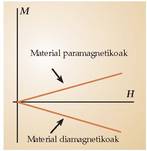
9.2. Irudia. Material paramagnetiko eta diamagnetikoen portaera kitzikadura magnetiko baten eraginpean
9.4.1. Material paramagnetikoak
Material paramagnetikoetan magnetizazioa eta kitzikadura magnetikoa proportzionalak dira; hau da, kitzikaberatasun magnetikoa konstantea da. Gainera, kitzikaberatasunaren balioa positiboa da:
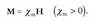
Eremu magnetiko baten eraginpean, beraz, materialak eremua indartzera joko du (ikus 9.2. irudia). Hau da, kanpoko eremuaz gain, materialak beste eremu magnetiko bat sortuko du norazko berberean.
Ikuspegi mikroskopikotik begiratuta, sustantzia paramagnetikoetan atomoek momentu magnetiko iraunkorrak dituzte. Momentu magnetiko horien arteko elkarrekintza oso ahula da. Kanpoko eremu magnetiko baten ezean, momentu magnetikoak arbitrarioki orientaturik daude. Baina sustantziari kanpotik eremu magnetiko bat aplikatzen baldin badiogu, momentuek kanpoko eremuaren norabidean lerrokatzera jotzen dute. Hala ere, bada kontuan hartu beharreko beste faktore garrantzitsu bat ere, atomoen higidura termikoa alegia. Horrek momentuen lerrokatzearen kontra egiten du, eta hori dela eta, lehia gertatzen da kanpoko eremuaren eta perturbazio termikoaren artean. Horregatik, kanpoko eremu magnetikoaren norabidean lerrokatzen diren momentu magnetikoen kopurua kanpoko eremuaren intentsitatearen eta tenperaturaren araberakoa da. Oso tenperatura apaletan eta oso eremu magnetiko handietan, momentu magnetiko gehienak eremuaren norabidean lerrokaturik daude. Kasu honetan, materialak sortzen duen eremu magnetikoa handia da. Tenperatura handietan eta eremu magnetiko txikietan, berriz, ia ez da momentu magnetiko lerrokaturik. Hori dela eta, materialak sortzen duen eremu magnetikoa txikia da. Tenperatura normalean eta kanpoko eremu arruntekin, oso momentu magnetiko gutxi dago lerrokaturik eremuaren norabidean.
Material paramagnetikoen portaera horiek guztiak lege batera laburtzen dira. 1885. urtean Pierre Curiek (1859-1906) material horien kitzikaberatasuna betetzen duen lege bat aurkeztu zuen. Material paramagnetikoen kitzikaberatasunak tenperaturaren mendekotasuna duela frogatzen da lege horretan. Lege horri Curieren legea esaten zaio. Hau da legearen adierazpen matematikoa:
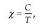
Adierazpen horretan C Curieren konstantea da. Kontuan hartu behar da ekuazioan ageri den tenperatura tenperatura absolutua dela. Beraz, tenperatura kelvinetan azaldu behar da ekuazioan.

9.1. Taula. Material paramagnetiko eta diamagnetiko batzuen kitzikaberatasun magnetikoa 20 °C-tan.
9.4.2. Material diamagnetikoak
Diamagnetismoaren fenomenoa M. Faradayk aurkitu zuen 1846. urtean. Garai hartan bismuto puska bat ikertzen ari zen, eta iman baten edozein polok alderatzen zuela ikusi zuen. Fenomeno bitxi hori ikustean, imanaren kanpoko eremu magnetikoak bismutoan eremuaren kontrako norabidea zuen dipolo magnetiko bat sortzen zuela pentsatu zuen. Material diamagnetikoen kasuan, beraz, materialak kanpotik aplikaturiko eremuaren kontrako erantzuna izaten du. Erantzuna, paramagnetikoena bezala, lineala da (ikus 9.2. irudia). Hori dela eta, material diamagnetikoek ere ekuazio hau bete behar dute:
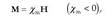
 materialaren magnetizazioa eta kitzikaberatasun magnetikoa dira; H, berriz, aplikaturiko
kitzikadura magnetikoa. 9.1. taulan zenbait material diamagnetikoren kitzikaberatasun magnetikoak ageri dira.
materialaren magnetizazioa eta kitzikaberatasun magnetikoa dira; H, berriz, aplikaturiko
kitzikadura magnetikoa. 9.1. taulan zenbait material diamagnetikoren kitzikaberatasun magnetikoak ageri dira.
Diamagnetismoa hobeto ulertzeko, Lenzen legea (ikus 8. gaia) erabiliko dugu maila mikroskopikoan. Material bat kanpoko eremu magnetiko baten eraginpean jartzean aldatu egiten dira bere atomoetako korronte elektronikoak, kanpoko eremuaren efektua txikitu ahal izateko. Eman dezagun bi karga positibo ditugula, eta beren higidura zirkularrean lastertasun berdina dutela, baina kontrako noranzkoa (ikus 9.3. a) irudia). Ezkerreko kargak higitzean sortzen duen momentu magnetikoa orritik ateratzen da perpendikularki, eta eskuineko kargarena orrian sartzen da perpendikularki. Hori dela eta, sortzen diren momentu magnetikoak konpentsatu egiten dira, eta ez dago momentu magnetiko garbirik. Ez da ahaztu behar material batean, edozeinetan, higitzen diren kargak negatiboak direla, elektroiak alegia. Adibide honetan, beraz, karga positiboak erabiltzeko arrazoia azalpena erraztekoa besterik ez da. Lehengo adibidea bera kanpoko eremu magnetiko baten eraginpean jarriko bagenu, interesagarria litzateke karga bien gaineko eragina aztertzea. 9.3. b) irudian, adibidez, kanpoko eremu magnetikoa orrian sartzen da. Orduan, Lenzen legearen arabera, eta zirkunferentziaren erradioa aldatzen ez dela ontzat hartuz, ezkerreko kargaren abiadura handitu behar da. Abiadura aldatze horrek agertzen den jario magnetiko berria berdinduko du. Eskuineko irudian, berriz, abiadura txikitu egiten da. Arrazoia berdina da; hau da, jario magnetikoaren aldaketa berdindu beharra. Eta hala, bi kargen higidura aldaketarengatik sortzen diren momentu magnetikoen aldaketak orritik irakurlearenganako noranzkoa du. Momentu magnetikoen aldaketak, beraz, kanpoko eremu magnetikoa berdintzera joko du. Ikusten denez, diamagnetismoa Lenzen legea atomoetan aplikatua dela esan daiteke.

9.4. Irudia. Material ferromagnetiko baten histeresi zikloa. Mr: erremanentzia magnetizazioa; Hc: eremu koertzitiboa; Ms: asetasun magnetizazioa
Diamagnetismoa materia guztian gertatzen da segur aski. Hala ere, material askotan paramagnetismo eta ferromagnetismo efektuakgerta daitezke aldi berean. Ferromagnetismoak diamagnetismokoak baino bortitzagoak direnez, diamagnetismoaren efektuak ezkutatuta geratzen dira. Diamagnetismoa, bestalde, oso garbi azaltzen da geruzak beteak dituzten atomoez osaturiko materialetan, atomo horiek ez baitute momentu magnetiko iraunkorrik. Horrela, efektu paramagnetiko guztiak ezereztu egiten dira, eta diamagnetismoa besterik ez da geratzen. Momentu iraunkorra duten atomoak ferromagnetikoak ez badira paramagnetikoak edo diamagnetikoak izango dira, materialean azaltzen den efektu nagusiaren arabera. Bestalde, diamagnetismoaren fenomenoak ez du inolako mendekotasunik tenperaturarekiko. Horrek eta tenperatura igotzean momentu iraunkorren lerrokatzea txikitzeak material guztiak —baita paramagnetikoak eta ferromagnetikoak ere— tenperatura handietan diamagnetikoak izatea eragiten dute.
Tximistorratza
Deskarga elektriko atmosferikoetatik babesteko sistema bakarra da. Eraikin baten goreneko puntan jartzen den metalezko ziri bat izaten da. Ziri hori, lurrera konektatuta dago kable baten bidez. Horrela, deskargari lurrera joateko bide erraz bat eskaintzen zaio, eta ez du eroalea ez den osagaietatik pasa beharrik (egurra, harria, zementua,...). Tximista mota desberdinak daudenez, ezin dezakegu esan tximistorratzaren instalazioa guztiz segurua denik. Baina, hala ere, tximistorratza edukita, tximistaren kalteak jasateko aukera asko jeisten da.
9.4.3. Material ferromagnetikoak
Ferromagnetismoa material gutxitan azaltzen da: burdina garbian (Fe), nikelean (Ni), kobaltoan (Co), metal horien arteko aleazioetan, beste zenbait elementutan (gadolinioa (Gd), disprosioa (Dy),...) eta material gutxi batzuetan. Kanpoko eremu magnetiko txiki batek magnetizazio handia eragiten du material horietan. Sortzen den magnetizazioa baino askoz handiagoa da aplikatzen den eremu magnetikoa.
Kanpoko eremu magnetiko baten aurrean material ferromagnetikoen erantzuna ez da lineala, material diamagnetikoen eta paramagnetikoen kasuan bezala. Beraz, ondoko adierazpena beteko da:

Bistan denez, material ferromagnetikoen kitzikaberatasun magnetikoa ez da konstantea, aplikatzen den kitzikadura magnetikoaren araberakoa baizik.
Material ferromagnetikoen portaera hobeto ulertzeko har dezagun horren zati bat.
Kanpotik eremu magnetiko bat aplikatzen baldin badiogu —H kitzikadura magnetikoaz adieraziko duguna—,
materialak nolabaiteko erantzuna izango du. Erantzun hori materialaren magnetizazioaren aldaketan nabarituko dugu.
Kanpoko kitzikadura magnetikoa zerotik hasita handituz doan heinean, materialaren magnetizaioa ere handitu egingo da
(ikus 9.4. irudia). Hala ere, balio handietan magnetizazioak asetasun balio batera joko du.
Balio horri asetasun magnetizazioa esaten zaio, eta
 ikurraz adierazten da. 9.1.
atalean adierazi denez, materialaren momentu magnetiko guztiak noranzko konkretu batean guztiz lerrokaturik
daudenean azaltzen den balioa da asetasun magnetizazioa.
Bestalde, kanpoko kitzikadura magnetikoa gutxinaka kentzen badugu, ferromagnetikoaren magnetizazioa ez da zerora itzuliko.
Beraz, nahiz eta kanpotik inolako eremu magnetikorik ez jarri, materialak
ikurraz adierazten da. 9.1.
atalean adierazi denez, materialaren momentu magnetiko guztiak noranzko konkretu batean guztiz lerrokaturik
daudenean azaltzen den balioa da asetasun magnetizazioa.
Bestalde, kanpoko kitzikadura magnetikoa gutxinaka kentzen badugu, ferromagnetikoaren magnetizazioa ez da zerora itzuliko.
Beraz, nahiz eta kanpotik inolako eremu magnetikorik ez jarri, materialak
 magnetizazioa erakutsiko du,
erremanentzia magnetizazioa, alegia. Ferromagnetikoan magnetizazioa berriro zero izango bada, kontrako noranzkoa
duen eremu magnetikoa aplikatu behar da kanpotik. Magnetizazioa desagertzeko aplikatu behar den eremu magnetikoari
eremu koertzitiboa esaten zaio, eta
magnetizazioa erakutsiko du,
erremanentzia magnetizazioa, alegia. Ferromagnetikoan magnetizazioa berriro zero izango bada, kontrako noranzkoa
duen eremu magnetikoa aplikatu behar da kanpotik. Magnetizazioa desagertzeko aplikatu behar den eremu magnetikoari
eremu koertzitiboa esaten zaio, eta  du ikurra. Kontrako noranzkoan aplikaturiko eremu magnetikoa handitzen bada, asetasun balio batera iritsiko da berriro
magnetizazioa. Beraz, eremu magnetiko aldakor baten aurrean, ferromagnetikoaren magnetizazioak 9.4. irudian ageri den
kurba egingo du. Kurba horri histeresi zikloa esaten zaio. Kurbaren itxura materialaren araberakoa da.
du ikurra. Kontrako noranzkoan aplikaturiko eremu magnetikoa handitzen bada, asetasun balio batera iritsiko da berriro
magnetizazioa. Beraz, eremu magnetiko aldakor baten aurrean, ferromagnetikoaren magnetizazioak 9.4. irudian ageri den
kurba egingo du. Kurba horri histeresi zikloa esaten zaio. Kurbaren itxura materialaren araberakoa da.
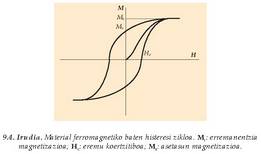
Material ferromagnetiko bakoitzak histeresi ziklo jakin bat du. Hori aprobetxatuz, material ferromagnetikoen sailkapena egin daiteke. Sailkapen hori egiteko, ondoko integral hau aztertzea komeni da:

Integral horretan, H kanpotik aplikaturiko kitzikadura magnetikoa aldakorra da; M, berriz, ferromagnetikoan agertzen den magnetizazioa. Integrala histeresi ziklo batean zehar egiten da, eta zikloaren azaleraren proportzionala da. Integralak zikloa burutzeko beharrezkoa den energia adierazten digu. Galdutako energia bero gisa azaltzen da materialean, eta hori dela eta, histeresiagatiko galera esaten zaio. Material ferromagnetikoen sailkapenarekin aurrera segituz, eta histeresi zikloa nolakoa den ikusita, bi motatako material ferromagnetikoak bereiz daitezke: ferromagnetiko gogorrak eta ferromagnetiko bigunak (ikus 9.5. irudia).
a) Ferromagnetiko gogorrak.
Ferromagnetiko hauek histeresi ziklo zabala dute. Hori dela eta, eremu koertzitiboak eta erremanentzia magnetizazioak balio handiak hartzen dituzte. Beraz,haien zikloaren azalera handia denez, histeresia galera handiak gertatzen dira. Baina haien ezaugarri positiboa beste bat da.erremanentzia magnetizazioa handia denez, materialaren magnetizazioa oso handia izaten da eremu magnetiko oso txikien aurrean. Horregatik, eremu magnetiko txikien aurrean oso sentikorrak baitira, neurgailuetan erabiltzen dira material horiek. Magneto iraunkorrak egiteko ere erabiltzen dira, haien eremu erremanente handia delako.
b) Ferromagnetiko bigunak.
Material hauetan histeresi zikloaren azalera txikia da; hau da, zikloa estua da. Hori dela eta, er emu koertzitiboa eta erremanentzia magnetizazioa txikiak izaten dira. Histeresi zikloaren azalera txikia denez, histeresia galera oso txikia da ferromagnetiko bigunetan. Hori dela eta, transformadoreetarako erabiltzen dira material horiek. Transformadoreetan dauden material magnetikoek ziklo asko egin behar izaten dituzte, eta garrantzi handiakoa da, horregatik, zikloaren azalera txikia izatea.

Ferromagnetismoa maila mikroskopikoan azaltzea ez da batere erraza. Nolanahi ere, materialaren momentu magnetikoen arteko elkarrekintzetan aurki daiteke haren oinarria. Quantumen Mekanikak momentuen arteko indar horien existentzia iragartzen du; ez, ordea, Mekanika Klasikoak. Momentuek beraien aldamenekoen artean oso indar bortitzak eragiten dituzte. Horrela, materialaren eskualde txikietan banatzen da. Eskualde horietan, nahiz eta kanpoko eremurik ez egon, momentu magnetiko guztiak lerrokaturik aurkitzen dira haien arteko elkarrekintzen ondorioz. Momentu magnetikoak lerrokaturik dauden eskualdeari dominio esaten zaio. Normalean, dominioen tamaina mikroskopikoa da. Beraz, ferromagnetiko zati makroskopiko batean dominio asko daude. Dominioetan momentu magnetikoak lerrokaturik daudenez, materialean nolabaiteko magnetizazioa aurkitu behar dugula pentsa genezake. Hala ere, dominio batetik beste batera aldatu egiten da lerrokatze norabidea. Horrela, material puska makroskopiko batean dominio asko daudenez, eta arbitrarioki orientaturik daudenez, momentu magnetiko garbia zero da (ikus 9.6. a) irudia). Kanpoko eremu magnetiko txiki batek materialaren momentu magnetikoen lerrokatze handia eragin dezake ferromagnetikoetan. Hori horrela izateko aldaketa batzuk gertatzen dira dominioetan. Kanpoko eremuaren eraginpean, dominioen mugak mugitzea da gertatzen den lehenengo aldaketa. Dominioen muga edohormak mugitu egiten dira kanpoko eremuaren eraginez (ikus 9.6. b) irudia).
Eta hala, momentu magnetikoak kanpoko eremurantz dituen dominioak handitu egiten du bere espazioa. Kontrako norabidean edo beste batean dituen dominioak, berriz, txikitu egiten du bere espazioa. Efektu horretaz gainera, beste bat ere gertatzen da dominioetan.
Bigarren prozesua dominioen lerrokatze norabideen aldatzea da. Norabide aldaketa biraketa baten bidez gertatzen da: dominioen lerrokatze norabideek kanpoko eremuaren norabidean jartzeko joera dute (ikus 9.6. c) irudia). Bestalde, kanpotik aplikatzen den eremu magnetikoa txikia bada ere, materialean lortzen den lerrokatzea handia da. Hori dela eta, normalean material barruan sortzen den eremu magnetikoa aplikatzen dena baino askoz handiagoa da.

9.6. Irudia. Dominioak aldatzean gertatzen den magnetizazioa: a) Magnetizaziorik gabeko ferromagnetikoa; b) Dominioen mugak aldatzean gertatzen den magnetizazioa; c) Dominioen errotazioaren bidez gertatzen den magnetizazioa
Ikerketak erakusten duenez, ferromagnetikoek tenperatura berezia dute. Tenperatura kritiko horri Curieren tenperatura esaten zaio; materialaren araberakoa da (ikus 9.2. taula). Tenperatura handitzean ferromagnetikoak Curieren tenperatura gainditzen badu, momentu horien arteko indarrak desagertu egiten dira, perturbazio termikoaren ondorioz. Hala bada, Curieren tenperatura baino handiagoetan, portaera ferromagnetikoa izatetik portaera paramagnetikoa izatera igarotzen da materiala. Hori dela eta, Curieren tenperatura gainditu eta gero, kitzikaberatasunak tenperaturaren mendekotasuna du, material paramagnetikoen kasuan bezala. 1907. urtean Pierre Weiss fisikari frantsesak (1865-1940) ferromagnetikoen portaera paramagnetikoaren legea aurkitu zuen. Curie-Weissen legea esaten zaio lege horri, eta honela adierazten da:

Adierazpen matematiko horretan C konstante bat da eta Tc, berriz, Curieren tenperatura

10. Gaia: uhin elektromagnetikoak
Argi ikuskorraren portaera azaltzeko bi teoria nagusi izan dira historian. Lehenengo teoria Isaac Newtonek (1642-1727) landu zuen 1669. urte inguruan. Argia zatikiz osatua zela proposatzen zuen teoria aurkeztu zuen, beste aurkikuntza batzuren artean. Argia zatikiz osatuta dagoela esaten duen teoriari argiaren gorpuzki eredua esaten zaio. Bigarren teoria, Christiaan Huygensek (1625-1695) landu zuen XVII. mendearen bukaeran. Haren ustez, argiak uhinen antzeko portaera zuen. Teoria horri, argiaren uhin eredu esaten zaio. Ondoren, James Clerk Maxwellek (1831-1879) argiaren uhin izaera finkatu zuen teoria elektromagnetikoaren bidez. Eta azkenik, Max Planckek (1858-1947) gorputz beltzaren irrada azaltzeko, eta Albert Einsteinek (1879-1955) efektu fotoelektrikoa argitzeko, frogatu zuten argia fotoi izeneko zatikiek osatzen dutela. Gaur egun, badakigu argiak ez ezik, irrada elektromagnetiko guztiek ere, bi eratara joka dezaketela, bai uhin modura bai zatiki modura. Beraz, eredu bakoitza irradaren fenomeno jakin batzuk azaltzeko egokia dela baiezta daiteke.
Irrada elektromagnetikoen barruan hainbat irrada mota daude: argi ikuskorra, irrati eta telebistan erabiltzen dena, mikrouhinak, X izpiak, eta abar. Gai honetan, uhin elektromagnetikoak nola hedatzen diren eta fisikan horrek zer esan nahi duen aztertuko da. Hala ere, irradaren uhin eredua aztertuko da bakarrik. Ezin ahaztu daitekeirrada elektromagnetikoek beste era bateko portaera ere badutela, zatiki eredua hain zuzen. Bestalde, uhin elektromagnetiko desberdinen ezaugarri nagusiak ere aipatuko dira.
Heinrich Rudolf Hertz
(Hamburg, 1857 - Bonn, 1894)
Fisikari alemana. Matematikan eta fisika esperimentalean prestakuntza bikaina izan zuen H. v. Helmholtz-i esker besteak beste. Uhin elektromagnetikoek argiaren ezaugarri berak dituztela frogatu zuen berak asmaturiko osziladorearen bitartez. Uhin elektromagnetikoak islatuak, errefraktatuak, difraktatuak eta polarizatuak izan daitezke beraz, argia bezala. Bere aurkikuntzek aurrerabidean jarri zuten hertziniar uhinen bidezko haririk gabeko telegrafia. Efektu fotoelektrikoa eta elektroiek materia nola zeharkatzen duten ere aztertu zuen.
10.1. Maxwellen ekuazioak
Zientzilariek aspaldi ekin zioten fenomeno elektrikoak eta magnetikoak aztertzeari. Hala, poliki-poliki elektrikaren eta magnetikaren lege esperimentalak lortu zituzten. 1864an J. C. Maxwellek ordu arte lortutako emaitza esperimentalak erabiliaz ondorio bat atera zuen. Arrazoiketa teorikoen laguntzaz, frogatu zuen edozein perturbazio elektriko argiaren lastertasunaz hedatu behar zela. Hala, argi uhinak uhin elektromagnetikoak zirela adierazi zuen. Eta lortutako emaitzak lau ekuaziotan formulatu zituen (Maxwellen ekuazioak). Maxwellen ekuazioetan batera azaltzen dira elektrikaren eta magnetikaren teoriak. Maxwellen ekuazioak honela adierazten dira:

Aurreko lau ekuazioak era diferentzialean adierazi dira; era integralean, berriz, honela idazten dira:
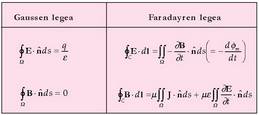
Lau ekuazio horien bidez, eremu elektrikoek eta eremu magnetikoek beren iturriekin duten lotura azaltzen da. Eremu elektrikoaren eta magnetikoaren iturriak hauek dira: kargak, korronte elektrikoak eta eremu aldakorrak.
Maxwellen ondorioak azaldu eta gero, 1887an, Heinrich Rudolf Hertz (1857-1894) fisikari alemaniarrak Maxwellen teoriak esperimentu bidez frogatu zituen. Horretarako, zirkuitu oszilatzaileak erabiliaz, uhin elektromagnetikoak sortu zituen. Gainera, maiztasun berarekin sintonizaturik zeuden beste zirkuitu batzuetan sortutako uhinak atzeman zituen. Uhin elektromagnetiko egonkorrak lortu zituen, eta elkarren ondoan zeuden nodoen arteko distantzia neurtuz, uhin luzera neurtu zuen. Erresonadoreen maiztasuna ezagutzen zuenez, uhinek hedatzeko zuten lastertasuna kalkulatzea lortu zuen. Hala, Maxwellek teoria bidez lortu zituen emaitzak Hertzek esperimentu bidez frogatu zituen.
Ordutik aurrera uhin elektromagnetikoei buruzko ikerketak ugariak izan dira eta aurrerabide handiak izan dira. Hala ere, aipatzekoa dira 1896an, Guglielmo Marconik (1874-1937) komunikatzeko bide gisa erabili zituen uhin elektromagnetikoak. Gaur egun, uhin elektromagnetikoak funtzezkoak dira gizartearen alor guztietan.
10.2. Uhin elektromagnetiko lauak
Aurretik aipatu denez, Maxwellen teorian irrada elektromagnetikoa argiaren lastertasunaz hedatzen dela frogatzen da. Horren froga hemen egingo da, baina lehenago komeni da gogoratzea nola ger - tatzen den uhin mekanikoen hedatzea. Bi motatako uhinak daude fisikan: elektromagnetikoak eta mekanikoak. Uhin mekanikoak izan daitezke: soka batek sortutakoak, uretako uhinak, soinua (presio uhinak airean), uhin elastikoak, eta abar. Uhin horien deskribapena egiteko funtzio bat erabiltzen da, uhin funtzioa deitua. Dimentsio bakar batean, X ardatzean adibidez, uhin funtzioa f( x, t) izan daiteke. Uhinen hedatzea beteko bada, uhin funtzioak deribatu partzialetako ekuazio bat bete behar du, uhin ekuazioa alegia. Uhin funtzioa f( x, t) izanik, ekuazioa ondoko hau da

non  uhinaren hedapen lastertasuna den. Beraz, uhin elektromagnetikoetarako, aurreko ekuazioaren moduko beste batera iritsi behar da.
uhinaren hedapen lastertasuna den. Beraz, uhin elektromagnetikoetarako, aurreko ekuazioaren moduko beste batera iritsi behar da.
Uhin elektromagnetikoen hedapena nola gertatzen den, eta hedapen lastertasuna zein den jakiteko, adibide erraza aztertuko da orain. Adibidea errazteko asmoz, aurretik aurkeztutako Maxwellen ekuazioek murriztapenak dituztela eduki behar da kontuan. Ekuazio horiek guztiz orokorrak dira, eta horregatik, hemen lortuko den emaitzaren berdina lortzeko beste bide korapilotsuagoa jarraitu beharko litzateke. Murriztapenetariko bat Maxwellen ekuazioak ikertuko direneko lekua hutsa izatea da. Hau da, materiarik gabeko lekua izan behar du. Bestetik, leku horretan ez kargarik ez korronterik ez dagoela onartuko da. Beraz, espazioko alde horretan ez da eremu elektrikoaren eta magnetikoaren iturririk izango. Baldintza horietan, Maxwellen ekuazioak era diferentzialean honako hauek dira:
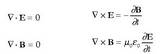
Ikusi denez, ekuazioak era integralean ere adieraz daitezke:

Zehaztapen horiek eginda, Maxwellen ekuazioen soluzio berezi bat ikertuko da. Ekuazio horientzat soluzioa lortzea, eremu bien adierazpen analitikoak lortzea da. Bestalde, bilatuko den soluzioan eremu elektrikoa eta eremu magnetikoa elkarrekiko zutak direla ontzat hartuko da. Demagun E eremu elektrikoa, Y ardatzaren norabidean dagoela, eta B eremu magnetikoa, berriz, Z ardatzean. Ondorioz, eremu elektrikoaren eta magnetikoaren osagaiak hauek izango dira:

Aurrerago ikusiko denez, kasu zehatz horretan jarri diren murriztapenek uhin lau bat sortuko dute. Beste murriztapen batzuk jarriz gero, beste motako uhinak aterako lirateke, adibidez, uhin esferikoak, zilindrikoak, etab.
Aurreko murriztapenak erabiliaz, Maxwellen ekuazioak ondoko era honetan azaltzen dira:
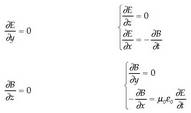
Aurreko ekuazioak arretaz aztertzen badira, E eremu elektrikoak eta B eremu magnetikoak, soilik x eta t aldagaien mendekotasuna dutela ikus daiteke. Beraz, E = E( x, t) eta B = B( x, t) erako soluzioak lortuko dira. Gainera, eremu biek aldiune guztietan X ardatzarekiko zuta den edozein planoko puntu guztietan balio bera dute.
Ekuazio horiek erabiliaz, aztertu daiteke E eta B eremuak x eta t aldagaiekin nola aldatzen diren.
Horretarako,  ekuazio hori x aldagaiarekiko deribatuz gero, era honetara gertzen da adierazpena:
ekuazio hori x aldagaiarekiko deribatuz gero, era honetara gertzen da adierazpena:
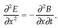
Bestalde,  ekuazio hori denborarekiko deribatuz gero, ondoko hau lortzen da:
ekuazio hori denborarekiko deribatuz gero, ondoko hau lortzen da:

Ikusten denez, azken ekuazio diferentzial hori eta atalaren hasieran aztertu den uhin ekuazioa berdinak dira. Hala ere, kasu horretanhedatzen ari den uhina eremu elektrikoa da. Beraz, eremu elektrikoa X ardatzaren norabidean hedatzen da, eta hedapenaren lastertasuna ondoko hau da:

non 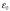 zeinuak permitibitatea hutsean,
eta
zeinuak permitibitatea hutsean,
eta  zeinuak irazkortasuna hutsean adierazten duten. Balio horiek aurreko adierazpenean ordezkatuz,
hedapen lastertasunarentzat honakoa lortzen da:
zeinuak irazkortasuna hutsean adierazten duten. Balio horiek aurreko adierazpenean ordezkatuz,
hedapen lastertasunarentzat honakoa lortzen da:
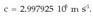
Beraz, c delakoaren balioa irrada elektromagnetikoak hutsean duen lastertasuna da,
argiaren lastertasuna hain zuzen. Askotan, lastertasun horrentzat
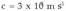 balio biribildua hartzen da.
balio biribildua hartzen da.
Eremu magnetikoarentzat antzeko prozedura erabiliz, ondoko hau lor daiteke:

Eremu magnetikoaren kasuan ere, hedapena uhinen moduan gertatzen da, X ardatzaren norabidean eta c lastertasunaz. Bestalde, kontuan hartu behar da bi eremuak hedapen norabidearekiko zutak direla. Halako ezaugarriak dituzten uhinei zeharkako uhinak esaten zaie. Horregatik, eta labur-labur hau esan daiteke:
Eremu elektrikoa eta magnetikoa X ardatzaren norabidean argiaren abiaduraz hedatzen diren zeharkako uhinak dira.
Bi eremuen hedatzea X ardatzaren norabidean 10.1. irudian ikus daiteke garbi.
Eremu elektrikoaren eta magnetikoaren ekuazioen soluzio analitikoak era honetakoak izan behar dute:

10.1. Irudia. X ardatzaren norabidean hedatzen diren eremuek uhin fronte planoa osatzen dute.

non  eta
eta  bi funtzio jarraituak diren.
Adibidea gehiago zehazteko, demagun aurreko bi funtzioak uhin armonikoak direla, hots:
bi funtzio jarraituak diren.
Adibidea gehiago zehazteko, demagun aurreko bi funtzioak uhin armonikoak direla, hots:

non  eta
eta
 eremuen anplitudeak diren.
Bi funtzio horiek Maxwellen ekuazioak bete behar dituzte. Hori dela eta,
eremuen anplitudeak diren.
Bi funtzio horiek Maxwellen ekuazioak bete behar dituzte. Hori dela eta,
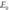 eta
eta
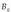 anplitudeak
ez dira bata bestearekiko independente. Adibidez, Maxwellen ekuazioetatik honako ekuazio hau hartzen bada:
anplitudeak
ez dira bata bestearekiko independente. Adibidez, Maxwellen ekuazioetatik honako ekuazio hau hartzen bada:

eta eremu elektriko eta magnetikoaren adierazpenak ordezkatzen baditugu, adierazpen hauetara irits daiteke:
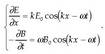
Eta hortik, ondoko erlazioa lor daiteke anplitudeentzat:

Baina erlazio hau ez da soilik anplitudeekin betetzen, aldiuneko balioekin ere betetzen da. Beraz:

Adierazpen horren bidez bi eremuen artean dagoen harremana ikus daiteke. 10.2. irudian harreman horren adierazpen grafikoa egiten da, eta uhin elektromagnetiko lauaren irudia erakusten du.
Irudi horretan ikusten denez, E eta B eremuak fasean daude eta hedapen lastertasunarekiko zutak diren norabidean aldatzen dira. Beraz,zeharkako uhinak dira. Gainera, kasu honetan E eremua etengabe dago XOY planoan eta B eremua XOZ planoan. Hori dela eta, uhina linealki polarizaturik dagoela esan daiteke.
Atal honetan aztertu den emaitza, hala ere, ez da Maxwellen ekuazioen ebazpen bakarra. Hemen, uhin laua aztertu da. Baina beste zenbaitetan, problemaren simetriaren arabera, uhin zilindriko edo esferikoak edo bestelakoak lor daitezke. Hala ere, uhin elektromagnetikoen iturritik nahiko urrun dauden puntuetan, edozein uhinaren zati bat uhin lautzat har daiteke. Hala, eremu elektrikoa eta eremu magnetikoa uhin lauaren kasuan bezala azter daitezke.

10.2. Irudia. Eremu elektrikoaren eta magnetikoaren hedatzea zeharkako uhinen modura. Bi eremuak elkarren artean eta hedapen norabidearekiko zutak direla argi ikusten da.
Guglielmo Marconi
(Bologna, 1874 - Erroma, 1937)
Italiar ingeniaria eta fisikaria, familia aberats batean jaio zen. Bolognako unibertsitatean egin zituen ikasketak, eta han hasi zen uhin elektromagnetikoak komunikazio telegrafikoan nola erabili aztertzen. Esperimentu horien emaitzak 1896an aplikatu ziren Bretaina Handian, Penarth-en eta Weston-en artean. Haririk gabeko telegrafiaren (irratiaren) sortzailea izan zen. 1901eko abenduaren 12an lortu zuen lehenengo aldiz irrati bidezko komunikazioa Atlantikoaren bi aldeen artean. 1909an Fisikako Nobel saria eskuratu zuen K. F. Braun-ekin batera, irrati-telegrafian eta uhin elektromagnetikoen ikerketan egin zituen ekarriengatik 1930ean Italiako Zientzia Akademiako lehendakari izendatu zuten.
James Clerk Maxwell
(Edinburgh, 1831 - Cambridge, 1879)
Eskoziar fisikaria. Edinburgheko eta Cambridgeko unibertsitateetako ikaslea izan zen. 1864an uhin elektromagnetikoei buruzko teoria eman zuen argitara. Teoria horren arabera, argiaren lastertasun berbera dute uhin elektromagnetikoek eterrean. Hura izan zen elektrizitatearen eta magnetismoaren teoriak bateratu zituen lehena, eremu elektromagnetikoaren lege orokorrak emanez (1873). Argia eremu elektromagnetiko batekin identifikatu zuen. Argiak eta uhin elektromagnetikoak lastertasun berbera zutela esperimentu bidez frogatu zenean onartu zuten zientzialariek Maxwellen teoria. Termodinamika ere landu zuen, eta lan batzuk egin zituen gas molekulen lastertasunaren banaketaz. Energia berdin nola banatzen den azaltzen duen legea eman zuen, eta koloreak nola sumatzen diren ere aztertu zuen.
10.3. Irrada elektromagnetikoaren espektroa
Uhin elektromagnetikoen uhin luzera,
 ,
edo maiztasuna,
,
edo maiztasuna,  ,
iturriaren arabera oso desberdinak izan daitezke uhin batetik bestera.
Horrez gainera, uhinak hainbat helburuetarako erabil daitezke. Hori dela eta, uhin elektromagnetikoak
uhin luzeraren arabera sailkatu ohi dira (edo, gauza bera dena, maiztasunaren arabera).
Jakina denez, bi magnitude horiek lotura dute hedapen lastertasunarekin, ondoko adierazpenaren bidez:
,
iturriaren arabera oso desberdinak izan daitezke uhin batetik bestera.
Horrez gainera, uhinak hainbat helburuetarako erabil daitezke. Hori dela eta, uhin elektromagnetikoak
uhin luzeraren arabera sailkatu ohi dira (edo, gauza bera dena, maiztasunaren arabera).
Jakina denez, bi magnitude horiek lotura dute hedapen lastertasunarekin, ondoko adierazpenaren bidez:

Bestalde, fotoien energia (E) uhinaren maiztasunarekin loturik dago, beste ekuazio honen bidez:

Hala, uhin elektromagnetikoen espektroa energiaren arabera ere adieraz daiteke. Energiekin erabili ohi den unitatea eV, elektronvolta, da. Ondorengo sailkapenean azaltzen diren uhin motek ez dute muga zehatzik. Izan ere, gerta daiteke iturri desberdinek sortutako uhinek inoiz maiztasun berbera izatea, eta horrenbestez, maiztasun tarteak gainka jartzea.
Beraz, uhin elektromagnetikoak uhin luzera edo maiztasunaren arabera honela sailkatzen dira:
- Irrati uhinak: Zenbait zentimetrotatik hasi eta hainbat kilometrora arteko tartea izaten dute uhin luzera. Irrati-telebistako sistemetan erabiltzen dira, batez ere; uhin mota hauek sortzeko tresna elektronikoak erabiltzen dira, zirkuitu oszilatzaileak gehienetan. Irrati uhinak, aldi berean, honela sailkatzen dira: uhin luzeak, erdi mailako uhinak eta uhin laburrak. Telebistan eta maiztasun modulatuzko (FM) igorpenetan maiztasun handiak eta, beraz, uhin luzera txikiak erabiltzen dira. Uhin horien uhin luzeran goiko mugarik ez dagoela esan behar da.
- Mikrouhinak: Mikrouhinen maiztasun tartea
 da eta uhin luzerakoa
da eta uhin luzerakoa  .
Uhin hauek ere tresna elektronikoz sortzen dira. Mikrouhin horiei UHF (Ultra High Frecuency) esaten zaie.
Azken urteetan, asko ugaldu dira uhin hauek erabiltzen dituzten labeak, eta etxe askotan ikus daitezke.
Beste hainbat arlotan erabiltzen dira, radar sistemetan adibidez. Ikerkuntzan egitura atomiko molekularrak
aztertzeko erabiltzen dira.
.
Uhin hauek ere tresna elektronikoz sortzen dira. Mikrouhin horiei UHF (Ultra High Frecuency) esaten zaie.
Azken urteetan, asko ugaldu dira uhin hauek erabiltzen dituzten labeak, eta etxe askotan ikus daitezke.
Beste hainbat arlotan erabiltzen dira, radar sistemetan adibidez. Ikerkuntzan egitura atomiko molekularrak
aztertzeko erabiltzen dira.
- Uhin infragorriak: Uhin luzeren tartea
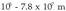 da,
eta maiztasunena
da,
eta maiztasunena  eta abarretan. Gizakiaren begiak ezin ditu izpi infragorriak
ikusi.
eta abarretan. Gizakiaren begiak ezin ditu izpi infragorriak
ikusi.
- Argi ikuskorra: Gizakiaren begiek ikus dezaketen uhin elektromagnetikoei esaten zaie horrela. Argiak begietan sortzen dituen sentipenei kolore esaten zaie. Hala, gizakiak maiztasun desberdinak kolore desberdin modura ikusten ditu. Argi ikuskorraren muturretanmorea eta gorria daude. Horien artean, oso maiztasun tarte txikia dago, eta horretan daude ostadarraren kolore guztiak (ikus 10.1. taula). Atal honetan, bi kontzeptu aipatu behar dira: alde batetik, argi zuria kolore edo uhin luzera desberdineko irradaz osatua, eta bestetik, argi monokromatikoa, uhin luzera bakarreko argiak osatua (beste hitzetan esanda, kolore bakarrekoa).

10.1. Taula. Koloreei dagozkien uhin luzerak, maiztasunak eta energiak.
- Izpi ultramoreak: Izpi hauen maiztasun tartea

 da,
eta uhin luzeratan emana,
da,
eta uhin luzeratan emana, 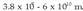 .
Uhin mota hauek atomo eta molekulen deskarga elektrikoetan sortzen dira; horiek sortzen duten energia erreakzio
kimiko askotan sortzen direnenergien mailakoa da. Hori dela eta, efektu kimiko asko sortzen dituzte:
oso ioitzaileak dira eta fluoreszentzia sortzen dute. Eguzkiak izpi ultramore asko sortzen ditu; horiek dira hain zuen
azala belzten dutenak. Hala ere, eguzkitik datozen izpi ultramore
gehienak eguratsaren goiko aldean zurgatzen dira. 80 km-tik gora
gertatzen da hori, eta ondorioz, eguratsaren inguru hori oso ionizaturik
dago, ionosfera esaten zaio. Eguratsean dagoen ozonoak,
O3, babesten gaitu izpi ultramoreen eraginetik, bestela kaltegarriak
izango lirakete. Hala ere, izpi hauek garrantzi handikoak izan dira
Lurraren bilakaeran. Gizakiaren begiak izpi ultramoreak ezin ditu
ikusi.
.
Uhin mota hauek atomo eta molekulen deskarga elektrikoetan sortzen dira; horiek sortzen duten energia erreakzio
kimiko askotan sortzen direnenergien mailakoa da. Hori dela eta, efektu kimiko asko sortzen dituzte:
oso ioitzaileak dira eta fluoreszentzia sortzen dute. Eguzkiak izpi ultramore asko sortzen ditu; horiek dira hain zuen
azala belzten dutenak. Hala ere, eguzkitik datozen izpi ultramore
gehienak eguratsaren goiko aldean zurgatzen dira. 80 km-tik gora
gertatzen da hori, eta ondorioz, eguratsaren inguru hori oso ionizaturik
dago, ionosfera esaten zaio. Eguratsean dagoen ozonoak,
O3, babesten gaitu izpi ultramoreen eraginetik, bestela kaltegarriak
izango lirakete. Hala ere, izpi hauek garrantzi handikoak izan dira
Lurraren bilakaeran. Gizakiaren begiak izpi ultramoreak ezin ditu
ikusi.
- X izpiak: Energia handiko izpiak dira, eta uhin luzera

 tartekoa dute, eta maiztasuna
tartekoa dute, eta maiztasuna 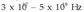 tartekoa.
X izpiak Wilhelm Röntgen fisikari alemaniarrak (1845-1923) izpi katodikoak aztertzen ari zela aurkitu zituen (1895).
X izpiak lortzeko hainbat metodo dago. Batetik, elektroi sorta batek metalezko oztopo baten kontra
talka egiten duenean, balaztaketa irrada (bremsstralhung izenaz ere ezaguna) sortzen da.
Balaztaketa irrada horiX izpiek osatzen dute. Beste metodo bat, lastertasun handiz higitzen den
kargen desbideratzea eta azelerazioa da. Bestalde, X izpiek materia zeharkatzeko ahalmen handia dute,
baita argazki xaflak inpresionatzeko ere. Medikuntzan erabiltzen dira, gorputzaren barruko ehun batzuek
(hezurretan adibidez) besteek baino izpi gehiago zurgatzen baitituzte. Horrela gorputzaren barruko
argazkiak lortzeko erabiltzen dira. Baina, X izpiak energia handikoak direnez gero, molekulak
ioitu egiten dituzte. Hori dela eta, kalteak sortzen dituzte bizidunetan. Beraz, dosi txikiak hartu behar dira,
ahal den gutxien erabiltzea komeni da. Beste arlo batzuetan ere erabiltzen dira, esate baterako
kristalografian kristalen egitura zehazteko.
tartekoa.
X izpiak Wilhelm Röntgen fisikari alemaniarrak (1845-1923) izpi katodikoak aztertzen ari zela aurkitu zituen (1895).
X izpiak lortzeko hainbat metodo dago. Batetik, elektroi sorta batek metalezko oztopo baten kontra
talka egiten duenean, balaztaketa irrada (bremsstralhung izenaz ere ezaguna) sortzen da.
Balaztaketa irrada horiX izpiek osatzen dute. Beste metodo bat, lastertasun handiz higitzen den
kargen desbideratzea eta azelerazioa da. Bestalde, X izpiek materia zeharkatzeko ahalmen handia dute,
baita argazki xaflak inpresionatzeko ere. Medikuntzan erabiltzen dira, gorputzaren barruko ehun batzuek
(hezurretan adibidez) besteek baino izpi gehiago zurgatzen baitituzte. Horrela gorputzaren barruko
argazkiak lortzeko erabiltzen dira. Baina, X izpiak energia handikoak direnez gero, molekulak
ioitu egiten dituzte. Hori dela eta, kalteak sortzen dituzte bizidunetan. Beraz, dosi txikiak hartu behar dira,
ahal den gutxien erabiltzea komeni da. Beste arlo batzuetan ere erabiltzen dira, esate baterako
kristalografian kristalen egitura zehazteko.
- Gamma izpiak: Izpi hauek  ikurraz adierazten dira gehienetan. Horien uhin luzerak
ikurraz adierazten dira gehienetan. Horien uhin luzerak
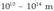 tartekoak izaten dira eta maiztasunak, berriz,
tartekoak izaten dira eta maiztasunak, berriz, 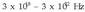 tartekoak. Gamma izpiak bi eratara sor daitezke. Batetik, atomo nukleoetan gertatzen diren zenbait fenomenoren
ondorioz ager daitezke. Adibidez, gai erradioaktiboen erreakzioetan sortzen dira. Bestetik, oinarrizko zatiekin
talken edo deuseztapenen ondorioz ere sor daitezke. Maiztasun handikoak direnez gero, X izpiek baino
energia handiagoa dute,
tartekoak. Gamma izpiak bi eratara sor daitezke. Batetik, atomo nukleoetan gertatzen diren zenbait fenomenoren
ondorioz ager daitezke. Adibidez, gai erradioaktiboen erreakzioetan sortzen dira. Bestetik, oinarrizko zatiekin
talken edo deuseztapenen ondorioz ere sor daitezke. Maiztasun handikoak direnez gero, X izpiek baino
energia handiagoa dute,  tartean hain zuzen.
Materian sartzeko ahalmen handia dute, X izpiek dutena baino handiagoa. Beraz, bizidunentzat oso
arriskutsuak dira, materia organikoa kaltetzen baitute.
tartean hain zuzen.
Materian sartzeko ahalmen handia dute, X izpiek dutena baino handiagoa. Beraz, bizidunentzat oso
arriskutsuak dira, materia organikoa kaltetzen baitute.
- Izpi kosmikoak: Irrada kosmikoak unibertsotik datoz, Lurraz kanpotik. Eta energia handia dute, 10 keV baino handiagoa baita. Lastertasun handiz higitzen ari diren zatiki kargatuek osatzen dute; batez ere, hidrogeno eta helio nukleoak dira. Izpi kosmikoak bi motatakoak izan daitezke, primarioak edo sekundarioak. Primarioak, lurrera zuzenean heltzen direnak dira. Sekundarioak, primarioek eguratsean dituzten erreakzioen ondorioz sortzen dira. Gaur egun, oraindik ez da ondo ulertzen izpi kosmikoak nola sortzen diren.
10.3. irudian espektro elektromagnetiko osoa azaltzen da, eta uhin elektromagnetikoen uhin luzerak eta maiztasunak ikus daitezke:

10.3. Irudia. Espektro elektromagnetikoa
Wilhelm Eduard Weber
(Wittenberg, 1804- Göttingen, 1891)
Fisikari alemana. Halleko eta Göttingengo unibertsitateetan egin zituen ikasketak. K. F. Gauss-ekin lan egin zuen Lurreko magnetismoa ikertzen, eta telegrafo elektromagnetikoa asmatzen. Higitzen ari diren partikula kargatuek eragiten dituzten indarren oinarrizko legea aurkitu zuen 1846an. Argiaren ikuspuntu elektromagnetikoaren oinarriak finkatu zituen. Uhinen higidura ikertu zuen Ernst Heinrich bere anaia nagusiarekin batera. Eduard Friedrich anaia gaztearekin, berriz, gizakien higiduraren fisiologia aztertu zen. Hari zor zaio banako elektrikoen sistema absolutua, gauss banako magnetikoan oinarritua.