Fisika-Kimika»Fisika - Kimika

4. Gasen teoria zinetikoa II

Batez besteko Ibilbide Askea

Molekula batek beste molekula batzuekin talka egiten duen unetik hurrengoz talka egiten duen arte egiten duen ibilbideari ibilbide askea esaten zaio. Ibilbide aske horretan zehar, lastertasun konstantean mugitzen da molekula, lerro zuzenean. Bi talkaren arteko batez besteko distantziari batez besteko ibilbide aske esaten zaio (24-1 irud.).

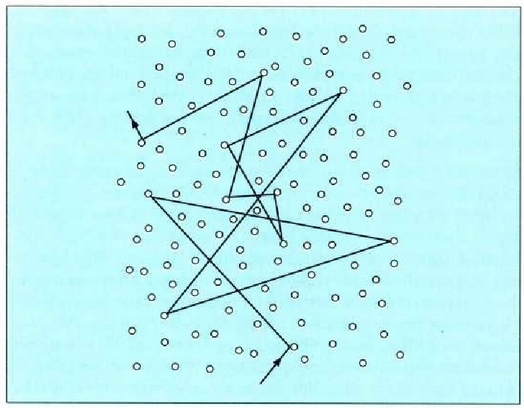
24.1: Gas batean mugitzen ari den molekula bat; mugitzean, bere ibilbidean beste molekula batzuekin talka egiten du. Gasa osatzen duen gainerako molekulak irudian agertzen denaren antzera mugitzen dira.

Molekulak puntuak balira, ez lukete inoiz elkarren kontra talka egingo eta infinitua izango litzateke haien batez besteko ibilbide askea. Molekulek hedadura finitua dute ordea, eta beraz, elkarren kontra talka egiten dute. Mugitzeko duten hutsartea zeharo betetzeko bezain handiak edo ugariak balira, ez litzateke batere tokirik geldituko translazio mugimendurako, eta batez besteko ibilbidea zero izango litzateke horrenbestez. Argi dago, beraz, batez besteko ibilbide askea molekulen neurriarekin eta materiaren trinkotasunarekin lotua dagoela.

Batez hesteko ibilbide askea erraz kalkulatzeko, d diametroko molekulak hartuz abia daiteke. Talka izan dadin 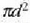izango da epai egokia. Hau da, bi molekulen zentroak elkarretatik d distantziara hurbiltzen direnean gertatuko da talka. Molekula batek izan ditzakeen talkak deskribatzeko, berdin izango litzateke molekula hori 2d diametroko molekula gisa eta gainerako guztiak zatiki puntual (puntuaren tamainako) gisa hartzea. 24-2 irudian erakusten dira bi ikuspegi baliokide horiek.

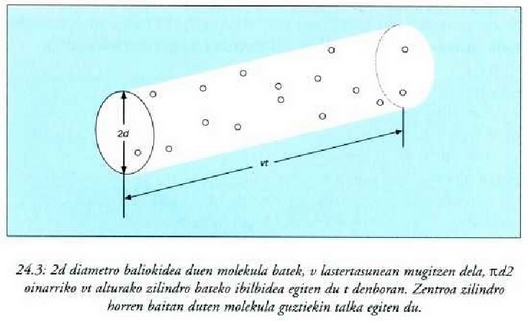
2d diametro baliokidea duen molekula bakar hori zatiki puntualez osaturiko gas batean zehar mugitzen denean jarraitzen bazaio, molekula horrek t denboran v lastertasunez zeharretarako epaia eta luzera vt dituen zilindro baten eremua igarotzen duela aterako da. Molekula horrek beren zentroa bolumen horretan duten molekulakula guztiekin egingo du talka t denboran (24-3 irud.).

24.2: Bi molekula d distantziara hurbiltzen bazaizkio elkarri (a), molekulak 2d diametroa izatearen eta beste molekula masa puntual bat izatearen (b) baliokidetzat har daiteke prozesu hori.

Bolumen banako bakoitzean n molekula baldin badaude, t denboran gertatuko den talka kopurua 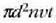zilindroan dauden gainerako molekulen kopurua adinakoa da.

l batez besteko ibilbide askea talken arteko batez besteko distantzia gisa defini daiteke. Beraz, t denboran egiten den vt distantzia osoa zati denbora horretan gertatzen den talka kopurua izango da l. Hau da:

Adierazpen horretan, ordea, molekula batek jotzen dituen jomuga puntuak finko zeudela irudikatu da. Molekulak, ordea, mugitzen ari den jomugak jotzen ditu. Hori dela eta, talka maiztasuna handiagoa da, izatez, eta batez besteko ibilbide askea ondoko adierazpenera murrizten da:

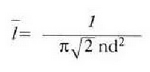
Adibidea. Batez besteko ibilbide askearen magnitudea eta talka maiztasuna aztertzeko, 23. ataleko datu tipikoak erabiliko dira. Molekularen d diametro eredu gisa 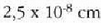hartzen bada, eta kontuan harturik baldintza arruntetan batez besteko lastertasun koadratikoa segundoko 105 cm dela eta gas batean 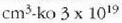atomo dagoela, orduan denbora banako bakoitzeko talka kopurua, hau da, talka maiztasuna ondoko ekuazio honek emango du:

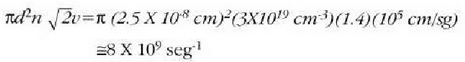
Gas baten molekulen batez besteko ibilbide askeak gasaren hutsune mailaren egiazko neurria erakusten du, talkarik gertatzen ez den batez besteko ibilbidea baitu neurtzen. Hutsune perfektua batez besteko ibilbide aske infinituari legokioke. Batez besteko ibilbide askea molekulen neurriaren, tenperaturaren eta presioaren araberakoa denez (trinkotasuna mugatzen duten ezaugarriak alegia), hobeto deskribatzen da hutsune maila molekularen batez besteko ibilbide askea zehaztuz presioa soilik aipatuz baino. Lurreko eguratsean airearen molekulek 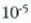cm inguruko batez besteko ibilbide askea egiten dute itsas mailan (760 mm Hg); Lurraren gainaldetik 100 kilometrora 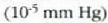, aldiz, batez besteko ibilbide askea 1 m-koa izaten da; 300 Km-ra 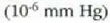talka arteko batez besteko ibilbidea 10 km-koa izango da, baina inguru horretan, zatiki daude oraindik ere zentimetro kuboko. Horrexek erakusten du ederki zein txikiak diren molekulak. Trinkotasuna, zentimetro kuboko, molekula batekoa da, gutxi gorabehera, Lurraren azaletik 2.500 km-ra. Zein balio izango luke batez besteko ibilbide askeak gune horretan?

Molekula lastertasunen banaketa

Aurreko atalean gas baten molekulen batez besteko lastertasun koadratikoa (rms) aztertu cla. Hala ere, uste izatekoa da molekulen lastertasunak desberdinak izango direla, batzuenak eta besteenak, lastertasun alde handiz, eta norabide guztietan. Ikusi den bezala, gas baten molekulen artean segundoko 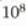talka gertatzen dira inguruko tenperaturan eta eguratsaren presiopean. Molekula baten lastertasuna aldatu egin daiteke, ordea, talka baten ondorioz. Edozein une harturik, une hartan molekula batzuen lastertasuna batez besteko balio koadratikoa baino handiagoa izango da; beste batzuena, berriz, hura baino txikiagoa. Gerta liteke, era berean, molekula batek ondoz ondoko mota guztietako talkak jasatea ere. Baina, oro har, molekulen lastertasun horiek ez dute balio oso handirik ez oso txikirik izaten. Adibidez, zerotik hurbileko lastertasunik nekez gertatzen da, edo batez besteko balio koadratikoa baino lastertasun handiagorik ere gutxitan; talka bereziak behar dira hori gerta dadin. Molekula gehienek batez besteko balioaren hurbilekoa izan ohi dute lastertasuna.

Clerk Maxwellek ebazpen matematiko bat eman zuen molekula asko dituen gas baten molekulen lastertasunen banaketa probableenak kalkulatzeko. Molekulen mugimenduak erabat irregularrak direla esan zuen, eta oinarri horretatik abiaturik, ondoko emaitza hau atera zuen:

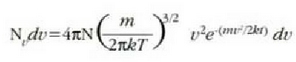
Ekuazio horretan v eta v + dv arteko lastertasuna duten molekulen kopurua da . T tenperatura absolutua cia, k Boltzmannen konstantea, eta m, berriz, molekula baten masa. Aipatzekoa da gas jakin batean, tenperaturaren mende bakarrik dagoela banaketa.

24-4 irudian gas baten molekula kopuru jakin batek bi tenperatura desberdinetan dituen lastertasunak agertzen dira, Maxwellen banaketaren arabera. v eta arteko latertasuna duen molekulen kopurua eta v eta aldagaiei dagozkien lerro bertikalen kurbaren azpiko area berdinak dira. Tenperatura jakin batentzat, molekula kopuruak gora egiten du buruz, lastertasun txikienak zero izan behar baitu, eta aldiz, ez da limite klasikorik molekula batek har dezakeen lastertasun gorenerako. Kasu horretan lastertasun guztien batez besteko balioa, , balio probableena bainohandixeagoa da. Eta batez besteko balio koadratikoa, , lastertasunen koadroen baturaren erroa denez, are handiagoa da oraindik.

24.4. Oxigenozko 1.000 molekularen lastertasunei dagokien Maxwellen banaketa bi tenperatura desberdinetarako. Lastertasun tarte jakin bateko molekula kopurua (eman dezagun 600 m/seg-etik 800 m/seg-era) kurbak zati horretan duen arearen baliokidea da

Tenperatura zenbat eta gorago, orduan eta handiagoa da lastertasun probableenaren balioa, tenperaturak eskala mikroskopikoan duen esanahiaren arabera. Aldiz, lastertasun aldaketa handiagoa da, eta molekulen zatikia txikiagoa, lastertasun probableenen Dv tartean. Aldaketa horrekin batera, handitu egiten da lastertasun jakin bat baino lastertasun handiagoa duten molekulen kopurua. Behaketetan aztertutako gertaera asko egiaztatzen ditu fenomeno horrek: adibidez, erreakzio kimikoen lastertasuna handitzea tenperatura hanclitzean.

Lastertasun oso handiko edo oso txikiko molekulak aurkitzea zaila den arren, ez da ezinezkoa. Aurki daitezke edozein unetan eta edozein tenperaturan lastertasun oso handia duten molekulak, eta aurki daitezke, halaber, ia geldirik daudenak. Isurkari bateko lastertasunen banaketa 24-4 irudian agertzen den kurben antzekoa da. Horrexek erakusten du ederki isurkari baten molekulek tenperatura apalean nola ihes egin dezaketen gainaldetik (nola lurrin daitezkeen, alegia). Molekula lasterrenek bakarrik dezakete gainaldeko molekulen erakarmen indarra saihestu eta, lurrinketa bidez, ihes egin. Gainerako molekulen batez besteko energia zinetikoak behera egiten du, eta isurkariaren tenperatura jaisten da. Horregatik esaten da lurrintzea hozte prozesu bat dela.

24-2 ekuazioan ikusten denez, molekula lastertasunen banaketa molekularen masaren araberakoa da, eta baita tenperaturaren araberakoa ere. Zenbat eta txikiagoa masa, orduan eta lastertasun handiko molekulen proportzio handiagoa izango da edozein tenperaturatan. Horrenbestez, Lurraren eguratsean, goratasun handian, handiagoa da hidrogeno gasak ihes egiteko probabilitatea oxigenoak edo nitrogenoak ihes egiteko dutena baino. Ilargiaren eguratseko molekulen artean, berriz, gai astunenen molekulak edo atomoak dira Ilargiaren erakarmen indar apaletik ihes egitekoprobabilitate gutxien dutenak, hango tenperatura apalak gorabehera. Izan ere, dirudienez, gas geldo astunak baitaude Ilargiaren eguratsean, Ilargiaren historiaren lehenengo aldietan izan zen desintegrazio erradiaktiboak sortuak gehienak: adibidez, kriptoia eta xenoia. Adituen ustez, Ilargiko egurats presioa Lurreko eguratsaren presioaren hamar bilioirena da , gutxi gorabehera.

Adibidea. Hamar zatikiren lastertasunak, m/seg eran adierazita, 0, 1,0, 2,0, 3,0, 3,0, 3,0, 4,0, 4,0, 5,0 eta 6,0 dira. Aurkitu: a) batez besteko lastertasuna; b) batez besteko lastertasun koadratikoa; eta c) zatiki horien lastertasun probableena.

a) Batez besteko lastertasuna, hau da:

b) Lastertasunen koadroen batez bestekoa, berriz:

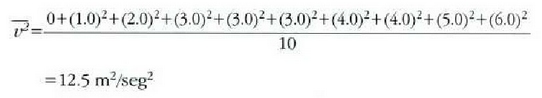
Eta batez besteko lastertasun koadratikoa:

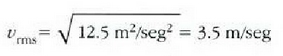
c) Hamar zatikietatik hiruk segundoko 3,0 m-ko lastertasuna dute, bik segundoko 4,0 m-ko lastertasuna, eta gainerako bostek, herriz, bakoitzak bere lastertasuna. Hortaz, zatiki baten lastertasun probableena, 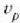, hau da:

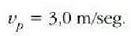
Adibidea. 24-2 ekuazioa erabiliz, zehaztu gas baten molekulen batez besteko lastertasuna, ; batez besteko lastertasun koadratikoa, 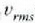; eta lastertasun probableena, , gasaren parametroen arabera.

aldagaiak v eta v +dv bitarteko lastertasuna duten molekulen kopurua adierazten du. 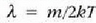adierazpena erabiliz, honela idatz daiteke Maxwellen banaketa legea (24-2 ekuazioa):

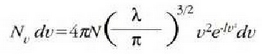
batez besteko lastertasuna kalkulatzeko, batez besteko balio bat lortzeko erabili ohi den metodo bera erabiltzen da: tarte bakoitzeko lastertasuna, batetik, eta lastertasun horri dagokion tartean dagoen molekula kopurua, bestetik, elkarrekin biderkatzen dira, eta, ondoren, biderkadura horren emaitza zati zatiki kopuru osoa kalkulatzen da. Batuketa prozesua, kasu honetan, integral gisa har daiteke; izan ere, lastertasunak ia etengabe aldatzen dira zerotik infinitora, eta zatiki kopuru osoa ere integral gisa adieraz daieke, honela:

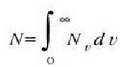
Hortaz,

24-3 ekuazioan jartzen bada eta integrala ebazten bada, hau ateratzen da:

(batez besteko lastertasuna)

Era berean, batez besteko lastertasun koadratikoa ondoko adierazpenak emango du:

(batez besteko lastertasun koadratikoa)

Azkenik, lastertasun probableena aurkitzeko funtzioak balio gorena zein lastertasunetan izango duen kalkula daiteke. Balio hori ondoko ekuazioak emango du

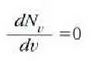
24-3 ekuaziotik beste adierazpen hau ateratzen da:

hau da:

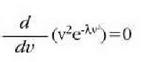
Eta hortik:

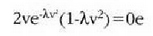
Horrenbestez:

(lastertasun probableena)

24-4 irudian adierazten dira balioak, dagokien ordenean an eta dagokien kokagunean, gutxi gorabehera.

Aipatzekoa da kopuru horiek guztiak T tenperaturaren arabera handitzen direla, eta guztiek gora egiten dutela, orobat, molekula pisua txikitzean. Izan ere, zenbat eta handiagoa gas baten tenperatura, orduan eta handiagoa da molekulen batez besteko energia zinetikoa ere. Horrez gainera, tenperatura berean dauden gas desberdinen molekulek batez besteko energia zinetiko bera dutenez, molekula arinenek lastertasun handiagoa izan behar dute batez beste.

Maxwellen banaketaren egiaztatze esperimentala

Atomo eta molekula sorten teknikari esker, Maxwellen molekula lastertasunen banaketatik ateratzen diren ondorio teorikoak frogatu ahal izan dira. Atomo eta molekula sorten metodoaren lorpenik garrantzitsuena teoria zinetikoan lastertasunen banaketa esperimentu bidez zehaztu ahal izatea izan zen. Zientzialari askok aztertu zuten gai hori, hainbat metodoren bidez; Sternek, 1926an, Eldridgek, 1927an eta Lammertek, 1929an, horretarako erabili zuten metodoa Fizeauk argiaren lastertasuna neurtzeko erabili zuen gurpil horztunaren metodoaren antzekoa (la. 24-5 irudian azaltzen da Sternek erabili zuen metodoa. Mekurioa berotzen da A labe txiki batean. Atomoen lastertasunaren banaketa tenperaturaren araberakoa da. Labean egindako irekiune txiki baten parean zirrikitu bertikal bat ireki da.

24.5. Sternen saioa, molekulek sorta batean duten lastertasunen banaketa zehazteko erabilia

Norabide egokian higitzen diren atomoak sorta bat eratuz ateratzen dira zirrikitutik, eta B eta C disko birakariak dauden ardatz bati buruz paralelo izango da, hain zuzen, sorta. Sistema guztian hutsunea egin da, hondakin gasen molekulen aurkako talkak saihesteko. Diskoek zirrikitu erradial bana dute, bigarrenarena lehenengoarenari buruz zenbait graclutan alboratua. Diskoen errotazio lastertasun konstante partikular bati buruz, hurbileko muga jakin batzuen arteko lastertasuna duten atomoak bakarrik igaro daitezke bi zirrikituetatik eta iritsi D xafla atzemailera. Beste errotazio mugimendu konstante batean, beste lastertasun tarte txiki bati

24.6. Lammertek Sternen metodoa erabiliz lorturiko emaitzak. Datuak 100°C-tan dagoen merkurio lurrinari dagozkio

dagozkion atomoak bakarrik igaroko dira. Horrenbestez, sistemak lastertasun hautatzaile gisa diharduela esan daiteke. D xaflan pilaturiko atomoen kopuru erlatiboak diskoaren lastertasunaren arabera aztertuz, labeko lastertasunen banaketa kalkula daiteke (ikus 10. galdera). 24-6 irudian Lammerten emaitzak azaltzen dira, Sternen teknika hobetuz lortuak. Intentsitate erlatiboak kalkulatzeko errotazio lastertasunaren arabera eraturiko irudian neurtzen den intentsitatea hartzen da oinarri, eta merkurio lurrinak 100 'C-tan duen intentsitateari dagokion banaketa teorikoarekin batera irudikatu dira. Emaitza esperimental horiek eta beste batzuk guztiz bat datoz teoriarekin.

Maxwellen banaketaren heste adibide bat atomo irradatzaileek igortzen duten argiaren behaketak ematen duen emaitza da. Atzemaileari buruz higitzen ari cien atomo batek argia igortzen duenean, detektatzen clen irradaren maiztasuna eta uhin luzera aldatu egiten dira Doppler efektuaren ondorioz. Maiztasuna atsedenean dagoen atomo batena baino handiagoa zein txikiagoa izan daiteke, atomoa atzemailerantz mugitzen ari den eclo handik urruntzen ari den. Horrenbestez, gas hodi batean presio txikitan gertatzen diren deskargetan atomoek igaorri ohi duten maiztasun irrada behatzen denean, maiztasunen barreiadura antzeman behar da, eta, hortaz, iturrian atomoek hartzen duten banaketaren arabera zehazten dira bai barreiadura maila bai maiztasun guztien intentsitate erlatiboa. Albert Abraham Michelsonek egin zituen (1895) Doppler efektuaren ondoriozko zabaltze horren lehenengo neurketak. Hidrogenoaren eta bismutoaren arteko 17 gaien zabaltzea iturriaren tenperaturaren arabera eta atomo masaren arabera aldatzen zela aurkitu zuen, lastertasunen banaketaz berak emandako teoriak eta argiari buruz Dopplerrek emandako formulak zioten bezala. Michelsonek atomoen batez besteko lastertasun koadratikoak ere kalkulatu zituen, bere datuez baliaturik, eta teoria zinetikoak aurreikusitako balioekin bat zetozela frogatu zuen.

Maxwellen lastertasunen banaketa, gasei buruz, baldintza arruntetan egindako behaketekin bat datorren arren, ez da betetzen, ordea, oso tenperatura apaletan eta oso dentsitate handietan, kasu horretan huts egiten baitu teoria zinetiko klasikoaren aurreikuspenak. Alor horietan quantumen fisikaren printzipioetan oinarrituriko banaketak -Fermi-Diracen banaketa eta Bose-Einsteinen banaketa- erabili behar dira. Quantumen arabrako banaketa horiek bat datoz Maxwellen banaketak alor klasikoan adierazten duenarekin, eta bat datoz, orobat, banaketa klasikoa betetzen ez den saioekin. Hortaz, Maxwellen banaketaren aplikazioak, beste edozein teoriak bezala, mugak ditu.

Brownen mugimendua

Zientzialari ospetsu askok ez zuten teoria atomikoei eta molekularrei XIX. mende amaieran eman zitzaien garrantzia aintzat hartu. Teoria zinetikoa eta gasen portaera gauza askotan bat zetozen arren, ez zen atomoak eta molekulak bi gauza desberdin eta bereizi zirela frogatzerik izan, eta ez zen, ezta ere, molekulen mugimendu jarraitua froga zezakeen behaketarik egin. Ernst Mach (1838- 1916) adituak zioen ezin zela "mundua mosaiko bat balitz bezala imajinatu, ezin baititugu aztertu haren harri puskak banan-banan". Teoria zinetikoaren hasieratik finkatua zegoen atomo batek 10 -7 edo 10- s cm-ko diametroa behar zuela izan. Inork ez zuen uste atomo bat ikusi ahal izango zuenik edo atomo bakar baten ondorioak aztertu ahal izango zirenik.

Wilhelm Ostwald izan zen teoria atomikoari aurre egin zion zientzialari ezagunena. Energiaren kontserbazioaren aldeko sutsua zen, eta kontserbazioa hartzen zuen azken errealitatetzat. Ostwaldek zioenez, prozesu baten trataera termodinamikoaren bitartez prozesu horri dagokion oinarrizko guztia jakin daiteke, eta errakzioen mekanismoari dagozkion hipotesi mekaniko guztiak frogatu gabeko hipotesiak dira. Teoria atomikoa eta molekularra alde batera utzi ondoren, zientzia ikuspegi hipotetikoetatik askatzeko ahalegina egin zuen, "ikuspegi horrek ez baitu aukerarik ematen esperimentu bidez ondorio egiaztagarriak ateratzeko". Beste fisikari ospetsu askok ez zuen atomoa gertaera zientifiko finkatu gisa onartzen.

Ludwig Boltzmann jarrera horren kontra agertu zen 1897an idatzitako artikulu batean, eta zientzia naturalean atomismoa ezinbestekoa zela azpimarratu zuen. Ikertzaileak bere adimenean izadiko prozesuekin egiten dituen analogien arabera gertatu da sarritan zientziaren aurreramendua. Eta teoria zinetikoa era horretako analogia mekanikoa zen haren ustez. Analogia gehienekin gertatzen den bezala, gure buru irudikapenen baliagarritasuna frogatzeko esperimentuak egitea iradokitzen du, eta ikerketa berrietarako eta ezaguera garbiagoetarako bidea zabaltzen du, gainera.

Zientziaren inguruko eztabaida guztietan gertatu ohi denez, esperimentuen emaitzen arabera hartzen da erabakia. Atomoen errealitatearen lehenengo froga esperimentala, eta zuzenena, Brownen mugimenduaren azterketa kuantitatiboek eskaini zuten teoria atomikoarena izan zen. Behaketa horiei esker konbentzitu ziren bai Mach bai Ostwald teoria zinetikoaren eta teoria horren oinarri den materiaren deskripzio atomikoaren baliagarritasunaz. Teoria atomikoak are indar handiagoa hartu zuen zenbait printzipio fisikotan oinarrituriko esperimentuek oinarrizko konstante atomikoen balio berberak eman zituztelarik.

Brownen mugimenduak Robert Brown botanikoari zor dio izena. 1827an polenak uretan mugimendu irregular jarraitua duela aurkitu zuen. Hasieran mugimendu hori bizi tankera baten arrastoa zela uste izan zuen, baina berehala ohartu zen zatiki inorganiko txikiek portaera hori bera dutela. Fenomeno horren azalpen kuantitatiborik ezin izan zen eman teoria zinetikoa zabaldu zen arte. Orduan, 1905ean, Albert Einsteinek Brownen mugimenduari buruzko teoria bat eman zuen, eta bere Ohar autobiografikoetan esan zuen: "Garai hartan nire helburu nagusia neurri zehatzeko atomoak bazirela egiaztatzea zen. Horretan ari nintzela ohartu nintzen, ezen, teoria atomistikoaren arabera, suspentsioan dauden zatiki mikroskopikoen mugimendu behagarriren bat egon behar zuela, jakin gabe Brownen mugimenduari buruzko behaketak aspalditik zirela ezagunak".

Einsteinek osatu zuen hipotesi nagusiaren arabera, isurkari edo gas batean suspentsioan dauden zatikiek ingurunearen mugimendu termiko berak dituzte, eta zatiki bakoitzaren energia zinetikoa, batez beste, 3/2kT da, energiaren banaketa baliokidearen printzipioaren arabera. Iritzi hori oinarritzat harturik, jariakariaren molekulen talkek sortzen dituzte Brownen mugimenduak, eta suspentsioan dauden zatikiek jariakariaren molekulen batez hesteko energia zinetiko bera hartzen dute.

Honelako zerbait gertatzen da: suspentsioan dauden zatikiak oso handiak dira jariakariaren molekulen aldean, eta molekulek etengabe bonbardatzen dituzte zatikiak alde guztietatik. Baldin eta zatikiak behar bezain handiak badira edo molekula kopurua aski handia bada, une bakoitzean talka kopuru hera izango da molekulen eta zatikien artean alde guztietatik. Zatiki txikiak badira, ordea, edo molekula gutxiago badago, une jakin batean zatikia alde guztietatik jotzen duten molekulen kopurua desberdina izango da, zorizko emaitza bat izango baita. Horrenbestez, une jakin bakoitzean orekarik gabeko indarra jasaten du zatikiak, eta alde batera eta bestera higiarazten du indar horrek. Beraz, zatikiek jariakariaren molekula oso handiak balira bezala dihardute, eta beren mugimenduak jariakariaren molekulen mugimenduen analogoak behar dute izan. Azpimarratu behar da Avogadroren zenbakia infinito balitz ez legokeela gorabehera estatistikorik eta ez legokeela Brownen mugimendurik. Avogadroren zenbakia oso txikia balitz, berriz, Brownen mugimendua oso handia litzateke. Ez du, beraz, Brownen mugimenduaren behaketetik Avogadroren zenbakia ateratzea ezinezkoa izan behar. Deskripzio honekin guztiz lotuta dago halaber molekulen mugimendua eta molekulen txikitasuna. Beraz, Brownen mugimendua teoria zinetikoaren hipotesien froga esperimentaltzat har daiteke.

Baina beste gauza bat ere erakusten du Brownen mugimenduak; hain zuzen ere, gorabeherak gertatzen direla. Izan ere, denbora tarte handi batean zehar, suspentsioan dagoen zatiki bat norabide desberdinetatik jotzen duten molekulek egiten duten indarrek orekan egon behar dute. Baina denbora tarte txiki batean zehar, gerta daiteke norabide jakin bateko talkak indartsuagoak eta ugariagoak izatea kontrako norabidekoak baino, eta, horrela, zatikia azeleratzea. Desoreka hori zoriaren arabera gertatzen denez, ez da iraunkorra, eta, horrela, zatikiak norabide baterako bultzada jasango du denbora tarte batean, eta beste norabide baterako bultzada beste batean.

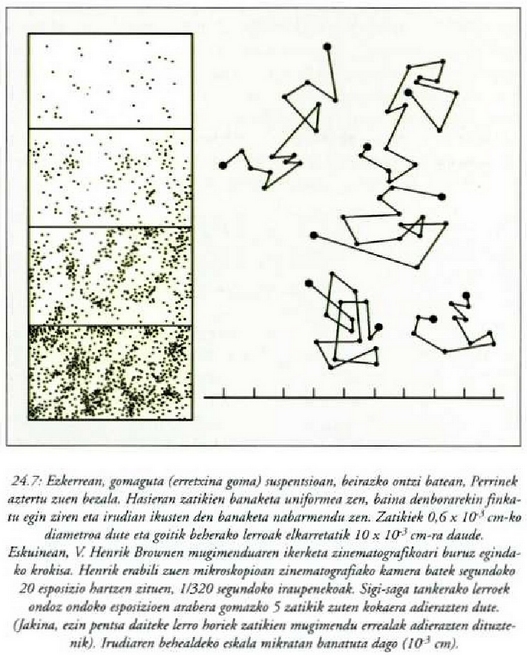
Suspentsioan dauden zatikiak grabitatearen eraginpean daude, eta hondoan jalkiko lirateke baldin eta molekulek, joera horri aurre eginez, zatikiak joko ez balituzte. Denbora bitarte baten ondoren, suspentsioan dauden zatikien dentsitatea ez da berdina izango jariakariaren sakonera guztian. Dentsitate aldaketa horretarako ekuazio zehatzak deriba daitezke (ikus 9. problema). Jean Perrin fisikari eta kimikari frantsesak egiaztatu zituen ekuazioak 1908an, eta isurkari tanta batean goratasun maila desberdinetan suspentsioan zeuden erretxina gomazko zatiki txikien kopurua zenbatekoa zen zehaztu zuen (24-7. irudia, ezkerrean). Bere datuak oinarri harturik Avogadroren zenbakiarentzat zatiki/mol balioa zehaztu zuen. Perrinek Brownen zatikien mugimendua ere neurtu zuen denbora tarte berdin a skotarako, eta, mugimendu horientzat, teoria zinetikoak eskatzen duen banaketa estatistikoa eta Einesteinek iragarri zuen batez besteko mugimendu koadratikoa betetzen direla aurkitu zuen (24-7. irudia, eskuinean).

Beste saio askoren artean aipagarria da E. Kapplerrek 1931n egin zuena. Bihurdura zuntz mehe baten gainean jarrita zegoen ispilu txiki-txiki baten Brown mugimendua behatu zuen, argi izpizko sorta bat ispilurantz bidaliz; argiak, islaturik, mugitzen ari zen argazki film bat jotzen zuen gero. Ispilua barrunbe batean zegoen, eta barrunbea gasez betea, presio apalean (10-2 mm Hg); film higikorraren errejistroak q(t) funtzioa (mugimendu angeluarra denboraren arabera) ematen zuen. Funtzio horrek ispiluaren errotaziozko Brown mugimendua -molekulen talkek eragindako angelu mugimenduen segida bat- islatzen du argi eta garbi. Gasaren presioa jaistean mugimendua murriztuz doa pixkana-pixkana. Argazki erregistroari esker q angelu mugimenduaren eta w angelu lastertasunaren balioak atera daitezke. Eta horrela, energiaren banaketa baliokideari ondoko ekuazioa dagokio

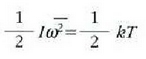
eta

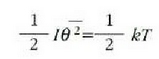
izan ere, s is temaren batez besteko energia zinetiko errotaziozkoa baita , eta sistemaren batez besteko energia potentziala, berriz, 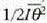. Adierazpen horietan, sistemaren inertzia momentua da I, eta k letrak, berriz, zuntzaren bihurdura konstantea adierazten du. Kapplerrek, bere saioaren bidez, Boltzmannen k konstantea kalkulatu zuen, eta, orobat, Avogadroren zenbakia kalkulatu ahal izan zuen 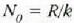harremanaren bidez. Balio hauek atera zituen: (gaur egun onartzen den balioa, , errore mugen barruan dago), eta 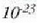zatiki/mol.

Saio asko egin dira Brownen mugimenduari buruz, baina hainbat saio desberdinetatik ateratako datuek Avogadroren zenbaki bera ematen dute, neurketei dagokien zehaztasunaren barruan. Eta materiaren atomo eta molekula egituraren kontzeptua argituta geratu da.

Van der Waalsen ekuazioa gas batean

Aurreko atalean gas idealaren portera izan da aztergai. Eskala makroskopikoan, gas ideal baten oinarrizko erlazioa egoera ekuazio honek ematen du:

Ekuazio honen eta termodinamikaren printzipioen ondorio bat da gas baten barne energia tenperaturaren mende dagoela soilik. Gas errealek nahiko ongi betetzen dute erlazio hori dentsitate apaletan, baina beren portaera oso desberdina da dentsitatea handitzen denean. Portaera idealari buruzko desbideratze horiek kontuan hartu beharrekoak dira zientzia lan zehatzak egiterakoan, desbideratze handiak izaten baitira sarritan. Adibidez, laboratorioan eskala termodinamiko absolutu bat finkatzeko, behar diren zuzenketak egiten jakin behar da gas termometro baten eskalan. Horrenbestez, zehatz-mehatz ezagutu behar da gas errealen portera. Eta bada oraindik garrantzi handiagoa duen beste gertaera bat ere: gas errealen portaerak molekula arteko indarren eta molekulen egituraren informazioa ematen duela, alegia.

Teoria zinetikoak gas ideal baten deskripzio mikroskopikoa ematen du. Aipatu da nola gera daitezkeen baliorik gabe teoria zinetikoarenzenbait oinarri. Baldintza jakinetan, gerta daiteke molekulek gasaren bolumen hutsaren zati bat betetzea eta molekula indarrak molekularen neurria baino handiagoak izatea. Dentsitate handietan kontuan hartu beharreko gertaerak dira horiek.

J. D. van der Waalsek (1838-1923) egoera ekuazio eraldatu bat osatu zuen, ezaugarri horiek kontuan hartzen zituena era soil batean. Eman dezagun molekulak d diametroko esfera gogorrak direla. Esfera horietako baten diametroa bat dator molekulen zentroak, talka indar gogorrak direla tartean, dauden distantziarekin. Molekula bat mugitzen denean molekula horren zentroa ezin da pareta batetik d/2 edo beste molekula baten zentrotik d baino distantzia txikiagora hurbildu. Hortaz, molekula batek bete dezakeen bolumen erreala txikiagoa da ontziaren bolumena baino. Zenbat txikiago, molekula kopuruak adierazten du. Adibidez, mol bakoitzeko bolumena, V/p, v letraz adieraziko da. Mol bakoitzeko "bolumen askea" balio hori baino txikiagoa izango da "kobolumen" deritzon b kopuru batentzat. Beraz, honela aldatzen da egoera ekuazioa, pv = RT erlazio idealari buruz:

aurretik esandakoa kontuan hartzeko. Bolumena txikiagoa denez, paretaren kontrako talka gehiago gertatzen dira, eta beraz, handitu egiten da presioa.

Orobat azter daiteke molekulen arteko erakarpen indarraren ondorioa ere. Har dezagun gas batetik igarotzen den plano bat eta gas horretan, edozein unetan, diharduten molekulen arteko indarrak; ezkerraldeko molekula bakoitzak eskuinean dauden n molekuletatik molekula kopuru txiki bat erakarriko du, eta eskuinaldeko molekula horiek ere berdin erakarriko dute ezkerraldeko molekula. Aldera dezagun orain egoera hori beste antzeko egoera batekin (alde bakarra: orain, bolumen banakoko molekula kopurua lehengoa halako bi izango da). Kasu honetan, ezkerreko molekula bakoitzeko eskuineko 2n molekula izango da elkarren eraginean; izan ere, molekula indarraren irispidea lehengo bera baita, baina orain lehen baino bi aldiz molekula gehiago dago irispidean.

Ezkerrean ere lehengo molekula kopurua halako bi daudenez eta horren araberako erakarpena gertatzen denez, argi dago planoan zeharreko erakarpen loturen kopurua lau halakotu egin dela. Horrenbestez, indar horien eragina bolumen banako bakoitzeko zatiki kopuruaren koadroaren arabera edo mol bakoitzeko bolumenaren koadroaren alderantzizko proportzioan, hau da, 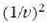proportzioan, aldatzen da. Molekulen arteko indarren loturak direla eta, kanpotik eragiten zaion presio jakin baterako, gasak gas ideala balitz hartuko lukeena baino bolumen txikiagoa hartu beharko luke. Edo beste era batera esanda, gasak kanpotik aplikatzen zaion presioa baino beste presio handiago baten eragina izango balu bezala dihardu. Presio gehiegi hori adierazpenaren proportzionala da, edo adierazpenaren baliokidea, bestela; a konstante bat da. Horrela, gas baten van der Waalsen ekuazioa lortzen da.

a eta b aldagaien zenbakizko balioak aztertu nahi den gasari buruz zehaztu behar dira, eta ikuspegi horren arabera, ekuazioa ekuazio enpirikoa dela esan daiteke. Kontuan hartu behar da gas idealaren legearen zuzenketak soilak direla, eta kasu partikular batzuetan van der Waalsen ekuaziorik ez izateak eredua gehiegi soildu dela esan nahi duela. Ez dago gas guztiei eta egoera guztietan aplika dakiokeen formula soilik.

Gas errealek ez dute zehatz-mehatz betetzen gas idealen legea. Esan daiteke gas errealentzat, barne energiaren funtzioa bolumenaren eta tenperaturaren mende dagoela. Izan ere, molekulen arteanerakarpen indarrik badago (urrunera eragina duela), energia potentzialak gora egiten du molekulen arteko batez hesteko distantziak gora egitean. Horrenbestez, gas erreal gehienen barne energia igo egingo da, gutxi hada ere, bolumenarekin batela tenperatura arruntetan. Jakina, talkak aldaratze indarren ondorioz gertatzen direla pentsa daiteke. Molekulak oso bizkor higitzen badira, halako eran non talka asko eragingo baitute, aldaratze indarren energia potentziala (irispide laburrekoa) handiagoa izan daiteke erakarpen indarrak baino, eta horrela, barne energia igo egin claiteke bolumena igotzean. Horrela gertatzen da hidrogenoaren kasuan eta helioaren kasuan tenperatura arruntetan. Hala ere, bai kasu batean bai bestean, U barne energiaren funtzioa ez clago tenperaturaren mende soilik, baizik eta baita bolumenaren mencle ere.

Adibidea. Presio-bolumenaren grafiko batean, alderatu gas ideal batek tenperatura konstantean duen portaera eta gas erreal batek cluena (Van der Waalsen gasa).

24-8 irudian pv = RT legearen araberako isotermak (T konstantearen kurbak) lerro etenez adierazi dira, eta legearen araberakoak lerro jarraituz. Gas ideal baten isoterma bakoitza pv = konstantea hiperbola aldekidearen adar bana cla. Gas errealen presioa honela aldatzen da bolumenaren arabera:

Balio handietatik abiatuta mol bakoitzeko bolumena txikitu ahala, presioa igo egiten cla, baina terminoa, presioa txikiarazten duena, bizkor igotzen cia, halako eran non presioak bere maila gorena iristen baitu A puntuan. Bolumena are gehiago txikitzen bada, RT/(v - b) terminoa bizkorrago igotzen cla, eta presioak bere maila apalena jotzen du B puntuan, baina berriro igotzen cla infinituraino, v aldagaia b baliora hurbildu ahala. Tenperatura igotzean, balio handien eta txikienak ez dira hain nabarmenak. Tenperatura kritikoan puntu kritiko esaten zaion inflexio puntu batean bat egiten clute. Tenperatura are beroagoetan 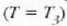inflexio puntu hori desagertu egiten da. Airearen tenperatura kritikoa -140 ° C cla, gutxi gorabehera, eta puntu kritikoko presioa, herriz, 37 atm, gutxi gorabehera.

Puntu kritikoaren Pcr presioa, vcr bolumen molarra eta Tcr tenperatura oro har kalkula daitezke baldintza hauek kontuan hartuz: alegia, isotermaren ukitzailea horizontala (lela (dp/dv = 0) T = konstante denean, cta puntua inflexio puntu bat dela (d2p/dv2 = 0) T = konstantea denean. Horrela lortzen da:

Eta hortik ateratzen da:

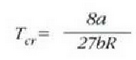
eta, balio horiek 24-8 ekuazioan jarriaz, herriz:

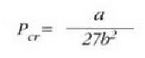
Isoterma multzoak isurkarien eta gasen portaera erreala nolakoa den erakusten du.

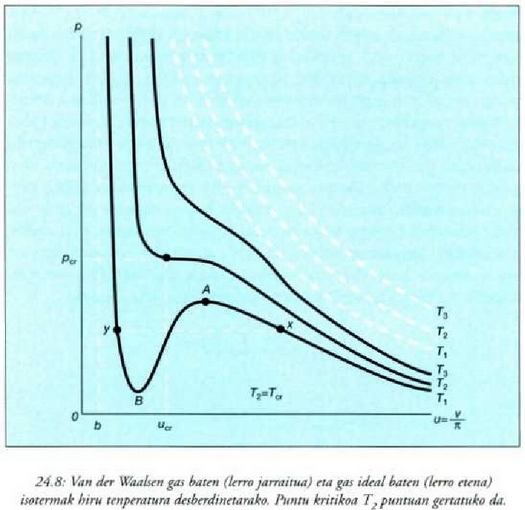
Oro har, saiakerak egitean ez dira ikusten tenperatura kritikoaz beherako handienak eta txikienak isotermetan. x punturen batean gasa trinkotzen hasten da. Bolumena murriztu ahala, presioak konstante irauten du (lerro etena), harik etar puntuan gas guztia isurkari bihurtzen den arte. y puntuaz haraindi, bolumena txikitzean, isurkari bat konprimatzen da, isurkarietan bolumen aldaketa oso txikiak eragiteko behar cien presio igoera handiarekin. Praktikan, isotermen xA eta Bv zatiak esperimentu bidez lor daitezke gas eta isurkari garbiak erabiliz. Neurrizgaindi asetako lurrin eta neurriz gaindi hoztutako isurkari deritze, eta egoera metaegonkorretan aurkitzen dira. AB zatia ezin da esperimentu bidez osatu eta ezegonkorra da.

Van der Waalsen ekuazioan a eta b konstanteak kopuru kritikoen balioetatik abiatuta kalkula daitezke. terminoari barne presio deritzo. Aireari dagozkion zenbait balio interes handikoak dira. Aireak, 0 °C-tan eta 1 atm-kop kanpo presioan, 0,0028 atm-ko barne presioa du; 0ºC-tan eta 100 atm-ko p kanpo presioan, herriz, 26,0 atm-kua da. Aireari dagozkion balioak -75 °C tenperaturan 0,0056 atm eta 84,5 atm-ko barne presioa dira. Gas bat presio jakin baten pean zabaltzen clenean eta konprimatzen duten kanpo indarren kontra lana egiten duenean, barne indar horien kontrako lana ere egin behar du. Airea -79 °C-tan eta 100 atm-ko presioan, barne indarren kontra egiten duen lana kanpo indarren kontra egiten duena bezain handia da ia. Baina badago garrantzi handiko desberdintasun bat barne eta kanpo lanen artean. Kanpo lanaren kasuan, gorputz batetik kanpoko beste gorputz batera igarotzen da energia; aldiz, barne lanaren kasuan, gorputz beraren baitan energia mota jakin batetik beste energia mota baterako aldaketa soilik gertatzen da; adibidez, energia potentziala energia zinetiko bihurtzen da. h konstantea ez da balio berekoa gas guztietan, baina oro har, moI bakoitzeko -kua izaten da. Beraz, egoera arruntean dagoen gas baten kobolumena bolumen aske hutsaren 0,15% ingurukoa da. Van der Waalsen formula tresna kualitatibo baliagarria izan daitekeen arren, esperimentuetan lortzen diren datu kuantitatiboak ez datoz erabat bat a eta b aldagaien balio konstanteekin. Eredua soilegia delako gertatzen da hori. Adibidez, molekulen diametroa ondo zehaztua dagoela pentsatu ordez, molekulen arteko indar erreala erabili behar da (23-3 irudia). Horrela gas idealaren legearen zuzenketa egokiagoa egin daiteke. Van der Waals berak bazekien hori egin beharra zegoela lan kuantitatibo zehatza lortuko bazen. Izan ere, era horretako ikerketek laguntzen dute molekula arteko indarren kurben benetako forma zehazten.

5. Entropia eta termodinamikaren bigarren legea

Sarrera

Termodinamikaren lehen legeak dio, funtsean, energia kontserbatu egiten dela. Hala ere, prozesu termodinamiko asko irudika daitezke energia kontserbatu behar luketenak, baina benetan inoiz gertatzen ez direnak. Adibidez, gorputz bero bat eta gorputz hotz bat elkar jotzenjartzen badira, inoiz ez da gertatzen gorputz beroa gehiago berotzea eta gorputz hotza gehiago hoztea. Edo, putzu bat ere ez da bat-batean izozten udako egun bero batean, ingurura beroa emanez. Eta esandako prozesu horiek ez dute termodinamikaren lehen legea hausten. Era berean, lehen legeak ez du inolako mugarik jartzen lana bero bihurtzeko ahalmenaz, edota beroa lan bihurtzekoaz, beti ere prozesuan energia kontserbatzen baldin bada. Praktikan ordea, lan kopuru jakin bat erabat bero energia bihurtu badaiteke ere, ezin izan da orain artean, bero energia kopuru jakin bat, guztiz lan bihurtu.

Entropia kontzeptuaren eta termodinamikaren bigarren legearen bitartez ulertu eta adierazi dira esandako muga horiek. Nahiz eta teoria hauek, zenbait alditan, abstraktuak eta ukiezinak diruditen, hauxe da fisikaren alor praktikoenetako eta emankorrenetako bat.

Prozesu itzulgarriak eta prozesu atzera ezinak

Har dezagun oreka termodinamikoan dagoen sistema bat. Ondorengo baldintzak betetzen dituenean dago sistema bat oreka termodinamikoan: (a) sistema oreka mekanikoan egotea -ez dago indar desorekaturik sistemaren barruan, ez eta sistemaren eta ingurunearen artean ere-; (b) sistema oreka termikoan egotea -sistemaren parte guztiak tenperatura berean claude eta baita ingurunea ere-; (c) sistema oreka kimikoan egotea -sistemak ez du barne egituraren berezko aldaketarik izateko joerarik-. Oreka termodinamikoan dagoen sistema bat zehazteko nahikoa da zenbait balio ematea, hala nola, presioa, bolumena, tenperatura eta gaiaren kopurua.

Eman dezagun orain, aldatu egiten dela sistemaren egoera. Sistemaren egoera aldatzen bada oreka termodinamikoa ere aldatu egingo da. Adibidez, eman dezagun sistema baten egoera aldatzen dugula pistoi batekin bortizki bultzatuta eta haren bolumena erdira jaisten dela. Sistema ez da oreka termodinamikoan geratuko; indarrak desorekatuta daudenez, sistemaren parte batzuk mugimenduan ibiliko dira; tenperatura diferentziak ere gerta daitezke, konpresioaren bero efektuek eragin desberdinak izan baititzakete sisteman; aldaketa kimikoak edo fase aldaketak ere gerta daitezke, kondentsazio bat, esate baterako. Jakina, bere horretan uzten bada denboran zehar, sistemak berriro ere oreka termodinamiko egoerara joko du. Baina aldaketa prozesuak dirauen bitartean ez dago oreka termodinamikorik.

Prozesu hauek gehienak, oreka egoeran hasi, oreka gabeko egoeratik pasa eta, beste oreka egoera batean amaitzen dira. Termodinamika, prozesu horiek interpretatzen saiatzen da. Baina, sistema oreka gaheko egoeratik oreka egoerara eramaten tiuten prozesu guztiz konplexuen xehetasunak argitzen baino gehiago, prozesu horiei buruzko informazio orokorra eta xinplea lortzen saiatzen (la termodinamika, portaera, prozesu itzulgarri deitzen den prozesu ideal batekin alderatuz. Prozesu itzulgarri batean, hurrenez hurrengo oreka egoera etengabeen bitartez lortzen cia sistema baten egoera aldatzea.

Adibidez, eman dezagun sistema baten bolumena erdira jaitsi nahi dela, hurrenez hurrengo aldaketa txikien bitartez. Lehenik, bultzada txiki bat emango diogu pistoiari. Horrek pixka bat txikituko du sistemaren bolumena; sistema orekatik aldentzen da, baina oso gutxi. Oso denbora laburrean sistema berriro orekatuko da. Orduan beste bultzada txiki bat emango diogu pistoiari, bolumena heste apur bat txikiagotzeko. Berriro ere itxaroten da oreka egoera ezarri arte, eta era horretan jarraitzen cla. Prozesu hori askotan errepikatuta azkenean lortuko dugu nahi genuen bolumen murrizketa. Prozesu horretan guztian sistema ez da inoiz egoten oreka egoeratik oso urrun. Prozedura hori hera, oraindik ere hurrenez hurrengo bultzada txikiagoak emanda egiten bada, tarteko egoerak oraindik gutxiago aldenduko dira oreka egoeratik. Aldaketa kopurua mugarik gahe gehiagotuta eta, ondorioz, aldaketa txikiagoak eginda, prozesu ideal batera iritsiko ginateke, zeinetan sistemak etengaheko oreka egoera hurrenkera bat pasako bailuke. Prozesu ideal horri prozesu itzulgarria esaten zaio. Praktikan asko hurbil daiteke prozesu itzulgarri batera, sistemaren egoera oso motel aldatuz.

Prozesu isotermiko batean sistemaren tenperaturak aldaketarik gahe dirau prozesu guztian zehar. Hala ere, sistema baten tenperaturak balio mugatua izango badu, nahitaezkoa da sistema oreka egoeran egotea, eta heraz, prozesu isotermiko bat, oreka egoera hurrenkera baten bitartez soilik gertatuko da. Argi geratzen da orduan, prozesu isotermikoa izateko prozesu itzulgarria izan behar duela. Prozesu isotermiko idealaren oso antzekoa, praktikan, sistema isurkari baten barruan sartu eta tenperatura iraunkorrean edukitzen den bitartean, presioa eta bolumena oso astiro aldatuz lortzen da.

Prozesu adiabatiko batean, ez da uzten sisteman berorik sartzen, ez eta dagoena ateratzen ere. Horregatik, prozesu adiabatiko bat itzulgarria bezala izan daiteke atzera ezina ere -definizioak ez du ukatzen, ez bat ez bestea-. Praktikan ezinezkoa da beroa erabat bakar dezakeen gairik aurkitzea. Prozesu adiabatiko bat, sistemak bero kopuru garrantzitsurik ez galdu ez irabazteko bezain azkar gauzatu behar litzateke. Prozesu itzulgarri bat, aldiz, egoera bakoitzean, sistemak ia orekara heltzeko behar duen denbora emateko bezain astiro egin beharko litzateke. Dena den, lor daiteke adiabatikoa eta itzulgarria izango den prozesu bat: horretarako, presioa berdintzeko edo beste zenbait prozesu orekatzeko behar den denborak oso laburra izan behar du bero eroatea gertatzen den azkartasunarekin alderatuta.

Bila dezagun orain prozesu itzulgarriei buruzko informazio kuantitatibo zehatz bat. Interpretazio horrek, gero, prozesu atzera ezinei buruzko informazio kualitatibo garrantzitsua emango digu. Nola prozesu natural gehienak atzera ezinak diren, izadiaren funtzionamenduari buruzko ezagutza hobea lortuko da horrela.

Carnoten zikloa

Sistema bat hasierako egoerara itzularazten duten prozesu sail bati esaten zaio zikloa. Baldin eta zikloak prozesu itzulgarriak baizik ez baditu, ziklo itzulgarria deitzen zaio. Irudika dezagun horrelakoziklo bat -gas bati dagokiona-, grafiko batean (25.1 irudia). Oreka egoeren hurrenkera, kurba itxi bateko puntuek irudikatzen dute.

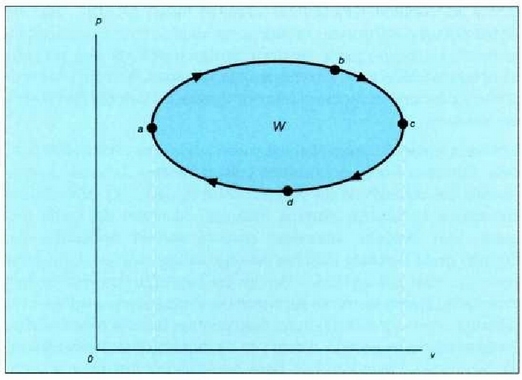
25.1: Ziklo itzulgarri bat jasaten duen gas baten V diagrama. Prozesuaren eraginez gasa bere hasierako egoerara itzultzen denez, zikloa deitzen zaio. Oreka egoera hurrenkera batez osatua dagoenez, itzulgarria esaten zaio. W izeneko gainalde ilunduak, gasak zikloan zehar egindako lan garbia adierazten du.

abc kurban zehar, sistema zabaltzen ari da, eta kurba horrek hartzen duen gainaldeak sistemak zabaltzerakoan egin duen lana adierazten du. cda kurban zehar, berriz -sistema hasierako egoerara itzultzekoa-, uzkurtu egiten da sistema eta kurba horrek hartzen duen gainaldeak, konprimatzekoan sistemari kanpotik egin zaion lana adierazten du.

Beraz, sistemak egindako lan garbia, kurbak ixtean hartzen duen gainaldeak adierazten du eta positiboa da. Zikloa aurkako noranzkoan egin izan balitz, hau da, adcn zehar zabalduz eta cban uzkurtuz, sistemak egindako lan garbia aurrez esan den lanaren balio negatiboa izango litzateke.

Teorian garrantzi handia duen ziklo itzulgarri bat, Carnoten zikloa da, Sadi Carnotek 1824an deskribatua. Aurrerago ikusiko dugu beroa lan bihurtzeko gaitasunaren muga zehazten duela ziklo horrek. "Lan egiten duen gai" bakar homogeneo bat dago -gas bat, adibidez- sistemaren oinarrian eta zikloa bi prozesu isotermiko eta bi prozesu adiabatiko itzulgarriz osatzen da. Lan egiten duen gaia -eman dezagun gas ideal bat dela- zilindro baten barruan dago. Zilindroaren oinarria bero eroale ona da eta pareta eta pistoia aldiz ez dira eroaleak. Giroa sortzeko behar dira, alde batetik, bero gordailu bat, oso bero gaitasun handiko gorputz baten formakoa eta T l tenperaturan dagoena, oso bero gaitasun handiko beste gordailu bat tenperaturan dagoena, eta eroaleak ez diren beste bi oinarri.

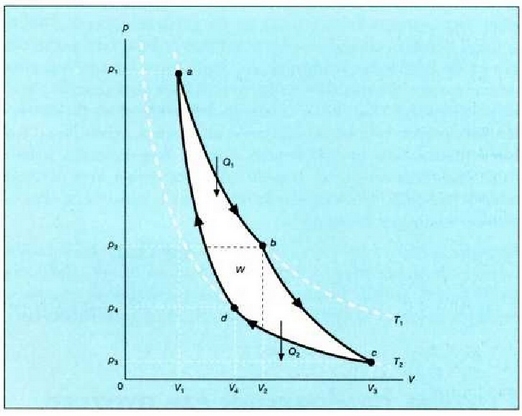
25.3: Aurreko irudian azaldutako Carnoten zikloa pV diagrama batean irudikatuta, gasa ideala den kasuan.

Carnoten zikloa lau alditan gertatzen da, 25.2 irudian erakusten den bezala. 25.3 irudian berriz, pV diagraman irudikatzen da zikloa, lan egiten duen gaitzat gas ideal bat hartu den kasuaz.

1. aldia. Gasa, hasieran 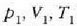balioek adierazten duten egoeran dago (a, 25-3 irudia). tenperaturan dagoen bero gordailuaren gainean jartzen da zilindroa, eta gasari astiro-astiro zabaltzen uzten zaio, balioetara iritsi arte (b, 25-3 irudia). Prozesuak irauten duen bitartean gasak balioko bero kopurua xurgatzen du, eroapenez, zilindroaren oinarritik. Zabaltze aldia isotermikoa da tenperaturan eta gasak lan egiten du pistoia altxatzean.

2. aldia. Eroalea ez den oinarri baten gainean jartzen da zilindroa eta gasari zabaltzen uzten zaio astiro-astiro 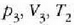balioetara iritsi arte (c, 25.3 irudia). Zabaltze aldia adiabatikoa da, ezin baita berorik sartu sistemara, ez eta irten ere. Gasak lan egiten du pistoia altxatzean eta bere tenperatura 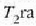jaisten da.

3. aldia. Zilindroa, tenperaturan (hotzago) dagoen bero gordailuaren gainean jartzen da eta gasa oso astiro konprimatzen da 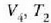balioetara iritsi arte (d, 25.3 irudia). Prozesuak irauten duenbitartean, tenperaturan, eta pistoiak kanpotik egiten du lana gasaren gainean.

4. aldia. Eroalea ez den oinarri baten gainean jartzen da zilindroa eta gasa astiro-astiro konprimatzen da hasierako 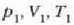balioetara iritsi arte. Konpresioa adiabatikoa da, ezin baita berorik sartu sistemara, ez eta irten ere. Gasaren gainean kanpotik egiten cla lana eta bere tenperatura igotzen da.

Zikloan zehar sistemak egindako W balioko lan garbia, 25.3 irudiko abcd ibilbideak hartzen duen gainaldeak adierazten du. Sistemak zikloan hartzen duen bero kopuru garbia da, da, delarik 1. aldian xurgatutako beroa eta 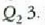aldian galdutako beroa. Hasierako eta amaierako egoerak berdinak dira, eta beraz, ez dago aldaketarik sistemaren barne energian. Ondorioz, termodinamikaren lehen legearen arabera,

Zikloaren emaitza da sistemak beroa lan bihurtu duela. Nahi den lan kopuru bat, edozein, lor daiteke, zikloa errepikatze hutsarekin. Beraz, sistemak, makina termiko batek bezala lan egiten du.

Gas ideal bat erabili dugu lan egiten duen gai baten adibidetzat. Baina, lan egiten duen gaia beste edozer izan daiteke. Jakina, pV diagramak desberdinak lirateke beste gai batzuetarako. Makina termikoek, eskuarki, ur lurrina, errekinez eta airez egindako nahasketa bat, edo errekinez eta oxigenoz egindako nahasketa erabiltzen dute lan egiten duen gaitzat. Tenperatura handiko gordailuari iturria esaten zaio eta tenperatura txikikoari irteera. Kasu praktiko gehienetan, gasolinaren edo ikatzaren gisako errekinak erretzetik lortzen da beroa. Berrikiago, fisiozko edo fusiozko prozesu nuklearretan masa desegitetik beroa lortzen duten instalazio termikoak ere egin dira. Nahiz eta egiazko makina termikoek ez duten ziklo itzulgarriekin lan egiten, Carnoten zikloak, itzulgarria denez, informazio erabilgarria ematen du edozein makina termikoren portaerari buruz.

Makina termiko baten e eraginkortasuna, zikloan zehar makinak egindako lan garbiaren eta tenperatura handiko iturritik hartutako bero kopuruaren arteko erlazioari esaten zaio. Beraz,

25.2 ekuazioak erakusten du makina termiko baten eraginkortasuna bat baino txikiagoa dela (%100), baldin eta deskargan itzulitako 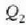bero kopurua zero ez bada. Esperientziagatik dakigu makina termiko orok bero kopururen bat botatzen duela gaiak ihes egiteko garaian. Kopuru hori, hain zuzen, makinak eskatzen duen beroa da, baina prozesuan lan bihurtzen ez dena.

Carnoten zikloa alderantziz ere egin daiteke. Kasu horretan, bero kopurua kentzen da, 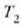tenperatura apaleneko gordailutik eta 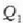bero kopurua ematen zaio 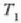tenperatura handieneko gordailuari; lana, eragileren baten bitartez, kanpotik egin behar zaio sistemari. Alderantzizko zikloaren emaitza zera da: sistemari kanpotik egiten zaio lana eta honek beroa ateratzen du tenperatura apaleneko gordailutik. Nahi den bero kopurua atera daiteke gordailu horretatik alderantzizko zikloa errepikatze hutsaren bitartez. Beraz, sistemak hozkailu papera jokatzen du, tenperatura apaleko gorputz batetik tenperatura handiagoko batera beroa pasatzen baitu, egiten zaion lanaren bitartez.

Adibidea. Froga ezazu, laneko gaitzat gas ideala erabiltzen duen Carnoten makina baten eraginkortasuna dela.

ab ibilbide isotermikoaren arabera, tenperaturak, eta ondorioz, gas idealaren barne energiak, lehenean irauten du. Lehen legea aplikatuz, gasak zabaltzekoan zurgatutako bero kopuruak, zabaltze horretan egindako W lanaren berdina behar du izan. 23. Kapituluko (*) 2. adibidetik, lan egiten duen gaiaren mol bat hartuta, zera ateratzen da,

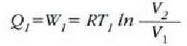
Era berean, cd ibilbidean zeharreko konpresio isotermikoan,

Lehen adierazpena zati bigarrena eginda, hona zer ateratzen den

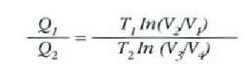
Gas ideal baten prozesu isotermikoa deskribatzen duen ekuaziotik, zera ateratzen da ab eta cd ibilbideetarako

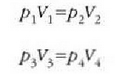
Gas ideal baten prozesu adiabatikoa deskribatzen duen ekuaziotik, zera ateratzen da bc eta da ibilbideetarako

Lau adierazpen horiek biderkatuta eta bietan agertzen den faktorea soilduta

eta hortik

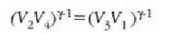
eta

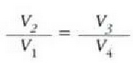
Emaitza hori gure 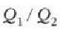adierazpenean erabilita, hona zer ateratzen den

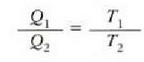
eta beraz

eta tenperaturak 21. Kapituluan (*) deskribatutako gas idealaren eskala termometrikoan neurtzen dira

Termodinamikaren bigarren legea

Egin ziren lehenengo makina termikoak oso eraginkortasun gutxikoak gertatu ziren. Tenperatura handiko iturritik zurgatutako bero zati txiki bat baizik ez zen bihurtzen lan erabilgarri. Injeniaritza diseinua hobetu eta gero ere, zurgatutako beroaren zati handi bat makinaren tenperatura apaleko ihesaldian galtzen zen, energia mekaniko bihurtu gabe. Bazen itxaropenik ordea, makina perfektua gauzatzeko. Horretarako oso gordailu oparo bat behar zen -ozeanoa, esate baterako- beroa hartzeko, eta gero, lan erabilgarri bihurtu, erabat. Kasu horretan ez zatekeen beharrezkoa izango, girokoa baino tenperatura handiagoko bero iturria sortzeak dakartzan -errekinak, e.a.- gastu guztietan sartzerik (25.4 irudia). Era berean, espero zitekeen, gizakia gai izango zela gorputz hotz batetik beste bero batera beroa pasatuko zuen hozkailu bat asmatzeko, kanpotik lanik egin beharrik gabe (25-5 irudia). Itxaropenez betetako bi nahi horiek ez baitute termodinamikaren lehen legea hausten. Makina termikoaren kasuan, bero energia, erabat eta zuzenean, energia mekaniko bihurtuko litzateke, eta prozesuan energia osoa kontserbatuko litzateke. Hozkailuaren kasuan, berriz, gorputz hotzetik gorputz berora pasako litzateke bero energia, prozesuan batere energiarik galdu gabe. Baina nahi hauek ezin izan dira inoizgauzatu, eta badira arrazoiak pentsatzeko ez direla inoiz gauzatuko. Termodinamikaren bigarren legeak, zuzenean, makina mota hauen ezinezkotasuna ezartzen du.

Bigarren legearen adierazpen asko eman dira, bakoitzak, beti ere, legearen alderdiren bat nabarmentzen duela, baina guztiak baliokideak dira, harritzekoa ez denez. Rudolph Clausiusek, esate baterako, honela adierazi zuen: Ezinezkoa da gorputz batetik tenperatura handiagoan dagoen beste batera etengabe beroa eramatea kanpotik energiarik jasotzen ez duen makina batean.

Adierazpen horrek gure itxaropenetako hozkailua ezinezko bihurtzen du, esaten baitu, alegia, gorputz hotz batetik gorputz bero batera etengabe beroa eramango bada, beharrezkoa dela eragile batek kanpotik lan egitea.

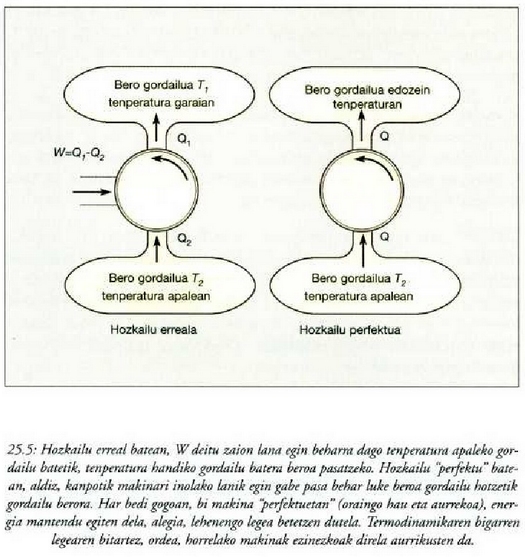
Esperientziagatik dakigu, bi gorputz elkar jotzen jartzen direnean, gorputz berotik gorputz hotzera pasatzen dela bero energia. Bigarren legearen indarrez, ezinezkoa da, adierazten den kasuan, gorputz hotzetik gorputz berora beroa pasatzea, eta era horretan, beroaren hedatze norabidea zehazten du. Alderantzizko norabidea ere har dezake, baina lana egiten bazaio, ez bestela. Termodinamikaren bigarren legea esperientziatik ondorioztatzen den lege orokor bat da.

Lord Kelvinek beste era honetara adierazi zuen bigarren legea: Ezinezkoa da eraldaketa baten azken emaitza bakarra, hedadura guztian tenperatura berean dagoen iturri batetik jasotako beroa lan bihurtzea izatea.

Adierazpen horrek gure itxaropenetako makina termikoa ezinezkoa bihurtzen du, esan nahi baitu, ezin dezakegula lan mekanikorik ekoiztu gordailu bakar batetik beroa jasota, eta tenperatura apalagoan dagoen beste gordailu batera bero haren zati bat pasa gabe.

Bi adierazpenak baliokideak direla frogatzeko nahikoa dugu frogatzea, bietako bat faltsua bada besteak ere hala izan behar duela. Eman dezagun Clausiusen adierazpena dela faltsua. Kasu horretan, errekinik edo lanik gabe funtzionatuko lukeen hozkailu bat izango genuke. Orduan, makina arrunt bat erabiliko genuke, gorputz beroari beroa kendu, lana egin eta bero zati bat gorputz hotzari pasako liokeena. Baina gure itxaropenetako hozkailua sistemari konektatuta, bero hori gorputz berora itzultzea legoke lanik egin beharrik gabe eta hala makina termikoak erabiliko zukeen berriro. Beraz, makina arrunt baten eta itxaropenetako hozkailuaren arteko konbinaziotik, Kelvinen adierazpena hausten duen makina termikoa aterako litzateke. Alderantziz ere egin daiteke arrazoiketa. Kelvinen adierazpena gezurra balitz, iturri batetik beroa hartu eta erabat lan bihurtuko lukeen makina termiko bat izango genuke. Horrelako makina termiko bat hozkailu arrunt bati konektatuta, gorputz berotik beroa ateratzea, erabat lan bihurtzea, lan hori erabiliz hozkailu arrunta ibilaraztea eta, gorputz hotzetik beroa atera eta gorputz beroari ematea legoke, hozkailuak bero bihurtutako lanarekin batera . Emaitza garbia zera izango litzateke: gorputz hotzetik gorputz berora beroa pasatzen dela lanik egin beharrik gabe, eta horrek Clausiusen adierazpena hausten du.

Bigarren legeak erakusten du prozesu asko atzera ezinak direla. Adibidez, Clausiusen adierazpenak berariaz baztertzen du, gorputz bero batetik gorputz hotz batera beroa pasatzearen alderantzizko prozesua, beste ezer egiten ez bazaio. Zenbait prozesutan, gainera, berez atzera ezinak izateaz aparte, ezein prozesu konbinazio bidez ere ezin daiteke konpondu prozesu atzera ezin baten efektua, heste tokiren batean beste aldaketaren bat eragin gabe.

Termodinamikaren bigarren legea esperientziatik ateratako orokortze zabal bat da. Zientziako alor guztietan du eragin handia, bero transmisioko arazo guztiak -dela astronomian, biologian, kimikan, geologian edo fisikan-, azken batean, makina termiko baten bidez bero energia energia mekaniko bihurtzera mugatzen baitira. Ondorengo artikuluetan ideia hauek luzeago garatuko dira eta era kuantitatiboan formulatuko da termodinamikaren bigarren legea.

Makinen eraginkortasuna

Sadi Carnot (1796-1832) izeneko ingeniari frantses batek idatzi zuen lehen aldiz, era zientifikoan, makina termikoen teoriaren gainean. 1824an argitaratu zituen bere Beroaren Indar Eragileari Buruzko Gogoetak. Garai hartan, industrian asko erabiltzen zen lurrin makina, haina ez garraioetan. Hara zer idatzi zuen Carnotek:

Lurrin makinan lan asko egin den arren eta egin zaizkion hobekuntza guztiak gorabehera, oso gutxi aurreratu da oraindik makina horren teorian...

Lurrin makinaren mugimendu produkzioa, beti, berariaz ohartarazi behar dugun egoera batean gertatzen da. Egoera hori, tenperatura handia duen gorputz batetik, tenperatura txikiagoa duen beste batera 'kalorikoa"pasatzea da...

Beroaren indar eragileak ez du zerikusirik hura lortzeko erabilitako agenteekin; "kaloriko" iragaitea gertatzen den bi gorputzen tenperaturak mugatzen du, indar horren kopurua, ez beste ezerk.

Beraz, Carnot ohartu zen tenperatura diferentzia zela "indar eragilearen" benetako iturria, beroaren iragaiteak paper garrantzizkoa jokatzen zuela, eta lanerako gaiak ez zuela garrantzirik teorian.

Carnotek egin zituen hutsegite batzuk, "kalorikoaren" teoria onartzen baitzuen, baina kontuan hartu behar da, beroaren baliokide mekanikoa eta energiaren kontserbazio legea ez zirela 1824an ezagutzen. Handik urte batzuetara Carnot ohartu zen "kalorikoaren" teoriaren faltsutasunaz. Carnot hil eta gero, 1872an argitaratu ziren haren idazlan batzuetan argi ikusten da, energiaren kontserbazio legea aurrez ikusi zuela eta doitasun osoz zehaztu zuela beroaren baliokide mekanikoa. Ikerketa egitarau oso bat pentsatuta zeukan, eta hartan sartzen ziren, ondorengo urteetan gainerako ikerlariek arlo horretan garatu zituzten garrantzizko aurrerapen guztiak. Baina kolera izurri batean hil zen 1832an, 36 urte zituela, eta beste batzuek jarraitu behar izan zuten hark hasitako lana. William Thompson izan zen (geroago Lord Kelvin) Carnoten arrazoiketak aldatu zituena, beroaren teoria mekanikoarekin bat etor zitezen, eta bera izan zen, Rudolph Clausiusekin (1822-1888) batera, termodinamikaren zientzia arrakastaz garatu zuena.

Carnotek, makina itzulgarri baten kontzeptua, eta bere izena daraman ziklo itzulgarria garatu zituen. Teorema garrantzitsu bat adierazi zuen ziklo horri buruz: Bi tenperatura berdinen artean lan egiten duten makina itzulgarri guztien eraginkortasuna berbera da, eta esandako tenperatura horien artean lan egiten duenezein makina atzera ezinek ez du izango makina itzulgarriek baino eraginkortasun handiagorik. Clausiusek eta Kelvinek frogatu zuten teorema hori termodinamikaren bigarren legearen haitezpadako ondorioa zela. Ohar gaitezen ez dela ezer esaten lan egiten duen gaiari buruz. Hortaz, makina itzulgarri baten eraginkortasunak ez du zerikusirik lan egiten cluen gaiarekin, haina aldiz tenperaturen mendekotasun osoan dago. Gainera, makina itzulgarri baten eraginkortasuna, tenperatura berberen artean lan egiten duen ezein makinena adinakoa bada, gutxienez ere. Ondoren teorema hau frogatuko da.

H eta H´ deituko diegu bi makina itzulgarriri. eta tenperaturen artean lan egiten dute, 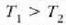delarik. Desberdinak izan claitezke, adibidez, lan egiten duten gaiak, hasierako presioak, eclota pistoien ibiltartea. H noranzko batean dabil eta H' alderantzizkoan. Aurreraka dabilen H makinak 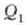beroa hartzen du tenperaturan eta heroa botatzen tenperaturan. H' alderantzizko makinak 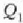beroa botatzen du tenperaturan eta beroa hartzen tenperaturan. Batu ditzagun orain bi makinak era mekanikoan, H-k egindako lana H'-k funtzionatzeko behar duen adinakoa izan dadin (25.6 irudia).

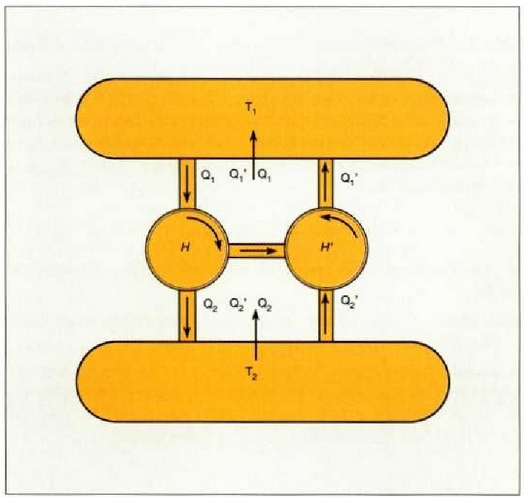
25.6: Carnoten teoremaren froga.

Eman dezagun H-ren e eraginkortasuna H'-ren e' eraginkortasuna baino handiagoa dela. Orduan:

Nola makina batek egindako lanak besteak egindakoaren berdina den,

Ekuazio horiek erkatuta, zera ikusten da

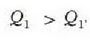
hau da

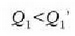
Hortaz (lanak berdinak izatera),

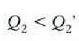
Hartara, iturri beroak 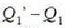(positiboa) balioko bero kopurua irabazten du eta hotzak, 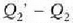(positiboa) balioko bero kopurua galtzen. Baina ez da lanik egiten prozesuan, eta beraz, tenperatura batean zegoen gorputz batetik, tenperatura handiagoan zegoen batera beroa pasa dugu lanik egin gabe, eta hori bigarren legea haustera dator. Beraz, e ezin daiteke e' baino handiago izan. Makinak alderantziz jarrita, eta arrazoiketa berbera erabiliz, e' ezin daitekeela e baino handiago izan frogatuko genuke. Hortaz

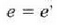
eta beraz, frogatuta geratzen da Carnoten teoremaren lehen partea.

Eman dezagun orain H makina atzera ezina dela. Aurreko prozedura berberaren bitartez froga daiteke ezin daitekeela e' baino handiago izan. Baina nola H ezin daitekeen alderantzikatu, ezin daiteke frogatu e', baino handiagoa izan ez daitekeenik. Hortaz, 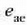, e'ren berdina edo txikiagoa izan behar du. Nola den, hau ateratzen da

eta horrela frogatuta geratzen da Carnoten teoremaren bigarren partea.

Ohar gaitezen, bigarren legetik, prozesu atzera ezinen tasun kualitatibo garrantzitsu bat lortu dela.

Adibidea. Lurrin makina batek 200 ° C-tan, 15,31 atm-tan eta presioan dagoen galdara batetik hartzen du lurrina eta zuzenean botatzen du airera (0,95 atm) ( presioa) 100°C-tara. Zein da makinaren eraginkortasun ideala?

Praktikan, %15 inguruko eraginkortasunak lortu ohi dira. Energia galera, marruskatzeagatik, zurrunbiloengatik eta beroa eroateagatik gertatzen da. Lurrin makina konplexuagoetako ihes tenperatura apalagoak direla eta, eraginkortasun ideala igo daiteke %35era eta erreala %20ra. Berebil motore arrunt baten eraginkortasuna %22koa da eta oliozko Diesel motore handi batena berriz %40 ingurukoa.

Tenperatura termodinamiko absolutuko eskala

Makina itzulgarri baten eraginkortasunak ez du zerikusirik lanerako erabiltzen den gaiarekin, baina aldiz, makinak lan egiten duen bi tenperatenperaturen arteko diferentziaren mende dago. Nola 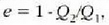orduan tenperaturen mende egon daiteke soilik. Honek eraman zuen Lord Kelvin, tenperatura eskala berri bat antolatzer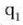a eta ikurrez adierazten baditugu bi tenperaturak, berorien definizio ekuazioa zera da:

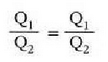
Alegia, eskala honetako bi tenperaturen arteko erlazioa, tenperatura berorien artean Carnoten zikloarekin lan egiten duen makina batek zurgatu eta botatako (hurrenez hurren) beroen artekoaren berdina da. Nola tenperatura eskala hori ez dagoen gai jakin baten, edozeinen, ezaugarrien mende, tenperatura termodinamiko absolutuko eskala deitzen zaio.

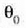
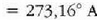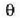Eskala absolutuaren definizioa osatzeko, 273,16 ° Absolutuko balio arbitrarioa izendatuko diogu uraren puntu hirukoitzari. Hortaz, . Orduan, eta arteko tenperaturetan ari den Carnoten makina batentzat, zera dugu

Adierazpen hori erkatzen badugu, gas idealaren T tenperaturari dagokion ekuazioarekin

ikusten dugu eskala absolutuan tasun termometriko baten papera jokatzen duela Q-k. Baina Q ez dago gai bereziren baten ezaugarrien mende, Carnoten makina batean ez baitu deus esan nahi lan egiten duen gaiaren izaerak. Beraz, lortu den tenperatura eskalari ez dago 21. kapituluko gas idealaren eskalari jar lezazkiokeen eragozpenak jartzerik, eta izatez, tenperaturaren funtsezko definiziora heldu gara.

Tenperatura termodinamikoaren definizioak bide ematen digu makina itzulgarri baten eraginkortasunaren ekuazioa berriro idazteko, beste era honetan

Baina frogatu dugu (1. Adib.), Carnoten makina baten eraginkortasuna, lanerako gaitzat gas ideal bat erabilita, ondoko hau dela

T, gas idealak duen bolumen konstanteko termometroak emandako tenperatura delarik. Hortaz, 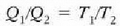eta 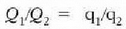izando da. Nol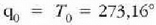a eta diren, q = T dela ondorioztatzen da. Beraz, bolumen konstanteko termometro batean erabiltzeko gas ideal bat balego, termometroak tenperatura termodinamiko absolutua emango luke.

25.7- Zero absolutu tenperaturarako joera duten Carnoten zenbait ziklo, tenperatura termodinamiko absolutuko eskala ezartzeko egiten den bezala. Isotermoen eta adiabatikoen malden arteko diferentzia handiagotu egin da, irudia argiagoa gerta dadin.

Ikusi dugu, gas ideala izan gabe ere, 25.4 ekuazioaren mugako prozesua erabilita, gas idealaren portaerari dagozkiola gas errealekin egindako neurketak. Hortaz, gas idealaren eskala eta eskala termodinamiko absolutua berdinak balira bezala tratatuko ditugu eta T K letrez adieraziko dira.

Praktikan ezin dezakegu gas bat 1 K-z azpitik eduki. 1 K-z azpitiko tenperaturak neurtzeko erabilitako metodoetako batek eskala absolutua erabiltzen du zuzenean. Bi tenperatura absolutuen arteko erlazioa, bi adiabatiko berberek mugatutako bi prozesu isotermikotan transmititutako beroen arteko erlazioaren berdina da (25.7 irudia). Muga adiabatikoen kokalekua (p-V diagraman) aurki daiteke esperimentu bidez eta bi prozesu isotermiko ia itzulgarritan transmititutako beroak doitasun handiz neur daitezke.

edo

ekuazioetatik garbi ondorioztatzen da bi adiabatiko jakinen arteko prozesu isotermiko batean transmititutako Q bero kopurua gutxitu egiten dela T tenperatura gutxitu ahala. Bestalde, Q zenbat eta txikiagoa, orduan eta txikiagoa da dagokion T tenperatura. Nolanahi ere, Q-k izan dezakeen balio txikiena zero da eta dagokion T tenperatura zero absolutua cla. Alegia, sistema batek prozesu isotermiko itzulgarri bat jasaten badu berorik transmititu gabe, prozesu hori gertatzen den tenperatura zero absolutua da. Beraz, zero absolutuan, berdin-berdinak dira prozesu isotermikoa eta prozesu adiabatikoa (25.7 irudia).

Zero absolutuaren definizio hau gai guztiei aplikatzen zaie eta ez du zerikusirik gai bereziren baten tasunekin. Ohar gaitezen ez dela molekularik edo molekula energiarik aipatzen, eta zero absolutuaren definizio makroskopikoa lortu dela.

Carnoten makinaren eraginkortasuna ondorengo hau da:

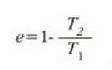
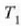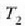zeina eta tenperaturen artean lan egiten duen edozein makinak izan dezakeen eraginkortasun handiena baita. % lOOeko eraginkortasuna lortzeko, 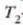-ek zero balio behar du. Tenperatura apaleko gordailua zero absolutuan dagoenean bestetan ez da lan bihurtuko, tenperatura altuko gordailutik zurgatutako bero guztia.

Hozte prozesu guztien funtsezko ezaugarria da, tenperatura zenbat eta txikiagoa, orduan eta zailagoa dela oraindik beherago jarraitzea. Esperientzia horrek termodinamikaren hirugarren legea formulatzea ekarri du. Honela adieraz daiteke: Ezinezkoa da, ezein prozeduraz, ezta idealizatuz ere, sistema bat zero absolutuaren tenperaturara jaistea, eragiketa kopuru finito bat erabiliz. Hortaz, nola ezin den lortu zero absolutuko tenperaturan dagoen gordailurik, ezinezkoa da praktikan, %100eko eraginkortasuna duen makina termikorik.

Entropia

Termodinamikaren bigarren legea modu kuantitatiboan adierazteko, kopuru bat behar da sistema batek lana egiteko duen aukera neur dezan. Neurtzeko premia hori adibide batzuen bidez argituko da. Adibiderik soilena gas ideal baten dilatazio librea da. Prozesu horretan (22-12 irudia) gas ideala dilatatu egiten da, hutsunea egiten bazaio eta ontzi bakartu zurrun baten barruan egonez gero. Dilatazio horretan gasak ez du inolako lanik egiten, eta prozesu horrek dirauen bitartean sisteman ez da berorik ez sartzen ez ateratzen. Sistema hori bakartuta dago. Beraz, termodinakaren lehenengo legearen arabera, gas horren barne energia ez da aldatzen, zeren eta dQ=O eta dW=O denez, dU-k berdin zero izan behar du. Gas ideal batean U tenperaturaren mende baizik ez dago, eta beraz prozesu horretan T-k ez du aldaketarik. Nolanahi ere, gas hori hasierako egoerara berriz eramateko, konprimatu egin behar izaten da. Beraz, dilatazio librearen ondorioz, gasak zertxobait galdu du lana egiteko duen gaitasuna. Ohar bedi dilatazio librea prozesu atzera ezina dela.

Beste adibide soil bat beroa eroatearena da. Gorputz bero batek eta gorputz hotz batek elkar ukitzen badute, oreka termikoan egongo dira azkenean. Prozesu horretan ez da energia galera garbirik izan. Baina sistemak lana egiteko gaitasuna galdu du oro har; makina termiko baten bidez gorputz bero horrek eta gorputz hotz horrek lan baliagarria egin zezaketen elkar ukitu aurretik, baina elkar ukitze horren ondoren ez dago alderik bi gorputz horien tenperaturaren artean, eta beraz ezin dute lanik egin. Beroa eroatea ere prozesu atzera ezina da.

Sistema jakin batek lana egiteko duen gaitasuna adierazten duen kopuru fisikoari entropia esaten zaio. Entropia tasun neurgarri bat da. Kontzeptu horrek energia berak bezain garrantzi handia du termodinamikan. Lehenik prozesu itzulgarri baten bidez era kuantitatiboan definituko da entropia, eta arestian deskribatu diren gisako prozesu atzera ezinetara nola aplika daitekeen ikusiko da gero.

Bi adiabatikoen arteko prozesu isotermikoetan hau gertatzen da:

Ekuazio horretan Q-k prozesu isotermiko batean T tenperaturan xurgatzen den beroa adierazten du. Carnoten zikloan beroa -n xurgatzen da eta -n botatzen da, halako moduan non Carnoten ziklo (itzulgarri) batean (bi adiabatikoen artean) Q, negatiboa baita eta

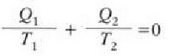
Ekuazio horren arabera, Q/T kopuruen batura zero da Carnoten ziklo batean.

Har dezagun orain 25-8 irudian ikusten denaren gisako ziklo itzulgarri bat. Beroa xurgatzen da, eta modu isortermikoan botatzen da tenperatura desberdinetan; prozesu adiabatikoek sortzen dituzte tenperatura aldaketa horiek, Carnoten zikloan bezala. Ziklo horrek Carnoten 3 zikloren balio bera du, abcdefghija zikloak Carnoten abia, bcghb, defgd 3 zikloen balio bera baitu, 3 ziklo horiek bh eta cg kurba adiabatikoak marraztuz lortu direlarik. Hortaz, ziklo oso horretan Q/T kopuruen batura Carnoten 3 zikloetako Q/T kopuruen batura da, besterik gabe. Beraz, ziklo oso horretan

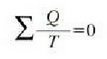
25.8: Carnoten 3 ziklok eratzen duten ziklo itzulgarria.

25.9: Edozein prozesu itzulgarri gutxi gorabehera Carnoten ziklo multzo baten bidez adieraz daiteke. Ziklo hori gero eta modu hurbilagoan adierazten da, zenbat eta handiagoa izan hurrenez hurreneko aldi adiabatikoen eta isotermikoen kopurua.

Edozein ziklo, izatez, prozesu isotermikoen eta adiabatikoen segidatzat har daiteke gutxi gorabehera (25-9 irudia), halako moduan non edozein ziklo itzulgarri Carnoten ziklo askoren batura gisa adieraz baitaiteke. Zenbat eta hurrenez hurrengo prozesu gehiago erabili, orduan eta laburragoak izaten dira aldi isotermikoak eta adiabatikoak, eta orduan eta zehatzagoa izango da hurbilketa. Integrala batura baten limitea denez, orduan edozein ziklo itzulgarritan hau gertatzen da:

ekuazio horretan zeinuak integrala zikloaren inguruan hartzen dela esan nahi du. Kasu honetan, dQ T tenperaturan xurgatu den beroaren kopuru infinitesimala da. 25-7 ekuaziotik ondorio hau ateratzen da balio bera du 1 egoeratik 2 egoerarako ibilbidean, zeinahi ere dela 1 etik 2ra aukeratu den ibilbidea. (ikus 12. problema). Ohar bedi 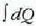ez dela ibilbidetik independentea, baina fdQ/T independentea dela ibilbidetik. Horra beraz berriz ere sistema baten tasun jakin bat, barneko energia bezalakoa, balioa sistemaren egoeraren mende baizik ez daukana, eta ez aldez aurretikako egoera batetik egoera horretara iritsi zen moduaren mende. Tasun horri sistemaren entropia esaten zaio, eta S letraz adierazten da. Orduan, baldin bada 2 egoeraren entropia, eta 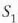baldin bada 1 egoeraren entropia,

hori da sistema baten entropiak duen aldea 1 egoeratik 2 egoerara ibilbide itzulgarri bat jarraituz igarotzen denean. Ibilbide itzulgarri baten segmentu infinitesimal batean

hori da entropiaren aldaketa infinitesimala. Hala bada, orain emaitza hitzez adieraz daiteke: ziklo itzulgarri baten entropia aldaketa zero da.

Entropia interpretatzea sistema batek lan egiteko duen gaitasunaren neurri gisa bat dator ziklo itzulgarri batean entropia aldaketa zero dela adierazten duen emaitzarekin, ziklo horretan barrena dabilen sistemak ez baitu lan egiteko gaitasuna galtzen.

Energia potentzialaren eta barne energiaren kasuan bezala, entropiaren arteko aldeak dira kontuan hartzekoak eta ez entropiaren balioak berak. Sistema baten egoera bati S-ren balio jakin bat ematen zaio, beste oreka egoeren balioak behin betiko definituta gelditzen dira. Kaloriak graduko edo jouleak graduko dira entropiaren ohiko banakoak.

Orain entropiaren kontzeptua prozesu atzera ezinei aplikatuko zaie. Lehenik gas ideal baten dilatazio librea aztertuko da. Gas horrek 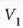bolumena, presioa, T tenperatura eta entropia ditu hasieran. Demagun gas hori libre dilatatzen dela 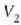bolumena iritsi arte, delarik. Gas horren presioa gutxitu egiten da izateko moduan, baina tenperaturak berdin dirau. Gas hori egoera desberdin batean dagoenez, haren entropia desberdina izan daiteke, eta esan dakioke. Gogora bedi dilatazio librea prozesu atzera ezina dela, eta sistema hori bakartua dagoela (ez dago eraginik sistemaren eta giroaren artean).

Har bedi berriz ere gas hori hasierako egoeran; konprimatze geldiko prozesu itzulgarri baten bidez tenperaturak konstante irauten du T balioan, Q bero kopuru jakin bat kenduz. Prozesu itzulgarrihori gasera itzultzen da presioan, 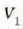bolumenean, T tenperaturan eta entropian, eta sistemaren eta bere giroaren arteko eraginaren bidez gertatzen da hori. Prozesu horretan gasaren entropia aldatu (la modu neurgarrian; Q bero kopuru jakin bat kenduz gero gasaren T tenperaturari, gas horren entropia Q/T gutxituko da kopuruz . Beraz, gas horrek dilatazio libre baten ondoren daukan entropia dilatazio libre hori baino lehenago zeukan entropia baino handiagoa da.

Sistema bakartu batean eta prozesu atzera ezin batean entropia zenbat gehitu cien neurtu da, gai jakin baten eta haren inguruaren elkarren arteko eraginez gai hori bere hasierako egoerara eramateko erabili den prozesu itzulgarrian gertatu den entropia aldaketa kalkulatuz. Entropiak behin betiko balioa du oreka definitua duen egoera batean, eta prozesu itzulgarri batez baizik ezin da neurtu, sistemara eta erreferentziazko egoera batera itzuliz. Dilatazio librea prozesu itzulgarria izan balitz, entropia aldaketa zero zatekeen, prozesu horretan dQ=O baita. Beraz, prozesu atzera ezin batean entropiak duen aldaketa sistemak lan egiteko gaitasunean duen galeraren neurritzat har daiteke.

Prozesu atzera ezin baten beste adibide bat aztertuko da orain: elkar ukitzen duten bi gorputzetan batetik bestera pasatzen den beroa. Demagun 1 eta 2 gorputzak girotik bakartuta daudela, baina elkar ukitzen dutela. 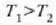baldin bada, 1 gorputzetik dQ bero kopuru jakin bat pasako da 2 gorputzera bitarte labur batean. Bitarte horretan 2 gorputzak entropia aldaketa hau du eta 1 gorputzak, berriz, halako moduan non sistema horren entropia aldaketa hau izango baita:

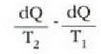
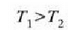denez, entropia aldaketa hori positiboa da, hau da, sistemaren entropia gehitu egiten da. Izan ere, entropia aldaketa prozesu itzulgarri baten bidez neurtu behar da, gorputz hotzenetik gorputz beroenerainoko transmisioa bezala. Horrek lan gastu bat dakar, eta, beraz, sistema horrek lan egiteko gaitasun pixka bat galdu du beroa batetik bestera pasatzeko prozesu atzera ezinean. Emaitza lehengo bera da: lan atzera ezina egiteko gaitasunaren galera jakin batek sistemaren entropia gehitzea dakar.

Oro har sistema bat 1 egoeratik 2 egoerara pasatzen denean, sistema horrek eta bere giroak elkarren arteko eragina baldin badute, sistema horrek entropia era honetara aldatzen duela froga daiteke:

(prozesu itzulgarria)

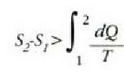(prozesu atzera ezina)

Sistema hori zeharo bakartuta baldin badago, orduan dQ=O, eta

(prozesu itzulgarria)

(prozesu atzera ezina)

Beraz, edozein dela ere aldaketa sistema bakartu batean, azken egoerako entropia sekula ez da izango hasierako egoerakoa baino txikiagoa. Aldaketa hori itzulgarria denean baizik ez da sistema hori entropia aldaketarik gabe geldituko. ekuazioa sistema bakartuetan bakarrik aplikatzen da. Gorputz jakin baten entropia kanpoko sistema baten laguntzaz gutxitu daiteke. Nolanahi ere, batera hartutako bi sistema horien entropia ezin da gutxitu.

Termodinamikaren bigarren legearen adierazpena aztertuko da orain; adierazpen hori kuantitatiboa da prozesu itzulgarrietan, baina kualitatiboa besterik ez da prozesu atzera ezinetan. Ekuazio horiek adierazpen honen bidez laburbil daitezke: prozesu natural bat norabide jakin batean gertatzen da beti, halako moduan non norabide horrek sistema horren entropia gehitzen baitu, eta gehitze horri giroaren entropiaren gehitzea ere erantsi behar baitzaio.

Prozesu natural guztiak atzera ezinak direnez, eta beraz entropia gehitzea dakartenez, era horretara badago ulertzea Clausiusen adierazpena: termodinamikaren bigarren legea eta Unibertsoaren entropia gehitzen ari dela dioen adierazpena berdinak dira, eta termodinamikaren lehenengo legea eta Unibertsoaren energia osoa konstantea dela dioen adierazpena berdinak dira orobat.

Zero absolutuan dagoen sistema baten entropiari zero puntuaren entropia esaten zaio. Entropiaren arabera, termodinamikaren hirugarren legea honela adieraz daiteke: Ezin da ezein prozeduraz sistema baten entropia zero puntuan duen baliora eragiketa kopuru mugatu baten bidez murriztu, prozedura hori ideala izanagatik.

Adibidea. O°C-tan dagoen kilogramo bat izotz O°C-tan dagoen ur bihurtzen da; izotzak urtzerakoan egoera fisikoaren aldaketako beroa 79.6 cal/gin. dela kontuan harturik, kalkulatu izotz horrek izan duen entropia aldaketa.

Tenperaturak konstante dirau, T=273 K. Beraz,

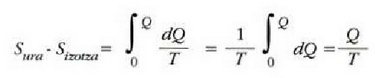
Baina

alegia,

Urtze prozesuan izotzak girotik hartzen clu beroa; giroaren tenperaturak O°C baino gorago egon behar du beraz. Beroa eroatearen adibideak erakusten duenez, izotzaren entropia gehitzea giroaren entropia galera baino handiagoa da, eta beraz prozesu horrek entropia gehitzea dakar guztira. Prozesu hori alderantziz egiteko, ura izozteko alegia, beroa uretatik 0°C baino gutxiagoko tenperaturan dagoen gorputz batera eraman behar litzateke. Sistema horretan (ura + gorputz hotza) entropia ere gehitu egingo litzateke guztira, beroa eroatearen adibideak frogatzen duen bezala.

Adibidea. Kalkulatu gas ideal baten n molen entropia nola aldatzen den bolumenetik bolumeneraino itzulgarria den dilatazio isotermiko batean.

Lehenengo legearen arabera:

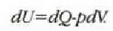
Baina dU=O, gas ideal bateanU tenperaturaren dago, eta tenperatura konstantea da. Beraz,

eta

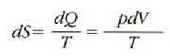
baina

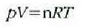
eta beraz,

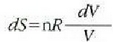
eta

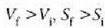, denez, gas horren entropia gehitu egiten da.

Prozesu hori egiteko, biltegi bat eduki behar da T tenperaturan; biltegi horrek sistema ukitzen du eta beroa ematen dio gasari. Beraz, biltegi horren entropia gutxitu egiten da kopuru honetan, eta beraz prozesu horretan sistemaren entropia + giroa ez dira aldatzen . Prozesu itzulgarri baten ezaugarria da hori

Entropia eta desordena

Freeman J. Dyson-ek beroari buruz idatzi zuen artikulu baten zati bat aldatuko dugu hona:

Beroa energia desordenatu bat da. Horrela azaltzen da bi hitzetan beroaren nolakotasuna...

Izan daiteke energia desordenarik gabe. Adibidez, eskopeta batekin tiro egindako balak edo U235 atomo batek desordenatua dute energia. Bala horren mugimendua zinetikoa esaten zaion motakoa da. Balak altzairuzko xafla bat jo ondorengelditzen denean, mugimendu horren energia balaren eta xaflaren mugimendu irregularretara transmititzen da. Energia desordenatu hori bero moduan adierazten da. Uranio atomoak duen energia potentziala esaten zaion motakoa da; osagaitzat dituen protoiak bereizteko joera duen indar elektrikoa da hori. Atomoa fisionatzen denean, askatzen diren zatien mugimenduaren energia, talken eraginez, elektroien eta inguruko materiako beste atomo hurbilen mugimendu irregular bihurtzen da -bestela esanda, bero bihurtzen da-. Energia potentzial hori bero bihurtzea du oinarri erreaktore nuklearren funtzionamenduak.

Bi adibide horiek garbi erakusten dute energia bero bihurtzen dela desordenatzen den ahala. Alderantziz ere gerta daiteke, izan daiteke desordena energiarik gabe, eta desordena bero bihurtzen da energia hartu ahala. U235 eta U238 atomoak modu irregularrean daude nahastuta uranio puska arrunt batean, baina desorden horrek ez du energiarik sortzen...

Gai honetan gehiago sakontzeko, kopuruari begiratu behar zaio. Beroa hain zuzen zenbakiekin neurtu behar da... Beroa ondo definitzeko bi zenbaki dago gutxienez erabili beharra; energia kopurua neurtzeko bata, desordenaren kopurua neurtzeko bestea. Energia kopurua kaloria izeneko banakoaren bidez neurtzen da... Desorden kopurua entropia izeneko kontzeptu matematikoaren arabera neurtzen da...

Azter dezagun orain entropiaren eta desordenaren arteko harremana. Lana, adibidez, kontzeptu makroskopiko bat da. Lana deskribatzeko, koordenada makroskopikoen -presioa eta bolumena- aldaketak erabiltzen dira. Lanak mugimendu ordenatua esan nahi du. Molekulen mugimendu desordenatuak ez dira lana. Baina lana barne energiaren baitan desagertzen denean, marruskatzean gertatzen den bezala, gehitu egiten da molekulen mugimendu desordenatua. Prozesu horrek desordena gehitzea dakar. Gas batek beste batean duen difusio naturalak, gas horiek nahasten direnean, desordena gehitzea dakar -handiagoa da desordena difusioaren ondoren, gasak bereizita zeudenean baino-. Izadian ikusten diren kasu guztietan desorden handiagoko egoera iristeko joera dago. Arestian esan da prozesu naturalek entropia handiagoko egoera iristeko joera dutela, eta, beraz, uste izatekoa da entropiaren kontzeptu termodinamikoaren eta desordenaren kontzeptu estadistikoaren artean badela harreman bat.

Mekanika estadistikoak frogatzen du bi kontzeptu horien arteko lotura erlazio honek definitzen duela

Ekuazio horretan, k Boltzmann-en konstantea da, S sistemaren entropia da, eta w egon daitekeen egoera posible guztien artean sistema horrek dagoen egoera horretxetan egoteko duen aukera da. Beraz, 25-13 ekuazioak harremanetan jartzen ditu kopuru termodinamiko edo makroskopiko bat, entropia, eta kopuru estatistiko edo mikroskopiko bat, probabilitatea.

Hori ondo ulertzeko, gas ideal batek dilatazio isotermikoan duen entropia aldaketa kalkulatuko da orain. Kasu honetan, molekula kopurua eta tenperatura ez dira aldatzen, baina bolumena bai. Molekula jakin batek V bolumena duen eremu batean egoteko duen aukera V-ren proportzioan dago; alegia, V zenbat eta handiagoa, orduan eta handiago da orobat molekula horrek V-n egoteko duen aukera. Beraz, V-n molekula bakarra egoteko dagoen aukera hau da"

ekuazio horretan c konstante bat da. V bolumenean N molekula aldi berean egoteko dagoen aukera -ren balioa N bider da. Alegia, V bolumen batean N molekula egoteko aukerak hauek dira:

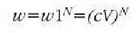
Adibidez, V-n molekula bakarra aurkitzeko aukera 1/2 baldin bada (alegia, %50eko aukera baldin badu V-n egoteko eta %50eko aukera V-tik kanpo egoteko) V-n bi molekula egoteko aukera 1/4 da. Kasu honetan badira 4 egoera orobat gertagarri (biak barruan; biak kanpoan; bata barruan, bestea kanpoan; bata kanpoan, bestea barruan), eta egoera horien artean bakarra baizik ez dago bi molekulak V-n dituena.

25-13 ekuazioa eta 25-14 ekuazioa konbinatzen badira, hau ateratzen da:

Beraz, V1 bolumenaren egoeran eta Vi bolumenaren egoeran (tenperatura eta molekula kopurua konstante irauten dutela) hau da entropiaren arteko aldea:

25-12 hori zehatz-zehatz dator bat ekuazioaren emaitza soil-soilik termodinamikoarekin.

Entropiaren definizio estatistikoaren bidez, sistema batek ez orekazko egoera baten duen entropiaren esanahia adieraz daiteke. Ez orekazko egoera batek entropia definitua du desorden maila definitu bat duelako. Beraz, bigarren legeak oinarri estatistiko bat du, eta, beraz, probabilitateen legeek definitzen dute (probabilitate gehiagoko egoera baterantz) prozesu naturalek gertatzean duten norabidea (entropia handiago baterantz). Ikuspuntu horretatik, zehatz esanda, ez da ezinezkoa bigarren legea haustea. Adibidez, bitarte aski luze batez itxoinez gero, gerta liteke urmael bateko ura udako egun bero batean batbatean izoztea. Gerta daitekeen zerbait da hori, baina hori gertatzeko aukera, kalkulatuz gero, ikaragarri txikia da; hori behin bakarrik gertatzeko, unibertsoaren adina aldiz izango litzatekeen bitarteak igaro beharko luke. Beraz, termodinamikaren bigarren legeak gertaeren modu gertagarriena erakusten du, eta ez gerta daitezkeen gertaera bakarrak. Baina lege horren aplikazio eremua hain da zabala, eta izadiak lege hori gezurtatzeko probabilitatea hain da txikia, non zientzia osoko legerik baliagarrienetako eta orokorrenetako bat izateko berezitasuna baitu.

Kelvin, William Thompson.

(Belfast, 1824 - Netherhall, 1907) Britainiar fisikari eta matematikaria. Glasgow-en eta Cambridgen egin zituen ikasketak. Glasgow-eko unibertsitatean filosofia naturaleko ikasle izan zen. 1 856an bero absortzioaren fenomenoa aurkitu zuen (Thomson efektua), eta horrekin zientzilari asko termodinamikaren alorrera eraman zituen. Handik gutxira energiaren barreiatzearen teoria azaldu zuen: teoria horren arabera sistema baten energia kopurua aldatzen ez bada ere, energia horretatik erabil daitekeen zatia etengabe gutxitzen da. Gasen konpresioa aztertuz, Joule-Thompson efektua aurkitu zuen: gasak presioz zulo txiki batetik igaro behar duenean izaten dituen tenperatura aldaketak. Esperientzia horien ondorioz zero absolutua 273 °C-tan zegoela aurkitu zuen, eta hala tenperatura eskala absolutua zero absolutuan oinarritua proposatu zuen zientzilarientzat. Geroago Atlantikoan zehar ezarri zuen lehenengo kablea jartzeko lanetan parte hartu zuen. Kelvin-en zientzia emaitzarik garrantzizkoenak energiaren kontserbazioari buruzko ikerketak, tenperatura absolutuaren eskala, beroaren teoria dinamikoa, elektrizitatearen eta magnetismoaren analisi matematikoa, Lurraren adina finkatzeko ikerketak, eta hidrodinamikazko oinarrizko lanak izan ziren. 600 lan zientifikotik gora argitaratu zituen. Kelvinen eskala zero absolutuan hasten da eta Celsius-en gradu bitarteak ditu. Zero absolutua da gas ideal baten bolumena zero izatera iritsiko litzatekeen tenperatura. Celsius eskalako zeroa (0 °C) Kelvin eskalako 273 °K baliokidea da.

Maxwell, James Clerk.

(Edinburgo, 1831-Cambridge, 1890) Eskoziar fisikaria. Aberdeen, Londres eta Cambridgeko unibertsitateetan irakasle izan zen. Maxwellek idatzi zituen teorien artean aipagarri dira elektrizitatearen, magnetismoaren eta gasen teoria zinetikoaren gainean egin zituenak. Elektrodinamikaren oinarriak finkatu zituen. Magnetismoari buruz haren izena daraman teoria landu zuen, 1855. urtean hasi eta urteetan zehar ikertu zuena. 1856. urtean bere izena duten ekuazioak formulatu zituen; haien bidez elektromagnetismo klasikoa matematikoki adieraztea lortu zuen. Gasen dinamika, astronomia eta koloreak ere ikertu zituen besteak beste. Maxwellen ekuazioek elektromagnetismoaren oinarrizko legeak Michael Faraday ingeles fisikariak finkatu zituen eremu elektriko eta eremu magnetiko kontzeptuetan oinarriturik, elektrizitatea eta magnetismoa erlazionatzen dituzte. Maxwellen ekuazioak Heinrich Hertz alemaniarrak aurkitu zituen uhin elektromagnetikoak badirela hartzen du oinarritzat. Maxwellen ekuazioen bidez eremu elektriko eta magnetikoaren balioa kalkula daiteke.

Carnot, Nicolas Leonard Sadi.

(Paris, 1796- Paris, 1832)Frantses fisikaria. Lazare Nicolas-en semea. Beroaren eta lanaren arteko lotura zehaztu zuen lehen fisikaria izan zen; tresna termikoak aztertzen ari zela, termodinamikaren bigarren printzipioa edo Carnoten legea eman zuen, eta horrela sortu zen termodinamika modernoa (Suaren motor indarraz eta indar hori garatzeko makinez gogoetak, 1824). • Carnoten zikloa: Bero motorretan, jariakari baten (motore batean erabilitako gasa, esate baterako) presio eta tenperatura aldaketen segida zikliko ideala, XIX. mendearen hasieran Sadi Carnot ingeniari frantsesak asmatua. Ziklo horretan motorrak erabiltzen duen gai jariakariak lau aldi izaten ditu hurrenez-hurren: espantsioaldia, gaia tenperatura bero aldagabean berotuz; espantsioaldi adiabatiko atzeragarria ; konpresioaldia, gaia tenperatura hotz aldagabean hoztuz; eta konpresioaldi adiabatiko itzulgarria. Motorrak beroa hartzen du (bero iturritik) tenperatura altuan espantsioaldian, lana egiten du espantsioaldi adiabatiko itzulgarrian, beroa kanporatzen du (bero isurtegira) tenperatura hotzeko konpresioaldian, eta lana jasotzen du konpresioaldia adiabatiko itzulgarrian. • Carnoten legea: Sadi Carnotek 1 824an idatzi zuen "proposamen orokorrean" jasorik dagen legea: "Beroaren higimena, jokoan jartzen diren eragileengandik aske da; batetik besterako bero garraioa geratatzen zaien gorputz beroaren eta gorputz hotzaren tenperaturen aldeak ematen du higimenaren zenbatekoa." Lege honen edukia, Rudolf Clausius-ek eta William Thomsonek (Lord Kelvin) apur bat orrazturik, Termodinamikako bigarren lege bihurtu zen, haiek termodinamikaren teoria garatu zutenean.

Clausius, Rudolf Emanuel.

(Koslin, 1822 - Bonn, 1888)Alemaniar fisikaria. Termodinamikaren alorrean egin zituen batez ere ikerketak. Termodinamikako bigarren printzipioaren adierazpen berri bat eman zuen 1850. urtean, entropia kontzeptu berria erabiltzen hasi zelarik. 1857. urtean gasaren teoria zinetikoa adierazi zuen. • Clausius-Clapeyron-en ekuazioa. Termodinamikaren oinarrizko ekuazioa, isurkari baten lurrin presioaren aldaketa tenperatura aldaketarekin lotzen duena.