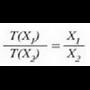Fisika-Kimika»Fisika - Kimika
1. Tenperatura
Deskripzio mikroskopikoa eta makroskopikoa
Egoera fisikoak aztertzeko, oro har, materia zati bat hartzen da eta kanpoko ingurutik banantzen da. Materia zati horri sistema esaten zaio. Sistematik kanpo dagoen guztiari eta sistemaren portaerarekin zerikusia duenari giroa esaten zaio. Sistemaren portaera aztertzeko, oro har, sistema horrek giroarekin duen harremana ikertzen da. Demagun sistema pilota bat dela, eta giroa, berriz, airea eta lurra. Pilota erortzen denean aireak eta lurrak pilotaren mugimenduan zein eragin duten aztertzen da. Demagun ontzi batean dagoen gasa dela sistema, eta enbolo mugikorra eta Bunsenen pizgailua direla giroa. Enboloaren eta pizgailuaren eraginez gasaren propietateak eta jokaera nola aldatzen diren aztertzen da. Adibide horietan guztietan zenbait kopuru hartu behar dira sistemaren portaera azaltzeko. Baina, kopuru horiek hautatzeko bi ikuspegi daude: makroskopikoa eta mikroskopikoa.
Bero gertakariak izaten diren prozesuetan, termodinamikak prozesuaren ikuspegi makroskopikoa ematen du eta beroaren teoria atomikoak, berriz, ikuspegi mikroskopikoa. Mekanikan erabiltzen den eraso makroskopikoaren metodoan, sistema baten ezaugarriak deskribatzen dira eta sistemaren hainbat tasun neurgarri, zentzumenek zuzenean edo zeharbidez hartzen dituztenak, zehazten dira. Esate baterako, ontzi batean dagoen gasarentzat, bolumena, presioa eta tenperatura kopuru makroskopikoak dira, zentzumenek zuzenean atzematen dituzten kopuruak baitira guztiak. Eraso mikroskopikoaren metodoaren bidez, sistema baten ezaugarri zehatzak aztertzen dira, eta azterketa horrekin zehazten dira zuzenean ezin neur daitezkeen kopuruak, eta oro har, gure zentzumenek hartzen ez dituztenak . Esate baterako, ontzi batean dagoen gasaren adibidean, molekula kopurua, horien lastertasuna edo energia, elkarren arteko harremanak, etab. zehazten dira. Azalpen mikroskopikoak zuzenean neur daitezkeen kopuru makroskopikoen balioak eta propietateak ematen ditu azkenean.
Eraso sistema horiek elkarri lotuta egon behar dute, izan ere, zuzenean atzeman daitezkeen propietate makroskopiko bakanak ezagugarri mikroskopiko askoren batez bestekoak baitira. Gas batek sortzen duen presioa adibidez, gas molekulek gainalde banakoko eragiten dituzten talka guztien ondoriozko mugimendu kopuru aldaketaren lastertasunaren batez bestekoa da. Gas baten tenperatura molekulen translazioaren ondoriozko energia zinetikoaren batez bestekoa da. Mekanikan, zenbaitetan, aldagai mikroskopikoak hartzen dira kontuan, hau da, aldagai horien batez bestekoak kopuru makroskopikoak edo zuzenean neurgarriak ematen dituzte . Marruskadura koefizientea, esaterako, kopuru mikroskopiko zehatzekin lotura duen ezaugarri makroskopikoa da.
Oreka termikoa. Termodinamikaren zero legea.
Ukimena da gorputz beroak gorputz hotzetatik bereizteko modurik arruntena eta sinpleena. Ukimenaren bidez, zehaztasun handirik gabe, berotasun mailaren arabera sailka daitezke gorputzak; A Bbaino beroagoa da, B C baino beroagoa, etab. esan daiteke. Ukimena tenperaturaren zentzumena dela esaten da. Dena dela, gorputz baten tenperatura zehazteko prozedura erabat subjektiboa eta kualitatiboa da hori; ez da balio handikoa prozedura helburu zientifikoak iritsi nahi direnean. John Lockek 1690ean frogatu zuen ukimenaren bidezko metodoa ez zela fidatzekoa. Horretarako esperimentu bat egin zuen: eskuak uretan sartzen dira, bat ur berotan eta bestea ur hotzetan; ondoren bi eskuak ur epeletan sartzen dira. Ur hotzetan egondako eskuak beroa sentituko du ura eta ur berotan egondakoak berriz hotza. Tenperaturari buruzko gure iritziak, beraz, nahasbidea sor dezake. Horrez gainera, gizakiak tenperaturaz duen pertzepzioa oso mugatua da. Hortaz, neurri objektiboagoak behar dira, tenperatura zenbaki bidez neurtuko dutenak alegia.
Ezer baino lehen tenperaturaren esanahia ulertu behar da. Demagun bi objektu ditugula: A objektua eskuaz ukitzean hotzaren sentipena dugu eta B objektua, aurrekoaren berdina, ukitzean beroaren sentipena dugu. Bi objektuak elkar ukitzen dutela jartzen badira, denbora bitarte nahikoa igaro ondoren, tenperatura sentipen bera izango da gorputz batekin zein bestearekin. Hori hala denean A eta B oreka termikoan daudela esaten da. "Bi gorputz oreka termikoan daude" esapidetik abiatuta hau esan daiteke: bi gorputz halako egoeran daude, ezen elkar ukitzen dutela jarriz gero sistema elkartuak oreka termikoan egongo lirateke. Oreka termikoaren froga logikoa egiteko hirugarren gorputz bat edo gorputz aitorle bat behar da, termometroa adibidez. Hori guztia termodinamikaren zero legea esaten zaion postulatuak azaltzen du: A eta B gorputzak C hirugarren gorputz batekin oreka termikoan badaude, orduan A eta B oreka termikoan daude. Azalpen horiek oinarrizko ideia bat osatzen dute: sistema baten tenperatura beste sistema batzuekin harremanean jartzen denean, sistema horiek duten tenperatura balio bera hartzen du. Kontzeptu hori bat dator beste ideia batekin, alegia tenperatura sistema baten bero edo hotz mailaren neurria dela esaten duenarekin, gorputz guztien bero maila berdindu egiten baita gorputzak denbora nahikoan elkarrekin harremanean egon ondoren. Zero legeak azaltzen duen ideia bakuna bada ere, ez da inolaz ere begien bistakoa. Esate baterako, joanek eta Joxek Pello ezagutzen dute, baina ez dute nahitaez elkar ezagutu beharrik. Bi burdin puskak, Ak eta Bek, C imana erakartzen dute, baina baliteke bi burdin puska horiek elkar erakartzea ala ez erakartzea. Ideia hori argi eta garbi azaltzea, beraz, ezinbestekoa da tenperatura neurtuko duen prozedura arrazionala osatuko bada.
Tenperatura neurria
Ezaugarri fisiko asko aldatu egiten dira tenperaturaren eraginez. Esate baterako, isurkari baten bolumena, ziri baten luzera, alanbre baten erresistentzia elektrikoa, bolumen konstantean irauten duen gas baten presioa eta lanpara hari baten kolorea. Propietate horien artetik edozein aplika daiteke termometro bat egiteko. Gai termometriko berezi bat eta gai horren ezaugarri termometriko berezi bat aukeratzen dira termometroa egiteko. Bestalde, oinarritzat hartzen da aukeratutako gaia tenperaturaren arabera etengabe aldatzen dela. Gai termometrikoa izan daiteke adibidez, isurkari bat beirazko hodi kapilar batean, eta ezaugarri termometrikoa, berriz, isurkari zutabearen luzera. Edo gai termometrikoa izan daiteke ontzi bateko gasa, bolumen konstantea duena, eta ezaugarri termometrikoa gasaren presioa; eta horrela hurrenez hurren.
X jarriko zaio erabiliko den edozein ezaugarri termometrikoari. X propietatearen funtzio lineal bat, edozein, hautatuko da, esaterako termometroaren T tenperatura, eta ondoren, propietate horrekin oreka termikoan dagoen edozein sistema:

Adierazpen horretan a konstante bat da. T(X) funtzioarentzat forma lineala hartuta funtzioa era honetan definitzen da: tenperatura alde berdinak, edo tenperatura tarteak, X-en aldaketa berdinei dagozkie. Horrek esan nahi du merkurioa termometro hodian luzera banako bat aldatzen denean, tenperatura ere kopuru jakin bat aldatzen dela, hasierako tenperatura edozein izanda ere. Baieztapen horretatik heste ondorio bat ere ateratzen da, alegia bi tenperatura eta horiei dagokien X' baliokideak harreman berean daudela, hau da
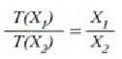

a konstantea zehazteko, eta termometroa kalibratzeko, puntu jakin bat hartzen da erreferentziatzat eta puntu horretan termometro guztiek T tenperaturaren irakurketa bera eman behar dute. Puntu horretan orekan egon behar dute izotzak, urak eta ur lurrinak; puntu horri uraren puntu hirukoitza esaten zaio. Puntu horretara presio kopuru jakin baten eraginaz iristen da bakarrik (irud. 21-1). Ur lurrinak puntu hirukoitzean duen presioa hau da: Hg-zko 4.58 mm. Ereduzko puntu horren tenperatura, zoriz, 273.16 K jarri da (hala erabaki zen 1954ko Pisu eta Neurrien Hamargarren Konferentzian, Parisen); 273.16 °K da horren laburdura. Kelvin gradua tenperatura bitartearen banakoa da.
Puntu hirukoitzaren balioak 0 azpi indizeaz adierazten badira, orduan
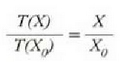
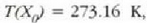 baita
baita
orduan

Beraz, ezaugarri termometrikoak X balioa duenean eta ekuazio horren bigarren aldean X eta
 -ren balioak jartzen direnean,
T(X)' funtzioak °K-etan ematen du T tenperatura.
-ren balioak jartzen direnean,
T(X)' funtzioak °K-etan ematen du T tenperatura.
Azken ekuazio hori edozein termometrorentzat aplika daiteke. Beiran sartutako isurkari termometro batentzat, X isurkari zerrendaren luzera da (L), eta

Presio konstantea duen gas batentzat X gasaren bolumena da (V), eta

Bolumen konstantea duen gas batentzat X gasaren presioa da (P) eta
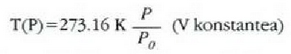
Platinozko erresistentzia duen termometro batentzat X erresistentzia elektrikoa da (R) eta

Baina sistema baten tenperatura neurtu ondoren lortutako balioa aukeratu den termometro motaren araberakoa den ala ez aztertu behar da. Onartu da termometroak ereduzko tenperaturan egokitu behar direla, baina ereduzkoak ez diren puntuetan zer gertatzen da? Sistema bateko tenperaturak hainbat termometro motaren bidez neurtu ondoren, termometro batzuek eta besteek ematen dituzten balioen artean desberdintasunak daudela ikus daiteke. Eta mota bereko termometroak batera jartzen direnean ere, esaterako gas mota desberdineko bolumen konstantezko gas termometroak, tenperatura neurri desberdinak lortzen dira sistema jakin batean eta egoera jakin batean.
Beraz, tenperatura eskala definitu bat lortzeko, termometro mota jakin bat hartu behar da eredu. Gasa hartzen da ereduzko gai termometriko gisa, bolumen konstantezko gas termometroek ematen dituzten neurrien arteko aldea txikia baita. Termometroan erabiltzen den gas kopurua gutxitu ahala presioa ere gutxitzen denez gero, gas mota desberdinak erabiltzen dituzten gas termometroen arteko neurri aldeak ere gutxitu egiten dira. Beraz, badirudi gasa presio txikian duen termometro baten jokaeran oinarrizko zerbait gertatzen dela.
• Adibidea. Merkuriozko termometro batean merkurio zutabeak 6.0 cm-ko luzera du puntu hirokoitzean. Zein luzera izango du eskalak 300 ° K-ko tenperatura ematen duenean?
 , orduan
, orduan
 ekuaziotik
ekuaziotik
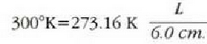 lortzen da.
lortzen da.
Beraz, L = 6.6 cm
Gas termometroa
Gas baten presioa, tenperatura edozein dela ere, bolumenaren araberakoa da. Bolumena konstantea bada, presioa tenperaturarenaraberakoa da, eta tenperatura igo ahala presioa ere etengabe igotzen da. Bolumen konstatea duen gas termometroak propietate termometriko gisa gas baten presioa bolumen konstantean erabiltzen du.

21.2.• Bolumen konstantezko gas termometroa
Bolumen konstantezko gas termometroaren atal nagusia anpulu bat da. Anpulua izan daiteke beirazkoa, portzelana nabartuzkoa, kuartzo urtuzkoa, platinozkoa edo platino iridioztatuzkoa (erabiliko den tenperaturaren arabera); anpulu hori merkuriozko manometro bati (irekia adibidez) lotuta egoten da hodi kapilar baten bidez. Anpulua, barruan gasa duela, bainuan edo neurtu nahi den giroan sartzen da. Ontzia halako eran jarri behar da non U irudia osatzen duen hodiaren ezkerreko adarreko merkurioak erreferentzia markaren parean gelditu behar baitu, era horretan, bolumen konstantean eduki ahal izango baita gasa. Orduan, merkurioaren altura eskuineko aldean ikus daiteke. Gordeta dagoen gasaren presioa hau izango da: merkurio zutabeen altura diferentziak (bider rg) gehi atmosfera presioa (barometro batekin neurtua). Praktikan hainbat zuzenketa egin behar dira anpuluaren uzkurtzearen edo dilatatzearen ondoriozko bolumen aldaketak direla-eta; bestalde, kontuan hartu behar da gas guztia ez dela bainuan sartu, hodi kapilarean dagoena esaterako. Demagun zuzenketa horiek guztiak eta beste hainbat egin direla eta P dela batez besteko presioa bainuaren tenperaturan. Orduan tenperatura honela lortzen da:

Presio konstantezko gas termometroa bolumen konstantezkoa baino zailagoa da erabiltzen eta konplexuagoa bai egiten bai zuzentzen. Bolumen konstantezko termometroa gehien erabiltzen den gas termometroa da zientzia ikerketetan
Gas idealaren tenperatura
Demagun bolumen konstantezko gas termometro batean gas kopuru jakin bat
dagoela anpulu batean sartuta halako eran non anpulua urez inguraturik dagoenean presio puntu hirukoitza
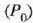 balio definitu baten berdina den, 80.0 cm Hg adibidez. Anpulua atmosfera 1eko presioan
kondentsatzen den lurrinaz inguratuz gero, gasaren presioa bolumen konstanteak aurretik duen balioa mantenduz
neurtzen da
balio definitu baten berdina den, 80.0 cm Hg adibidez. Anpulua atmosfera 1eko presioan
kondentsatzen den lurrinaz inguratuz gero, gasaren presioa bolumen konstanteak aurretik duen balioa mantenduz
neurtzen da  .
Ondoren, berdintza honetatik abiatuta, tenperatura kalkulatzen da:
.
Ondoren, berdintza honetatik abiatuta, tenperatura kalkulatzen da:
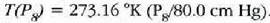 .
Gero,
.
Gero,  -ak
balio txikiagoa izan dezan, gas piska bat kentzen da, 40.0 cm Hg adibidez.
Orduan
-ak
balio txikiagoa izan dezan, gas piska bat kentzen da, 40.0 cm Hg adibidez.
Orduan 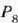 -ren
balio berria neurtu eta tenperatura kalkulatzen da:
-ren
balio berria neurtu eta tenperatura kalkulatzen da:
 .
Anpuluko gas kopurua jaisten da berriro, eta
.
Anpuluko gas kopurua jaisten da berriro, eta  -ren
balio berriaren tenperatura irakite puntuan kalkulatzen da
-ren
balio berriaren tenperatura irakite puntuan kalkulatzen da
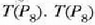 balioak
balioak
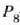 balioak P ren
arabera marrazten badira, lortzen den kurbaren estrapolazioa egin daiteke,
harik eta kurbak x ardatzarekin intersekzioa egiten duen arte, non
balioak P ren
arabera marrazten badira, lortzen den kurbaren estrapolazioa egin daiteke,
harik eta kurbak x ardatzarekin intersekzioa egiten duen arte, non
 baita.
baita.
(21.3) irudian hainbat gasezko eta bolumen konstantezko termometroetatik eta prozedura horren bidez jasotako kurbak azaltzen dira. Kurba horiek erakusten dute bolumen konstantezko gas termometro baten tenperaturaren irakurpenak erreferentziazko presioaren ohiko balioentzat erabiltzen den gasaren araberakoak direla. Dena dela, erreferentziazko presioa txikitu ahala, bolumen konstantezko gas termometroak (hainbat gasezkoak) balio berera hurbiltzen dira. Beraz, estrapolazioa egin den tenperaturaren balioa gasen ezaugarri orokorren araberakoa da bakarrik, eta ez gas jakin baten araberakoa. Hortaz, gas idealaren tenperatura honela definitzen da:
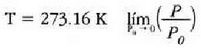

Beraz, termometro eredu gisa bolumen konstantezko gas termometroa erabiltzen da, hau da, azken ekuazio horren arabera definitutako tenperatura eskalan oinarritzen dena
Gogoan hartu behar da aukeratutako tenperatura eskala ez dela gas jakin baten ezaugarrien araberakoa, gasen ezaugarri orokorren aaberakoa baizik (hau da, gas ideal baten ezaugarrien aaberakoa). Beraz, tenperatura bat neurtzeko, tenperatura horretan dagoen gas bat erabili behar da. Gas termometro batekin neur daitekeen gutxieneko tenperatura T= 1 K da, gutxi gorabehera. Hain tenperatura baxua neurtzeko helioa erabili behar da, presio apalean, beste edozein gas baino tenperatura txikiagoetan urtzen baita helioa. Horren arabera, beraz, ezin zaio T=O K terperaturari, zero absolutua deiturari, esanahirik eman
Zero absolutua definitzeko edozein gairen ezaugarrien mendekoa ez den tenperatura eskala behar da. Tenperatura termodinamikoaren eskalak, Kelvin eskala deituak, ezaugarri hori du; beraz, badago inguru guztietako tenperaturari esanahi jakina ematea, gai termometrikoa kontuan hartu gabe. Hala, fisikaren ikuspegitik zuzena den erara definitu daiteke zero absolutua. Eta frogatu ahal izango da gas idealaren eskala eta Kelvin eskala termodinamikoa berdin-berdinak direla gas termometro bat erabil daitekeen tenperatura mugen barruan. Arrazoi horregatik, gas idealaren tenperaturaren atzetik K idatz daiteke
Dena dela, zero absolutuaren bidez ez da zero energia duen eta mugimendurik ez duen egoera adierazten. Eta ez da zuzena molekulen ekintzak zero absolutuan eteten direlako ustea. Ideia horrek azaltzen du tenperaturaren ikuspegi makroskopioak molekula mugimenduen ikuspegi mikroskopikoarekin harreman zuzena duela. Baina harreman hori zehaztu nahi denean, zero absolutuan dagoen gai baten molekulek energia zinetiko kopuru finitua dutela -zero puntuaren energia deitua- ikus daiteke. Zero absolutuan energia molekularra txikia da, baina ez hutsa.
Celsius eta Fahrenheit eskalak
Gaur egun gehien erabiltzen diren tenperatura eskalak Celsius eskala, antzina zentigradu deitua, eta Fahrenheit eskala dira. Bi eskala horiek Kelvin eskala absolutuaren arabera definitzen dira; azken hori da, hain zuzen, oinarrizko eskala zientzian.
Celsius tenperatura eskalak erabiltzen duen gradua (tenperatura banakoa) Kelvin eskalak (edo gas idealaren eskalak) erabiltzen duen magnitudearen berdina da. Celsius tenperatura t letraz adieraziz gero, orduan

adierazpenak Celsius t ° C tenperatura eta Kelvin T K tenperaturak lotzen ditu. Horren arabera, uraren puntu hirukoitza 0.01 ° C da. Celsius eskalaren zero puntuan airez betetako ura eta izotza orekan daude atmosfera presioarekin; izotzaren fusio puntua esaten zaio horri. Ur lurrina 1 atm presioaz kondentsatzeko behar den tenperatura lortzeko, hau idazten da
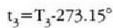 eta
eta
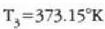 adierazpenarekin 21-3 irudian hau lortzen da
adierazpenarekin 21-3 irudian hau lortzen da
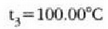
Laboratorio lanetarako hau hartzen da Celsius gradutzat: termometroa izotzaren fusio puntutik uraren irakite punturaino berotzen denean, une horretan gertatzen den propietate termometrikoaren aldaketaren ehunenak sortzen duen tenperatura aldaketa.
Fahrenheit eskala ingeles hizkuntza erabiltzen duten herrialdeetan erabiltzen da,
baina zientzian ez du legezko estatusik. Bi puntu finkoetan oinarritzen den eskala da:
izotzaren fusio puntua (32 °) eta uraren irakite puntua (212 °F).
Beraz, Fahrenheit gradu bat Celsius gradu baten 5/9 da.
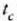 (tenperatura Celsius eskalan) eta
(tenperatura Celsius eskalan) eta
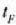 (tenperatura Fahrenheit eskalan)
tenperaturen arteko harremana hau da:
(tenperatura Fahrenheit eskalan)
tenperaturen arteko harremana hau da:
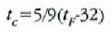

21.4: Kelvin, Cetsrus eta Fahrenheit tenperatura eskakn arteko konparazioa.
(21-4) irudian Kelvin, Celsius eta Fahrenheit eskalak konparatzen dira.
Nazioarteko Tenperatura Eskala
Termometrian erabiltzen den ereduzko puntu finkoa uraren puntu
hirukoitza da, 273.16 ° K-ko balioa eman zaiona.
Ereduzko termometroa bolumen konstantezko gas termometroa da.
Gas estrapolatuen eskala erabiltzen da eta
 ekuaziotik gas idealaren tenperatura lortzen da. Froga daiteke gas termometro bat
erabil daitekeen bitarteetan, eskala hori eta Kelvinen eskala termodinamiko
absolutua berdinak direla.
ekuaziotik gas idealaren tenperatura lortzen da. Froga daiteke gas termometro bat
erabil daitekeen bitarteetan, eskala hori eta Kelvinen eskala termodinamiko
absolutua berdinak direla.
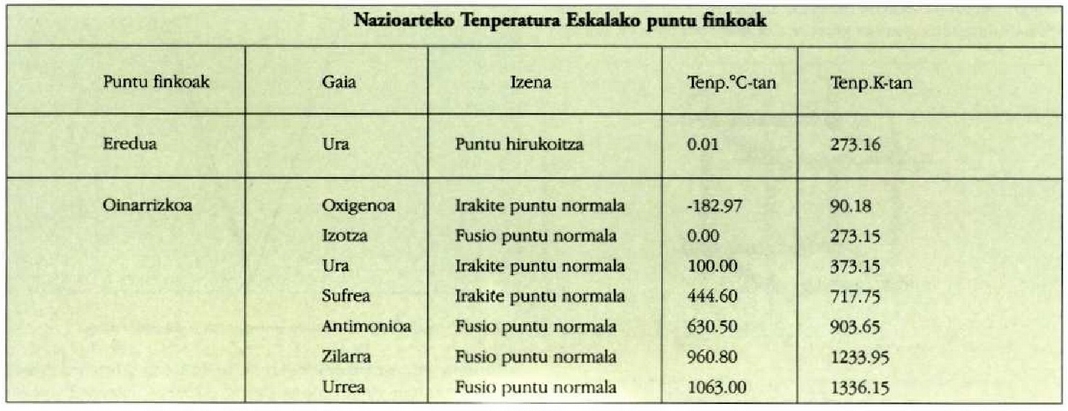
Ereduzko termometro hori harturik, esperimentu bidez tenperatura neurrientzat beste erreferentzia puntuak zehazten dira, puntu finkoak deituak. Oinarrizko erreferentzia puntu finkoak 21-1 taulan azaltzen dira, eta oinarritzat hartzen da atmosfera presio normalean daudela puntu horiek. Tenperaturak Celsius eskalan adierazteko, Kelvin ternperatura zehaztu behar da lehenbizi, eta 21-5 ekuazioa ebatzi behar da ondoren.
Tenperaturak era horretara zehazteak lan handia ematen du. Lan mota guztietarako prozedura hori erabiltzeak ez du zentzurik. Horregatik, 1927an Nazioarteko tenperatura eskala osatu zen (1948an aztertu zen berriz); eskala horrek erabiltzen erraza izan behar zuen. Eskala hori metodo sail batek osatzen du; metodo sail horretan Kelvinen eskalara gehien hurbiltzen diren datuak ematen dituzten metodoak biltzen dira. Hainbat puntu finko zehaztu ziren, 21-1 taulako oinarrizko puntuak, eta hainbat tresna zehaztu ziren, puntu finko horien arteko interpolazioa egiteko beharrezkoak. Bestalde, hainbat formula eman ziren oinarrizko tenperaturak neurketa uneko irakurketa barometrikoen arabera zuzentzen zituztenak. Nazioarteko eskala Celsius eskalatik urruntzen da puntu finkoen arteko tenperaturak neurtzen direnean; aldea, ordea, ez da kontuan hartzekoa. Nazioarteko eskala ia munduko herrialde guztietan hartu da eredutzat.
Dilatazio termikoa
Tenperatura aldaketak dituen ondorio nagusiak bi dira: tamaina aldaketak eta gaien egoera aldaketak. Egoera aldatu gabe tamaina nola aldatzen den aztertuko da lehenbizi.
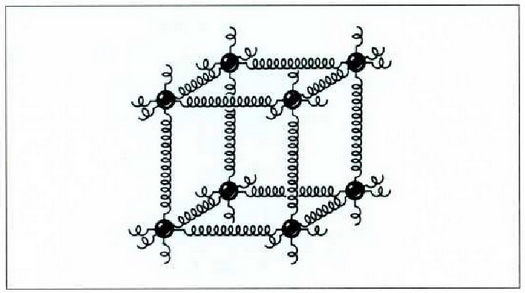
Bedi gai gotorraren eredu soil bat. Gai gotor batean atomoak elkarri lotuta egoten dira
jatorri elektrikoa duten idarren bidez. Gai gotor batek malguki koltxoi
mikroskopiko baten itxura duela esan daiteke (21-5 irud.). "Malguki" horiek trinkoak dira
eta zentimetro kubiko batean 1023 malguki inguru dago. Tenperatura edozein dela ere,
gai gotorraren atomoak dardarrean egoten dira. Dardarraren anplitudea 10-9 cm-koa da
gutxi gorabehera, eta maiztasuna 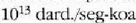 .
.
Tenperaturak gora egiten duenean, atomoen dardaren anplitudeak ere gora egiten du, eta atomoen arteko batez besteko distantzia ere handitu egiten da. Horren ondorioz, tenperatura igotzen den neurrian dilatatzen da gorputz gotorra. Gai gotorraren neurri linealen
(luzera, zabalera edo altura) edozein aldaketari dilatazio lineala esaten zaio.
Neurri lineal horren luzera 1 bada,  tenperatura aldaketa batek sortutako luzera aldaketari
tenperatura aldaketa batek sortutako luzera aldaketari
 esaten zaio.
Esperimentuen bidez ikus daiteke
esaten zaio.
Esperimentuen bidez ikus daiteke  luzera aldaketa
luzera aldaketa 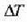 tenperatura aldaketaren proportzionala dela, eta zalantzarik gabe, jatorrizko
tenperatura aldaketaren proportzionala dela, eta zalantzarik gabe, jatorrizko
 luzeraren proportzionala.
Beraz, idatz daiteke
luzeraren proportzionala.
Beraz, idatz daiteke
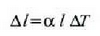
 dilatazio linealaren
koefizientea da. Koefiziente horren balioak, noski, gai batetik bestera aldatu egiten dira.
Aurreko formula hori berriz idatziz gero:
dilatazio linealaren
koefizientea da. Koefiziente horren balioak, noski, gai batetik bestera aldatu egiten dira.
Aurreko formula hori berriz idatziz gero:
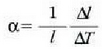
non  tenperatura graduaren
aldaketaren ondorioz gertatutako luzera aldaketaren zatikia baita.
tenperatura graduaren
aldaketaren ondorioz gertatutako luzera aldaketaren zatikia baita.
 -ren balioa
gorputz batek une jakin batean duen tenperaturaren eta 1 zehazteko hartu den erreferentziazko
tenperaturaren araberakoa da. Dena dela, bariazioa oso txikia da eta garrantzi gutxikoa ingeniaritzako
neurriak hartzeko behar den zehaztasunaren aldean. Gai jakin baten konstantetzat har daiteke,
tenperatura kontuan izan gabe. 21-2 taulan hainbat gai gotorrek 0°C-100 °C tenperatura bitartean
duten batez besteko dilatazio linealerako balioak zehazten dira (izotzarena salbu, horrentzat
tenperatura bitartea -10 ° C-0 ° C baita). Zerrenda horretako gai guztiek, tenperaturak gora
egin ahala gertatzen den dilatazioaren eraginez, tamainaz aldatzen dira, a positiboa baita.
Dilatazioaren magnitude ordena hau da: milimetro bat luzera metroko 100 Celsius moduluko.
Celsius modulu bat (1 Ce) Celsius eskala batean neurtutako tenperatura bitartea da
-ren balioa
gorputz batek une jakin batean duen tenperaturaren eta 1 zehazteko hartu den erreferentziazko
tenperaturaren araberakoa da. Dena dela, bariazioa oso txikia da eta garrantzi gutxikoa ingeniaritzako
neurriak hartzeko behar den zehaztasunaren aldean. Gai jakin baten konstantetzat har daiteke,
tenperatura kontuan izan gabe. 21-2 taulan hainbat gai gotorrek 0°C-100 °C tenperatura bitartean
duten batez besteko dilatazio linealerako balioak zehazten dira (izotzarena salbu, horrentzat
tenperatura bitartea -10 ° C-0 ° C baita). Zerrenda horretako gai guztiek, tenperaturak gora
egin ahala gertatzen den dilatazioaren eraginez, tamainaz aldatzen dira, a positiboa baita.
Dilatazioaren magnitude ordena hau da: milimetro bat luzera metroko 100 Celsius moduluko.
Celsius modulu bat (1 Ce) Celsius eskala batean neurtutako tenperatura bitartea da
 .
Celsius gradu bat (1 ° C) eskala horretan irakurritako tenperatura espezifikoa da (T).
.
Celsius gradu bat (1 ° C) eskala horretan irakurritako tenperatura espezifikoa da (T).


21.6..: Bi metalez osatutako zerrenda baten makurdura erradioa.
Adibidea. Bi zerrenda metaliko mehe, bakoitza
 luze eta d lodi,
luze eta d lodi,
 tenperaturan elkarri
lotuta daude (iltzeekin itsatsiak), halako eran non baten muturra eta bestearena bat datozen.
Zerrenda mehetako bat
tenperaturan elkarri
lotuta daude (iltzeekin itsatsiak), halako eran non baten muturra eta bestearena bat datozen.
Zerrenda mehetako bat  dilatazio linealaren koefizientea duen metal batez egina da eta bestea
dilatazio linealaren koefizientea duen metal batez egina da eta bestea
 koefizientea duen metalaz;
koefizientea duen metalaz;
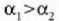 da.
Bi metalez osatutako zerrenda lodia
da.
Bi metalez osatutako zerrenda lodia 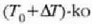 tenperaturara berotzen bada, zerrenda bat beste baino gehiago luzatzen da, eta bi metalez osatutako zerrenda lodia
zirkunferentzia arku bat eratzen duela tolesten da. Kalkulatu zerrenda lodiaren kurbaturaren r erradioa.
tenperaturara berotzen bada, zerrenda bat beste baino gehiago luzatzen da, eta bi metalez osatutako zerrenda lodia
zirkunferentzia arku bat eratzen duela tolesten da. Kalkulatu zerrenda lodiaren kurbaturaren r erradioa.
Zerrenda lodian tentsioak eta konpresioak izango dira. Esan daiteke zerrenda mehe bakoitzaren
lerro zentralak ez duela indar eraginik eta lerroak dilatatuko direla zerrenda osoa aske egongo balitz bezala.
Goiko zerrenda mehearen dilatazioaren luzera  da eta behekoarena
da eta behekoarena 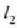 (21-6 irud).
(21-6 irud).
Lerro horien arteko bereizkuntza d da. Demagun d oso txikia dela r erradioaren aldean. Orduan
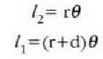
Beraz,

Baina

Beraz,
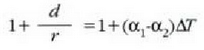
hau da

Kontuan hartu  bada,
edo
bada,
edo  bada,
orduan
bada,
orduan 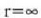 , eta halakotan
bi metalez osatutako zerrenda zuzena dela.
, eta halakotan
bi metalez osatutako zerrenda zuzena dela.
Bi metalezko zerrenda osagai erregulatzailea da termostatoetan. Erabil al daiteke termometro gisa?
Gai gotor bat isotropoa bada, tenperatura aldaketa jakin batean gertatzen
den luzera aldaketaren ehunekoa berdina da gai gotorraren
edozein lerrorentzat. a harremanean, bi punturen arteko distantzia
gradu bateko tenperatura aldaketa bakoitzeko aldatzen da. Dilatazioa
argazki bat handitzearen antzeko prozesua cla, baina gai gotorra
hiru dimentsiokoa da. Demagun xafla lau bat dagoela zulo batekin,
 batentzat
batentzat  balioa berdina da luzerarako, lodierarako, aurpegiaren diagonalerako, gorputzaren digonalerako eta zuloaren
balioa berdina da luzerarako, lodierarako, aurpegiaren diagonalerako, gorputzaren digonalerako eta zuloaren

21.7.- Altzairuzko erregela bera bi tenperatura desberdinetan. Irudian ikus daiteke erregelak dilatatzen direnean dimentsio guztiak proportzio berean handitzen direla. Eskala, zenbakiak, zuloa eta lodiera, guztiak faktore berberaz biderkatzen dira ((a)-tik (b)-ra dagoen dilatazioa 100.000°C-ko tenperatura igoerari dagokiol
diametrorako. a erlazioan, tenperatura gradu bat igotzen den bakoitzean, luzatu egiten da lerroa, zuzena izan edo makurra izan. Demagun izen bat jartzen dela xafla batean; izenak lerro bat osatzen du, eta lerro horren luzera aldaketaren frakzioa beste edozein lerroren berdina da. 21-7 irudian ikus daiteke argazki bat handitzeak prozesu horrekin duen antzekotasuna.
Hori guztia kontuan hartuta, froga daiteke, hurbiltasun handiaz, gai gotor isotropo
batean A arearen aldaketaren frakzioa gradu bateko tenperatura aldaketako
 dela, hau da
dela, hau da

eta gai gotor isotropo batean V bolumen aldaketaren frakzioa gradu bateko tenperatura aldaketako
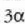 dela, hau da
dela, hau da

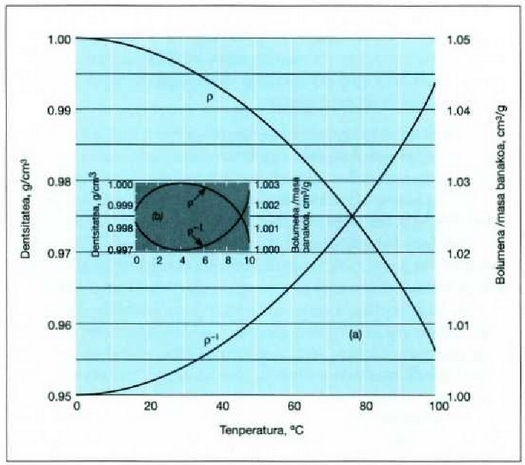
21.8. (a) Uraren dentsitatearen aldaketa ohiko atmosfera presioan eta dentsitatearen erreziprokoaren aldaketa (hau da, 1 gm batek hartzen duen bolumena). (b) 0°-ren eta 10°-en arteko aldearen xehetasuna.
Jariakariei dagokienez, tenperaturarekin jasaten duten bolumen aldaketa hartzen da bakarrik kontuan, jariakari baten forma ez baita beti berdina. Gasek era eraginkorrean erantzuten diote tenperatura edo presio aldaketari. Gai gotor baten bolumen dilatazioaren koefizientea R ikurraz adierazten bada, hau da,
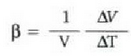
ikus daiteke  askea dela tenperaturi buruz, maila batean behintzat.
Isurkari gehienak tenperaturak gora egiten duenean dilatatzen dira, eta
horien bolumenaren dilatazioa gai gotorrena baino 10 aldiz handiagoa da.
askea dela tenperaturi buruz, maila batean behintzat.
Isurkari gehienak tenperaturak gora egiten duenean dilatatzen dira, eta
horien bolumenaren dilatazioa gai gotorrena baino 10 aldiz handiagoa da.
Dena dela, isurkarietan arruntenak, urak alegia, ez du gainerako isurkariek duten portaera hera.
21-8 irudian uraren dilatazio kurba ikus daiteke. Tenperatura 4°C-tik gora igo ahala dilatatzen da ura,
linealki ez bada ere. Tenperatura 4-tik O°C-ra jaisten denean ura, uzkurtu beharrean, dilatatu egiten da.
Tenperatura jaistean gertatzen den dilatazio hori ez cla beste isurkarietan gertatzen, ezta beste gai
gotor arruntetan ere, goma eta antzeko zenbait gaitan salbu. Urak 4°C-tan du gehieneko dentsitatea; une horretan
 balioa du, hau da
balioa du, hau da
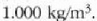 Beste tenperatura guztietan dentsitate txikiagoa du.
Uraren portaera hori dela-eta, aintzirak azaletik hasten dira izozten.
Beste tenperatura guztietan dentsitate txikiagoa du.
Uraren portaera hori dela-eta, aintzirak azaletik hasten dira izozten.
2. Beroa eta termodinamikaren lehen legea
Beroa, energia iturri bat
Tenperatura desberdineko bi sistema elkarren ondoan jartzean, bi sistemek iristen duten azken tenperatura hasierako tenperaturen tarteko tenperatura bat da. Esperientzia arrunta da hori. Aurreko atalean tenperatura gisa zer ulertzen den eragiketa bidez azaltzeko oinarri hori erabili da hain zuzen.
XIX. mendea arte era horretako gertaerak gorputz guztiek zuten gai berezi bati esker, gai kaloriko delakoari esker, gertatzen zirela uste izan zen. Tenperatura beroa duen gorputz batek kaloriko asko zuela uste zen, eta gorputz hotzek kaloriko gutxi zutela. Gorputz bero bat eta gorputz hotz bat elkarren alboan jartzean, kaloriko gehien zuen gorputzak bere kalorikoaren parte bat ematen zion gorputz hotzari, harik eta bi gorputzek tenperatura bera iristen zuten arte. Kalorikoaren teoriari esker zenbait prozesu argitu ahal izan ziren, baina beroaren kontzeptua, beroa sustantzia gisa harturik definitzen zuena, bazterrera gelditu zen zenbait saiakera egin ondoren. Hala ere, tenperatura aldaketa asko deskribatzen dira tenperatura altuko gorputz batetik tenperatura hotzagoko baterako "zerbaiten" igarotze gisa, eta "zerbait" horri beroa esaten zaio. Beraz, beroaren definizio gisa, esan daiteke sistema baten eta bere ingurunearen artean igarotzen den zerbait dela, eta tenperatura diferentzia dela gertaera horren ondorio bakarra.
Urte asko igaro ziren kalorikoaren teoria osatu zenetik beroa energia mota bat dela onartu zen arte, beroa gai bat zela zioen ideia baztertu zen arte alegia. Beroa gai bat ez zela esateko lehenengo froga erabakiorrak Thompson iparamerikarrak (1753-1814) egin zituen. Thompsonek egindako ikerketei esker jakin zen prozesu batean xahutzen den lan mekanikoak sortzen duela beroa, nahiz eta ideia hori askoz geroago azaldu zen argi eta garbi. Energia mekanikoa etengabe desagertu eta beroa sortu ordez -kontserbazioaren printzipioa urratzen baitzuten prozesu horiek zeinek bere aldetik- prozesu guztia energia eraldatze gisa hartu zen, prozesuan zehar energia osoak bere horretan irauten zuela onartu zen.
Energiaren eta energia kontserbazioaren printzipioa ez zen XIX. mende amaiera arte onartu eta zabaldu; Galileo, Newton eta maila handiko beste hainbat ikerlari ez zen kontzeptu horretaz ohartu. Energiaren kontserbazioaren printzipioa Julius Robert von Mayer ikerlariak (1814-1878) eman zuen, baina joulek ere (1818-1889) hark atera zituen ondorio berberak atera zituen bere aldetik Ingalaterran, Helmholtzek (1821-1894) Alemanian eta Coldingek (1815- 1888) Danimarkan.
Joulek energia mekaniko kopuru jakin bat bero bihurtzen denero bero kopuru bera sortzen dela beti frogatu zuen esperimentu bidez. Horrela finkatu zen behin betiko beroaren eta lan mekanikoaren arteko baliokidetasuna, biak energia mota gisa harturik.
Helmholtzek adierazi zuen lehenengo beroa eta energia mekanikoaez ezik, gainerako energia motak ere elkarren baliokide direla, eta energia mota jakin baten kopurua ez dela murrizten, harik eta hesteenergia mota bat agertzen ez den arte galduriko energia kopuru horren kopuru berean.
Bero kopurua eta bero espezifikoa
Prozesu fisiko batean parte hartzen duen bero kopurua neurtzeko prozesu horretan zehar gertatzen den aldaketa bat hartzen da oinarri gisa. Edo, zehatzago esanda, eredu gisa harturiko aldaketa bat eragiteko behar den beroa hartzen da beroaren banako gisa. Hiru banako hauek erabiltzen dira bero kopurua neurtzeko: kaloria, kilokaloria eta britainiar banako termikoa (Btu).
Kaloriak (cal) ur gramo baten tenperatura 14.5 ° C-tik 15.5 ° C-ra igotzeko behar den bero kopurua adierazten du.
Kilokaloria (kcal) ur kilogramo baten tenperatura 14.5 ° C-tik 15.5°Cra igotzeko behar den bero kopurua da.
Eta Btu banakoak, berriz, libra eredu bat (1/32 slug gutxi gorabehera) 63 ° F-tik 64 °F-ra igotzeko behar den bero kopurua adierazten du.
Goiko adierazpenetan erreferentziazko tenperaturak zehaztu dira, izan ere, zein tenperatura tarte hartzen den, ez baita beti bero kopuru bera behar tenperatura grado batean igoarazteko. Baina, oro har, ez da aintzat hartzen gorabehera hori. Bero kopurua adierazteko Q letra erabiltzen da. Goian aipatu diren hiru banakoen arteko harremana hau da:

Gaien arteko desberdintasuna gai bakoitzaren masa jakin bat tenperatura maila
jakin batean igoarazteko behar den bero kopuruak ematen du aditzera.
Gorputz bati ematen zaion  bero kopuruaren eta gorputz horren
bero kopuruaren eta gorputz horren  tenperatura igoeraren arteko harremanari gorputzaren bero ahalmena deritzo, eta honela adierazten da:
tenperatura igoeraren arteko harremanari gorputzaren bero ahalmena deritzo, eta honela adierazten da:

Gorputz baten bero ahalmena eta gorputz horren tenperatura gradu bat igotzeko behar den bero kopurua berdinak dira, zenbakiz. Masa banako bakoitzeko bero ahalmena, bero espezifiko ere deitua, gorputzaren materialari dagokion ezaugarria da:
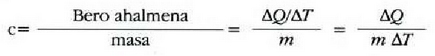
Material baten bero ahalmen espezifikoa eta materialaren tenperatura gradu bat igotzeko material horren masa banakoari eman behar zaion bero kopurua berdinak dira, zenbakiz.
Zehatz neurtuta, gorputz baten bero ahalmena eta material baten bero espezifikoa ez dira konstanteak,
tenperatura tarteen arabera aldatzen dira. Beraz, aurreko ekuazioek
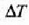 tenperatura tarteari dagozkion batez besteko kopuruen balioa ematen dute. Material batek edozein
tenperaturan duen c bero espezifikoa honela definitzen da:
tenperatura tarteari dagozkion batez besteko kopuruen balioa ematen dute. Material batek edozein
tenperaturan duen c bero espezifikoa honela definitzen da:
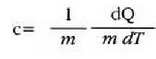
Horrenbestez, m masa duen gorputz baten tenperatura 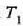 tenperaturarik
tenperaturarik 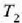 tenperaturara igo dadin gorputz horri eman behar zaionberoa honela kalkulatzen da,
gorputz horren materialaren bero ahalmena c dela kontuan harturik:
tenperaturara igo dadin gorputz horri eman behar zaionberoa honela kalkulatzen da,
gorputz horren materialaren bero ahalmena c dela kontuan harturik:

non c tenperaturaren funtzio bat baita. Ohiko tenperaturetarako eta ohiko tenperatura tarteetarako, bero espezifikoa konstantetzat har daiteke.
Material baten bero espezifikoak ez du balio bakar bat, ordea.
Balio bat baino gehiago izan ditzake, beroa zein baldintzetan ematen zaion. m eta
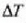 jakin batzuetarako
jakin batzuetarako
 balio asko izan daitezke, beraz.
Adibidez, gas bat bolumen konstantean berotuz, gas horren tenperatura gradu bat igotzeko bero kopuru handiagoa
behar da neurri bereko igoera eragiteko gorputza presio konstantean berotzen denean baino.
Horrenbestez, c aldagaiak balio bakar bat izan dezan baldintzak zehaztu behar dira,
adibidez presio konstantean duen bero espezifikoa,
balio asko izan daitezke, beraz.
Adibidez, gas bat bolumen konstantean berotuz, gas horren tenperatura gradu bat igotzeko bero kopuru handiagoa
behar da neurri bereko igoera eragiteko gorputza presio konstantean berotzen denean baino.
Horrenbestez, c aldagaiak balio bakar bat izan dezan baldintzak zehaztu behar dira,
adibidez presio konstantean duen bero espezifikoa,  ,
edo bolumen konstantean duen bero espezifikoa, Cv
,
edo bolumen konstantean duen bero espezifikoa, Cv
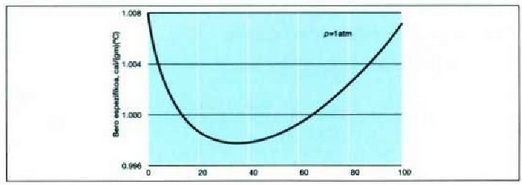
Uraren bero espezifikoaren aldaketa atmosfera bateko presio konstantean tenperatura aldatu ahala.

22.1 taula
22-1 taulan gai gotor batzuen bero ahalmen espezifikoak azaltzen dira, cn presio konstantepean neurturik ahalmen horiek. banakoak cal/(g)(°C) edo Btu/(Ib)(°F) banakoak dira.
Aipatzekoa da uraren bero espezifikoa -zeinaren balioa 1 baita bero kopuruaren banakoa aukeratu zen moduari jarraituz- oso handia dela gainerako gai guztiek dutenaren aldean. Izotzaren balioak erakusten du gai hera isurkari egoeratik gotor egoerara aldatzean bero espezifikoan aldaketa aski nabarmena izan daitekeela. Orobat, nabarmentzekoa da bero espezifikoa tenperaturaren arabera aldatzen dela, eta tenperatura oso hotzetan bero espezifikoen balioak askoz ere txikiagoak direla tenperatura arruntean baino. Gasen bero espezifikoak hurrengo atalean aztertuko dira.
Gai gotorren bero ahalmen espezifikoak materialaren arabera aldatzen direla dirudi. Hala ere, mol bakoitzeko bero ahalmena aztertzen bada, hau da bero ahalmen molarra, eta ez masa banako bakoitzeko bero ahalmena, zera ikusiko da: 0 ° C-tik gorako tenperaturan, gai gotor gehienek 6 cal/(mol) (C°) inguruko bero ahalmen molarra dute. Molekula kopurua bera da edozein gairen mol batentzat, eta beraz, esan daiteke gai gotor baten tenperatura neurri jakin batean igoarazteko behar den beroa molekulen arabera, ia berdina dela gai gotor guztien kasuan. Horrenbestez, gai gotor baten tenperatura igoarazteko behar den bero kopurua ez dago molekula bakoitzaren masaren mende, gai gotorraen laginean dagoen molekula kopuruaren mende baizik.
Adibidea. 75 gramoko kobre puska bat labe batetik atera eta 300 gramoko beirazko onzi batean sartzen da, 200 gramo ur hotzetan. Ontziko uraren tenperatura 12 ° C-tik 27C-ra igotzen da. Zenbatekoa da labeko tenperatura, gutxi gorabehera?
Adibide honetan bi sistema azaltzen dira; hasieran sistema bakoitzak zeinek bere tenperatura zuen, baina elkar ukitzean oreka termikoa iristen dute. Ez dago energia mekanikoaren parte hartzerik, bero energiaren trukea baizik. Beraz,
kobreak galdutako beroa = irabazitako beroa (ontzia + ura)

C azpi indizeak kobrea adierazten du,
G azpi indizeak beira eta W azpi indizeak ura. Kobrearen hasierako tenperatura
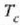 da, ontziko uraren hasierako tenperatura
da, ontziko uraren hasierako tenperatura
 eta amaierako oreka tenperatura
eta amaierako oreka tenperatura
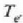 Emandako balioen ordezkaketa eginez,
Emandako balioen ordezkaketa eginez,

 (ikus 22-1 taula), horrela gelditzen da ekuazioa:
(ikus 22-1 taula), horrela gelditzen da ekuazioa:

Bero eroatea
Gai baten bi parte tenperatura desberdinean daudenean bien arteko tenperatura banaketa gertatzen da etengabean. Gai baten elkarren ondoz ondoko bi parteren arteko tenperatura diferentziatik datorren energia garraioari bero eroate esaten zaio.
Eman dezagun material jakin baten xafla bat hartzen dela,
A zeharretarako epaia eta Dx lodiera duena, eta xaflaren aurpegi bakoitza tenperatura batean dagoela.
t denboran zehar aurpegietara perpendikularrean jariatzen den Q bero kopurua neurtzen da.
Saiakera honek erakusten du Q bero kopurua t denborari eta A zeharretarako epaiari buruz proportzionala dela
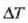 tenperatura diferentzia jakin baterako, eta Q proportzionala dela
tenperatura diferentzia jakin baterako, eta Q proportzionala dela
 zatikiari buruz t eta A
aldagaien balio batzuetan,
zatikiari buruz t eta A
aldagaien balio batzuetan,  eta
eta  aldagaien balioak
apalak diren kasuetan. Hau da,
aldagaien balioak
apalak diren kasuetan. Hau da,
gutxi gorabehera.
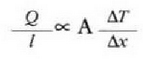
Eman dezagun dx lodiera infinitesimala duen xafla batean xafla horren ertz baten eta bestearen artean dT tenperatura diferentzia dagoela. Adibide horrek ematen du bero eroatearen oinarrizko legea:
Adierazpen horretan beroaren barreiadura lastertasuna dQ/dt zatikiak adierazten du, dT/dx zatikiari tenperatura gradiente esaten zaio eta k konstante proportzionala bero eroamena da. Bero jarioarennorabidetzat x aldagaia igotzen den norabidea hartzen da. Kontuan harturik bero jarioa T aldagaia murriztuz doan norabidean gertatzen dela, ken zeinua sartzen da 22-4 ekuazioan (hau da, dQ/dt positiboa da dT/dx negatiboa denean).
k bero eroamen handiko gai bat beroaren eroale ona da; k beroeroamen txikiko gaia, berriz, beroaren eroale txarra izango da,bakartzaile ona, beraz. k konstantearen balioa tenperaturaren arabera aldaten da, tenperaturak gora egiten konstanteak ere goraegiten baitu, maila apalean izan arren; dena dela, gai baten parteentenperaturen diferentzia oso handia ez denean ia konstantetzat hardaiteke. 22-2 taulan gai batzuei dagokien k eroamenaren balioakadierazi dira;

22.2 Taula
Taula horretan ikusten denez, metalak beroaren eroale hobeak dira, oro har, gai ez metalak baino, eta gasak beroaren oso eroale txarrak dira.
22-2 irudian 22-4 ekuazioa aplikatu zaio L luzera eta A zeharretarako epai konstantea dituen barra bati,
barra hori errejimen egonkorrean dagoela (22-2. irudia). Errejimen egonkorrean tenperaturak konstante
dirau denbora tarte guztian zehar eta puntu guztietan. Horrenbestez, dQ/dt zatikiaren emaitza berbera
izango dute zeharretarako epai guztiek. Baina dQ/dt = -kA(dT/x) denez, k eta A aldagaien balioa
konstante denean dT/dx bera izango da zeharretarako epai guztietan. Horren ondorioz, T murriztuz doa barran zehar eta
 betetzen da Hori dela eta,
t denboran zehar transmititzen den Q beroa kalkulatzeko ondoko ekuazioa erabiltzen da:
betetzen da Hori dela eta,
t denboran zehar transmititzen den Q beroa kalkulatzeko ondoko ekuazioa erabiltzen da:

Bero eroateak erakusten du beroaren eta tenperaturaren kontzeptuak elkarren desberdinak direla, nahiz eta batak bestearekin zerikusia duen. Barra batean zehar gertatzen den bero jarioa eta barraren mutur baten eta bestearen arteko tenperatura diferentzia ez dira gauza bera. Tenperatura diferentzia bera duten barra desberdinek bero kopuru desberdina eroan dezakete denbora tarte berean.
Adibidea. Bedi xafla bat bi materialez osatua;
materialek  eta
eta 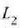 lodiera desberdinak
dituzte eta
lodiera desberdinak
dituzte eta  eta
eta  bero eroamen
desberdinak.
bero eroamen
desberdinak.

22.2: Bero eroatea, barra eroale bakartu batean zehar
Baldin eta kanpoaldeko gainaldeetako tenperaturak 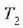 eta
eta  bat badira, aurkitu errejimen
egonkorrean beroa zein lastertasunetan igarotzen den xafla horretan zehar.
bat badira, aurkitu errejimen
egonkorrean beroa zein lastertasunetan igarotzen den xafla horretan zehar.
Bedi  tenperatura bi
materialen arteko interfasean. Orduan,
tenperatura bi
materialen arteko interfasean. Orduan,

eta

Errejimen egonkorrean, beroaren jarioa  da,
eta horrenbestez,
da,
eta horrenbestez,

betetzen da.
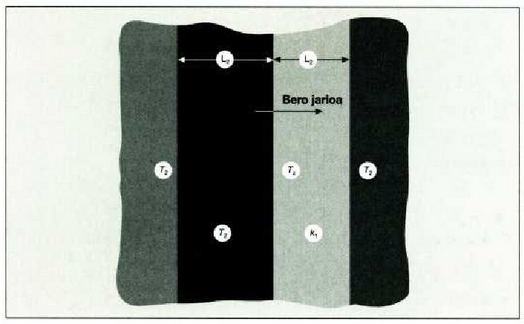
22.3: Bero eroatea eroamen desberdineko bi materialgeruzetan zehar
Beroa Q/t lastertasunean igarotzen da (epai guztietan bera). Orduan, T2 bakartuz, eta aurreko ekuazioetako edozeinetan ordezkaketa eginez, adierazpen hau lortuko da:

Jakina, serieko edozein epai kopuru hartzen dela orokor daiteke hori, beraz hau ateratzen da:

Beroaren Baliokide Mekanikoa
Beroa energia mota bat dela kontuan harturik, edozein energia banako har daiteke beroa neurtzeko banakotzat Kaloria eta Btu banakoak beroa energia mota bat zela onartu aurretik sortu ziren. Joulek neurtu zuen lehenengo bero energiari energia mekanikoan dagokion baliokidea, eta horrela finkatu zen kaloria bati dagokion joule kopurua edo 1 Btu-ri dagokion oin/libra kopurua.
"Beroaren banakoen" eta "banako mekanikoen" neurri erlatiboa saiakera bidez aurki daiteke, adibidez neurtzen den bero kopurutik zenbat bihurtzen den energia mekaniko aztertuz. Joulek paleta sistema bat erabili zuen, pisu batzuek urez beteriko ontzi batean mugiarazten zutena (22-4. irudia). Zenbat energia mekaniko galtzen zen neurtzeko, pisuak, pisu horiek zein alturara erortzen ziren eta zenbat bero energia irabazten zen kalkulatzen zen, urari zegokion masa eta uraren tenperatura igoera zehaztuz. Joulek frogatu nahi zuen lan jakin bat egitean, lan hori egiteko edozein metodo erabilita ere, bero energia bera lortzen zela beti.
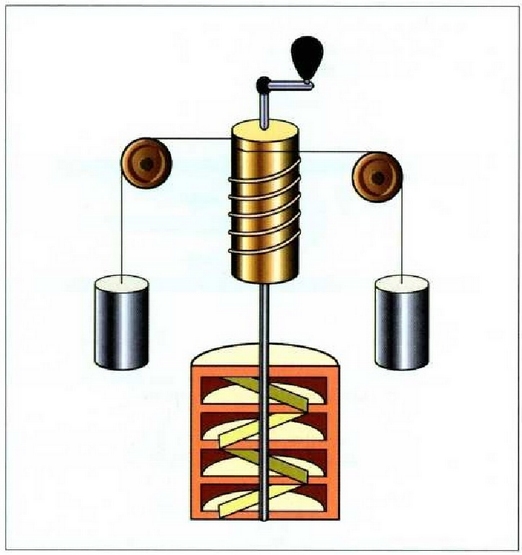
22. 4: Beroaren baliokide mekanikoa zehazteko Jouleren tresna. Pisuek, erortzean, ontzi barneko ura astintzen duten paleta batzuk mugiarazten dituzte, eta horrela uraren tenperatura igotzen da
Horrela, merkurioa astinduz, merkuriozko bainu batean burdinazko eraztunak elkar igurtziz, energia elektrikoa uretan sarturiko alanbre batean bero bihurtuz, eta beste hainbat eratara lortu zuen beroa. Eta sorturiko beroaren eta egindako lanaren arteko konstante proportzionala beti berdina izan zela ikusi zuen, %5eko errorearen muga esperimentalaren barnean. Izan ere, Joulek ez zituen gaur egun dauden termometro zehatzak, eta ezin zuen zuzenketa fidagarririk egin sistemaren bero galeraz. Baina haren ikerketak garrantzi handikoak izan ziren, bai hark erakutsi zuen trebetasunagatik eta baita eragin handia izan zuelako beroaren teoria mekanikoa zuzena zela erakusteko. Gaur egun onartzen diren balioak, hauek dira:
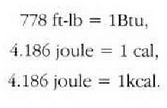
Hau da, 4.186 joule bero energia mekaniko bihurtzen direnean, ur gramo baten tenperatura 1°C igotzen da. Beraz, edozein eratako energia, adibidez, mugitzen ari den bala baten energia zinetikoa, edo malguki konprimatu batean pilatutako energia potentzial elastikoa, kaloria banakoetan adieraz daiteke joule banakoetan adieraz daitekeen bezalaxe.
Beroa eta Lana
Ikusi denez, tenperatura desberdina izatearen ondorioz gorputz batetik bestera igarotzen den energia da beroa. Beroa gorputz baten barnean dagoen zerbait dela dioen ideia, kalorikoaren teoria alegia, baztertu egin zen zenbait saiakeraren ondoren. Tenperatura gorputz batetik bestera aldaketa baten ondorioz igarotzen denean bakarrik ematen zaio energia horri bero energia izena. Beroa gai bat balitz edo energia mota definitu bat, sistema baten baitan bere identitatea gordetzen duena, ezingo litzateke berorik lortu batere aldatzen ez den sistema batetik. Hala ere, Rumfordek erakutsi zuen hori posible zela. Izan ere, Jouleren tresna etengabean jarrita lanean, bero kopuru zehazgabea atera daiteke uretatik, sistema hotzago batekin harremanean jarriz adibidez, uraren ezaugarriak aldatu gabe.
Era berean, lana ez da kopuru zehatz batean agertzen sistema batean. Hau da, sistema bati lan kopuru zehazgabe bat aplika dakioke bere egoera aldarazi gabe, Jouleren tresnak erakusten duenez. Lanak, beroak bezala, energia jario bat eskatzen du. Mekanikan, lana egiten zen tenperaturak zerikusirik ez zuen energia aldaketetan. Baldin eta bero energia tenperatura diferentziaren arabera transmititzen bada, beroa eta lana bereizteko hau esan daiteke: sistema batetik bestera tenperatura diferentziak zuzenean zerikusirik izan gabe transmititzen den energia da lana. Definizio hori bat dator aurretik termino honetaz esan denarekin. Hau da, dW = F dx adierazpenean, F indarraren iturria iturri magnetikoa, elektrikoa, grabitatezkoa edo bestelakoa izan daiteke. Lanak energia eraldaketaren prozesu horiek guztiak hartzen ditu bere baitan, baina tenperatura diferentziek eragindako energia eraldaketak baztertzen ditu.

22.5: (a) Sistema bat hasierako oreka egoera dago bere inguruneari buruz. (b) Prozesu termodinamiko batean zehar elkarri eragiten diote sistemak eta bere inguruneak eta Q bero edo W lan trukea, edo bien trukea, gertatzen da. (e) Prozesua amaitzen delarik, sistema orekan gelditzen da berriro.
Beste adibide bat emango da orain, eskuak igurtzitzean edo bi gainalde elkarren kontra igurtzitzean gertatzen dena. Ez dago sistema horretatik atera daitekeen bero kopuruan mugarik eta ezta sistema horri aplika dakiokeen lan kopurua zehazturik ere, beraz ez dute zentzurik "sistemak duen beroa" edo "sistemaren lana" esapideek. Q eta W kopuruak ez daude sistemarekin lotuak, sistemak bere ingurunearekin duen elkar eraginaren mende daude. Elkar eragin horrek ematen die zentzua lanari eta beroari. Horrela, sistemarekin komunikaturiko beroarekin edo sistematik ateratako beroarekin identifika daiteke Q, eta W, berriz, sisteman kanpotik egindako lanarekin edo elkar eraginean zehar sistemak egindako lanarekin. Prozesu askotan bero jarioa gertatzen da eta lan bat egiten da. Elkar eragin horiek dira, lana egitean gertatzen diren energia aldaketak eta bero jarioa hain zuzen, termodinamikaren aztergaiak.
22-5 irudian termodinamikako prozesu orokor baten azalpena egin da. Lehenik eta behin, sistema zein den eta sistemaren ingurunea nolakoa den definitu behar da. Irudian gainalde itxi espezifiko bat irudikatu da sistemaren inguruan, definizioa egin ahal izateko. (a) eskeman, jatorrizko oreka egoeran dago sistema bere inguruneari buruz. (b) eskeman sistemaren eta bere ingurunearen arteko elkar eragina gertatzen da, prozesu espezifiko baten ondorioz. Prozesu horretan zehar, beroa eta lana, edo bi gauzak, sar daitezke sisteman edo atera daitezke hartatik. Q edo W aldagaien jarioa adierazten duten geziek sistema inguratzen duen gainaldea igaro behar dute. (c) eskeman sistemaren amaierako egoera ematen da aditzera, berriro inguruneari buruzko oreka egoera dagoela.

22.6: Beroa eta lana. Pisu batek, erortzean, lan jakin bat egiten du generadore elektriko baten gainean eta generadoreak korrontea bidaltzen du erresistentzia baten bidez; erresistentziak, korrontearen eraginez ontziko ura berotzen du
Eman dezagun adibide espezifiko bat. 22-6. irudian pisu bat azaltzen da, erortzean generadore bat martxan jartzen duena; pisuak martxan jartzen duen generadoreak korronte elektrikoa igortzen du urez beteriko ontzi batean sartu den erresistentzia batera, sistema gisa zirkuito elektrikoa, ura eta ontzia harturik, sistemaren egoera aldatu egingo da, eta aldaketaren eragilea erortzen den pisuak sistema horretan egindako lana izango da, kanpo lana beraz. Energia eraldaketa hauetan ez du zerikusi zuzenik sistemaren ingurunearen eta sistemaren beraren arteko tenperatura diferentziak. Baina eman dezagun orain sistema gisa ontzia eta ura bakarrik hartzen direla, eta sistemaren ingurunea edo inguruneko baliabideak zirkuitu elektrikoa eta pisua direla. Orduan, erresistentziaren eta uraren arteko tenperatura diferentzia dela eta, ingurunetik sistemarako bero jarioa gertatzen da; kasu honetan ez da lanik egiten zuzenean sistemaren gainean. Hortaz, argi gelditzen da lehenik sistema zein den eta ingurunea zein den zehaztu beharra dagoela sistemaren egoeraren aldaketa beroaren jarioak edo lanak edo biek eragina den erabakitzeko. Sistemaren eta bere ingurunearen artean, bien artean tenperatura diferentzia dagoenean naozol ez da gertatuko bero trukea; tenperatura diferentziarik ez bada, lana behar da batetik bestera energiarik igaroko bada.
Eman dezagun termodinamikako prozesu espezifiko batean Q edo W aldagaien balioa kalkulatu behar dela.
Enbolo mugikor bat duen zilindro formako ontzi batean gas bat dagoela, sistema gisa gasa hartzen bada,
hasieran sistema kanpo ingurunearekin orekan dagoela ikus daiteke;
 presioa eta
presioa eta
 . bolumena ditu sistemak kasu horretan.
Ontziaren paretak sistemaren muga direla esan daiteke. Sisteman beroa sar daiteke eta beroa atera daiteke bertatik,
ontziaren paretetan zehar; era berean, sistemari lana egin dakioke kanpotik, enboloa zapalduz,
edo lana sistemak berak egin dezake, enboloaren kontra dilatatuz. Eman dezagun prozesu jakin bat
gertatzen dela eta prozesu horretan sistemaren eta ingurunearen arteko elkar eraginean
. bolumena ditu sistemak kasu horretan.
Ontziaren paretak sistemaren muga direla esan daiteke. Sisteman beroa sar daiteke eta beroa atera daiteke bertatik,
ontziaren paretetan zehar; era berean, sistemari lana egin dakioke kanpotik, enboloa zapalduz,
edo lana sistemak berak egin dezake, enboloaren kontra dilatatuz. Eman dezagun prozesu jakin bat
gertatzen dela eta prozesu horretan sistemaren eta ingurunearen arteko elkar eraginean
 presioa eta
presioa eta
 bolumena duen amaierako
oreka egoera bat iristen dela.
bolumena duen amaierako
oreka egoera bat iristen dela.

22.7- p presioa duen gas batek dW lana egiten du A area duen enbolo baten gainean, eta pA indarra eta ds lerradura eragiten ditu.
22-7 irudian gas bat azaltzen da, pistoiaren kontra dilatatzen ari dena. Gasak enboloa ds distantzia infinitesimal bat higitzean egiten duen lanari

adierazpena dagokio, non dV gasaren bolumen diferentziala baita. Oro har, presioa ez da konstantea izango mugimendu batean zehar. Gasak mugimendu batean zehar enboloaren gainean egindako W lan osoa zenbatekoa den jakiteko, mugimenduaren ondoriozp nola aldatzen den jakin behar da lehenengo. Horretarako integral hau ebatzi beharko da, bolumen tartean:

Integral horren adierazpen grafikoa p - V grafiko batean kurbaren azpian eratzen den area gisa eman daiteke, 22-8. irudiak agertzen duen kasu bereziak erakusten duenez.
Dena dela, modu askotara eraman daiteke sistema bat hasierako i egoeratik amaierako
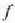 egoerara.
Adibidez, 22-9. irudian presioak konstante iraun dezake i egoeratik a egoerara eta ondoren,
bolumena konstante izan daiteke a egoeratik
egoerara.
Adibidez, 22-9. irudian presioak konstante iraun dezake i egoeratik a egoerara eta ondoren,
bolumena konstante izan daiteke a egoeratik 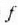 egoerara bitartean. Orduan, gasa dilatatzean egindako lana ia lerroaren azpiko arearen baliokidea da,
eta kasu horretan gasak egindako lana
egoerara bitartean. Orduan, gasa dilatatzean egindako lana ia lerroaren azpiko arearen baliokidea da,
eta kasu horretan gasak egindako lana 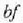 lerroaren azpiko area izango da. i-tik f-rako kurbak beste ibilbide posible bategiten du, zeinetan gasak
egindako lana aurreko bi ibilbideetan
egindakoaren desberdina baita. Beraz, sistema jakin batek egindako
lana ez dago hasierako eta amaierako egoeren mende soilik,
baizik eta baita tarteko egoeren mende ere bai, hau da, ibilbidearen
mende.
lerroaren azpiko area izango da. i-tik f-rako kurbak beste ibilbide posible bategiten du, zeinetan gasak
egindako lana aurreko bi ibilbideetan
egindakoaren desberdina baita. Beraz, sistema jakin batek egindako
lana ez dago hasierako eta amaierako egoeren mende soilik,
baizik eta baita tarteko egoeren mende ere bai, hau da, ibilbidearen
mende.

22. 8: Gas batek egindako lana p-V kurba baten azpian eratzen den arearen baliokidea da
Ondorio bera aterako da prozesuan zehar gertatzen den bero jarioa kalkulatzen bada ere
 egoeraren ezaugarria
egoeraren ezaugarria 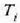 tenperatura eta
tenperatura eta  egoerarena
egoerarena  tenperatura.
Sistemara jariatzen den beroa, esaterako, sistema nola berotzen den, halakoa izango da.
tenperatura.
Sistemara jariatzen den beroa, esaterako, sistema nola berotzen den, halakoa izango da.
 presio konstantean berotu daiteke,
adibidez,
presio konstantean berotu daiteke,
adibidez, 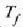 tenperatura iristen duen arte,
eta orduan presioa tenperatura konstantera aldatu,
tenperatura iristen duen arte,
eta orduan presioa tenperatura konstantera aldatu,  amaierako balioa iritsi arte.
Edo presioa
amaierako balioa iritsi arte.
Edo presioa  baliora jaitsi
eta ondoren sistema presio horretan berotu daiteke
baliora jaitsi
eta ondoren sistema presio horretan berotu daiteke  Tamaierako tenperatura iritsi arte. Edo beste hainbat bide ere egin daitezke.
Bide bakoitzak emaitza jakin bat izango du sistemara jariatzen den beroari dagokionez.
Horrenbestez, sistema batek galtzen edo irabazten duen beroa ez dago hasierako eta amaierako
egoeren mende soilik, baizik eta baita tarteko egoeren mende ere, hau da ibilbidearen mende ere.
Gertaera esperimental bat da hori.
Tamaierako tenperatura iritsi arte. Edo beste hainbat bide ere egin daitezke.
Bide bakoitzak emaitza jakin bat izango du sistemara jariatzen den beroari dagokionez.
Horrenbestez, sistema batek galtzen edo irabazten duen beroa ez dago hasierako eta amaierako
egoeren mende soilik, baizik eta baita tarteko egoeren mende ere, hau da ibilbidearen mende ere.
Gertaera esperimental bat da hori.
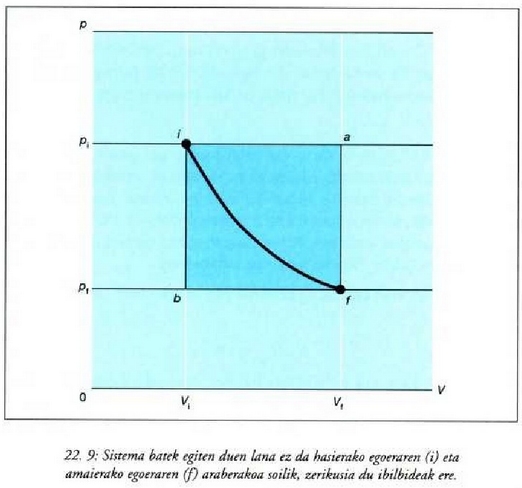
Bai beroa eta bai lana "ibilbidearen araberakoak" izango dira; ez bata eta ez bestea ez dira ibilbideari buruz askeak, eta bata ezin da bestea gabe kontserbatu.
Termodinamikaren Lehen Legea
Aurretik azaldu diren ideiak elkarri lotuko zaizkio orain. Eman dezagun sistema bat i egoeratikf egoerara aldatzen dela, adibidez, halako eran non sistemak bereganatzen duen beroa Q eta sistemak egindako lana W diren. Beroaren banakoak edo energiaren banako mekanikoak erabiliz, Q-W diferentzia kalkulatzen da. Berriro sistemaren egoera aldaketa bat azalduko da orain, i egoera beretik abiatuta f egoerara bitarteko aldaketa hau ere, baina oraingoan beste ibilbide bat jarraituz lortua. Behin eta berriro egingo da gauza bera, bide desberdinak eginez aldiko. Kasu guztietan Q - W diferentzia berdina dela ikusiko da. Hau da, nahiz eta Q eta W, zein bere aldetik, ibilbidearen mende dauden, Q - W kopurua berbera izango da jarraitzen den bidea edozein dela ere; hau da, Q - W balioa ez dago sistema i egoeratikf egoerara nola eramaten den, horren mende, baizik eta hasierako eta amaierako egoeren mende soilik.
Mekanikan, objektu bat i hasierako puntu batetik f amaierako puntura grabitate eremuan eta marruskadurarik gabe mugitzen denean, lana bi puntuen kokagunearen araberakoa bakarrik izango da eta ez gorputzak mugitzean egindako ibilbidearen araberakoa. Horren ondorioz, esan daiteke funtzio bat badela zeinetan gorputzaren espazioaren koordenatuen hasierako balioa gorputza mugitzeko egiten den lanaren berdina baita. Funtzio horri energia potentzialaren funtzioa esaten zaio. Termodinamikan, sistema bat i egoeratikfegoerara aldatzen denean, Q -W kopurua hasierako eta amaierako koordenatuen mende dago bakarrik, eta ez muturreko bi puntu horien artean egindako ibilbidearen mende. Horren ondorioz, esan daiteke badela koordenatu termodinamikoen funtzio bat zeinetan amaierako balioaren eta hasierakoaren arteko kenketaren emaitza prozesuan zehar gertatzen den Q - W kenduraren berdina baita. Funtzio horri barne energiaren funtzio deritzo.
Baina sistemari beroa ematean eransten zaion energia adierazten
duenez Q aldagaiak, eta W sistemak lana egitean ematen duen energia,
Q -W kenketak sistemaren barne energiaren aldaketa adierazi
behar du. Barne energia adierazteko U letra erabiltzen da.
Horrela,f egoeran dagoenean sistemak duen barne energia,
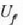 ken i egoerandagoenean duena,
ken i egoerandagoenean duena,
 sistemaren barne energiaren aldaketa izango da, eta kopuru horrek balio definitu edo zehatza du,
sistema i egoeratik f egoerara nola aldatzen den kontuan hartu gabe.
Beraz,
sistemaren barne energiaren aldaketa izango da, eta kopuru horrek balio definitu edo zehatza du,
sistema i egoeratik f egoerara nola aldatzen den kontuan hartu gabe.
Beraz,
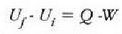
Energia potentzialaren kasuan bezala, barne energiaren kasuan aldaketa da kontuan hartu behar dena. Zorizko balio bat hartzen bada barne energiarentzat erreferentziazko egoera ereduzko batean, balio zehatz bat eman dakioke beste edozein egoeretarako.
Erlazio hori adierazteko ekuazio hau ere erabil daiteke:

Ekuazio horri termodinamikaren lehen legea esaten zaio. 22-6 ekuazioa aplikatzean gogoan izan behar da Q positibotzat hartzen dela sistemara beroa sartzen uzten duenean eta W positiboa dela sistemak lana egiten duenean.
Sistemaren egoeraren aldaketa infinitesimala bada, dQ bero infinitesimala bakarrik bereganatzen du eta dW lan infinitesimala bakarrik egiten du, beraz, dU barne energia ere infinitesimala izango da. Kasu horretan, lehen legearen adierazpen diferentziala erabiltzen da:
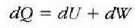
Termodinamikaren lehen legea izadiko edozein prozesuri aplika dakioke. Jakina, oso orokorra denez, ematen duen informazioa ez da osoa, nahiz eta zehatza eta zuzena den. Badira oso gai orokor batzuk lege honen bidez azaldu ezin daitezkeenak. Adibidez, prozesu orotan energia kontserbatzen dela esaten duen arren, ez du esaten prozesu jakin bat gertatuko den ala ez. Oso bestelako orokortze bat, termodinamikaren bigarren legea, da informazio hori ematen duena, eta bigarren lege horren bidez aztertzen dira termodinamikaren gai asko.
Termodinamikaren Lehen Legearen zenbait erabilera
Lehenago ikusi dugunez, gas batek, zabaltzen denean, lan hau egiten du bere inguruan
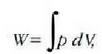
Formula horretan, gasari eragiten zaion presioa (edo gasak eragiten duena) da p,
eta gas bolumenean dagoen gorabehera edo diferentziala, berriz, dV.
Har dezagun orain kasu berezi bat: presioak aldagabe iraungo du eta bolumena, berriz,
kopuru finitu batez aldatuko da,  -etik
-etik
 -ra, adibidez.
Horren arabera:
-ra, adibidez.
Horren arabera:
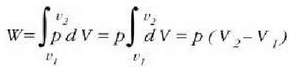
Presio konstantean gertatzen den prozesua prozesu isobarikoa dela esaten da. Adibidez: berotu ura lurrin makina baten galdaran, irakite puntura iritsi eta lurrindu arte; gero, berotu gehiago lurrina, eta presio konstantean egin egin beharreko prozesu guztiak.
Hurrengo irudia prozesu isobariko
baten azalpena da. Ontzi zilindriko baten barruan  dago;
dago; 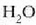 da sistema.
Bada enbolo bat ere, ontzian sartuta -ontzia osorik ixten eta marruskatu gabe-,
hareaz zamatzen dena
da sistema.
Bada enbolo bat ere, ontzian sartuta -ontzia osorik ixten eta marruskatu gabe-,
hareaz zamatzen dena  -ri
eragin nahi zaion presioaren arabera. Bunsen erregailu baten bidez beroa pasaraz daiteke ingurunetik sistemara.
Prozesua behar beste luzatzen bada, urak irakin egingo du eta parte bat lurrin bihurtuko da. Sistema, azkenean,
dilatatu egingo da, zabaldu, eta lana eragingo dio pistoiari. Nolanahi ere, enboloari eragiten dion presioa berdina da beti;
izan ere, presio hori eta enboloak sistemari eragiten dion presio konstantea berdinak izan behar baitute.
Enboloa finkatuko bagenu, edota berotze prozesuan harea gehitu edo kenduko bagenu, prozesua ez litzateke,
noski, isobarikoa izango.
-ri
eragin nahi zaion presioaren arabera. Bunsen erregailu baten bidez beroa pasaraz daiteke ingurunetik sistemara.
Prozesua behar beste luzatzen bada, urak irakin egingo du eta parte bat lurrin bihurtuko da. Sistema, azkenean,
dilatatu egingo da, zabaldu, eta lana eragingo dio pistoiari. Nolanahi ere, enboloari eragiten dion presioa berdina da beti;
izan ere, presio hori eta enboloak sistemari eragiten dion presio konstantea berdinak izan behar baitute.
Enboloa finkatuko bagenu, edota berotze prozesuan harea gehitu edo kenduko bagenu, prozesua ez litzateke,
noski, isobarikoa izango.
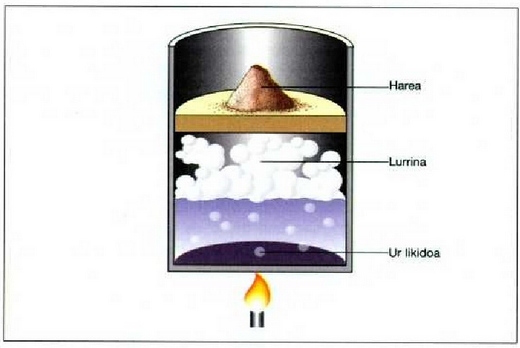
22.10: Ura presio konstantean irakiten (modu isobarikoan). Presioak konstante irauten du harearen eta enboloaren zamapean
Har dezagun irakite prozesua. Fisika edo kimika oinarrizkoaren arabera dakigun bezala, gaiak presio
eta tenperatura balioen konbinazio jakin baten arabera aldatzen dira isurkari egoeratik lurrin egoerara.
Urak, adibidez, 100 'C-tan eta egurats presio normalean dagoenean irakiten du. Sistema batek fase aldaketa izan dezan,
beroa eman edo kendu behar zaio, duen tenperatura eskatzen den tenperaturara eramanarazteko
behar denaz aparte. Eman dezagun m masa duen isurkari bat lurrin egoerara aldarazten dela tenperatura
eta presio konstantean. Bedi 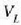 isurkariaren bolumena, eta
isurkariaren bolumena, eta 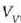 , berriz,
lurrinaren bolumena. Hau da gai horrek
, berriz,
lurrinaren bolumena. Hau da gai horrek  -tik
-tik
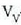 -era hedatzean, presio konstatean,
egiten duen lana.
-era hedatzean, presio konstatean,
egiten duen lana.

Ekuazio horretan lurrintze beroa da L; hau da, gai bat, tenperatura eta presio konstantean, isurkari egoeratik lurrin egoerara aldatzeko, masa banako bakoitzeko behar den beroa. Hauxe da, berriz, egoeraz aldatzean m masak xurgatzen duena:

Termodinamikaren lehen legearen arabera:
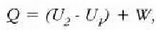
halako moduan ezen, prozesu horrentzat
 baita.
baita.
• Adibidea. Egurats presio normalean dagoen gramo bat ur
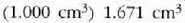 ur lurrin bihurtzen da irakiten duenean.
Uraren lurrintze beroa 539 cal/g-koa da atmosfera bateko presioan. Beraz, baldin m = 1 g, orduan
ur lurrin bihurtzen da irakiten duenean.
Uraren lurrintze beroa 539 cal/g-koa da atmosfera bateko presioan. Beraz, baldin m = 1 g, orduan
Q = mL = 539 cal (sistemari erantsitako bero energia),
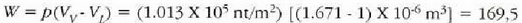 joule (sistemak bere ingurunearen kontra zabaltzean egindako kanpo lana).
joule (sistemak bere ingurunearen kontra zabaltzean egindako kanpo lana).
Baldin 1 cal = 4.186 joule, W = 41 cal.
Orduan, 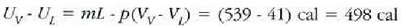 (sistemaren barne energiaren handitzea).
(sistemaren barne energiaren handitzea).
Hala beraz, gramo bat ur (100 'C-tan eta atmosfera bateko presiopean) irakiten jartzeko behar diren 539
kalorietatik 41 cal dilatatze lanari dagozkio, kanpo lanari alegia; gainerako 498 kaloriek, berriz, sistemari
erantsi zaion barne energia osatzen dute. Isurkari egoeran
 molekulen artean dagoen erakarpen
indar handia hausteko egiten den barne lana adierazten du energia horrek.
molekulen artean dagoen erakarpen
indar handia hausteko egiten den barne lana adierazten du energia horrek.
Hortaz, nola banatuko dira izotz gramo bat ur bihurtzeko (0° C eta 1 atm) behar diren 80 kaloriak? Hau da, 80 cal horietarik zenbat dagozkio kanpo lanari eta zenbat, berriz, barne energiari?
Aldiz, sisteman berorik sartu edo atera gabe gertatzen den prozesuari prozesu adiabatiko esaten zaio. Halako prozesu bat lortzeko, bere ingurunetik bakartu behar da sistema, nahiz material bakartzailea erabiliz, nahiz azkar-azkar eraginez prozesua. Eta bero isuriaren "moteltasuna" dela eta, behar bezain azkar eginez gero, ia edozein prozesu bihur daiteke prozesu adiabatiko.
Prozesu adiabatiko batean Q zero da, eta hala lortzen da lehenengo legea:

Hala, beraz, prozesu adiabatiko bateko sisteman egiten den lana adinaxe handitzen da sistema baten barne energia. Baldin sistema lana prozesu adiabatiko batean egiten duena bada, egiten duen kanpo lana adina jaisten da sistemaren barne energia. Barne energia handitzeak sistemaren tenperatura goratzen du, eta, aldiz, barneenergia txikitzeak sistemaren tenperatura jaisten du. Modu adiabatikoan zabaltzen den gas batek kanpo lana egiten du eta barne energia galtzen du; horren antzeko prozesu bat erabiltzen da oso tenperatura apalak lortzeko. Bizikleta gurpilen puzgaila nola berotzen den ikustea aski da airearen konpresio adiabatikoan tenperatura igotzen dela frogatzeko.

22.11: Prozesu adiabatiko batean ez da berorik sartzen sistemara, ez sistematik ateratzen ere. Ontzia ingurunetik bakartua dago, eta harea gehitzen edo kentzen zaionean, modu adiabatikoan aldatzen da gas bolumena
Aurreko irudia prozesu adiabatiko erraz baten adibide da. Zilindro batean, berotik bakartua, gasa dago, eta gas hori da sistema. Ez dago berorik sartzerik ingurunetik sistemara ez eta sistematik ingurunera ateratzerik. Zilindroan enbolo bat dago -zilindroa osorik ixten eta marruskatu gabe-, eta harea pilatxo bat, enboloaren gainean. Eta sistemaren eta ingurunearen artean eraginik izango bada, lanaren ondorioz izango da. Bai enboloari harea erantsiz bai kenduz egin daiteke hori, eta horren arabera, gasa enboloaren kontra konprimitu edo dilatatuko da.
Lurrin makina bateko zilindro baten lurrinaren dilatazioa, barne errekuntzako makina baten gas beroen dilatazioa eta Diesel motor bateko edo aire konpresore bateko airearen konpresioa, esate baterako, prozesu adiabatikoen ingeniaritzaren adibideak dira. Prozesu horiek oso-oso azkar gertatzen dira, eta apenas sartzen (ateratzen) den berorik sisteman (sistematik), paretetan zehar, denbora bitarte labur horretan. Soinu uhin baten konpresioak eta errefrakzioak hain dira azkarrak ezen hura igortzen den gasak portaera adiabatikoa baitu.
Hala ere, prozesu adiabatikoak aztertzeko dagoen arrazoi nagusia prozesu horiek makina idealetan zehatz-mehatz betetzen direla jakitea da.
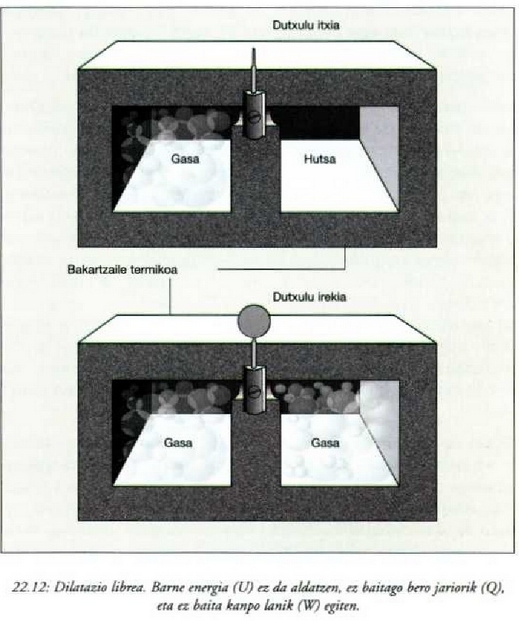
Interes teoriko handiko beste prozesu bat dilatazio librearena da.
Sistemak lanik ez hartzen ez egiten ez duen prozesu adiabatiko bat da hau;
horretarako bi biltegi behar dira, gasez betea bat, eta hutsik, herriz, bestea, biak dutxulu batez lotuak;
bakartzaile termiko batean sarturik egon behar du, gainera, sistema osoak (ikus irudia).
Dutxulua irekiz gero, hutsik dagoen biltegira zabalduko da, libre, gasa.
Bakartzaile termikoa dela eta, prozesua adiabatikoa da, eta, ontzien paretak zurrunak izanik,
ez da kanpo lanik egiten. Beraz, lehenengo legearen arabera, Q = 0 eta W = 0, halako moduan ezen,
prozesu horrentzat  .
Dilatazio librean berdinak dira hasierako eta bukaerako barne energiak.
.
Dilatazio librean berdinak dira hasierako eta bukaerako barne energiak.
3. Gasen teoria zinetikoa
Sarrera
Materiaren egitura filosofoen aztergai izan zen antzina. Leuzipo greziarra eta haren ikasle Demokrito (K.a. 460-370) hartzen dira materiaren teoria atomikoaren lehen sortzailetzat. Haiena da materia zatiki zatiezinez osatua dagoela eta zatikiak hutsartez bereizita daudela zioen hipotesia; zatiki zatiezin horiei atomo izena jarri zieten, atomo hitzak zatiezin esan nahi baitu, hain zuzen ere, grekoz. Ideia horiek espekulazio hutsa ziren, noski; ez zen xehetasunik ematen, eta ez ziren esperimentuetan oinarritzen. Baina 2.000 urte baino gehiago geroago berriro kontuan hartu ziren, hala ere, Berpizkundearen ondoren, filosofia naturalean ere esperimentua erabiltzen hasi zenean. 1600. urte inguruan, Gassendi eta Boyle gasen tasunak azaltzen saiatu zirenean, gasen osagai txikienen hidez azaldu nahi izan zituzten; hau da, haiek "molekula" deitu zieten zatikien bidez. Nolanahi ere, molekula haien tamainari, tasunei eta izaerari zegoztion xehetasunetan, ez zetozen denak bat.
Daniel Bernoulli (1700-1782) izan zen Boylek aurkitu zituen gasen legeak azaltzen eta tenperaturaren eta molekulen mugimenduaren artean lotura zuzena dagoela adierazten lehena. Gas baten presioa kalkultzeko, molekulek paretetan egiten dituzten talketan oinarritu zen, eta molekulen lastertasuna tenperatura igo ahala handitzen dela atera zuen ondorioz. Joulek asko argitu eta zabaldu zuen Bernoulliren lana: gas baten molekulen energia zinetikoaren eta haren tenperaturaren artean kuantitatiboki dagoen lotura azaldu zuen. A. Kronig (1822-1879) eta Rudolph Clausiusek (1822-1888) are gehiago findu eta zabaldu zituzten ideia horiek, eta, gasen teoria zinetikoari dagokionez, gaur egun erabiltzen den teoria molde bera atera zuten funtsean. Clerck Maxwellek (1831-1879) Ingalaterran, Ludwig Boltzmannek (1844-1906) Austrian eta J. Willard Gibbsek (1839-1903) Estatu Batuetan, osatu zuten teoria hura.
Gasen teoria zinetikoak atomoen mailara zabaldu zuen, beraz, Newtonen mekanikaren teoria. Horra, beraz, makroskopikoki aztertuta dauden neurri asko aurrez zuzen iragartzen dituen teoria mikroskopiko bat. Baina gas baten zatiki bakoitzaren kokalekua eta lastertasuna zehazteko nekez espero daiteke emaitza onik Newtonen ideiak soilik aplikatzen badira. Metodo estatistiko bat erabili da horren ordez, eta kopuru askoren batez besteko balioak atera dira. Izan ere, gasen zatikien batez besteko balioak baitira, eta ez gas zatikien tasunen banakako balioak, esperimentu bidez ikusten eta neurtzen direnak.
Gas idealaren egoeraren ekuazioa
Esperimentuek erakusten clutenez, gas guztiek -oso dentsitate handia ez badute, behintzat- portaera bera dute funtsean. Hau da, tenperatura oso-oso apala eta presioa oso-oso handia ez badira behintzat, portaera sinple berbera dute izatez diren gas erreal guztiek. Gas ideal baten kontzeptua iradokitzen du horrek, baldintza guztietan portaera bakuna izango duen gas batena, alegia. Atera dezagun lehenbizi gas idealaren legea. Gero saiatuko gara, eskala mikroskopikoan, eta gasen teoria zinetikoa lagun, lehenengo teoria hori interpretatzen.
Metodo bat baino gehiago dago gas baten presioa, p, bolumena, V, tenperatura, T, eta masa, m, neurtzeko. V/m balioari bolumen espezifikoa esaten zaio. Har ditzagun orain gas batean dentsitate apealean egindako esperimentuak. Esperimentu horiek erakusten dutenez, gas baten presioak -tenperatura aldagabean- alderantzizko proportzioa du bolumen espezifikoari buruz (Boyleren legea); presioaren eta bolumen espezifikoaren arteko biderkadurak, berriz, zuzeneko proportzioa du gasaren tenperaturari buruz (Charlesen legea). Honela labur daitezke emaitza horiek:
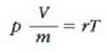
Ekuazio horretan, proportzionaltasun aldagabea da r, eta zein gas erabiltzen den, halako balioa hartzen du.
Gas batekin eta besterekin r konstanteak hartzen dituen balioak elkarrekin konparatzen direnean, hau erakusten du esperimentuak, alegia, r-k alderantzizko proportzioa duela gasaren pisu molekularrari, M-ri, buruz: r = R/M dela, beraz. Ekuazio horretan R -proportzionaltasun konstantea- berdina da gas guztientzat. R, beraz, ez da gas motaren arabera aldatzen; konstante unibertsal bat da. Hortaz, beste era honetara ere idatz daiteke lehengo ekuazio hori:
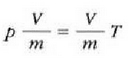
hau da,
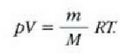
Gogoan izan molekula pisuak, M-k, ez duela dimentsiorik, ez dela zenbaki abstraktu bat besterik. Kimikaren oinarrizko printzipioen arabera, molekula baten molekula pisua molekula horren masaren eta oxigeno atomo baten masaren hamaseirenaren arteko erlazioa da. Molekula pisua hitza, beraz, ez da kasu horretan egokia.
Kimikan beste masa banako bat definitu beharra dago. "Mola" edo "molekula gramoa", hain zuzen ere; hau da, molekula pisuak atomo adina gramo dituen masa (M gramo). Gai bakoitzaren mol batek, beraz, gramo kopuru jakin bat du; gaiaren masa moletan adierazteko n letra erabili ohi da. Hala, beraz, m baldin bada gas baten masa gramotan, orduan, n (molak) = m (gramoak)/M.
Eta, gasaren masa n mol gisa adierazten denean, ohiko itxura hartzen du aurreko formulak:
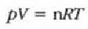
Gasen konstante unibertsalaren zenbaki balioa, berriz, hau da:
R = 8.314 joule/(mol)(K) = 1.986 cal/(mol)(K)
Gas mol batek duen bolumena presioaren eta tenperaturaren, eta ez besteren, mende dago, beraz, ez gasaren izaeraren mende, alegia (hau da, V/n = RT/p). Baldintza normaletan (hau da,p = 1 atm, eta T = 273 K), gas baten, edozeinen, mol batek 22,4 litroko bolumena hartzen du.
Gas errealek ia beti betetzen dute pV = nRT ekuazioa, tarte zabal batean bai behintzat, baina gasen dentsitatea oso handia denean aldendu egiten da hartatik. Gas ideal batek, herriz, egoera guztietan betetzen du ekuazio hori. Horregatik,

ekuazioa gas idealaren egoera ekuazioa da, eta gas idealaren definiziotzat hartzen da eskala makroskopikoan.
• 1. Adibidea. Zilindro bat gas oxigenoz betea dago. Gasa 20 °Cko tenperaturan eta 15 atm-ko presioan dago, eta 100 litroko bolumena hartzen du.
Zilindroan enbolo bat sartzean 80 litrora murriztu da gasaren bolumena, eta 25 'C-ra igo, berriz, tenperatura. Zein izango da orduan gasaren presioa?
Honela adieraz daiteke lehengo ekuazioa:
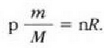
Gas kopurua ez baita aldatzen, 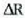 konstantea da, eta, beraz,
konstantea da, eta, beraz,

Hau zen hasierako egoera:

Eta hau da, berriz, bukaerako egoera:
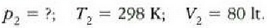
Hortaz,

• 2. Adibidea. Kalkulatu zenbat lan egiten duen gas idealaren mol batek tenperatura konstantean zabaltzen bada,
hasierako bolumena 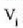 bada, eta bukaerakoa, berriz,
bada, eta bukaerakoa, berriz, 
Honela adieraz daiteke egindako lana:
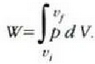

Gas idealaren legearen arabera, eta n = 1 bada, orduan:
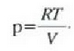
Horrenbestez,
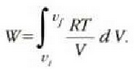
Eta tenperatura konstantea denez,

Hori da, beraz, gas ideal baten mol batek tenperatura konstantean hasierako
 bolumenetik bukerako
bolumenetik bukerako
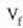 bolumeneraino dilatatzean egiten duen lana.
bolumeneraino dilatatzean egiten duen lana.
Gasa zabaltzen denean, alegia,  denean, gas horren mol
batek egiten duen lana positiboa da; konprimitzen denean, aldiz,
hau da Vf < V, denean, gasak egiten duen lana negatiboa da. Hori
bat dator termodinamikaren lehenengo legean W-rentzat hartutako
ikurren konbentzioarekin. Goiko irudian alde ilunak adierazten du
lanaren zenbatekoa. Lerro beltz lodia isotermia bat da, hau da, tenperatura
konstantean p-tik V-ra dagoen erlazioa adierazten duen
kurba. Egiatan, baina, nola eduki daiteke gas bat tenperatura konstantean
gas hori dilatatu edo uzkurtu egiten bada?
denean, gas horren mol
batek egiten duen lana positiboa da; konprimitzen denean, aldiz,
hau da Vf < V, denean, gasak egiten duen lana negatiboa da. Hori
bat dator termodinamikaren lehenengo legean W-rentzat hartutako
ikurren konbentzioarekin. Goiko irudian alde ilunak adierazten du
lanaren zenbatekoa. Lerro beltz lodia isotermia bat da, hau da, tenperatura
konstantean p-tik V-ra dagoen erlazioa adierazten duen
kurba. Egiatan, baina, nola eduki daiteke gas bat tenperatura konstantean
gas hori dilatatu edo uzkurtu egiten bada?
Gas baten eredua teoria zinetikoaren arabera
Har dezagun orain gas baten eredu mikroskopikoa. Eredu hori prestatzean hartzen diren hipotesiak onargarriak izango dira baldin eta ereduan iragartzen diren ondorio makroskopikoak bat badatoz esperimentu makroskopikoekin.
Hona hemen, laburbilduta, gas baten ereduari buruzko hipotesiak teoria zinetikoaren arabera.
Gas bat molekulez osatua dago; zatiki horiei molekula esaten zaie. Zer gas mota den, atomo batez edo atomo talde batez osatua egongo da molekula bakoitza. Baldin gasa elementu garbia bada, edo gai elkartu bat bada, eta egoera egonkorrean badago, haren molekula guztiak berdintzat hartzen dira.
Molekulak modu irregularrean mugitzen dira eta Newtonen mugimendu legeak betetzen dituzte. Gas baten molekulak alde guztietara mugitzen dira, lasterrago edo motelago. Mugimendu horren tasunak kalkulatzeko, Newtonen mekanika eremu mikroskopikoan ere betetzen dela joko da. Kalkulua aurretiazko uste horren arabera eginez lorturiko emaitzak esperimentu bidez betetzean diren ala betetzen ez diren, horrek egiten du uste hori onargarri edo arbuiagarri.
Molekula kopuru osoa handia da. Molekula baten mugimenduaren norabidea eta lastertasuna tupustean alda daiteke, molekulak paretaren kontra edo beste molekula baten kontra jotzean. Talka horiek direla eta, siga-sagaka mugitzen dira molekulak. Hala ere, hainbeste molekula izanik, talka asko izango da, eta hori dela eta, molekula lastertasunen banaketa orokorrean ez da gorabeherarik izango. Mugimendua hain da irregularra ezen, batez beste, norabide jakin bakoitzean beste edozein norabidetan adina molekula mugitzen baita.
Gasak hartzen duen bolumenaren aldean molekulek betetzen duten espazioa oso-oso txikia, hutsa, da. Molekula asko badago ere, oso molekula txikiak dira. Gas batek hartzen duen bolumena asko handi edo txiki daiteke zailtasun handirik gabe. Bestalde, gas bat kondentsatzen denean, geratzen den likidoak hartzen duen bolumena gas bolumena baino milaka aldiz txikiagoa da. Hala beraz, gure hipotesia onargarria da.
Molekulen arteko indarrak ez dira, talka batek irauten duen bitartean salbu, kontuan hartzeko modukoak. Molekula bat, beraz, lastertasun uniformez eta lerro zuzenean mugitzen da bi talken artean. Molekulak hain txikiak badira, haien artean dagoen tartea, berriz, oso handia izango da tamainaren aldean. Beraz, uste izatekoa da, orobat, molekula indarraren helmena (indar horiek zehazten baitute talkaren zeharkako epaia) molekula tamainaren araberakoa izango dela.
Talkak osoki elastikoak dira eta hutsa irauten dute. Bai molekulek elkar jotzean bai pareten kontra talka egitean aldagabe irauten dute energia zinetikoak eta mugimendu kopuruak. Bi talken artean igarotzen den denboraren aldean talkak berak oso-oso denbora bitarte laburra irauten duenez, eta talka bitartean energia potentzial bihurtzen den energia zinetikoa handik denbora bitarte labur-labur batera berriro energia zinetiko gisa prest geratzen denez, kontuan hartu ere egin gabe utz daiteke aldaketa edo gorabehera hori.
Aurreko ahapaldietan letra etzanean jarri diren adierazpen horiek gasen teoria zinetikoaren aurretiazko ustetzat har daitezke. Gasek esperimentuetan egiaz duten portaera teoria zinetikoaren bidez azaltzeak hain arrakasta handia izan du, ezen beldurrik gabe esan daiteke teoria zinetikoa gutxi gorabehera zuzena dela gas errealen kasuan ere. Hala beraz, aurretiazko uste horiek zuzenak balira bezala jokatzen du gas ideal batek.
Presioaren kalkulu zinetikoa
Gas ideal baten presioa kalkulatzen hasi baino lehen, labur ditzagun gauzak.
Eman dezagun gas bat ontzi kubo batean sartuta dagoela eta ontziaren paretak osoki elastikoak direla.
Kuboaren ertz bakoitzaren luzerari l esango diogu; x ardatzari buruz zutak diren aurpegiei (ikus 23-2 irudia),
berriz,  eta
eta  esango diegu,
bakoitzak
esango diegu,
bakoitzak  -ko area duela.
Har dezagun molekula partikular bat, v lastertasuna duena; v horren osagaiak -
-ko area duela.
Har dezagun molekula partikular bat, v lastertasuna duena; v horren osagaiak -
 -bereiz daitezke, ertzen norabideetan.
Baldin zatikiak
-bereiz daitezke, ertzen norabideetan.
Baldin zatikiak 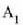 aurpegiaren
kontra talka egiten badu, errebote egingo du, eta lastertasunaren x osagaiak kontrako norabidea hartuko du.
Ordea, ez
aurpegiaren
kontra talka egiten badu, errebote egingo du, eta lastertasunaren x osagaiak kontrako norabidea hartuko du.
Ordea, ez 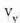 ez
ez
 ez dira aldatuko.
Zatikiaren mugimendu kopuruaren
ez dira aldatuko.
Zatikiaren mugimendu kopuruaren  aldaketa,
beraz, Al buruz zuta, hau izango da:
aldaketa,
beraz, Al buruz zuta, hau izango da:

Beraz, 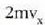 izango da
izango da
 aurpegiari buruzko
mugimendu kopuru proportzionala, mugimendu kopuru osoa kontserbatzen baita.
aurpegiari buruzko
mugimendu kopuru proportzionala, mugimendu kopuru osoa kontserbatzen baita.

23.1: Tenperaturak aldagabe irauten duenean gas idealaren mol batek Vi bolumena hartzetik Vf bolumena hartzeraino zabaltzean egin duen lana adierazten du alde ilunak irudi honetan.
Eman dezagun orain zatiki hori  paretaraino iristen dela, bidean zatiki bat bera ere topatu edo jo gabe.
Zatikiak
paretaraino iristen dela, bidean zatiki bat bera ere topatu edo jo gabe.
Zatikiak  denbora
beharko du kuboa alderik alde igarotzeko.
denbora
beharko du kuboa alderik alde igarotzeko.  pareta jotzean, ordea, berriro aldatuko da zatikiaren lastertasunaren x osagaia,
eta
pareta jotzean, ordea, berriro aldatuko da zatikiaren lastertasunaren x osagaia,
eta 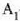 -era itzuliko da atzera.
Eman dezagun ez dela batere talkarik gertatzen itzulerako bidean; orduan, joan-etorri osoa egiteko,
-era itzuliko da atzera.
Eman dezagun ez dela batere talkarik gertatzen itzulerako bidean; orduan, joan-etorri osoa egiteko,
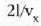 denbora beharko da.
Hala beraz, zatiki horrek
denbora beharko da.
Hala beraz, zatiki horrek  paretaren kontra denbora banako batean egiten duen talka kopurua
paretaren kontra denbora banako batean egiten duen talka kopurua
 izango da,
beraz zatiki horrek denbora banako batean
izango da,
beraz zatiki horrek denbora banako batean  paretaren kontra egiten duen talka kopurua hau izango da:
paretaren kontra egiten duen talka kopurua hau izango da:
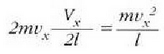
Orain,  paretaren kontra egiten
den indar osoa -hau da, gasaren molekula guztiek denbora banako batean eragiten dioten mugimendu kopurua- kalkulatzeko,
zatiki guztien
paretaren kontra egiten
den indar osoa -hau da, gasaren molekula guztiek denbora banako batean eragiten dioten mugimendu kopurua- kalkulatzeko,
zatiki guztien  batu beharko da.
Gero, berriz, presioa jakiteko,
batu beharko da.
Gero, berriz, presioa jakiteko,  aurpegiaren arearen
aurpegiaren arearen 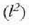 eta indar
horren arteko zatiketa egingo da.
eta indar
horren arteko zatiketa egingo da.
Eman dezagun gas homogeneo bat dugula eta gasaren molekula bakoitzaren masa m dela. Orduan,
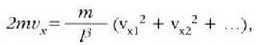
Adierazpen horretan, 1 zatikiaren lastertasunaren x osagaia da
 zatikiaren lastertasunarena da
zatikiaren lastertasunarena da 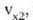 etab.
Baldin ontzian dauden zatikien kopuru osoa N bada, eta n, berriz, bolumen banako bakoitzeko kopurua, orduan,
etab.
Baldin ontzian dauden zatikien kopuru osoa N bada, eta n, berriz, bolumen banako bakoitzeko kopurua, orduan,
 ; hau da,
; hau da,
 .
Beraz,
.
Beraz,

Baina zatikien bolumen banako bakoitzeko masa -hau da, p dentsitatea- besterik ez da
 kopurua, berriz,
kopurua, berriz,
 -ren batez besteko balioa da,
ontziko zatiki guztientzat.
-ren batez besteko balioa da,
ontziko zatiki guztientzat. 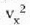 deituko diogu balio horri. Horren arabera
deituko diogu balio horri. Horren arabera
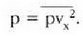
Zatiki batentzat, edozeinentzat, 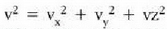 betetzen da.
Zatiki asko dagoenez, eta norabide guztietan eta lastertasun desberdinetan mugitzen ari direnez,
betetzen da.
Zatiki asko dagoenez, eta norabide guztietan eta lastertasun desberdinetan mugitzen ari direnez,
 eta
eta
 -ren batez besteko
balioak berdin-berdinak dira. Hortaz, vz-ren batez besteko balioaren heren bat balio du horietako bakoitzak.
Diren hiru ardatzen artean molekulek ez dute bat beste bat baino nahiago.
Beraz,
-ren batez besteko
balioak berdin-berdinak dira. Hortaz, vz-ren batez besteko balioaren heren bat balio du horietako bakoitzak.
Diren hiru ardatzen artean molekulek ez dute bat beste bat baino nahiago.
Beraz,  eta, hortaz,
eta, hortaz,
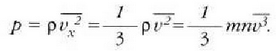
Emaitza hori zatikien arteko talkak kontuan hartu gabe atera bada ere, aurreko azterketak ederki
asko frogatzen du emaitza zuzena dela, talkak kontuan hartu gabe utzi badira ere. Izan ere, talka elastiko batean,
zatiki berdinen artean dagoen lastertasun trukea dela eta, beti izango da
 aurpegiaren kontra
aurpegiaren kontra
 mugimendu kopuruz
joko duen molekularen bat:
mugimendu kopuruz
joko duen molekularen bat:  aurpegitik mugimendu kopuru horrexekin irtendako zatikia bera, hain zuzen. Talka batek oso denbora bitarte
laburra irauten du bi talken artean igarotzen den denboraren aldean. Beraz, talkak kontuan ez hartzea
kalkulua errazteko modu bat besterik ez da. Ontziak ere ez du zertan kubo bat izanik, baina lana erraztearren
aukeratu da halakoa.
aurpegitik mugimendu kopuru horrexekin irtendako zatikia bera, hain zuzen. Talka batek oso denbora bitarte
laburra irauten du bi talken artean igarotzen den denboraren aldean. Beraz, talkak kontuan ez hartzea
kalkulua errazteko modu bat besterik ez da. Ontziak ere ez du zertan kubo bat izanik, baina lana erraztearren
aukeratu da halakoa.
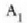 aurpegiari eragiten zaion presioa baino ez da kalkulatu, baina Pascalen printzipioaren arabera, presioa berdina izango
da aurpegi guztietan eta barneko puntu guztietan. Emaitza hori berdin froga daiteke abiapuntutzat teoria
zinetikoa harturik.
aurpegiari eragiten zaion presioa baino ez da kalkulatu, baina Pascalen printzipioaren arabera, presioa berdina izango
da aurpegi guztietan eta barneko puntu guztietan. Emaitza hori berdin froga daiteke abiapuntutzat teoria
zinetikoa harturik.
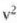 -ren bigarren
erroari molekulen batez besteko lastertasun koadratikoa esaten zaio, eta batez besteko molekula lastertasun
moduko bat-edo da. Batez besteko lastertasun hori gasaren batez besteko presio eta dentsitate balioetatik
abiaturik kalkula daiteke 223-3 ekuazioa aplikatuz gero. Eta, hala,
-ren bigarren
erroari molekulen batez besteko lastertasun koadratikoa esaten zaio, eta batez besteko molekula lastertasun
moduko bat-edo da. Batez besteko lastertasun hori gasaren batez besteko presio eta dentsitate balioetatik
abiaturik kalkula daiteke 223-3 ekuazioa aplikatuz gero. Eta, hala,

Behin puntu honetaraz gero, interesgarria dateke teoria kritikoaren heste bi ezaugarri aipatzea.
Batetik, metodo eta argumentu estatistikoak erabiltzen dira erantzun bat lortzeko. Hala ere,
gure estatistiken azpian Newtonen mekanika clago, horrek arautzen du banakako efektu bakoitza.
Gasen teoria zinetikoaren ekarpen nagusia mekanika estatistikoari eman zion bultzada da.
Gero, quantumen fisikaren aurrerapena dela eta, metodo estatistikoak erabili elira gehienbat fisikan,
prozesu estatistiko horrek Newtonekin zerikusi handirik ez izan arren. Eta bestetik, kopuru makroskopikoak
(presioa, esaterako) kopuru mikroskopikoen batez besteko balioekin (hala nola
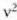 ) lotzen ditu.
Baina batez besteko balio horiek denbora bitarte laburretan edo denbora bitarte luzeetan har daitezke,
eta espazioko gune txikietan edo espazioko gune handietan. Gune txiki batean denbora bitarte labur batean
kalkulatutako batez bestekoa denboraren edo aukeratzen den eskualdearen mende egon zitekeen,
halako moduan non gerta baitzitekeen horrela lorturiko balioek gorabeherak izatea.
Hori erraz gerta zitekeen oso dentsitate apaleko gas batean, esaterako.
Gorabeherak, baina, ez daude soilik teoria zehatz bateko "batez besteko" balio horietan;
gorabehera horiek oso handiak baitira kasu batzuetan. Hala ere, gorabehera horiek guztiak alde batera
utz daitezke kasurik gehienetan, hutsa baitira sistemak zatiki kopurua osoa handia duenean.
) lotzen ditu.
Baina batez besteko balio horiek denbora bitarte laburretan edo denbora bitarte luzeetan har daitezke,
eta espazioko gune txikietan edo espazioko gune handietan. Gune txiki batean denbora bitarte labur batean
kalkulatutako batez bestekoa denboraren edo aukeratzen den eskualdearen mende egon zitekeen,
halako moduan non gerta baitzitekeen horrela lorturiko balioek gorabeherak izatea.
Hori erraz gerta zitekeen oso dentsitate apaleko gas batean, esaterako.
Gorabeherak, baina, ez daude soilik teoria zehatz bateko "batez besteko" balio horietan;
gorabehera horiek oso handiak baitira kasu batzuetan. Hala ere, gorabehera horiek guztiak alde batera
utz daitezke kasurik gehienetan, hutsa baitira sistemak zatiki kopurua osoa handia duenean.
• 3. Adibidea. Kalkulatu hidrogeno molekulen batez besteko lastertasun koaclratikoa, tenperatura 0 °C
eta presioa 1 atm direnean; hau da, gas. ideal gisa harturik. Hidrogenoaren dentsitatea, baldintza normal horietan,
 da.
Orduan,
da.
Orduan,
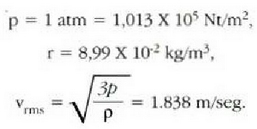
Milia bat segunduko-edo (hau da, 3.600 milia/orduko) cla balio hori.
23 taulan ikus daitezke 0 ° C-tan dauden heste gas batzuei buruz eginclako kalkuluen emaitzak. Orobat adierazten dira energia zinetikoaren balioak, 0 'C-tan, gas mol bakoitzeko. Kontuan hartu: tenperatura berean gasen batez besteko lastertasunek gorabeherak dituztenean, mol bakoitzeko energia zinetikoa ia berdina da gas guztientzat tenperatura berean.
Kontuan hartu behar da, baita ere,
molekula lastertasun horiek soinuaren hedatze lastertasunaren magnitude ordena bera dutela presio
eta tenperatura berdinean. Adibidez, airean, 0 'C-tan eta 1 atmko presioan, vrms = 485 m/seg da,
eta soinuaren lastertasuna 331 m/seg; hidrogenoan vrms = 1.838 m/seg eta soinuaren lastertasuna 1.286 m/seg;
oxigenoan, berriz,  eta soinuaren lastertasuna 317 m/seg.
eta soinuaren lastertasuna 317 m/seg.

23. taula
Emaitza horiek espero izatekoak dira gure gas ereduarentzat. Molekulak denak batera eta norabide baterantz mugituko balira bezala irudikatzen ditugu soinu uhinak. Beraz, soinu uhinaren energia energia zinetiko gisa igarotzen da molekula batetik hurrengora, alegia, molakula batek talka egiten duen hurrengo molekulara. Molekulek berek, oso laster mugitzen badira ere, ez dute asko aurreratzen denbora luze samar batean; espazio mugatu batean dabiltza bateko eta besteko talkak direla eta. Soinu uhinaren energia, ordea, bai komunikatzen da molekula batetik hurrengora lastertasun handi horrekin. Soinuaren lastertasunak ez du, baina, vrms-ren balio berbera izango; soinuaren teoria zehatzak berak iragartzen du zenbateko aldea dagoen.
• 4. Adibidea. Eman dezagun, gas batean, soinuaren lastertasuna molekulen batez besteko lastertasun koadratikoaren berdina dela. Galdera: zer neurritan dago uhinaren lastertasuna tenperatura absolutuaren mende?
Ekuazio honen arabera,
 edo
edo 
hona zer ateratzen den:
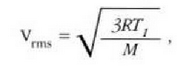
 halako eran non
halako eran non
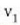 soinuaren lastertasunak,
soinuaren lastertasunak,
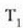
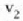
 tenperaturan,
adierazpen honetan agertzen den erlazioa duten:
tenperaturan,
adierazpen honetan agertzen den erlazioa duten:
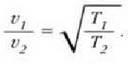
Adibidez, baldin soinuaren lastertasuna 273 K-tan 332 m/seg bada airean, zenbatekoa izango da lastertasuna tenperatura 300 K denean?
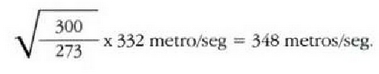
Zein izango litzateke emaitza baldin soinuaren lastertasuna gasaren molekulen batez besteko lastertasun koadratikoaren proportzionala halitz, berdina izan ordez?
Tenperaturaren interpretazio zinetikoa
Ontzian dagoen gasaren masa osoari M esango diogu. Orduan, M = Nm izango da. Baldin n = NN bada, honela ere adieraz dezakegu 23-3 ekuazioa:

Molekulen translazioaren energia zinetiko osoaren bi heren -hau da,
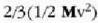 - da
- da
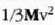 kopurua.
Hala beraz, honela idatziko dugu orain erlazioa:
kopurua.
Hala beraz, honela idatziko dugu orain erlazioa:
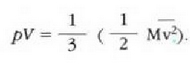
Gauzak errazteko, eman dezagun gas mol bat dugula (n = 1 mol), halako moduan ezen M-ren ordez M -hau da, molekula gramoaren pisua- jar baitaiteke. Gas ideal baten mol batentzat hau da egoera ekuazioa:
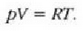
Bi adierazpen horiek parez pare jarriz gero, hau ateratzen da:

Hau da, gas baten molekulen translazioko energia zinetiko osoak zuzeneko proportzioa du tenperatura
absolutuari buruz. Teoria zinetikoa gasen legearekin bat etorriko bada, emaitzak
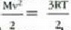 izan beharko du nahi eta nahiez. Bestela, teoria zinetikoan Zhau da, oinarri mikroskopiko batean-
oinarri hartuta dagoen gas baten tenperaturari buruzko definiziotzat har daiteke ekuazio hori.
Era batera edo bestera izan, zer edo zer sakontzen da tenperaturaren esanahia gasen kasuan.
izan beharko du nahi eta nahiez. Bestela, teoria zinetikoan Zhau da, oinarri mikroskopiko batean-
oinarri hartuta dagoen gas baten tenperaturari buruzko definiziotzat har daiteke ekuazio hori.
Era batera edo bestera izan, zer edo zer sakontzen da tenperaturaren esanahia gasen kasuan.
Molekula baten batez besteko energia zinetikoa 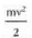 da.
Lehen azaldu den bezala, molekularen energia zinetiko osoa tenperaturaren proportzionala da.
Idatz dezagun, bada, 23-7 ekuazioari dagokion adierazpena halako molekula batentzat:
da.
Lehen azaldu den bezala, molekularen energia zinetiko osoa tenperaturaren proportzionala da.
Idatz dezagun, bada, 23-7 ekuazioari dagokion adierazpena halako molekula batentzat:
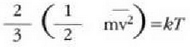
Ekuazio horretan konstante unibertsal bat da k, Boltzmannen konstantea hain zuzen ere. 23-5 ekuaziotik ondorioztatzen denez,
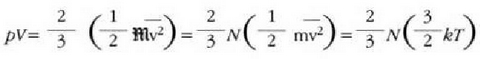
Ekuazio hau gas ideal baten egoera ekuazioarekin alderatuz gero, adierazpen hau ateratzen da:
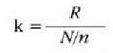
Baina molekula kopuruaren (N) eta mol kopuruaren (n) arteko erlazioa mol bakoitzeko
molekula kopurua da; hau da, Avogadroren zenbakia
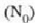 . Beraz,
. Beraz,

Avogadroren zenbakia neurtzeko metodo bat baino gehiago erabil daiteke, hamalau bat metodo; baina metodo horiek guztiek zerikusia dute elkarrekin, eta kimikako eta fisikako gertaera asko -zehaztasun maila bertsukoak denak- gertatzen da haietan. Hau da Avogadroren zenbakiari hitzarmenez eman ohi zaion balioa, 4 zifra esangarrikoa:
 molekula/mol.
molekula/mol.
Eta hau da, beraz, Boltzmannen konstantea:
 joule/molekula k
joule/molekula k
23-7 ekuazioak zuzenean iragartzen du aurreko atalean esperimentu bidez egin den behaketa, zeinaren arabera mol bakoitzeko energia zinetikoa (ia-ia) berdina baita gas guztientzat tenperatura berean. 23-8 ekuazioaren arabera, berriz, T tenperatura berean, bi gas desberdinen molekulen lastertasun koadratikoen erlazioa molekula horien masen alderantzizko erlazioaren bigarren erroaren berdina da. Hau da,

23-10 ekuazioa betetzen da espazio huts batean dagoen eta pareta porotsuak dituen biltegi
batean dauden bi gasen barreiatzean. Gasik arinenak gas astunak baino lasterrago aldegingo du.
Denbora bitarte labur batean pareta porotsuetan zehar igarotzen den molekula kopuruaren erlazioa ere
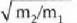 izango da.
Barreiatze prozesu hori erabiltzen da, adibidez,
izango da.
Barreiatze prozesu hori erabiltzen da, adibidez,  uranioz (fisionagarria) (%0,7) eta
uranioz (fisionagarria) (%0,7) eta 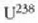 uranioz (fisionagaitza) (%99,3) osaturiko uranio lagin normal batean bi isotopo horiek bereizteko.
Hona zer esaten duen gai honi buruz Smyth Reportek:"
uranioz (fisionagaitza) (%99,3) osaturiko uranio lagin normal batean bi isotopo horiek bereizteko.
Hona zer esaten duen gai honi buruz Smyth Reportek:"
1896an Lord Rayleighek erakutsi zuenez, atomo pisu desberdineko gasez osaturiko nahastura bat nahastura horren parte bat pareta porotsu batean zehar espazio huts batera hedatzen utziz bereiz zitezkeen. Gas arinaren molekulak, batez besteko lastertasun handiagoa baitute gas astunaren molekulek baino, azkarrago hedatzen dira paretan zehar, halako moduan ezen paretatik igaro den gasa (hau da, "barreiatua") osagai arinenez aberasten baita, eta, aitzitik, paretatik igaro ez den hondakin gasa osagai arinenez gabetzen da. Osagai arinenez aberasturiko gasari aldiuneko barreiatu esaten zaio; hondakina antzutzen ari dela sumatu aurretik hedatzen den partea da hori. Baldin barreiatze prozesu horrek gas guztia paretatik igaro arte jarraitzen badu, barreiatuaten batez besteko aberastea ere txikiagoa da... Baldin barreiatze lastertasunak molekula pisuen bigarren erroen alderantziz proportzionalak balira, hau izango litzateke aldiuneko barreiatuaren banatze faktorea, banatze idealaren faktore ere deitua:

Ekuazio horretan 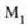 gasik arinenaren molekula pisua da;
gasik arinenaren molekula pisua da;  berriz,
astunenarena. Formula hori uranioaren kasuari aplikatuz argiago erakutsiko dugu banaketaren arazoa.
Uranioa bera ez baita gas bat, uranioa duen gasen bat erabili behar da. Hartarako gas egoki bakarra uranio hexafluoruroa da,
berriz,
astunenarena. Formula hori uranioaren kasuari aplikatuz argiago erakutsiko dugu banaketaren arazoa.
Uranioa bera ez baita gas bat, uranioa duen gasen bat erabili behar da. Hartarako gas egoki bakarra uranio hexafluoruroa da,
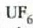 ... Fluorrak isotopo bakarra duenez,
... Fluorrak isotopo bakarra duenez,
 eta
eta
 dira dauden bi uranio hexafluoruro
bakarrak (molekula pisua: 349 eta 352). Eta hala, uranio hexafluoruroren kopuru jakin bateko zati txiki bat pareta
porotsu batean zehar hedatzen bada,
dira dauden bi uranio hexafluoruro
bakarrak (molekula pisua: 349 eta 352). Eta hala, uranio hexafluoruroren kopuru jakin bateko zati txiki bat pareta
porotsu batean zehar hedatzen bada,  uranio hexafluoruroz aberastuko da barreiatua:
uranio hexafluoruroz aberastuko da barreiatua:

Uranioaren isotopoak bereizteko barreiatze aldi asko aplikatu behar dira bata bestearen ondotik.
Gohenek-eta egin zituzten azterketen arabera, aldi bakoitzean ponpaturiko gasaren erdia paretan zehar barreiarazi behar da,
eta beste erdia (antzuturik) hurrengo aldiari gehitzeko utzi..., baldin eta
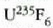 garbia (%99) lortu nahi bada
behintzat. Baina barreiatze aldi bakoitzaren aberastasun faktorea
kontuan hartzeko modukoa bada, 4.000 aldi inguru beharko dira.
Barreiatze aldien bukaeran ateratzen den material gehiena askotan
pasarazi da zikloan zehar. Uranioa banatzeko lantegi batean ehun
mila aldiz ere pasarazi behar izaten da barreiatze aldien ondoren
geratzen den gas bolumena lehenengo aldian barreiadura gertatu
den paretetan zehar".
garbia (%99) lortu nahi bada
behintzat. Baina barreiatze aldi bakoitzaren aberastasun faktorea
kontuan hartzeko modukoa bada, 4.000 aldi inguru beharko dira.
Barreiatze aldien bukaeran ateratzen den material gehiena askotan
pasarazi da zikloan zehar. Uranioa banatzeko lantegi batean ehun
mila aldiz ere pasarazi behar izaten da barreiatze aldien ondoren
geratzen den gas bolumena lehenengo aldian barreiadura gertatu
den paretetan zehar".
Molekularteko indarrak
Jakina denez, molekulen arteko indarrek jatorri elektrikoa eta magnetikoa dute. Molekula guztietan daude karga elektrikoak mugitzen. Molekula horiek neutroak dira, elektrikoki neutroak hain zuzen; hau da, elektroien karga negatibo osoak nukleoen karga osoaren balio bera du, baina aurkakoa. Horrek ez du esan nahi, ordea, molekulen artean eragin elektrikorik ez dagoenik. Adibidez, bi molekula elkarrengana hurbiltzen direnean, bakoitzaren karga mugitu egiten da pixka bat bere ohiko lekutik, eta, horren eraginez, bi molekula horien artean dauden aurkako kargen arteko batez besteko tartea karga berdinen arteko tartea baino txikiagoa izaten da. Molekularteko erakarpen indarra da hori. Molekulak elkarretatik hurbil samar direnean baizik ez da haien barne egitura aldatzen; indar horiek, beraz, tarte txikietan baizik ez dira eraginkorrak; irismen laburrekoak dira. Molekulak elkarri asko hurbiltzen bazaizkio, ordea, eta haien kanpoko kargak elkarren gainean jartzen badira, molekularteko indarra aldaratze indar bilakatzen da. Molekulek elkar aldaratzen dute, ez baitute barne antolamendua berrantolatzeko -kanpoko elektroien aldaratzea eragozteko- modurik aurkitzen. Gasen molekulak elkar ukitzean gertatzen den aldaratze horrexek eragiten du molekulen arteko talka, elkar jotzen duten bi billar bolen artekoa bezalakoa. Aldaratzerik gertatuko ez balitz, batak bestea zeharkatuz mugituko lirateke bolak, elkar jo gabe.
Eman dezagun molekulak biribilak direla, gutxi gorabehera. Grafiko
baten bidez azaldu ahal izango dira orduan molekularteko indarrak.bi molekulek duten
elkarganako energia potentzialaren (U) grafikoa eginez, haien erdiguneen artean dagoen distantziaren (r) arabera.
Molekula bakoitzari eragiten dion indarra (F) energia potentzialarekin (U) lotua dago, adierazpen honen bidez:
 .
23- 3a irudiak U(r) tipiko baten grafikoa agertzen du. Irudika dezagun molekula bat O puntuan finko.
Beste molekula O puntutik aldaratuko da U malda negatiboa denean, eta malda positiboa denean, herriz,
O punturantz erakarria izango da.
.
23- 3a irudiak U(r) tipiko baten grafikoa agertzen du. Irudika dezagun molekula bat O puntuan finko.
Beste molekula O puntutik aldaratuko da U malda negatiboa denean, eta malda positiboa denean, herriz,
O punturantz erakarria izango da.  puntuan ez da indarrik molekulen artean, malda zero da. Energia potentzialaren funtzio horri
dagokion elkarganako indarra F(r) irudikatu da 23-3b irudian. Bi molekula berdinek elkarganako
energia potentziala zero duten punturaino dagoen tartea talka batean egon daiteken hurbiltze handieneko
distantziatzat -hau da, molekularen gutxi gorabeherako diametrotzat- hartzen da askotan. Molekula sinpleen diametroa
puntuan ez da indarrik molekulen artean, malda zero da. Energia potentzialaren funtzio horri
dagokion elkarganako indarra F(r) irudikatu da 23-3b irudian. Bi molekula berdinek elkarganako
energia potentziala zero duten punturaino dagoen tartea talka batean egon daiteken hurbiltze handieneko
distantziatzat -hau da, molekularen gutxi gorabeherako diametrotzat- hartzen da askotan. Molekula sinpleen diametroa
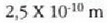 m da, gutxi gorabehera.
Molekulen arteko indarrak huts bihurtzen dira
m da, gutxi gorabehera.
Molekulen arteko indarrak huts bihurtzen dira 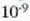 m-ko
distantziara, hau da 4 diametroko distantziara. Beraz, molekula indarrek oso irismen laburra dute.
Potentzial minimoa duen
m-ko
distantziara, hau da 4 diametroko distantziara. Beraz, molekula indarrek oso irismen laburra dute.
Potentzial minimoa duen  distantzia (oreka puntua)
distantzia (oreka puntua) 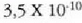 da molekula sinpleentzat. Molekulek tamaina eta barne egitura desberdinak dituzte beren kargetan,
eta molekularteko indarrak desberdinak dira molekula batetik bestera. Hala ere, irudietan adierazi den
portaera kualitatibo hori dute beti.
da molekula sinpleentzat. Molekulek tamaina eta barne egitura desberdinak dituzte beren kargetan,
eta molekularteko indarrak desberdinak dira molekula batetik bestera. Hala ere, irudietan adierazi den
portaera kualitatibo hori dute beti.

Har dezagun molekula mota jakin bat. Egoera gotorrean molekula horiek dar-dar egiten dute beren oreka puntuari
 buruz,
eta ez dute potentzial hondotik (hau da, erakarpen indarretik) ihes egiteko adina energiarik.
Gorputz gotor batean dardaraldi zentroak (0) finko daude, gutxi gorabehera. Isurkari batean, berriz,
dardaraldi energia handiagoa dute zentroei buruz, eta zentroak mugitzeko aske badira ere,
bata bestearekiko distantzia berean gelditzen dira, gutxi gorabehera. Molekula horiek gas egoeran
dute energia zinetiko handiena. Gas batean molekulen arteko batez besteko distantzia molekularteko
indarren irismena baino askoz handiagoa da, eta molekulak lerro zuzenetan mugitzen dira talken artean.
Clerk Maxwellek honela adierazi zuen gas baten teoria zinetikoaren ereduaren eta molekularteko
indarren arteko lotura: "Zatikiak gogorrak, biribilak eta elastikoak direla esan beharrean, indar zentroak
direla esan dezakegu; haien eragina ez dela nabari, oso tarte txiki katera ez bada behintzat,
eta eragin hori intentsitate handikoaldaratze indar bilakatzen dela bat-batean.
Hipotesi batak zein besteak emaitza bera izango du".
buruz,
eta ez dute potentzial hondotik (hau da, erakarpen indarretik) ihes egiteko adina energiarik.
Gorputz gotor batean dardaraldi zentroak (0) finko daude, gutxi gorabehera. Isurkari batean, berriz,
dardaraldi energia handiagoa dute zentroei buruz, eta zentroak mugitzeko aske badira ere,
bata bestearekiko distantzia berean gelditzen dira, gutxi gorabehera. Molekula horiek gas egoeran
dute energia zinetiko handiena. Gas batean molekulen arteko batez besteko distantzia molekularteko
indarren irismena baino askoz handiagoa da, eta molekulak lerro zuzenetan mugitzen dira talken artean.
Clerk Maxwellek honela adierazi zuen gas baten teoria zinetikoaren ereduaren eta molekularteko
indarren arteko lotura: "Zatikiak gogorrak, biribilak eta elastikoak direla esan beharrean, indar zentroak
direla esan dezakegu; haien eragina ez dela nabari, oso tarte txiki katera ez bada behintzat,
eta eragin hori intentsitate handikoaldaratze indar bilakatzen dela bat-batean.
Hipotesi batak zein besteak emaitza bera izango du".
Oso gauza interesgarria da molekularteko
indarrak molekulen arteko grabitate erakarpen indarrarekin konparatzea. Adibidez, elkarretatik
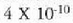 m-ko distantziara dauden
bi helio atomoren arteko indarra
m-ko distantziara dauden
bi helio atomoren arteko indarra 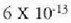 nt-koa da,
gutxi gorabehera. Distantzia horretarako kalkulatu den grabitate indarra
nt-koa da,
gutxi gorabehera. Distantzia horretarako kalkulatu den grabitate indarra
 nt da gutxi gorabehera;
hau da, molekularteko indarra baino
nt da gutxi gorabehera;
hau da, molekularteko indarra baino 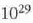 aldiz gutxiago! Emaitza hori tipikoa da; molekularteko indarren aldean grabitate indarrak oso txikiak direla erakusten du.
Hala ere, kontuan izan behar da, molekula baten masa hain dela txikia
aldiz gutxiago! Emaitza hori tipikoa da; molekularteko indarren aldean grabitate indarrak oso txikiak direla erakusten du.
Hala ere, kontuan izan behar da, molekula baten masa hain dela txikia
 ezen indar horiek
ezen indar horiek
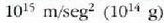 -ko azelerazioak eragin ditzakete bat-batean.
Azelerazio horiek oso denbora bitarte laburra iraun dezakete, zeren
molekula batek berehala aldegin baitezake beste baten eragin eremutik.
-ko azelerazioak eragin ditzakete bat-batean.
Azelerazio horiek oso denbora bitarte laburra iraun dezakete, zeren
molekula batek berehala aldegin baitezake beste baten eragin eremutik.
Gas idealaren bero espezifikoak
Gas ideal baten molekulak esfera gogor elastikoak balira bezala irudikatu ditugu. Molekulen artean ez dago indarrik, talkak irauten duen bitartean izan ezik, eta molekulen itxura ez da talken ondorioz aldatzen. Hortaz, ez dago barne energia potentzialik. Gas ideal baten barne energia, beraz, guztiz zinetikoa da. Lehen esan dugun bezala, molekula baten batez besteko energia zinetikoa 3/2kT da, eta N molekula dituen gas ideal baten barne energia (U), berriz,

Emaitza horrek garrantzi handia du, gas ideal baten barne energia Kelvin tenperaturaren proportzionala dela eta, presioa eta bolumena gorabehera, bakarrik tenperaturaren mendeko dela adierazten baitu. Emaitza horren bidez gas ideal baten bero espezifikoei buruzko informazioa lor dezakegu orain.
Gai baten bero espezifikoa gai horren tenperatura
gradu bat igotzeko masa banako bakoitzeko behar den beroa da.
Gasen masa neurtzeko mol banakoa erabiltzen da. Dagokion bero espezifikoari bero
kapazitate molarra esaten zaio eta C batez adierazten da.
Bi kapazitate espezifiko erabiltzen dira gasentzat: alegia, batetik, kapazitate
espezifiko molarra bolumen konstantean  ,
eta, bestetik, kapazitate espezifiko molarra presio konstantean Cp
,
eta, bestetik, kapazitate espezifiko molarra presio konstantean Cp
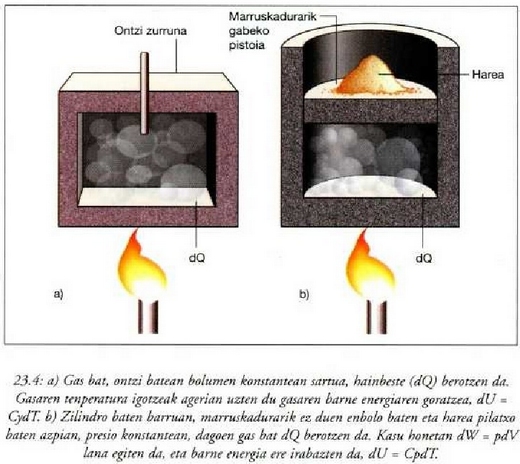
Baldin gas ideal baten n mol baditugu, haren mol kapazitate espezifikoa tenperatura konstantean
 bada eta dT igotzen bada haren
tenperatura bolumen konstantean,
bada eta dT igotzen bada haren
tenperatura bolumen konstantean, 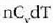 da ematen zaion beroa, eta zero, berriz, egiten den kanpo lana (23-4a irudia). Termodinamikaren lehenengo legearen arabera:
da ematen zaion beroa, eta zero, berriz, egiten den kanpo lana (23-4a irudia). Termodinamikaren lehenengo legearen arabera:
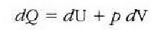
Baina
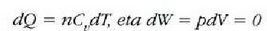
eta horrenbestez,
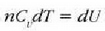
Baldin gas kopuru bera tenperaturak aldaketa bera egin arte presio konstantean (p) berotuko balitz,
 beroa emango litzateke.
Aldiz, kasu honetan, gasa dilatatu egingo litzateke eta kanpo lana egingo luke (23-4b irudia).
Eta lehenengo legearen arabera,
beroa emango litzateke.
Aldiz, kasu honetan, gasa dilatatu egingo litzateke eta kanpo lana egingo luke (23-4b irudia).
Eta lehenengo legearen arabera,
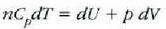
Tenperatura aldaketa berbera da kasu bietan. Gas ideal batentzat, U tenperaturaren mende baizik ez dagoenez,
barne energiaren aldaketa, dU, berbera da prozesu bietan.
Orduan,  eta
eta
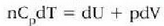 ekuazioak konbinatuz,
ekuazioak konbinatuz,
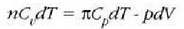
hau da,

Dilatazio batean presio konstantean egindako lana da pdV Baldin pV = nRt egoera ekuazioan p aldagabe gordetzen bada eta bi atalak bereizten badira, hau ateratzen da:
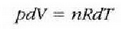
eta horrenbestez, honela gelditzen da 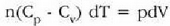 ekuazioa:
ekuazioa:

hau da,

Azken ekuazio horrek erakusten duenez, presio konstantean dagoen
gas ideal baten bero ahalmen molarra bolumen konstantean
dagoenarena baino handiagoa da gasen konstante unibertsala (R)
adinako kopuruan. Baina R = 8,31 joule/mol K, edo, bestela, 1,99
cal/mol K, eta, horrenbestez, 2 cal/mol K da, gutxi gorabehera, bi
bero ahalmen horien artean dagoen aldea. Nahiz eta (23-15) ekuazioa
gas ideal batentzat baizik ez izan zehatza, ia zehatza da presio
moderatuan dauden gas errealentzat (ikus 23-2 taula). Kontuan izan,
emaitza hori lortzeko, ez dela U=(3/2)nRT ekuazio espezifikoa baliatu,
U tenperaturaren eta ez beste ezeren mendeko izatea baizik.
Baldin orain  ,
kalkulatzeko moduren bat badugu, 23-15 ekuazioak
,
kalkulatzeko moduren bat badugu, 23-15 ekuazioak  emango digu, eta alderantziz.
emango digu, eta alderantziz. 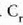 ere lor dezakegu, 23-12 ekuazioa gas ideal baten barne energiarako teoria zinetikoaren
emaitza espezifikoarekin konbinatuz: U = 3/2nRT (23-11 ekuazioa). Eta hala:
ere lor dezakegu, 23-12 ekuazioa gas ideal baten barne energiarako teoria zinetikoaren
emaitza espezifikoarekin konbinatuz: U = 3/2nRT (23-11 ekuazioa). Eta hala:

Emaitza hori (3 caI/mol K, gutxi gorabehera) nahikoa zuzena da gas atomobakarren kasuan. Gas atomobiko eta atomoanitzen kasuan lortu diren balioentzat, ordea, ez dator guztiz bat. Horren arabera, beraz, 23-11 ekuazioa ez da, oro har, zuzena. Erlazio hori teoria zinetikoaren eredutik atera denez zuzenean, aldatu egin beharko da eredua, gas errealen portaera azaltzeko hurbiltze baliagarria izango bada.
5. adibidea. Soinu uhin baten konprimatze eta arrarotze prozesuak ia adiabatikoak dira audiomaiztasunetarako. Froga ezazu halakoetan hau dela soinuaren lastertasuna gas ideal batean:
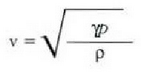

Lehenago frogatu denez, 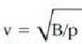 da soinu uhinen
lastertasuna jariakari batean; ekuazio horretan jariakariaren dentsitatea da p,
eta
da soinu uhinen
lastertasuna jariakari batean; ekuazio horretan jariakariaren dentsitatea da p,
eta  jariakariaren
modulu boluntarioa, berriz, B.
jariakariaren
modulu boluntarioa, berriz, B.
Sisteman berorik sartzen edo ateratzen uzten ez duen prozesua da prozesu adiabatikoa.
Beraz, 
Gas ideal batentzat,  tenperatura aldaketak
tenperatura aldaketak 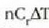 -ren
bidez ematen dituen prozesu bat da barne energiaren aldaketa. Beraz, termodinamikaren lehenengo legearen arabera,
-ren
bidez ematen dituen prozesu bat da barne energiaren aldaketa. Beraz, termodinamikaren lehenengo legearen arabera,

adierazpen hau lortzen da prozesu horrentzat:

hau da,

Gas idealaren legea 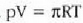 da.
Beraz, p, V eta T-k gorabehera txikiren bat izanez gero,
da.
Beraz, p, V eta T-k gorabehera txikiren bat izanez gero,
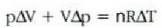
ateratzen da diferentzialak hartuz. Baina  ekuazioaren arabera,
ekuazioaren arabera,
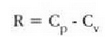
Adierazpen diferentzialean R eta 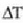 ordezkatuz,
hau lortzen da:
ordezkatuz,
hau lortzen da:

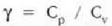 , ekuazioari
bero espezifikoen erlazio esaten zaio. Osagaiak aldatu, eta zati pV eginez, hau ateratzen da:
, ekuazioari
bero espezifikoen erlazio esaten zaio. Osagaiak aldatu, eta zati pV eginez, hau ateratzen da:

Beraz, prozesu adiabatikoetan,
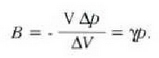
Hau da, beraz, soinuaren lastertasuna gas ideal batean baldintza adiabatikoetan:
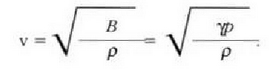
Zer alde dago emaitza honen eta laugarren adibidean atera denaren aldean? Zergatik ez dira berdinak soinuaren lastertasuna gas batean eta gasaren molekulen batez besteko lastertasun koadratikoa?
6. adibidea. Froga ezazu prozesu adiabatikoan dagoen gas ideal bati pVg konstantea dagokiola. Bosgarren adibidearen arabera,

betetzen du aldaketa adiabatikoa izan duen gas ideal batek. Gehikuntza txikien limitean
 jar dezakegu d ordez, eta, orduan:
jar dezakegu d ordez, eta, orduan:

Integratu, eta hau ateratzen da:
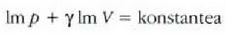
hau da,
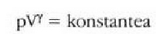
Konstante hori gas kopuruaren arabera zehazten da, eta, beraz, aldaketa adiabatikoa izan duen edozein gas kopururen presioaren eta bolumenaren artean dagoen erlazioa azaltzeko erabil daiteke azken ekuazio hori. 23-5 irudian gas ideal baten portaera isotermikoa eta adiabatikoa alderatzen dira.

Energiaren banaketa baliokidea
1857an Clausiusek teoria zinetikoaren ereduari aldaketa bat egin zion gasen bero espezifikoak azaldu ahal izateko. Gogoan izan, hemen erabili den ereduan esfera elastiko gogor baten portaera zuela molekulak, eta haren energia zinetikoa translazio hutsekoa balitz bezala hartzen zela. Ateratzen zen bero espezifikoa nahikoazen molekula atomobakar batentzat, eta molekula horientzat adierazpen hori egokia dela esan nahi du horrek. Gainera, era guztietako gasen portaera tenperatura tarte zabal baten barruan iragartzeko bide gisa eredu horrek izan duen arrakasta dela eta, iruditzen zaigu translazioko batez besteko energia zinetikoa dela gas baten tenperatura gisa neurtzen dugun hori.
Baina bero espezifikoen kasuan, tenperatura aldaketak ez ezik beroa (energia) trukatzeko prozesua interesatzen zaigu, eta, beraz, galdera da, ea molekulak meta dezakeen barruan energiarik, translazioko energia zinetiko gisa ez bestela. Hori hala zatekeen baldin eta molekula, zatiki gogor baten gisa hartu ordez, barne egituraren bat duen gauzatzat hartuko balitz. Izan ere, translazio mugimenduaz gainera errotazio eta dardaraldi mugimenduak izateko gauza izango bailitzateke, orduan, molekula. Talkek errotazio mugimendua eta dardaraldiak eragiten dituzte, eta horrek gasaren barne energia handitzen, aldi berean. Horra, beraz, gas baten barne energiarako teoria zinetikoa alda dezakeen eredu bat.
Bila dezagun orain molekula asko duen sistema baten energia osoa zenbatekoa den molekula
bakoitza barne egitura duen objektu gisa harturik. Molekula banakoen translazioaren energia
zinetikoa izango da energia  ; edo,
bestela, molekula banakoen errotazioaren energia zinetikoa
; edo,
bestela, molekula banakoen errotazioaren energia zinetikoa
 ;); edo atomoen dardaraldiaren
energia zinetikoa molekula batean
;); edo atomoen dardaraldiaren
energia zinetikoa molekula batean  );
edo atomoen dardaraldiaren energia potentziala molekula batean
);
edo atomoen dardaraldiaren energia potentziala molekula batean
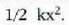 .
Energia beste energia mota batzuez -energia magnetikoaz, esaterako- osa baliteke ere, gasentzat eta
are gai elkartu bakunentzat eta kristal metalikoentzat ere, zehatz samar eman daiteke energia osoa,
aipatu diren energia mota horien arabera. Nahiz eta gaiek jatorri fisiko desberdina izan, matematika
adierazpide bera dute denek: alegia, balio negatiboak edo positiboak har ditzakeen kopuru baten koadroa bider
konstante bat. Azterketa estatistiko baten bidez froga daitekeenez, zatiki asko dagoenean eta Newtonen
mekanika baliagarria denean, gai horien guztien batez besteko balioa bera da, eta tenperaturaren mende dago
bakarrik. Hau da, energia erabilgarria tenperaturaren mende dago bakarrik, eta proportzio berean banatzen
da molekulek energia xurgatzeko dituzten modu independenteen artean. Teorema hori, energiaren banaketa baliokidea deitua,
Clerck Maxwellek deduzitu zuen mekanika estatistikoari buruz egin zuen teoria matematikoan.
Energia xurgatzeko modu independente horietako bakoitzari askatasun maila esaten zaio.
.
Energia beste energia mota batzuez -energia magnetikoaz, esaterako- osa baliteke ere, gasentzat eta
are gai elkartu bakunentzat eta kristal metalikoentzat ere, zehatz samar eman daiteke energia osoa,
aipatu diren energia mota horien arabera. Nahiz eta gaiek jatorri fisiko desberdina izan, matematika
adierazpide bera dute denek: alegia, balio negatiboak edo positiboak har ditzakeen kopuru baten koadroa bider
konstante bat. Azterketa estatistiko baten bidez froga daitekeenez, zatiki asko dagoenean eta Newtonen
mekanika baliagarria denean, gai horien guztien batez besteko balioa bera da, eta tenperaturaren mende dago
bakarrik. Hau da, energia erabilgarria tenperaturaren mende dago bakarrik, eta proportzio berean banatzen
da molekulek energia xurgatzeko dituzten modu independenteen artean. Teorema hori, energiaren banaketa baliokidea deitua,
Clerck Maxwellek deduzitu zuen mekanika estatistikoari buruz egin zuen teoria matematikoan.
Energia xurgatzeko modu independente horietako bakoitzari askatasun maila esaten zaio.
23.7 ekuaziotik dakigu gas bateko molekula moI baten translazio energia zinetikoa 3/2 RT dela.
Translazioko energia zinetikoa, baina, hiru gai hauen batura da:
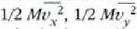 eta
eta
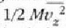 .
Banaketa baliokidearen teorema beteko bada, gai horietako bakoitza neurri berean gehitu behar zaio
energia osoari: alegia, 1/2RT neurri bat askatasun maila bakoitzeko.
.
Banaketa baliokidearen teorema beteko bada, gai horietako bakoitza neurri berean gehitu behar zaio
energia osoari: alegia, 1/2RT neurri bat askatasun maila bakoitzeko.
Gas atomobakarretan molekulek ez dute translazio mugimendua besterik
(ez dute barne egiturarik teoria zinetikoaren arabera); hala, beraz: U = 3/2 RT mol bakoitzeko.
23-12 ekuaziotik ateratzen denez:  (mol)(K).
Orduan, 23-14 ekuazioaren arabera,
(mol)(K).
Orduan, 23-14 ekuazioaren arabera,  ;
eta bero espezifikoen erlazioa hau da:
;
eta bero espezifikoen erlazioa hau da:
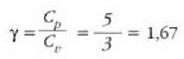
Gas atomobikoetan molekulek palankatxo baten itxura dute (bi esfera, haga zurrun batez lotuak).
Molekula horiek hiru ardatz elkarzuten inguran bira dezakete. Baina ardatz bati buruzko inertzia momentua
harra zurrunean zehar hutsaren hurrengo litzateke barrari perpendikular dauden ardatzei buruzko
inertzia momentuarekin konparatuta; errotazio energiak, beraz, ez du bi gai besterik izango:
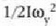 eta
eta
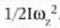 .
Banaketa baliokidea beteko bada, errotazioko askatasun maila bakoitzak translazioko askatasun mailak beste
energia gehitu behar clu. Hala, beraz, errotaziomugimendu adina translazio mugimendu dituen gas atomobiko batentzat,
.
Banaketa baliokidea beteko bada, errotazioko askatasun maila bakoitzak translazioko askatasun mailak beste
energia gehitu behar clu. Hala, beraz, errotaziomugimendu adina translazio mugimendu dituen gas atomobiko batentzat,
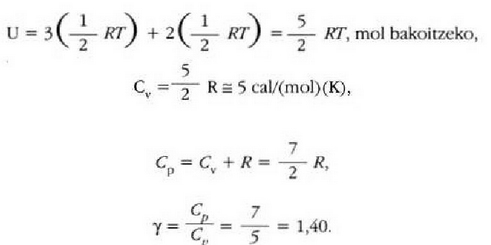
Gas atomoanitzetan, berriz, molekula bakoitzak hiru esfera (atomo) edo gehiago ditu barra batez lotuak gure ereduan; beraz, elkarzut dauden hiru ardatzetako bakoitzaren inguruan energiaz biratzeko gauza da molekula. Eta, hala, errotazio eta translazio mugimenduak dituen gas atomoanitz batentzat,

Har ditzagun orain datu esperimentalak ideiak egiaztatzeko. Ondoko taulan hainbat gasen bero espezifiko molarra adierazi da, tenperatura 20 °C eta presioa 1 atm direnerako.

Gas atomotiko batzuetan -kloroan, esaterako- eta gas atomoanitz gehienetan, aurreikusi direnak baino handiagoak dira bero espezifikoak. g-k ere ez du erregulartasun bakunik gas poliatomokioentzat. Horrek esan nahi du gure eredua ez dagoela behar bezala cloitua molekulen egitura errealera.
Oraindik ez da, noski, molekula atomobikoetan eta atomoanitzetan atomoen dardaraldiak eragiten duen energia kontuan hartu. Orain artean erabili dugun eredua -palankaren eredua- alda daiteke, eta barra baten ordez malgukien bidez lotu esferak. Eredu herri horri esker asko hobetuko clira gure emaitzak aipatu ditugun kasu horietako batzuetan. Hala ere, kontuan izan behar (la, gas guztientzat eredu teoriko bat bera izan ordez eredu enpiriko bat dugula orain, gas batetik bestera desberdina dena. Molekulen portaeraren irudikapen egokia lor daiteke horrela; ereclu enpirikoa erabilgarria da, beraz, baina ez da jada funtsezkoa.
Kontuan hartu, gainera, esperimentu bidez frogatu Gien bezala, gasen bero espezifikoak tenperaturaren mende daudela. 23-6 irudiak erakusten du hidrogenoaren bero molarra tenperaturaren arahera nola aldatzen den. Adibidez, gure ereduan molekula atomobikoentzat eskatzen den 5 cal/(mol)(K) balioa 250-750 K bitarteko tenperaturan bakarrik dagokio hidrogenoari. 750 K-tik gora C„ modu konstantean handitzen cla 7 cal/(mol)(K) balioraino, eta 250 K-tik behera, herriz, berehala txikitzen cla 3 cal/(mol)(K)-raino.

Beste gas batzuen bero espezifikoan ere antzeko gorabeherak gertatzen dira tenperaturarekin
Gorabehera horiek zergatik gertatzen diren, aurreko azterketa horrek azal dezake. Tenperatura apaletan hidrogeno molekulak translazio energia besterik ez clute eta ezin clute biratu. Errotazioa tenperatura igo ahala hasten (la. Tenperatura arruntetan, hidrogeno molekula batek lehengo palankatxoaren araberako portaera clu. Oso tenperatura hanclian, berriz, molekulek energia handiko talkak dituzte, talka horiek atomoak dardarazten dituzte eta molekulek ez dute gehiago gorputz zurrunen portaera izaten. Gasek, bakoitzak molekula egitura bat izanik, tenperatura desberdinetan erakuts ditzakete efektu horiek. Horregatik egin ditzake kloro molekula batek dardaraldiak inguruneko giro tenperaturan.
Nahiz eta deskripzio hau funtsean zuzena izan, eta molekulen portaeraren xehetasun asko aztertu izan, portaera hau ez dator bat teoria zinetikoak dioenarekin. Izan ere, teoria zinetikoa Newtonen mekanikan oinarritzen da, zatiki kopuru handi bati aplikaturik, eta energiaren banaketa baliokidea mekanika estatistiko klasiko horren ondorio cla, ezinbesteko onclorioa gainera. Baina energiaren banaketa baliokidea beteko bada, energiaren zati bakoitzak -translazio, errotazio eta clardaraldi energiakzati berdinak hartu beharko lituzke, tenperatura aldatzean barne energia osoan gertatzen den aldaketa gorabehera. Gasen bero espezifikoak tenperaturaren mende ez egotea eskatzen baitu teoria zinetikoak.
Atomoaren (edo molekularen) egitura azaltzen saiatzean mekanika klasikoaren baliotasunaren mugara iristen gara, beraz. Oso lastertasun handien muncluan bezala dimentsio txikien munduan ere, Newtonen printzipioak baliogabetu egiten dira. Erlatibitatearen teoriak Newtonen ideiak aldatzen ditu lastertasun handien munduan sistema fisikoek duten portaera azaltzeko, eta quantumen fisikak, herriz, dimentsio txikietan sistema fisikoek Gluten portaera azaltzeko. Bai erlatibitatearen teoria bai quantumen mekanika, teoria klasikoaren orokortzeak dira; izan ere, Newtonen fisikak esperimentu bidezko behaketen deskribapen zehatza egin cluen alorretan bat baitatoz Newtonen emaitzekin (emaitza zuzenak).