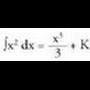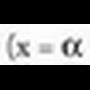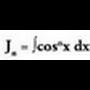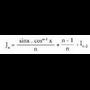Matematika»Analisiak
Jatorrizkoak eta integralak
Integrazioa, hasiera hasieratik, barruti baten azaleraren edo kurba
baten luzeraren kalkuluarekin erlazionaturik egon zen. XVII. mendearen
bukaeran sortu zen, batez ere Leibniz eta Newtonen aurkikuntzei
esker. Bakoitzak bere aldetik lan eginez, eta sarritan elkarren
aurka ibili arren, hemen ematen diren emaitzetara iritsi ziren. Integrazioaren
tasun eta arauak Newtonek lehenago aurkitu bazituen
ere, gaur egun erabiltzen den notazioa Leibnizengandik dator. Teoria
hauetara iristeko, XVII. mendean zehar Kepler, Fermat, Cavalieri
eta beste matematikari batzuk, Arkimedesek (K. a. 111. m.) lortutako
emaitzaz baliatu ziren.Lehen aro hau pasa ondoren ere luzaroan izan ziren integrazioak
ikerketagai. XIX. mendean, integral kontzeptuaren definizio zehatz
bat eman beharraren arazoari irtenbidea eman zitzaion. Gaur egun
definizio honen oinarri diren ideia gehienak Riemann (1826-
1866) alemaniarrak aurkitu zituen, nahiz eta oinarrizko matematikatan
erabiltzen dena Darboux (1842-1917) frantziarrarena izan.
Definitutako tartean, funtzioak jarraitasun uniformea duenean,
definizio hau erraza da, baina etenguneak dituzten funtzioei aplikatzerakoan
korapilatu egiten da. Integrazioaren teoriaren inguruan
geroago egin diren lanak, definizio hau orokortzera jo dute,
gero eta irregularrago diren funtzioetarako baliagarria izan dadin.
Stieljes (1856-1.894) holandarrak, eta batez ere Lebesgue (1.875-
1.941) frantziarrak, integralaren ideia hobetu dute, topologian eta
neurriaren teorian izandako aurrera pausoak bereganatuz. Bestalde,
XVIIL mendeaez geroztik jakina da integrazioa deribazioaren alderantzizko
eragiketa dela. Integrala definitzeko era hau, bere aplikazioengatik
oso urruti dago, baina errazagoa da, eta berari esker, integralak
errazago kalkula daitezke. Gai honetan integralak era
honetara azalduko dira, eta integral mugagabeak landuko dira.
Hurrengo gaian berriz, integralaren eta azalera edo desplazamenduaren
arteko erlazioa eta integral mugatuaren definizioa landuko
dira.
I. Funtzio baten jatorrizko funtzioa
tarte itxi batean definitutako f(x) edozein funtzio emanda,
f(x) funtzioaren jatorrizkoa, F(x) beste funtzio bati esaten zaio, non
tarte horretan, F(x) funtzioaren deribatua f(x) den. Hau da, [a,b]
tarteko x guztientzat F(x) = f(x) da.? Adibideaksin x funtzioa cos x funtzioaren jatorrizko bat da, izan ere,
(sin x)' = cos x da.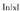 funtzioa,
funtzioa, funtzioaren jatorrizko banda, izan ere ,
funtzioaren jatorrizko banda, izan ere ,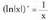 da.
da.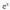 ex funtzioa bere jatorrizko bat da, izan ere
ex funtzioa bere jatorrizko bat da, izan ere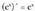 da.
da.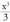 funtzioaren deribatua
funtzioaren deribatua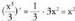 da. Horrela,
da. Horrela,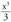 funtzioa
funtzioa
Funtzio baten jatorrizkoen tasunak
Lehenengo tasuna
F(x) funtzioa f(x) funtzioaren jatorrizko bat bada, eta K konstante
bat bada, F(x) + K funtzioa f(x)-en beste jatorrizko bat da.
463Frogapena:Funtzioen baturaren deribatua funtzioen deribatuen batura, eta
konstante baten deribatua beti zero dela gogoan izatea nahikoa da.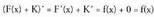 ? Adibidea1. Bila itzazu
? Adibidea1. Bila itzazu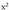 funtzioaren hiru jatorrizko.Ebazpidea :
funtzioaren hiru jatorrizko.Ebazpidea :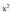 funtzioaren jatorrizko bat
funtzioaren jatorrizko bat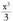 da.
da. -ren hiru jatorrizko, adibidez, hauek dira :
-ren hiru jatorrizko, adibidez, hauek dira :
Bigarren tasuna
Funtzio batek jatorrizko bat badu, orduan, infinitu jatorrizko
ditu.Frogapena :F(x) funtzioa f(x)-en jatorrizko bat bada,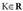
Hirugarren tasuna
Funtzio bereko bi jatorrizkoren arteko aldea, konstante bat da.
Hau da, F(x) eta G(x) funtzioak f(x) funtzioaren bi jatorrizko badira,
orduan, F(x) - G(x) = K = konstantea da.Frogapena :Edozein tartean definitutako f(x) funtzio baten deribatua, tarteko
puntu guztietan, zero bada, orduan f(x) konstantea dela kontuan
hartu behar da; hau da, f '(x) = 0 bada orduan f(x) = K dela.Hau horrela izanik,F(x) funtzioa f(x)-en jatorrizko bat bada, F' (x) = f(x) izango da, etaG(x) funtzioa f(x)-en beste jatorrizko bat bada, G' (x) = f(x) izango da.Atalez-atal kenketa eginez,
I I. Funtzio baten integral mugagabea
f(x) funtzio baten integral mugagabea, f(x) funtzioaren jatorrizko
guztien multzoari esaten zaio. Horrela adierazten da: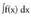 Espresio hau honela irakurtzen da : "efe ixa diferentzial ixaren
integrala"Jatorrizko funtzioaren tasunak direla eta, F(x) funtzioa f(x) funtzioaren
jatorrizko bat bada,
Espresio hau honela irakurtzen da : "efe ixa diferentzial ixaren
integrala"Jatorrizko funtzioaren tasunak direla eta, F(x) funtzioa f(x) funtzioaren
jatorrizko bat bada,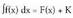 da, K integrazio-konstantea delarik.Batzutan aldagaia adierazteko beste letra edo hizki bat erabiltzen
da ; adibidez :
da, K integrazio-konstantea delarik.Batzutan aldagaia adierazteko beste letra edo hizki bat erabiltzen
da ; adibidez :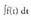 edo
edo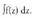 ? Adibideak1. Bila ezazu
? Adibideak1. Bila ezazu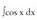 Ebazpidea :cos x funtzioaren jatorrizko bat sin x denez,
Ebazpidea :cos x funtzioaren jatorrizko bat sin x denez,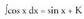 2. Bila ezazu
2. Bila ezazu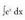 Ebazpidea :
Ebazpidea :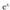 funtzioaren jatorrizkoa
funtzioaren jatorrizkoa bera denez,
bera denez,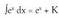 3. Bila ezazu
3. Bila ezazu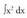 Ebazpidea:funtzioa
Ebazpidea:funtzioa -ren jatorrizko bat denez,
-ren jatorrizko bat denez,
I I I. Integralen kalkulua. Integral berehalakoak
Edozein funtzioren integrala ebatzita dago integratu behar den
funtzioaren jatorrizko bat ezagutzen denean. Jatorrizko bat bilatuz
gero, jatorrizko horri konstante bat gehituz ateratzen da integral
orokorra.Integrazioa deribazioaren alderantzizko eragiketa denez, oinarrizko
funtzioen funtzio deribatuen integralak berehala bilatzen dira.
Baina, zoritxarrez, edozein funtzioren integrala ezin da, deribazioan
gertatzen den bezala, oinarrizko funtzio batzuen integralak ezagutuaz
eta arau batzuk erabiliz kalkulatu.Integrala kalkulatzeko, integral berehalakoak eta funtzioen baturaren
integralak eta konstante eta funtzio arteko integralak betetzen
dituzten arau orokorrak ezagutzeaz gain beste metodo batzuk ezagutu
behar dira. Integralak berehalakoak ez direnean, edo arauak
erabiliz berehalako bihurtu ezin direnean, aldagai-aldaketaren
metodoa edo zatikako integrazio metodoa erabili daiteke. Metodo
bat edo beste, zein erabili behar den jakiteko, ez dago araurik, eta
metodo hauekin funtzio denak integratu daitezkeenik ere ezin da
ziurtatu. Integrazio metodoa, integratu behar den funtzioaren arabera
dago.Gai honetan, besteak beste, funtzio razionalen integrazioa,
Integral berehalakoak
Oinarrizko funtzioen deribaziotik abiatuz, integral berehalako
deritzatenak lortzen dira. Hain errazak ez diren integralen kalkulua
arin egin nahi bada, emaitza hauek nahitaez ikasi behar dira.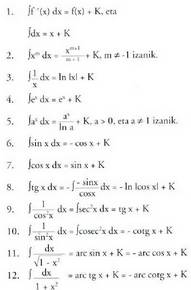 ? Adibideak (Integral berehalakoak)1. Kalkula ezazu
? Adibideak (Integral berehalakoak)1. Kalkula ezazu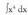 Ebazpidea :Berehalako integralen zerrendako bigarren kasua da, m= 4 delarik.
Ebazpidea :Berehalako integralen zerrendako bigarren kasua da, m= 4 delarik.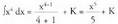 2. Bila ezazu
2. Bila ezazu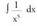 Ebazpidea :
Ebazpidea :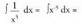 (Kasu honetan m = -5 da).
(Kasu honetan m = -5 da).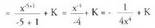 3. Kalkula ezazu :
3. Kalkula ezazu :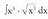 Ebazpidea:
Ebazpidea: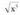 berreketa eran idatziz:
berreketa eran idatziz: Oinarri bereko berreketen biderkaduraren tasuna dela eta
Oinarri bereko berreketen biderkaduraren tasuna dela eta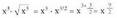 (kasu honetan m = 2 da)Beraz
(kasu honetan m = 2 da)Beraz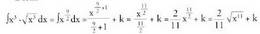 4. Bila ezazu
4. Bila ezazu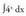 Ebazpidea :
Berehalako integralen zerrendako bosgarrena da, a = 4 delarik.
Ebazpidea :
Berehalako integralen zerrendako bosgarrena da, a = 4 delarik.
I V. Deskonposaketa bidezko integrazioa
Integralek, oinarrizko bi tasun betetzen dituzte :
Lehenengo tasuna
Funtzio arteko baturaren (kenduraren) integrala funtzioen integralen
batura (kendura) da. Hau da,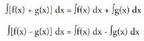 FrogapenaF(x) funtzioa, f(x) funtzioaren jatorrizko bat bada,
FrogapenaF(x) funtzioa, f(x) funtzioaren jatorrizko bat bada,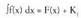 G(x) funtzioa, g(x) funtzioaren jatorrizko bat bada,
G(x) funtzioa, g(x) funtzioaren jatorrizko bat bada,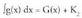 Orduan F(x) + G(x) funtzioa, f(x) + g(x) funtzioaren jatorrizko
bar da, eta F(x) - G(x) funtzioa, f(x) - g(x) funtzioaren jatorrizko bar
da, izan ere :
Orduan F(x) + G(x) funtzioa, f(x) + g(x) funtzioaren jatorrizko
bar da, eta F(x) - G(x) funtzioa, f(x) - g(x) funtzioaren jatorrizko bar
da, izan ere :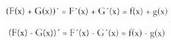 Beraz
Beraz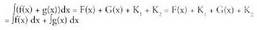 Eraberean
Eraberean
Bigarren tasuna
Konstante eta funtzio baten arteko biderkaduraren integrala,
konstantearen eta funtzioaren integralaren arteko biderkadura (la.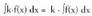 Frogapena :F(x) funtzioa f(x) funtzioaren jatorrizko bat bada,
Frogapena :F(x) funtzioa f(x) funtzioaren jatorrizko bat bada,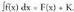 Baina (k.F(x))' = k.F'(x) = k.f(x) da, beraz, k.F(x) funtzioa k-f(x)en
jatorrizko bat da. Beraz,
Baina (k.F(x))' = k.F'(x) = k.f(x) da, beraz, k.F(x) funtzioa k-f(x)en
jatorrizko bat da. Beraz,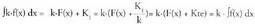 Adibidea. (Tasun hauen aplikazioak)1. Kalkula ezazu
Adibidea. (Tasun hauen aplikazioak)1. Kalkula ezazu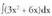 Ebazpidea :Lehenengo tasuna dela medio,
Ebazpidea :Lehenengo tasuna dela medio,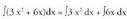 Bigarren tasuna dela medio,
Bigarren tasuna dela medio, eta
eta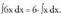 Baina
Baina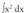 eta fx dx, berehalako integralen zerrendako bigarren kasukoak dira.Lehenengoan ni = 2, eta bigarrenean m = 1 da.
eta fx dx, berehalako integralen zerrendako bigarren kasukoak dira.Lehenengoan ni = 2, eta bigarrenean m = 1 da.
Horrela, Beraz,
Beraz,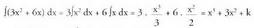 2. Kalkula ezazu
2. Kalkula ezazu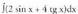 Ebazpidea:
Ebazpidea: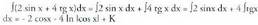 3. Kalkula ezazu
3. Kalkula ezazu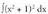 EbazpideaBinomio baten karratuaren formula erabiliz
EbazpideaBinomio baten karratuaren formula erabiliz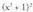 garatuko da :
garatuko da : Horrela,
Horrela,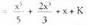 4. Kalkula ezazu
4. Kalkula ezazu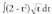 Ebazpidea:(Oraingo honetan t da aldagaia, eta ez x )
Ebazpidea:(Oraingo honetan t da aldagaia, eta ez x )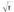 berreketa eran jarriz :
berreketa eran jarriz :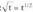 Biderkaketaren banakortasun legea erabiliz :
Biderkaketaren banakortasun legea erabiliz :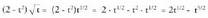 Orduan, rduan,
Orduan, rduan,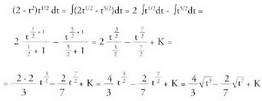 5. Kalkula ezazu f
5. Kalkula ezazu f Ebazpidea:Emandako zatikia zatikien baturetan banatuz edo deskonposatuz
:
Ebazpidea:Emandako zatikia zatikien baturetan banatuz edo deskonposatuz
: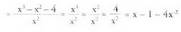 Beraz,
Beraz,
- Ariketak
V. Aldagai-aldaketa edo ordezkapen metodoa
Metodo honen bidez, aldagaiaren aldaketa bat eginez, emandako
integrala beste errazago batean bihurtzen da. Kasu batzutan egin
behar den aldaketa zehatz daiteke, baina gehienetan, praktikak erakusten
du komenigarriena zein den.Hasteko, ia berehalakoak diren integralak aztertuko dira.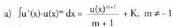 denean.
denean.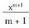 inserted textfuntzioaren deribatua,
inserted textfuntzioaren deribatua,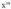 da.x-en ordez u(x) funtzio bat bagenu,
da.x-en ordez u(x) funtzio bat bagenu,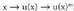 katearen erregelak,
katearen erregelak,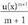 funtzioaren deribatua
funtzioaren deribatua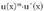 dela ziurtatzen du.
dela ziurtatzen du.
Beraz,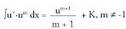
Adibideak (Mota honetako integraletan, ordezkapen metodoaren aplikazioa)
1. Kalkula ezazu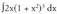 Ebazpidea
Ebazpidea aldaketa egiten bada,
aldaketa egiten bada,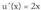 da.Horrela,
da.Horrela,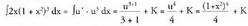 2. Kalkula ezazu
2. Kalkula ezazu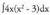 Ebazpidea:
Ebazpidea: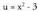 aldaketa egiten bada, orduan
aldaketa egiten bada, orduan da.Baina integralean 2x-en ordez 4x azaltzen da. Hori oso erraz konpontzen da, izan ere,
da.Baina integralean 2x-en ordez 4x azaltzen da. Hori oso erraz konpontzen da, izan ere,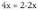 da.
da.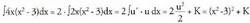 3. Bila ezazu
3. Bila ezazu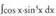 Ebazpidea :
Ebazpidea :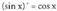 dela kontuan izanik, u = sin x eginez,
dela kontuan izanik, u = sin x eginez,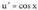 da.
da.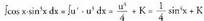 b)
b)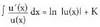 Berehalako integralen zerrendako hirugarrenean,
Berehalako integralen zerrendako hirugarrenean,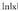 -en deribatua
-en deribatua dela azaltzen da.
dela azaltzen da.
X x-en ordez x-en funtzio bat bagenu, u(x),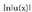 funtzioarenderibatua, katearen erregela aplikatuz,
funtzioarenderibatua, katearen erregela aplikatuz,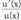 da. Beraz
da. Beraz
Adibideak (Mota honetako integraletan, ordezkapen metodoaren aplikazioa)
1. Kalkula ezazu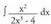 Ebazpidea :
Ebazpidea :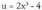 aldaketa egiten bada,
aldaketa egiten bada,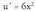 da.Zatikia 6-z biderkatu eta zatitzen da.
da.Zatikia 6-z biderkatu eta zatitzen da.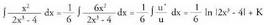 2. Ordezkapen metodoa erabiliz,
2. Ordezkapen metodoa erabiliz,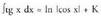 dela egiaztatu.Ebazpidea :
dela egiaztatu.Ebazpidea :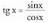 denez, u = cos x aldaketa egiten bada, u' = - sin x da.
denez, u = cos x aldaketa egiten bada, u' = - sin x da.
Orduan funtzioaren deribatua
funtzioaren deribatua funtzio bera da. x-en ordez u(x) funtzioa bagenu,
funtzio bera da. x-en ordez u(x) funtzioa bagenu,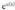 funtzioaren deribatua, katearen erregela aplikatuz,
funtzioaren deribatua, katearen erregela aplikatuz,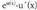 da.Beraz,
da.Beraz,
Adibideak (Funtzio esponentziala ematen duten integraletan ordezkapen metodoa erabiliz)
1. Kalkula ezazu J7x2 ?ex3 dx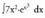 Ebazpidea:Hasteko, 7 konstantea integraletik ateratzen da.
Ebazpidea:Hasteko, 7 konstantea integraletik ateratzen da. aldaketa eginez,
aldaketa eginez, lortzen da.3-z biderkatu eta zatitzen da :
lortzen da.3-z biderkatu eta zatitzen da :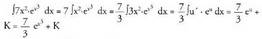 2. Bila ezazu
2. Bila ezazu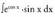 Ebazpidea:u = cos x aldaketa egiten da, orduan u' _ - sin x da.-1-ez biderkatu eta zatitzen da.
Ebazpidea:u = cos x aldaketa egiten da, orduan u' _ - sin x da.-1-ez biderkatu eta zatitzen da.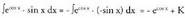 3. Kalkula ezazu
3. Kalkula ezazu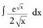 Ebazpidea :
Ebazpidea :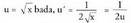 da
da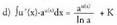 Aurrekoetan egindako azterketen antzeko bat eginez, hau ateratzen
da :
Aurrekoetan egindako azterketen antzeko bat eginez, hau ateratzen
da :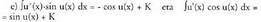 - cos x funtzioaren deribatua sin x da. Katearen erregela aplikatuz, cos u funtzioaren deribatua
- cos x funtzioaren deribatua sin x da. Katearen erregela aplikatuz, cos u funtzioaren deribatua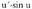 da. Era berean, sin u funtzioaren deribatua
da. Era berean, sin u funtzioaren deribatua da.Horrela lortzen dira :
da.Horrela lortzen dira :
Adibidea (Mota honetako integraletan, aldagai-aldaketa metodoaren aplikazioa)
1. Kalkula ezazu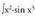 Ebazpidea :inserted text
Ebazpidea :inserted text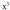 eta
eta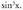 Lehenengoak
Lehenengoak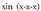 adierazten du, bigarrenak berriz
adierazten du, bigarrenak berriz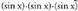 adierazten du.
adierazten du.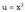 aldaketa egiten da ; orduan
aldaketa egiten da ; orduan da.3-z biderkatu eta zatitzen da.
da.3-z biderkatu eta zatitzen da.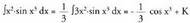 f) Beste kasuak bezala, honako hauek ere erraz froga daitezke :
f) Beste kasuak bezala, honako hauek ere erraz froga daitezke :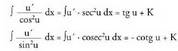 ? Adibideak1. Kalkula ezazu
? Adibideak1. Kalkula ezazu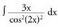 Ebazpidea :3 konstantea integraletik kanpora ateratzen da.
Ebazpidea :3 konstantea integraletik kanpora ateratzen da.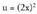 aldaketa egiten da ; orduan u' = 4x da.4-z biderkatu eta zatitzen da.
aldaketa egiten da ; orduan u' = 4x da.4-z biderkatu eta zatitzen da.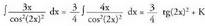 2. Kalkula ezazu
2. Kalkula ezazu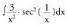 Ebazpidea:3 konstantea integraletik ateratzen da.
Ebazpidea:3 konstantea integraletik ateratzen da.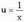 aldaketa egiten da ; orduan
aldaketa egiten da ; orduan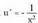 da.
da.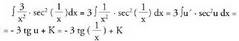 g) u, x-en funtzio bat bada, katearen erregela erabiliz, sec u funtzioa
deribatuz, u' ?sec u ? tg u ateratzen da.Hain zuzen,
g) u, x-en funtzio bat bada, katearen erregela erabiliz, sec u funtzioa
deribatuz, u' ?sec u ? tg u ateratzen da.Hain zuzen,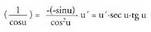 Beraz:
Beraz: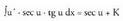 ? Adibideak1. Kalkula ezazu
? Adibideak1. Kalkula ezazu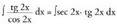 Ebazpidea:u = 2x aldaketa egiten bada, orduan u' = 2 da.2-z biderkatu eta zatitzen da
Ebazpidea:u = 2x aldaketa egiten bada, orduan u' = 2 da.2-z biderkatu eta zatitzen da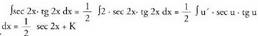 2. Kalkula ezazu
2. Kalkula ezazu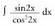 Ebazpidea:
Ebazpidea: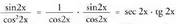 dela kontuan izanik, integral hau aurreko integralera bihurtzen da.Beraz:
dela kontuan izanik, integral hau aurreko integralera bihurtzen da.Beraz: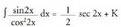 inserted text
inserted text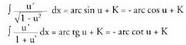 ? Adibideak1. Kalkula ezazu
? Adibideak1. Kalkula ezazu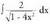 Ebazpidea :
Ebazpidea :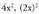 eran idazten da. Horrela argi gelditzen da egin behar den aldaketa u = 2x dela. Orduan, u' = 2 da.
eran idazten da. Horrela argi gelditzen da egin behar den aldaketa u = 2x dela. Orduan, u' = 2 da.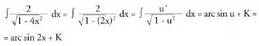 2. Kalkula ezazu
2. Kalkula ezazu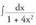 Ebazpidea:
Ebazpidea: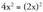 da. u = 2x aldaketa egiten da ; orduan u' = 2 da.2-z biderkatu eta zatitzen da.
da. u = 2x aldaketa egiten da ; orduan u' = 2 da.2-z biderkatu eta zatitzen da.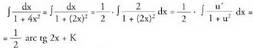 3. Kalkula ezazu
3. Kalkula ezazu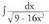 Ebazpidea:Hasteko, integral honek, azken bi kasuen antzik ez duela dirudi,
baina lehenengo kasu bezala ebatzi daiteke.
Ebazpidea:Hasteko, integral honek, azken bi kasuen antzik ez duela dirudi,
baina lehenengo kasu bezala ebatzi daiteke.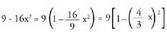 Beraz
Beraz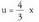 aldaketa egiten da. Orduan
aldaketa egiten da. Orduan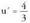 da.
da.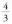 -z biderkatu eta zatitzen da.
-z biderkatu eta zatitzen da. Integratzeko teknika hau maiz erabiltzen da era honetako integralak kalkulatzerakoan.
Integratzeko teknika hau maiz erabiltzen da era honetako integralak kalkulatzerakoan.
4. Bila ezazu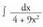 Ebazpidea:
Aurreko adibidean emandako urratsak emanez,
Ebazpidea:
Aurreko adibidean emandako urratsak emanez,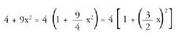 Integral honek bigarren kasuko integralen antza dauka.
Integral honek bigarren kasuko integralen antza dauka.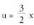 aldaketa egiten da ; orduan
aldaketa egiten da ; orduan .
.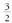 -z biderkatu eta zatitzen da.
-z biderkatu eta zatitzen da.
f Ja 2 - x2 dx erako integralak
Integral hau bi arrazoirengatik azaltzen dugu hemen ; alde batetik,
aldagai-aldaketa baten bidez ebazten delako, eta, bestetik, hurrengo
gaian ikusiko diren eta integral mugatuaren bidez kalkulatzen diren
azalera eta bolumenen kalkulutan sarri azaltzen delako.a konstante bat izanik,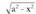 erako integralak ebazteko,
erako integralak ebazteko,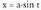 aldagai aldaketa egiten da.Diferentziala eginez,
aldagai aldaketa egiten da.Diferentziala eginez,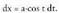 Horrela,
Horrela,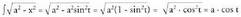 Beraz,
Beraz,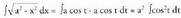 Trigonometrian ikusten denez hau betetzen da :
Trigonometrian ikusten denez hau betetzen da :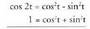 Bi berdintzak atalez atal batuz,
Bi berdintzak atalez atal batuz,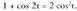 Beraz,
Beraz,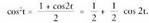 Honen ondorioz
Honen ondorioz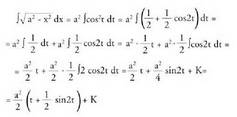 sin 2t = 2 sin t.cos t dela gogoan izanik,
sin 2t = 2 sin t.cos t dela gogoan izanik,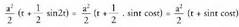 Baina
Baina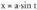 da, orduan
da, orduan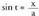 , eta
, eta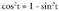 denez,
denez,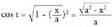 Bestalde,
Bestalde,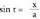 denez,
denez,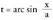 izango da.Azkenik, hona iristen da :
izango da.Azkenik, hona iristen da :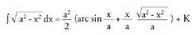 ? Adibidea1. Kalkula ezazu
? Adibidea1. Kalkula ezazu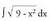 Ebazpidea :Aldagai aldaketa :
Ebazpidea :Aldagai aldaketa :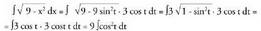 Baina
Baina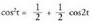 denez,
denez,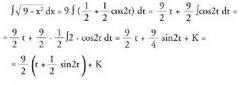 Aldaketa deseginez :
Aldaketa deseginez :
Aldagai aldaketaren bidez lortutako integral berehalakoak
- Ariketak
VI. Zatikako integrazioa
Metodo honen bidez, berehalakoak ez diren integral asko ebatzi
daitezke.Izan bitez u eta v, x aldagaiaren mendeko diren bi funtzio ; hau da
u = f(x) eta v = g(x).Bi funtzioren biderkaduraren deribatua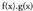 -i aplikatuz, hau ateratzen da :
-i aplikatuz, hau ateratzen da :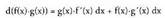 Bi atalak integratuz
Bi atalak integratuz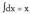 den bezalaxe,
den bezalaxe,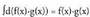 da.Beraz,
da.Beraz,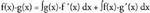 da. Hemendikhau ateratzen da :
da. Hemendikhau ateratzen da :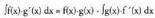 u = f(x) bada, orduan du= f '(x) dx da, eta v = g(x) bada, dv = g' (x)
dx da. Bi emaitza hauek azkeneko berdintzan ordezkatuz,
u = f(x) bada, orduan du= f '(x) dx da, eta v = g(x) bada, dv = g' (x)
dx da. Bi emaitza hauek azkeneko berdintzan ordezkatuz,
Zatikako integral bat ebazteko era
Metodo hau erabiltzen denean, integratu behar den funtzioaren
zati bat "u" bezala, eta beste dena "dv" bezala hartu behar da, eta
bigarren atalean aterako den integralak lehenengo atalean dagoena
baino errazagoa izan behar du. Zati hautaketa egokia egiteko arau
finkorik ez dago. Praktika da kasu honetan, arau hau nola eta noiz
erabili behar den jakiteko erarik hoberena. Dena dela, beti-beti
baliagarriak ez badira ere, hona aholku batzuk :1. Integratu behar den espresioan faktore bezala funtzio trazendente
bat azaltzen bada, eta funtzio honen deribatuaren integrala
eman dutena baino errazagoa bada, funtzio hau u bezala hartuko
da, eta beste dena dv bezala. Hau baliagarria izan daiteke, adibidez,
faktore gisa arc sin x edo In x azaltzen bada.2. Integratu behar den espresioan faktore bezala polinomio bat
azaltzen bada, eta gainerantzekoa integratzerakoan zailtzen ez bada,
polinomioa u bezala hartuko da, eta beste dena dv bezala. Prozesu
hau birritan egiten da, eta polinomioaren maila jaitsiz joaten da,
konstante bihurtu arte. Hau baliagarria da x 3.ex erako funtzioetan.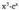 erako funtzioetan.3. Aldaketa bera birritan eginez, edo funtzio arteko baliokidetasunen bat erabiliz, hasierako espresioa bider bata ez den konstante batera iristen bada, zatikako integrazioaren bidez, zuzenean ez bada ere, kalkula daiteke integrala. Horretarako, sortzen den berdintzan hasierako integrala bakandu edo despejatu behar da. Hau baliagarria da
erako funtzioetan.3. Aldaketa bera birritan eginez, edo funtzio arteko baliokidetasunen bat erabiliz, hasierako espresioa bider bata ez den konstante batera iristen bada, zatikako integrazioaren bidez, zuzenean ez bada ere, kalkula daiteke integrala. Horretarako, sortzen den berdintzan hasierako integrala bakandu edo despejatu behar da. Hau baliagarria da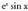 erako funtziotan.4. Azkenik, zatikako integrazioa erabiltzen da, integratu behar den espresioa zenbaki arrunt baten mende, berretzaile baten mende, adibidez, azaltzen denean. Halakoetan, prozesu bera behin eta berriz errepikatuz, n-ren balioa txikituz joaten da. Hau
erako funtziotan.4. Azkenik, zatikako integrazioa erabiltzen da, integratu behar den espresioa zenbaki arrunt baten mende, berretzaile baten mende, adibidez, azaltzen denean. Halakoetan, prozesu bera behin eta berriz errepikatuz, n-ren balioa txikituz joaten da. Hau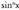 erako integraletan aplikatzen da.? Adibideak1. Kalkula ezazu
erako integraletan aplikatzen da.? Adibideak1. Kalkula ezazu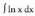 Ebazpidea:Kasurik errazenetako bat da hau. Integralak funtzio bakarra du :
Ebazpidea:Kasurik errazenetako bat da hau. Integralak funtzio bakarra du :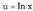 egiten da, diferentziatuz, du
egiten da, diferentziatuz, du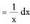 Nahitaez dv = dx izango da. Bi atalak integratuz,
Nahitaez dv = dx izango da. Bi atalak integratuz,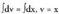 ateratzen da.Formula aplikatuz,
ateratzen da.Formula aplikatuz,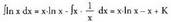 2. Ebatzi
2. Ebatzi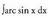 Ebazpidea:Nahitaez u = arc sin x hartu behar da ; orduan du
Ebazpidea:Nahitaez u = arc sin x hartu behar da ; orduan du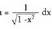 da etadv = dx ; orduan
da etadv = dx ; orduan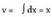 Formula aplikatuz,
Formula aplikatuz,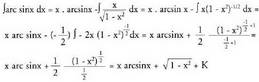 3. Kalkula ezazu
3. Kalkula ezazu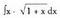 Ebazpidea :u = x egiten da ; orduan du = dx da, eta
Ebazpidea :u = x egiten da ; orduan du = dx da, eta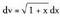 izango da ; orduan
izango da ; orduan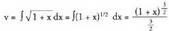 Formula aplikatuz:
Formula aplikatuz: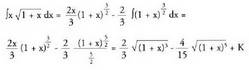 4. Bila ezazu
4. Bila ezazu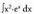 Ebazpidea:
Ebazpidea: egiten da, diferentziala kalkulatuz, du = 2x dx ateratzen daBestalde
egiten da, diferentziala kalkulatuz, du = 2x dx ateratzen daBestalde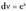 , integrala kalkulatuz,
, integrala kalkulatuz,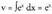 Formula aplikatuz,
Formula aplikatuz,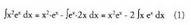 zatikako integrazio metodoa berriro erabiliz integratzen da.
zatikako integrazio metodoa berriro erabiliz integratzen da.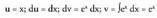 Horrela,
Horrela,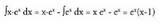 Emaitza hau (1) integralean ordezkatuz,
Emaitza hau (1) integralean ordezkatuz,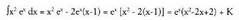 5. Kalkula ezazu
5. Kalkula ezazu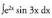 Ebazpidea :Hasteko u = sin 3x hartzen da, beraz du = 3 cos 3x dx da, eta
Ebazpidea :Hasteko u = sin 3x hartzen da, beraz du = 3 cos 3x dx da, eta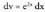 hartzen da, integrala eginez
hartzen da, integrala eginez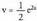 da.Formula aplikatuz,
da.Formula aplikatuz,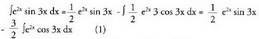 Gelditzen den integrala,
Gelditzen den integrala,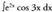 , zatikako integrazio metodoa erabiliz integratzen da berriro.Oraingo honetan ere, u = cos 3x hartzen da ; orduan du = - 3 sin
3x dx da, eta
, zatikako integrazio metodoa erabiliz integratzen da berriro.Oraingo honetan ere, u = cos 3x hartzen da ; orduan du = - 3 sin
3x dx da, eta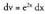 dv = e2x dx hartzen da, integrala eginez v =
2
e 2 x da.
dv = e2x dx hartzen da, integrala eginez v =
2
e 2 x da.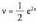 da.(Alderantziz hartu izan bagenitu, hau da
da.(Alderantziz hartu izan bagenitu, hau da eta
eta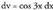 hartu izan bagenitu, hasierako espresiora itzuliko ginateke, ezer aurreratu gabe)Berriro formula aplikatuz,
hartu izan bagenitu, hasierako espresiora itzuliko ginateke, ezer aurreratu gabe)Berriro formula aplikatuz,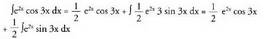 Emaitza hau (1) integralean ordezkatuz,
Emaitza hau (1) integralean ordezkatuz,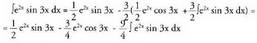 Integrala lehenengo atalera pasatuz :
Integrala lehenengo atalera pasatuz :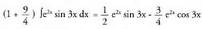 Eta integrala bakanduz, emaitza lortzen da :
Eta integrala bakanduz, emaitza lortzen da :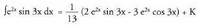 6. Bila ezazu
6. Bila ezazu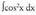 Ebazpidea :u eta dv honela hartzen dira :u = cos x ; orduan du = -sin x dx, etadv = cos x dx ; orduan v = sin xFormula aplikatuz :
Ebazpidea :u eta dv honela hartzen dira :u = cos x ; orduan du = -sin x dx, etadv = cos x dx ; orduan v = sin xFormula aplikatuz :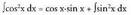 Orain
Orain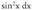 integrala kalkulatu behar da ; baina berriro zatikako metodoa erabiliz integrala kalkulatzeko ordez, eta
integrala kalkulatu behar da ; baina berriro zatikako metodoa erabiliz integrala kalkulatzeko ordez, eta denez, integralean ordezkatzen da :
denez, integralean ordezkatzen da :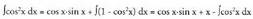 Integrala lehenengo atalera pasatuz :
Integrala lehenengo atalera pasatuz : Eta integrala bakanduz :
Eta integrala bakanduz :
- Ariketak
4. Bila itzazu :
VII. Funtzio razionalen integrazioa
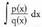 erako integralak ebatzi behar dira, p(x) eta q (x) poliomioak direla.Oro har, polinomioetan, p(x) zatikizuna bada, q(x) zatitzailea,
z(x) zatidura eta h(x) hondarra bada,
erako integralak ebatzi behar dira, p(x) eta q (x) poliomioak direla.Oro har, polinomioetan, p(x) zatikizuna bada, q(x) zatitzailea,
z(x) zatidura eta h(x) hondarra bada,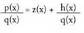 Beraz,
Beraz,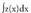 polinomio baten integrala da.
polinomio baten integrala da.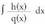 berehalakoabalitz, integrala ebatzita legoke.? Adibideak1. Kalkula ezazu
berehalakoabalitz, integrala ebatzita legoke.? Adibideak1. Kalkula ezazu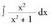 Ebazpidea :
Ebazpidea :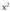 polinomioa eta
polinomioa eta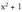 polinomioaren arteko zatiketa egiten da :
polinomioaren arteko zatiketa egiten da :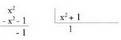 Zatidura 1 da, eta hondarra - 1.
Zatidura 1 da, eta hondarra - 1.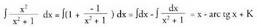 2. Bila ezazu
2. Bila ezazu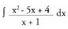 Ebazpidea:Polinomioen arteko zatiketa egiten da
Ebazpidea:Polinomioen arteko zatiketa egiten da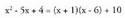 Zatidura x - 6 da, eta hondarra 10.
Zatidura x - 6 da, eta hondarra 10.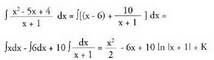
Zatiki sinpletan deskonposatzea
Zatiki sinple bat polinomioz osatutako zatiki bat da, baina zenbakitzailearen mailak, hertsiki, izendatzailearen maila baino txikiagoa izan behar du, eta izendatzaileak erakoa edo
erakoa edo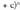 erakoa,
erakoa,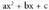 polinomioak erro edo soluzio errealik ez badu, n zenbaki arrunta delarik.
polinomioak erro edo soluzio errealik ez badu, n zenbaki arrunta delarik.
Horrela,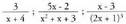 ; zatiki sinpleak dira.
; zatiki sinpleak dira.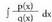 erako integralen aterketa egiterakoan, p(x) zenbakitq (x) zailearen maila q(x) izendatzailearen maila baino txikiagoa dela hartuko da abiaburutzat. Zenbakitzailearen maila izendatzailearen mailaren berdina edo handiagoa balitz, p(x) eta q(x)-en arteko zatiketa egin beharko litzateke, eta z(x) zatidura eta h(x) hondarra aterako
erako integralen aterketa egiterakoan, p(x) zenbakitq (x) zailearen maila q(x) izendatzailearen maila baino txikiagoa dela hartuko da abiaburutzat. Zenbakitzailearen maila izendatzailearen mailaren berdina edo handiagoa balitz, p(x) eta q(x)-en arteko zatiketa egin beharko litzateke, eta z(x) zatidura eta h(x) hondarra aterako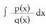 integrala
integrala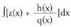 integralean bihurtzen da.
integralean bihurtzen da.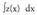 polinomio baten integrala denez, berehalakoa da, eta
polinomio baten integrala denez, berehalakoa da, eta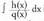
Zatiki sinpletan deskonposatze bidezko integrazioa
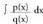 erako integralak ebazteko honela egiten da :
1. q(x) polinomioaren faktorketa egiten da, horretarako q(x) = 0 ekuazioaren erro edo soluzioak bilatzen dira.2. Adibidetan ikusiko den eran,
erako integralak ebazteko honela egiten da :
1. q(x) polinomioaren faktorketa egiten da, horretarako q(x) = 0 ekuazioaren erro edo soluzioak bilatzen dira.2. Adibidetan ikusiko den eran,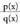 zatikia, zatiki sinpleenbatura bezala deskonposatzen da.3. Ateratzen diren batugaien integralak kalkulatzen dira.Baina q(x) = 0 egiterakoan hiru erako emaitzak atera daitezke :- erro edo soluzio bakunak, sinpleak (soluziorik ez da errepikatzen).- erro edo soluzio anizkoitzak (gutxienez soluzio bat errepikatzen da).- erro edo soluzio irudikariak (zenbaki konplexuak).Kasu bakoitza bere aldetik ikasi behar da.A) Erro erreal sinpleak ateratzen direnean.q(x)-en erro sinpleak
zatikia, zatiki sinpleenbatura bezala deskonposatzen da.3. Ateratzen diren batugaien integralak kalkulatzen dira.Baina q(x) = 0 egiterakoan hiru erako emaitzak atera daitezke :- erro edo soluzio bakunak, sinpleak (soluziorik ez da errepikatzen).- erro edo soluzio anizkoitzak (gutxienez soluzio bat errepikatzen da).- erro edo soluzio irudikariak (zenbaki konplexuak).Kasu bakoitza bere aldetik ikasi behar da.A) Erro erreal sinpleak ateratzen direnean.q(x)-en erro sinpleak inserted text
inserted text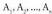 zehaztu behar diren konstanteak dira. Ikusi daitekeenez, ateratzen diren integralak berehalakoak dira.? Adibidea1. Kalkula ezazu
zehaztu behar diren konstanteak dira. Ikusi daitekeenez, ateratzen diren integralak berehalakoak dira.? Adibidea1. Kalkula ezazu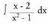 Ebazpidea:
Ebazpidea: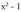 izendatzailearen erroak hauek dira :
izendatzailearen erroak hauek dira :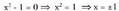 Beraz, bi erro sinple desberdin ditu : 1 eta - 1.
Beraz, bi erro sinple desberdin ditu : 1 eta - 1.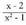 zatiki sinpletan deskonposatzen da :
zatiki sinpletan deskonposatzen da :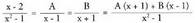 Izendatzaileak berdinak direnez, zenbakitzaileek ere berdinak
izan behar dute :
Izendatzaileak berdinak direnez, zenbakitzaileek ere berdinak
izan behar dute :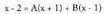 A eta B mugatzeko x-ri balioak emango dizkiogu :
A eta B mugatzeko x-ri balioak emango dizkiogu :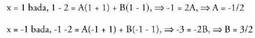 x-ri nahi den balio eman diezaiokegu, baina kalkuluak errazteko,
batugaietariko bat anulatzen duen balioa eman zaio. Prozedura hau
oso hedatua dago.Horrela bada:
x-ri nahi den balio eman diezaiokegu, baina kalkuluak errazteko,
batugaietariko bat anulatzen duen balioa eman zaio. Prozedura hau
oso hedatua dago.Horrela bada: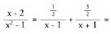 Beraz :
Beraz :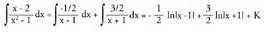 B) Erro erreal anizkoitzak ateratzen direnean.a erroa n aldiz errepikatzen bada,
B) Erro erreal anizkoitzak ateratzen direnean.a erroa n aldiz errepikatzen bada,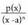 zatikiaren deskonposatzea zatiki sinpletan hau da :
zatikiaren deskonposatzea zatiki sinpletan hau da :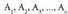 orain ere, zehaztu behar diren konstanteak dira.
orain ere, zehaztu behar diren konstanteak dira.
Berriro ere,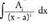 erako integralak berehalakoak dira.? Adibidea1. Kalkula ezazu
erako integralak berehalakoak dira.? Adibidea1. Kalkula ezazu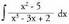 Ebazpidea:Zenbakitzailearen maila (2), izendatzailearena (3) baino txikiagoa
denez, ez da polinomio arteko zatiketarik egin behar.
Ebazpidea:Zenbakitzailearen maila (2), izendatzailearena (3) baino txikiagoa
denez, ez da polinomio arteko zatiketarik egin behar.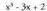 polinomioaren erroak Ruffiniren erregela erabiliz lortzen dira :
polinomioaren erroak Ruffiniren erregela erabiliz lortzen dira : Polinomioak erro sinple bat, -2, eta erro anizkoitz (bikoitz) bat, 1, du.Emandako zatikia honela deskonposatzen da zatiki sinpletan :
Polinomioak erro sinple bat, -2, eta erro anizkoitz (bikoitz) bat, 1, du.Emandako zatikia honela deskonposatzen da zatiki sinpletan :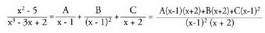 Lehengo kasuan bezalaxe, zenbakitzaileak berdindu egiten dira,
eta A, B eta C zehazteko, x-ri balio arbitrarioak ematen zaizkio.
Lehengo kasuan bezalaxe, zenbakitzaileak berdindu egiten dira,
eta A, B eta C zehazteko, x-ri balio arbitrarioak ematen zaizkio.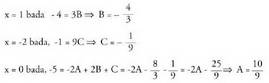 Beraz
Beraz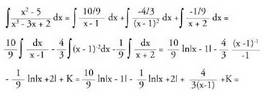 C) Erro irudikariak ateratzen direnean.Koefiziente errealak dituen polinomio baten erro irudikari
C) Erro irudikariak ateratzen direnean.Koefiziente errealak dituen polinomio baten erro irudikari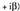 bat badu, bere konjokatua
bat badu, bere konjokatua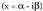 ere, polinomioaren erro da.
ere, polinomioaren erro da.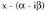 eta
eta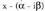 arteko biderkaketa egiten bada, hau lortzen da:
arteko biderkaketa egiten bada, hau lortzen da: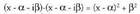 (i zenbaki irudikiariak
(i zenbaki irudikiariak egiaztatzen du).
egiaztatzen du).
Erro irudikari konjokatu bikote bakoitzak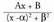 erako zatikisinple bat eratzen du, beraz, kasu honetan honako hau ulatu behar da :
erako zatikisinple bat eratzen du, beraz, kasu honetan honako hau ulatu behar da :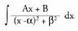 1. Zenbakitzaileari Aa gehitu eta kentzen zaio eta jarraian azaltzen
den bezala bi integraletan deskonposatzen da :
1. Zenbakitzaileari Aa gehitu eta kentzen zaio eta jarraian azaltzen
den bezala bi integraletan deskonposatzen da :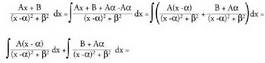 Bi integral hauek berehalako integral bihurtzen dira aldagai-aldaketa bat eginez gero.2.
Bi integral hauek berehalako integral bihurtzen dira aldagai-aldaketa bat eginez gero.2.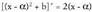 delako,
delako,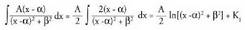 3.
3.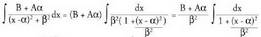 Baina
Baina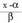 -ren deribatua
-ren deribatua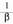 delako,
delako,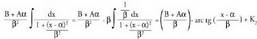 4. Bukatzeko :
4. Bukatzeko :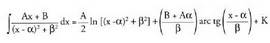 (
(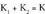 egiten delarik)Hirugarren kasu hau izendatzaileko erro irudikariak sinpleak
direnean bakarrik landuko da.? Adibidea1. Kalkula ezazu
egiten delarik)Hirugarren kasu hau izendatzaileko erro irudikariak sinpleak
direnean bakarrik landuko da.? Adibidea1. Kalkula ezazu Ebazpidea :
Ebazpidea :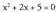 bigarren mailako ekuazioa ebazterakoan, -1 + 2i eta -1 - 2i soluzioak lortu dira, beraz
bigarren mailako ekuazioa ebazterakoan, -1 + 2i eta -1 - 2i soluzioak lortu dira, beraz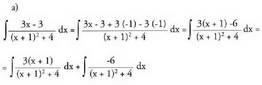 Integral bakoitza bere aldetik ebazten da
Integral bakoitza bere aldetik ebazten da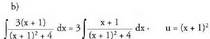 egiten bada,egiten bada,u'=2(x+1)daBeraz
egiten bada,egiten bada,u'=2(x+1)daBeraz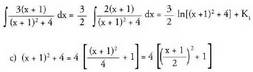 inserted text
inserted text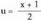 egiten badu
egiten badu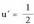 da, eta
da, eta -z biderkatu eta zatituz :
-z biderkatu eta zatituz :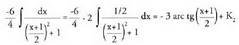 d) b) eta c) ataletan ateratako emaitzak batuz, eta
d) b) eta c) ataletan ateratako emaitzak batuz, eta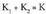 eginez :
eginez :
- Ariketak
4. Bila itzazu :
VIII. Laburketa formulak
Integral batzuk ezin dira ebatzi azaldutako metodoak erabiliz,baina n zenbaki arrunta baten mende dauden zenbait integral,laburketa deritzan formula batzuen bidez ebatzi daitezke. Kasuhauetan, nahitaez, n - 1 edo n - 2 denean integrala ebazten jakinbehar da.
integralaren kalkulua
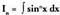 Ikusten denez,
Ikusten denez,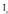 -ren n azpindizea,
-ren n azpindizea,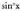 berretzailearekin bat dator.Jakina denez,
berretzailearekin bat dator.Jakina denez,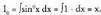 eta
eta -ri dagokion laburketa formula aurkitzeko zatikako integrazio metodoa erabiliko da :
-ri dagokion laburketa formula aurkitzeko zatikako integrazio metodoa erabiliko da :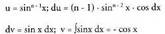 Beraz,
Beraz,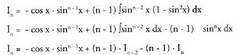 -
-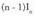 lehenengo atalera pasatuz, eta
lehenengo atalera pasatuz, eta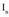 bakanduz,
bakanduz,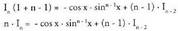 Eta beraz,
Eta beraz,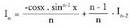 Horrela
Horrela
integralaren kalkulua
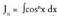 kalkulatzeko cos x = sin(90º - x) egiten da, eta era horretara aurreko kasu berean gaude.Ebazteko, 90° - x = y aldagai aldaketa egiten da; orduan dx = - dy
da eta hau lortzen da :
kalkulatzeko cos x = sin(90º - x) egiten da, eta era horretara aurreko kasu berean gaude.Ebazteko, 90° - x = y aldagai aldaketa egiten da; orduan dx = - dy
da eta hau lortzen da :
integralaren kalkulua
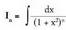 Zenbakitzaileari xz gehitu eta kenduz,
Zenbakitzaileari xz gehitu eta kenduz,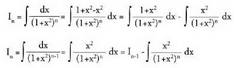 Bigarren integrala zatikako integrazio metodoa erabiliz ebatzi
behar da:
Bigarren integrala zatikako integrazio metodoa erabiliz ebatzi
behar da: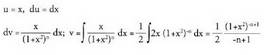 Eta beraz,
Eta beraz,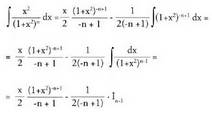 (1) adierazpenean ordezkatuz, hau ateratzen da :
(1) adierazpenean ordezkatuz, hau ateratzen da :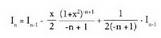 Eragiketak eginez :
Eragiketak eginez :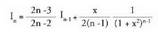 n = 1, 2 eta 3 denean, emaitza hauek lortukoonlYrateke :
n = 1, 2 eta 3 denean, emaitza hauek lortukoonlYrateke :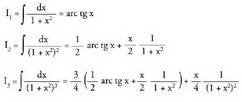
- Ariketak
4. Bila itzazu:
Soluzioak