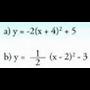Matematika»Analisiak
Oinarrizko funtzioak
I. Sarrera
Gai honetan oinarrizko funtzio batzuk aztertuko dira. Lehenbizi
funtzio konstanteak ikusten dira, garrantzi handikoak baitira beste
funtzioekin batu eta kendu daitezkelako funtzio berriak sortzeko.
Ondoren funtzio linealak aztertuko dira; garrantzi handia dute proportzionaltasun
zuzena aztertzeko, eta gainera, bi ezezaguneko
ekuazio linealen interpretazio grafikoa egiteko balio dute.Ondoren bigarren mailako funtzio polinomikoak aztertzen dira.
Funtzio horien grafikoa parabola bat da. Funtzio linealekin batera
aztertzean, bigarren mailako sistemen adierazpen grafikoak interpretatzeko
balioko dute. Horiekin amaitzen da oraingoz funtzio
polinomikoen azterketa.Ondoren proportzionaltasun alderantzizkoaren funtzioa eta
funtzio horri funtzio konstante bat batzean edo funtzio konstante
batekin konposatzean ateratzen diren funtzioak aztertzen dira.Gaiaren osagarri bezala beste funtzio mota batzuk azaltzen dira : erakoak, y = E(x) zati osoaren funtzioa,
erakoak, y = E(x) zati osoaren funtzioa,
I I. Funtzio konstantea
Funtzio konstanteak zero mailako polinomio baten bidez definiturik
daude : f(x)=kFuntzio horren bidez, edozein baliori k zenbaki berdina dagokio
edozein baliori k zenbaki berdina dagokio Adibidea
Adibidea
Proportzionaltasun zuzenaren funtzioa
Bi aldagaiak proportzionalak dituzten funtzioak dira. Produktu
batetik ordaindu behar den B.E.Z-a prezioaren funtzioa da ; bi
kopuru horiek proportzionalak dira, produktu baten prezioa erositako
kantitatearen funtzioa da, etab.1. adibideaEspainian, produktu askoren B.E.Z-a salneurriaren %16-a da.
Kalkulatu, gaiaren salneurria jakinda, zein adierazpenen bitartez
ezagutu daitekeen B.E.Z-a.EbazpenaBitez x salneurria eta y ordaindu beharreko B.E.Z.-a. y = x-en %16-a da, hau da, y = 0´16 x. Hortaz, da proportzionaltasun konstantea.2. adibideaAuto bat 80 kilometro orduko lastertasunean doa. Zein erlazio
dago horretarako behar izan den denboraren (ordutan) eta egindako
bidearen (kilometrotan) artean?EbazpenaDistantziari e eta denborari t esanez gero, e = 80 t. Kasu honetan
80 da proportzionaltasun konstantea.Lortutako ekuaziotik abiatuta, ibilitako distantzia atera daiteke
t aldagaiaren balio desberdinetarako. Hala, balio taula bat ateratzen
da :
da proportzionaltasun konstantea.2. adibideaAuto bat 80 kilometro orduko lastertasunean doa. Zein erlazio
dago horretarako behar izan den denboraren (ordutan) eta egindako
bidearen (kilometrotan) artean?EbazpenaDistantziari e eta denborari t esanez gero, e = 80 t. Kasu honetan
80 da proportzionaltasun konstantea.Lortutako ekuaziotik abiatuta, ibilitako distantzia atera daiteke
t aldagaiaren balio desberdinetarako. Hala, balio taula bat ateratzen
da : Balio horiek ardatz koordenatu ortogonaletan adieraz daitezke,
denbora (aldagai askea) abzisa ardatzean jartzen da, eta distantzia
ordenatu ardatzean.Beraz :Proportzionaltasun funtzioa y=mx ekuazioak ematen du. Funtzioa aztertzeko m-ren balio desberdinei dagozkien grafikoak egiten dira.
Balio horiek ardatz koordenatu ortogonaletan adieraz daitezke,
denbora (aldagai askea) abzisa ardatzean jartzen da, eta distantzia
ordenatu ardatzean.Beraz :Proportzionaltasun funtzioa y=mx ekuazioak ematen du. Funtzioa aztertzeko m-ren balio desberdinei dagozkien grafikoak egiten dira.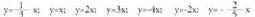 adieraziko dira, eta horretarako balio taulak egingo dira.
adieraziko dira, eta horretarako balio taulak egingo dira.
y = mx + n funtzio afina
y = mx funtzioari y = n funtzio konstantea batzen bazaio, funtzio
afina ateratzen da. Horren ekuazioa "y = mx + n" da. Grafikoa eta
haren parametroen interpretazioa aztertuko da orain.Ardatz berdinetan y = 2x, y = 2x - 2, y = 2x + 3, eta y = 2x - 5 adieraziz
gero, horien grafikoak lerro zuzen paraleloak direla ikusten
da, izan ere malda berdina baitute : guztietan m = 2. Gainera x = 0
denean, y-k n balioa hartzen du eta hori dela eta, parametro horri
jatorrian ordenatua esaten zaio. P (0,n) puntua zuzenaren eta y
ardatzaren arteko ebakidura puntua da. eta
eta funtzioen grafikok eginez gero.
funtzioen grafikok eginez gero.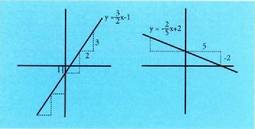
Zuzen baten ekuazioa puntu bat eta malda ezagututa
Orain artekoaren arabera, grafikoa lortzeko, funtzioaren ekuaziotik abiatu eta balio taula bat egiten da; guztien adierazpen grafikoa zuzen bat izango da. Baina bada beste bide bat. Demagun zuzeneko malda m eta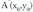 puntua ezagutzen direla eta ekuazioa eta dagokion funtzioa ezagutu nahi direla.Bedi P(x,y) zuzeneko edozein puntu ; 4c irudian ikus daiteke A P- ra pasatzean x-en gehikuntza
puntua ezagutzen direla eta ekuazioa eta dagokion funtzioa ezagutu nahi direla.Bedi P(x,y) zuzeneko edozein puntu ; 4c irudian ikus daiteke A P- ra pasatzean x-en gehikuntza dela eta y-ri dagokion gehikuntza
dela eta y-ri dagokion gehikuntza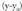 dela ; hortaz, aurreko atalean ikusitakoaren arabera, m malda
dela ; hortaz, aurreko atalean ikusitakoaren arabera, m malda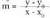 eginez ateratzen da;
eginez ateratzen da; m malda da,eta
m malda da,eta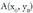 puntutik pasatzen den zuzenaren ekuazioa. Dagokion funtzioaren ekuazioa ateratzeko y bakantzen da.
puntutik pasatzen den zuzenaren ekuazioa. Dagokion funtzioaren ekuazioa ateratzeko y bakantzen da. Adibideak1. Bilatu funtzio baten ekuazioa, kontuan harturik grafikoa zuzen
bat dela A(-3, 1) puntutik pasatzen dena, eta malda -4 duela.Ebazpena
Adibideak1. Bilatu funtzio baten ekuazioa, kontuan harturik grafikoa zuzen
bat dela A(-3, 1) puntutik pasatzen dena, eta malda -4 duela.Ebazpena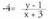 berdintzatik hasten da,eta y bakanduz y = 1 - 4(x + 3) lortzen da, hau da, y = -4x - 11 ;
malda -4 da eta jatorriaren ordenatua -11.2. Bilatu funtzio baten ekuazioa, funtzio horren grafikoa A(-1,3)
eta B(2,1) puntuetatik doan zuzena dela kontuan hartuta.EbazpenaMalda lortzeko y-ren gehikuntzaren eta x-en gehikuntzaren
(A-tik B-ra pasatzerakoan gertatutakoa) arteko zatiketa egiten da.
berdintzatik hasten da,eta y bakanduz y = 1 - 4(x + 3) lortzen da, hau da, y = -4x - 11 ;
malda -4 da eta jatorriaren ordenatua -11.2. Bilatu funtzio baten ekuazioa, funtzio horren grafikoa A(-1,3)
eta B(2,1) puntuetatik doan zuzena dela kontuan hartuta.EbazpenaMalda lortzeko y-ren gehikuntzaren eta x-en gehikuntzaren
(A-tik B-ra pasatzerakoan gertatutakoa) arteko zatiketa egiten da. formula erabili da, (xO, y0) bezala A hartuz (B hartuta ere egin daiteke) ;
formula erabili da, (xO, y0) bezala A hartuz (B hartuta ere egin daiteke) ;
- Ariketak
1. Ondoko funtzioetan esan zein den malda, eta jatorriaren
ordenatua eta grafikoa egin. 2. Ondoko funtzio afinen ekuazioa bilatu.a) A(2,-3) puntutik doa eta
2. Ondoko funtzio afinen ekuazioa bilatu.a) A(2,-3) puntutik doa eta
Funtzio kuadratikoa
Horrela esaten zaio definitzen duen ekuazioaren 2. atala 2. mailako polinomioa delako. Hau da da.Funtzio kuadratiko sinpleena hau da :
da.Funtzio kuadratiko sinpleena hau da : Funtzio horri dagokion grafikoari parabola esaten zaio. Ezaugarri
hauek ditu :Funtzio bikoiti bat da, f(-x) = f(x) baita; horregatik, y ardatzarekiko
simetrikoa du grafikoa.• O(0,0) puntua, funtzioak minimo erlatiboa duena, parabolaren erpina da.• Funtzioa hertsiki beherakorra da
Funtzio horri dagokion grafikoari parabola esaten zaio. Ezaugarri
hauek ditu :Funtzio bikoiti bat da, f(-x) = f(x) baita; horregatik, y ardatzarekiko
simetrikoa du grafikoa.• O(0,0) puntua, funtzioak minimo erlatiboa duena, parabolaren erpina da.• Funtzioa hertsiki beherakorra da tartean, eta hertsiki gorakorra
tartean, eta hertsiki gorakorra
y = x2 + c funtzioa
 funtzioari y = c konstantea gehituz ateratzen da.
funtzioari y = c konstantea gehituz ateratzen da.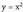 -ren bidez ere lor daiteke
-ren bidez ere lor daiteke bektore traslazioa eginez.Hala,
bektore traslazioa eginez.Hala, -ren grafikoa lortzen da
-ren grafikoa lortzen da -ren grafikotik abiatuta eta puntu guztiak hiru banako jasoz.
-ren grafikotik abiatuta eta puntu guztiak hiru banako jasoz.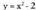 grafikoa,
grafikoa, -ren grafikotik abiatuta, puntu guztiak bi banako jaitsiz ateratzen da.
-ren grafikotik abiatuta, puntu guztiak bi banako jaitsiz ateratzen da.
y = (x - p) 2 funtzioa
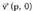 bektoretzat duen traslazioa eginez eta
bektoretzat duen traslazioa eginez eta funtziotikabiatuta atera daiteke.
funtziotikabiatuta atera daiteke. Hain zuzen ere, egiazta daiteke V(p, 0) puntua duela erpina, horixe
baita funtzioaren minimoa.
Hain zuzen ere, egiazta daiteke V(p, 0) puntua duela erpina, horixe
baita funtzioaren minimoa. funtzioaren y-ren balioak negatiboak ez direnez gero, balio minimoa y = 0 izango da, eta hori x = p-rako gertatzen da.• Simetria ardatza x = p zuzena du.• Funtzioa beherakorra da
funtzioaren y-ren balioak negatiboak ez direnez gero, balio minimoa y = 0 izango da, eta hori x = p-rako gertatzen da.• Simetria ardatza x = p zuzena du.• Funtzioa beherakorra da tartean, eta gorakorra
tartean, eta gorakorra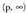 tartean.• Grafikoaren forma
tartean.• Grafikoaren forma -renaren berdina da.AdibideaBilatu ondoko funtzio hauen erpina, simetria ardatza eta grafikoa
.
-renaren berdina da.AdibideaBilatu ondoko funtzio hauen erpina, simetria ardatza eta grafikoa
.
y = (x - p) 2 + q funtzioa
Funtzio hau, funtzioari
funtzioari bektoretzat duen traslazioa eginez ateratzen da; edo
bektoretzat duen traslazioa eginez ateratzen da; edo funtziotik abiatuz,
funtziotik abiatuz, bektorearen traslazioaren bidez.
bektorearen traslazioaren bidez. Egiazta daiteke, beraz, funtzio horren erpina V (p, q) puntua dela, eta horixe da funtzioaren balio minimoa. q konstantea denez, minimoa
Egiazta daiteke, beraz, funtzio horren erpina V (p, q) puntua dela, eta horixe da funtzioaren balio minimoa. q konstantea denez, minimoa balio txikienentzat lortuko da, eta adierazpen hori negatiboa ez denez balio txikiena zero izango du, eta horretarako egiaztatu behar da x = p. x-en balio horretarako, y = q ; hortaz erpina V(p, q) da.Hala, funtzio honen grafikoa
balio txikienentzat lortuko da, eta adierazpen hori negatiboa ez denez balio txikiena zero izango du, eta horretarako egiaztatu behar da x = p. x-en balio horretarako, y = q ; hortaz erpina V(p, q) da.Hala, funtzio honen grafikoa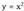 -ren grafikoa p banako eskubira (ezkerrea p < 0 bada) eta q banako gora (behera q < 0 bada) eramanez ateratzen da.• Simetria ardatza x = p zuzena da.• Funtzioa beherakorra da
-ren grafikoa p banako eskubira (ezkerrea p < 0 bada) eta q banako gora (behera q < 0 bada) eramanez ateratzen da.• Simetria ardatza x = p zuzena da.• Funtzioa beherakorra da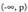 -n eta gorakorra
-n eta gorakorra -n.• Grafikoaren forma
-n.• Grafikoaren forma -renaren berdina da.Adibidea
-renaren berdina da.Adibidea funtzioen erpina, simetria ardatza eta grafikoa bilatu.
funtzioen erpina, simetria ardatza eta grafikoa bilatu.
y = ax 2 funtzioa. "a" parametroa
"a" parametroak funtzioaren grafikoan duen eragina ulertzeko, a-ren
balioa desberdina duten zenbait funtzioaren grafikoak eginez hasiko
gara.a < 0 kasuetatik hasita : grafikoak ematen dira.
grafikoak ematen dira. Ikusten denez a-ren balioa handitu ahala, y-ren hazkuntza
Ikusten denez a-ren balioa handitu ahala, y-ren hazkuntza tartean bizkorragoa da, eta aldi berean y-ren txikitzea bizkorragoa da
tartean bizkorragoa da, eta aldi berean y-ren txikitzea bizkorragoa da tartean. Beraz, a-ren balioa zenbat eta txikiagoa izan, orduan eta zapalagoa izango da parabola, eta a-ren balioa zenbat eta handiagoa izan, orduan eta estuagoa da parabola.Parabola horiek guztiak O(0, 0) puntuan dute erpina eta
tartean. Beraz, a-ren balioa zenbat eta txikiagoa izan, orduan eta zapalagoa izango da parabola, eta a-ren balioa zenbat eta handiagoa izan, orduan eta estuagoa da parabola.Parabola horiek guztiak O(0, 0) puntuan dute erpina eta tartean beherakorrak dira eta
tartean beherakorrak dira eta -n gorakorrak, hau da, erpina funtzioaren minimo erlatibo bat da.a < 0 kasua aztertzeko a-ren balio desberdinetarako
-n gorakorrak, hau da, erpina funtzioaren minimo erlatibo bat da.a < 0 kasua aztertzeko a-ren balio desberdinetarako motako funtzioen grafikoak egingo dira.
motako funtzioen grafikoak egingo dira.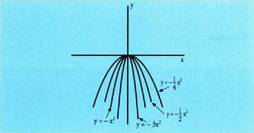 Ikusten denez, guztiek O (0, 0)-an dute erpina.• Hertsiki gorakorrak dira
Ikusten denez, guztiek O (0, 0)-an dute erpina.• Hertsiki gorakorrak dira -an• Hertsiki beherakorrak dira
-an• Hertsiki beherakorrak dira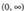 -an• a-ren balioa zerotik zenbat eta gertuago egon, orduan eta makalagoa
izango da gorakortasuna eta beherakortasuna.•
-an• a-ren balioa zerotik zenbat eta gertuago egon, orduan eta makalagoa
izango da gorakortasuna eta beherakortasuna.• zenbat eta handiagoa izan, orduan eta arinagoa izango da gorakortasuna eta beherakortasuna.• Erpina funtzioaren maximo erlatibo bat da.Hortaz, a-ren balioak finkatzen du parabolaren forma.
zenbat eta handiagoa izan, orduan eta arinagoa izango da gorakortasuna eta beherakortasuna.• Erpina funtzioaren maximo erlatibo bat da.Hortaz, a-ren balioak finkatzen du parabolaren forma.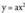 -tik abiatuz, eta traslazioz, hau lortzen da, hurrenez hurren :
-tik abiatuz, eta traslazioz, hau lortzen da, hurrenez hurren : bektoreko traslazioa aplikatzean
bektoreko traslazioa aplikatzean bektoreko traslazioa aplikatzean
bektoreko traslazioa aplikatzean bektoreko traslazioa aplikatzeanHortaz, a-ren balio berdinerako, parabolek forma bera dute, eta
kokaeraren arabera bereizten dira ; erpinak mugatzen du kokaera.Hala,
bektoreko traslazioa aplikatzeanHortaz, a-ren balio berdinerako, parabolek forma bera dute, eta
kokaeraren arabera bereizten dira ; erpinak mugatzen du kokaera.Hala, , erpina E(0, c)-n du.
, erpina E(0, c)-n du. , erpina E(p, 0)-n du.
, erpina E(p, 0)-n du. , erpina E(p, q)-n duLaburtuz :• a > 0 bada, erpina minimo erlatiboa izango da, eta parabolaren
adarrak gorantz egongo dira.• a < 0 bada, erpina maximo erlatiboa izango da, eta parabolaren
adarrak beherantz egongo dira.Ariketa ebatziak1) Balio taula bat egin
, erpina E(p, q)-n duLaburtuz :• a > 0 bada, erpina minimo erlatiboa izango da, eta parabolaren
adarrak gorantz egongo dira.• a < 0 bada, erpina maximo erlatiboa izango da, eta parabolaren
adarrak beherantz egongo dira.Ariketa ebatziak1) Balio taula bat egin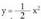 parabola irudikatzeko. Egin grafiko hauek parabolaren arabera :
parabola irudikatzeko. Egin grafiko hauek parabolaren arabera : Ebazpena
Ebazpena 2) Taula bat egin
2) Taula bat egin parabola irudikatzeko, eta parabolatik abiaturik, grafiko hauek egin :
parabola irudikatzeko, eta parabolatik abiaturik, grafiko hauek egin : Ebazpena
Ebazpena Kasu orokorraBedi funtzio koadratiko hau :
Kasu orokorraBedi funtzio koadratiko hau : Parabola horren erpina aurkitzeko,
Parabola horren erpina aurkitzeko, eran adierazi behar da bigarren atala.Ikus adibide hauek :Adibideak1) Bedi
eran adierazi behar da bigarren atala.Ikus adibide hauek :Adibideak1) Bedi . Binomio baten karratua gehi konstante bat bezala adierazi behar da :
. Binomio baten karratua gehi konstante bat bezala adierazi behar da : konparatuz gero, 2p = 4 da, eta p = 2. Orduan,
konparatuz gero, 2p = 4 da, eta p = 2. Orduan, , eta honela idatz daiteke :
, eta honela idatz daiteke : Hortaz, parabola horrek
Hortaz, parabola horrek forma du, baina erpina E(-2,-5) puntuan du.2) Bedi
forma du, baina erpina E(-2,-5) puntuan du.2) Bedi . Kasu honetan
. Kasu honetan eginez gero,
eginez gero, , eta orduan :
, eta orduan :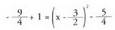 kasu honetan ere parabolaren bora
kasu honetan ere parabolaren bora -ren berdina izango da eta erpina
-ren berdina izango da eta erpina 3) Bedi
3) Bedi , erpina bilatu nahi da eta horretarako
, erpina bilatu nahi da eta horretarako eran idatzi behar dugu 2. mailako polinomioa. 2 biderkagai komuna ateraz hasten da :
eran idatzi behar dugu 2. mailako polinomioa. 2 biderkagai komuna ateraz hasten da : Hortaz, parabola horrek
Hortaz, parabola horrek forma du, baina erpina E(-1, -1) puntuan
forma du, baina erpina E(-1, -1) puntuan Hortaz, erpina
Hortaz, erpina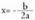 denan lortzen da eta
denan lortzen da eta da.Nola egiten da parabola baten grafikoa? °a) Erpinaren abzisa lortzen da. Horretarako,
da.Nola egiten da parabola baten grafikoa? °a) Erpinaren abzisa lortzen da. Horretarako,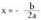 formula erabiltzen da.b) Erpinaren ordenatu lortzen da. Horretarako, x-en balioa funtzioaren
ekuazioan ordezkatzen da.AdibideaBedi
formula erabiltzen da.b) Erpinaren ordenatu lortzen da. Horretarako, x-en balioa funtzioaren
ekuazioan ordezkatzen da.AdibideaBedi Beraz,
Beraz, Eta horrenbestez, simetria ardatza
Eta horrenbestez, simetria ardatza zuzena da.c) Balio taula egiten da.Parabolak bere erpinetik pasatzen den zuzen bertikalarekiko
duen simetria kontuan hartuz, erpina taularen zentroan jarri, eta
x-i 3 edo 4 balio eskuinera eta beste horrenbeste ezkerrera ematen
zaizkio
zuzena da.c) Balio taula egiten da.Parabolak bere erpinetik pasatzen den zuzen bertikalarekiko
duen simetria kontuan hartuz, erpina taularen zentroan jarri, eta
x-i 3 edo 4 balio eskuinera eta beste horrenbeste ezkerrera ematen
zaizkio Nahiz eta orain arte ikustakoarekin nahikoa den parabola marraz-
teko, interesgarria da beste puntu garrantzitsu batzuk ezagutzea.d) Ardatzekin dituen ebakidura puntuak kalkulatzen dira.y ardatzarekin (x = 0 ekuazioa duena) duen ebakidura puntua P(0, c) izango da. Adibide honetan P(O, 2) izango da.x ardatzarekin (y = 0 ekuazioa duena) dituen ebakidura puntuak.
Nahiz eta orain arte ikustakoarekin nahikoa den parabola marraz-
teko, interesgarria da beste puntu garrantzitsu batzuk ezagutzea.d) Ardatzekin dituen ebakidura puntuak kalkulatzen dira.y ardatzarekin (x = 0 ekuazioa duena) duen ebakidura puntua P(0, c) izango da. Adibide honetan P(O, 2) izango da.x ardatzarekin (y = 0 ekuazioa duena) dituen ebakidura puntuak. sistema ebazteko,
sistema ebazteko, ekuazioa ebazten da. Dakigunez, ekuazio horrek bi soluzio (bi ebakidura puntu), soluzio bat (x ardatza parabolari buruz ebakitzailea denean, erpina ukitze puntua delarik), edo batere ez (parabola osorik x ardatzaren gainetik edo azpitik dagoenean) atera daitezke.
ekuazioa ebazten da. Dakigunez, ekuazio horrek bi soluzio (bi ebakidura puntu), soluzio bat (x ardatza parabolari buruz ebakitzailea denean, erpina ukitze puntua delarik), edo batere ez (parabola osorik x ardatzaren gainetik edo azpitik dagoenean) atera daitezke. -rentzat soluzioak x = 1 eta x = 2 dira, hortaz, ebakidura puntuak Q, (1, 0) eta Q,(2, 0) dira.e) Lortu diren datu guztiekin grafikoa egiten da.
-rentzat soluzioak x = 1 eta x = 2 dira, hortaz, ebakidura puntuak Q, (1, 0) eta Q,(2, 0) dira.e) Lortu diren datu guztiekin grafikoa egiten da.
- Ariketak
3. Hurrengo funtzio hauetan, kalkulatu erpina, esan maximoa edo minimoa den, aurkitu simetria ardatza, eta balio taula bat eta haren grafikoa egin :
Parabolaren eta zuzenaren arteko ebakidura puntuak
Oro har, parabola baten eta zuzen baten arteko ebakidura puntuak,
edo bi parabolen artekoak, kalkulatzeko, bi ekuazioek osatzen
duten sistema ebazten da.Parabolaren eta zuzenaren artekoak :Hiru aukera daude :Bi soluzio : zuzena parabolaren ebakitzailea denean bi ebakidura
puntu daude.• Soluzio bakarra : zuzena parabolaren ukitzailea denean ukitze
puntu bat dago.• Soluziorik ez : zuzena parabolaz kanpokoa da.Adibideak1) Bilatu ebakidura puntuak: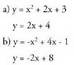 Ebazpena :
Ebazpena :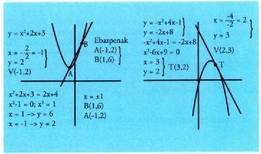 Bi parabolen artekoakBi parabolen ekuazioek osaturiko sistema bat ebazterakoan
ondoko hiru kasu hauek gerta daitezke :Lehen mailako ekuazio bat gelditzen bada, parabolek puntu
bakar batean ebakitzen dute elkar.Adibidea
Bi parabolen artekoakBi parabolen ekuazioek osaturiko sistema bat ebazterakoan
ondoko hiru kasu hauek gerta daitezke :Lehen mailako ekuazio bat gelditzen bada, parabolek puntu
bakar batean ebakitzen dute elkar.Adibidea • 2. mailako ekuazio bat gelditzen bada, bi soluzio edo soluzio
bakarra izan ditzake, edo bat ere ez.- Bi soluzio baditu, parabolek bi puntutan ebakitzen dute elkar.- Soluzio bakarra badu, parabolak elkarren ukitzaileak dira.- Soluziorik ez badu, parabolek ez dute puntu komunik.Adibideaka) Bitez
• 2. mailako ekuazio bat gelditzen bada, bi soluzio edo soluzio
bakarra izan ditzake, edo bat ere ez.- Bi soluzio baditu, parabolek bi puntutan ebakitzen dute elkar.- Soluzio bakarra badu, parabolak elkarren ukitzaileak dira.- Soluziorik ez badu, parabolek ez dute puntu komunik.Adibideaka) Bitez b)Bitez
b)Bitez Ebazpena
Ebazpena Alderantzizko proportzionaltasunaren funtzioaBitez bi neurri, x eta y, y x-en alderantzizkoaren proportzionala dela,
Alderantzizko proportzionaltasunaren funtzioaBitez bi neurri, x eta y, y x-en alderantzizkoaren proportzionala dela, . Orduan esaten da x eta y alderantziz proportzionalak direla.AdibideaBaserritar batek 3 hilabetetan 35 animalia bazkatzeko adina belar
du baserrian bilduta. Zenbat animalia saldu beharko ditu baldin etaa) belar kopuru horrekin bere animaliak 4 hilabetez bazkatu nahi
baditu?b) eta bost hilabeterako bazka izan nahi badu?Egin taula bat animalia kopurua eta animalia horiek bazka ditzakeen
egun kopuruaren arteko erlazioa adieraziz.EbazpenaDenbora egunetan adierazten badugu -30 eguneko hilabeteak harturik-, animalia kopuruari n esaten badiogu eta egun kopuruari d, erlazio hau izango dugu :
. Orduan esaten da x eta y alderantziz proportzionalak direla.AdibideaBaserritar batek 3 hilabetetan 35 animalia bazkatzeko adina belar
du baserrian bilduta. Zenbat animalia saldu beharko ditu baldin etaa) belar kopuru horrekin bere animaliak 4 hilabetez bazkatu nahi
baditu?b) eta bost hilabeterako bazka izan nahi badu?Egin taula bat animalia kopurua eta animalia horiek bazka ditzakeen
egun kopuruaren arteko erlazioa adieraziz.EbazpenaDenbora egunetan adierazten badugu -30 eguneko hilabeteak harturik-, animalia kopuruari n esaten badiogu eta egun kopuruari d, erlazio hau izango dugu : . Ekuazio horretatik
. Ekuazio horretatik ateratzen da. Hortaz, baserritarrak bere animalientzako bost hilabeterako bazka izan dezan :
ateratzen da. Hortaz, baserritarrak bere animalientzako bost hilabeterako bazka izan dezan : egun ;
egun ;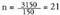 , beraz 14 animalia saldu beharko ditu.
, beraz 14 animalia saldu beharko ditu.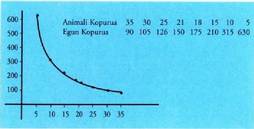 Alderantzizko funtzioa
Alderantzizko proportzionaltasuna aztertzeko aukera ematen duen funtzioa
Alderantzizko funtzioa
Alderantzizko proportzionaltasuna aztertzeko aukera ematen duen funtzioa funtzioa da.
funtzioa da.
Era horretako funtziorik sinpleena da, eta hori erabiliko dugu, hasteko.Funtzio horren izate eremua
da, eta hori erabiliko dugu, hasteko.Funtzio horren izate eremua Balio taula bat egingo dugu :
Balio taula bat egingo dugu : Ezaugarri hauek nabarmentzen dira :• Funtzioa beherakorra da bere izate eremu guztian.• Etengune bakarra du, x = 0 puntuan ; jarraia da
Ezaugarri hauek nabarmentzen dira :• Funtzioa beherakorra da bere izate eremu guztian.• Etengune bakarra du, x = 0 puntuan ; jarraia da eta
eta tarteetan.
tarteetan.
- Ariketa
4. Adierazi funtzio hauen arteko ebakidura puntuak analitikoki eta grafikoki :
- Ariketa
5. Irudikatu eta deskribatu
y= 1/x + a funtzioa
 funtziotik abiatuta lortzen da,
funtziotik abiatuta lortzen da,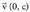 bektore traslazioz, edo funtzioari y =a funtzio konstantea batuz.Adibidez,
bektore traslazioz, edo funtzioari y =a funtzio konstantea batuz.Adibidez, funtzioa
funtzioa funtzioaren grafikoko puntu guztiak hiru banako goratuz lortzen da. Hortaz:
• Izate eremua D = R - {0} du.• Etengune bakarra x =0 da, beraz, jarraia da
funtzioaren grafikoko puntu guztiak hiru banako goratuz lortzen da. Hortaz:
• Izate eremua D = R - {0} du.• Etengune bakarra x =0 da, beraz, jarraia da eta
eta tarteetan.
tarteetan.
• Beherakorra da bere izate eremu guztian.
• Asintota bertikala x = 0 ekuazioko ardatza da.
• Asintota horizontala y = a zuzena da. Adibidea
Adibidea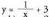 funtzioa aztertu (izate eremua, gorakortasuna, asintotak) eta grafikoa egin.Ebazpena :D = R - {0}, beherakorra eta jarraia
funtzioa aztertu (izate eremua, gorakortasuna, asintotak) eta grafikoa egin.Ebazpena :D = R - {0}, beherakorra eta jarraia eta
eta tarteetan.Asintotak x = 0 eta y = 3
tarteetan.Asintotak x = 0 eta y = 3
y = 1/x-c funtzioa
 funtziotik abiatuta lortzen da,
funtziotik abiatuta lortzen da, bektoreko traslazioz.• Bere izate eremua
bektoreko traslazioz.• Bere izate eremua da eta jarraia eta beherakorra da izate eremu horretan.• Bere asintota bertikala x = c ekuazioko zuzena da.• Bere asintota horizontala x ardatza da.Adibidea
Aztertu
da eta jarraia eta beherakorra da izate eremu horretan.• Bere asintota bertikala x = c ekuazioko zuzena da.• Bere asintota horizontala x ardatza da.Adibidea
Aztertu funtzioa eta grafikoa egin.
funtzioa eta grafikoa egin.
Ebazpena
D = R - {-2}. Jarraia eta beherakorra da bere izate eremuan. Asintota bertikala x = -2 da, eta horizontala y = 0 (x ardatza)
Y= 1/x-c + a funtzioa
 funtziotik abiatuta lortzen da, v (c, a) bektore traslazioz.
funtziotik abiatuta lortzen da, v (c, a) bektore traslazioz.
• Bere izate eremua D = R - {c} da.• Jarraia eta beherakorra da bere izate eremuan.• Asintota bertikala x = c ekuazioko zuzena da.• Asintota horizontala y = a ekuazioko zuzena da.AdibideaAztertu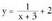 funtzioa eta grafikoa egin.EbazpenaD = R - {-3}. Asintotak x = -3, y = 2
funtzioa eta grafikoa egin.EbazpenaD = R - {-3}. Asintotak x = -3, y = 2 Orain k parametroak
Orain k parametroak funtzioaren grafikoan duen eragina aztertuko dugu, eta horretarako k-ren zenbait balio hartzen dituzten funtzio batzuk irudikatuko ditugu :Bitez
funtzioaren grafikoan duen eragina aztertuko dugu, eta horretarako k-ren zenbait balio hartzen dituzten funtzio batzuk irudikatuko ditugu :Bitez funtzioak.
funtzioak. funtzioen bitartez,
funtzioen bitartez, bektoreko traslazioz
bektoreko traslazioz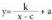 erako funtzio guztiak lortzen dira.Mota honetako funtzioek ezaugarri hauek dituzte :• Izate eremua D = R - {c} da, eta x = c etengune bakarra.
erako funtzio guztiak lortzen dira.Mota honetako funtzioek ezaugarri hauek dituzte :• Izate eremua D = R - {c} da, eta x = c etengune bakarra. • Asintota bertikala x = c zuzena da.• Asintota horizontala y = a zuzena da.• Simetria zentroa asintoten P(c, a) ebakidura puntua da.• Bi simetria ardatz dituzte, P(c, a) puntutik igarotzen direnak.
• Asintota bertikala x = c zuzena da.• Asintota horizontala y = a zuzena da.• Simetria zentroa asintoten P(c, a) ebakidura puntua da.• Bi simetria ardatz dituzte, P(c, a) puntutik igarotzen direnak. Hortaz, c eta a parametroek kurbaren kokagunea adierazten digute ; k parametroak kurbaren forma zein den esaten digu, eta horren zeinuak kurbak asintotei buruz zuen kokaera.
Hortaz, c eta a parametroek kurbaren kokagunea adierazten digute ; k parametroak kurbaren forma zein den esaten digu, eta horren zeinuak kurbak asintotei buruz zuen kokaera.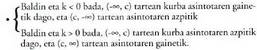 AdibideaEgiaztatu ezaugarri hauek guztiak
AdibideaEgiaztatu ezaugarri hauek guztiak eta
eta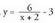 funtzioen grafikoen bidez.
funtzioen grafikoen bidez.
Kasu orokorra y = ax+b/x+c funtzioa
Funtzio hau aztertzeko zenbakitzailearen eta izendatzailearen arteko zatiketa egiten da lehendabizi. Adibide batekin ikusiko dugu :Adibideaa) Izan bedi , eta era honetan ikusten dugu emandako funtzioa
, eta era honetan ikusten dugu emandako funtzioa bektoreko traslazioz lortzen dela.Bere izate eremua D = R - {2} da, beherakorra da izate eremuan
eta bere asintotak x = 2 eta y = 3 dira.
bektoreko traslazioz lortzen dela.Bere izate eremua D = R - {2} da, beherakorra da izate eremuan
eta bere asintotak x = 2 eta y = 3 dira.
- Ariketa

Oinarrizko beste funtzio mota bat
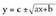 funtzioaOrain oinarrizko funtzio irrazional mota bat aztertuko dugu, errokizuna lehenengo mailako polinomio bat denean.
funtzioaOrain oinarrizko funtzio irrazional mota bat aztertuko dugu, errokizuna lehenengo mailako polinomio bat denean. erako funtzioak dira eta parametro bakoitzak funtzio horietan duen eragina aztertuko dugu.Lehenengo 4 sinpleenak adieraziko ditugu.
erako funtzioak dira eta parametro bakoitzak funtzio horietan duen eragina aztertuko dugu.Lehenengo 4 sinpleenak adieraziko ditugu.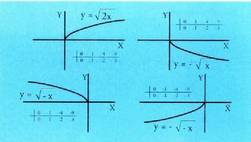 Lehenengo bi funtzioen izate eremua
Lehenengo bi funtzioen izate eremua da.c) eta d) funtzioen izate eremua
da.c) eta d) funtzioen izate eremua da.a) eta c) funtzioen ibilbidea
da.a) eta c) funtzioen ibilbidea da.b) eta d) funtzioen ibilbidea
da.b) eta d) funtzioen ibilbidea da.a parametroaren eragina zein den ikusteko, parametro horren
balio desberdinak hartu eta zenbait funtzio aztertuko ditugu :
da.a parametroaren eragina zein den ikusteko, parametro horren
balio desberdinak hartu eta zenbait funtzio aztertuko ditugu : Ikusi den bezala a-ren zeinuak funtzioaren izate eremua mugatzen
du.Zenbat eta handiagoa izan
Ikusi den bezala a-ren zeinuak funtzioaren izate eremua mugatzen
du.Zenbat eta handiagoa izan , orduan eta arinagoa izango da funtzioaren gorakortasun edo beherakortasuna.Orokorrean,
, orduan eta arinagoa izango da funtzioaren gorakortasun edo beherakortasuna.Orokorrean,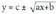 erako funtzio baten grafikoa egiteko :D izate eremua kalkulatzen da, errokizuna positiboa egiten duten x-en balioak osatzen dute :
erako funtzio baten grafikoa egiteko :D izate eremua kalkulatzen da, errokizuna positiboa egiten duten x-en balioak osatzen dute : • Balio raula bat egiten da x-ari izate eremuko balioak emanezAdibideaFuntzioak aztertu era beren grafikoak irudikatu.
• Balio raula bat egiten da x-ari izate eremuko balioak emanezAdibideaFuntzioak aztertu era beren grafikoak irudikatu.
Tarteka definituriko funtzioak
Tarte desberdinetan formula desberdinez definituriko funtzioa ; dira.Era honetako funtzioen grafikoa egiteko balio taula bat egiten da formula bakoitzeko dagokion tarteko balioak x-i emanez.Adibideak
y = E(x) - [x] zati osoa funtzioa
Funtzio hau da x zenbaki erreal bakoitzari x baino txikiagoa den
zenbaki oso handien, hau da bere zati osoa, egokitzen diona.Honela, E(2,7) = 2, E(3,42222...) = 3, E(-5,4) =-G, E(0,67) = 0,
E(-0,3G) = -i defini daiteke.Bere grafikoa etengune infinitoko funtzio mailakatu bat du.Irudian ikus daitekeenez, x-eko puntu guztiak etenguneak dira.
defini daiteke.Bere grafikoa etengune infinitoko funtzio mailakatu bat du.Irudian ikus daitekeenez, x-eko puntu guztiak etenguneak dira. Grafiko bitxia da, 1lalabet, y E(x) - x funtzioarena.
Grafiko bitxia da, 1lalabet, y E(x) - x funtzioarena.
y = |ax + b| funtzioa
Funtzio hau R guztian dago definitua eta da positiboa, eta tartekako
funtzio gisa ere defini daiteke honela : Adibidea
Adibidea
- Ariketak
8. Aurkitu ondoko funtzioen izate eremua, balio taula eta
grafikoa 9. Egin funtzio honen grafikoa :
9. Egin funtzio honen grafikoa :
Emaitzak:
LEONHARD EULER
(1707-1783)Basilean jaio zen, eta Basilean bertan egin zituen
ikasketak : teologia, medikuntza, fisika, sortaldeko
hizkuntzak eta matematika. Johan Bernoulli izan
zuen matematika irakasle, eta haren seme Daniel
eta Nikolaus, ikaskide. 1727an lana lortu zuen San
Petersburgoko Akademian, medikuntza sailean.
Nikolaus eta Daniel ere han ari ziren, matematikari
gisa. Nikolaus, baina, gazterik hil zen, eta Danielek
katedra lortu zuelarik Basileako Unibertsitatean,
matematika arduradun geratu zen Euler, San
Petersburgon. 1741ean, Federiko Handiak deituta,
Berlingo Akademian hasi zen lanean, eta hogeitabost
urte eman zituen han. 1766an Katalina
Handiak lana eskaini zion berriro San Petesburgon,
eta Errusiara itzuli zen atzera. Eulerrek, nahiz
eta Errusian eta Berlinen bizi, eta alemana izan
haren ama hizkuntza, frantsesez eta latinez idatzi
zituen lanik gehienak. Hiru dira garrantzitsuenak,analisi matematikoaren oinarriak : Introductio in
analysin infinitorum (1748), funtzioei buruzkoa,
Institutiones calculi differentialis (1755), deribatu
eta ekuazio diferentzialei buruzkoa, eta Institutiones
calculi integralis (1768-1770), integralei
buruzkoa.Eulerren irizitz, funtzioak ziren analisiaren
aztergai nagusia. Problema bat ebaztea, problema
horri dagokion ekuazio diferentzialaren soluzio
izango den funtzioa aurkitzea zen.Dardar ari den soka baten mugimenduaren
kasuan, esate baterako, horri dagokion ekuazio
diferentziala, hau da, dx = zdz/(a-z) ebazteko,
Eulerren ustez aski zen ekuazioaren soluzioak x + z
+ a.log (a-z) = konstantea funtzioak zirela jakitea.Haren maisu Joan Bernoulliren ustez, ordea, urrats bat besterik ez zen hori, eta funtzio horien interpretazio geometrikoa behar zen ezagutu, problema osorik ebatziko bazen. Eulerrek funtzio trigonometrikoak, esponentzialak eta logaritmikoak landu zituen, eta berdintza hauek proposatu zituen :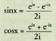 D'Alemberten eta Johan Bernoulliren iritziz
bestera, funtzio multibaluatu gisa definititu zituen
zenbaki konplexuen logaritmoak. Eraiki zuen teoria,
baina, ez zen oso sendoa oinarrietan, eta funtzioaz
eman zuen definizoa ere ez oso zehatza :
"kopuru aldakorrez eta zenbaki edo kopuru lconstanteez osaturiko edozein adierazpen analitiko"
gisa definitu zuen. Oso emaitza baliagarriak lortu
zituen serie konbergente edo dibergenteetako
emaitzak funtzioetan aplikatuz. Baina frogatu
zuen beste biderik ere, segidak batuketa finitoak
balira bezala tratatuz, eta bide horrek zenbait huts
eginarazi zion.Bestalde, gaur egun matematiketan erabiltzen diren ikurretako asko, berak erabili zituen lehenengoz: x-en funtzioa f(x) bidez adieraziz, e zenbakia e letraren bidez, irudizko banakoa i letraren bidez. Zirkunferentzia eta diametroaren arteko zatidura adierazteko, berriz, n zenbakia erabiltzea zabaldu zuen. Geometrian, triangelu baten angeluak adierazteko, A, B, C letrak erabili zituen, eta aldeak adierazteko, berriz, a, b, c ; halaber erabili zituen, zirkunferentzia inskribatuaren erradiorako, r letra, zirkunferentzia zirkunskribatuaren erradiorako, R, eta erdiperimetrorako, s. Triangeluetan 4Rs=abc betetzen dela aurkitu zuen berriro.
D'Alemberten eta Johan Bernoulliren iritziz
bestera, funtzio multibaluatu gisa definititu zituen
zenbaki konplexuen logaritmoak. Eraiki zuen teoria,
baina, ez zen oso sendoa oinarrietan, eta funtzioaz
eman zuen definizoa ere ez oso zehatza :
"kopuru aldakorrez eta zenbaki edo kopuru lconstanteez osaturiko edozein adierazpen analitiko"
gisa definitu zuen. Oso emaitza baliagarriak lortu
zituen serie konbergente edo dibergenteetako
emaitzak funtzioetan aplikatuz. Baina frogatu
zuen beste biderik ere, segidak batuketa finitoak
balira bezala tratatuz, eta bide horrek zenbait huts
eginarazi zion.Bestalde, gaur egun matematiketan erabiltzen diren ikurretako asko, berak erabili zituen lehenengoz: x-en funtzioa f(x) bidez adieraziz, e zenbakia e letraren bidez, irudizko banakoa i letraren bidez. Zirkunferentzia eta diametroaren arteko zatidura adierazteko, berriz, n zenbakia erabiltzea zabaldu zuen. Geometrian, triangelu baten angeluak adierazteko, A, B, C letrak erabili zituen, eta aldeak adierazteko, berriz, a, b, c ; halaber erabili zituen, zirkunferentzia inskribatuaren erradiorako, r letra, zirkunferentzia zirkunskribatuaren erradiorako, R, eta erdiperimetrorako, s. Triangeluetan 4Rs=abc betetzen dela aurkitu zuen berriro.
Zenbakien teorian Fermaten teorema frogatu zuen : a eta p zenbaki lehenak badira, ap-1 eta p zatitzean, zatiketaren hondarra 1 da. Orobat frogatu zuen oker zebilela Fermat, n lehena baldin bada zenbaki lehena dela zioenean, zeren n=5 denean
zenbaki lehena dela zioenean, zeren n=5 denean