Matematika»Analisiak

Funtzioak. Gai orokorrak

Sarrera

Eguneroko hizkuntzan, askotan erlazionatzen dira bi kantitate ; esan ohi da, adibidez, zerbait erostean ordaintzen den zerga salneurriaren mende dagoela, edo postaz pakete bat bidaltzeko prezioa pisuaren araberakoa dela. Adierazpen horiek nahiko ondo azaltzen dute matematikan funtzio bat zer den ; ideia hori azalduko da hain zuzen, atal honetan eta hurrengoan.Funtzio kontzeptua garrantzi handiko kontzeptua da matematika modernoan (XVII. mendeko bigarren erdialdetik aurrera zabaldu zen bezala hartuta). Leibniz (1646-1716) izan zen funtzio hitza lehenengo erabili zuena, baina Euler (1707-1783) izan zen kontzeptu hori gehien sakondu zuena. Haientzat erlazio funtzionalaren ideia bat zetorren formula matematiko batekin, erlazioaren nolakotasuna adierazten zuen formularekin hain zuzen. Baina kontzeptu hori oso mugatua zen, eta zabaldu egin zen gaur egungo kontzeptura iritsi arte.

Definizioa, Izate-eremua, Ibilbidea, Grafikoa

Bedi D zenbaki errealen multzo bat. D-n definitutako funtzio erreala, D-ko elementuei R-ko elementu bana dagokien D-ren eta R-ren arteko aplikazioa da. D multzoari izate-eremu esaten zaio.

Funtzioak hartzen dituen balio multzoari funtzioaren ibilbidea esaten zaio.Funtzio bat honela adierazten da :x aldagai askea day (x-en irudia f-ren bitartez) mendeko aldagaia da.Ondoren adibide batzuk azaltzen dira.Adibideak:1.funtzioa hartuko da lehenbizif-ren izate-eremua R da.x-ek R-ko balio guztiak hartzean, x2+1-ek 1 baino handiagoak diren zenbaki erreal guztiak hartzen ditu. Hortaz, ibilbideainserted text2.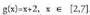. g-ren izate-eremua emanik dator[2,7] tarte bezala.x = 2 denean g(2) = 2+2 = 2x = 7 denean g(7) = 7+2 = 9 = 3, x-ek 2 eta 7-ren artean dauden balio guztiak hartzen dituenean, g(x)-k 2 eta 3 artean dauden balio guztiak hartzen ditu. g-ren ibilbidea [2,3] tarte itxia da. Hau da:Bedi f funtzio bat izate-eremua D duena ; f-ren grafikoa, definizioz, P(x,f(x)) puntuen multzoa da,izanik. Hala,funtzioaren grafikoa la irudiko parabola da, eta g(x)= x+2funtzioaren grafikoa l b irudiko arkua da.Oharra : garrantzi handikoa da azpimarratzea, baldin eta x-en funtzioa y bada,bakoitzeko y-ren balio bakar bat dagoela, izan ere, hala ez balitz ez bailitzateke funtzio izango.y x-en funtzioa den erraz jakin daiteke grafika ezagutzen denean.. x-en funtzio bada, ez dago zuzen bertikalik grafikoa puntu batean baino gehiagotan ebakitzen duenik. Beraz, 2,2a) 2d) eta 2e) grafikoetakoak funtzioak dira, 2c) eta 2f) grafikokoak, berriz, ez.Askotan funtzioaren izate-eremua ez dator esplizitoki emanda,edo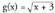idatz daiteke, ezer gehiago erantsi gabe. Kasu horietan f(x) zenbaki erreala duten x zenbaki errealen multzo handiena hartzen da izate-eremu bezala. Beraz,funtzioarentzatetafuntzioarentzat berriz,Horien grafikoak hauek diraAriketa ebatziaka) Bilatufuntzioaren izate-eremua eta ibilbidea.Ebazpena Izate-eremua bilatzeko kontuan hartzen dazenbaki erreala izatekoizan behar duela, hau da,. Baina x = 1 denean,da etaez da existitzen ; hortaz,Orain ibilbidea kalkulatzen da. 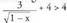x-ektarteko balioak harterakoan,-ek zenbaki erreal positiboak guztiak hartzen ditu eta gauza bera-ek, hortazeta f-ren ibilbidea =da.b)funtzioaren izate-eremua eta ibilbidea bilatu.Ebazpena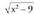zenbaki erreala izango da, baldin etabada; hortaz,izan behar du eta hori x < -3 etadenean betetzen da. Beraz, funtzioaren izate-eremua bitarte hauek bilduz lortzen da:x-ek izate-eremuko balioak hartzerakoan g(x)-ek zenbaki erreal positibo guztiak eta zero balioak hartzen ditu, hau da, g-ren ibilbidea

- Ariketak

1) Bilatu ondoko funtzioen izate-eremua eta ibilbidea2) Bilatu ondoko funtzioen grafikoa

Funtzio bikoitiak, funtzio bakoitiak

Definizioak

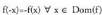f funtzio bat bikoitia dela esaten dabetetzen denean.f funtzio bat bakoitia dela esaten dabetetzen denean.Funtzio bikoiti baten grafikoa simetrikoa da y ardatzari buruz (5.. rudia). Funtzio bakoiti baten grafikoa, O koordenatuen jatorriari buruz simetrikoa da (6. irudia).Adibideak:a)funtzio bikoitiak dira :b)h(x) = sen x, funtzioak bakoitiak dira :

- Ariketak

3. Esan ondoko funtzioak bakoitiak edo bikoititak diren, edo ez bata ez bestea :4. f funtzio bat zenbaki erreal positiboentzat ondoko eran definitzen da :

Funtzioen arteko eragiketak

Izate-eremu bereko funtzioak batu eta ken daitezke :Biderka daitekeEtabada,kalkula daiteke eta.a zenbaki erreala bada eta f funtzio bat,.Etaetazenbaki errealak badira, konbinazio linealak egin daitezke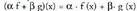Adibideak :a) Bitezb) Tarteka definitutako bi funtzio hartuz gero :(f+g), (f-g) eta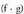bilatzeko bi funtzioen izate-eremua tarte berdinetan banatu behar da.Hortik aurrerakoa erraza da :

- Ariketak

Funtzioen konposaketa

Orain arte funtzioen arteko eragiketa aljebraikoak nola egiten diren aztertu da ; ondoren, bi funtzioen arteko konposaketa f " g azalduko da.

Definizioa

Bitez f eta g funtzioak, g-ren ibilbidea. f-ren izate-eremuaren azpimultzo bat izanik, hau dakonposaketa ("g konposatua f-rekin" irakurtzen da) g-ren izate-eremuan honela definitutako funtzioa izango da :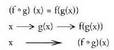Hortaz,balioaren irudia bilatzeko lehenbizi g(x) bilatzen da eta ondoren horren irudia f-ren bitartez.Adibideaka) Bitez g(x)=2x+1 eta, orduanOndorenkalkulatzen daIkusten denez, trukakortasunaren propietatea ez da betetzen izan ere,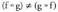baita.. ) Bitezeta. Orduan :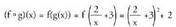c) Bitezeta, orduand) Bilatu f eta g bi funtziobeteko dutenak, baldin etabada.Ebazpenaeta f(x) = 2x+5, izan ere

- Ariketak

6) Ondoko funtzioekinetakonposaketak kalkulatu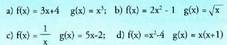7) Bilatueta h(x) = 3x izanik8) Bilatu f, baldin etabada.

Funtzio injektiboak. Alderantzizko funtzioa

Funtzio injektiboak

Zenbait funtziotan x aldagaiaren balio desberdinek y irudi berdina dute. Hori, esate baterako, funtzio konstanteetan gertatzen da, f(x) = 3 funtzioan izate-eremuko balio guztiak irudia 3 dute.funtzioan,

Definizioa

Funtzio bat injektiboa dela esaten da, baldin eta soilik baldin ez badaude izate-eremuan bi puntu irudi berdina dutenak.Era honetan ere idatz daiteke :Adibideaketainjektiboak dira.f funtzioa injektiboa da ez daudelako bi zenbaki desberdin kubo berdina dutenak; g funtzioa injektiboa da, ez daudelako erro koadroa berdina duten bi zenbaki desberdin.Behin grafikoa ezagutzen denean, erraza da funtzio bat injektiboa den ala ez jakitea. Zuzen horizontal batek grafikoa behin baino gehiagotan ebakitzen duenean funtzioa ez da injektiboa (7. irudia).

Baina ez badago zuzen horizontalik grafikoa behin baino gehiagotan ebakitzen duenik, orduan funtzioa injektiboa da (8. irudia).

Alderantzizko funtzioa

funtziotik abiatuta, demagun badakigula puntu baten irudia 8 dela, hau da,, badago galdetzea ea zein den x-en balioa, eta horren erantzuna x = 2 da. Funtzioa injektiboa denez gero,-ren balio bakoitzeko x-en balio bakarra dago.

Hortaz, badago funtzio bat definitzea f-ren ibilbideko puntu bakoitzari bere aurreirudia egokituko diona. Funtzio horri f-ren alderantzizkoa esaten zaio etaadierazten da. Kasu horretan funtzioada.

.funtzioarekin gauza bera egin nahi izanez gero, g-ren ibilbideko puntu bat ezagutzen da eta horren aurreirudia aurkitu nahi da ; bedi, x-entzat bi aukera daude 2 eta -2, eta hori dela eta ezin aurki daiteke

Alderantzizko funtzioaren definizioa.

Bedi f funtzio injektibo bat. f-ren alderantzizkoa,adierazten dena, funtzio bakarra da izate-eremutzat f-ren ibilbidea duena eta ekuazio hau betetzen duena :ere egia da.Frogapenahartzen da etadenez gero :y-ren ordez f(x) jarriz gero,. Horrek esan nahi du f-k x-en eta-en balioa hartzen duela, eta horrenbestez,f injektiboa denez,izan behar du, frogatu nahi zen bezala.

Berdintza horrek esan nahi du-ek f-ren lana desegiten duela (9. irudia).Era berean,definizioak adirazten du f-ek-en lana desegiten duela (10. irudia).Konposaketan ikusi bezalaIbil(f), hortaz,identitate funtzioa da (elementu bakoitzaren irudia, elementua bera da).Era berean,, hortaz,identitate funtzioa da f-ren izate-eremuan definitua.Adibideak1) Egiaztatu f(x) = 4x-3 funtzioa injektiboa dela eta alderantzizkoa kalkulatu.EbazpenaInjektiboa dela egiaztatzekodela suposatzen da, hau da:, beraz injektiboa da :Alderantzizko funtzioa bilatzeko,definitzen da eta f(t)=x ekuazioa ebazten da.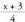, ten ordezjarriz gerolortzen da.

2) Egiaztatu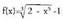injektiboa dela eta alderantzizkoabilatu.Ebazpena Injektiboa dela egiaztatzekodela hartzen da oinarritzat, hau da :, hortaz f injektiboa da,betetzen baitaAlderantzizko funtzioa bilatzekodefinitzen da eta f(t)=x ekuazioa ebazten daeta t-ren ordezjarriz gero :f eta f-1 grafikoen arteko harremana f funtzio injektiboaren etaharen alderantzizko funtzioaren grafikoen artean harreman estua dago. f funtzioaren grafikoa P ( x , f ( x ) ) erako puntuek osatzen dute etafuntzioarenaerako puntuek. 11. marrazkian ikus daitekeenez, P etapuntuak simetrikoak dira y = x zuzenari buruz (1. eta 3. kuadranteetako erdikaria).Behin f funtzioaren grafikoa ezagututa, berehala ateratzen daen grafikoa. 12. marrazkian f funtzioaren grafikoa ematen da eta 13. marrazkian-en grafikoa lortu da f-ren grafikotik abiatuta.Ondoren funtzio ez injektiboak aztertzen dira, kasu batzuetan posible da emandako funtziotik abiatuta funtzio injektibo bat bilatzea. Horretarako nahikoa da tarte egoki batean definitzea.

Ondoren alderantzizko funtzioa kalkula daiteke. Hori azaltzeko adibide batzuk jarriko dira :Ariketa ebatziakfuntzioa ematen da. Funtzio hori ez da injektiboa f(0) = f(2) = -1 delako.Nola defini daiteke, izate-eremua murriztuz, injektiboa den funtzio bat, eta halakotan zein da alderantzizkoa?EbazpenaKarratuak osatuz, funtzio horiidatz daiteke.Funtzio hori, izate-eremua R duena, simetrikoa da x=1 ardatzari buruz, izan ere, f(0) = f(2) = -1, f(-1) = f(3) = 2, f(-2) = f( 4) = 7 baita eta, oro har, 1 -etik distantziakide diren x-en balioentzat balio berdina hartzen du funtzioak. Ibilbidea kalkulatzeko kontuan hartzen dadela; hortaz,eta Ibil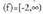Hortaz,funtzioa defini daiteke, injektiboa dena, edo defini daiteke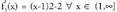ere, hori ere injektiboa. Emandako funtziotik abiatuta, bi funtzio injektiboaketadefinituko dira.inserted text-en izate-eremuada.-ren izate-eremuadaBien ibilbideada.funtzioak-en alderantzizkoak, izate-eremua-en ibilbidea izango dueta ibilbidea, berriz,-en izate-eremua izango du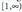Kalkulatzeko, honela idatzi behar da:bete beharko da, eta ondoko hau lortzen da :, eta t-ren ordezjarriz gero,lortzen da, ibilbideaduena.Baina, erroa aukeratzean bi aukera zeuden, eta bazegoen erro negatiboa hartzea ; horrela eginez gero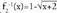ateratzeko litzateke, ibilbidealukeena, alegia

- Ariketak

9) Esan ondoko funtzio hauek injektiboak diren ala ez ; injektiboak direnetan kalkulatu alderantzizkoa.

- Ariketak

Bedifuntzioa, kalkulatua) izate-eremua eta ibilbidea.b) Definitueta

Funtzio gorakorrak eta beherakorrak

Definizioak

Bitez f funtzioa eta D bere izate-eremua.tartean f gorakorradela esaten da, baldin eta soilik baldinHorrez gainera,bada, f hertsiki gorakorra delaesaten da.Bedi f funtzioa eta D bere izate-eremua.tartean f beherakorra dela esaten da, baldin eta soilik baldin; horrez gainera,bada, f hertsiki beherakorra dela esaten da.AdibideaOndoko grafikoko funtzioa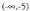eta (-1,3) tarteetan gorakorra da eta (-5,-1) etatarteetan beherakorra.

Funtzioaren muturrak. Maximoak eta minimoak

Definizioak

Bitez f funtzioa eta D izate-eremua. f-k a CED puntuanmaximoerlatibo bat duela esaten da, baldin eta a-k ingurunea badu, erradioaduena, hau da,non(f-k a puntuan inguruko puntu guztietan baino balio handiagoa du).Bitez f funtzioa eta D izate-eremua. f-k aCED puntuan minimo erlatibo bat duela esaten da, baldin etanonbetetzen den (funtzio horren balioa a puntuan inguruko puntu guztietan baino txikiagoa da).

Periodizitatea

Atal hau funtzio trigonometikoei dagokie batez ere, eta horregatik, mota horretako funtzioak erabiliko dira adibideetan.

Ondorengo kapituluan, berriz, periodiko trigonometriko ez diren zenbait funtzio aztertuko dira.

Definizioak

Funtzioa bat periodikoa dela esaten da, baldin eta edozein x-entzat zenbaki erreal bat, zero ez dena, esistitzen bada :betetzen duena, T zenbakia funtzioaren zenbakia da.Adibideaky=sen x eta y=cos x funtzio periodikoak dira eta periodoa 2p da.

Hau da :y = tg x funtzioa periodikoa da eta periodoada,da eta edozein x-entzatOro har,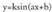etaerako funtzioak periodikoak dira eta periodoadute.erako funtzioak periodikoak dira eta periodoa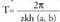Grafikoki f funtzio bat periodikoa bada eta bere periodoa T badu, eta bere grafikoa G, puntu batemanik,erako puntu guztiak G-koak dira orobat.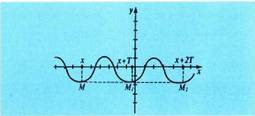AdibideaBedi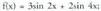; kasu horretan (2,4) zkh = 2 da, hortaz, hortaz, periodikoa da eta periodoa