Matematika»Analisiak
Segida konbergenteak eta dibergenteak. segiden limiteak
Beste ikuspegi batetik aztertuko ditugu orain segidak. Haien gaien arteko erlazioa aztertu ordez, segidak gorakorrak edo beherakorrak diren jakiten saiatuko gara, eta batez ere oso aurrera diren gaiei buruz zer nolako jokabidea duten argitzen.
I. Segida gorakorrak, segida beherakorrak.
Definizioa :
Bedi , zenbaki errealen segida bat.
, zenbaki errealen segida bat.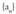 segida gorakorra da baldin
segida gorakorra da baldin , eta gorakor hutsa, baldin
, eta gorakor hutsa, baldin .
. segida beherakorra da baldin
segida beherakorra da baldin , eta beherakor hutsa, baldin
, eta beherakor hutsa, baldin Segida bat gorakorra edo beherakorra denean monotonoa dela esaten da.Segida monotono bateko gaiak honela ordenatzen dira :Segida gorakor batean :
Segida bat gorakorra edo beherakorra denean monotonoa dela esaten da.Segida monotono bateko gaiak honela ordenatzen dira :Segida gorakor batean : Segida beherakor batean :
Segida beherakor batean :
Nola jakin segida bat gorakorra edo beherakorra den gai orokorra ezaguturik?
inserted text N edota, bestela, baldin
N edota, bestela, baldin , edozein n-rentzat
, edozein n-rentzat dela.Segida beherakorra da baldin:
dela.Segida beherakorra da baldin: edota, bestela, baldin
edota, bestela, baldin , edozein n-rentzat
, edozein n-rentzat dela.• Adibideaka) Aztertu segida hau,
dela.• Adibideaka) Aztertu segida hau, ,gorakorra edo beherakorra den.SoluzioaKenketaren bidez :
,gorakorra edo beherakorra den.SoluzioaKenketaren bidez : Beraz, segida gorakorra da.b) Aztertu segida hau,
Beraz, segida gorakorra da.b) Aztertu segida hau, , gorakorra ala beherakorra den.SoluzioaZatiketaren bidez :
, gorakorra ala beherakorra den.SoluzioaZatiketaren bidez :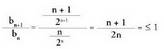 zeren
zeren
I I. Segida bornatua, goiko bornea eta beheko bornea
• Adibideaka) Har dezagun segida hau : Agerikoa denez, segida horretako gai guztiak 6 baino handiagoak
dira. 6a, beraz, beheko borne bat da segida horretan ; -la, 5a eta 7a
bera ere, beheko borneak dira. Segida batek beheko borneak baldin
baditu behetik bornatua dela esaten da.Bestalde, ikusten denez, ez dago zenbakirik segidako gainerako guztiak baino handiagoa denik ; hau da, ez dago goiko bornerik ;
Agerikoa denez, segida horretako gai guztiak 6 baino handiagoak
dira. 6a, beraz, beheko borne bat da segida horretan ; -la, 5a eta 7a
bera ere, beheko borneak dira. Segida batek beheko borneak baldin
baditu behetik bornatua dela esaten da.Bestalde, ikusten denez, ez dago zenbakirik segidako gainerako guztiak baino handiagoa denik ; hau da, ez dago goiko bornerik ; segida ez dago, beraz, goitik bornaturik.b) Bedi orain beste segida bat :
segida ez dago, beraz, goitik bornaturik.b) Bedi orain beste segida bat : Segida honetan 1 zenbakia goiko bornea da, eta ez dago beheko
bornerik. Segida beherakor bat da, lehenengo gaiak goitik bornatua.Aurreko bi adibide horien ondorioz pentsa daiteke segida gorakor
batek ezin dezakeleea goiko bornerik izan eta, era berean, segida
beherakor batek ezin dezakeela beheko bornerik izan. Hori, ordea,
ez da hala. Ikusi, bestela, beste adibide hau :c) Bedi
Segida honetan 1 zenbakia goiko bornea da, eta ez dago beheko
bornerik. Segida beherakor bat da, lehenengo gaiak goitik bornatua.Aurreko bi adibide horien ondorioz pentsa daiteke segida gorakor
batek ezin dezakeleea goiko bornerik izan eta, era berean, segida
beherakor batek ezin dezakeela beheko bornerik izan. Hori, ordea,
ez da hala. Ikusi, bestela, beste adibide hau :c) Bedi Segida hau segida beherakor bat da, eta hala ere, badu beheko bornerik, 2, hain zuzen ere, zeren zenbakitzailea izendatzailea halako bi baino handiagoa baita beti. Gainera, beherakorra den aldetik, goiko bornea du,
Segida hau segida beherakor bat da, eta hala ere, badu beheko bornerik, 2, hain zuzen ere, zeren zenbakitzailea izendatzailea halako bi baino handiagoa baita beti. Gainera, beherakorra den aldetik, goiko bornea du,
Definizioak
 segida goitik bornatua izango da baldin eta bada
segida goitik bornatua izango da baldin eta bada zenbakirik eta betetzen bada
zenbakirik eta betetzen bada dela.
dela. segida behetik bornatua izango da baldin eta bada
segida behetik bornatua izango da baldin eta bada zenbakirik eta betetzen bada
zenbakirik eta betetzen bada dela.Goiko eta beheko borneak dituen segida bat segida bornatua dela
esaten da.Adibide eta definizio horiek kontuan harturik ondorio hauek atera daitezke :
a) Gai orokorreko segidetan,
dela.Goiko eta beheko borneak dituen segida bat segida bornatua dela
esaten da.Adibide eta definizio horiek kontuan harturik ondorio hauek atera daitezke :
a) Gai orokorreko segidetan, , goiko eta beheko borneak beti 1 eta 0 dira, hurrenez hurren.b) Segida gorakor batean, edozeinetan, segidako lehenengo gaia
da beheko bornea.c) Bedi
, goiko eta beheko borneak beti 1 eta 0 dira, hurrenez hurren.b) Segida gorakor batean, edozeinetan, segidako lehenengo gaia
da beheko bornea.c) Bedi denerako definiturik dagoen gai orokorreko segida bat :
denerako definiturik dagoen gai orokorreko segida bat :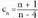 .Segida beherakor huts bat da, eta, beraz, goitik bornatua dago, bere lehenengo gaiak, 6ak bornatua alegia. Bestalde, zenbakitzailea beti izendatzailea baino handiagoa denez, gai guztiak 1 baino handiagoak dira, eta 1 segidako beheko borne bat da : Beraz :
.Segida beherakor huts bat da, eta, beraz, goitik bornatua dago, bere lehenengo gaiak, 6ak bornatua alegia. Bestalde, zenbakitzailea beti izendatzailea baino handiagoa denez, gai guztiak 1 baino handiagoak dira, eta 1 segidako beheko borne bat da : Beraz : eta
eta
- Ariketak
1. Aztertu segida hauek gorakorrak ala beherakorrak diren
kenketaren teknika baliatuz: 2. Aztertu segida hauek gorakorrak ala beherakorrak diren
zatiketaren teknika baliatuz :
2. Aztertu segida hauek gorakorrak ala beherakorrak diren
zatiketaren teknika baliatuz : 3. Aurkitu segida hauentzat beheko eta goiko borne bana :
3. Aurkitu segida hauentzat beheko eta goiko borne bana : 4. Froga ezazu segida hau ez dela monotonoa eta ez dagoela bornatua ez goitik ez behetik :
4. Froga ezazu segida hau ez dela monotonoa eta ez dagoela bornatua ez goitik ez behetik : 5. Segida hau emanik :
5. Segida hau emanik :
I I I. Segida bateko limitea.
Segida konbergenteak eta dibergentak.
Segida bateko gaiak zer baliotarantz jotzen duten aztertu behar
dugu atal honetan. Horretarako segidan oso aurrera diren gaiak
aztertzea da egokiena.• Adibideaka) Segida honek, adibidez, gai guztiak positiboa eta gero eta txikiagoa dituenez, argi dago zerorantz jotzen duela. Oso aurrera diren gaiak kalkulatzean ere,
gai guztiak positiboa eta gero eta txikiagoa dituenez, argi dago zerorantz jotzen duela. Oso aurrera diren gaiak kalkulatzean ere, eta
eta , gero eta zerotik hurbilago diren zenbakiak lortzen dira. Hala beraz, segidaren limiteak zerorantz jotzen duela esaten da, eta honela adierazten da hori :
, gero eta zerotik hurbilago diren zenbakiak lortzen dira. Hala beraz, segidaren limiteak zerorantz jotzen duela esaten da, eta honela adierazten da hori : b) Beste segida honetan, berriz,
b) Beste segida honetan, berriz, , 2 zenbakiari gero eta kopuru txikiagoak kenduz lortzen dira gaiak (aurreko adibidean ikusi denez, zerorantz jotzen dute kopuru horiek). Segidak, beraz, logikoa denez, 2-rantz joko du. Hori frogatzeko, segidan aski aurrean diren gaiak kalkulatu behar dira :
, 2 zenbakiari gero eta kopuru txikiagoak kenduz lortzen dira gaiak (aurreko adibidean ikusi denez, zerorantz jotzen dute kopuru horiek). Segidak, beraz, logikoa denez, 2-rantz joko du. Hori frogatzeko, segidan aski aurrean diren gaiak kalkulatu behar dira : . Espero izatekoa zen bezala, lortu diren zenbakiak gero eta hurbilago daude 2 zenbakitik. Segidan aurrerago diren gaiak harturik baina, are txikiago ere egin daiteke tarte hori. Hala beraz, kasu honetan, segidaren limiteak birantz jotzen duela esaten da, eta honela adierazten da :
. Espero izatekoa zen bezala, lortu diren zenbakiak gero eta hurbilago daude 2 zenbakitik. Segidan aurrerago diren gaiak harturik baina, are txikiago ere egin daiteke tarte hori. Hala beraz, kasu honetan, segidaren limiteak birantz jotzen duela esaten da, eta honela adierazten da : .
. eta
eta bezalako segida mugatu edo limitedunak segida konbergenteak direla esaten da.
bezalako segida mugatu edo limitedunak segida konbergenteak direla esaten da. c) Beste segida honetan, ordea,
c) Beste segida honetan, ordea, , segidako gaiek bi balio baino ez dituzte hartzen, 5 eta -5, eta bi balio horien artean mugitzen dira, orain batera, orain bestera, etengabe oszilatzen. Horregatik segida mota hauek segida oszilatzaileak direla esaten da. Gisa honetako segida gehiago aztertuko da aurrerago.
, segidako gaiek bi balio baino ez dituzte hartzen, 5 eta -5, eta bi balio horien artean mugitzen dira, orain batera, orain bestera, etengabe oszilatzen. Horregatik segida mota hauek segida oszilatzaileak direla esaten da. Gisa honetako segida gehiago aztertuko da aurrerago. Azter ditzagun orain beste bi segida hauek :
Azter ditzagun orain beste bi segida hauek : d) Bietako lehena,
d) Bietako lehena, segida beherakorra da eta ez nago behetik bornatua. Edozein -k balioa baino balio txikiagoak har ditzake, den handiena izanik ere k hori.
segida beherakorra da eta ez nago behetik bornatua. Edozein -k balioa baino balio txikiagoak har ditzake, den handiena izanik ere k hori.
Halakoetan segidak minus infiniturantz jotzen duela esaten da eta honela adierazten da :
jotzen duela esaten da eta honela adierazten da : e) Beste segida, berriz,
e) Beste segida, berriz, gorakorra da eta ez dago goitik bornatua.
gorakorra da eta ez dago goitik bornatua.
Edozein -k balioa baino balio handiagoak har ditzake, denik eta handiena izanik ere k hori. Halakoetan segidak plus infiniturantz jotzen duela esaten da eta honela adierazten da :
jotzen duela esaten da eta honela adierazten da : .
. eta
eta
Segida konbergenteak. Limiteren definizioa.
Limiteren definizio zehatzago bat lortzeko kontuan hartu behar dira segida konbergenteei buruz esanak : alegia, segidako gaien eta limitearen arteko distantzia gero eta txikiagoa dela eta are txikiago ere zitekeela, aurrera eginez gero segidan. Segidako gai baten, , eta horren limitearen, a, arteko distantzia kalkulatzeko, batari bestea kentzen zaio eta kenduraren balio absolutua kalkulatzen da,
, eta horren limitearen, a, arteko distantzia kalkulatzeko, batari bestea kentzen zaio eta kenduraren balio absolutua kalkulatzen da, .
.
Bestalde, matematiketan, kopuru positibo txiki-txiki bat adierazteko, e letra erabiltzen da, . Beraz, a segidaren limitea a izango da, baldin eta edozein e-rentzat, den txikiena izannik ere,
. Beraz, a segidaren limitea a izango da, baldin eta edozein e-rentzat, den txikiena izannik ere, betetzen bada segidako
betetzen bada segidako gaitik aurrera (
gaitik aurrera ( -ren arabera kalkulatuko da
-ren arabera kalkulatuko da
Definizioa:
 segidaren limitea a izango da, alegia,
segidaren limitea a izango da, alegia, , baldin eta
, baldin eta ,eta
,eta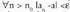 izatea betetzen bada. Definizioak zera adierazten du : segidako gaien eta limitearen arteko distantzia nahi bezain txikia izan daitekeela, e baino txikiagoa izan daitekeela, alegia, edozein eta oso-oso txikia izanik ere e hori, eta horretarako, segidan
izatea betetzen bada. Definizioak zera adierazten du : segidako gaien eta limitearen arteko distantzia nahi bezain txikia izan daitekeela, e baino txikiagoa izan daitekeela, alegia, edozein eta oso-oso txikia izanik ere e hori, eta horretarako, segidan gaiaz aurrera diren gai guztiak hartu beharko direla, zenbat eta txiloago e, orduan eta handiago izango delarik
gaiaz aurrera diren gai guztiak hartu beharko direla, zenbat eta txiloago e, orduan eta handiago izango delarik • Adibideak
a) Segida bateko n-garren gaia harturik,
• Adibideak
a) Segida bateko n-garren gaia harturik, , segidaren limitea 2 dela frogatzeko,
, segidaren limitea 2 dela frogatzeko, inekuazioa ebatzi behar da:
inekuazioa ebatzi behar da: . Beraz,
. Beraz, eta
eta - ren balio bakoitzarentzat
- ren balio bakoitzarentzat zenbat den aterako da hortik. Adibidez,
zenbat den aterako da hortik. Adibidez, , orduan
, orduan , hots,
, hots, Hala,
Hala, -tik aurrera,
-tik aurrera, inserted text
inserted text . Aldiz, e= 0,001 hartzen bada, orduan
. Aldiz, e= 0,001 hartzen bada, orduan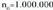 eta, hala,
eta, hala, gairaino aurreratu beharko da
gairaino aurreratu beharko da . izan dadin.b) Segida hau emanik,
. izan dadin.b) Segida hau emanik, , frogatu segidaren limitea3 dela, eta aurkitu segidako zer gaitik aurrera betetzen den
, frogatu segidaren limitea3 dela, eta aurkitu segidako zer gaitik aurrera betetzen den izatea.Soluzioa
izatea.Soluzioa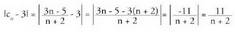 eta zatidura hori nahi adina txiki daiteke. Adibidez, O'001 baino txikiago izan dadin,
eta zatidura hori nahi adina txiki daiteke. Adibidez, O'001 baino txikiago izan dadin, gaiak izan beharko lukeen balioa kalkula daiteke inekuazio hau ebatziz :
gaiak izan beharko lukeen balioa kalkula daiteke inekuazio hau ebatziz : ; beraz, n+2 > 11.000, eta n > 10.988. Izan ere, froga daitekeenez,
; beraz, n+2 > 11.000, eta n > 10.988. Izan ere, froga daitekeenez, ; alegia, gai horretatik 3-ra dagoen tartea O'001 baino txikiagoa da. Alegia, segidan 10.998. lekua hartzen duen gairaino aurreratu behar da segidako azken gaietatik 3 limiterainoko tartea e- ren balioa (e = 0'001, aurrez zehaztua) baino txikiagoa izan dadin.
; alegia, gai horretatik 3-ra dagoen tartea O'001 baino txikiagoa da. Alegia, segidan 10.998. lekua hartzen duen gairaino aurreratu behar da segidako azken gaietatik 3 limiterainoko tartea e- ren balioa (e = 0'001, aurrez zehaztua) baino txikiagoa izan dadin.
Jakina, e-ri beste balio bat emango balitzaio, -k ere beste balio bat hartuko luke. Bi balio horien arteko erlazioa inekuazio hau ebatziz lortzen da, 0'001-en lekuan e jarriz :
-k ere beste balio bat hartuko luke. Bi balio horien arteko erlazioa inekuazio hau ebatziz lortzen da, 0'001-en lekuan e jarriz :
- Ariketak
6. Segida hau emanik, , frogatu segidaren limitea 2 dela, eta kalkulatu zenbat aurreratu behar den segidan, limiterainoko tartea 0'01 baino txikiagoa izan dadin, batetik, eta O'001 baino txikiagoa izan dadin, bestetik.7. Segida hau emanik,
, frogatu segidaren limitea 2 dela, eta kalkulatu zenbat aurreratu behar den segidan, limiterainoko tartea 0'01 baino txikiagoa izan dadin, batetik, eta O'001 baino txikiagoa izan dadin, bestetik.7. Segida hau emanik, , frogatu segidaren limitea
, frogatu segidaren limitea
Limiteen kalkulurantz
Artean ikusiriko adibideetan, limitea aurretik ematen zen, eta
definizioko baldintzak betetzen zituela frogatzea eskatzen zen.
Gehienetan ordea limitea ez da ezagutzen, huraxe da kalkulatu
behar izaten dena. Kalkulagailu batez, ez da zaila limitea zein izango
den jakitea. Izan ere, segidan oso aurrera diren gaiak kalkulatuz
lortzen diren hurbilketetatik atera baitaiteke, adibide hauetan ikusiko
den bezala, zein den limitea. • Adibideaka) Kalkulatu segida honen limitea :
• Adibideaka) Kalkulatu segida honen limitea : Soluzioa
Nola
Soluzioa
Nola gaiek ez digutenaskorik lagunduko limitea aurkitzen, askoz arrerago diren gaietara joko dugu:
gaiek ez digutenaskorik lagunduko limitea aurkitzen, askoz arrerago diren gaietara joko dugu: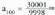 . Beraz, limitea 3 dela esan daiteke.Ohartu nola,
. Beraz, limitea 3 dela esan daiteke.Ohartu nola, adierazpenean, zenbat eta handiago izan n, orduan eta eragin gutxiago dute 1 eta -2 batugaiek zatikian. Beraz, berdin idatz daiteke :
adierazpenean, zenbat eta handiago izan n, orduan eta eragin gutxiago dute 1 eta -2 batugaiek zatikian. Beraz, berdin idatz daiteke : Ondorio bera ateratzen da zenbakitzailea eta izendatzilea zati
Ondorio bera ateratzen da zenbakitzailea eta izendatzilea zati egiten badira :
egiten badira : .Izan ere, n gaiakinfiniturantz jotzen duenean
.Izan ere, n gaiakinfiniturantz jotzen duenean eta
eta gaiek zerorantz jotzen dute,eta zatidurak 3-rantz, beraz.b) Kalkulatu segida honen limitea :
gaiek zerorantz jotzen dute,eta zatidurak 3-rantz, beraz.b) Kalkulatu segida honen limitea : Soluzioa
Soluzioa eta
eta kalkulatuko ditugu:
kalkulatuko ditugu: . Ematen du segida handi tuz doala, baina ez dakigu edozein zenbaki gainditzeko gauza izango den -eta beraz, infiniturantz joko duen-, edota balio jakin baterantz joko duen, oso handia bada ere.Kontuan hartu,
. Ematen du segida handi tuz doala, baina ez dakigu edozein zenbaki gainditzeko gauza izango den -eta beraz, infiniturantz joko duen-, edota balio jakin baterantz joko duen, oso handia bada ere.Kontuan hartu,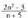 adierazpenean, zenbat eta handiago izan n, orduan eta eragin gutxiago dutela emaitzan zenbakitzailea eta izendatzailea batzen dituzten -3 eta 5 batugaiek. Beraz, berdin idatz liteke :
adierazpenean, zenbat eta handiago izan n, orduan eta eragin gutxiago dutela emaitzan zenbakitzailea eta izendatzailea batzen dituzten -3 eta 5 batugaiek. Beraz, berdin idatz liteke : Emaitza bera lortzen da zenbakitzailea eta izendatzailea zati n (n ber bietarik berretzaile maila txikiena duenaren berretzailerik handiena, izendatzailearena kasu honetan) egiten badira :
Emaitza bera lortzen da zenbakitzailea eta izendatzailea zati n (n ber bietarik berretzaile maila txikiena duenaren berretzailerik handiena, izendatzailearena kasu honetan) egiten badira : , zeren n gaiak infinituarantz jotzen duenean
, zeren n gaiak infinituarantz jotzen duenean gaiek zerorantz lotzen baitute.c) Kalkulatu segida honen limitea :
gaiek zerorantz lotzen baitute.c) Kalkulatu segida honen limitea : Soluzioa
Soluzioa eta
eta . Limitea minus infinitu
. Limitea minus infinitu dela esan daiteke. Hala den edo ez frogatzeko, zenbakitzailea eta izendatzailea zati
dela esan daiteke. Hala den edo ez frogatzeko, zenbakitzailea eta izendatzailea zati (alegia, n ber bietatik berretzaile maila txikiena duenaren berretzailerik handiena, izendatzailearena ere bai, kasu honetan) egingo ditugu :
(alegia, n ber bietatik berretzaile maila txikiena duenaren berretzailerik handiena, izendatzailearena ere bai, kasu honetan) egingo ditugu : zeren n gaiak infiniturantzantz jotzen duenean
zeren n gaiak infiniturantzantz jotzen duenean ,
, eta
eta , gaiek zerorantz jotzen dute.• Adibidead) Kalkulatu segida honen limitea :
, gaiek zerorantz jotzen dute.• Adibidead) Kalkulatu segida honen limitea : Soluzioa
Soluzioa eta
eta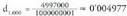 Dirudienez, 0 zero izango du limitea. Hala den egiaztatzeko, zenbakitzailea eta izendatzailea
Dirudienez, 0 zero izango du limitea. Hala den egiaztatzeko, zenbakitzailea eta izendatzailea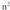 -ren artean zatitzen dira :
-ren artean zatitzen dira :
Segida dibergenteak
Hasieran, sarrera gisa-edo, jarritako adibideetan, eta baita aztertu
berri ditugun b) eta c) adibideetan ere, limite finituko segidak ez
ezik -limite konbergentak, alegia- plus edo minus infinturantz jotzen
duten segidak ere azaldu dira, segida dibergenteak alegia.
Orain, horiek zer diren definitzen saiatuko gara.Segida batek infinturantz jotzen duela
infinturantz jotzen duela esaten da, baldin eta K balio batentzat, edozeintzat, den handiena izanik ere, segidako gai batetik aurrera, alegia
esaten da, baldin eta K balio batentzat, edozeintzat, den handiena izanik ere, segidako gai batetik aurrera, alegia -tik aurrera gai guztiak K baino handiagok badira. Hau da :
-tik aurrera gai guztiak K baino handiagok badira. Hau da : . Eta limite finituaren definiziorako erabili den notazioa baliatuz :Definizioa :
. Eta limite finituaren definiziorako erabili den notazioa baliatuz :Definizioa : , baldin eta soilik baldin
, baldin eta soilik baldin non
non Minus infiniturantz jotzen duten segiden definizioa ere antzekoa da.Definizioa :
Minus infiniturantz jotzen duten segiden definizioa ere antzekoa da.Definizioa : baldin eta soilik baldin
baldin eta soilik baldin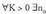 non
non da.• AdibideaLimitea
da.• AdibideaLimitea duen segida hau emanik,
duen segida hau emanik, , aurkitu segidako zer gaitik aurrera den an < -100.000.SoluzioaInekuazioa ebatzi : 5 - 3n < -100.000, -3n < -100.005, n > 33.335.
, aurkitu segidako zer gaitik aurrera den an < -100.000.SoluzioaInekuazioa ebatzi : 5 - 3n < -100.000, -3n < -100.005, n > 33.335.
Beraz, , eta
, eta . gaitik aurrea, segidako gai guztiak - 100.000 baino txikiagoak ira.
. gaitik aurrea, segidako gai guztiak - 100.000 baino txikiagoak ira.
- Ariketak 3n- 1 1 + n
8. Kalkulatu ondoko limiteak balio handiak emanez n-ri.
Frogatu emaitza bera ateratzen den zenbakitzailea eta
izendatzailea zati berretzaile maila txikiena duenaren
berratzaile handiena egitean edo n handitzean garrantzia
galtzen duten gaiak arbuiaturik.
IV Segiden arteko eragiketak
Bitez bi segida: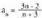 eta
eta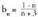 .
.
Kalkula ditzagun haien limiteak : . Bi segidak gaiz gai batuta edo haien n-garren gaiak batuta,emaitza bera da :
. Bi segidak gaiz gai batuta edo haien n-garren gaiak batuta,emaitza bera da : eta limitea, beraz :
eta limitea, beraz : . Bestalde, n-garren gaien limitea ere :
. Bestalde, n-garren gaien limitea ere :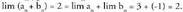 Batuketari buruz esanak biderketarako ere berdin-berdin balio
du :
Batuketari buruz esanak biderketarako ere berdin-berdin balio
du :
Segida konbergenteen tasunak
Baldin , orduan...:1.
, orduan...:1. 2.
2.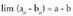 3.
3. 4.
4. eta
eta 5.
5. , non eta a eta b ez diren biak zero.6.
, non eta a eta b ez diren biak zero.6. , non eta ez den a < 0 eta p bikoiti.Tasun horiek aplikatuz limite asko kalkula daitezke, ez denak ordea. Zer gertatzen da, adibidez, lim
, non eta ez den a < 0 eta p bikoiti.Tasun horiek aplikatuz limite asko kalkula daitezke, ez denak ordea. Zer gertatzen da, adibidez, lim denean, baldin eta
denean, baldin eta bada? Ikus ditzagun adibide batzuk :a ) Bitez bi segida,
bada? Ikus ditzagun adibide batzuk :a ) Bitez bi segida, eta
eta ,eta horien limiteak,
,eta horien limiteak, eta
eta Beraz,
Beraz, b) Aldiz, baldin
b) Aldiz, baldin bada (
bada ( b) Aldiz, baldin b n = - 2 bada (b -k zerorantz jotzen duela orainere, eta
b) Aldiz, baldin b n = - 2 bada (b -k zerorantz jotzen duela orainere, eta -k, berriz, aldagabe irauten duela), orduan :
-k, berriz, aldagabe irauten duela), orduan : c) Gauzak are gehiago korapilatzen dira, ordea,
c) Gauzak are gehiago korapilatzen dira, ordea, denean. Orduan,
denean. Orduan,
0/0 indeterminazioa
Zenbakitzaileak ez ezik izendatzaileak ere zerorantz jotzen duenean
azaltzen da kasu hau. Indeterminazioaz, ordea, ez dago erregela
orokor bat ; kasu partikular bakoitza aztertu behar da, zeren, zenbakitzailearen
eta izendatzailearen segidak nolakoak, limitea zenbaki
finito, zero edo infinitu izan baitaiteke. Hiru adibide aztertuz ikusiko
da hori :• 1. adibidea Bitez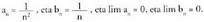 Orduan,
Orduan,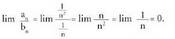 • 2. adibideaBitez
• 2. adibideaBitez eta
eta eta
eta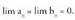 Orduan,
Orduan, • 3. adibideaBitez
• 3. adibideaBitez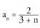 eta
eta eta
eta Orduan,
Orduan,
Zenonen paradoxak
Zenon Eleakoa filosofo greziarra K.a. V mendean bizi zen. Parmenidesen
ikasle eta laguna izan zen, eta Eleako filosofia eskolako filosofo nagusia.
Eskola horretako filosofoek izatearen batasuna eta iraunkortasuna
defenditzen zuten bitartean, beste filosofo batzuek, aldiz, Pitagorasen
jarraitzaileek, esate baterako, aniztasuna eta mudantza defenditzen zuten.
Batzuen eta besteen arteko tirabira horietan, Zenon gailendu zen : metodo
filosofiko berri bat asmatu zuen, dialektika, eta higidura ezinezkoa dela
frogatu zuen, behatze hutsak bestela erakusten badu ere. Baina higidura
izan, badenez, arrazoibide itxuraz egiazko horiei "Zenon paradoxak" esaten
zaie. Horien artean ezagunenetako bat Akilesen eta dortokaren arteko
pasadizoa da. Zenonek segidaren ideia erabili zuen paradoxa horretan eta
horregatik da guretzat interesgarria. Honela dio :"Akiles hanka-arinak dortoka bat ikusi eta hura harrapatzea erabaki
zuen. Lasterka abiatu zen haren atzetik, baina dortokoa zegoen lekura iritsi
orduko, dortoka, oso-oso poliki mugitzen bazen ere, mugitu zen pixka
bat aurrera, lekuz aldatu zen. Akiles, orduan, berriz abiatu zen haren atzetik,
baina dortoka ikusi zuen lekura iristean, hura ez zegoen jada han, lekuz
aldatua zen berriro. Nahi adina aldiz errepika daiteke prozesua, baina Akiles
eta dortoka ez dira sekula leku berean aldi berean egongo : Akiles iristerako
dortoka alde egina izango da. Akilesek ezingo du sekula harrapatu. "Higidura ez da esistitzen, dena da batasuna eta egonkortasuna, bukatzen
zuen Zenonek. Akilesek ez duela dortoka harrapatuko esatea, Akilesen eta dortokoaren arteko distantzien segidak ez duela zerorantz jotzen esatea bezala da, edo zerorantz jotzen duela baina ez duela limiterik esatea.
Akiles dortoka baino esate baterako hamar aldiz bizkorrago joango balitz, distantzia -ren arabera gutxituz joango litzateke (d = hasierako distantzia ; n = Akiles zenbat aldiz saiatzen den). Zerorantz jotzen duen segida bat da. Zenonek adierazi nahi duena da, dortoka harrapatuko bazuen, Akilesek infinitu ahalegin egin beharko zituela. Zenonek Akilesen ahalegin guztiek denbora jakin bat behar dutelako ideia erabili zuen, kontuan hartu gabe denbora, ahaleginetik ahaleginera, laburtuz doala, hau da, ahalegin bakoitzeko zerorantz jotzen duen beste segida bat osatzen dutela denborek. Gainera, denbora partzial infinituen batura -alegia, matematiketan segida esaten dena- konbergentea da, eta, beraz, Akilesek harrapatu, harrapatzen du dortoka.
-ren arabera gutxituz joango litzateke (d = hasierako distantzia ; n = Akiles zenbat aldiz saiatzen den). Zerorantz jotzen duen segida bat da. Zenonek adierazi nahi duena da, dortoka harrapatuko bazuen, Akilesek infinitu ahalegin egin beharko zituela. Zenonek Akilesen ahalegin guztiek denbora jakin bat behar dutelako ideia erabili zuen, kontuan hartu gabe denbora, ahaleginetik ahaleginera, laburtuz doala, hau da, ahalegin bakoitzeko zerorantz jotzen duen beste segida bat osatzen dutela denborek. Gainera, denbora partzial infinituen batura -alegia, matematiketan segida esaten dena- konbergentea da, eta, beraz, Akilesek harrapatu, harrapatzen du dortoka.
- Ariketak
9. Kalkulatu limite hauek: 10. Asmatu bi segida, limitea 0 eta haien arteko zatiduraren
limitea 0 ez beste dutenak.11. Asmatu bi segida, limitea 0 izan eta lim
10. Asmatu bi segida, limitea 0 eta haien arteko zatiduraren
limitea 0 ez beste dutenak.11. Asmatu bi segida, limitea 0 izan eta lim
V. Segida dibergenteen arteko eragiketak
Infiniturantz edo minus infiniturantz jotzen duten bi segida
dibergenteen artean ere egin daiteke zenbait eragiketa.Baldin eta
eta . Hau da,
. Hau da, Baldin
Baldin eta
eta Hau da,
Hau da, Ordea, baldin bietako batek infiniturantz eta besteak minus infiniturantz jotzen badute, orduan, bi segiden baturaren limitea
Ordea, baldin bietako batek infiniturantz eta besteak minus infiniturantz jotzen badute, orduan, bi segiden baturaren limitea eta
eta
Infinituen arteko konparatzea
Hasteko, ikus ditzagun adibide batzuk :Bedi eta
eta . Orduan :
. Orduan : .
. , eta
, eta ,eta
,eta arteko baturak norantz jotzen duen jakiteko, segidan oso aurrera diren gaiak kalkulatuko ditugu, zeren,
arteko baturak norantz jotzen duen jakiteko, segidan oso aurrera diren gaiak kalkulatuko ditugu, zeren, -ren koefiziente 100 dela eta, lehenengo gaiek huts eginaraz diezagukete :
-ren koefiziente 100 dela eta, lehenengo gaiek huts eginaraz diezagukete : . Baina
. Baina . Beraz,
. Beraz, . Aitzitik, baldin
. Aitzitik, baldin , eta
, eta , orduan :
, orduan :
Definizioa
Baldin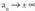 , eta
, eta , eta , gainera,
, eta , gainera, ; orduan
; orduan da ordena goragoko infinitua.
Baldin
da ordena goragoko infinitua.
Baldin , eta
, eta , eta, gainera,
, eta, gainera,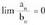 ; orduan
; orduan da ordena goragoko infinitua.
da ordena goragoko infinitua.
Baldin , eta
, eta , eta gainera,
, eta gainera,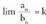 ; orduan
; orduan eta
eta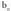 ordena bereko infinituak dira.Definizio hori kontuan harturik, infinituak konparatzeko erregela
hauek eman daitezke.a) Bi segiden gai orokorra n-ren berredura positibo bat biderkonstante bat baldin bada, bietatik zeinek duen berretzaile handiena,hori da goren ordenako infinitua. Baldin
ordena bereko infinituak dira.Definizio hori kontuan harturik, infinituak konparatzeko erregela
hauek eman daitezke.a) Bi segiden gai orokorra n-ren berredura positibo bat biderkonstante bat baldin bada, bietatik zeinek duen berretzaile handiena,hori da goren ordenako infinitua. Baldin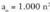 , eta
, eta , esate baterako; orduan, b ,, da ordena gorenekoa da, zeren :
, esate baterako; orduan, b ,, da ordena gorenekoa da, zeren : Baldin eta segida baten gai orokorra polinomio bat bada, goren ordenako gaiak -maila handiena duenak, alegia- adieraziko du haren limitea. Hala,
Baldin eta segida baten gai orokorra polinomio bat bada, goren ordenako gaiak -maila handiena duenak, alegia- adieraziko du haren limitea. Hala, segidak, maila handieneko gaiaren koefizientea positiboa denez, infiniturantz jotzen du.
segidak, maila handieneko gaiaren koefizientea positiboa denez, infiniturantz jotzen du.
Aitzitik, ; segidak minus infiniturantz jotzen du.b) Bi segiden gai orokorrak n mailako berreketak baldin badira (berrekizuna 1 baino handiagoa duelarik), berrekizun handiena duena goren ordenako infinitu bat da. Adibidez :
; segidak minus infiniturantz jotzen du.b) Bi segiden gai orokorrak n mailako berreketak baldin badira (berrekizuna 1 baino handiagoa duelarik), berrekizun handiena duena goren ordenako infinitu bat da. Adibidez :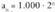 , eta
, eta baldin badira ; orduan, b goren ordenakoa da, zeren :
baldin badira ; orduan, b goren ordenakoa da, zeren : Beraz, hortik ateratzen denez halaber :
Beraz, hortik ateratzen denez halaber : segidak minus infiniturantz
segidak minus infiniturantz jotzen du, eta infiniturantz
jotzen du, eta infiniturantz , aldiz,
, aldiz, segidak.c) Bi segidetatik, baten gai orokorra n mailako berreketa baldin bada (berrekizuna 1 baino handiagoa duelarik), eta bestearena n- ren berreketa (berretzailea positiboa duela), esponentziala duena goren ordenakoa da. Adibidez :
segidak.c) Bi segidetatik, baten gai orokorra n mailako berreketa baldin bada (berrekizuna 1 baino handiagoa duelarik), eta bestearena n- ren berreketa (berretzailea positiboa duela), esponentziala duena goren ordenakoa da. Adibidez : , eta
, eta baldin badira ; orduan,
baldin badira ; orduan, goren ordenakoa da. Hori n-ri balio handiak emanez (75-tik gorakoak) frogatzen da. Beraz,
goren ordenakoa da. Hori n-ri balio handiak emanez (75-tik gorakoak) frogatzen da. Beraz, segidak minus infiniturantz
segidak minus infiniturantz joko du zeren eta beste honek, berriz,
joko du zeren eta beste honek, berriz, , infinturantz
, infinturantz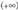 Biderkadurak, ordea, ez du aparteko arazorik :
Biderkadurak, ordea, ez du aparteko arazorik :
a) n mailako polinomioen arteko zatidura.
 indeterminazioaErregela eman aurretik, izan daitezkeen hiru kasuak aztertuko
dira adibide banaren bidez.• 1. adibidea
indeterminazioaErregela eman aurretik, izan daitezkeen hiru kasuak aztertuko
dira adibide banaren bidez.• 1. adibidea zeren
zeren eta
eta Lehenbizi izendatzailearen eragiketa burutu da ; gero, zenbakitzailea eta izendatzailea zati berretzailea handiena duen n-ren berredura egiten da (
Lehenbizi izendatzailearen eragiketa burutu da ; gero, zenbakitzailea eta izendatzailea zati berretzailea handiena duen n-ren berredura egiten da ( , kasu honetan). Ondorioa : n maila bera duten bi polinomioen arteko zatiduraren limitea maila handieneko koefizienteen arteko zatiduraren berdina da.• 2. adibidea
, kasu honetan). Ondorioa : n maila bera duten bi polinomioen arteko zatiduraren limitea maila handieneko koefizienteen arteko zatiduraren berdina da.• 2. adibidea Zenbakitzailea eta izendatzailea zati bietatik berretzaile txikiena
duenaren n-ren berredura handiena egiten da (n, kasu honetan).
Zenbakitzailea eta izendatzailea zati bietatik berretzaile txikiena
duenaren n-ren berredura handiena egiten da (n, kasu honetan).
Araua : n mailako bi polinomioen zatiduraren limitea, zenbakitzailearen
maila izendatzailearena baino txikiago denean, zero da.• 3. adibidea Aurreko kasuan bezala, zenbakitzailea eta izendatzailea zati bietan berretzaile txikiena duenaren n-ren berredura egiten da (
Aurreko kasuan bezala, zenbakitzailea eta izendatzailea zati bietan berretzaile txikiena duenaren n-ren berredura egiten da ( kasu honetan).• 4. adibidea
kasu honetan).• 4. adibidea Zenbakitzailea eta izendatzailea zati
Zenbakitzailea eta izendatzailea zati egin da, hori baita izendatzailearen berredura handiena. Horretarako, parentesi barruan, zati n egiten da.Emaitza orokortuz, zera esan daiteke : zenbakitzailearen maila izendatzailearena baino handiagoa denean, n mailako bi polinomioen arteko zatiduraren limitea
egin da, hori baita izendatzailearen berredura handiena. Horretarako, parentesi barruan, zati n egiten da.Emaitza orokortuz, zera esan daiteke : zenbakitzailearen maila izendatzailearena baino handiagoa denean, n mailako bi polinomioen arteko zatiduraren limitea da baldin zenbakitzailearen eta izendatzailearen maila handieneko gaiak zeinu bera baldin badute eta
da baldin zenbakitzailearen eta izendatzailearen maila handieneko gaiak zeinu bera baldin badute eta da, berriz, kontrako zeinua badute.Laburbilduz :Bedi
da, berriz, kontrako zeinua badute.Laburbilduz :Bedi n mailako bi polionomioenarteko zatidura, orduan :
Baldin
n mailako bi polionomioenarteko zatidura, orduan :
Baldin Baldin
Baldin Baldin p > q, eta a-ren eta b-ren zeinuak berdinak
Baldin p > q, eta a-ren eta b-ren zeinuak berdinak Baldin p > q, eta a-ren eta b-ren zeinuak desberdinak
Baldin p > q, eta a-ren eta b-ren zeinuak desberdinak • Adibideak
• Adibideak Ohar zaitez zenbakitzailea eta izendatzailea zati n egiten badira erro barruan diren gaiak zati
Ohar zaitez zenbakitzailea eta izendatzailea zati n egiten badira erro barruan diren gaiak zati
b) Infiniturantz jotzen duten segiden kendura.
 indeterminazioaKasu honetan ere ez da erregela orokorrik limiteak kalkulatzeko.
indeterminazioaKasu honetan ere ez da erregela orokorrik limiteak kalkulatzeko.
Izan ere, eta
eta aldatzean aldatu egiten baita limitea ere. Badira ordea arau batzuk. Limite hauek bi kasuren arabera sortzen dira.
aldatzean aldatu egiten baita limitea ere. Badira ordea arau batzuk. Limite hauek bi kasuren arabera sortzen dira.
Ikus dezagun, beraz, adibide batzuen bidez, nola ebazten diren limiteok.• 1. adibidea • 2. adibidea
• 2. adibidea • 3. adibidea
• 3. adibidea c) Segiden berredura.
c) Segiden berredura. 1. kasua
Baldin
1. kasua
Baldin , eta
, eta Adibidea:
Adibidea: 2. kasua
Baldin
2. kasua
Baldin , eta
, eta Adibidea :
Adibidea : 3. kasua
Baldin
3. kasua
Baldin Adibidea :
Adibidea : Adibidea :
Adibidea : 4. kasua
Baldin
4. kasua
Baldin , eta
, eta Adibidea :
Adibidea : 5. kasua
Baldin
5. kasua
Baldin izanik 0 < a < 1 , eta
izanik 0 < a < 1 , eta Adibidea :
Adibidea :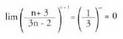 6. kasua
Baldin
6. kasua
Baldin , izanik 0 < a < 1, eta
, izanik 0 < a < 1, eta Adibidea:
Adibidea: 7. kasua
Baldin
7. kasua
Baldin eta
eta Adibidea:
Adibidea: 8. kasuaBaldin
8. kasuaBaldin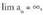 , eta
, eta Adibidea:
Adibidea:
Limite indeterminatuak
Limiteen berreduretan, zenbait kasutan, limitea indeterminatua
da, eta kasuz kasu aztertu behar da. Kasu hauek izan daitezke :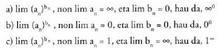 Hori guztia taula batera bil daiteke :
Hori guztia taula batera bil daiteke :
- Ariketak
12. Kalkulatu limite hauek, limiteak konparatzeko erregelak kontuan hartuz :
- Ariketak
13. Kalkulatu !imitC hauek : 14. Kalkulatu limite hauek :
14. Kalkulatu limite hauek :
V I. 1´ indeterminazioa. e zenbakia
 eta gisako limiteez arituko gara orain, hau da, berrekizunak 1-erantz eta berretzaileak infiniturantz
eta gisako limiteez arituko gara orain, hau da, berrekizunak 1-erantz eta berretzaileak infiniturantz jotzen duten berreketa gisa adierazten diren horiez.Azter dezagun, adibidez, segida hau,
jotzen duten berreketa gisa adierazten diren horiez.Azter dezagun, adibidez, segida hau,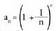 , eta kalkula ditzagun hura osatzen duten gaietako batzuk:
, eta kalkula ditzagun hura osatzen duten gaietako batzuk: Segida gorakorra eta goitik bornatua da, limiteduna, beraz. Limite
horren hurbileko bat lortzeko, segidan oso aurrera diren gaiak
kalkulatuko beharko dira.
Segida gorakorra eta goitik bornatua da, limiteduna, beraz. Limite
horren hurbileko bat lortzeko, segidan oso aurrera diren gaiak
kalkulatuko beharko dira. Ikusten denez, hirugarren zifra hamartarrak aldagabe irauten du
10.000. gaiaz geroztik, eta berdin 5. zifra hamartarrak 100.000.. aiaz geroztik. Segida horren limitearen 6 zifra zehatz lortu da,
beraz. Limite horri e zenbakia esaten zaio, eta zenbaki transzendentea
da.Esandakoaren arabera :
Ikusten denez, hirugarren zifra hamartarrak aldagabe irauten du
10.000. gaiaz geroztik, eta berdin 5. zifra hamartarrak 100.000.. aiaz geroztik. Segida horren limitearen 6 zifra zehatz lortu da,
beraz. Limite horri e zenbakia esaten zaio, eta zenbaki transzendentea
da.Esandakoaren arabera : Aurreko segida horren limitea ez ezik berrekizunak 1-erantz eta berretzaileak infiniturantz
Aurreko segida horren limitea ez ezik berrekizunak 1-erantz eta berretzaileak infiniturantz jotzen duen berredura gisa adierazita dauden -hau da,
jotzen duen berredura gisa adierazita dauden -hau da, indeterminazioa ematen duten- segida gehienen limitea kalkulatzeko bidea emango digu horrek.Ikus dezagun zenbait kasu :
indeterminazioa ematen duten- segida gehienen limitea kalkulatzeko bidea emango digu horrek.Ikus dezagun zenbait kasu : eta oro har
eta oro har ORO HARBaldin
ORO HARBaldin , eta
, eta Froga :
Froga : Adibideak
Adibideak Limiteak kalkulatzeko, prozesu hau jarraitu da :a)
Limiteak kalkulatzeko, prozesu hau jarraitu da :a) gisako indeterminazioa den frogatzen da.b) Zenbakitzailea zati izendatzailea egiten da, eta gisa honetara adierazten oinarria :
gisako indeterminazioa den frogatzen da.b) Zenbakitzailea zati izendatzailea egiten da, eta gisa honetara adierazten oinarria : d) Berretzailea bider zenbakitzailean geratu den adierazpena eta horren alderantzizkoa egiten da, berretzailea alda ez dadin. Eta
d) Berretzailea bider zenbakitzailean geratu den adierazpena eta horren alderantzizkoa egiten da, berretzailea alda ez dadin. Eta izendatzen bada, gisa honetako adierazpen bat r(n) geratzen da :
izendatzen bada, gisa honetako adierazpen bat r(n) geratzen da : Segiden berredura baten limitea oinarriaren limitea ber berretzailaren limitea dela aplikatuz, eta kontuan hartuz e zenbakia dela oinarriaren limitea, hau emaitza da :
Segiden berredura baten limitea oinarriaren limitea ber berretzailaren limitea dela aplikatuz, eta kontuan hartuz e zenbakia dela oinarriaren limitea, hau emaitza da :
e zenbakia
Zenbaki erreala da e zenbakia, eta, gutxi gorabehera, balio hau du :e = 2,71828182845904523536028Zenbaki traszendentea da e, hau da, ezin da adierazi zenbaki osoen erro
edota zatidura kopuru finitu baten bidez.XVII. mendean azaldu zen lehenbiziko aldiz, logaritmo nepertarren
oinarri gisa. Harrezkero matematikaren alor guztietara zabaldu da. Izena,
e zenbakia, Euler matekari suitzarrak jarri zion 1748an, bere Introductio in
Analysis Infiniturum liburuan.Modu askotara lor daiteke e zenbakia.Segiden limite gisa, adibidez :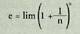 Serie gisa :
Serie gisa : Zatiki jarrai ez-periodiko gisa :
Zatiki jarrai ez-periodiko gisa : Eta beste era askotara.Erabili ere, gauza akostarako erabil daiteke. Analisian adibidez sarritan erabiltzen da oinarritzat e zenbakia duen berreketa funtzioa :
Eta beste era askotara.Erabili ere, gauza akostarako erabil daiteke. Analisian adibidez sarritan erabiltzen da oinarritzat e zenbakia duen berreketa funtzioa : Kontu batean, kapitalizatze Jarraiko interes finkoan ezarrita dagoen
kapitalaren bilakaera adierazteko balio dezake, adibidez, funtzio horrek.
Kontu batean, kapitalizatze Jarraiko interes finkoan ezarrita dagoen
kapitalaren bilakaera adierazteko balio dezake, adibidez, funtzio horrek.
Gai baten urritzea adierazteko era balio dezake, baldin eta, gai erradiaktiboen
desintegrazioan bezala, geratzen den masaren arabera urritzen bada.
Edo populazioaren gehikuntza adierazteko, baldin eta, aldeko ingurunean
eta harraparirik gabe bizi diren espezieetan gertatzen den bezala, duen
banako kopuruaren arabera gehitzen bada.Bi gakotatik zintzilik dagoen soka edo katea baten forma adierazteko ere
balio du. Forma hori bera du funtzioaren grafikoak. Kateanaria deitzen
zaio, eta ekuazio honen bidez adierazten da : Stirling-en formulan ere, n oso handia denean n-ren faktoriala hurbiltzeko
erabiltzen den formulan alegia, azaltzen da e zenbakia :
Stirling-en formulan ere, n oso handia denean n-ren faktoriala hurbiltzeko
erabiltzen den formulan alegia, azaltzen da e zenbakia : Baita probabilitate problemetan ere. Idazkari batek n karta n pertsonei zuzenduriko sobre banatan aliritzira sartzen baditu, nork berea ez duen karta hartzeko probabilitatea, n asko handitzen denean, hau da gutxi gorabehera: 1/e =_ 0,367...Baina berdintza harrigarriena, zenbaki konplexuak erabiliz lortzen dena
da:
Baita probabilitate problemetan ere. Idazkari batek n karta n pertsonei zuzenduriko sobre banatan aliritzira sartzen baditu, nork berea ez duen karta hartzeko probabilitatea, n asko handitzen denean, hau da gutxi gorabehera: 1/e =_ 0,367...Baina berdintza harrigarriena, zenbaki konplexuak erabiliz lortzen dena
da: Matematikan diren hiru zenbaki famatuenak elkarrekin batera daude berdintza horretan : e zenbakia, i irudizko banakoa, eta
Matematikan diren hiru zenbaki famatuenak elkarrekin batera daude berdintza horretan : e zenbakia, i irudizko banakoa, eta
- Ariketak
15. Kalkulatu limite hauek :
Eranskina
a) Gai orokorra duen segida beherakor hutsa da.Froga
Frogatu behar da
duen segida beherakor hutsa da.Froga
Frogatu behar da izatea, eta horretarako, elkarrekin konparatu behar dira bi gaiak, `Newtonen binomioaren" formulaz baliatuz :
izatea, eta horretarako, elkarrekin konparatu behar dira bi gaiak, `Newtonen binomioaren" formulaz baliatuz : .
. segidako gai bakoitza
segidako gai bakoitza segidan dagokiona baino txikiagoa da, edo berdina. Lehenego biaI berdinak dira, baina gero :
segidan dagokiona baino txikiagoa da, edo berdina. Lehenego biaI berdinak dira, baina gero :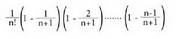 Gainera,
Gainera, , segidak gai bat gehiago du
, segidak gai bat gehiago du baino:
baino: Beraz,
Beraz, ; segidagorakorra da.b)
; segidagorakorra da.b) segida goitik bornatua dago, 3-k bornatua hainzuzen.Froga
segida goitik bornatua dago, 3-k bornatua hainzuzen.Froga SOLUZIOAK1.. )
SOLUZIOAK1.. ) Gorakorra, beraz.. )
Gorakorra, beraz.. ) . Gorakorra, beraz.2.. )
. Gorakorra, beraz.2.. ) Beherakorra, beraz.. )
Beherakorra, beraz.. ) . Beherakorra, beraz.3.a) Beheko bornea zero edo zero baino txikiagoa, eta goiko bornea
1 edo 1 baino handiagoa.b) Beheko bornea 2 edo 2 baino txikiagoa, eta goiko bornea
. Beherakorra, beraz.3.a) Beheko bornea zero edo zero baino txikiagoa, eta goiko bornea
1 edo 1 baino handiagoa.b) Beheko bornea 2 edo 2 baino txikiagoa, eta goiko bornea edo
edo ren baino handiagoa.c) Beheko bornea
ren baino handiagoa.c) Beheko bornea edo
edo baino txikiagoa, eta goiko bornea 1 edo 1 baino handiagoa.4.Ez da monotonoa, gaiek zeinuak txandakatzen dituzte. Ez dago
goitik bornatua, zeren edozein K kota K-aren zati osoaren ondoko
zenbaiki bikoiti osoa K baino termino handiagoa baita, eta azpitik
ere ez dago bornatuta, zeren -K-aren zati osoaren ondoko zenbaiki
bakoiti osoari K baino termino txikiagoa baitagokio.5..Goiko borneak : 3 eta 3 baino handiagoak. Beheko bornea: 2 edo 2 baino txikiagoak. 2,999999 ez da goi-borneetako bat,
baino txikiagoa, eta goiko bornea 1 edo 1 baino handiagoa.4.Ez da monotonoa, gaiek zeinuak txandakatzen dituzte. Ez dago
goitik bornatua, zeren edozein K kota K-aren zati osoaren ondoko
zenbaiki bikoiti osoa K baino termino handiagoa baita, eta azpitik
ere ez dago bornatuta, zeren -K-aren zati osoaren ondoko zenbaiki
bakoiti osoari K baino termino txikiagoa baitagokio.5..Goiko borneak : 3 eta 3 baino handiagoak. Beheko bornea: 2 edo 2 baino txikiagoak. 2,999999 ez da goi-borneetako bat, eta hurrengoak handiagoak baitira hura baino.6.
eta hurrengoak handiagoak baitira hura baino.6. , baldin eta
, baldin eta Beraz, limitea 2 du. Baldin e = 0,01, orduan
Beraz, limitea 2 du. Baldin e = 0,01, orduan Baldin 0,00005, orduan
Baldin 0,00005, orduan 7.
7. , baldin
, baldin Baldin e = 0,001, orduan
Baldin e = 0,001, orduan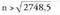 Baldin e = 0,00005, orduan
Baldin e = 0,00005, orduan . Beraz,
. Beraz, edo hurrengoak.8.a) 1 = 5 ; 1/n duen batugaia arbuiatuz lortzen da.b) 1 = -2 ; zenbakitzailea eta izendatzailea zati
edo hurrengoak.8.a) 1 = 5 ; 1/n duen batugaia arbuiatuz lortzen da.b) 1 = -2 ; zenbakitzailea eta izendatzailea zati egitean eta
egitean eta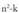 zatitzen dituen batugaiak arbuiatzean geratzen dena da.c)
zatitzen dituen batugaiak arbuiatzean geratzen dena da.c) ; zenbakitzailea eta izendatzailea zati
; zenbakitzailea eta izendatzailea zati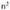 egitean, zenbakitzailea eta izendatzailea 3n eta -1 dira hurrenez hurren.d)
egitean, zenbakitzailea eta izendatzailea 3n eta -1 dira hurrenez hurren.d) . Zenbakitzailea eta izendatzailea zati n egitean, zenbakitzailea eta izendatzailea 5n eta 3 dira hurrenez hurren.e) 1 = 5. Lehenengo batugaia 2 da, eta bigarrena, zenbakitzailea eta
izendatzailea zati n egitean, 3/1.9.
. Zenbakitzailea eta izendatzailea zati n egitean, zenbakitzailea eta izendatzailea 5n eta 3 dira hurrenez hurren.e) 1 = 5. Lehenengo batugaia 2 da, eta bigarrena, zenbakitzailea eta
izendatzailea zati n egitean, 3/1.9. c) 0 ;
c) 0 ;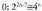 gaiak menperatzen baitu.f)
gaiak menperatzen baitu.f) zenbakitzailean eta -3n izendatzailean baitira indartsuenak.g)
zenbakitzailean eta -3n izendatzailean baitira indartsuenak.g) bider erroen batura.h) 9i) 0j) 1, izendatzaile komuna ateraz
bider erroen batura.h) 9i) 0j) 1, izendatzaile komuna ateraz