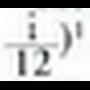Matematika»Analisiak
Analisiak
Zenbaki segidak
Askotan erabiltzen dira, eguneroko bizitzan, zenbaki segidak : dendari batek eguneko irabazien zerrenda egiten duenean, autopistako bidesarien ordain lekutik orduro zenbat auto igarotzen den zenbatzen, eta abar. Matematikan ere askotan erabiltzen dira zenbaki segidak: zenbaki bakoitien segidak, zenbaki lehenenak, zenbaki naturalen koadroenak... Baina matematikan ez ezik zientzien beste alor batzuetan ere, asko erabiltzen dira, hala nola biologian -ameba haztegi batean, hango ameba kopurua ordurik ordu nola aldatzen den zenbatzean-, giza geografian -herrialde bateko urteko biztanle gehikuntza zenbatzean- edo ekonomia geografian -herrialde bateko azken hamarraldiko labore ekoizpena zenbatzean-.
Definiziorako sarrera
Aurreko adibideetatik atera daitekeen bezala, zenbaki katea ordenatuak besterik ez dira segidak : {2, 4, 6, 8, 10,... }, adibidez, zenbaki bikoitien segida da ; {1, 4, 9, 16, 25,...}, berriz, zenbaki naturalen koadroena. Beste segida batzuk, ordea, hala nola {2, 3, 5, 8, 12, 17, 23,...} eta , zerenak diren zehaztea ez da batere erraza. Are gehiago, b irulan gogorra egin beharko da horien jarraipena asmatzeko, eta inoiz, azkenekoan, adibidez, ez da asmatzerik izango.Segida osatzen duten elementuei gai esaten zaie. Segidaren hurrenkeran gaiak zer tokia duen adierazten duen letra azpi-indizedun batez izendatzen dira,
, zerenak diren zehaztea ez da batere erraza. Are gehiago, b irulan gogorra egin beharko da horien jarraipena asmatzeko, eta inoiz, azkenekoan, adibidez, ez da asmatzerik izango.Segida osatzen duten elementuei gai esaten zaie. Segidaren hurrenkeran gaiak zer tokia duen adierazten duen letra azpi-indizedun batez izendatzen dira, edo laburburen bidez, bestela:
edo laburburen bidez, bestela: edo , besterik gabe,
edo , besterik gabe,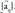
Definizioa
Zenbaki natural bakoitzari zenbaki erreal bat egokitzen dion aplikazioa
da zenbaki errealen segida, hau da : n-ren irudia adierazteko, aplikazioen ohiko notazioa erabili ordez
n-ren irudia adierazteko, aplikazioen ohiko notazioa erabili ordez , azpi-indizeen notazioa erabiltzen da, goraxeago aipatu den bezala.Segida baten hurrenkera argituko bada, hura osatzen duten gaiak
ateratzeko bete beharreko araua aurkitu behar da. Nolako segida
halako araua :• Adibideaka) {-1, 3, 7, 11, 15,...} segidan, adibidez, gai bakoitza aurrekoari 4 batuz lortzen da. Hori honela adierazten da :
, azpi-indizeen notazioa erabiltzen da, goraxeago aipatu den bezala.Segida baten hurrenkera argituko bada, hura osatzen duten gaiak
ateratzeko bete beharreko araua aurkitu behar da. Nolako segida
halako araua :• Adibideaka) {-1, 3, 7, 11, 15,...} segidan, adibidez, gai bakoitza aurrekoari 4 batuz lortzen da. Hori honela adierazten da : b) {1, 4, 9, 16, 25,...} segidan, berriz, gai bakoitza hurrenkeran duen lekuaren koadroa da. Hau da:
b) {1, 4, 9, 16, 25,...} segidan, berriz, gai bakoitza hurrenkeran duen lekuaren koadroa da. Hau da: c) {2, 3, 5, 7, 11, 13, 17, 19, 23,...} zenbaki lehenen segida da.
c) {2, 3, 5, 7, 11, 13, 17, 19, 23,...} zenbaki lehenen segida da.
Segida horretan ez dago biderik, zenbaki lehen bat hurrenkeran
duen lekuaren edo aurrean duen gaiaren arabera lortzeko.d) 11, 1, 2, 3, 5, 8, 13,...1 edo Fibonacciren segida deituan gai bakoitza aurreko bien batura da. Beraz,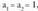 eta
eta f)
f) segidan honela adieraz daiteke n-garrenterminoa :
segidan honela adieraz daiteke n-garrenterminoa : Aurreko adibideetako batzuetan, b) edo f) adibideetan, esate baterako, duen kokalekuaren araberako formula baten bidez lortzen da n- garren terminoa; segidaren gai orokorra esaten zaio formulari eta aukera ematen du segidako edozein gai, aurrekoak ez ezagututa ere, zuzenean kalkulatu ahal izateko. Beste adibide batzuetan, berriz, a), d) eta e) adibideetan, esaterako, n-garren gaia aurreko gai(eta)tik ateratzen da ; errekurrentzia esaten zaio gaiak lortzeko bide horri. Segida baten hurrenkera bide hori erabiliz zehaztu nahi bada, n-garrenaren aurrekoa ez ezik segidako lehenengo (edo lehenengo bi) gaia(k) ere ezagutu behar d(ir)a. Metodo horrek, baina, badu eragozpen bat, segidan aurrera den gai bat ezagutzeko haren aurreko guztiak kalkulatu behar izatea aurretik. Azkenik, beste kasu batzuetan, a) edo d) adibideetan, esate baterako, errekurrentzia legea ez ezik gai orokorra ere kalkula daiteke. Kalkulu hori ordea, oso erraza den bezala lehenengo kasurako
Aurreko adibideetako batzuetan, b) edo f) adibideetan, esate baterako, duen kokalekuaren araberako formula baten bidez lortzen da n- garren terminoa; segidaren gai orokorra esaten zaio formulari eta aukera ematen du segidako edozein gai, aurrekoak ez ezagututa ere, zuzenean kalkulatu ahal izateko. Beste adibide batzuetan, berriz, a), d) eta e) adibideetan, esaterako, n-garren gaia aurreko gai(eta)tik ateratzen da ; errekurrentzia esaten zaio gaiak lortzeko bide horri. Segida baten hurrenkera bide hori erabiliz zehaztu nahi bada, n-garrenaren aurrekoa ez ezik segidako lehenengo (edo lehenengo bi) gaia(k) ere ezagutu behar d(ir)a. Metodo horrek, baina, badu eragozpen bat, segidan aurrera den gai bat ezagutzeko haren aurreko guztiak kalkulatu behar izatea aurretik. Azkenik, beste kasu batzuetan, a) edo d) adibideetan, esate baterako, errekurrentzia legea ez ezik gai orokorra ere kalkula daiteke. Kalkulu hori ordea, oso erraza den bezala lehenengo kasurako , Fibonacciren segidaren kasurako, berriz, zaila da; orain ez baino aurrerago aztertuko da kasu hori polikiago.
, Fibonacciren segidaren kasurako, berriz, zaila da; orain ez baino aurrerago aztertuko da kasu hori polikiago.
- Ariketak
1. Gehitu Ona gai segida hauetako bakoitzari : 2. Aurkitu gai orokor hauei dagozkien segiden lehenengo 5 gaiak :
2. Aurkitu gai orokor hauei dagozkien segiden lehenengo 5 gaiak : 3. Kalkulatu errekurrentzia lege hauei dagozkien segiden
lehenengo 6 gaiak:
3. Kalkulatu errekurrentzia lege hauei dagozkien segiden
lehenengo 6 gaiak: 4. Asmatu errekurrentzia lege bat eta adierazi lege horri
legozkiokeen segidaren lehenengo 6 gaiak.5. Aurkitu segida hauen gai orokorra :
4. Asmatu errekurrentzia lege bat eta adierazi lege horri
legozkiokeen segidaren lehenengo 6 gaiak.5. Aurkitu segida hauen gai orokorra : 6. Aurkitu segida hauen errekurrentzia legea :
6. Aurkitu segida hauen errekurrentzia legea :
Fibonacciren segida
Leonardo Pisano (1180-1250?), Fibonacci ere deitua -Bonacciren seme,
alegia-, Pisan sortu zen, merkatari familia batean. Gaztetan arabiar
herrialdeetan ibili zen eta hango matematika ezagutzeko aukera izan zuen.
1202an Liber abaci idatzi zuen, garrantzi handiko liburua, besteak beste
arabiar edo indiar zifren erabilera zabaldu zuelako Europako Mendebalean.
Leonardo Pisanok problema asko planteatu zituen, eta gaur egun problema
horietako batengatik da batez ere ezaguna :"Gizon batek untxi bikote bat jarri du hesiz inguraturiko leku batean.
Zenbat untxi bikote izango dira urte baten buruan, baldin eta, hilabetero,
bikote bakoitzarengandik beste bat sortzen bada eta bikote berria ere bigarren
hilabetez gero umeak egiten hasten bada?"Hasieran bikote bat egongo da, eta nola bikoteak bi hilabete behar
dituen umeak egiten hasi baino lehen, bat bakarrik egongo da lehenengo
eta bigarren hilabeteetan. Hirugarrenerako ordea bikote bat sortuko da ;
hilabete horretan, beraz, 2 bikote izango dira. Laugarrenean berriro umetuko
da : hiru bikote, beraz. Gainera, aurrena sorturiko ume bikotea ere
umeak egiten hasiko da, eta, hala, bosgarren hilabeterako 5 bikote izango
dira, bi berri eta lehengo hirurak. Hurrengo hilabetean bi hilabete lehenago
bazirenak umetuko dira eta, beraz, zortzi untxi bikote izango dira guztira.
Hala, handik hara eta hilez hil, bi hilabete lehenago zegoen untxi
bikote adina ume bikote berri gehituko zaizkie lehendik ziren bikoteei.
Bikote kopurua, beraz, segida errepikari bat izango da, non... : Joan den mendeko matematikariek arretaz aztertu zuten segida hori,
oso ezaugarri bereziak zituela konturatu baitziren.Hauek dira segidaren lehenengo hogeitabost gaiak :
Joan den mendeko matematikariek arretaz aztertu zuten segida hori,
oso ezaugarri bereziak zituela konturatu baitziren.Hauek dira segidaren lehenengo hogeitabost gaiak : Zenbait ezaugarri berezi :- Ondoz ondoko bi gai lehenak dira elkarrekin.- 4ren anizkoitz diren lekuetan dauden gaiak hiruz zati daitezke, 5en
anizkoitz diren lekuetan daudenak bostez, 8ren anizkoitz diren lekuetan
daudenak zazpiz.Hirugarren, bosgarren, zazpigarren, hamaika eta hamairugarren lekuetan diren gaiak zenbaki lehenak direla eta, n zenbaki lehena baldin bada a erelehena dela pentsa daiteke. Ez da hala, ordea :
Zenbait ezaugarri berezi :- Ondoz ondoko bi gai lehenak dira elkarrekin.- 4ren anizkoitz diren lekuetan dauden gaiak hiruz zati daitezke, 5en
anizkoitz diren lekuetan daudenak bostez, 8ren anizkoitz diren lekuetan
daudenak zazpiz.Hirugarren, bosgarren, zazpigarren, hamaika eta hamairugarren lekuetan diren gaiak zenbaki lehenak direla eta, n zenbaki lehena baldin bada a erelehena dela pentsa daiteke. Ez da hala, ordea : Fibonacciren segidaren gaien artean oso harreman bitxiak sortzen dira.
Fibonacciren segidaren gaien artean oso harreman bitxiak sortzen dira.
Esate baterako :- - zati daiteke baldin m a-z zati badaiteke.-
- zati daiteke baldin m a-z zati badaiteke.- -
- Segida gero eta handiagoa da, baina froga daitekeenez :
Segida gero eta handiagoa da, baina froga daitekeenez : Hau da,
Gai orokorra formula baten bidez lor daiteke, baina ez da oso baliagarria bide hori, zer adierazpena duen kontuan harturik:
Hau da,
Gai orokorra formula baten bidez lor daiteke, baina ez da oso baliagarria bide hori, zer adierazpena duen kontuan harturik: Non
Non eta
eta
Progresio aritmetikoak
Definizioa
Gai bakoitza aurrekoari kopuru bera gehituz lortzen den zenbaki
segida da progresio aritmetikoa. Kopuru horri diferentzia esaten zaio.Aztertu arretaz segida hauek : Progresio aritmetikoak dira guztiak. Lehenengoan gai bakoitza aurrekoari 5 batuz lortu da. Beraz,
Progresio aritmetikoak dira guztiak. Lehenengoan gai bakoitza aurrekoari 5 batuz lortu da. Beraz,
Nola jakin segida bat progresio aritmetikoa den?
Segidako gai bakoitzaren eta aurrekoaren arteko kendurak konstantea
izan behar du ; konstante hori bera da hain zuzen progresioaren
diferentzia.Hau da :
Progresio aritmetikoaren gai orokorra
Ikusi nola lortzen diren segida bateko gaiak lehenengo gaiaren eta
diferentziaren bidez : Beraz, segidako gai bat lortzeko, lehenengo gaiari, haren eta aurkitu
nahi denaren artean dagoen leku diferentzia adinbat aldiz batu
behar zaio d. Orobat lor daiteke beste edozeinetatik abiatuz :
Beraz, segidako gai bat lortzeko, lehenengo gaiari, haren eta aurkitu
nahi denaren artean dagoen leku diferentzia adinbat aldiz batu
behar zaio d. Orobat lor daiteke beste edozeinetatik abiatuz : • AdibideakAurkitu segida hauen gai orokorrak :
• AdibideakAurkitu segida hauen gai orokorrak : Soluzioak
Soluzioak ; ordezkatu, eta : 21 = -7 + 4d ; 28 = 4d; d = 7.
; ordezkatu, eta : 21 = -7 + 4d ; 28 = 4d; d = 7.
Gai orokorra, beraz, hau da : an = -7 + 7(n-4) = -7 + 7n-28 = 7n - 35 a eta b zenbakien artean n erdikari diferentzial interpolatzea da lehenengo gaia a duen eta b, berriz,
a eta b zenbakien artean n erdikari diferentzial interpolatzea da lehenengo gaia a duen eta b, berriz,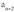 gaia den progresio aritmetikoa eratzea.• AdibideaEman dezagun 10 gai interpolatu nahi ditugula 504 eta 691 artean. Goiko definizioaren arabera,
gaia den progresio aritmetikoa eratzea.• AdibideaEman dezagun 10 gai interpolatu nahi ditugula 504 eta 691 artean. Goiko definizioaren arabera, izango da, eta
izango da, eta
- Ariketa
7. Interpolatu 15 gai -3 eta 109 artean.
Progresio aritmetiko bateko n aien arteko batura
Mutur banatatik distantzia berera diren gaien baturak betetzen
duen ezaugarri bat erabiliko da n gaien baturaren formula lortzeko.
Hurrengo segidan ikus daiteke nola :{1 7, 13, 9, 5, 1, -3, -7, -11,...1 segidan froga daiteke ezen 17 + (-11)
=13+(-7)=9+(-3)=5+1=6dela.Alegia : ,non
,non segidaren erdiko gaia baita (segidako gai kopurua bakoitia denean bakarrik izaten da).Ezaugarri hori erabiliko da, beraz, n gaien baturaren formula ateratzeko
:
segidaren erdiko gaia baita (segidako gai kopurua bakoitia denean bakarrik izaten da).Ezaugarri hori erabiliko da, beraz, n gaien baturaren formula ateratzeko
: Ordena aldatu, eta :
Ordena aldatu, eta : Berdintza biak gaiz gai batu, eta :
Berdintza biak gaiz gai batu, eta : Baina frogatu berri denez, batugai horiek beti dira
Baina frogatu berri denez, batugai horiek beti dira Hortaz,
Hortaz, Eta, beraz :
Eta, beraz : • AdibideakAurkitu lehenengo n zenbaki naturalen baturaSoluzioa :
• AdibideakAurkitu lehenengo n zenbaki naturalen baturaSoluzioa :
- Ariketak
8. Kalkulatu lehenengo n zenbaki bakoitien batura.
Harrituta zaude emaitzagatik?9. Progresio aritmetiko batean eta d = 2 direla kontuan harturik, kalkulatu al eta lehenengo 15 gaien batura.10. Kalkulatu zenbat diren hiru zifra esangarriz osaturiko
Tren anizkoitzak. Kalkulatu zifra horien batura.inserted text
eta d = 2 direla kontuan harturik, kalkulatu al eta lehenengo 15 gaien batura.10. Kalkulatu zenbat diren hiru zifra esangarriz osaturiko
Tren anizkoitzak. Kalkulatu zifra horien batura.inserted text eta
eta direla kontuan harturik, kalkulatu
direla kontuan harturik, kalkulatu eta
eta
Progresio geometrikoak
Definizioa
Gai bakoitza aurrekoari kopuru bera biderkatuz lortzen den zenbaki
segida da progresio aritmetikoa. Kopuru horri arrazoi esaten zaio.• Adibideaka) {1, 3, 9, 27, 8 1,...} progresio geometrikoan arrazoia 3 da.b) {2, 2'2, 2'42, 2'662, 2'9282,...} progresio geometrikoan arrazoia 1'1 da.c) progresio geometrikoan arrazoia da
progresio geometrikoan arrazoia da
Nola jakin segida bat progresio geometrikoa den?
Segidako gai bakoitzaren eta horren aurrekoaren arteko zatidurak
konstantea izan behar du ; konstante hori da hain zuzen progresioaren
arrazoia. Hau da : c) adibidean
c) adibidean
- Ariketak
14. Aurkitu zenbaki segida hauek progresio geometrikoak diren edo ez. Hala baldin badira, aurkitu progresioaren arrazoia ere :
Gai orokorra nola kalkulatu
Gai batetik hurrengora igarotzeko delako gaia eta arrazoia biderkatu
behar direla kontuan harturik, berdintza hauek lortuko dira : Hau da, segidako lehenengo gaia jakinik beste edozein gai jakiteko,
lehenegoari arrazoia ber bien arteko leku diferentzia (n-1) biderkatu
behar zaio.Orobat lor daiteke n-garren gaia beste edozein gaitik (a k ), abiatuz.
Hau da, segidako lehenengo gaia jakinik beste edozein gai jakiteko,
lehenegoari arrazoia ber bien arteko leku diferentzia (n-1) biderkatu
behar zaio.Orobat lor daiteke n-garren gaia beste edozein gaitik (a k ), abiatuz.
Horretarako aski da gai hori arrazoia ber bien arteko leku diferentziaz
(n-k) bideraktzea. Honela adierazten da hori : • Adibideaka) Kalkulatu {3, 9, 27,...} progresioaren zazpigarren gaia.(Soluzioa :
• Adibideaka) Kalkulatu {3, 9, 27,...} progresioaren zazpigarren gaia.(Soluzioa : b) Progresio geometriko batean zortzigarren gaia 1.280 baldin
bada, eta arrazoia 2, kalkulatu segidaren lehenengo gaia.(Soluzioa :
b) Progresio geometriko batean zortzigarren gaia 1.280 baldin
bada, eta arrazoia 2, kalkulatu segidaren lehenengo gaia.(Soluzioa : beraz
beraz c) Progresio geometrikoa batean
c) Progresio geometrikoa batean baldin bada, eta
baldin bada, eta kalkulatu arrazoia.(Soluzioa :
kalkulatu arrazoia.(Soluzioa : zenbakiaren zortzigarren erroa da, alegia r = ±5)
zenbakiaren zortzigarren erroa da, alegia r = ±5)
- Ariketak
15. Kalkulatu progresio honen 10. gaia : 16. Progresio geometriko batean
16. Progresio geometriko batean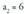 eta
eta
Interpolazio geometrikoa
a eta b zenbakien artean n erdikari geometriko interpolatzea da
lehenengo terminoa a duen eta b, berriz, n+2 lekuan duen progresio
geometriko bat eratzea.• AdibideaInterpolatu 3 erdikari geometriko
5
eta 20 artean. eta
eta artean.Soluzioa
artean.Soluzioa r, beraz,
r, beraz, -ren laugarren erroa izango da,
-ren laugarren erroa izango da, .Eta bi zenbakien artean interpolatu nahi diren hiru zenbakiak, berriz,
.Eta bi zenbakien artean interpolatu nahi diren hiru zenbakiak, berriz, eta
eta izango dira baldin
izango dira baldin bada, eta ,
bada, eta , eta
eta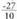 berriz, baldin
berriz, baldin
- Ariketak
17. a) Interpolatu 5 erdikari geometriko eta
eta
Mutur banatatik distantzia berean diren bi gaien legea
 progresio geometrikoan lege hau betetzen da :
progresio geometrikoan lege hau betetzen da :
Progresio geometriko bateko n gaien biderkaketa
Aurreko legeaz baliatuko gara berdintza hau frogatzeko :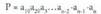 Biderkagaien ordena aldatu, eta....
Biderkagaien ordena aldatu, eta.... Bi berdintzak gaiz gai biderkatu, eta...
Bi berdintzak gaiz gai biderkatu, eta...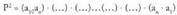 Mutur banatatik distantzia berean diren gaien biderkaketaren legea dela eta,
Mutur banatatik distantzia berean diren gaien biderkaketaren legea dela eta, bezalako n biderkagai daude azken berdintzan. Beraz,
bezalako n biderkagai daude azken berdintzan. Beraz, Eta hortik, formula hau ateratzen da.
Eta hortik, formula hau ateratzen da. • AdibideaProgresio hau emanik,
• AdibideaProgresio hau emanik, kalkulatu segidarenlehenengo 9 gaien biderkadura.Soluzioa
kalkulatu segidarenlehenengo 9 gaien biderkadura.Soluzioa
- Ariketa
18. Kalkulatu progresio hauen lehenengo 7 gaien biderkadura .
Progresio geometriko bateko n gaien batura
Batuketa hau egin behar da : Biderkatu berdintza horretako osagai guztiak r arrazoiaz :
Biderkatu berdintza horretako osagai guztiak r arrazoiaz : Baina r-z biderkatzean, progresioko gai bakoitza hurrena bihurtzen da. Beraz, ordezkatu batuketako gaiak, salbu eta azkena -hori berdin utzi-:
Baina r-z biderkatzean, progresioko gai bakoitza hurrena bihurtzen da. Beraz, ordezkatu batuketako gaiak, salbu eta azkena -hori berdin utzi-: Kendu adierazpen honi(1) eta ezabatu berdinak diren gai guztiak:
Kendu adierazpen honi(1) eta ezabatu berdinak diren gai guztiak: Atera berdintzako lehenengo atalaren biderkatzaile komuna :
Atera berdintzako lehenengo atalaren biderkatzaile komuna : Bakandu S, eta formula hau ateratzen da :
Bakandu S, eta formula hau ateratzen da : Adierazpen hau aldatueta lehenengo gaiaren eta arrazoiaren arabera adieraz daiteke
Adierazpen hau aldatueta lehenengo gaiaren eta arrazoiaren arabera adieraz daiteke -ren ordez
-ren ordez jarriz:
jarriz: • AdibideaSegida hau emanik,
• AdibideaSegida hau emanik,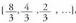 , kalkulatu lehenengo 7 gaien batura.Soluzioa
, kalkulatu lehenengo 7 gaien batura.Soluzioa
- Ariketak
19. Kalkulatu progresio hauen lehenengo...a) 6 gaien batura {6, 12, 24,...}b) 7 gaien batura {8'1, 27, 0'9,...}
c) 8 gaien batura d) 9 gaien batura
d) 9 gaien batura 20. Kalkulatu
20. Kalkulatu dituen progresio geometrikoaren lehenengo 8 gaiak.2 1. Kalkulatu a, = 972 eta r = 3 dituen progresio geometrikoaren
lehenengo 5 gaien batura.22. Kalkulatu lehenengo 5 gaien batura 1.452 eta r = 3 diruen progresio geometrikoaren
dituen progresio geometrikoaren lehenengo 8 gaiak.2 1. Kalkulatu a, = 972 eta r = 3 dituen progresio geometrikoaren
lehenengo 5 gaien batura.22. Kalkulatu lehenengo 5 gaien batura 1.452 eta r = 3 diruen progresio geometrikoaren eta
eta
Progresio geometriko mugagabe baten gaien batura
Dakigunez, progresio geometriko baten n gaien batura honela da : Baldin n mugagabe handitzen bada, lau aldaera izan ditzake batuketaren
kalkuluak, r-k zer balio duen.Baldin r>7 bada,
Baldin n mugagabe handitzen bada, lau aldaera izan ditzake batuketaren
kalkuluak, r-k zer balio duen.Baldin r>7 bada, -ren balioa mugagabe handitzen da, progresioa gorakorra da eta baturak infiniturantz jotzen du.Baldin r = 1 bada, gai guztiak berdinak dira eta haien baturak,
-ren balioa mugagabe handitzen da, progresioa gorakorra da eta baturak infiniturantz jotzen du.Baldin r = 1 bada, gai guztiak berdinak dira eta haien baturak,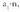 , infiniturantz jotzen du.
, infiniturantz jotzen du.
Baldin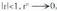 zeren 1 baino zenbaki txikiagoen berredurak txikituz doaz berretzailea handitu ahala, eta zerorantz hurbiltzen dira.
zeren 1 baino zenbaki txikiagoen berredurak txikituz doaz berretzailea handitu ahala, eta zerorantz hurbiltzen dira.
Infinitu gaien batura lortzeko aurreko formula erabiliko da, -ren ordez 0 jarriz :
-ren ordez 0 jarriz : Baldin
Baldin bada, segida oszilatzailea da, eta batura, indeterminatua.• Adibideaka) Aurkitu progresio geometriko indefinitu honen batura :
bada, segida oszilatzailea da, eta batura, indeterminatua.• Adibideaka) Aurkitu progresio geometriko indefinitu honen batura : Soluzioa
Soluzioa b) Erabili formula hori zenbaki hamartar periodiko honen frakzio
edo zatiki sortzailea aurkitzeko : 2'4090909... = 2'4 + 0,0009 +
O'00009 + O'0000009...=Bigarren batugaiaz aurrerrako infinitu batugaiek progresio geometrikoa
eratzen dute, arrazoia r = 0'01 dutela. Formula batugai
horietara aplikatuz gero, hau lortzen da :
b) Erabili formula hori zenbaki hamartar periodiko honen frakzio
edo zatiki sortzailea aurkitzeko : 2'4090909... = 2'4 + 0,0009 +
O'00009 + O'0000009...=Bigarren batugaiaz aurrerrako infinitu batugaiek progresio geometrikoa
eratzen dute, arrazoia r = 0'01 dutela. Formula batugai
horietara aplikatuz gero, hau lortzen da :
- Ariketak
23. Aurkitu progresio mugagabe hauen gaien batura : 24. Progresio geometriko beherakor bateko infinitu gaien batura 3 da, eta lehenengo gaia
24. Progresio geometriko beherakor bateko infinitu gaien batura 3 da, eta lehenengo gaia , Kalkulatu arrazoia.25. Elezahar batek dioenez, xake jokoa asmatu zuenak
zera eskatu omen zuen ordainetan : gari ale bat taulako
lehenengo laukitxoarengatik, bi ale bigarren laukitxoarengatik,
lau ale hirugarrenarengatik, eta horrela
hurrenez hurren, aurreko laukitxoko ale kopurua
bikoiztuz beti, taulako 64. laukira iritsi arte. Kalkulatu
zenbat ale pilatu zuen guztira eta zenbat pisatuko
zuen, tonatan, guztiak. Eman dezagun ale bakoitzak
dezigramo bat (1 dg) pisatzen duela.26. Alde bakoitzak 3 cm dituen lauki baten aldeen erdiko
puntuak marra batez zein bere ondokoarekin lotu eta
lauki bat eratu da aurrenekoaren barruan. Bigarrenean
gauza bera eginez, beste bat lortu da gero, eta beste
bat hurrena, eta horrela hurrenez hurren, ezin bukatu
ahalean. Kalkulatu lauki guztien areen batura.27. Behinola eskale batek hau proposatu omen zion diruzale
zeken bati : nik pezeta bat emango dizut hilaren
lehenean, 2 pezeta bigarren egunean, 3 hirugarrenan,
eta horrela hurrenez hurren, pezeta bat gehiago egunero,
hilak 30 arte. Zuk ordainez 0'001 xentimo
eman beharko didazu lehenengo egunean, O'0002
xentimo bigarrenean, O'0004 hirugarrenean eta
horrela, aurrekoaren bikoitza egunero, hila bukatuarte. Zekenak pentsatu zuen sekulako negozioa egin
behar zuela eta bi aldiz pentsatu gabe onartu zuen trukea
. Erabaki zuzena hartu zuen? Kalkulatu zenbat
diru ordaindu zuen bakoitzak.28. Aldeak 2 cm-koak dituen triangelu ekilatero bateko
aldeen erdiko puntuak marra batez lotu eta beste
triangelu ekilatero bat eratu da aurrekoaren barruan.
, Kalkulatu arrazoia.25. Elezahar batek dioenez, xake jokoa asmatu zuenak
zera eskatu omen zuen ordainetan : gari ale bat taulako
lehenengo laukitxoarengatik, bi ale bigarren laukitxoarengatik,
lau ale hirugarrenarengatik, eta horrela
hurrenez hurren, aurreko laukitxoko ale kopurua
bikoiztuz beti, taulako 64. laukira iritsi arte. Kalkulatu
zenbat ale pilatu zuen guztira eta zenbat pisatuko
zuen, tonatan, guztiak. Eman dezagun ale bakoitzak
dezigramo bat (1 dg) pisatzen duela.26. Alde bakoitzak 3 cm dituen lauki baten aldeen erdiko
puntuak marra batez zein bere ondokoarekin lotu eta
lauki bat eratu da aurrenekoaren barruan. Bigarrenean
gauza bera eginez, beste bat lortu da gero, eta beste
bat hurrena, eta horrela hurrenez hurren, ezin bukatu
ahalean. Kalkulatu lauki guztien areen batura.27. Behinola eskale batek hau proposatu omen zion diruzale
zeken bati : nik pezeta bat emango dizut hilaren
lehenean, 2 pezeta bigarren egunean, 3 hirugarrenan,
eta horrela hurrenez hurren, pezeta bat gehiago egunero,
hilak 30 arte. Zuk ordainez 0'001 xentimo
eman beharko didazu lehenengo egunean, O'0002
xentimo bigarrenean, O'0004 hirugarrenean eta
horrela, aurrekoaren bikoitza egunero, hila bukatuarte. Zekenak pentsatu zuen sekulako negozioa egin
behar zuela eta bi aldiz pentsatu gabe onartu zuen trukea
. Erabaki zuzena hartu zuen? Kalkulatu zenbat
diru ordaindu zuen bakoitzak.28. Aldeak 2 cm-koak dituen triangelu ekilatero bateko
aldeen erdiko puntuak marra batez lotu eta beste
triangelu ekilatero bat eratu da aurrekoaren barruan.
Bigarren triangeluan gauza bera egin eta beste bat,
hirugarrena, eratu da gero, eta horrela eginez segitu da
ezin bukatu ahalean. Kalkulatu triangelu horien guztien
areen batura.
Interes elkartua - Kapitalizatzea - Kredituaren amortizazioa
Lantzera goazen gai hau finantza eta merkataritza matematikaren
alorrari dagokio. Egin behar duguna, funtsean, zera da : segidak
aplikatu, interes elkartuko kapitalizazioari buruzko problemetan.
Progresio geometrikoak aztertzean ikasi ditugun formulak oso
baliagarri gertatuko zaizkigu horretarako, batez ere kredituen amortizaziorako
urteroko finkoak kalkulatzeko.
Interes elkartuko kapitalizatzea
Kapital bat interes elkartuan jartzean kapitalizazio aldi bakoitzaren
buruan eskuraturiko interesak kapitalari gehitzen zaizkio interes
gehiago eman dezaten.Kapital C bat banku batean uzten da, eta interes elkartuan jartzen,
denbora t batez (urtetan adierazia), % hainbateko r korrituarekin.100 pezetek urte baten buruan ematen duten etekina da r (korritua edo ehuneko zenbatekoa). Kalkuluak errazteko, bateko zenbatekoa erabiliko da,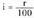 ; hau da, zenbat ematen duen pezeta batek urte batean.Hortik formula bat ateratzen da, C kapitala hainbat t urteren
buruan zenbat bihurtzen den kalkulatzeko.Baldin pezeta lek i pezeta ematen badu urte baten buruan, eta (1
+ i) pezeta bihurtzen bada...Lehenengo urtean C pezetek
; hau da, zenbat ematen duen pezeta batek urte batean.Hortik formula bat ateratzen da, C kapitala hainbat t urteren
buruan zenbat bihurtzen den kalkulatzeko.Baldin pezeta lek i pezeta ematen badu urte baten buruan, eta (1
+ i) pezeta bihurtzen bada...Lehenengo urtean C pezetek pezeta emango duta, eta
pezeta emango duta, eta pezeta bihurtuko dira.Bigarren urtean C (1 + i) pezetek
pezeta bihurtuko dira.Bigarren urtean C (1 + i) pezetek pezeta emango dute, eta
pezeta emango dute, eta pezeta bihurtuko dira.Hirugarren urtean
pezeta bihurtuko dira.Hirugarren urtean pezetek
pezetek emango dute, eta
emango dute, eta ; pezeta bihurtuko dira.Eta horrela hurrenez hurren, t-garren urtearen bukaeraraino.
; pezeta bihurtuko dira.Eta horrela hurrenez hurren, t-garren urtearen bukaeraraino.
Kapitala, orduan, hau izango da : Ikusten denez, hasierako kapitalak eta lehenengo, bigarren, hirugarren,
... t-garren urtearen buruan lortutakoek progresio geometriko
bat eratzen dute. Progresioaren arrazoia (1 + i) da, eta horrek
esan nahi du kapitala, urtez urte, kopuru horrez biderkatuko dela :
Ikusten denez, hasierako kapitalak eta lehenengo, bigarren, hirugarren,
... t-garren urtearen buruan lortutakoek progresio geometriko
bat eratzen dute. Progresioaren arrazoia (1 + i) da, eta horrek
esan nahi du kapitala, urtez urte, kopuru horrez biderkatuko dela : Hasierako kapitala 0. urtearen buruan (eta 1. urtearen hasieran) dagoen kapitala da, eta
Hasierako kapitala 0. urtearen buruan (eta 1. urtearen hasieran) dagoen kapitala da, eta , berriz, t-garren urtearen buruan dagoena.• AdibideaZenbat diru bihurtuko da, 4 urteren buruan, milioi bat pezeta,
interes elkartuan (%7) jarria?Soluzioa
, berriz, t-garren urtearen buruan dagoena.• AdibideaZenbat diru bihurtuko da, 4 urteren buruan, milioi bat pezeta,
interes elkartuan (%7) jarria?Soluzioa pezeta
pezeta Azaldu berri denaren arabera, interesak kapitalari gehitzen zaizkio
urte bakoitzaren bukaeran. Kapitalizazio aldia urte batekoa dela
esan nahi du horrek. Baina ez du zertan urte batekoa izan beti ; izan
daiteke hiru hilabetekoa, edo hil batekoa.Eman dezagun hiru hilabetez behin egiten dela kapitalizazioa.
Azaldu berri denaren arabera, interesak kapitalari gehitzen zaizkio
urte bakoitzaren bukaeran. Kapitalizazio aldia urte batekoa dela
esan nahi du horrek. Baina ez du zertan urte batekoa izan beti ; izan
daiteke hiru hilabetekoa, edo hil batekoa.Eman dezagun hiru hilabetez behin egiten dela kapitalizazioa.
Pezeta batek hiru hilabeteren buruan pezeta emango lituzke, hau da, urte batean ameten duenaren laurden bat. C pezetek, beraz,
pezeta emango lituzke, hau da, urte batean ameten duenaren laurden bat. C pezetek, beraz, pezeta emango lituzkete, eta
pezeta emango lituzkete, eta bihurtuko lirateke hiru hilabeteren buruan,
bihurtuko lirateke hiru hilabeteren buruan, pezeta sei hilabeteren buruan eta
pezeta sei hilabeteren buruan eta pezeta lehenengo urtearen buruan. Prozesu hori muturreraino eremanez, hau da t. urteren buruan metatuko litzatekeen kapital berria :
pezeta lehenengo urtearen buruan. Prozesu hori muturreraino eremanez, hau da t. urteren buruan metatuko litzatekeen kapital berria : . Arrazoibide bera erabiliz t urteren buruan metatuko zen kapitalaren formula lor daiteke edozein kapitalizio aldirako. Adibidez, hil batekokapitalizorako,
. Arrazoibide bera erabiliz t urteren buruan metatuko zen kapitalaren formula lor daiteke edozein kapitalizio aldirako. Adibidez, hil batekokapitalizorako,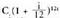 da formula, sei hilabeteko kapitalizaziorako C
da formula, sei hilabeteko kapitalizaziorako C , eta, oro har, m alditan zatitzen bada urtea, hau izango da kapital berria t urteren buruan :
, eta, oro har, m alditan zatitzen bada urtea, hau izango da kapital berria t urteren buruan :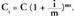 • Adibidea500.000 pezeta jartzen badira 10 urtez interes elkartuan, %4ko korrituarekin eta se hilabeteko kapitalizazio aldiekin. Zenbat izango da azkenerako kapitala?
Soluzioa
Urtean bi aldiz kapitalizatzen denez:
• Adibidea500.000 pezeta jartzen badira 10 urtez interes elkartuan, %4ko korrituarekin eta se hilabeteko kapitalizazio aldiekin. Zenbat izango da azkenerako kapitala?
Soluzioa
Urtean bi aldiz kapitalizatzen denez: Epe finkoan ezarritako kapital bat zenbat bihurtzen den jakiteko
ere balio du arrazoibide horrek. Baina badira beste kapitalizazio
metodo batzuk ere, hala nola diru kopuru finko bat ezartzea hilero
hainbat urtez, ezartzen den diruarekin eta horrek ematen duen
korrituarekin kapital bat osatzen joateko. Horretarako dira, adibidez,
etxebizitzaren aurrezkirako kontuak.Bedi C osatu nahi den kapitala, a hilero ezarriko den diru kopurua
eta t urte kopurua.Hasieran ezarri den diru kopurua, a alegia, handik 12t hiletara, a
Epe finkoan ezarritako kapital bat zenbat bihurtzen den jakiteko
ere balio du arrazoibide horrek. Baina badira beste kapitalizazio
metodo batzuk ere, hala nola diru kopuru finko bat ezartzea hilero
hainbat urtez, ezartzen den diruarekin eta horrek ematen duen
korrituarekin kapital bat osatzen joateko. Horretarako dira, adibidez,
etxebizitzaren aurrezkirako kontuak.Bedi C osatu nahi den kapitala, a hilero ezarriko den diru kopurua
eta t urte kopurua.Hasieran ezarri den diru kopurua, a alegia, handik 12t hiletara, a bihurtuko da.Bigarren hilean ezartzen den a dirua, handik 12t-1 hiletara, a
bihurtuko da.Bigarren hilean ezartzen den a dirua, handik 12t-1 hiletara, a bihurtuko da.
bihurtuko da.
Hirugarren hilean ezartzen den a dirua, handik 12t-2 hiletara, a bihurtuko da.Eta horrela hurrenez hurren, ezartzekoa den azken kopurura iristeraino
.12t-garren hilean ezartzen den a dirua, handik hil batera, a
bihurtuko da.Eta horrela hurrenez hurren, ezartzekoa den azken kopurura iristeraino
.12t-garren hilean ezartzen den a dirua, handik hil batera, a bihurtuko da.Hilero-hilero ezarri diren diru kopuru guztien baturak C eman
behar du.
bihurtuko da.Hilero-hilero ezarri diren diru kopuru guztien baturak C eman
behar du. Berdintzaren bigarren atala progresio geometriko bateko 12tgaien batura da, eta progresioaren arrazoia da
Berdintzaren bigarren atala progresio geometriko bateko 12tgaien batura da, eta progresioaren arrazoia da Formula aplikatu, eta...
Formula aplikatu, eta... C jakinda, a kopurua kalkulatu nahi bada, berdintzatik bakandu
behar da. Dirua hilero ezarri ordez hiru hilabez behin edota urtean
behin ezartzen bada, aski da i-ren izendatzailea eta t berretzailearen
biderkatzailea aldatzea edo kentzea.Adibideaka) Zer kapital metatuko du pertsona batek 5 urteren buruan baldin
hiru hilabetez behin 150.000 jartzen baditu %4ko korrituan?SoluzioaFormula aplikatu, eta...
C jakinda, a kopurua kalkulatu nahi bada, berdintzatik bakandu
behar da. Dirua hilero ezarri ordez hiru hilabez behin edota urtean
behin ezartzen bada, aski da i-ren izendatzailea eta t berretzailearen
biderkatzailea aldatzea edo kentzea.Adibideaka) Zer kapital metatuko du pertsona batek 5 urteren buruan baldin
hiru hilabetez behin 150.000 jartzen baditu %4ko korrituan?SoluzioaFormula aplikatu, eta... b) Zenbat diru jarri bahar da hilero %5eko korrituarekin 8 urteren
buruan 5 mililoiko kapitala osatzeko?Soluzioa
b) Zenbat diru jarri bahar da hilero %5eko korrituarekin 8 urteren
buruan 5 mililoiko kapitala osatzeko?Soluzioa
- Ariketa
30. Pertsona batek 5 milioi pezeta interes elkartuan jarri ditu, urteko %6ko korrituarekin. Zenbat diru jasoko du handik bost urtera?
Zorren amortizazioa
Orain hurrena zorrak nola amortizatu aztertuko da. Gauzak epetan
erostean, kredituak itzultzean edota hipotekak ordaintzean,
zorrak amortizatzen ari gara. Modu bat baino gehiago dago horretarako
. Hona hemen hiru aukera :a) Epe jakin baten buruan zorra aldi batean kitatzea. Alegia, mailegaturiko
dirua eta maileguak iraun duen denboran gehituriko
interesak, dena batera itzultzea.• AdibideaEman dezagun 2 milioiko mailegua eskatu dugula % 1 Oeko korrituarekin,
eta lau urteren buruan itzuli behar dugula.SoluzioaGuztira, hau itzuli beharko dugu: pezeta.Ez da hau asko erabiltzen den bidea, zeren batek ez badauzka 2
milioi gaur, nekez itzuliko ditu ia 3 milioi, 4 urte geroago.b) Mailegaturiko kapitala zati berdinetan zatiturik, epe jakin
baten buruan ordaintzen da zati bakoitza (hilabetero, hiru
hilabetero, urtero), ordaintzea falta den zatiaren interesekin
batera.• Adibidea2 milioiko mailegua, %10eko korritua duela, urte beteko lau
alditan ordaindu behar da.SoluzioaUrte bakoitzaren buruan, beraz, 500.000 pezeta ordaindu beharko
dira, eta kapital zati horri zor den zatiari dagozkion interesak
gehitu beharko zaizkio. Lehenengo urtean bi milioi zorko dira baina
epeak ordaindu ahala gutxituz joango da zor den zatia.Ikus hori, argiago, taula honetan :
pezeta.Ez da hau asko erabiltzen den bidea, zeren batek ez badauzka 2
milioi gaur, nekez itzuliko ditu ia 3 milioi, 4 urte geroago.b) Mailegaturiko kapitala zati berdinetan zatiturik, epe jakin
baten buruan ordaintzen da zati bakoitza (hilabetero, hiru
hilabetero, urtero), ordaintzea falta den zatiaren interesekin
batera.• Adibidea2 milioiko mailegua, %10eko korritua duela, urte beteko lau
alditan ordaindu behar da.SoluzioaUrte bakoitzaren buruan, beraz, 500.000 pezeta ordaindu beharko
dira, eta kapital zati horri zor den zatiari dagozkion interesak
gehitu beharko zaizkio. Lehenengo urtean bi milioi zorko dira baina
epeak ordaindu ahala gutxituz joango da zor den zatia.Ikus hori, argiago, taula honetan : Lau ordainketek, beraz, beherako progresio geometriko bat eratzen
dute. Progresioaren diferentzia -50.000 da, -500.000 pezetaren
-zorra urtetik urtera gutxitzen den kopuruaren- %lOa.c) Kasu honetan, epe bakoitzaren buruan, kopuru berdina
ordaintzen da, halako moduan non hilez hil ordaindu beharreko
kopuru berdin horiek amortizazio aldiaren buruan eta interesaren
arabera emango luketen kopuruen baturak, batetik, eta mailegaturiko
kapitalak epe horretan berean emango lukeenak, bestetik, berdinak
izan beharko baitute.• AdibideaPertsona batek 105.000 pezetako hozkailua erosi du, eta bi urtean
ordaindu behar du, hilabeteko epetan, %l2ko korrituarekin.
Lau ordainketek, beraz, beherako progresio geometriko bat eratzen
dute. Progresioaren diferentzia -50.000 da, -500.000 pezetaren
-zorra urtetik urtera gutxitzen den kopuruaren- %lOa.c) Kasu honetan, epe bakoitzaren buruan, kopuru berdina
ordaintzen da, halako moduan non hilez hil ordaindu beharreko
kopuru berdin horiek amortizazio aldiaren buruan eta interesaren
arabera emango luketen kopuruen baturak, batetik, eta mailegaturiko
kapitalak epe horretan berean emango lukeenak, bestetik, berdinak
izan beharko baitute.• AdibideaPertsona batek 105.000 pezetako hozkailua erosi du, eta bi urtean
ordaindu behar du, hilabeteko epetan, %l2ko korrituarekin.
Zenbat ordaindu beharko du hilero?Soluzioa105.000 pezeta, bi urteren buruan, 133.322 pezeta bihurtuko
lirateke, zeren... Bedi a hilero ordaindu beharreko kopurua, eta kalkula dezagun
zenbat den :1. hilean : hilaren bukaeran ordaindu beharreko a kopurua
Bedi a hilero ordaindu beharreko kopurua, eta kalkula dezagun
zenbat den :1. hilean : hilaren bukaeran ordaindu beharreko a kopurua bihurtuko da 23 hilabete geroago.2. hilean : hilaren bukaeran ordaindu beharreko a kopurua
bihurtuko da 23 hilabete geroago.2. hilean : hilaren bukaeran ordaindu beharreko a kopurua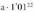 bihurtuko da 22 hilabete geroago.3. hilean : hilaren bukaeran ordaindu beharreko a kopurua
bihurtuko da 22 hilabete geroago.3. hilean : hilaren bukaeran ordaindu beharreko a kopurua bihurtuko da 21 hilabete geroago.Eta horrela hurrenez hurren. Ikus dezagun zer kopuru bihurtuko
diren azkeneko biak :23. hilean : hilaren bukaeran ordaindu beharreko a kopurua
bihurtuko da 21 hilabete geroago.Eta horrela hurrenez hurren. Ikus dezagun zer kopuru bihurtuko
diren azkeneko biak :23. hilean : hilaren bukaeran ordaindu beharreko a kopurua bihurtuko da hilabete bat geroago.24. hilean : a kopurua kreditua ordaintzeko epea bukatzearekin
batera ordaintzen da, eta, beraz, ordaindu beharreko kopurua a bera
da.Kopuru horien guztien baturak
bihurtuko da hilabete bat geroago.24. hilean : a kopurua kreditua ordaintzeko epea bukatzearekin
batera ordaintzen da, eta, beraz, ordaindu beharreko kopurua a bera
da.Kopuru horien guztien baturak eman behar du.
eman behar du. Berdintzaren lehenego atala progresio geometriko bat da, eta progresioaren
arrazoia 1'01 da.Formula aplikatu, eta...
Berdintzaren lehenego atala progresio geometriko bat da, eta progresioaren
arrazoia 1'01 da.Formula aplikatu, eta...
- Ariketak
31. a) Aurkitu zenbat ordaindu beharko duen urtero pertsona batek 40 milioiko mailegua %9 korrituarekin 5 urtebeteko epetan itzultzeko.b) Eta urtebeteko epetan ez baina hilabateko epetan ordaintzen badu?32. Pertsona batek autoa erosi du eta lau urtean hilerohilero 45.000 pezeta jarriz ordaindu behar du. Diruak urteko % 12 balio badu, zenbat balio du autoak?33. Zenbat diru bihurtuko da 5 urteren buruan 2 milioi pezeta, baldin eta urteko interesa % 12koa baldin bada eta kapitalizatzea hiru hilabetez behin egiten bada?34. Zenbateko korrituan jarri behar da 3 milioi pezeta 3.675.130 pezeta bihur dadin hiru urteren buruan interes elkartuan?35. Pertsona batek 15 milioiko hipoteka kreditua eskatu du etxebizitza bat erosteko. Bankuak dirua aurreratu dio %10'Seko korrituarekin eta 12 urteko epean eskuratzeko baldintzaz. Zenbat ordaindu beharko du hilero?36. Zenbateko korrituan jarri beharko da 1.500.000 pezetako kapitala, jarri eta 12 urtera 3.049.191 pezetakoa bihur dadin, baldin eta kapitalizatzea hiru hilabetez behin egiten bada?37. Zenbat denboran eduki behar da milioi bat pezeta %seko korrituarekin 2,5 milioi pezetatik gora bihurtzeko? Oharra : Kalkulagailua erabiliz iritzira kalkulatzea ere onartzen da.38. Kontu batean, urtero, 100.000 pezeta jartzen dira %7ko interes elkartuan. Zenbat diru izango da kontuan bosgarren ordainketa egin ondoren?
Gaiari buruzko zenbait problema
1. Argitu hurrengo progresio hauek progresio aritmetikoak
ala progresio geometrikoak diren, eta zenbakitzaileek
eta izendatzaileek, zein bere aldetik, progresioa osatzen
duten ala ez. Bestalde, bakoitza zer den, kakulatu diferentzia
edo arrazoia, eta, guztietan, gai orokorra. 2. Kalkulatu, 25 zenbakitik aurrera, 3ren lehenengo 20
anizkoitzen batura.3. Progresio aritmetiko batean
2. Kalkulatu, 25 zenbakitik aurrera, 3ren lehenengo 20
anizkoitzen batura.3. Progresio aritmetiko batean eta
eta
Ariketen soluzioak
1. 2.
2. 3.
3. 4. Soluzio posible asko dago.5.
4. Soluzio posible asko dago.5. 6)
6) 7) 4, 11, 18, 25, 32, 39, 4G, 53, 60, G7, 74, 81, 88, 95, 1028)
7) 4, 11, 18, 25, 32, 39, 4G, 53, 60, G7, 74, 81, 88, 95, 1028) . Hala da, bai, zenbaki bakoitiak batu ahala zenbaki naturalen koadroak lortzen dira hurrenez hurren : 1, 4, 9,...9)
. Hala da, bai, zenbaki bakoitiak batu ahala zenbaki naturalen koadroak lortzen dira hurrenez hurren : 1, 4, 9,...9) 10)
10)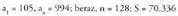 11) Nola
11) Nola , orduan,
, orduan, , eta, beraz, d = 4,
, eta, beraz, d = 4, 12)
12) -en formulan,
-en formulan, adierazpen ordezkatu eta d lortzen da : d = 7/2. Eta pentagonoaren aldeen neurriak dira : 3 ; 6,5 ; 10 ; 13,5 ; 17 cm13) Oktogono ganbil baten angeluen batura da : 180 (8 - 2) =
1.080°. Zeren A erpinetik diagonalak marraztuz eratzen
diren 6 triangeluetako bakoitzaren angeluen batura 180°
baita.
adierazpen ordezkatu eta d lortzen da : d = 7/2. Eta pentagonoaren aldeen neurriak dira : 3 ; 6,5 ; 10 ; 13,5 ; 17 cm13) Oktogono ganbil baten angeluen batura da : 180 (8 - 2) =
1.080°. Zeren A erpinetik diagonalak marraztuz eratzen
diren 6 triangeluetako bakoitzaren angeluen batura 180°
baita. formulan
formulan adierazpena ordezkatu, eta
adierazpena ordezkatu, eta lortzen da:
lortzen da: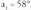 . Beraz, poligonoaren angeluen neurriak dira : 80°, 102°, 124°, 168°, 190° eta 212°.14)a) Bai, progresio geometrikoa da ; r = 1'2.b) Ez, ez da.c) Bai, progresio geometrikoa da eta arrazoia -0'3 da.15)
. Beraz, poligonoaren angeluen neurriak dira : 80°, 102°, 124°, 168°, 190° eta 212°.14)a) Bai, progresio geometrikoa da ; r = 1'2.b) Ez, ez da.c) Bai, progresio geometrikoa da eta arrazoia -0'3 da.15) 16) Nola
16) Nola , orduan
, orduan , eta beraz,
, eta beraz, 17) a) Bitez
17) a) Bitez eta
eta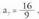 , eta r ateratzen da :
, eta r ateratzen da : Hauek dira interpolatu beharreko zenbakiak, beraz :
Hauek dira interpolatu beharreko zenbakiak, beraz : 17)
17) eta
eta , eta beraz, r = 3. Hauek dira interpolatu beharreko zenbakiak : 3, 9, 27, 81, 243, 729.
, eta beraz, r = 3. Hauek dira interpolatu beharreko zenbakiak : 3, 9, 27, 81, 243, 729. 19) b)
19) b) eta
eta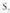 -ren formula aplikatu eta bakundu ondoren,
-ren formula aplikatu eta bakundu ondoren, lortzen da :
lortzen da : 19 ) d )
19 ) d ) 20.
20. 21.
21. 22.
22. -en formulan balio ezagunak ordezkatu, eta
-en formulan balio ezagunak ordezkatu, eta lortzen da :
lortzen da : . Hortik, gero,
. Hortik, gero, ateratzen da:
ateratzen da: 24. Sren formulan r bakandu, eta r ateratzen da :
24. Sren formulan r bakandu, eta r ateratzen da : 25.
25. gari ale xake jokoaren taularen azkene o laukitxoan, 9 trilioi gutxi gorabehera.
gari ale xake jokoaren taularen azkene o laukitxoan, 9 trilioi gutxi gorabehera. gari ale guztira, hau da : 18'45 trilioi ale. Eta horren pisua : 18'45 trilioi dezigramo edo -hori zati
gari ale guztira, hau da : 18'45 trilioi ale. Eta horren pisua : 18'45 trilioi dezigramo edo -hori zati bilioi tona, gutxi gorabehera.26. Lehenengo laukiak
bilioi tona, gutxi gorabehera.26. Lehenengo laukiak area du, eta bigarren laukiak aurrekoaren erdia. Argi ikusten da hori marrazkian. Beraz,
area du, eta bigarren laukiak aurrekoaren erdia. Argi ikusten da hori marrazkian. Beraz, eta
eta 27. Eskaleak zekenari 465 pezeta pagatu beharko dizkio :
27. Eskaleak zekenari 465 pezeta pagatu beharko dizkio :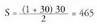 Zekenak eskaleari ordaindu beharko diona kalkulatzeko, berriz, badakigu
Zekenak eskaleari ordaindu beharko diona kalkulatzeko, berriz, badakigu dela, progresio geometriko baten aurrean gaudela, eta progresioaren arrazoia 2 dela.
dela, progresio geometriko baten aurrean gaudela, eta progresioaren arrazoia 2 dela.
Hortik : pezeta.
pezeta. 31) a)
31) a) . Baturaren formula erabili bigarren atalaren eragiketa egiteko, eta bakandu a berdintzan : a = 10.283.698 pezeta.3 1) b) Aurekoaren berdina baina honetan hilabeteko korritua
. Baturaren formula erabili bigarren atalaren eragiketa egiteko, eta bakandu a berdintzan : a = 10.283.698 pezeta.3 1) b) Aurekoaren berdina baina honetan hilabeteko korritua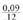 da. Hilabeteko epean ordaindu beharrekoa m = 830334 da.32. 2.160.000 pezeta ordaintzen ditu. Baina eskura ordaindurik, interesengatik ordaintzen duena kenduta :
da. Hilabeteko epean ordaindu beharrekoa m = 830334 da.32. 2.160.000 pezeta ordaintzen ditu. Baina eskura ordaindurik, interesengatik ordaintzen duena kenduta :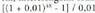 zati
zati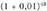 berdin 1.708.828 pezeta.
berdin 1.708.828 pezeta. 34.
34. . Eta hortik i ateratzen da : i = 0,07 ; %7, alegia.35. M = 183.621,136.
. Eta hortik i ateratzen da : i = 0,07 ; %7, alegia.35. M = 183.621,136. Beraz, i = 0,06 ; %6, alegia.37. Kalkuladora zein logaritmoak erabiliz, erantzuna da : 19 urte
baino gehiago.
Beraz, i = 0,06 ; %6, alegia.37. Kalkuladora zein logaritmoak erabiliz, erantzuna da : 19 urte
baino gehiago.
Gaiari buruzko problemen soluzioak S -(1 + 30) 30 - 465 2
1. a. Progresio aritmetikoa : 1. b. Progresio geometrikoa:
1. b. Progresio geometrikoa: 1c. Ez da progresio aritmetikoa ez geometrikoa, baina... :- Zenbakitzaileek progresio aritmetikoa dute :
1c. Ez da progresio aritmetikoa ez geometrikoa, baina... :- Zenbakitzaileek progresio aritmetikoa dute : - Izendatzaileek progresio aritmetikoa dute :
- Izendatzaileek progresio aritmetikoa dute : -Beraz, progresioaren gai orokorra da :
-Beraz, progresioaren gai orokorra da : ld. Progresio geometrikoa da :
ld. Progresio geometrikoa da : 4. A (1. lauki zuzena) =
4. A (1. lauki zuzena) = , A (1. erronboa) =
, A (1. erronboa) = , A (2. lauki zuzena) =
, A (2. lauki zuzena) = , A (2. erronboa) =
, A (2. erronboa) = . Beraz, areek progresio geometrikoa dute :
. Beraz, areek progresio geometrikoa dute : eta
eta 5. Formula aplikatu eta :
5. Formula aplikatu eta : biztanle. Hau da, hazkunde erritmo horri eutsiko baliote, herrialdeak 94 milioi pertsona baino gehiago izango lituzke.6. Azkeneko kapitalak 2C izan beharko du. Beraz,
biztanle. Hau da, hazkunde erritmo horri eutsiko baliote, herrialdeak 94 milioi pertsona baino gehiago izango lituzke.6. Azkeneko kapitalak 2C izan beharko du. Beraz,