Matematika»Geometria
Planoko Eraldaketak
Eraldaketak, planoko puntuen arteko korrespondentziak dira.
Distantzien aldaketak eta irudien forma aldaketak burutzera, edo
burutu gabe uztera, eraman dezaketen planoko puntuen kokapen
aldaketen moduan har daitezke. Antzinatean, geometrialariek, errezeloz
ikusten zituzten, izan ere, geometriako problemak eta gaiak
tratatzeko modu fisikoegia zela baitzirudien. Baina, mekanikako
higiduretara jo gabe defini daitezke eta oso erabilgarria den geometria
ikusteko modu berria eskaintzen dute. Berez, beti erabili izan
dira irudien ezaugarriak aztertzeko eta ikasteko. Euklidesek, bere
garairako, onartu zuen higidura baten ondorengo bat etortzea irudien
arteko berdintasuna frogatzeko eta Elementuak deitu laneko 8.. xioman, zera baieztatu zuen : "8. beren artean bat datozen gauzak,
beren artean ere berdinak dira." Joan zen mendeaz geroztik, eraldaketek
leku garrantzitsua hartu dute geometrian. Beste zientzia batzuetan
ere, hala nola fisikan, egoera solidoak edo partikula elementalak
edota kristalografiak, garrantzizko laguntzailea dute
geometriako eraldaketen ikasketa eta azterketa.Planoan eta espazioan buru daitezkeen eraldaketetatik, isometriak
dira garrantzitsuenak. Isometrietan, eraldaketa baten imajina
diren puntuen arteko distantzia jatorrizko puntuen artean dagoen
distantziaren berdina da eta angelua ere, anplitude edo zabaltasun
bereko beste angelu baten moduan eraldatzen da. Isometriak edo
higidurak, bi motatakoak daude : zuzeneko higidurak, irudien
orientazioa ere gordetzen dutenak, hala nola, traslazioa edota biraketa
bezalakoak eta alderantzizko edo aurkako higidurak, hala nola
simetria edota lerradura, irudien norantza aldatzen dutenak.Higiduren edo isometrien ondoren, antzekotasunen multzoa ikusiko
da. Kasu honetan, irudien eitea edo forma mantendu egiten da
eta angeluak edota zuzenen arteko paralelotasunak gorde egiten
dira, baina ez distantziak. Bereziki homoteziak aztertuko dira, irudi
bat forma edo eite bereko beste batean eraldatzen dutenak baina
jatorrizkoa baino handiagoa edo txikiagoa eginez.Hemen ez dira aztertuko zabalkuntza edota murriztapen koefizienteak
hartutako norabidearen arabera aldatzen diren eraldaketak.
Eraldaketa hauekin ateratzen diren irudiak, jatorrizkoen antzekoak
dira, baina norabide batzuetan beste batzuetan baino
luzatuagoak daude. Irudien eitea gordetzen ez duten eraldaketetatik,
alderanzketa aztertuko da, zuzenak zirkunferentzia bihur ditzakeena
eta orientazioa aldatzen duena, baina angeluak gordetzen
dituena. Azken atala proiekzioen azterketari eskainia da, planoko
puntu guztiak lerro batera daramatzan eraldaketa moduan alegia.
I. Eraldaketak.
Planoko eraldaketa, planoko puntuekin beren buruen baitan
egindako aplikazio oro da. Planoa p letraz adierazita, T eraldaketa
zera da : T eraldaketak alegia,
T eraldaketak alegia,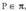 (
( planokoa den P puntu) bakoitzari, beste
planokoa den P puntu) bakoitzari, beste puntu bat egoki arazten dio ; honela idazten da :
puntu bat egoki arazten dio ; honela idazten da : Eraldaketak aztertzeko, beren artean bereiztaratzen dituzten elementuak
zeintzuk diren ikusiko dugu, aldatu gabe gelditzen diren
puntuak edo irudiak zeintzuk diren, koordenatu sistema batean
dituzten ekuazioak zeintzuk diren eta beren osaketa nolakoa den,hau da, aplikazio bat planoko puntuei behin eta berriz aplikatzearen
ondorioak.Geometriako eraldaketa batean, puntu aldagabe, atzera lehengo
berbera izatera eraldatzen denari deritzo, hau da planoa eraldatzean
aldatzen ez denari. Adibidez, biraketa batean, biraketa zentroa ez da
aldatzen. Eraldaketa motaren arabera, puntu, zuzen, zirkunferentzia
edo beste irudi batzuek ere izan daitezke aldagabe. Kasu batzuetan,
irudi baten aldagabetasuna, bere puntu guztiak aldagabe
izatetik dator, beste batzuetan aldiz, irudiak aldatu gabe irauten du
puntuek bere barnean kokaera aldaketak izan arren.Bi eraldaketa hurrenez hurren egitearen emaitza, egindako bi
eraldaketen konposizio deritzon beste eraldaketa berri bat da. Mota
jakin bateko eraldaketen konposizioak dituen ezaugarriak jakiteak,
errepikatutako aplikazioak sinplifikatzeko, alderantzizko eraldaketarik
ba al den jakiteko, edota eraldaketen ordenak lortutako emaitza
aldatzen duen ala ez jakiteko aukera ematen du.Eraldaketen konposizioa adierazteko modua hau da :
Eraldaketak aztertzeko, beren artean bereiztaratzen dituzten elementuak
zeintzuk diren ikusiko dugu, aldatu gabe gelditzen diren
puntuak edo irudiak zeintzuk diren, koordenatu sistema batean
dituzten ekuazioak zeintzuk diren eta beren osaketa nolakoa den,hau da, aplikazio bat planoko puntuei behin eta berriz aplikatzearen
ondorioak.Geometriako eraldaketa batean, puntu aldagabe, atzera lehengo
berbera izatera eraldatzen denari deritzo, hau da planoa eraldatzean
aldatzen ez denari. Adibidez, biraketa batean, biraketa zentroa ez da
aldatzen. Eraldaketa motaren arabera, puntu, zuzen, zirkunferentzia
edo beste irudi batzuek ere izan daitezke aldagabe. Kasu batzuetan,
irudi baten aldagabetasuna, bere puntu guztiak aldagabe
izatetik dator, beste batzuetan aldiz, irudiak aldatu gabe irauten du
puntuek bere barnean kokaera aldaketak izan arren.Bi eraldaketa hurrenez hurren egitearen emaitza, egindako bi
eraldaketen konposizio deritzon beste eraldaketa berri bat da. Mota
jakin bateko eraldaketen konposizioak dituen ezaugarriak jakiteak,
errepikatutako aplikazioak sinplifikatzeko, alderantzizko eraldaketarik
ba al den jakiteko, edota eraldaketen ordenak lortutako emaitza
aldatzen duen ala ez jakiteko aukera ematen du.Eraldaketen konposizioa adierazteko modua hau da : Baldin eta
Baldin eta eta
eta badira, T eta
badira, T eta eraldaketen konposiziotzat zera hartzen da, alegia, beste
eraldaketen konposiziotzat zera hartzen da, alegia, beste eraldaketa bat, non
eraldaketa bat, non den.Hori, honela idazten da :
den.Hori, honela idazten da : bete egiten da, baldin eta
bete egiten da, baldin eta eta
eta badira eta orduan :
badira eta orduan : da.
da. Traslazioen eta zentro bera duten biraketa edo homotezien konposizioek,
multzo trukakorren egitura dute. Zuzeneko higiduren
multzoa, edota higidura guztien multzoa edo antzekotasun guztiena
ere taldeak dira, baina ez-trukakorrak dira. Beste kasu batzuetan,
simetrien kasuan adibidez, konposizioa ez da itxia, hau da, bi simetrien
konposizio edo biderkadura ez da simetria. Irudi bat aldatu
gabe uzten duten higiduren konposizioa, karratu bat adibidez, maiz
finitua edo amaieraduna den taldea da. Karratuarentzat adibidez,
zortzi eraldaketa daude aldatu gabe uzten dutenak.Eraldaketa multzo baten konposizioa aztertzean, taldea osatzen
dutela esaten da ondoko baldintza hauek betetzen dituztela adierazteko
:- Eragiketa itxia izatea : hau da, mota bereko bi eraldaketa egiten badira, bi traslazio adibidez, mota bereko beste eraldaketa bat lortzen da, beste traslazio bat alegia. Bestela esanda, T eta
Traslazioen eta zentro bera duten biraketa edo homotezien konposizioek,
multzo trukakorren egitura dute. Zuzeneko higiduren
multzoa, edota higidura guztien multzoa edo antzekotasun guztiena
ere taldeak dira, baina ez-trukakorrak dira. Beste kasu batzuetan,
simetrien kasuan adibidez, konposizioa ez da itxia, hau da, bi simetrien
konposizio edo biderkadura ez da simetria. Irudi bat aldatu
gabe uzten duten higiduren konposizioa, karratu bat adibidez, maiz
finitua edo amaieraduna den taldea da. Karratuarentzat adibidez,
zortzi eraldaketa daude aldatu gabe uzten dutenak.Eraldaketa multzo baten konposizioa aztertzean, taldea osatzen
dutela esaten da ondoko baldintza hauek betetzen dituztela adierazteko
:- Eragiketa itxia izatea : hau da, mota bereko bi eraldaketa egiten badira, bi traslazio adibidez, mota bereko beste eraldaketa bat lortzen da, beste traslazio bat alegia. Bestela esanda, T eta ezaugarri hori duen multzo bateko bi eraldaketa badira, beren konposizioa,
ezaugarri hori duen multzo bateko bi eraldaketa badira, beren konposizioa,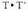 ere, multzo horretakoa da.Dena delako eraldaketen konposizioak, taldeen tasun edo ezaugarriak
ditu :a) Elkarkortasuna :
ere, multzo horretakoa da.Dena delako eraldaketen konposizioak, taldeen tasun edo ezaugarriak
ditu :a) Elkarkortasuna : b) Unitate edo elementu neutro bat badago : I identitatea,
b) Unitate edo elementu neutro bat badago : I identitatea, egiten duena.c) T elementu bakoitzak, bere
egiten duena.c) T elementu bakoitzak, bere alderantzizkoa du eta ondorengoa betetzen du :
alderantzizkoa du eta ondorengoa betetzen du : Zenbaki oso, razional erreal edo konplexuen multzo askoren baturak, talde egitura du eta beste multzo batzuetan definitutako eragiketek ere hala dute. Zenbakien baturak trukakorrak dira, batugaien ordenak ez du aldatzen batura, geometriako eraldaketetan badaude hainbat kasu konposizioa trukakorra ez dutenak, hots,
Zenbaki oso, razional erreal edo konplexuen multzo askoren baturak, talde egitura du eta beste multzo batzuetan definitutako eragiketek ere hala dute. Zenbakien baturak trukakorrak dira, batugaien ordenak ez du aldatzen batura, geometriako eraldaketetan badaude hainbat kasu konposizioa trukakorra ez dutenak, hots, eta
eta
I I. Traslazioak.
Definizioa:
 bektorearen traslazioa, planoko eraldaketa da eta edozein P punturi,
bektorearen traslazioa, planoko eraldaketa da eta edozein P punturi, puntua egoki arazten zaio,
puntua egoki arazten zaio,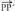 bektorea
bektorea bektorearen ekipolentea dela.
bektorearen ekipolentea dela. Traslazioak, bera definitzen duten
Traslazioak, bera definitzen duten bektorearen arabera bereizten dira. Horregatik, bektore traslazioa
bektorearen arabera bereizten dira. Horregatik, bektore traslazioa bidez adieraziko da.
bidez adieraziko da. AB zuzenkiaren zuzenki lekualdatua, beste
AB zuzenkiaren zuzenki lekualdatua, beste zuzenki bat da, paralelogramoaren parez pareko aldea izateagatik lehenaren luzera berdinekoa dena, izan ere, beste bi aldeak paraleloak eta a luzerakoak baitira.
zuzenki bat da, paralelogramoaren parez pareko aldea izateagatik lehenaren luzera berdinekoa dena, izan ere, beste bi aldeak paraleloak eta a luzerakoak baitira. BAC angeluaren angelu lekualdatua, beste
BAC angeluaren angelu lekualdatua, beste angelu bat da, aldeak paraleloak eta norantza berekoak dituena, beraz, angelu bat eta bere angelu lekualdatua berdinak dira.
angelu bat da, aldeak paraleloak eta norantza berekoak dituena, beraz, angelu bat eta bere angelu lekualdatua berdinak dira. Planoko puntu guztiei, traslazio baten bitartez, beste puntu desberdinen bat dagokie, bektore lekualdatzailea den bektorea
Planoko puntu guztiei, traslazio baten bitartez, beste puntu desberdinen bat dagokie, bektore lekualdatzailea den bektorea bektore hutsala ez bada behintzat. Kasu horretan, hutsala ez den bektoredun traslazioak, ez du puntu aldagaberik.Edozein traslaziok ere, irudi aldagabeak ditu. Traslazioa definitzen duen bektorearen paraleloak diren lerro guztiak aldagabeak dira. Errepikatzen diren marrazkidun frisoek, traslazio bektorea dute aldagabetasuna dutenarekiko. Saretek, lauzek, paper pintatuek edota bestelako pareta estaldura batzuek, bi traslazioekiko aldagabetasunaz jokatu ohi dute beren m arrazkian. b i kasuetan ere, irudia traslazioarekiko aldagabea bada,
bektore hutsala ez bada behintzat. Kasu horretan, hutsala ez den bektoredun traslazioak, ez du puntu aldagaberik.Edozein traslaziok ere, irudi aldagabeak ditu. Traslazioa definitzen duen bektorearen paraleloak diren lerro guztiak aldagabeak dira. Errepikatzen diren marrazkidun frisoek, traslazio bektorea dute aldagabetasuna dutenarekiko. Saretek, lauzek, paper pintatuek edota bestelako pareta estaldura batzuek, bi traslazioekiko aldagabetasunaz jokatu ohi dute beren m arrazkian. b i kasuetan ere, irudia traslazioarekiko aldagabea bada, bektorea ere hala da
bektorea ere hala da bektorearekiko eta orokorki
bektorearekiko eta orokorki
Traslazioaren ekuazioa.
Traslazioa egiten den planoan erreferentzi sistema bat baldin badago, hasierako puntuaren eta eraldaketa ondorengo azkenekoaren arteko korrespondentzia, ekuazioen bitartez adieraz daiteke.Traslazio definiziotik ondorioztatzen da, alegia, puntu baten kokaerabektorearen eta bere eraldatuaren arteko erlazioa hau dela :
erreferentzi sistema bat baldin badago, hasierako puntuaren eta eraldaketa ondorengo azkenekoaren arteko korrespondentzia, ekuazioen bitartez adieraz daiteke.Traslazio definiziotik ondorioztatzen da, alegia, puntu baten kokaerabektorearen eta bere eraldatuaren arteko erlazioa hau dela : Erlazio hori, emandako oinarriko koordenatuak hartuta eta
Erlazio hori, emandako oinarriko koordenatuak hartuta eta bektoreak dituen
bektoreak dituen koordenatuak erabiliz, honako ekuazio hauen bidez adieraz daiteke :
koordenatuak erabiliz, honako ekuazio hauen bidez adieraz daiteke : non, P(x,y) jatorrizko puntua den eta
non, P(x,y) jatorrizko puntua den eta puntu lekualdatua
puntu lekualdatua Bektore batuketa moduan adierazita :
Bektore batuketa moduan adierazita : Oinarri batean, biraketa, simetria edo homotezien konposizioak,
matrize biderkaketa bihurtzen dira. Horregatik, traslazioen konposiziorako
oso erabilgarria ez den arren, aurreko berdintza, matrize
moduan ere ematen da :
Oinarri batean, biraketa, simetria edo homotezien konposizioak,
matrize biderkaketa bihurtzen dira. Horregatik, traslazioen konposiziorako
oso erabilgarria ez den arren, aurreko berdintza, matrize
moduan ere ematen da :
Traslazioen konposizioa.
P puntua bektoredun traslazio batez eraldatua baldin bada eta emaitza ostera
bektoredun traslazio batez eraldatua baldin bada eta emaitza ostera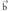 bektoredun eraldaketa berri batez berriro eraldatua, emaitza,
bektoredun eraldaketa berri batez berriro eraldatua, emaitza, bektoredun traslazio bidez eraldatu izan balitz bezalakoa izango da :
bektoredun traslazio bidez eraldatu izan balitz bezalakoa izango da : Traslazioak korrespondentzia dute bektoreekin eta traslazioen
konposizioak bektoreen baturarekin. Beraz, eraldaketa konposizio
bidezko eragiketa eginez burututako planoko traslazio multzoak,
bektore batuketako eragiketa bidez planoko bektore askeen multzoak
dituen ezaugarri berberak ditu :Elkarkortasuna :
Traslazioak korrespondentzia dute bektoreekin eta traslazioen
konposizioak bektoreen baturarekin. Beraz, eraldaketa konposizio
bidezko eragiketa eginez burututako planoko traslazio multzoak,
bektore batuketako eragiketa bidez planoko bektore askeen multzoak
dituen ezaugarri berberak ditu :Elkarkortasuna : Trukakortasuna :
Trukakortasuna : Elementu neutroa ere badute, bektore traslazioko
Elementu neutroa ere badute, bektore traslazioko bektorea,
bektorea, Eta traslazio bakoitzak bere aurkakoa ere badu, aurkako bektoreari dagokion traslazioa noski.
Eta traslazio bakoitzak bere aurkakoa ere badu, aurkako bektoreari dagokion traslazioa noski. bektorearen aurkako
bektorearen aurkako da, izan ere :
da, izan ere :
- Ariketak
1.- Kalkula itzazu P(2,1) puntuaren eraldatua denaren koordenatuak traslazio bektoreak eragindako traslazioaren ondoren. Adieraz itzazu traslazio horren ekuazio cartesiarrak eta matrize ekuazioak.2.- Kalkula ezazu 2x - y + 4 = 0 zuzenak aurreko eraldaketa
dela bide izango duen zuzen eraldatuaren ekuazioa.3.- Kalkula ezazu
traslazio bektoreak eragindako traslazioaren ondoren. Adieraz itzazu traslazio horren ekuazio cartesiarrak eta matrize ekuazioak.2.- Kalkula ezazu 2x - y + 4 = 0 zuzenak aurreko eraldaketa
dela bide izango duen zuzen eraldatuaren ekuazioa.3.- Kalkula ezazu zirkunferentziak aurreko eraldaketa dela bide izango duen zirkunferentzia eraldatuaren ekuazioa :a) Traslazio ekuazioak erabiliz.b) Erradioaren aldagabetasuna eta zentroaren eraldatua
erabiliz.4.- Kalkula ezazu
zirkunferentziak aurreko eraldaketa dela bide izango duen zirkunferentzia eraldatuaren ekuazioa :a) Traslazio ekuazioak erabiliz.b) Erradioaren aldagabetasuna eta zentroaren eraldatua
erabiliz.4.- Kalkula ezazu
I I I. Biraketak.
Biraketa zentro deituriko O puntu bat eta a zenbaki errealeko biraketa angelu bat emanik, O zentrodun eta biraketa angeludun biraketa esaten zaio planoko P puntu bakoitzari beste
biraketa angeludun biraketa esaten zaio planoko P puntu bakoitzari beste puntu eraldatu bat egoki arazten dion eraldaketari, baina ondoko baldintza hauek betez beti ere :a)
puntu eraldatu bat egoki arazten dion eraldaketari, baina ondoko baldintza hauek betez beti ere :a) angeluak
angeluak balio du.
balio du. angelua,
angelua, tartean hartuta ulertzen da erradianetan ematen bada eta [0, 360°) tartean hartuta gradutan ematen bada.
tartean hartuta ulertzen da erradianetan ematen bada eta [0, 360°) tartean hartuta gradutan ematen bada. O zentrodun eta
O zentrodun eta angeludun biraketak P puntua
angeludun biraketak P puntua - era daramala adierazteko, honela idazten da :
- era daramala adierazteko, honela idazten da : .
.
Biraketak, biraketa zentroaren edota biratutako angeluaren arabera bereizten dira. Horregatik idazten dira bi datu horiek azpindize moduan. Halere, kasu askotan, biraketak, ezaguntzat jotzen den puntu baten inguruan, koordenatu jatorriaren inguruan adibidez, ematen dira eta O azpindizea kendu egiten da : AB zuzenkia biratzean, luzera bereko beste
AB zuzenkia biratzean, luzera bereko beste zuzenki bat lortzen da. Hain zuzen ere, AOB eta
zuzenki bat lortzen da. Hain zuzen ere, AOB eta triangeluak berdinak baitira
triangeluak berdinak baitira eta
eta aldeak eta beren arteko
aldeak eta beren arteko angeluak berdinak izateagatik, ezen, hiru berdintzak ere biraketaren definiziotik ondorioztatzen baitira. Triangeluen berdintasunetik ateratzen da
angeluak berdinak izateagatik, ezen, hiru berdintzak ere biraketaren definiziotik ondorioztatzen baitira. Triangeluen berdintasunetik ateratzen da OAC eta
OAC eta triangeluekin arrazoiketa berbera erabiliz gero, OAC angelua =
triangeluekin arrazoiketa berbera erabiliz gero, OAC angelua = angelua dela ateratzen da. OAB eta
angelua dela ateratzen da. OAB eta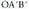 triangeluen berdintasunetik berriz,
triangeluen berdintasunetik berriz, ateratzen da. Bi berdintzen kenketa eginda, edozein angelurentzat ere, BAC =
ateratzen da. Bi berdintzen kenketa eginda, edozein angelurentzat ere, BAC = dela ateratzen da.
dela ateratzen da.
Bestalde, biraketa norantza ez da aldatzen irudi eraldatuetan. Jatorrizko irudian biraketa norantza positiboa BAC baldin bada, eraldatuan ere positiboa izango da norantza.
norantza. Laburbilduz, biraketa, zuzeneko isometria da, hau da, distantziak,
angeluak eta biraketa norantza gordetzen dituen higidura alegia
.Biraketa zentroa da aldatzen ez den puntu bakarra zero ez den
angelua duen edozein biraketarentzako. 00-ko angelua duen biraketan,
puntu guztiak errepikatu egiten dira eta identitatea berbera da.
Laburbilduz, biraketa, zuzeneko isometria da, hau da, distantziak,
angeluak eta biraketa norantza gordetzen dituen higidura alegia
.Biraketa zentroa da aldatzen ez den puntu bakarra zero ez den
angelua duen edozein biraketarentzako. 00-ko angelua duen biraketan,
puntu guztiak errepikatu egiten dira eta identitatea berbera da.
Zentroa, biraketa zentrotzat duten zirkunferentziak, aldatzen ez
diren irudi dira, nahiz eta beren puntuak lekuz edo kokaeraz aldatu.. alde dituzten poligono erregularrak ere aldagabeak dira irudiaren
zentroan biraketa zentroa eta 3600/n biraketa angelua duten biraketetan
. Adibidez, karratua, aldagabea da 90°ko biraketan.
Biraketaren ekuazioak:
Planoan erreferentzi sistema definitu baldin bada, lehendabizi, biraketa zentroa koordenatu jatorria dela suposatzen da.a angeludun biraketa batean hasierako P(x,y) puntuaren koordenatuen eta
erreferentzi sistema definitu baldin bada, lehendabizi, biraketa zentroa koordenatu jatorria dela suposatzen da.a angeludun biraketa batean hasierako P(x,y) puntuaren koordenatuen eta puntu eraldatuaren koordenatuen arteko korrespondentzia aurkitzeko, era honetara jokatzen da :
puntu eraldatuaren koordenatuen arteko korrespondentzia aurkitzeko, era honetara jokatzen da : Hasierako puntuarentzat, ondorengoa betetzen da :
Hasierako puntuarentzat, ondorengoa betetzen da : Azken puntuak,
Azken puntuak, angelua eratzen du abzisa ardatzarekin, izan ere, P-tik abiatuta jatorri puntuaren inguruan
angelua eratzen du abzisa ardatzarekin, izan ere, P-tik abiatuta jatorri puntuaren inguruan angelua biratuz lortzen baita. Beraz, ondorengoa betetzen du :
angelua biratuz lortzen baita. Beraz, ondorengoa betetzen du : Trigonometriaz badakigu :
Trigonometriaz badakigu : Ordezkatuta, hau lortzen da :
Ordezkatuta, hau lortzen da : Biraketaren definizioa dela bide,
Biraketaren definizioa dela bide, denez,
denez, Era berean kalkulatzen da :
Era berean kalkulatzen da : Beraz, koordenatuen jatorri puntua zentrotzat eta a biraketa
angelutzat duen biraketa egitean, puntu eraldatuak jatorrizko puntuaren
koordenatuen arabera izango dituen koordenatuak honako
hauek izango dira:
Beraz, koordenatuen jatorri puntua zentrotzat eta a biraketa
angelutzat duen biraketa egitean, puntu eraldatuak jatorrizko puntuaren
koordenatuen arabera izango dituen koordenatuak honako
hauek izango dira: Berdintza hauek era honetan idazten dira matrize moduan :
Berdintza hauek era honetan idazten dira matrize moduan : Hau da,
Hau da, ; A ondorengo determinantea duen matrizea dela : det
; A ondorengo determinantea duen matrizea dela : det . Biraketa matrizearen determinanteak 1 balio du, zuzeneko higidura guztietan balio duen bezalaxe.
. Biraketa matrizearen determinanteak 1 balio du, zuzeneko higidura guztietan balio duen bezalaxe. da, non I, 2x2 mailako unitate-matrizea den eta
da, non I, 2x2 mailako unitate-matrizea den eta matrize antisimetrikoa, diagonal bigarrenean - 1 eta 1 dituela.Zentroa jatorri puntua ez den kasuan ere, aurreko formulak baliozkoak dira, baina lehendabizi ardatz traslazioa egin behar da jatorri puntua eta biraketa zentroa bat etor daitezen. Beraz, aurreko formulekin, ardatz lekualdatuetan biratutako puntuaren koordenatuak kalkulatzen dira eta azkenik, traslazioa desegin egiten da biratutako puntuaren koordenatuak jatorrizko koordenatuetan izateko.
matrize antisimetrikoa, diagonal bigarrenean - 1 eta 1 dituela.Zentroa jatorri puntua ez den kasuan ere, aurreko formulak baliozkoak dira, baina lehendabizi ardatz traslazioa egin behar da jatorri puntua eta biraketa zentroa bat etor daitezen. Beraz, aurreko formulekin, ardatz lekualdatuetan biratutako puntuaren koordenatuak kalkulatzen dira eta azkenik, traslazioa desegin egiten da biratutako puntuaren koordenatuak jatorrizko koordenatuetan izateko.
Ardatz traslazioa egiteko, kontuan hartu behar da, bektoredun ardatz traslazioak, koordenatuetan puntuak
bektoredun ardatz traslazioak, koordenatuetan puntuak
Biraketa konposizioa.
Zentro beraren inguruan egindako bi biraketek, zentro bera eta
biraketa angelua angeluen batura duen biraketa bihurtzen da : Zentroa desberdina baldin bada, bi biraketen konposizioak
Zentroa desberdina baldin bada, bi biraketen konposizioak angeludun beste biraketa bat da oraindik ere,
angeludun beste biraketa bat da oraindik ere,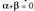 eta
eta den kasuan salbu, kasu horretan emaitza traslazioa da eta. Orokorki, biraketen konposizioa aztertzeko, lehendabizi simetriak aztertzea komeni da.Zentroa bi biraketetan berbera baldin bada, aurreko emaitza frogatu
egin daiteke zentroa koordenatuen jatorri puntua dela suposatuz
eta a eta b angeluekin egindako biraketetako formulak bi aldiz
aplikatuz.Hau suposatzen da :
den kasuan salbu, kasu horretan emaitza traslazioa da eta. Orokorki, biraketen konposizioa aztertzeko, lehendabizi simetriak aztertzea komeni da.Zentroa bi biraketetan berbera baldin bada, aurreko emaitza frogatu
egin daiteke zentroa koordenatuen jatorri puntua dela suposatuz
eta a eta b angeluekin egindako biraketetako formulak bi aldiz
aplikatuz.Hau suposatzen da : Frogatu nahi dena hau da :
Frogatu nahi dena hau da : Hain zuzen ere,
Hain zuzen ere, koordenatuetan jarrita :
koordenatuetan jarrita : Gauza bera
Gauza bera rentzat:
rentzat: eta
eta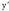 - arentzat lortutakoa
- arentzat lortutakoa - aren adierazpenean ordezkatuz :
- aren adierazpenean ordezkatuz : Trigonometrian gauza jakina da :
Trigonometrian gauza jakina da : Aurreko berdintzetan ordezkatuta :
Aurreko berdintzetan ordezkatuta : Era berean ateratzen da :
Era berean ateratzen da : Hauek dira beraz,
Hauek dira beraz, biraketari dagozkion formulak.Konposizio lege honekin, zentro finko baten inguruan egindako biraketek, multzo abeldar edo trukakorraren egitura dute. Biraketa unitatea, 0 angeluaren biraketa alegia,
biraketari dagozkion formulak.Konposizio lege honekin, zentro finko baten inguruan egindako biraketek, multzo abeldar edo trukakorraren egitura dute. Biraketa unitatea, 0 angeluaren biraketa alegia,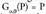 da eta biraketa baten alderantzizkoa edo aurkakoa berriz, zentro berbera eta aurkako angelua duen biraketa da :
da eta biraketa baten alderantzizkoa edo aurkakoa berriz, zentro berbera eta aurkako angelua duen biraketa da : biraketaren aurkakoa,
biraketaren aurkakoa, da.Biraketa angeluen artean, honako erlazio hau ere badago :
da.Biraketa angeluen artean, honako erlazio hau ere badago : , hau da, bira oso bat norantza batean ala bestean biratzeak, ez du emaitzarik aldarazten. Aurkako biraketarako erosoagoa gertatzen da
, hau da, bira oso bat norantza batean ala bestean biratzeak, ez du emaitzarik aldarazten. Aurkako biraketarako erosoagoa gertatzen da erabiltzea, baina biraketa angeluarentzat onartutako balioekiko zorrotzak izatekotan, bere balioa
erabiltzea, baina biraketa angeluarentzat onartutako balioekiko zorrotzak izatekotan, bere balioa da. Era berean, bi biraketen konposizioak
da. Era berean, bi biraketen konposizioak baino biraketa angelu handiagoa ematen badu,
baino biraketa angelu handiagoa ematen badu,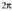 kentzen zaio.Zentro berberarekin egindako biraketen multzoa trukakorra da,
hots :
kentzen zaio.Zentro berberarekin egindako biraketen multzoa trukakorra da,
hots :
- Ariketak
G.- Kalkulatu biraketak emango duen P(1,2) puntuaren eraldatua.7.- Kalkulatu
biraketak emango duen P(1,2) puntuaren eraldatua.7.- Kalkulatu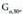 biraketak emango duen x + 2y = 38.- Kalkulatu
biraketak emango duen x + 2y = 38.- Kalkulatu biraketak emango duen
biraketak emango duen zirkunferentziaren eraldatua.9.- Egiazta ezazu, traslazioen bidezko biraketen biderkadura ez dela trukakorra,
zirkunferentziaren eraldatua.9.- Egiazta ezazu, traslazioen bidezko biraketen biderkadura ez dela trukakorra, eta
eta , P(2,0) puntuarentzat erabiltzean
, P(2,0) puntuarentzat erabiltzean eta
eta
I V. Simetriak
Planoan bi simetria mota daude. Simetria zentrala, 180o-ko biraketaren edota -1 arrazoia duen homoteziaren berdina dena, eta ardatz simetria edo zuzen (ardatz) batekikoa, orientaziorik gordetzen ez duen alderantzizko higidura da azken hau.
Zentro batekiko simetria.
Planoko O puntua emanik, zentro batekiko simetria, planoko P puntu bakoitzari beste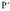 bat egoki arazten diona da eta ondokoak betez egoki arazi ere :- P, O eta
bat egoki arazten diona da eta ondokoak betez egoki arazi ere :- P, O eta lerrokatuta egonez,-
lerrokatuta egonez,- , izanez,- P eta
, izanez,- P eta O zentroarekiko alde banatan egonez.Eraldaketa honetan, ezaugarri den elementua zentroa da.Zentroa da aldatzen ez den puntu bakarra. Zentrotik igarotzen
diren zuzenak eta zentroa simetria zentroan duten zirkunferentziak
aldagabeak dira. Irudi bat mota honetako simetria batekiko aldagabea
baldin bada, simetria zentroa duela esaten da. Adibidez, karratuak
simetria zentroa du eta aldiz triangelu aldekideak ez du.Eraldaketa honek, gorde egiten ditu luzerak eta angeluak eta ABC triangeluari, orientazio bera duen beste
O zentroarekiko alde banatan egonez.Eraldaketa honetan, ezaugarri den elementua zentroa da.Zentroa da aldatzen ez den puntu bakarra. Zentrotik igarotzen
diren zuzenak eta zentroa simetria zentroan duten zirkunferentziak
aldagabeak dira. Irudi bat mota honetako simetria batekiko aldagabea
baldin bada, simetria zentroa duela esaten da. Adibidez, karratuak
simetria zentroa du eta aldiz triangelu aldekideak ez du.Eraldaketa honek, gorde egiten ditu luzerak eta angeluak eta ABC triangeluari, orientazio bera duen beste triangelu bat dagokio. Hau guztia, zentro batekiko simetria, zentro horrekiko 180o-ko biraketaren gauza berdina izatetik ondorioztatzen da.
triangelu bat dagokio. Hau guztia, zentro batekiko simetria, zentro horrekiko 180o-ko biraketaren gauza berdina izatetik ondorioztatzen da. Simetria zentroa koordenatuen jatorri puntua baldin bada, ekuazio
hauek ditu :
Simetria zentroa koordenatuen jatorri puntua baldin bada, ekuazio
hauek ditu :
Zuzen batekiko simetria.
Planoko P puntu bakoitzari beste puntu bat egoki arazi eta r zuzena
puntu bat egoki arazi eta r zuzena zuzenkiaren erdibitzailea izan arazten dion eraldaketari, r zuzenarekiko (ardatzarekiko) simetria deritzo.Irudi simetrikoak beren artean bereizi arazten dituen elementua, r zuzena da, horregatik, r zuzenarekiko simetria,
zuzenkiaren erdibitzailea izan arazten dion eraldaketari, r zuzenarekiko (ardatzarekiko) simetria deritzo.Irudi simetrikoak beren artean bereizi arazten dituen elementua, r zuzena da, horregatik, r zuzenarekiko simetria, idatziz adieraziko dugu.
idatziz adieraziko dugu. Simetriak distantziak eta angeluak gorde egiten ditu, baina orientazioa alderanztu egiten du. Hain zuzen ere, AB zuzenkiaren simetrikoa den
Simetriak distantziak eta angeluak gorde egiten ditu, baina orientazioa alderanztu egiten du. Hain zuzen ere, AB zuzenkiaren simetrikoa den zuzenkiak, luzera bera du.
zuzenkiak, luzera bera du. Hori frogatzeko, nahikoa da A eta
Hori frogatzeko, nahikoa da A eta alde batetik eta B eta
alde batetik eta B eta bestetik elkartzea.
bestetik elkartzea. zuzenkia, r zuzenari buruz zuta da eta Q bere erdiko puntua da, simetriaren definizioz. Arrazoi horretxengatik,
zuzenkia, r zuzenari buruz zuta da eta Q bere erdiko puntua da, simetriaren definizioz. Arrazoi horretxengatik, zuta da r-ri buruz eta P bere erdiko puntua da. A-tik eta
zuta da r-ri buruz eta P bere erdiko puntua da. A-tik eta - etik
- etik zuzenkiari perpendikularrak marratzen bazaizkio, AMB eta
zuzenkiari perpendikularrak marratzen bazaizkio, AMB eta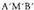 triangeluak ateratzen dira, eta biak berdinak dira, izan ere,
triangeluak ateratzen dira, eta biak berdinak dira, izan ere, angelua =
angelua = angelua da, AM aldea eta
angelua da, AM aldea eta aldea berdinak baitira, paralelogramo bateko parez pareko aldeak izateagatik. MB eta
aldea berdinak baitira, paralelogramo bateko parez pareko aldeak izateagatik. MB eta aldeak berriz, bi zuzenki berdinen arteko diferentzia izateagatik dira berdinak.
aldeak berriz, bi zuzenki berdinen arteko diferentzia izateagatik dira berdinak. da simetrikoak direlako eta
da simetrikoak direlako eta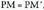 , bi paralelogramoetan AQ eta
, bi paralelogramoetan AQ eta aldeen parez parekoak direlako.
aldeen parez parekoak direlako.
Azkenik, da simetrikoak direlako.
da simetrikoak direlako. eta
eta angeluak ere berdinak dira eta antzeko arrazoiketa erabiliz froga daiteke, alegia,
angeluak ere berdinak dira eta antzeko arrazoiketa erabiliz froga daiteke, alegia, bezalako edozein angelu eta 15. irudiko bere simetrikoa den
bezalako edozein angelu eta 15. irudiko bere simetrikoa den ere berdinak direla. Baina AB-tik BC-ra joateko biraketa angelua, biraketa positiboarena da eta
ere berdinak direla. Baina AB-tik BC-ra joateko biraketa angelua, biraketa positiboarena da eta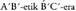 joatekoa berriz negatiboa, hau da, orientazioa aldatu egiten dela irudi simetrikoan.
joatekoa berriz negatiboa, hau da, orientazioa aldatu egiten dela irudi simetrikoan.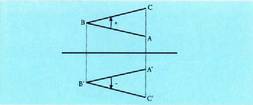
Simetria baten ekuazioak
Geometria analitikoan, simetria ardatzaren ekuazioa emanda eta alde batetik
simetria ardatzaren ekuazioa emanda eta alde batetik zuzenaren norabide bektorea dela eta bestetik A zuzen horretako puntu bat dela jakinda, planoko P puntu baten simetrikoa aurkitzeko, P-tik igarotzen den eta r zuzenari buruz zuta den zuzena aurkitzen da. Perpendikular horrek ardatza ebakitzen duen M puntua aurkitzen da. Azkenik, P puntuaren simetrikoa den
zuzenaren norabide bektorea dela eta bestetik A zuzen horretako puntu bat dela jakinda, planoko P puntu baten simetrikoa aurkitzeko, P-tik igarotzen den eta r zuzenari buruz zuta den zuzena aurkitzen da. Perpendikular horrek ardatza ebakitzen duen M puntua aurkitzen da. Azkenik, P puntuaren simetrikoa den aurkitzen da,
aurkitzen da, zuzenkiaren erdiko puntua izan behar duela baliatuz.
zuzenkiaren erdiko puntua izan behar duela baliatuz. Prozedura horrek ez du balio hasierako puntuaren koordenatuak
jakinik puntu simetrikoaren koordenatuak emateko formula orokorra
lortzeko, nahiz eta puntu simetrikoa aurkitzeko kasu guztietan
balio duen prozedura soila izan.Hasierako puntuen eta simetrikoen koordenatuen artean dagoen
erlazioa aurkitzeko, simetria ardatza jatorri puntutik igarotzen
zaion erreferentzi sistema ortonormal bat hartzen da, edozein a
inklinazioarekin. Norabide bektoreak, ardatzaren u banako modulua
duenak, balio hau du :
Prozedura horrek ez du balio hasierako puntuaren koordenatuak
jakinik puntu simetrikoaren koordenatuak emateko formula orokorra
lortzeko, nahiz eta puntu simetrikoa aurkitzeko kasu guztietan
balio duen prozedura soila izan.Hasierako puntuen eta simetrikoen koordenatuen artean dagoen
erlazioa aurkitzeko, simetria ardatza jatorri puntutik igarotzen
zaion erreferentzi sistema ortonormal bat hartzen da, edozein a
inklinazioarekin. Norabide bektoreak, ardatzaren u banako modulua
duenak, balio hau du : P planoko puntu bat bada eta
P planoko puntu bat bada eta haren simetrikoa,
haren simetrikoa, bektore banakoa denez, hau dugu:
bektore banakoa denez, hau dugu: izan ere,
izan ere, zuzenkia simetria ardatzari buruz zuta baita eta
zuzenkia simetria ardatzari buruz zuta baita eta eta
eta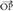 bektoreek modulu berbera baitute.Aurreko bektoreen batura, bi berdintzetan deskonposatzen da,
koordenatu bakoitzarentzat banatan hain zuzen ere :
bektoreek modulu berbera baitute.Aurreko bektoreen batura, bi berdintzetan deskonposatzen da,
koordenatu bakoitzarentzat banatan hain zuzen ere : Lehenengoan
Lehenengoan askatu eta eragiketak eginda :
askatu eta eragiketak eginda : Baina trigonometrian gauza jakina da :
Baina trigonometrian gauza jakina da : dela eta
dela eta Orduan, hau gelditzen da :
Orduan, hau gelditzen da : .
. - aren balioan ere antzeko eraldaketa batzuek eginda, hauek ateratzen dira :
- aren balioan ere antzeko eraldaketa batzuek eginda, hauek ateratzen dira : Matrize bitartez adierazita :
Matrize bitartez adierazita :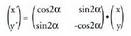 Matrizeak A-ren det = -1 baldintza betetzen du eta simetrikoa da, hau da, bere
Matrizeak A-ren det = -1 baldintza betetzen du eta simetrikoa da, hau da, bere matrize irauliaren berdina
matrize irauliaren berdina
Simetrien konposizioa.
Simetria inboluzioa da. Puntu baten simetrikoaren simetrikoa
jatorrizko puntua bera da, hots, simetriaren alderantzizkoa, elementu
berbera da.
- Ariketak
10.- Aurki ezazu :a) OX ardatzaren ardatz simetrikoarena ekuazioab) OY ardatzaren ardatz simetrikoarena ekuazioac) lehen koadranteko erdikariaren ardatz simetrikoarena?d) bigarren koadranteko erdikariaren ardatz simetrikoarena?.Aplikatu P(2,1) puntuari.11.- Kalkulatu y = 2x + 1 zuzenaren eraldatua zuzenaren ardatz simetriarekiko.12.- Kalkulatu
zuzenaren ardatz simetriarekiko.12.- Kalkulatu
Bilaua hiru aldagaien arabera eta biderik laburrena.
Traslazioak eta simetriak erabiliz, lehen begiradan oso konplexuak diren
arazoak edo ariketak, oso soil eta erraz bihur daitezke. Adibidez, ibilbiderik
laburrenen arazo batzuek.Mota horretako ariketarik soilena, A puntutik B puntura gutxieneko
luzera duen ibilbidea zein den aurkitzea da. Erantzuna, bistan denez, zera
da, AB zuzenkia dela distantziarik txikiena.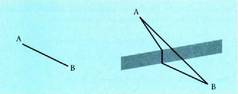 Halere ordea, baldintzaren bat erantsiz gero, arazoa bihurruago hasten
da bihurtzen. Bedi adibidez, A herritik B herrira lursail lau eta oztoporik
gabean errepidea marratzeko ariketa, baina tartean 1 zabalera duen ibaia
dela. Ibaia igarotzeko zubia egin beharra dago. Kostua, korrontearekiko
erresistentziarik handiena eta iraupena kontuan hartuta, zubia, paralelotzat
hartzen diren ibaiertzei buruz zuta izan behar duela suposatuko da.
Halere ordea, baldintzaren bat erantsiz gero, arazoa bihurruago hasten
da bihurtzen. Bedi adibidez, A herritik B herrira lursail lau eta oztoporik
gabean errepidea marratzeko ariketa, baina tartean 1 zabalera duen ibaia
dela. Ibaia igarotzeko zubia egin beharra dago. Kostua, korrontearekiko
erresistentziarik handiena eta iraupena kontuan hartuta, zubia, paralelotzat
hartzen diren ibaiertzei buruz zuta izan behar duela suposatuko da.
Zein da orain ibilbiderik laburrena?Ibaiertzei buruz zuta den zubiaren 1 luzera, ezinbestekoa da, beraz, bidearen gainerako ibilbide txikiena aurkitzea da kontua. Hori egiteko, B herriaren traslazioa egiten da planora, ibaiertzari buruz zut 1 luzeran, eta horrela puntura igarotzen da. Ibaia kontuan hartu gabe,
puntura igarotzen da. Ibaia kontuan hartu gabe, doana da ibilbide laburrena. Ibilbide hori ordea, ibaiertzera iritsi arte bakarrik da benetakoa. Ibaiertzera iristean, ibaia perpendikular gurutzatu behar da eta beste ibaiertzean zubia iristen den puntutik B-rainoko zuzena marratu behar da. Lurreko ibilbidea
doana da ibilbide laburrena. Ibilbide hori ordea, ibaiertzera iritsi arte bakarrik da benetakoa. Ibaiertzera iristean, ibaia perpendikular gurutzatu behar da eta beste ibaiertzean zubia iristen den puntutik B-rainoko zuzena marratu behar da. Lurreko ibilbidea da, horixe da eta lurreko ibilbide txikiena.
da, horixe da eta lurreko ibilbide txikiena. Ibilbideak bi ibai gurutzatu behar baldin baditu, A herria ibaiari buruz zut aldatu behar da eta beste ibaiari buruz zut B herria.
Ibilbideak bi ibai gurutzatu behar baldin baditu, A herria ibaiari buruz zut aldatu behar da eta beste ibaiari buruz zut B herria. eta
eta puntuak zuzen batez lotzen dira. Zuzenki hori da bi ibaien arteko ibilbiderik laburrena. Ibaietara iristean, ibaiertzei buruz zutak diren zubietan zehar igarotzen da bidea eta ibaiak gurutzatuta iristen den puntuetatik A eta B herriekin elkartzeko zuzenak marrazten dira.
puntuak zuzen batez lotzen dira. Zuzenki hori da bi ibaien arteko ibilbiderik laburrena. Ibaietara iristean, ibaiertzei buruz zutak diren zubietan zehar igarotzen da bidea eta ibaiak gurutzatuta iristen den puntuetatik A eta B herriekin elkartzeko zuzenak marrazten dira. Ariketa honen beste aldagai bat zera da, ibilbideak zuzen bat ukitu
behar duena. Bedi adibidez hegazkin bat A puntuan aireportua duena eta
B puntuan sutea itzali behar du. B-ra joan aurretik ordea, ura hartu behar
du r ibaian. Non hartu behar du ura ibilbiderik laburrena egiteko?
Ariketa honen beste aldagai bat zera da, ibilbideak zuzen bat ukitu
behar duena. Bedi adibidez hegazkin bat A puntuan aireportua duena eta
B puntuan sutea itzali behar du. B-ra joan aurretik ordea, ura hartu behar
du r ibaian. Non hartu behar du ura ibilbiderik laburrena egiteko?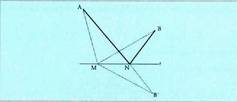 Ibaiko ura ukitzea nahikoa badu, A-tik B-ra ura ukituz lortzen den biderik laburrena,
Ibaiko ura ukitzea nahikoa badu, A-tik B-ra ura ukituz lortzen den biderik laburrena, aurkituz ateratzen da,
aurkituz ateratzen da, hori, zuzentzat hartzen den ibaiarekiko B puntuaren simetrikoa delarik. A eta
hori, zuzentzat hartzen den ibaiarekiko B puntuaren simetrikoa delarik. A eta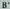 elkartuta, zuzen horrek N puntuan ebakitzen du ibaia (r zuzena). Ibilbiderik laburrena, ANB da, hain zuzen ere
elkartuta, zuzen horrek N puntuan ebakitzen du ibaia (r zuzena). Ibilbiderik laburrena, ANB da, hain zuzen ere - ren luzera berdinekoa baita NB-k eta
- ren luzera berdinekoa baita NB-k eta - ak duten simetria bidezko berdintasunarengatik. Hain zuzen ere, beste edozein puntuk, M-k adibidez,
- ak duten simetria bidezko berdintasunarengatik. Hain zuzen ere, beste edozein puntuk, M-k adibidez, emango luke eta bere balioa beti ere
emango luke eta bere balioa beti ere triangeluaren bi aldeen batura izango litzateke, beti
triangeluaren bi aldeen batura izango litzateke, beti hirugarren aldea baino handiago dena.Aurreko ariketan hegazkinak ibaian zehar 1 luzerako distantzia behar baldin badu ur-gordailuak betetzeko, B-ren simetrikoa den
hirugarren aldea baino handiago dena.Aurreko ariketan hegazkinak ibaian zehar 1 luzerako distantzia behar baldin badu ur-gordailuak betetzeko, B-ren simetrikoa den puntua aurkitzen da eta
puntua aurkitzen da eta puntu hori 1 luzera aldatzen da A-rantz, eta horrela B "aurkitzen. A eta B" elkartuz, ibairainoko AP ibilbidea lortzen da. Gero, ibaian zehar 1 distantzia egingo du, PQ hain zuzen ere. Azkenik, Q-tik zuzenzuzen B-ra joango da.
puntu hori 1 luzera aldatzen da A-rantz, eta horrela B "aurkitzen. A eta B" elkartuz, ibairainoko AP ibilbidea lortzen da. Gero, ibaian zehar 1 distantzia egingo du, PQ hain zuzen ere. Azkenik, Q-tik zuzenzuzen B-ra joango da. Simetriez baliatuz ebazten den beste ariketa bat, bilar jokokoa da, alegia,
ea non jo behar duen bolak mahai ertza gero beste bola bat jotzeko.
Simetriez baliatuz ebazten den beste ariketa bat, bilar jokokoa da, alegia,
ea non jo behar duen bolak mahai ertza gero beste bola bat jotzeko.
Hori, bolari gurpil bereizirik eman gabe eginda noski. Ebazpena zera da,
alegia, jo nahi den bolak mahai ertzaz bestaldean izango lukeen simetrikorantz
apuntatu behar dela.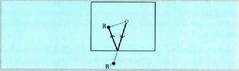 Bi ertzetan jo nahi baldin bada, bi simetria joko egin behar dira jo nahi
diren ertzak simetria ardaztzat hartuta.
Bi ertzetan jo nahi baldin bada, bi simetria joko egin behar dira jo nahi
diren ertzak simetria ardaztzat hartuta. Hiru ertzetan jo nahi bada berriz, hiru simetria joko hartu behar dira
kontuan. Beti ere, ertzen ordena gordez noski.
Hiru ertzetan jo nahi bada berriz, hiru simetria joko hartu behar dira
kontuan. Beti ere, ertzen ordena gordez noski.
V Higiduren multzoa.
Luzerak eta angeluak gordez egindako eraldaketen konposizioak, beste isometria bat ematen du. Konposizio horiek aztertzeko, bi simetria, biraketa, traslazioa, bi biraketa eta azkenik biraketa eta traslazioa dituen simetria erabiltzearen ondorioak aztertuko ditugu.
Bi simetriazko konposizioa :
a) Kasurik soilena lehen ikusia da, hain zuzen ere, bi simetriek ardatz berbera dutenekoa. Kasu horretan, da eta I-k identitatea adierazten du.b ) Konposatzen diren bi simetrien ardatzak paraleloak badira,
da eta I-k identitatea adierazten du.b ) Konposatzen diren bi simetrien ardatzak paraleloak badira, , orduan, konposizioaren emaitza, traslazioa da :
, orduan, konposizioaren emaitza, traslazioa da : non
non bektorea, r-tik
bektorea, r-tik - erako distantzia modulutzat duena den, norabidea berriz r-tik
- erako distantzia modulutzat duena den, norabidea berriz r-tik - erako lerroaren perpendikularra eta norantza r-tik
- erako lerroaren perpendikularra eta norantza r-tik - erakoa.
- erakoa. Adibide baten bidez ikusita :
Adibide baten bidez ikusita : P puntua, r ardatzaren simetriaz,
P puntua, r ardatzaren simetriaz, bihurtzen da eta
bihurtzen da eta ardatzaren simetriaz
ardatzaren simetriaz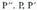 eta
eta puntuak lerrokatuta daude eta gainera,
puntuak lerrokatuta daude eta gainera, da eta
da eta , beraz :
, beraz : Traslazioaren norantza, A-tik, lehenengo simetria ardatzarekin duen ebakiduratik,
Traslazioaren norantza, A-tik, lehenengo simetria ardatzarekin duen ebakiduratik, - erakoa, bigarren simetria ardatzarekin duen ebakidurarakoa da. Hortik zera ondoriozta daiteke, alegia, simetrien konposizioa ez dela trukakorra, izan ere, S r S , balitz, bektorearen norantza
- erakoa, bigarren simetria ardatzarekin duen ebakidurarakoa da. Hortik zera ondoriozta daiteke, alegia, simetrien konposizioa ez dela trukakorra, izan ere, S r S , balitz, bektorearen norantza - etik A-rakoa izango bailitzateke, hau da,
- etik A-rakoa izango bailitzateke, hau da, Ez da oso zaila egiaztatzea, alegia, P puntuaren beste jatorrizko
kokaera batzuentzat, emaitza berbera dela.Ardatz paraleloen bi simetria,
Ez da oso zaila egiaztatzea, alegia, P puntuaren beste jatorrizko
kokaera batzuentzat, emaitza berbera dela.Ardatz paraleloen bi simetria, bektorearen traslazioaren baliokideak dira, non
bektorearen traslazioaren baliokideak dira, non bi ardatzei buruz zuta den bektorea den, modulutzat beren arteko distantzia duena eta norantza lehenengotik bigarrenerakoa.c) r eta
bi ardatzei buruz zuta den bektorea den, modulutzat beren arteko distantzia duena eta norantza lehenengotik bigarrenerakoa.c) r eta simetria ardatzek a angelua eratuz elkar ebakitzen badute, orduan
simetria ardatzek a angelua eratuz elkar ebakitzen badute, orduan eta
eta . simetrien konposizioa,
. simetrien konposizioa, angeludun biraketa da, zentroa simetriak eratzen dituzten bi zuzenen ebaki puntua delarik, eta biraketa norantza r lehen ardatzetik
angeludun biraketa da, zentroa simetriak eratzen dituzten bi zuzenen ebaki puntua delarik, eta biraketa norantza r lehen ardatzetik bigarren ardatzera doana.
bigarren ardatzera doana. Hain zuzen ere, P puntua, S r simetriaren bidez
Hain zuzen ere, P puntua, S r simetriaren bidez izatera pasatzen bada, POA eta
izatera pasatzen bada, POA eta triangeluak berdinak direla egiaztatzen da, izan ere, A angeluzuzena baita, OA alde komuna eta PA eta
triangeluak berdinak direla egiaztatzen da, izan ere, A angeluzuzena baita, OA alde komuna eta PA eta aldeak berdinak simetrikoak direlako. Beraz,
aldeak berdinak simetrikoak direlako. Beraz,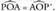 Bigarren simetriarentzat ere antzeko arrazoiketa erabiliz,
Bigarren simetriarentzat ere antzeko arrazoiketa erabiliz, eta
eta angeluak berdinak dira. Beraz, hau betetzen da :
angeluak berdinak dira. Beraz, hau betetzen da : angelua, bi simetrien ardatzek elkarren artean eratzen duten
angelua, bi simetrien ardatzek elkarren artean eratzen duten angelua da.Biraketa norantza, r-tik
angelua da.Biraketa norantza, r-tik
Biraketa eta traslaziozko edota traslazio eta biraketazko konposizioa
Traslazioak eta biraketak bi simetrien biderkadura bihurtu eta deskonposatzeak, erraztu egiten du konposizio horien emaitzen lorpena.a) Lehenik biraketa eta gero traslazioa : - ren emaitza jakin nahi bada, bi mugimenduak simetrien biderkaduran deskon posatzen dira. Hau lortzen da :
- ren emaitza jakin nahi bada, bi mugimenduak simetrien biderkaduran deskon posatzen dira. Hau lortzen da : elkar ebakitzen duten r eta
elkar ebakitzen duten r eta simetria ardatzek eratzen duten angelua izanik eta b
simetria ardatzek eratzen duten angelua izanik eta b - etik t-ra perpendikular daraman bektorea.
- etik t-ra perpendikular daraman bektorea.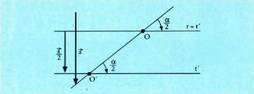 Ondoko konposizioa kalkulatzeko :
Ondoko konposizioa kalkulatzeko : hartzen da, traslazioko
hartzen da, traslazioko bektoreari buruz zuta dela eta biraketa zentro den O puntutik igarotzen dela.
bektoreari buruz zuta dela eta biraketa zentro den O puntutik igarotzen dela. zuzena marrazten da,
zuzena marrazten da, - etik r-rako biraketa
- etik r-rako biraketa - koa izanez eta t zuzena,
- koa izanez eta t zuzena, - etik t-ra perpendikular daraman bektorea
- etik t-ra perpendikular daraman bektorea - koa izanez. Orduan, hau betetzen da :
- koa izanez. Orduan, hau betetzen da : Baina
Baina da, beraz,
da, beraz, Orduan, honako hau gelditzen da :
Orduan, honako hau gelditzen da : Hau da,
Hau da, angeludun beste biraketa bat da, t eta
angeludun beste biraketa bat da, t eta paraleloak direlako eta
paraleloak direlako eta - aren eta r-ren arteko angelua, t zuzenaren arteko berbera dena alegia,
- aren eta r-ren arteko angelua, t zuzenaren arteko berbera dena alegia, delako : Biraketa zentroa
delako : Biraketa zentroa puntua izango da, t eta
puntua izango da, t eta - aren ebaki puntua hain zuzen ere.b) Lehenik traslazioa eta gero biraketa. Konposizioaren emaitza lortzeko modua antzekoa da.
- aren ebaki puntua hain zuzen ere.b) Lehenik traslazioa eta gero biraketa. Konposizioaren emaitza lortzeko modua antzekoa da. bektoredun traslazioa eta O zentrodun a angeluko biraketa baditugu, simetria biderkaduratan deskonposatzen dira bi eraldaketak, baina traslazioaren bigarren simetria biraketaren lehenengoarekin bat etorraraziz eta beren ondorioak hutsal bihurturik identitatea emanaraziz.
bektoredun traslazioa eta O zentrodun a angeluko biraketa baditugu, simetria biderkaduratan deskonposatzen dira bi eraldaketak, baina traslazioaren bigarren simetria biraketaren lehenengoarekin bat etorraraziz eta beren ondorioak hutsal bihurturik identitatea emanaraziz. Kasu honetan, aurrekoan bezalaxe :
Kasu honetan, aurrekoan bezalaxe : Emaitza,
Emaitza, zentro eta
zentro eta angelua duen biraketa da. Baina biraketak desberdinak dira, izan ere,
angelua duen biraketa da. Baina biraketak desberdinak dira, izan ere, eta
eta
Zentro desberdineko bi biraketazko konposizioa.
Bi biraketek zentro berbera baldin badute, konposizioa beste biraketa bat da, angelua angeluen batura duena eta eta zentroa beste biraketekin komuna duena. Bi zentroak desberdinak badira, emaitzaez da hain begibistakoa. Emaitza zein den ikusteko, aurreko kasuan bezalaxe, simetrietan deskonposatzen dira. eta
eta biraketak baldin baditugu, bi biraketak, bi simetrietan deskonposa daitezke.
biraketak baldin baditugu, bi biraketak, bi simetrietan deskonposa daitezke. biraketarentzat, bi ardatzak, O-n gurutzatu eta elkarren artean
biraketarentzat, bi ardatzak, O-n gurutzatu eta elkarren artean angelua eratu behar duten bi zuzen dira.
angelua eratu behar duten bi zuzen dira. biraketarentzat, bi ardatzek
biraketarentzat, bi ardatzek - etik pasa eta bien artean
- etik pasa eta bien artean angelua eratu behar dute. Konposizioa ondorengoa bada :
angelua eratu behar dute. Konposizioa ondorengoa bada : O-tik eta
O-tik eta - etik igarotzen den zuzena hartzen da eta lehen biraketako bigarren simetriaren nahiz bigarren biraketako lehen simetriaren ardatz moduan jartzen. Hau da, bi biraketak definitzen dituzten simetriak hartzen dira ondoko baldintza hau betez :
- etik igarotzen den zuzena hartzen da eta lehen biraketako bigarren simetriaren nahiz bigarren biraketako lehen simetriaren ardatz moduan jartzen. Hau da, bi biraketak definitzen dituzten simetriak hartzen dira ondoko baldintza hau betez : Simetria hori desagertu egingo da, izan ere, bere buruarekin konbinatzean, identitatea ematen baitu. Orduan, lehenengo biraketari dagokion lehen simetria eta azkeneko biraketari dagokion bigarren simetria geldituko dira. Bi zuzen horiek
Simetria hori desagertu egingo da, izan ere, bere buruarekin konbinatzean, identitatea ematen baitu. Orduan, lehenengo biraketari dagokion lehen simetria eta azkeneko biraketari dagokion bigarren simetria geldituko dira. Bi zuzen horiek ebakitzen dute elkar eta eratzen duten angeluak
ebakitzen dute elkar eta eratzen duten angeluak balio du,
balio du, triangeluko
triangeluko erpineko kanpoangelua delako eta horren ondorioz beste bi barneangeluen
erpineko kanpoangelua delako eta horren ondorioz beste bi barneangeluen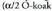 eta
eta batura balio duelako.
batura balio duelako.
Beraz, bi biraketa horien konposizioa, beste biraketa bat izango da, simetrien ebaki puntua zentrotzat duena eta
simetrien ebaki puntua zentrotzat duena eta angeluduna.
angeluduna.
Simetriaren konposizioa traslazioz edo biraketaz.
Traslazioz edo biraketaz egindako simetriaren kasuan, azken irudiak,
hasierakoaren aurkako orientazioa izan behar du. Simetria
berriren bat ere izan daiteke, baina orokorki, alderantzizko higidura
berria izan ohi da, lerradura. Lerradura, simetria baten eta simetria
ardatzarekiko paraleloa den traslazio baten konposizioa da : Eraldaketa hau ezin daiteke simetria bat izan, izan ere, eraldaketaren irudia lekualdatuta baitago. A eta
Eraldaketa hau ezin daiteke simetria bat izan, izan ere, eraldaketaren irudia lekualdatuta baitago. A eta - ren erdibitzailea, B eta
- ren erdibitzailea, B eta - aren edo C eta
- aren edo C eta
Frisoak eta mosaikoak.

Frisoak
Frisoa edo zerrenda modulua d eta norabidea frisoarena bera dituen
bektore baten arabera lekualdatuz doan marrazki bat da. Marrazkia printzipioz,
bi norantzetan errepikatzen da mugagabe, baina izatez frisoa kokatuta
dagoen lekuak berak mugatu ohi du haren luzera.Frisoak oso maiz azaltzen dira arkitekturan eta baita barne apaindura,
paper pintatu, alikatatu edo oihaletan ere.Horrela egiten diren marrazkiak, sortzen dituen bektorearen luzeraren
eta norabidearen araberakoak dira. Errepikatzen den oinarrizko marrazkia
berriz, marrazki erraz eta soilago batean oinarrituta egin ohi da. Frisoak
oinarrizko irudia lortzeko elementu sortzaileari egiten zaizkion eraldaketen
arabera sailkatzen dira :- Traslazio frisoak, oinarrizko marrazkia bakarrik dauka lekualdatua.- Simetria horizontala duen frisoak, irudi soil batez eta bere simetria
horizontalaren araberako irudi simetrikoaz osatua du oinarrizko marrazkia,
hots, traslazio bektorearekiko paraleloan.- Traslazioak eta simetria bertikala dituen frisoak, elementu sortzaile
bati simetria bertikala aplikatuta lortutako oinarrizko irudia du.- Lerraduradun traslazio frisoak, marrazki soila den oinarrizko irudia
eta simetria horizontal baten eta traslazio baten emaitza ditu, hau da, bere
lerradurarena hain zuzen ere.- Traslazioak eta simetria zentrala dituen frisoa berriz, oinarrizko irudia
marrazki sortzailez eratua izan eta 1800 biratzean berarengandik lortzen
dena da.- Biraketa eta lerradurak dituen traslazio frisoa. Irudi elementalari simetria
bertikala aplikatzen zaio eta emaitzari lerradura, edota 180°-ko biraketa,
kasu honetan gauza bera da eta.
- Friso osoa berriz marrazki elementaletik lortzen da simetria horizontal
bat eta simetria bertikal bat edo biraketa bat eta simetria horizontal bat
aplikatuz.
Mosaikoak
Irudi batean oinarritu eta plano osoa bete arte errepikatuz egiten dira.
Mosaiko batek, ongi egina izango bada, ez du hutsune librerik utzi behar
ez eta irudi bat beste baten gainean jarrita eduki ere. Oinarrizko irudia,
errepikatuz mosaikoa sortzen duena, poligono erregularra izan daiteke ala
ez. Halaber, hutsunerik utzi gabe eta zatiak bata bestearen gainean jarri
gabe perimetroa aldatu zaion poligono erregularra ere izan daiteke.Mosaiko erregularrak, oinarrizko irudi gisa poligono erregularra dutenak
dira. Hiru poligono bakarrik izan daitezke mosaikoaren oinarri, trianelu
aldekidea, karratua eta hexagono erre g ularra. Hain zuzen ere, erpin
batean elkartzen diren poligonoen angeluek, 360°-ko batura eman behar
dute inolako hutsunerik eta gainjartzerik izan ez dadin. Hori, sei triangelu
aldekiderekin, 6x60° = 360°, lau karraturekin 4x90° = 360°, edo hiru
hexagonorekin, 3x1200 = 360° lortzen da. Baina pentagonoa adibidez, ezin daiteke izan mosaiko baten oinarrizko
irudi, izan ere barne-angelua 108° baita eta 3x108° = 324° da eta 4x108°
= 432°. Hiru pentagonorekin ez da betetzen erpina eta laurekin berriz pasa
egiten da edo gainjarri egiten dira.Baldosa pentagonalek ez dute betetzen planoa osorik eta zehatz.
Baina pentagonoa adibidez, ezin daiteke izan mosaiko baten oinarrizko
irudi, izan ere barne-angelua 108° baita eta 3x108° = 324° da eta 4x108°
= 432°. Hiru pentagonorekin ez da betetzen erpina eta laurekin berriz pasa
egiten da edo gainjarri egiten dira.Baldosa pentagonalek ez dute betetzen planoa osorik eta zehatz. Poligono erregular horietan, mosaikoaren oinarrizko irudia lortzeko,
90° eta 180°-ko biraketak konbina daitezke, simetriekin eta ertzetako
irudi aldaketekin, horrela, bi norabidetako traslazio bidez baino erakargarriagoak
diren oinarrizko irudiak lortzeko. Planoa bete arte errepikatzen
da oinarrizko irudia.
Poligono erregular horietan, mosaikoaren oinarrizko irudia lortzeko,
90° eta 180°-ko biraketak konbina daitezke, simetriekin eta ertzetako
irudi aldaketekin, horrela, bi norabidetako traslazio bidez baino erakargarriagoak
diren oinarrizko irudiak lortzeko. Planoa bete arte errepikatzen
da oinarrizko irudia. Mosaiko erdierregularrakMosaiko erdierregularrak, ondorengo baldintzak betetzen dituzten bi
poligono erregularrez eratuta daude :Erpin guztietan, poligono berberak eta ordena berean daude.
Mosaiko erdierregularrakMosaiko erdierregularrak, ondorengo baldintzak betetzen dituzten bi
poligono erregularrez eratuta daude :Erpin guztietan, poligono berberak eta ordena berean daude.
Poligono erregular guztiek alde berdina dute. Mosaiko erdierregularretan, triangelu aldekideak, karratuak,hexagonoak,
oktogonoak edo dodekagonoak izan daitezke. Erpin bakoitzeko, 360°
izan behar du angeluen baturak, poligono erregularretan bezala, eta
horrek, 8 konbinazio baizik ez ditu uzten posible.Mosaiko erregularretan bezala, alde, irudi eta koloreekin era askotara
joka daiteke, era askotako mosaiko ugari lortzeko.Mosaikoak batez ere arabiar kulturan loratu dira, izan ere, kultura
horretan ez baita zilegi erlijio eraikinetan giza irudia irudikatzea. Arabiar
mosaikoen artean, sonatuak dira Nazari garaiko Granadakoak eta horien
artean bereziki Alhambrakoak. Alhambrako mosaikoen hiru irudi petu,
petalo, hezur eta paper txori deituak dira, irudi karratu edo triangeluarretatik
lortuak.
Mosaiko erdierregularretan, triangelu aldekideak, karratuak,hexagonoak,
oktogonoak edo dodekagonoak izan daitezke. Erpin bakoitzeko, 360°
izan behar du angeluen baturak, poligono erregularretan bezala, eta
horrek, 8 konbinazio baizik ez ditu uzten posible.Mosaiko erregularretan bezala, alde, irudi eta koloreekin era askotara
joka daiteke, era askotako mosaiko ugari lortzeko.Mosaikoak batez ere arabiar kulturan loratu dira, izan ere, kultura
horretan ez baita zilegi erlijio eraikinetan giza irudia irudikatzea. Arabiar
mosaikoen artean, sonatuak dira Nazari garaiko Granadakoak eta horien
artean bereziki Alhambrakoak. Alhambrako mosaikoen hiru irudi petu,
petalo, hezur eta paper txori deituak dira, irudi karratu edo triangeluarretatik
lortuak.
Irudi bat aldatzen ez duten eraldaketak.
Irudi lau erregularrenak aldagabeak dira, baldin eta eraldaketa geometriko
batzuek egiten bazaizkie. Adibidez, zirkunferentzia bat ez da aldatzen
diametro batekiko irudi simetrikoa egiten bazaio edota bere zentroaren
inguruan edozein biraketa egiten bazaio. Kasu honetan, zirkunferentzia
bat aldatzen ez uzten duten eraldaketen kopurua, infinitua da. Poligonoa
baldin bada berriz, eraldaketak finituak eta mugatuak dira. Adibidez,
triangelu aldekidea, honako hauek bihurtzen dute aldagabe :Hiru ardatz simetriek, aldeen hiru erdibitzaileek.Triangeluaren zentroa zentrotzat duten hiru biraketek : 0°, 120° eta
240°-koek alegia.Hala ere ordea, ez du simetria zentrorik.Karratua aldagabea da honako kasu hauetan :- Lau ardatzekiko simetrien kasuetan: bi diagonalen kasuan eta aldeen
bi erdibitzaileenean.- Karratuaren zentroan zentro duten lau biraketetan : 0°, 90°, 180° eta
270°-ko angeludunetan.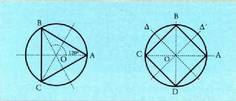 180°-ko biraketarekin simetrikoa denez, karratuaren zentroa, bere
simetrien zentro da. Eta horrela jarrai daiteke beste poligono batzuekin
ere.Irudi bat aldatzen ez duten bi eraldaketa konposatzen badira, aldagabe
uzten duen beste eraldaketa bat lortzen da. Bestela esanda, eraldaketen
konposizioa, eragiketa itxia da irudi bat aldagabe uzten duten eraldaketen
multzoarentzat. Bestalde, identitateak edozein irudi uzten du aldagabe eta
higidura batek aldagabe uzten badu, bere alderantzizkoak ere bai. Era
horretan, eraldaketen multzo finituak edo mugatuak lortzen dira.ABCD karratua aldagabe uzten duten eraldaketen konposizioa, ondoko taulan dago laburtuta. Lehenengo eraldaketa, lerroetan doana da eta bigarrena zutabeetan, hots, i errenkadaren eta j zutabearen gurutzaduran,
180°-ko biraketarekin simetrikoa denez, karratuaren zentroa, bere
simetrien zentro da. Eta horrela jarrai daiteke beste poligono batzuekin
ere.Irudi bat aldatzen ez duten bi eraldaketa konposatzen badira, aldagabe
uzten duen beste eraldaketa bat lortzen da. Bestela esanda, eraldaketen
konposizioa, eragiketa itxia da irudi bat aldagabe uzten duten eraldaketen
multzoarentzat. Bestalde, identitateak edozein irudi uzten du aldagabe eta
higidura batek aldagabe uzten badu, bere alderantzizkoak ere bai. Era
horretan, eraldaketen multzo finituak edo mugatuak lortzen dira.ABCD karratua aldagabe uzten duten eraldaketen konposizioa, ondoko taulan dago laburtuta. Lehenengo eraldaketa, lerroetan doana da eta bigarrena zutabeetan, hots, i errenkadaren eta j zutabearen gurutzaduran, , dago. Taulan, r,s,t,u erabili dira diagonalen araberako aldeen erdibitzaileen simetrientzat,
, dago. Taulan, r,s,t,u erabili dira diagonalen araberako aldeen erdibitzaileen simetrientzat, edo
edo erabili ordez eta horrela emaitzak irakurterrazagoak dira.
erabili ordez eta horrela emaitzak irakurterrazagoak dira.
VI. Homoteziak. Antzekotasun multzoak.
O zentrodun eta k arrazoidun (k zero ez dela) homotezia, planoko edozein P punturi beste puntu bat egoki arazten dion eraldaketa da
puntu bat egoki arazten dion eraldaketa da izanez.Homotezia bat zehazteko, haren zentroa eta arrazoia jakin behar dira. Horregatik, P puntua
izanez.Homotezia bat zehazteko, haren zentroa eta arrazoia jakin behar dira. Horregatik, P puntua bilakarazten duen homotezia, era honetan adieraziko da :
bilakarazten duen homotezia, era honetan adieraziko da : Homotezia bat duen AB zuzenkia,
Homotezia bat duen AB zuzenkia, zuzenki bihurtzen da.
zuzenki bihurtzen da.
Homoteziaren definizioz, da. O angelua komuna denez, OAB eta
da. O angelua komuna denez, OAB eta antzekoak dira bi alde proportzional eta aldeen arteko angelua berdina dituztelako. Horren ondorioz,
antzekoak dira bi alde proportzional eta aldeen arteko angelua berdina dituztelako. Horren ondorioz, zuzenkia, AB zuzenkiaren eraldatua, honekiko paralelo a da eta BC zuzenkia berriz
zuzenkia, AB zuzenkiaren eraldatua, honekiko paralelo a da eta BC zuzenkia berriz zuzenkiarekiko paraleloa. Beraz,
zuzenkiarekiko paraleloa. Beraz,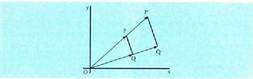 angelua =
angelua = Homotezian beraz, angeluek iraun egiten dute aldeak paraleloak direlako.
Homotezian beraz, angeluek iraun egiten dute aldeak paraleloak direlako. 1 arrazoidun simetria, identitatea da, izan ere, puntu baten eraldatua,
puntua berbera baita. -1 arrazoidun homotezia, simetria zentrala
da edota O zentrodun eta 1800-ko angeludun biraketa.Arrazoi negatibodun homoteziarekin, irudi eraldatua, homotezia
zentroaz beste (aurkako) aldera igarotzen da.
1 arrazoidun simetria, identitatea da, izan ere, puntu baten eraldatua,
puntua berbera baita. -1 arrazoidun homotezia, simetria zentrala
da edota O zentrodun eta 1800-ko angeludun biraketa.Arrazoi negatibodun homoteziarekin, irudi eraldatua, homotezia
zentroaz beste (aurkako) aldera igarotzen da.
Ekuazioak:
Homoteziaren O zentroa, koordenatu ardatzen jatorri puntua
baldin bada, ekuazioa honako hau da : edota matrize bidez azalduta :
edota matrize bidez azalduta : Homoteziaren zentroa koordenatu ardatzen
Homoteziaren zentroa koordenatu ardatzen jatorri puntua ez bada, aurreko ekuazioak, matrize honetara bihurtzen dira :
jatorri puntua ez bada, aurreko ekuazioak, matrize honetara bihurtzen dira :
Konposizioa :
Zentroa berbera baldin bada, homoteziek multzoa osatzen dute. Unitatea,
homoteziek multzoa osatzen dute. Unitatea, da eta
da eta - ren alderantzizkoa
- ren alderantzizkoa da. Alderantzizkoa beti dago, izan ere, k ezin baitaiteke 0 izan.
da. Alderantzizkoa beti dago, izan ere, k ezin baitaiteke 0 izan.
Orokorki, da,
da, denean salbu, izan ere, kasu horretan, traslazioa baita.
denean salbu, izan ere, kasu horretan, traslazioa baita. zentroak lerrokatuta egon behar du O eta
zentroak lerrokatuta egon behar du O eta
- Ariketak
15.- Kalkula ezazu 0(1,1) zentrodun eta k=2 arrazoidun
homoteziak eragindako P(3,2) puntuaren eraldatua.16.- Kalkula ezazu aurreko ariketako homoteziak eragindako
x+3y=5 zuzenaren eraldatua.17.- Kalkula ezazu aurreko ariketako homoteziak eragindako zuzenaren eraldatua.18.- Froga ezazu matrize bidez
zuzenaren eraldatua.18.- Froga ezazu matrize bidez
VII. Alderanzketak
Planoko O puntua emanda eta den zenbaki bat, alderanzketa izena ematen zaio planoko A puntu bakoitzari, A puntu horrekin
lerrokatuta dagoen eta
den zenbaki bat, alderanzketa izena ematen zaio planoko A puntu bakoitzari, A puntu horrekin
lerrokatuta dagoen eta egiten duen beste
egiten duen beste puntu bat egoki arazten dion eraldaketari.
puntu bat egoki arazten dion eraldaketari. betetzen duten P puntuak, puntu aldagabeak dira, hots, puntu eraldatua jatorrizko puntu berbera da. Ardatz simetrian simetria ardatzaren zuzena bazen aldagabe irauten zuena, hemen zirkunferentzia bat da eta horregatik deitu ohi zaio alderanzketari simetria zirkularra edo zirkulu simetria.Alderanzketa bat ongi finkatuta dago, zentroa eta
betetzen duten P puntuak, puntu aldagabeak dira, hots, puntu eraldatua jatorrizko puntu berbera da. Ardatz simetrian simetria ardatzaren zuzena bazen aldagabe irauten zuena, hemen zirkunferentzia bat da eta horregatik deitu ohi zaio alderanzketari simetria zirkularra edo zirkulu simetria.Alderanzketa bat ongi finkatuta dago, zentroa eta ezagutzen badira, edota zentroa eta puntu aldagaben zirkunferentzia ezagutzen badira. Zirkunferentziaren barneko A puntuak, zirkunferentziaz kanpoko
ezagutzen badira, edota zentroa eta puntu aldagaben zirkunferentzia ezagutzen badira. Zirkunferentziaren barneko A puntuak, zirkunferentziaz kanpoko puntua du iruditzat eta alderantziz, zirkunferentziaz kanpoko puntu batek barruan du bere irudia. O jatorri puntuak, berez ez du irudirik, izan ere,
puntua du iruditzat eta alderantziz, zirkunferentziaz kanpoko puntu batek barruan du bere irudia. O jatorri puntuak, berez ez du irudirik, izan ere, da eta
da eta ekuazioak ez du emaitzarik. Baina A puntua jatorri punturantz hurbiltzen bada, OA distantzia txikiago bihurtzen da eta
ekuazioak ez du emaitzarik. Baina A puntua jatorri punturantz hurbiltzen bada, OA distantzia txikiago bihurtzen da eta geroz eta handiago bihurtu behar du biderkadura konstante iraunarazteko.
geroz eta handiago bihurtu behar du biderkadura konstante iraunarazteko.
Horregatik da erosoa jatorri puntuaren irudia infinituko puntua dela esatea.Alderanzketa inboluzio bat da : Baldin eta alderanzketa batek sortutako P-ren eraldatua bada, P, P'-arena da. Eraldatuaren eraldatua, jatorrizkoa da.Alderanzketa, ez distantziak ez eta irudiak edo formak ere gordetzen
ez dituen eraldaketa da, baina angeluak bai gordetzen ditu,
beren orientazioa aldatu arren. Alderanzketaren cartesiar ekuazioak
ez dira errazak ; horregatik haien ezaugarriak aipatuko dira, baina ez
dira erabiliko.Alderanzketa batean zuzenek eta zirkunferentziek izandako eraldaketak,
kokaeraren araberakoak dira :- Alderanzketaren zentrotik igarotzen diren zuzenak, beren buru bihurtzen dira. A eta
alderanzketa batek sortutako P-ren eraldatua bada, P, P'-arena da. Eraldatuaren eraldatua, jatorrizkoa da.Alderanzketa, ez distantziak ez eta irudiak edo formak ere gordetzen
ez dituen eraldaketa da, baina angeluak bai gordetzen ditu,
beren orientazioa aldatu arren. Alderanzketaren cartesiar ekuazioak
ez dira errazak ; horregatik haien ezaugarriak aipatuko dira, baina ez
dira erabiliko.Alderanzketa batean zuzenek eta zirkunferentziek izandako eraldaketak,
kokaeraren araberakoak dira :- Alderanzketaren zentrotik igarotzen diren zuzenak, beren buru bihurtzen dira. A eta puntuek, O jatorri puntuarekin lerrokatuta egon behar dutenez, A eta
puntuek, O jatorri puntuarekin lerrokatuta egon behar dutenez, A eta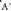 zuzen berberean daude, beraz, eraldatzen diren puntuak zuzen batean badaude, haien eraldatuak zuzen berberean egongo dira. Zuzena aldagabea da, nahiz eta puntu bikoitzak edo aldagabeak
zuzen berberean daude, beraz, eraldatzen diren puntuak zuzen batean badaude, haien eraldatuak zuzen berberean egongo dira. Zuzena aldagabea da, nahiz eta puntu bikoitzak edo aldagabeak betetzen duten bi puntuak bakarrik izan.
betetzen duten bi puntuak bakarrik izan. - Zentrotik igarotzen ez diren zuzenak, zentrotik igarotzen diren
zirkunferentzia bihurtzen dira.Bedi O alderanzketaren zentroa. P puntua, jatorri puntutik igarotzen ez den r zuzenean dagoena,
- Zentrotik igarotzen ez diren zuzenak, zentrotik igarotzen diren
zirkunferentzia bihurtzen dira.Bedi O alderanzketaren zentroa. P puntua, jatorri puntutik igarotzen ez den r zuzenean dagoena, bihurtzen da. O-tik, r-ri buruz zuta den zuzena marrazten da,
bihurtzen da. O-tik, r-ri buruz zuta den zuzena marrazten da, . Zuzen horrek, r, M puntuan ebakitzen du. M-ren alderantzizko puntua bilatzen da eta demagun
. Zuzen horrek, r, M puntuan ebakitzen du. M-ren alderantzizko puntua bilatzen da eta demagun dela. Alderanzketaren definizioz, hau betetzen da :
dela. Alderanzketaren definizioz, hau betetzen da : Eta hortik lortzen da
Eta hortik lortzen da . Bestalde,
. Bestalde, eta
eta berdinak dira bat datozelako, beraz, OPM triangelua eta
berdinak dira bat datozelako, beraz, OPM triangelua eta antzekoak dira. Horren ondorioz,
antzekoak dira. Horren ondorioz,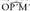 angelua,
angelua, angeluaren berdina da.
angeluaren berdina da. angeluak ordea, 900 balio du eraikuntzaz, beraz,
angeluak ordea, 900 balio du eraikuntzaz, beraz, angeluak ere 90° balio du, alderanztutako r zuzenaren P puntua edozein delarik ere.
angeluak ere 90° balio du, alderanztutako r zuzenaren P puntua edozein delarik ere. angeluak 90° balio izateko puntuek ordea,
angeluak 90° balio izateko puntuek ordea, angeluaren arku kapaza eratzen dute 90°-ko angeluarekin,
angeluaren arku kapaza eratzen dute 90°-ko angeluarekin, diametrodun zirkunferentzia hain zuzen ere. Beraz, alderanzketa batean, jatorri puntutik igarotzen ez den zuzen batek, jatorri puntutik igarotzen den zirkunferentzia du iruditzat.
diametrodun zirkunferentzia hain zuzen ere. Beraz, alderanzketa batean, jatorri puntutik igarotzen ez den zuzen batek, jatorri puntutik igarotzen den zirkunferentzia du iruditzat.
- Jatorri puntutik igarotzen diren zirkunferentziek, jatorri puntutik igarotzen ez diren zuzenak dituzte iruditzat. Esandakoaren ondorio zuzena da eta baita alderanzketa inboluzio erako eraldaketa izatea ere. Beraz, irudi eraldatuak, kasu honetan jatorri puntutik igarotzen den zirkunferentziak, berriro eraldatzen bada, hasierako irudia ematen du, jatorri puntutik igarotzen ez den zuzena alegia. - Jatorri puntutik igarotzen ez diren zirkunferentziak jatorri puntutik
igarotzen diren zirkunferentzia bihurtzen dira.Demagun c zirkunferentzia dugula eta alderanzketa zentroak zirkunferentzia horrekiko duen potentzia,
- Jatorri puntutik igarotzen ez diren zirkunferentziak jatorri puntutik
igarotzen diren zirkunferentzia bihurtzen dira.Demagun c zirkunferentzia dugula eta alderanzketa zentroak zirkunferentzia horrekiko duen potentzia, dela. c zirkunferentziako A eta B puntuak hartzen dira (bi edozein), baina O-rekin lerrokatuta daudenak. Beren eraldatuak
dela. c zirkunferentziako A eta B puntuak hartzen dira (bi edozein), baina O-rekin lerrokatuta daudenak. Beren eraldatuak eta
eta dira eta hau betetzen da :
dira eta hau betetzen da : Bestalde, zirkunferentziaren potentzia
Bestalde, zirkunferentziaren potentzia delako, hau betetzen da :
delako, hau betetzen da : Lehenengo berdintzak bigarren honekin zatituta, hau dugu :
Lehenengo berdintzak bigarren honekin zatituta, hau dugu : Beraz,
Beraz, Hori, begiratzen ari garen A eta B puntuekiko zerikusirik gabe.
Hori, begiratzen ari garen A eta B puntuekiko zerikusirik gabe.
Hori ordea, arrazoia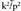 eta zentrotzat alderanzketa zentroa duen homoteziaren ekuazioa da.Orduan, alderanzketa zentrotik igarotzen ez den zirkunferentziaren alderantzizko irudia berarekiko homotetikoa den zirkunferentzia da, zentrotzat alderanzketakoa eta arrazoia
eta zentrotzat alderanzketa zentroa duen homoteziaren ekuazioa da.Orduan, alderanzketa zentrotik igarotzen ez den zirkunferentziaren alderantzizko irudia berarekiko homotetikoa den zirkunferentzia da, zentrotzat alderanzketakoa eta arrazoia dituen homotezian,
dituen homotezian, alderanzketa arrazoia dela eta
alderanzketa arrazoia dela eta zentroak lehen zirkunferentziarekiko duen potentzia.Kasu partikular moduan zera aipatu behar da, alegia, berekiko potentzia
zentroak lehen zirkunferentziarekiko duen potentzia.Kasu partikular moduan zera aipatu behar da, alegia, berekiko potentzia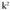 dela betetzen duten zirkunferentzia guztiak, zirkunferentzia bikoitzak direla, izan ere, 1 arrazoia duten homotezia baitagokie.Azken zirkunferentzia eraldaketa honetan, alderanzketaren beste bi ezaugarri ikusten dira. Jatorrizko zirkunferentziaren puntuak A- tik B-ra badoaz, alderantzizkoarenak
dela betetzen duten zirkunferentzia guztiak, zirkunferentzia bikoitzak direla, izan ere, 1 arrazoia duten homotezia baitagokie.Azken zirkunferentzia eraldaketa honetan, alderanzketaren beste bi ezaugarri ikusten dira. Jatorrizko zirkunferentziaren puntuak A- tik B-ra badoaz, alderantzizkoarenak doaz. Hau da, alderanzketak aldatu egiten du irudien orientazioa, ez da beraz zuzeneko higidura. Bestalde, zirkunferentziaren A puntuko ukitzaileak koordenatuen jatorri puntutik igarotzen den zuzenarekiko eratzen duen angelua, zuzen horrek
doaz. Hau da, alderanzketak aldatu egiten du irudien orientazioa, ez da beraz zuzeneko higidura. Bestalde, zirkunferentziaren A puntuko ukitzaileak koordenatuen jatorri puntutik igarotzen den zuzenarekiko eratzen duen angelua, zuzen horrek - eko ukitzailearekin eratzen duenaren berdina da, zeren, homotezia batean bere irudia baita. Angelu hori aldi berean,
- eko ukitzailearekin eratzen duenaren berdina da, zeren, homotezia batean bere irudia baita. Angelu hori aldi berean, - ean eratzen denaren berdina da, korda beraren muturrak dira eta. Beraz, A-n eratutako angelua eta
- ean eratzen denaren berdina da, korda beraren muturrak dira eta. Beraz, A-n eratutako angelua eta - ean eratutakoa berdinak dira, orientazioa aldatua badute ere.Emaitza hori, bi kurbak, edozeintzuk, eratutako angeluaren eta
beren eraldatuek eratzen dutenaren arlora pasa eta orokortu daiteke :
Alderanzketa, angeluak gordetzen dituen eraldaketa da. Angeluak
gordetzen dituzten eraldaketa hauei, forma edo eitea gordetzen
duten eraldaketak deitzen zaie.
- ean eratutakoa berdinak dira, orientazioa aldatua badute ere.Emaitza hori, bi kurbak, edozeintzuk, eratutako angeluaren eta
beren eraldatuek eratzen dutenaren arlora pasa eta orokortu daiteke :
Alderanzketa, angeluak gordetzen dituen eraldaketa da. Angeluak
gordetzen dituzten eraldaketa hauei, forma edo eitea gordetzen
duten eraldaketak deitzen zaie.
- Ariketak
19. Zentrotzat jatorri puntua eta ekuaziodun puntu bikoiztun zirkunferentziaren alderanzketa batean, kalkulatu :a) P(0,1) puntuaren alderantzizkoa.b) y = 6 zuzenaren alderantzizkoa.20. Zentrotzat jatorri puntua duen alderanzketa batean, A(1,2) eta
ekuaziodun puntu bikoiztun zirkunferentziaren alderanzketa batean, kalkulatu :a) P(0,1) puntuaren alderantzizkoa.b) y = 6 zuzenaren alderantzizkoa.20. Zentrotzat jatorri puntua duen alderanzketa batean, A(1,2) eta puntuak homologoak dira. Kalkula itzazu alderanzketaren potentzia eta autoalderanzketaren zirkunferentzia.2 1. Erradioa 2 duen zirkulu batean inskribatutako triangelu
aldekidea emanda, zentroa triangelu aldekidearena eta
arrazoia 4 duen alderanzketa egiten bada, kalkula itzazu
aldeen (zuzen) eraldatuak.22. Peaucellier-en alderanzketa tresnak, OB eta OC zuzenki giltzatu berdinak ditu, eta horiei elkartuta beste lau zuzenki
puntuak homologoak dira. Kalkula itzazu alderanzketaren potentzia eta autoalderanzketaren zirkunferentzia.2 1. Erradioa 2 duen zirkulu batean inskribatutako triangelu
aldekidea emanda, zentroa triangelu aldekidearena eta
arrazoia 4 duen alderanzketa egiten bada, kalkula itzazu
aldeen (zuzen) eraldatuak.22. Peaucellier-en alderanzketa tresnak, OB eta OC zuzenki giltzatu berdinak ditu, eta horiei elkartuta beste lau zuzenki erronboa eratuz eta hori ere giltzaturik B,C,A eta
erronboa eratuz eta hori ere giltzaturik B,C,A eta puntuetan. Zuzenkiak zurrunak badira eta O puntua plano batean finkatzen bada, froga ezazu, alegia,
puntuetan. Zuzenkiak zurrunak badira eta O puntua plano batean finkatzen bada, froga ezazu, alegia, -ak irudi bat deskribatzen badu, A'-ak haren alderantzizkoa deskribatzen duela.(Kasu partikular moduan, Peaucellier-en alderanzketak,
higidura zuzenak higidura zirkular bihurtzeko edota alderantzizkoa
lortzeko balio du).
-ak irudi bat deskribatzen badu, A'-ak haren alderantzizkoa deskribatzen duela.(Kasu partikular moduan, Peaucellier-en alderanzketak,
higidura zuzenak higidura zirkular bihurtzeko edota alderantzizkoa
lortzeko balio du).
VIII. Proiekzioa
P puntuak r zuzenean duen proiekzio ortogonala deitzen zaio (orokorki d norabide jakin batekiko paraleloa den proiekzioa) P-tik igaro eta eta r zuzenari buruz zuta den zuzenak (d norabideko zuzenak orokorki) r zuzenarekin duen ebaki puntuari.
ebaki puntuari. Proiekzioa ez da higidura, ez eta planoko puntuak beren buru
bihurtzeko egindako eraldaketa ere. Proiekzioa planoko puntuetatik
zuzenera egindako aplikazioa da.Proiekzioa ezaugarritu eta mota desberdinen artean desberdintzen
duten elementuak honako hauek dira : r zuzena eta d proiekzio
norabidea.Ekuazioak ardatz cartesiarretan.Proiekzioa egin nahi den zuzena, jatorri puntutik igarotzen dela
suposatu da : y = mxZuzenaren norabideko bektore unitarioa,
Proiekzioa ez da higidura, ez eta planoko puntuak beren buru
bihurtzeko egindako eraldaketa ere. Proiekzioa planoko puntuetatik
zuzenera egindako aplikazioa da.Proiekzioa ezaugarritu eta mota desberdinen artean desberdintzen
duten elementuak honako hauek dira : r zuzena eta d proiekzio
norabidea.Ekuazioak ardatz cartesiarretan.Proiekzioa egin nahi den zuzena, jatorri puntutik igarotzen dela
suposatu da : y = mxZuzenaren norabideko bektore unitarioa, da, m=tga malda duela.
da, m=tga malda duela.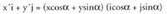 eta matrize moduan jarrita :
eta matrize moduan jarrita :
Traslazioak, biraketak, simetriak, hormoteziak, alderanzketak eta proiekzioak
Emaitzak :
 zentroa (-1,4) izatera igarotzen da eta erradioak r=3 jarraitzen du, edota ordezkatuta ,
zentroa (-1,4) izatera igarotzen da eta erradioak r=3 jarraitzen du, edota ordezkatuta , 22.
22. zuzena, COB angeluaren erdibitzailea da.
zuzena, COB angeluaren erdibitzailea da. eta CB marrazten dira eta M puntuan elkar ebakitzen dute perpendikular,
eta CB marrazten dira eta M puntuan elkar ebakitzen dute perpendikular, erronboa delako.OMB triangelua, angeluzuzena da M-n, beraz,
erronboa delako.OMB triangelua, angeluzuzena da M-n, beraz, da.
da. triangeluan,
triangeluan, Goian MB ordezkatuz eta sinplifikatuta, ondorengoa gelditzen da :
Goian MB ordezkatuz eta sinplifikatuta, ondorengoa gelditzen da : konstantea, beraz, A eta A' alderantzizkoak dira.
konstantea, beraz, A eta A' alderantzizkoak dira.





































