Matematika»Estatistika

Estatistika

Sarrera

Taulak eta grafikoak

Estatistika, datu multzo handiak bildu, landu eta aztertu ondoren, ondorioak ateratzen dituen matematikaren adar bat da.

Errolda batetik, inkesta batetik, edo informazio motaren bateko bilketa batetik jasotako emaitzen bildumari ere estatistika deitzen zaio. Datuak tratatzeko era kontuan hartuz gero, bi zatitan banatzen da estatistika :Estatistika deskribatzailea : lortutako emaitzak ordenatuta ematen saiatzen da, eta ordenatze horren ondorio bezala, datu multzo handi horien esanahia azkar eta erraz ulertzeko eta horietatik ondorioak ateratzeko baliagarri diren zenbakiak edota banaketa taulak eskaintzen ditu. Estatistika deskribatzailearen lehenengo egitekoa emaitzak laburbiltzea eta ordenatzea da. Datu laburbildu edo ordenatu horietatik abiatuz, lortutako datuen laburpen diren taulak prestatzen dira. Taulak erabiliz diagramak egiten dira, eta horiei esker, estatistikaren aztergai zen arazoari buruzko atal garrantzitsuenak argiago ikusten dira. Bestalde, datu multzo mordoa zenbaki bakar batzutan laburtuko duten guztizkoak edo totalak, batezbestekoak edo aldakuntza koefizienteak aurki daitezke.

Erakunde ofizial gehienek izaten dute zeinek bere estatistika saila, populazioari, enpleguari, produkzioari eta abarri dagozkien gai orokorrei buruzko datu bilketak egiteko.Estatistika inferentziala : datu estatistikoak erabiliz lortu diren emaitzen zentzu orokorra atera edo aurrikuspenak egiten ditu. Kasuhauetan, ezagutzen dena kontuan hartuz, erabat ziurrak ez izanda ere baliagarri diren ondorioak proposatzen dira. Estatistika inferentzialean datu estatistikoen bilketa eta zoria batera nahasten da. Laginen teoria deritzan estatistikaren alor honetan, lagin edo erakusgarri deritzan multzo txiki bat aztertuz, azterketa horren ondorioak aztergai den multzo osorako baliagarritzat eman ohi dira. Batzuetan ordea, ilaren teorian adibidez, hasierako egoera bat ezagutuz eta ezaguera estatistikoaz baliatuz, prozesuak izango duen bilakaera ikertzen saiatzen da. Beste batzuetan berriz, erabaki bat hartzeak izan ditzakeen ondorioak baloratu eta bakoitzak duen probabilitatea ezagutzen saiatzea da egiten den estatistikaren helburua. Oro har hartuz, gertaeren bilakaerak jarraitzen duen legea ezagutzen ez delako edo lege hori zailtasun handikoa delako, gertaeren bilakaera ziur ezagutzen ez denean -inkesta (galdeketa), zundaketa edo erroldatan (zentsutan) lortutako datuak extrapolatuz zein bilakaera izango den aurrikusi nahiz- erabiltzen da indukzio estatistikoa.Estatitiska desbribatzailea egiteko aski dira oinarrizko matematikari dagozkion ezaguerak. Datuak biltzeko, zentralizazio edo barreiadura neurriak lortzeko edo grafikoak marrazteko, aski da oinarrizko aritmetika. Estatistika inferentzialak datu guztiak ezagutzen ez diren egoeretan ondorioak ateratzen ditu ; bere ziurtasuna aleatorioa da, eta probabilitatearen teoriaren barruan ez bada, ezin da zientzia bezala garatu. Estatistika deskriptiboak kapitulu hau eta hurrengoa, biak hartzen ditu ; bien artean Estatatistikari dagokion atala osatzen dute. Zorizko estatistika probabilitatearekin batera ikusiko da

Estatistikaren historia

Estatistika hitza estatu hitzetik dator ; izan ere, estatuek, errepublikek, erresumek edo inperioek bere mendekoak zenbat ziren, haien ondasunak edo soldadu kopuruak jakiteko zuten beharrean du jatorria matematikaren adar honek.

Guk dakigunez, lehenengo estatistikak zentsu edo erroldak izan ziren.

Dirudienez, Txinako Yao enperadoreak, K. a. 2238. urtean zentsu bat egiteko agindua eman zuen. Egipto, Babilonia edo Pertsia eta beste inperio batzuetan ere egin ziren erroldak. Erromatarrek egindako errolden artean, Augusto enperadoreak gure aroko 0. urtean agindu zuena, hau da, Jesus Belenen jaio arazi zuena, aipa daiteke : "Garaia hartan, mundu guztiko errolda egiteko agindua eman zuen Augusto enperadoreak. Lehen errolda hau Siriako gobernari Kirino zela egin zen. Beraz, erroldatzera joan ziren denak, nor bere herrira." (Lukas 2, 1-3)Estatistika ez zen matematikaren garapenerako laguntza handiko izan ; izan ere kontaketa edo oinarrizko eragiketak erabiliz ebatzi zitezkeen hark sortzen ziren problemak. Baina hedatu samarra zegoen ekintza bat zenez, zenbakiak idazteko era desberdinen ezagutza edota antzina kalkulurako erabiltzen ziren abakoak edo harkoskorrezko taulatxoak bezalako tresna lagungarrien erabilera zabaltzen lagundu zuen. Adibide gisa, Kipuak erabiliz garatutako zenbakikuntza sistema, Inken inperioan estatistikak mantendu beharrarekin loturik zegoen. Kipu hauek kolore desberdinetako sokatxoak ziren, gorde nahi zen zifraren arabera korapiloak zituztenak.

Hari korapilatu hauetan hiri edo barrutietako datu estatistikoak gordetzen ziren. Datuak kopiatu, gorde eta ulertzeko, Quipucamayoc zeritzan inperioko funtzionarioak zeuden, gaur egungo estatistikarien antzeko eginkizuna zutenak.

Erroldatan erabiltzen zen estatistika deskribatzailetik estatistika inferentzial modernorako urratsa, 1662. urtean John Grauntek (1620-1674) Londresen argitara eman zuen Natural and Political Observations liburuarekin egin zela uste da. John Graunt oihalgina zen ; oinarrizko ikasketak baizik ez zituen, baina oso sen fina zuen kalkulurako. Bere liburuan, alde batetik, 1592tik 1662ra Londreseko parrokia orrietan jaiotza, ezkontza eta heriotzen berri azaltzen zen informazioa bildu zuen, eta bestetik, horrela bildutako datuetan oinarrituta bururatzen zitzaizkion oharpeneta proposamenak azaldu zituen. Honi esker estatistikak urrats bat aurrera eman zuen : lortutako datuetatik abiatuz ondorioak atera eta aurrikuspenak egin ziren. Graunten arabera Londres ez zen 400.000 biztanletara iristen ; familia batzkoitzak 4 seme-alaba zituen batez beste, eta jaiotako 100 pertsonatik 64 pertsona iristen zen 6 urtetara, baina 70 urtetara 7 baizik ez. Londresko heriotzen zergatiak ere aztertu zituen : ondorio bezala, 200dik 1 gutxi gorabehera bestek hila izan zela eta 500dik 1 gutxi gorabehera erotasunaren ondorioz hiltzen zela ikusi zuen. 400dik 1 gutxi gorabehera gosez hiltzen zela ere konturatu zen, eta ondorio bezala eskaleak kalean eskean ibiltzea baino gobernuak eskaleei ordaintzea hobe zela erabaki zuen. Zortzigarren atalean, Londresen, gizonezko eta emakumezkoen arteko proportzioa 14/13, hau da 13 emakumezkorentzat 14 gizonezko zeudela konturatu zen eta, ondorioz, giza espeziearen ugalketarako poligamia desegokia zela erabaki zuen. Londresen zeuden izurrite, jaiotza, heriotza eta emigrazioari buruzko datuak, parrokien tamainak eta antzeko bestelako datu asko ere eskaintzen zituen.

John Graunten lanak, datuetatik ondorioetara igarotzea oinarri matematikorik ez izatea du akatsik handiena. Datu estatistikoetatik abiatuz, orduantxe garatzen hasi berria zen probabilitatearen teoria erabiliz baizik ezin atera zitezkeen ondorioak. 1669. urtean, probabilitate kalkuluaren aitzindarietako bat den Huygens matematikari holandarrak, Grauntek bizi itxaropenari buruz lortutako datuetan oinarrituz, haur batek 6 urte beteko zituen alde 64 eta kontra 36ko apustua egin zitekeela, baina 16 urte beteko zituen alde 40 eta kontra 60ko apustua bakarrik egin zitekeela esan zuen. Geroago Bernouillik, banaketa binomialarekin, etaGaussek erroreen estudioa eta banaketa normalarekin, eta beste matematikari batzuek, saiakuntza estatistikoen emaitzetarako eredugarri izan daitezkeen probabilitate egiturak landuz joan ziren. Baina XX. mendean, beste askoren artean, Karl Pearson-ek (1857-1936) herentzia eta biologiako problemak aztertuz prestatuko koerlazioaren eta erregresioaren teoriei esker, Fisher-ek (1890-1962) nekazaritzan erabili zituen saiakuntza estatistikoen diseinuei esker, eta Abraham Waldek (1902-1950) bigarren mundu gerratean erabili eta lehenago garatutako erabakien teoriei esker lortzen du estatistikak gaur egun duen balioa. Bestalde, XX. mende honetan lortu da orobat XVII. mendeaz geroztik estatistika inferentzialaren oinarria den probabilitate teoriaren oinarri teoriko sendoa.

I. Populazioa, banakoa eta lagina

Ikerketa estatistiko batean, aztertu nahi den elementu, pertsona, animalia edo gauza guztiek osatzen duten multzoa da Populazioa.Banakoa, populazio hori osatzen duen elementu bakoitza da.

Populazio batek duen banako kopuruak populazio horren tamaina adierazten du.Batzuetan, populazioko banako guztiak aztertu ordez, populazioaren azpimultzo bat den zati bat aztertzen da. Aztertzen den elementu multzo horri lagina edo erakusgarria deitzen zaio.Donostiarrek zein egunkari irakurtzen duten jakin nahi balitz, adibidez, Donostiako biztanle guztiek osatzen duten multzoa izango litzateke populazioa, eta estatistika horretako banakoak bertako biztanleak izango lirateke. Inkesta edo galdeketa egiteko 500 pertsona hautatuko balira, horiek osatuko lukete estatistika horren lagina.Ikastetxe bateko ikasle guztiekin tuberkulina test bat egiten bada, ikastetxe horretako ikasleek osatzen dute populazioa, eta ikasle bakoitza banako bat izango litzatee test horretan. Kasu honetan ez da laginik, populazio osoa baizik.Populazio osoa erabiltzen bada, errolda egiten dela esaten da ; baina batzuetan, bestela ezinezkoa edo hala komenigarriagoa delako, lagina erabiltzen da ikerketak egiteko. Askotan populazioaren tamaina handia delako, lagina bat erabili behar da derrigor. Banako bat erabilita hura desegiten denean ere lagina erabili behar izaten da derrigor. Oro har, lagin batekin lan egiteak baditu bere alde onak ; alde batetik dirua eta denbora aurrezten da, eta bestetik banako gutxiago ikertzen denez, hobeto iker daitezke horiek. Baina baditu bere alde txarrak ere, izan ere, bestela gerta zitezkeen emaitza batzuk ez dira agian azalduko, eta batez ere, agian, gerta daitekeelako lortutako emaitzak populazio osoari ongi ez egokitzea.

Laginaren tamaina txikia bada, edo lagina ikertu nahi den populazioaren adierazgarri ez bada, gerta daiteke lagin horrekin lortutako emaitzak populazio osoa erabiliz lortuko liratekeen emaitzetatik oso desberdinak izatea. Adierazgarri diren laginak, hau da lagin "lerratu gabeak" lortzea da estatistikan laginak erabili nahi direnean konpondu behar izaten den arazo nagusia.Adibidez, Iruñeko etxeetan garbiketa egiteko zein xaboi marka erabiltzen den jakin nahi izanez gero, garestia eta luzea izango litzateke etxez etxe galdeketa egitea. Beraz kasu honetan, eta aztergaiak kontsumoarekin zerikusia duenean orohar, lagin bat erabiliz egiten dira inkestak. Gauza bera egiten da telebista programa bat Espainia guztiko zenbat ikuslek ikusi duten ala ez duten ikusi jakin nahi denean. Egunean 100.000 pospolo egiten dituen fabrika bateko produkzioaren kalitatea jakin nahiko balitz, merkeagoa izango litzateke eta diru eta denbora asko aurreztuko litzateke pospolo guztiak aztertu ordez 1.000 pospoloko lagin bat hautatuko balitz.

Gainera, kasu honetan, probatzerakoan pospoloa erre eta berriro erabiltzeko balio ez duela uzten denez, lagina komenigarri ez ezik beharrezkoa da orobat. Produkzio osoa erabiliz gero, agian, denak oso kalitate onekoak direla frogatuko genuke, baina piztu ondoren ezingo ditugu berriro erabili.Lagin bat albo batera lerratua izango ez dela ziurtatzea oso gauza zaila da. Batzuetan nabarmena izaten da lerratzea. Euskal Herriko futbol talderik maitatuena zein den jakiteko galdera egingo balitz San Mameseko irteeran, Athleticen partidu baten ondoren, inkesta horrek ez luke deusik balioko. Beste batzuetan ez da hain nabarmena izaten lerratzea, aurreko adibide beretan, zein xaboi erabiltzen den edo telebistako programa gustagarriena zein den galdetuta lortutako datuak oso desberdinak izan daitezke auzune batetik bestera. Pospolo fabrikan erabiltzen den lagina zaintzen ez bada ere antzeko zerbait gerta daiteke ; horrela ekoizten diren lehenengo 1.000 pospoloak hartzen badira, agian, gerta daiteke emaitzak errealitatea baino hobeak izatea, makinak berotzerakoan okerrago egiten dituelako, edo alderantziz errealitatea baino txarragoak ere izan daitezke, berotzerakoan makinak hobeto lan egiten dutelako.

I I. Aldagai estatistikoak

Populazio batean ikertzen den ezaugarri bakoitzari aldagai estatistikoa deitzen zaio. Aldagai estatistikoak kualitatiboak ala kuantitatiboak izan daitezke. Kolorea, sexua edota batek gogokoen duen abeslariaren izena, adibidez, zenbakien bidez adierazi ezin direnak, aldagai estatistiko kualitatiboak dira. Aldagai estatistiko kuantitatiboak zenbakizko balioak hartzen dituztenak dira, eta diskretuak edo jarraiak izan daitezke. Diskretuak balio desberdin bakar batzuk hartzen dituzten aldagaiak dira. Adibidez, dado bat 500 aldiz bota eta aurpegi bakoitza zenbat aldiz ateratzen den kontatzen bada, sei emaitza desberdin ditu bakarrik. Emaitzak, luzerak eta pisuak bezala, zenbaki errealak direnean, aldagai horiek jarraiak direla esaten da. Aldagaien balioak zenbaki osoak izan arren, aldagai asko direnean, bakarka lantzea zaila denez, aldagai estatistiko jarrai bezala hartzen dira. Lana erosoagoa izan dadin, aldagai estatistiko jarraiak tarteka taldekatzen dira. Batzuetan, aldagai kualitatiboak edo kuantitatibo diskretuak adierazgarriak ez direlako edota bakarka landuz gero lana astunagoa egiten delako, taldekatu egiten dira.Aurten soldaduzkara joan behar duten kintoen alturen estatistika egin nahi bada, balioak, luzerak direnez, zenbaki errealak izango dira, beraz aldagai estatistikoa jarraia da. Errealitatean ordea, alturen neurriak zentimetrotan ematen dira, balio errealak goiti beheiti bateratuta ; beraz aldagai horiek diskretuak balira bezala landu daitezke. Baina emaitzak oso barreiatuak izango lirateke, 140 eta 210 zentimetroen arteko ia zenbaki guztiak aterako bailirateke. Hori horrela izanik, 5 zentimetrotako bitartetan multzokatu eta aldagai jarraiak balira bezala lantzea da egokiena. Zenbakiosoak ere batzuetan taldekatu egin behar izaten dira. Europako udalerrietako biztanle kopuruen estatistika egiten bada, emaitzak zenbaki osoak izango dira, baina hainbeste kopuru desberdin izango direnez, aldagai jarrai bezala lantzea izango da komenigarriena.Ikastetxe bateko ikasleek duten anai-arreba kopurua ikertzen bada, emaitzak 1 eta 10 bitartean izango dira gutxi gorabehera, baina 1 eta 4 bitartean egongo dira emaitza gehienak. Halakoetan, aldagai horiek aldagai estatistiko diskretuak balira bezala lantzea izaten da komenigarriena, eta lautik gorako kopuruak elkartuta landu.

- Ariketak:

1.- Xaboi fabrika batek egunean 10.000 xaboi pastila ekoizten ditu. Egun batean, kontrol sailak, enpresak dituen produkzio arauen arabera, pastilen pisua egokia den ala ez egiaztatu nahi du, eta horretarako ehun pastiletik bat pisatzen du.

Zein da populazioa, zein aldagai estatistikoa eta zein lagina?2. Nekazari batek 15 behi ditu, eta hilabete batean egunero-egunero, behi bakoitzak emandako esnea neurtu eta idatzita jasotzen du. Esan ea saiakuntza hori lagin bat erabiliz egin den edo populazio osoa erabiliz egin den, eta ea aldagai estatistikoa kualitatiboa, kuantitatibo diskretua ala kuantitatibo jarraia den.3. Bonbilagin batek bonbilen iraupena eta kostua egiaztatu nahi ditu. Proba egiteko zer erabiliko du, populazio osoa ala lagin bat?

I I I. Metodologia estatistikoa: lagin prestaketa

Estatistika ikerketa bat egiterakoan urrats hauek dira bete beharrak.1.- Ikertu nahi den populazioa eta ezagutu nahi diren ezaugarri edo aldagaiak zehaztu behar dira, hasteko.2.- Galdeketa edo inkesta populazio osoari ala haren lagin bati egin behar zaion erabaki behar da. Lagin bat hautatu behar bada, alderatua atera ez dadin zein metodo erabili behar den erabakiko da.3.- Ondoren populazio edo lagineko datuak bildu behar dira.

Datu bilketa, zuzenean, galdeketa bat prestatu ondoren inkestariak erabiliz, edo zeharka, erakunde ofizialek argitaratutako taulak edota norberak dituen datu zerrendak erabiliz burutu daiteke.4.- Datuak lortu ondoren, bildu eta tabulatu egin behar dira ; ondoren emaitzak laburtuta azalduko dituzten grafikoak egin behar dira.5.- Emaitzak aztertzeko batezbesteko balioa, emaitzen sakabanatze neurriak, simetria edo asimetria, eta aldagai bat baino gehiago ikertzen denean beraien arteko erlazioari dagozkien datuak kalkulatu behar dira.6.- Azkenik, datuak extrapolatu egin behar dira, eta bereziki, lortu diren datuak banaketa aleatorioren bati, edo probabilitate banaketa bati, edo probabilitate atalean ikusiko diren banaketa binomial, Poisson-en banaketa edo banaketa normal bati, edo liburu berezituetan aurkitu daitekeen beste banaketa bati hurbiltzen den ikusi behar da.Lagin bat erabiliz lan egin bada, estrapolazio honi esker, emaitzak, populazio osoari estimatu edo zenbatetsi daitezke. Estrapolazio horretan lortu diren ondorioak onartzeko edo baztertzekotest bat ere egin daiteke ; horretarako, galdeketa edo inkesta berri bat egiten da, eta emaitza berriak egindako hipotesiarekin bat datozen ala ez ikusten da.Zientzia desberdinetarako saiakuntza estatistikoen diseinu desberdinak egiten dira. Erroreen kalkuluak, biologiak, medikuntzak, edo prozesu estokastikoak, hau da, hurrengo emaitza aleatorioak aurreko baldintzekin zerikusia duten prozesuak, bere garapen propioak dituzte. Laginen teoria berdina da eremu askotan. Lagin bat lortzeko biderik errazena zorizko lagin sinple bat aukeratzea da.

Horretarako populazioko elementu denak ordenatu egiten dira eta zenbaki aleatorioen taula bateko zenbakiekin bat datozen ordinalak hartzen dira.

- Ariketak:

4. Aduanari batek Amerikatik eta ezer aitortu behar ez dutela dioten 100 bidaiarietatik lauren maletak miatzeko aginduak ditu. Lagin aleatorio bat lortzeko era bat azaldu.5. Koarteletako janariaren kalitatea egiaztatzeko, agintean dagoen koronelari lagin bat eramaten zaio. Lagin hori adierazgarria al da?

Kalkulagailuak

RAND, RAN#, edo RANDOM izena daraman tekla bat izaten dute. Tekla hau sakatzerakoan 0 eta 999 edo 0,000 eta 0,999 zenbakien arteko zenbaki aleatorio bat ateratzen da. Horrela, kalkulagailua erabiliz, zenbaki aleatorioen taulen erabilpena saihestu daiteke.

IV Datu bilketa eta maiztasunak

Aldagai estatistiko bat ikertzerakoan, inkesta egin ondoren edo datuak era batera edo bestera jaso ondoren, lortu diren emaitzak bildu eta ordenatu egin behar dira. Horretarako lortu diren emaitzak zeintzuk diren eta emaitza horietariko bakoitza zenbat aldiz ateratzen den ikusi behar da.Atera diren emaitza desberdinak ikusteko era antzekoa da aldagai estatistiko kualitatiboetan eta kuantitatibo diskretuetan.

Aldagaiak jarriak direnean, emaitzak, tarteka taldekatzen direnez, zailxeagoa da. Dena delarik, bai batzuetan eta bai bestetan jaso behar diren datu garrantzitsuenak maiztasunak dira :Maiztasun absolutua, emaitza bakoitza edo, emaitzak taldekatuta badaude, emaitza multzo bakoitza zenbat aldiz azaltzen den adierazten duen zenbakia da. Maiztasun absolutua adierazteko n ; erabiltzen da.Emaitza baten maiztasun erlatiboa, maiztasun absolutua eta banako edo elementu kopuruaren arteko zatidura da. Maiztasun erlatiboa adierazteko f; erabiltzen da.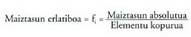Maiztasun erlatiboa 100ekin biderkatuez gero emaitza baten portzentaia lortzen da.Aldagaiak hartzen dituen balio desberdinak ordenatu daitezkeenean, eta hau aldagaiak kuantitatiboak direnean behintzat egin daiteke, emaitza baten maiztasun metatua, emaitza hori eta txikiago diren emaitzen maiztasun absolutuen batura bezala definitzen da.Maiztasun taula aldagai estatistikoak kualitatiboak direnean.

Datu bilketa egin ondoren emaitzen zerrenda egiten da. Lortutakoemaitzak sakabanatuegiak badira, taldekatu egiten dira eta, kontrako arrazoirik ez badago, maiztasun txikiena duten balioak aukera berezi batean biltzen dira.Emaitza bakoitzaren maiztasun absolutua lortzeko, emaitza hori zenbat aldiz ateratzen den kontatu behar da. Kontaketa hori behar bezala burutzeko horrela egingo dugu : hasteko emaitza posible guztien zerrenda egiten da; ondoren emaitzak banan-banan irakurtzen ditugun aldi berean, dagokion emaitzaren eskuinaldean marra bertikal bat jarriko dugu. Ez nahasteko, marrak bosnaka elkartuko ditugu eta emaitza asko ditugunean maiztasun partzialak kalkulatuko ditugu. Ordenadore programa askotan kontaketa hau automatikoki egiten da.Adibidez, ikasgela bateko 25 ikasleei gogokoen duten kirolari buruz galdetu zaie, emaitza hauek lortu direlarik : EB (Eskubaloi), SB (Saskibaloi), EB, F (Futbol), SB, F, BB (Boleibol), E (Eski), F, BB, SB, H (Hockey), F, F, R (Rugby), BB, I (Igeriketa), BB, j (Judo), SB, F, EB, F, SB, F. Emaitza hauekin taula hau lortzen dugu :Emaitza bakoitza zenbat aldiz azaltzen den adierazten duen zenbakia maiztasun absolutua da. Maiztasun absolutu guztien batura, lanean ari garen populazio edo lagineko banako edo elementuen batura da ; hau da populazioaren edo laginaren tamaina. Gure adibidean 25.9 kiroletatik 5 kirolek aldeko kide bakarra dute, beraz, oso emaitza zehatzak behar ez badira behintzat, azken hauek "beste kirolak" izeneko atalean bilduz, lehentasunak argiago ikusiko dira :Ez da gauza bera 25etik 8 futbolzaleak izatea edo 300 edo 3.000tik 8 futbolzaleak izatea. Tamaina desberdina duten populaziotako maiztasunak alderatu nahi direnean,maiztasun erlatiboak erabiltzen dira. Taulari zutabe berri bat, maiztasun erlatiboen zutabea, gehitzen zaio. Maiztasun erlatiboa lortzeko emaitza bakoitzari dagokion maiztasun absolutua elementu kopuruarekin zatitzen da.Maiztasun taula aldagai estatistikoa kuantitatibo diskretuak direnean. Aldagaia zenbakizkoa bada, maiztasun absolutuak eta erlatiboak aurreko atalean bezala kalkulatzen dira. Maiztasun metatuak ere erabili ahal izateko, aldagai estatistikoaren emaitza desberdinak ordena gorakorra (batzuetan beherakorra) gordeaz idazten dira. Adibidez, letik 6ra zenbakituta dagoen dato bat 25 aldiz bota eta lortzen den emaitza idatzi saiakuntza egiten da.

Suposa dezagun lortutako emaitzen laburpena ondoko taulan azaltzen dena dela :Kasu honetan maiztasun metatuak kalkula ditzakegu. Emaitza baten maiztasun metatua lortzeko bere maiztasun absolutuari, bere gainetik dauden maiztasun absolutu denak batuko dizkiogu.

Maiztasun absolutu metatuak eta maiztasun erlatibo metatuak kalkula daitezke.Aurreko adibideanMaiztasun absolutu metatu handiena elementu kopuruaren berdina da, eta maiztasun erlatibo metatu handiena 1 da.Aldagai estatistiko diskretuak balio desberdin asko izan arren gehienak bakar batzuetan bildu daitezkeenean, sakabanatuta dauden balioak, kualitatiboan egiten den bezala, "besteak" izeneko aukeran biltzen dira, baina aldagaiak zenbakizkoak direnean emaitzak ordenatuta edukitzea komeni denez, baliorik txikienak edo handienak bakarrik taldekatzen dira.Suposa dezagun 40 etxebizitza dituen etxe batean bizi diren pertsonen estatistika bat egiten dela. Emaitza hauek lortu dira : 5 etxebizitzetan pertsona bakarra bizi da, 8 etxebizitzetan 2 pertsona bizi dira, loetan 3 bizi dira, beste Setan 4, lean 5, 6 etxebizitzetan 6 bizi dira, etxebizitza batean 7 bizi dira, 2tan 8 bizi dira, beste batean 9 bizi dira, eta azkenik beste batean 11 bizi dira. 7 edo gehiago bizi direnak talde batean bildu ditzakegu, horrela :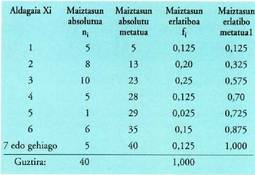"7 edo gehiago"ren ordez "besteak" jarri izan bagenu, bertan 5 emaitzari dagokion maiztasun absolutua gehituz, ezingo genituzke maiztasun metatuak kalkulatu.Maiztasun taula aldagai estatistikoa kuantitatibo jarraiak direnean. Zenbakizko aldagai estatistikoak jarraiak, edo emaitza desberdin asko dituzten diskretuak, direnean, datuak berdin ordenatzen dira, baina azken kasuan aldagai estatistikoaren balioak tarteka taldekatu behar dira ; izan ere, galdeketa bat egiterakoan, balio desberdin asko har ditzakeen aldagai bat bi aldiz azaltzea zaila da, baina azalduko balitz ere ez litzateke adierazgarria izango.Aldagai kuantitatibo jarrai bati dagokion maiztasun taula bat egiterakoan, aldagaiak har ditzakeen balio multzoa zenbat tartetan zatituko den erabaki behar da hasteko. Tarte denak elkartzerakoan lortutako emaitzen ibiltarte osoa lortu behar da. Bestalde, zatiketa honekin lortuko ditugun taulak edo grafikoak argiak eta zehatzak izan behar dute. Tarte kopurua, lortu diren balioen eta emaitzen bilketarekin lortu nahi dena kontuan hartuz erabakitzen da.

Zenbat eta tarte gehiago orduan eta zehaztasun handiagoa, baina argitasun txikiagoa, izango dugu. Tarte kopurua erabaki ondoren lortutako balio handienari txikiena kentzen zaio. Ateratzen den zenbaki hori, aldagai estatistikoaren ibiltartea da, eta tarte kopuruaz zatituz tarte bakoitzaren zabalera lortuko dugu. Kalkulu neketsuak alde batera uztekoa zabalerarako lortu den balioa hori biribildu egiten da. Hau da tarteak lortzeko biderik errazena, eta gainera tarte denak zabalera bera dute. Aurreko kasuan bezala, balioren bat oso sakabanatua badago, zabalera desberdineko tarteren bat sor daiteke muturren batean. Bestalde, ibiltarteko zatiren batean zehaztasun handiagoa nahi bada tarte batzuen zabalera txikitu daiteke.Klase ordezkaria tarte bakoitzeko muturren batezbesteko balioa da. Tartea ordezkatzen duen balioa da, eta estatistika horrekin egiten diren kalkulutan tarteko balio denak batezbesteko balio hori balio dutela suposatuko da. Horrela banaketa kuantitatibo diskretu bat balitz bezala lan egiteko aukera izango dugu.Adibidea : Pikondo sail batetik 40 pikok osatutako lagin bat hartu eta pisatu egin da. Gramotan pisu hauek lortu dira :Balioak taldekatuko ez balira, 49 gramotako 1, 50eko 1, 54ko 1, 56ko 1, 58ko 2, 59ko 1, 60ko 3, 6leko 1, 62ko 2, 63ko 4, 64ko 1, 65eko 5, 66ko 1, 67ko 3, 68ko 2, 69ko 2, 70eko 2, 7lko 1, 72ko 1, 73ko 1, 74ko 1, 75eko 1 eta 78ko 1 lortuko genituzke. Emaitzak sakabanatuegiak eta desberdinegiak direnez, banaketa ez da batere argia izango. Lortutako emaitzak 6 tartetan bildu nahi izanez gero, 78-49=29 eta 29/6=4,83... egingo dugu. Biribilduz, tarteak Seko zabalera izango dute, eta tarteak 48tik 53ra, 53tik 58ra, 58tik Ora, eta abar izango dira. Baina horrela eginez gero, tartetako muturretako balioekin arazoak izango genituzke. Horrelako arazoak saihesteko tarteko muturretariko bat irekia eta beste itxia hartzen dira : (48,53] ; (53,581 ; (58,63] ; eta abar. Hau egiterakoan emaitza denak sartzen direla kontuan hartu behar dugu. Alderantziz, [48,53) ; [53,58) ;... ; [73,78) egin izan bagenu 78 emaitza hurrengo tartean, [78,83) tartean, sartuko litzateke, eta horrela 6 tarte izateko ordez 7 tarte izango genituzke. Estatistikan lortutako balioak biribilduak izaten direnez, beste batzuetan, tarteko muturrei zifra bat gehitzen zaie. Horrela, gure adibidean, tarteak horrela geldituko lirateke : 48,5tik 53,5era ; 53,5etik 58,5 era ;... eta 73,5etik 78,5era. Era honetan mugak tartearen barruan edo kanpoan egoteak, edo tarteak irekiak edo itxiak izateak ez du axola, izan ere, ez dugu muturren balio bera izango duen emaitzik izango. Kontuan hartu behar da baita ere klase ordezkariak hartzen duen balioa, izan ere kalkulu gehienak bera erabiliz egiten dira, eta gure adibidean lehenengo eran (48+53)/2=51,5 da eta bigarren eran berriz (48,5+53,5)/2=51 da. Azken hau osoa denez, kalkuluak errazagoak izango dira.Maiztasun taula horrela geldituko da :

- Ariketak :

6. 1950etik 1989ra Frantziako Toureko txapeldunak hauek izan dira :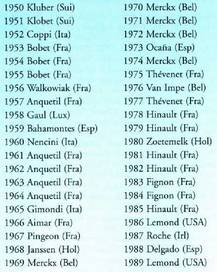a) Egizu txapeldunen nazioen zerrenda.b) Txirrindulariak nazioa ordezkatzen duela suposatuz, zenbat aldiz irabazi du zerrendako nazio bakoitzak? Datu hauek erabiliz, nazioa eta garaipen kopurua adieraziko duen taula egin [maiztasun absolutuak].c) Hurrengo urtetako txapeldunak gehituz datuak eguneratu.7. 1930 urtetik 1970 urtera munduko futbol kopako garaileak hauek izan dira :Uruguai (1930)Italia (1934) Italia (1938)Uruguai (1950) Mendebaldeko Ale. (1954) Brasil (1958)Brasil (1962)Inglaterra (1966) Brasil (1970)Mendebaldeko Alemania (1974) Argentina (1978)Italia (1982) Argentina (1986)Mendebaldeko Alemania (1990)a) Osa ezazu hurrengo taula :EstatuaUruguai ItaliaAlemania BrasilInglaterra ArgentinaKopa kopurua8. Inkestari batek herri bateko familia bakoitzak duen seme-alaba kopurua idatzi du zerrenda honetan.Datu hauek erabiliz txosten bat egin behar du. Lagun iezaiozu inkestariari maiztasun taula osatzen :Familia kopurua%Zein da populazioa? Zeintzuk banako edo elementuak? Zein da ikertzen den aldagaia?Taula osatu ondoren seme-alaben kopuruari dagozkion maiztasun absolutuak eta portzentaiak izango dituzu. Bila maiztasun erlatiboak.9. Bere txostena osatzeko inkestariak bi zenbaki errenkada gehitu dizkio bere taulari :

V. Grafikoak

IInkesta bateko emaitzen adierazpen grafikoa bere maiztasun taula edo beste taula estatistiko bat baino ulerterrezagaoa izaten da.

Datuak era askotara irudikatu daitezke. Aldagaiak kualitatiboak edo kuantitatibo diskretuak direnean barra diagramak erabiltzen dira, aldiz aldagaik kuantitatibo jarraiak direnean histogramak erabiltzen dira. Aldaketak nabarmendu nahi direnean maiztasun poligonoak erabiltzen dira, eta balio bakar batzuk grafiko erraz batean azaldu nahi direnean sektore diagrama erabiltzen da. Grafikoak atsegina- 1 7 8goak egin nahi badira, ikertutako aldagaia adierazten duten irudiarekin osatzen den piktograma erabiltzen da, eta aldagai baten banaketa geografikoa azaldu nahi denean kartogramak erabiltzen dira.

Pertsona talde baten adin banaketa azaltzeko biztanleriaren piramideak erabiltzen dira. Aipatutako hauek, garrantzitsuenak, ondoren azalduko ditugu, baina diagrama desberdin gehiago badaude. Dena delarik nahiz batzuk eta nahiz besteak irakurterrazak izan behar dute alde batetik eta egiazko adierazpena eskaini behar dute bestetik, hau da, ez dute estatistikaren ondoriorik ezkutatu behar eskalak aldatuz edo beste trikimailu batzuk erabiliz.Barra diagrama. Barra diagrama bat egiterakoan bi ardatz marraztuko ditugu, ardatz horizontalean aldagai estatistikoaren balioak kokatuko ditugu, balio batetik bestera distantzia berdina mantentzen dugularik. Balio bakoitzaren gainean barra bertikal bat irudikatzen da. Barra hauen luzerak bere maiztasunarekiko zuzenki proportzionalak dira.Ikasle batzuk gogokoen zuten kirolari buruz egindako inkestako datuak hartzen baditugu, eta luzera bezala maiztasun absolutuak zentimetrotan hartzen baditugu :Hartutako luzerak maiztasunekiko zuzenki proportzionalak dira.

Barrak luzeagoak edo motzagoak nahi badira, unitate bakoitzari dagokion luzera aldatuko genuke. Onartu ditugun unitateak OY ardatzean markatuko ditugu. Adibide honi dagokion barra diagrama hau da :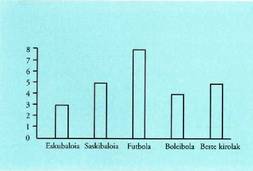Kasu batzuetan barrak bertikalak izateko ordez horizonatalak nahi izaten dira, eta halakotan aldagaiaren balioak ardatz bertikalean jartzen dira.Diagrama mota honetan berehala ikusten da maiztasun handiena eta txikiena duena zein den.Histograma. Aldagaiak kuantitatibo jarraiak direnean barra diagramen ordez histogramak erabiltzen dira. Kasu honetan, ardatz horizontalean tartetako muturrak idazten dira, eta tarte bakoitza adierazten duen zuzen zati bakoitzaren gainean, maiztasunarekikozuzenki proportzionala den laukizuzen bat irudikatzen da. Tarte denak zabalera bera baldin badute, maiztasunarekiko proportzionala den altuera edo azalera har daiteke, baina tarteak zabalera desberdinekoak badira maiztasunarekiko proportzional diren azalerak hartu behar dira nahi eta nahi ez. Altuera hartuko balitz zabalera handiena duten tarteek behar baino azalera handiagoa izango lukete.

Pikuen pisua lantzen zuen adibidean :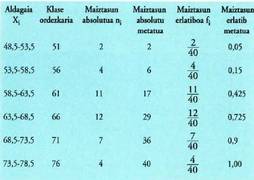Dagokion histograma hau izango da :Maiztasun poligonoak. Batzuetan emaitzen arteko aldaketa nabarmendu nahi izaten da. Halakotan barra diagrama edo histogramak baino egokioagoak dira maiztasun poligonoak. Aldagai estatistikoa diskretua denean barratako goi muturrak elkartuz lortzen da maiztasun poligonoa, eta aldagai estatistikoa jarrai denean, histogrametan, laukizuzenetako goi aldetako erdiko puntuak elkartuz lortzen da. "Gogokoen zuten kirola"ren adibideari maiztasun poligono hau dagokio :Ohizkoa denez, poligonoa zerotik hasi eta batzuetan zeron bukatzen da, horretarako lehenengo emaitzaren aurreko balioa eta azken emaitzaren hurrengo balioa zero egiten dira.Maiztasun metatuen poligonoa : Sarritan maiztasun metatuen poligonoa erabiltzen da. Poligonoa maiztasun poligonoa bezala eraikitzen da, baina oraingo honetan maiztasun metatuak erabiltzen dira. Mota honetako poligonotan zerotik hasten da, baina azken baliora iritsi ondoren ez da zerora jaisten. Aldagai kuantitatibo diskretuaren adibide bezala jarri dugun datoaren adibideari maiztasun metatuen poligono hau dagokio :Aldagaiak kuantitatibo jarraiak direnean, maiztasun metatuen poligonoa, lehenengo laukizuzeneko beheko ezker muturretik hasita, zero maiztasun metatutik, eta hurrenez hurren, abzisa bezala tarte bakoitzeko eskuineko muturra eta ordenatu bezala tarte horretako maiztasun metatua duten puntuak elkartuz eraikitzen da. Pikuen pisua lantzen zuen adibideari maiztasun metatuen poligono hau dagokio :Sektore diagrama. Sektore diagramak oso egokiak dira aldagaiak balio desberdin gutxi dituenean eta bat bateko ustea eman nahi denean. Diagrama mota hauetan zirkulu bat aldagaiak dituen balio hainbat sektoretan zatitzen da, eta sektore bakoitzari dagokion angelu zentralak, saiakuntza estatistikoaren emaitzen maiztasunekiko zuzenki proportzionala izan behar du.Ikasgela bateko ikasleek gogokoen zuten kirolaren adibidean guztira 25 erantzun jaso dira. Zirkulua 25 zatitan banatuz, zatibakoitzari 360°/25 = 14° 24'ko angelu zentral bat dagokio.

Orduan kirol desberdinei honako angelu zentral hauek dagozkie :Beraz sektore diagrama hau dagokio :Biztanleriaren piramidea. Herri bateko biztanleriaren berri ematen duten bi histograma dira, bata gizonezkoentzat eta bestea emakumezkoentzat . Bi histogramak tarteak markatuta dituen ardatz bertikal berean kokatzen dira. Herri bateko biztanleriaren ezaugarri asko eta bere historia ere bertatik atera daitekeenez, oso egokiak dira demografian.Garaiko zentsuko arazoak direla eta tarteak desberdinak dira.

Piramide honen oinarri zabalak haur asko zeudela adierazten digu.

15 etik 25 era biztanleria gutxitzen doala ikusten da, lehen karlistadaren ondorioa hain zuzen. Eta 40tik 50era gizonezko baino emakumezko gehiago dago, gerra horretan parte hartu zuten gehienak gizonezkoak zirela adieraziz. Oso gutxi dira 70 urtetik gorakoak. Biztanleria gazte samarra da. Krisialdi garrantzitsu bat pasa duen herri gazte baten piramidea da.Zentsuak hobeak eta sarriago egiten dira, tarteak 5 urtekoa direlarik.

Haur gutxiago ditugu 0 urtetik 5 urtera ia berdintsu diren 5etik 10era edo lOetik 15era baino. 40tik 45era bitarteko biztanleria nabarmen gutxitzen da, izan ere 1936-39ko gerra zibilaren garaiko jaiotzak dira. 70 urtetik gorako biztanleria garrantzitsuagoa da, eta emakumezkoak gizonezkoak baino askozez gehiago dira.

Etorkizuna baikortasun gutxirekin ikusten duen biztanleri zaharra eta duela 40 urte krisialdi garrantzitsu bat izan zuenaren berri ematen digu piramideak. 60tik 75 urte bitartean gizonezko baino emakumezko gehiago izatearen arrazoia, agian gerra zibilari egotzi behar zaio, baina egoera adin handiagotan errepikatzen denez, emakumeak gizonezkoak baino gehiago bizi direla esan nahi du agian.Azalpen hauek, estatistikaren ondorio guztiekin gertatzen den bezala, azalpen posibleetariko batzuk besterik ez dira. Haur gehiago egon daitezke pediatriak aurrera egin duelako, eta biztanleria jaitsi da izurriteak eta emigrazioak izan direlako. Gizonezko baino emakumezko gehiago egotearen arrazoia ere emigrazioak izan daitezke . Hipotesiarik seguruena estatistikan baino historian eta soziologian aurki dezakegu.Kartograma. Ikertzen ari garen ezaugarria geografikoki banatzen denean, mapak oso egokiak izaten dira adierazpena egiteko. Bertan maiztasun desberdinetako kolore edo irudi desberdinak erabiltzen dira. Adibidez, hurrengo mapa honetan goi ikasketak dituzten pertsonak estatuko batezbestekoarekin erlazionatzen dira.Piktograma. Barra diagramen antzekoa da, baina barren ordez ikertzen ari garena irudikatzen duten marrazkiak jartzen dira.

Batzuetan, oinarria oso desberdina denean bereziki, maiztasuna irudiaren azalarekiko eta ez altuerarekiko proportzionala da.Diagramen alderaketa. Batzuetan populazio batzuen emaitzak alderatuz aldi baterako bilakaera ikertu edo populazio baten eta besteen arteko diferentzia ikusi nahi izaten da. Kasu hauetan diagramak ardatz beretan irudikatzen dira. Alderaketa hauek errazagoak eta garbiagoak dira maiztasun poligonoak edo barra diagramak erabiliez gero.Grafikoen alderaketa eginez ondorioak erraz ateratzen dira, baina ikerketa egin zenean erabili ziren baldintzak azaltzen ez direnez, sarri samar, argitasun hori engainagarria izan daiteke. Adibidez : goiko irudian benetan datu berberak alderatzen ari direla zehazteko, 'jasotako langabetu"ak zer esan nahi zuen urte horietan, bai Europako estatu desberdinetan eta bai USAn, egiaztatu beharko dugu.Aldagai estatistiko baten aldi baterako bilakaera, beste batzuekin alderatuz, ikertu nahi denean, estatistikaren arabera lehenengo urtean, edo hilabetean, edo egunean 100 balio duen indizea erabili daiteke, hurrengo balioak jatorrizko balioaren portzentai bezala kalkulatzen direlarik.

- Ariketak:

11. 1989. urtean espazio gauzetarako onartu ziren aurri kontuak hauek izan ziren :Japonia: 1.200 milioi dolar S.E.S.B. : 9.000 milioi dola :EE.BB. :25.000 milioi dolarEuropa : 3.600 milioi dolarAurrekontu hauek barra diagrama batean irudikatzeko :a) Ondoko proportzionaltasun taula osatu :b) Barra diagrama eraiki.12. 1989. urtean jaurtiki ziren 18 koheteak horrela banat ziren :Europa (Ariane) : 10 jaurtiketaS.E.S.B. : 2 jaurtiketaEE.BB. : 5 jaurtiketaJaponia: Jaurtiketa lJaurtiketa hauek sektore diagrama batean irudikatzeko :a) Ondoko proportzionaltasun taula osatu :b) Sektore diagrama eraiki.13. Ondoko taulan, enpresa bateko 200 langilek hilez o pezetatan irabazten dutena azaltzen da. Eraiki ezazu tau. a horri dagokion histograma.Histograma egiteko neurri hauek erabili :- Abzisa ardatzean : 4.000 pezeten ordez unitate 1 [adib dez 2 cm.]- Ordenatu ardatzean : 10 langileren ordez unitate 1 [adib dez cm. 1 ]Tarte bakoitzarentzat langile kopuruarekiko proportzionala duen altuerako laukizuzen bat irudikatu.14. Fabrika batean egiten dituzten bonbilak ordutan irauten dutena jakiteko proba bat egin nahi dute. 2.000 bonbilako lagin batekin egindako ikerketak emaitza hauek eman ditu :Taula histograma batean irudikatu, horretarako 201 ; 203 ; 198 ; 199 ; 201 ; 199 ; 201 ; 199 ; 202 ; 202 ;- abzisa ardatzean, 100 orduren ordez unitate 1 [cm.] 198 ; 199 ; 200 ; 200 ; 201 ; 200 ; 198 ; 200 ; 200 ; 199 ;- ordenatu ardatzean, 100 bonbilaren ordez unitate 1 [cm.]15. Arantxaren gelako ikasleak bere altueraren arabera sailkatu dira :- 3 ikaslek 1,30 m. edo gehiago baina 1,40 m. baino gutxiago neurtzen dute.- 4 ikaslek 1,40 m. edo gehiago baina 1,50 m. baino gutxiago neurtzen dute.- 15 ikaslek 1,50 m. edo gehiago baina 1,60 m. baino gutxiago neurtzen dute.- 7 ikaslek 1,60 m. edo gehiago baina 1,70 m. baino gutxiago neurtzen dute.- 2 ikaslek 1,70 m. edo gehiago baina 1,80 m. baino gutxiago neurtzen dute.Datu hauek erabiliz taula egin eta dagokion histograma eraiki.16. 9. ariketako inkestariak taula hau lortu du :Maiztasun poligonoa eta maiztasun metatuen poligonoa irudikatu.17. Dato bat bota eta jaurtiketa bakoitzean lortu dena ondorengo zerrendan idatzi da :a) Emaitza hauek, balio bakoitzaren maiztasun absolutuak eta erlatiboak (% tan) agertzen dituen taula batean antolatu.b) Barra diagrama bat eta maiztasun poligonoa egin.c) Taula berean maiztasun absolutu metatuen zutabez gehitu.d) Datu hauek erabiliz maiztasun metatuen poligonoa irudikatu.e) Zenbat jaurtiketa atera dira 3 edo zenbaki txikiagoekin? f) Zer adierazten digu 20 maiztasun metatuak?18. Zilindroak ekoizten dituen fabrika batean pieza batzuen diametroa neurtu eta idatzi da:a) Emaitza hauek, balio bakoitzaren maiztasun absolu- tuak eta erlatiboak (% tan) agertzen dituen taula bate- an antolatu.b) Barra diagrama bat eta maiztasun poligonoa egin.c) Taula berean maiztasun absolutu metatuen zutabea gehitu.d) Datu hauek erabiliz maiztasun metatuen poligonoa (% tan) irudikatu ; (baliorik handiena % 100 izango da). e) Zenbatekoa da, diametrotzat 200 edo gutxiago neurtzen duten, zilindroen portzentaia?f) Zer adierazten digu % 92ko maiztasun metatuak?g) Zenbatekoa da, diametrotzat 201 edo gehiago neurtzen duten, zilindroen portzentaia?19. Maiztasun absolutu metatuak ezagutuz, bila balio bakoitzari dagokion maiztasun absolutua.20. Ikasgela bateko ikasleen anai-arreben kopuruari buruzko datoen laburpena hurrengo maiztasun metatuen poligonoan biltzen da :Maiztasun metatuen poligonoa aurrean duzularik, eta behar izanez gero goiko taula osatuz, hurrengo baieztapenak zuzenak ala okerrak diren esan :a) 23 ikaslek 3 anai-arreba baino gutxiago dituzte.b) Ikasleen % 2ak 3 anai-arreba ditu.c) Ikasleen % 40a seme-alaba bakarra da.d) Ikasleen % 20ak bi anai-arreba ditu.e) 18 ikaslek anai-arreba bakar bat dute.21. Erretzaileen adinaMaiztasun erlatiboen zutabea (% tan) eta maiztasun erlatibo metatuen zutabeak gehituz, hurrengo taula osatu eta hurrengo baieztapenak zuzenak ala okerrak diren esan :a) Erretzaileen heren bat baino gehiago 25-39 adin tartekoa da.b) Erretzaileen laurden bat baino gutxiago 40-54 adin tartekoa da.c) Erretzaileen % 12a 12-14 adin tartekoa da.d) Erretzaileen % 10ak 55 urte baino gehiago ditu.e) Erretzaileen bi herenak gutxi gora behera 40 urte baino gutxiago dituzte.f) Erretzaileen % 30ak 25 urte baino gutxiago ditu.g) Erretzaileen % 80ak 55 urte baino gutxiago ditu.h) Erretzaileen % 60a 25-54 adin tartekoa da.i) Erretzaileen % 70ak 24 urte baino gehiago ditu.22. Zigarroak egiten dituen makina baten irteeran 1.000 zigarro, banaka-banaka, pisatu dira.a) Zer adierazten dute hamargarren lerroko emaitzek?b) Maiztasunak bilduz, zabalera bereko lau tartetan banatu.c) Lau tarte horiei dagozkien maiztasun erlatiboak % tan kalkulatu.23. Hurrengo taula honetan 1970 etik 1990era milaka milioi kilowat-ordutan izandako elektrizitate kontsumoa azaltzen da :a) 100 oinarri indize bezala 1970. urtekoa hartzen bada, kalkulatu beste urteri dagokiena.b) 1970etik 1990era kontsumoaren bilakaera azaltzen duen indizeen grafikoa egin. (Abzisa : 10 urteren ordez 3 unitate [cm.] ; ordenatuan indizeko 100aren ordez 2 unitate [cm.]24. Petrolio produkzioa, milioi tonatan, hau izan zen :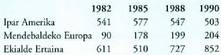a) Hiru lurralde horietan 1982 eta 1990 bitartean petrolioaren produkzioak izan duen bilakaera aztertzeko 100 oinarri indize bezala 1982. urtekoa hartuz, kalkulatu beste urteri dagozkien indizeak.b) Lurralde desberdinei dagozkien grafikoak koordenatu ardatz berean irudikatu. Iruzkinak egin.25. Ikastetxe bateko bigarren hezkuntzako 3. mailako ikasleek 60 m. korritzeko behar dituzten denborak taula honetan jaso dira:a) Zer kalkulatzen da eragiketa hauek egiten direnean?b) Egiazta ezazu, ikastetxe horretako ikasleen % 90ak 60 m.ak korritzeko 11 segundo baino gutxiago behar dutela.26. Kristala eta plastikoakTaula honetan estatu mailan kristala eta plastikoaren produkzioen bilakaera (milaka tonatan) azaltzen da.

Ebazpide edo soluzioak

1. Populazioa : produzitutako 10.000 pastilak. Aldagai estatistikoa : pisua da. Lagina : pisatzen diren 100 pastilak.2. Saiakuntza populazio osoa erabiliz egiten da. Aztertzen den ezaugarria, litrotan, behiek ematen duten esne produkzioa da.

Aldagaia kuantitatibo jarraia da.3. Lagin bat ; izan ere bonbilaren iraupena aztertzerakoa, bonbila hondatu egiten da.4. Zenbaki aleatorioko taula bateko zutabe batetik bi zifratako lau zenbaki hartuz miatu behar dituen lau pertsonen posizioa zehaztuko du. 0 0 ateratzen bada, 100. posizioan dagoen pertsona miatu beharko du.5. Ez. Ez da zoriaren arabera hautatutako lagin bat, koronelak ontzat eman dezan sukaldariak aukeratutakoa baizik.8. Ebazpena 9.ariketan azaltzen den taula da. Populazioa : herriko familiak. Banakoak : familia bakoitza. Aldagai estatistikoa: seme-alaben kopurua.9. Hirugarren errenkadan maiztasun absolutu metatuak azaltzen dira. Bostgarrenean berriz, portzentaietan emanda, maiztasun erlatibo metatuak azaltzen dira.e) % 60f) bere diametroa 202 edo txikiago duten zilindro kopuruag) % 4022.a) 112 zigarroren pisua 1,22 gramo eta 1,24 gramoren artean dagoela adierazten du, 1,22 gramo pisatzen baditu kontuan hartzen delarik eta 1,24 gramo pisatzen baditu sartzen ez delarik.25.a) A : Ikasle kopurua.B : 11 segundo baino azkarrago korritzen duten ikasleak.

C : 60 m.ak korritzeko 10 segundo edo gehiago behar duten ikasleak.

D : 11 segundo edo gehiago behar dutenen maiztasun erlatiboa .

E: D-ko gauza bera baina ehunekotan.

F : 11 segundo baino azkarrago korritzen dutenen portzentaia.hori da 90%b)26. Barra diagrama bat edo maiztasun poligono bat eraikiko dugu. Plastiko produkzioa azkarrago hazten dela ikusiko da.

Parametro estatistikoak.

Bi dimentsioko banaketak

Lehenengo kapituluan aztertutako maiztasun taulak eta grafikoak datuak biltzeko eta banaketaren azalpen orokorra emateko balio dute. Baina lortutako datuekin azteketa sakonagoak egin nahi izanez gero, taula eta grafiko horiek motz geratzen dira. Datu horiekin matematika kalkuluak egiteko zenbaki gutxi batzuk behar dira banaketaren ezaugarriak adierazteko. Zenbaki horiei parametro estatistiko esaten zaie ; zentralizazio eta barreiadura neurriak dira parametro estatistiko nagusiak.Lortutako datu guztiak balio batez ordezkatu nahi badira, balio hori datuen zentroan egongo dela pentsatzea zentzuzkoa dirudi.

Zentroko balio hori era batera baino gehiagotara defini daiteke, eta ondorioz zentralizazio neurri bat baino gehiago sor daitezke : batez beste aritmetikoa, mediana, moda eta gutxiago erabiltzen diren beste hainbat. Komenigarria da, bestalde, zentralizazio neurriarekin batera datuen barreiadura neurtzen duen balio bat izatea. Gela bateko batez besteko nota 5 dela esatea oso adierazgarria da gela horretako ikasle guztien nota 5 denean, baina gelaren erdiak 10 eta beste erdiak 0 badu ez da hain adierazgarria izango. Datuak zentroaren inguruan biltzen diren edo datuak zentrotik urrun dauden jakiteko barreiadura neurriak erabiltzen dira. Hauek dira barreiadura neurriak : ibiltartea, desbideratze tipikoa eta batez besteko desbideratzea balio absolutuan.Badira beste parametro estatistiko batzuk : "alborapena", datuen simetria edo asimetria adierazten duena ; "kurtosia", zentroko balioaren inguruan dagoen datu kontzentrazioa adieraztenduena; edo oinarrizko estatistikan gutxiago erabiltzen diren beste batzuk.Esperientzia estatistiko batean aldi berean bi aldagai aztertzen badira, bi aldagai horien artean harremana dagoen edo ez dagoen jakitea interesgarria izaten da, eta harremana dagoenean zein motakoa den jakitea ere komeni da. Koerlazio koefizienteak eta erregresio zuzena bi dimentsioko banaketetan aztertzen diren gaiak dira.

I. Batez beste aritmetikoa

Aldagai estatistiko baten balio guztiak batu eta balioen kopuruaz zatitzean lortzen den balioari batez beste aritmetikoa edo batez bestekoa esaten zaio. Batez bestekoa x edo m-z adierazten da.Adibidez, saskibaloiko talde bateko jokalarien adinak 20, 22, 22, 24, eta 27 dira ; batez besteko adina hau izango da :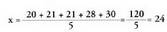Beste talde batean adinak 20, 21, 21, 28 eta 30 badira, batez bestekoa hau izango da :Hau da, bigarren taldearen batez besteko adina handiagoa da.Oro har, aldagai estatistikoak n balio hartzen baditu, balio horietako bat; bidez adierazten da, non i azpi-indizeak 1-etik n-ra bitarteako balioak har ditzakeen. Aldagai horren batez bestekoa kalkulatzeko n balioak batu eta n-z zatitzen da. Hau da :nonbatura adierazten duen, aldagaiak hartzen dituen n balioen batura alegia.Lortutako datuak taldetan bilduta badaude kalkulua datuen maiztasunak erabiliz sinplifika daiteke.Adibidez, aurreko kapituluan ikusitako adibide baten arabera dado bat 25 aldiz bota eta emaitzak taldekatuta hauek ziren :Batez bestekoa kalkulatzeko aldagaiak hartzen dituen balio guztiak batu ordez, balio bakoitza bere maiztasunaz biderka daiteke eta ondoren batu, hau da :Nahiz eta dadoan ateratzen diren zenbakiak osoak izan, horien batez bestekoa ez da zenbaki osoa.Kalkulua egiteko, ordea, maiztasunak erabiltzea arinagoa izaten da. Beraz, taula estatistikoan datuak taldetan bilduta daudean, batez bestekoa kalkulatzeko era errezena hau da : balio bakoitza bere maiztasunaz biderkatu eta ondoren biderkadura horiek batu. Batura horren emaitza datuen kopuruaz zatitu eta batez bestekoa lortzen da. Maiztasun erlatiboak erabiliz ere egin daiteke ; halakoetan, balioak bere maiztasun erlatiboaz biderkatu eta batu egiten dira :Aurreko formuletan, suposatzen da aldagaiak p balio desberdin hartzen dituela, eta p balioen maiztasunen batura n dela. n esperientzian lortutako emaitzen kopurua da.Aldagai estatistiko kuantitatiboa jarraitua denetan ere berdin kalkulatzen da. Har dezagun aurreko kapituluko beste adibide bat, baratza bateko pikuena, hain zuzen ; pikuen pisuak hauek dira :Datuak ondoko taulan bil daitezke :Batez bestekoa kalkulatzeko datu guztiak banan-banan batu daitezke :Edo tartearen marka eta maiztasuna biderkatu. Modu hori askoz ere sinpleagoa da :Bi emaitzen arteko diferentzia txikia da ; askotan zehaztasuna galtzea merezi du, batez ere datu asko direnean, kalkuluak asko errazten baitira.Beraz, aldagaia jarraitua denean erabiltzeko formula hau da :non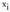

Batukaria

E ikurra batuketen idazketa sinplifikatzeko era da. Batugai guztiak idatzi ordez, balio bakoitzari azpi-indizearen balio bat elkartzen zaio, iesaterako ;ikurrak adierazten du zehaztutako limiteen artean azpi-indizearenbalioak aldatzean lortzen diren kopuru guztiak batu egin behar direla. Esate baterako,x= {2,4,6,8,10,12,14,1G,18,20} multzoa osatzen duten lehenengo 10 zenbaki bikoitiak batzeko. Zenbaki horiek azpi-indize bidez idatz daitezke :. Horien batura honela adieraz daiteke :Lehenengo n zenbaki naturalen batura honela idazten da :Batugaiak adierazten duen indizea zein den argi ikusten denean, ez dabeharrezkoa batukaria ikurraren gainean eta azpian jartzea, eta i=l edo i=n-ren ordez bakarrik 1 edo n idazten da. Batura zein balioen artean egitenden aurretik esan bada eta balioak ezagunak badira,ikurra jartzea nahikoa da.Batura ikur hori batugaien multzoa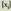finitoa eta ordenatua deneanBatura ikurra batuketaren adierazpen laburra denez gero, batuketaren propietate berak ditu :Estatistikan aurreko bi propietateetatik beste bat ateratzen da :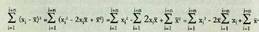Batukari batetik bestera batez bestekoa aldatzen ez denez gero, azkenekoBatez bestekoaren definizioa kontuan hartuta,da.

Beraz hau lortzen da :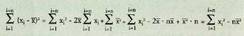Propietate horrek bariantza eta desbideratze tipikoaren kalkuluak laburtzeko balio du.

I I. Bariantza eta desbideratze tipikoa

Banaketa batean, datuen batez bestekoaz gainera komenigaria da ezagutzea zein den datuen desbideratzea batez besteareiko . Hau da, datuen barreiadura ematen duen neurria.. dibidez, saskibaloi talde bateko jokalarien adina kontuan harurik (20, 22, 22, 24 eta 27 ; batez bestekoa 23 urte), neurri bataurkitu nahi da adieraziko duena adin horiek beste talde batekojokalarien adinak (22, 23, 23, 23, 24 ; batez bestekoa 23urte) baino barreiatuagoak daudela, baina ez daudela beste taldebatekoenak bezain barreiatuak (19, 20, 21, 26, 29 ; batez bestekoa 23 urte).Lehenbiziko ideia datu bakoitzaren eta batez bestekoaren artekokendura bilatzea da.Lehen taldean : 20 - 23 = -3 ;Baina, datu horien batez bestekoa egiten bada, batez besteko desbideratzea lortzen da, zero hain zuzen :Esperientzia estatistiko batean, datuen eta batez bestekoaren arteko kenduren batura zero da. Hori batez bestekoaren definizioaren ondorio da :Kendura positiboak eta negatiboak elkar baliogabetzen dira, eta horien batura zero da.BariantzaBanaketa bateko datuen barreiamendua ezagutzeko, garrantzi handiagoa du kenduren balioak kenduren zeinuak baino. Zeinu horiek alboratzeko kenduren karratuak edo kenduren balio absolutuak erabil daitezke. Batez bestekoa egiteko karratuak erabiltzen dira, hau da : kendurak ber bi egiten dira, ondoren batu, eta azkenik emaitza hori datuen kopuruaz, n-z, zatitzen da.Desbideratzearen karratuen batez bestekoari bariantza esaten zaio. Bariantza batez bestekoarekin erabiltzen den barreiamendu neurria da. Bariantza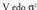adierazten da.Saskibaloiko lehenengo taldearen bariantza hau da :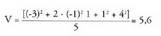Bigarrenarena :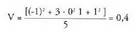eta hirugarrenarena:Desbideratze tipikoaBariantza aldagai estatistikoaren karratuaren mailakoa da, horregatik zaila da bariantzaren balioak eta batez bestekoarenak konparatzea.

Hori dela eta, barreiadura neurri gisa gehiago erabiltzen da desbideratze tipikoa (bariantzaren erro karratua) ;bidez adierazten da. Ikusitako adibideetan desbideratze tipikoak hauek dira :Datuak taldean bilduta daudenean, kalkulua erraztu daiteke maiztasunak erabiliaz :Kalkulua errazteko, estatistika bateko datuak ezagutzen direnean, komenigarria da taula bat egitea, non bilduko baitiren batez bestekoa eta bariantza kalkulatzeko behar diren eragiketa guztiak.Demagun maiztasun taula batean jaso direla dado bat 25 aldiz botatzean lortu diren emaitzak :Bigarren zutabean ikus daiteke emaitzak 25 direla guztira ; hirugarrengoan batez bestekoa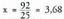dela eta azkenekoan bariantzaHortaz desbideratze tipikoada.Aldagaia estatistiko kuantitatibo jarraitua baldin bada, balio diskretuen ordez tarteen markak hartzen dira kontuan eta balio diskretuen maiztasunen ordez tarteen maiztasunak. Aldaketa horiekin formula berak baliagarriak dira.Bariantzaren kalkulua errazagoa izaten da, batez ere batez bestekoa osoa ez denean, ondoko propietatea aplikatzen bada :Formula horrela gelditzen da :Aldagai estatistiko jarraitu baten adibidea hartuko dugu, pikuen pisuarena esaterako.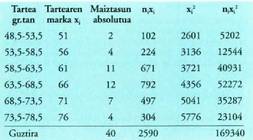Adibide horretan, batez bestekoa 2590/40 = 64,75 da, eta bariantza; desbideratze tipikoa, beraz,da.Azkeneko bi zutabeak aldatu egin dira, kalkuluen amaiera arte aldagaia sar ez dadin ; izan ere, batez bestekoak zenbaki hamartar gehiago izaten ditu datuak baino.

Zenbait liburutan, aldagai estatistikoa aldatu egiten da kalkuluak sinplifikatzeko. Aldagai estatistiko batean eskala aldaketa bat edo jatorri aldaketa bat egiten bada, hau da, x-en batez bestekoa eta bariantza bilatu beharrean beste aldagai s=ax+b baten batez bestekoa eta bariantza bilatzen badira, hau betetzen da :

- Ariketak

1. 40 familiren artean inkesta bat egin da zenbat semealaba dituzten jakiteko. Inkesta horien emaitzak taula honetan jaso dira :Bilatu batez bestekoa, bariantza eta desbideratze tipikoa2. Espazioaren ikerketarako 1989ko aurrekontuak hauek izan ziren :Japonia: 1.200 milioi dolar Errusia : 9.000 milioi dolar Estatu Batuak: 25.000 milioi dolar Europa : 3.600 milioi dolarKalkula ezazu inbertsioen batez bestekoa, bariantza eta desbideratze tipikoa.3. Ondoko taulan enpresa bateko 200 langileren hileko soldata zehazten da, milakako pezetatan :Bilatu batez besteko soldata, bariantza eta desbideratze tipikoa .4. 7 laguneko hiru familiatan garaierari buruzko azterketa egin da, eta ondoko parametroak lortu dira :Histograma hauek dira :

Batez bestekoaren eta desbideratzearen kalkulua kalkulagailuarekin

Ia kalkulagailu zientifiko guztiak gauza dira banaketa estatistiko baten batez bestekoa eta desbideratze tipikoa kalkulatzeko. Horretarako eman beharreko pausuak hauek dira :Era estatistikora aldatu: Horretarako lehendabizi aldaketa tekla sakatu (gehienetan MODE hitzarekin adierazten da) eta ondoren estatistikako aukera (sarritan SD hitzarekin adierazten da).Pantailan agertzen den SD txiki batek adierazten du kalkulagailua era estatistikoan dagoela.Aurreko datuak ezabatu: kalkulagailua itzaltzerakoan memorian gordeta dauden datu estatistikoak ez dira galtzen. Hori dela eta, datu berriak sartu aurretik, datu zaharrik ez dagoela ziurtatu behar da. Horretarako datuak ezabatzen duen tekla sakatzen da : askotan [SHIFT] + [SAC].Daturik gordeta dagoen jakiteko n teklari eman behar zaio, pantailan 0 agertzen bada ez dago daturik; daturik egotekotan datu kopurua agertzen da pantailan.Datuak sartu: lehenbizi balioa idazten da, ondoren biderkaketa tekla sakatzen, gero maiztasuna eta azkeniktekla kalkulagailu batzuetan edo DATA besteetan.Hurrengo balioa sartzeko berdin egiten da, eta horrela datu guztiak sartu arte.Balioak taldetan bilduta ez badaude, nahikoa da lehen balioa idatzi eta ondorentekla sakatzea:Gaizki sartu den datu bat zuzentzeko, berriro datu okerra idatzi eta ondoren [M+] teklaren ordez [M-] tekla sakatzen da.Parametro estatistikoak lortu : Datu guztiak sartu ondoren,teklek maiztasun taulari dagozkion balioak adierazten dituzte.

Gehienetan tekla horiek bigarren aukera bezala ematen dituzte balio estatistikoak, hari da :Parametro horiez gainera, kalkulagailuek beste parametro estatistiko batzuk izaten dituzte, esate baterako- laginentzat erabiltzen dena - edo, eta beste hainbat bi dimentsioko banaketetan erabiltzen direnak.

I I I. Mediana

Estatistikan erabiltzen den beste zentralizazio neurri bat mediana da. Datuak txikienetik handienera ordenatzen baditugu, mediana erdian dagoen balioa da. Me erabiltzen da mediana adierazteko.Datu kopurua txikia eta bakoitia denean, erraz kalkulutzen da mediana. Hala, saskibaloiko jokalarien adinak azaltzen direneko adibidean -20, 22, 22, 24 eta 27- datuak ordenaturik daude eta erdian dagoena hirugarrena da. Hau da, mediana 22 da. Adibide honetan, beraz, mediana batez bestekoa -23- baino txikiagoa da.Beste talde batean jokalarien adinak 18, 20, 24, 25 eta 28 badira, mediana 24 da eta batez bestekoa 23 ; beraz, mediana batez bestekoa baino handiagoa da. Medianan eragin gutxiago dute muturreko balioek batez bestekoan baino. Lehenengo adibidean jokalari zaharrenak 27 urte eduki beharrean 37 urte balitu mediana ez litzateke aldatuko, ezta ere gazteenak 20 urte eduki beharrean 15 urte balitu.Datu kopurua bikoitia bada, erdian bi balio izaten dira, eta mediana bi balio horien batez bestekoa da. Adibidez, abesbatza bateko kideen adinak hauek dira : 32, 33, 25, 46, 23, 25, 39 eta 42.

Mediana kalkulatzeko adinak ordenatzen dira : 23, 25, 25, 32, 33, 39, 42 eta 46. Erdian 32 eta 33 gelditzen dira ; hortaz, mediana32 + 33 / 2 = 32,5 da. Adibide horretan, mediana ez dator bat bildutako inongo daturekin. Gerta daiteke erdian gelditzen diren bi gaiak berdinak izatea, halakotan medianak balio hori hartzen du.

Adibidez, sei familiatan seme-alaben kopuruak 0, 3, 2, 1, 2, 4 dira.

Datuak ordenatzean, 0, 1, 2, 2, 3, 4, erdian 2 eta 2 gelditzen dira ; mediana, beraz, 2 da.Datuak taldetan bilduta daudenean, kontuan hartu behar da erdiko posizioak zein baliori dagokion. Dadoa 25 aldiz botatzearen adibidea aztertuko ditugu. Emaitzak hauek dira :25 zenbakitatik erdiko tokia hamairugarrena da; adibide honetan 4 dago hamairugarren lekuan. Maiztasun metatuekin errazagoa da media bilatzea. 3a arte 12 datu daude, hortaz 13. datua hurrengo balioari dagokio.Datuak taldekatuta badaude eta kopurua bikoitia bada, eragiketa bera egiten da erdian gelditzen diren bi balioak berdinak izenez gero. Adibidez, hurrengo taulan herri batean bizi diren 40 familien seme-alaben kopurua azaltzen da :Erdiko posizioak 20 eta 21 dira eta lehenengoaren maiztasun metatua 11-tik 24-ra pasatzen da. Hortaz, bi erdiko posizioak 1-i dagozkio, eta mediana seme bat izango litzateke.Beste herri bateko emaitzak hauek dira :Berriro ere 40 familia dira, baina oraingoan 20. tokian 1 dago eta 21. tokian 2a; adibide honetan, beraz, 1,5 seme-alaba da mediana, nahiz eta, banaketan ez dagoen halako baliorik eta ezin den 1,5 seme-alabarik eduki.Aldagai estatistikoa jarraitua denean eta datuak tarteetan taldekatuta daudenean, mediana tarte horietako bat izan daiteke eta ez tarte horretako kopuru jakin bat. Datu guztiak ordenatuz gero, mediana tarte horren barruan egongo da.• Adibidez:Datu kopurua 40 da, 20. tokia eta 21. tokia [63,5-68,51 tarteari dagozkio eta tarte hori da mediana. Tartearen ordez zenbakia nahi bada, 66 tartearen marka har daiteke mediana gisa. Baina, zehaztasun handiago nahi izanez gero, tartearen zabalera -5- 12 zatitan banatzen da, tartearen maiztasuna 12 baita. Bestalde, 20,5ri (mediana posizioa) 17 kentzen zaio, aurreko tartearen maiztasun metatua dela, eta 3,5 lortzen da. Ondoren biderkadura egiten da 3,5(5/12) = 1,458... eta tartearen ezkerreko muturrari batuta (63,5+1,455)= 64,958 ematen du. Horixe da mediana zehatza.Banaketa estatistiko baten mediana erraz lortzen da maiztasun metatuen diagramatik abiatuta, horretarako erdiko posiozioko ardenatua zein abzisari dagokion begiratu behar da. Adibide honetan erdiko posizioa Y=20,5 da.

IV. Batez besteko desbideratzea

Datu multzo baten barreiadura neurtzeko bada beste era bat : datuen eta erdiko balioaren arteko kendurak kalkulatu, eta kendura horien balio absolutua hartu. Saskibaloiko taldeko jokalarien adinak 20, 22, 22, 24 eta 27 kontuan hartzen badira, mediana 22 da. Medianarekiko desbideratzeak hauek dira : 20-22=-2 ; 22-22=0 ; 24-22=2 ; 27-22=5. Medianarekiko desbideratzearen balio absolutuen batez bestekoa hau da : (2 + 0 + 0 + 2 + 5)/5 = 1,8Medianaren ordez batez bestekoa -23- hartzen bada, desbideratzeak hauek izango dira : 20-23=-3 ; 22-23=-1 ; 22-23=-1 ; 24- 23=1 ; 27-23=4. Desbideratze horien balio absolutuen batez bestekoa hau da : (3+1+1+1+4)/5=2Beraz, desbideratzeen balio absolutuen batez bestekoa txikiagoa da medinarekiko.Dadoaren adibidea aztertzen bada :Batez beste aritmetikoa 3,68 da eta mediana 4. 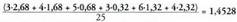Batez besteko desbideratzea batez beste aritmetikoarekikoda.

Batez besteko desbideratzea medianarekiko

- Ariketak.

5. 7 lagunen matematikako notak hauek dira : 7, 2, 8, 9, 3, 5, 6. Bilatu mediana eta batez besteko desbideratzea.6. Dado bat 32 aldiz botatzerakoan lortutako emaitzak hauek izan dira:Kalkulatu mediana eta batez besteko desbideratzea.7. Ikastetxe bateko 3. D.B.H.ko ikasleek 60 m korrika ibiltzeko erabili duten denbora taula honetan jaso da :

V moda

Beste zentralizazio neurri bat moda da. Mo-z adierazten da.

Banaketa estatistiko batean, maiztasun handiena duen balioari esaten zaio moda. Saskibaloi taldeko kideen adinak (20, 22, 22, 24 eta 27) azaltzen ziren adibidean, maiztasun handiena duen balioa 22 da ; medianaren berdina da, baina batez bestekoa baino txikiagoa.Datuak taldekatuta daudenean, moda kalkulatzeko nahikoa da kustea maiztasun haindiena zein baliori dagokion.Dadoa 25 aldiz botatzen den adibidean, emaitzak hauek ziren :Maiztasun handiena 6 da, 5. balioari dagokiona. Hortaz, moda 5 da. Adibide honetan, batez bestekoa eta mediana baino handiagoa da.

Modak abantaila bat du, aldagai estatistikoa kualitatiboa denean ere erabil daitekeela alegia.Adibidez, gela bateko ikasleen gustuko kirolak biltzen direnaula honetan :Erraz ikusten da moda futbola dela.Moda barra-diagrama batean irakur daiteke. Azkeneko adibidearen barra-diagrama hau da :Barra luzeena futbolarena dela berehala ikusten da.Datuak taldetan bilduta daudenean, tarte modala edo klase modala lor daiteke. Tarte modala maiztasun handiena duen tartea da. Pikuen adibidean :[63,5-68,51 tartea da moda ; tartearen marka 66.

Banaketa estatistiko batzuetan bi moda daude, hau da, bi balio desberdin maiztasun handienarekin.Adibidez, dadoa 25 aldiz botatzerakoan emaitzak hauek badira :

- Ariketak

8. 25 ikasleko gela batean notak hauek izan dira :Bilatu batez bestekoa, besbideratze tipikoa, mediana eta moda.9. D.B.H.ko maila bateko ikasleen adinak taula honetan jaso dira :Bilatu mediana eta moda.10. Bonbila fabrika batean, lagin bat hartu eta horien iraupena neurtu da. 2.000 bonbilako laginarekin egin da azterketa eta lortutako emaitzak hauek izan dira :

VI. Zentralizazio edo barreiadura beste neurri batzuk.

Koartilak, dezilak eta pertzentilakBanaketaren datu guztiak txikienetik handienera ordenaturik badaude, lehenengo koartilak datuen laurdena ezker aldean uzten du. Hau da, datuen laurdena lehenengo koartila baino txikiagoa da. Bigarren koartila medianarekin bat dator eta hirugarren koartilak datuen 3/4-a ezker aldean uzten du, hau da, datuen 3/4-a hirugarren koartila baino txikiagoa da.Adibidez, 15 datuko multzo hau, 3, 1, 5, 5, 2, 7, 1, 10, 7, 9, 14, 12, 13, 15, 10, ordenatu ondoren honela gelditzen da : 1, 1, 2, 3,5, 5, 7, 7, 9, 10, 10, 13, 13, 14, 15. Datu kopuruen laurdena 3,75 da, hortaz laugarren datua izango da 1. koartila, 3 balioa duena alegia. Erdiko tokia 8. datuak hartzen du, 7 balioari dagokiona. Datu kopuruaren 3/4 11,25 da, hortaz 12. datua da hirugarren koartila -13 balio-. Zehaztasun handiagoa nahi bada, batez ere datuak taldekatuta daudenean, interpolazio lineal bat egin daiteke koartil guztietan eta 1. koartil gisa 2,75 hartu eta 3 koartil gisa

- Ariketak

11. Ondoko nota multzoan -l, 3, 6, 8, 6, 7, 5, 6, 2, 10kalkulatu koartilak. Zein da banaketaren ibiltartea?12. 100 gizonezkoren garaiera taula honetan jaso da :

VII. Alborapena eta kurtosia

Banaketa estatistiko batean, asimetria neurriari alborapen esaten zaio. Banaketa simetrikoetan alborapena zero da. Era asko daude alborapena neurtzeko ; gehien erabiltzen dena asimetria koefizientea da. Hau da asimetria koefizientearen definizioa :nondesbideratze tipikoa.; aldagaiaren balioak.batez besteko aritmetikoaAlborapena neurtzeko, ordea, bada beste modu errazago bat : lehenbizi moda eta batez bestekoaren arteko kendura kalkulatu eta ondoren emaitza horren eta desbideratze tipikoaren arteko zatidura egin. Era hori, dena dela, modulu bakarreko banaketetan erabil daiteke soilik.Bi kurba honen irudia alborapen positibo eta negatiboko maiztasun poligonoak bi kurba hauen irudia hartuko lukete :Banaketa simetrikoenak probabilitatean erabiltzen den banaketa normalari hurbiltzen zaizkie. Aldagai estatistiko bat aldagai normalera hurbiltzen denean eta bere tarteen zabalerak txikitzen direnean, aldagai estatistiko horrek histogramak kanpaiaren itxura hartzen du. Grafiko horri "Gaussen kanpaia" esaten zaio, Gauss suitzarrak proposatu zuelako bere errore teorian.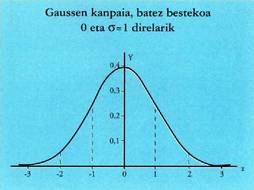Banaketa normal batean batez bestekoa=mediana=moda da, eta x batez bestekoa bada eta a desbideratze tipikoa,tartean datuen %68a dago etatartean, berriz, %95a.Banaketa bat normalera hurbiltzen bada, interesgarria da jakitea normala baino zapalagoa den. Horretarako kurtosi koefizientea erabiltzen da ; 4. mailako momentuaren eta desbideratze tipikoaren laugarren berreiaduraren arteko zatidura da kurtosi koefizientea :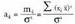Banaketa normal batean koefiziente horrek 3 balio du. Banaketa normala baino zapalagoa bada, kurtosia 3 baino txikiagoa da eta zorrotzagoa bada, berriz, 3 baino handiagoa.

VIII. Batez bestekoa, mediana eta moda.

Gehien erabiltzen den zentralizazio neurria batez bestekoa da, eta gehien erabiltzen den barreiadura neurria desbideratze tipikoa.

Banaketa normalera hurbiltzen diren banaketa estatistikoetan, banaketari buruzko gauza asko ezagut daitezke datu horien bidez.

Dena dela, beste egoera batzuetan beste zentralizazio neurri bat erabiltzea komeni da. Esaterako, batez bestekotik asko urruntzen den datu bat dagoenean hobe izaten da mendiana erabiltzea.

Aldagaia kualitatiboa denean, edo gehien errepikatzen den datua jakin nahi denean, egokiagoa moda izaten da.Enpresa batean espezializatu gabeko sei langile daude, hilean 100.000 pezeta irabazten dutenak, bost langile espezializatu 130.000 pezeta irabazten dutenak, hiru arduradun 140.000 pezeta irabazten dutenak, eta zuzendari bat 580.000 pezeta irabazten duena.

Enpresaren batez besteko soldata 150.000 pezetakoa da. Datu hau interesgarria izan daiteke soldatak ordaindu behar dituen nagusiarentzat, ez ordea lanean hasi behar duenarentzat, 15 lagunetik 14 baitira batez bestekoa baino gutxiago irabazten dutenak. Adibide honetan, mediana -130.000- lantegi horretan irabazten denaren adierazgarriagoa da ; baina, langileen gehiengoari atsegin eman nahi bazaio 100.000 pezeta irabazten dutenen alde egin beharko litzateke, moda hartu beharko litzateke, hain zuzen ere, kontuan.Era berean gela bateko 20 ikasletatik 10 badira 1 atera dutenak eta 10 ikasle 10 atera dutenak ; batez bestekoa eta mediana 5,5 dira, baina adierazgarriagoa da esatea bi modako banaketa dela, eta modak 10 eta 1 direla.

- Ariketak

13. 100 familia artean inkesta bat egin da jakiteko zenbat gelatako etxeetan bizi diren. Datuak ondoko taulan jaso dira.a) Egin barra diagrama eta maiztasun metatuen poligonoa.b) Batez bestekoa eta desbideratze tipikoa kalkulatu.c) Mediana eta batez besteko desbideratzea.d) Zein da moda?14. Errepideetako istripuen kopurua eguneko orduaren arabera azaltzen da taula honetan :Informazio estatistiko hau bildu nahi da gidatzen dutenei emateko. Horretarako adierazgarria den zentralizazio neurri bat bilatu behar da.a) Zein esanahi izango du batez bestekoak? Erabilkorra al da ematen duen informazioa?b) Zein esanahi du kasu honetan moda den tarteak? Gidarientzat interesgarria al da datu hori?c) Taula horretan, maiztasun erlatibo metatuen zutabea erantsi, eta maiztasun horiekin maiztasun metatuen poligonoa (%-tan) eraiki.d) Bilatu grafikoan %50 ordenatua duen puntua.

Jakingo al zenuke esaten zer adierazten duen abzisa horrek? Interesgarria al da gure txostenerako?e) 15 eta 21 artean dauden istripuen portzentaia kalkulatu . Adierazgarria al da datu hori?15. 32 ikasleko 2 gelatan, A eta B, azterketa bera egin da eta horien batez bestekoak eta desbideratze tipikoak hauek izan dira:a) Gela batean 12 gutxiegi eta 5 bikain daude, bestean 4 gutxiegi eta bikain bat. Zein da A gela eta zein B?b) Zein gelatan daude 4 eta 6 arteko nota gehiago?16. Saskibaloiko talde bateko jokalarien garaierak hauek dira.a) Batez bestekoa x eta desbideratze tipikoakalkulatu.b)etabalioak kalkulatu eta esan zenbat jokalari dauden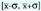tartean. %tan zenbat dira?c) Zenbat jokalari daudetartean? Zenbateko portzentaia da?d) Egiaztatu lortutako emaitzak hurrengo baieztapenarekin bat datozen :"Banaketa kopuru handi batean zera ziurtatu daiteke1)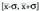tartean, %50 eta %75 arteko datuen portzentaia dago2)

Estatistiko arrunta

Estatistika deskribatzaileak, erabiltzen duen datu trataerarekin, existitzen ez den elementu hipotetikoa sortzen du, indibiduo arrunta hain zuzen ere. Multzoan ezertan nabarmentzen ez den kidea izango litzateke, gauza guztietan arrunta. Esate baterako, estatistikan espezializatuak direnen artean profesional arruntaren deskribapena hau izango litzateke :estatistiko ertainak 39,7 urte ditu, 1,2 senar/emazte ditu eta 1,87 seme-alaba (horietatik 0,94 mutilak dira eta 0,93 neskak). Bizi den etxeak 3,27 gela, sukalde bat eta 1,47 bainu ditu, eta berea da %47,3 kasutan. Familiak 1,07 auto ditu eta 0,04 aparkalekuren jabe da ; hori dela era, egunean 0,34 ordu pasatzen du autoa non utzi bila. Egunean 0,82 ordu ematen ditu autoan lanerako joan-etorrian. Astean 42,4 ordulan egiten du eta hilean garbi 153.245,7 pezeta irabazten du. Lagunekin astean 0,3 egun ateratzen da afaltzera eta bere senar/emaztearekin 1,9 aldiz joaten hilean zinemara. Astean telebista 2,8 ordu ikusten du eta egunean 3,2 aldiz eztabaidatzen du bere senarlemaztearekin. Egunean 7,1 ordu lo egiten du. Bere bizi-esperantza 74,3 urtekoa da gizonezkoa bada eta 76,2 emakumea bada.

IX. Bi dimentsioko banaketa estatistikoak.

Multzo batean aldi berean bi aldagai estatistiko aztertzen direnean, bi egoera desberdin gerta daitezke. Lehenengoan, aldagai baten emaitzak erabat finkatzen ditu bestearenak. Adibidez, zilindro bat urez betetzen bada, zilindroaren pisua urak hartzen duen garaieraren mende egongo da. Adibide horretan, bi aldagaien artean mendekotasun funtzionala dago ; egoera hori arrunta da, bai mekanikan, bai zientzia zehatzetan. Baina pertsona baten garaiera eta pisuaren artean zein erlazio dagoen bilatu nahi bada, erlazioa ez da hain sinplea izango. Orokorrean bi aldagai hauek erlazionaturik daudela esan daiteke, hau da, pertsona garaiek baxuek baino pisu gehiago dutela. Baina hori ez da beti egia izaten, eta ezin da formula bakar batean jaso. Kasu horretan erlazio estatistiko bat dago, baina ez dago funtzio bat erlazio hori adierazteko. Era horretako erlazioak arruntak izaten dira psikologia, ekonomia, biologia eta medikuntzan. Adibidez, bizi mailaren eta bizitza iraupenaren arteko erlazioa, produktu baten kontsumoaren eta propagandaren arteko erlazioa, gurasoen eta semeen garaieraren artekoa, tabakoaren eta biriken minbiziaren arteko erlazioa edo futbol talde batek gastatutako milioien eta lortzen duen postuaren arteko erlazioa, horiek guztiak erlazio estatistikoak dira.Lehenbizi, bi aldagaien artean erlazio estatistikorik baden edo ez den jakin behar da, edo erlazioa zein neurrian dagoen. Horretarako koerlazio-koefizientea definitzen da. Ondoren, erlazio estatistiko hori funtzio batera, eta bereziki funtzio lineal batera hurbiltzen den aztertzen da.

X. Sarrera bikoitzeko taulak. Barreiadura diagramak edo puntu hodeiak

Balio bikote gutxi badaude, eta errepikatzen den bikoterik ez badago, edo oso gutxi badira, emaitzak emateko era sinpleena hiru zutabetan jartzea da. Lehenengo zutabeak aztertzen den elementua identifikatzen du, bigarrenak elementu horretarako lehenengo aldagaiak hartzen duen balioa, eta hirugarrenak, bigarren aldagaiak hartzen duen balioa.Adibidez, sei ikasleren frantsesezko eta ingelesezko notak horrela jar daitezke :Errepikapenak ugariagoak badira eta datu kopurua handiagoa, emaitzak sarrera bikoitzeko taulan ematen dira. Errenkadaren eta zutabearen gurutzean balio bikoteari dagokion maiztasuna jartzen da. Adibidez, 20 emakumeren garaiera eta erabiltzen duten zapata zenbakia aztertu da, eta emaitzak hauek izan dira :Datu hauek ondoren agertzen diren sarrera bikoitzeko taula batean eman daitezke :Emaitzak grafikoki adierazteko, ardatz kartesiarrak erabiltzen dira; lehenengo aldagaia OX ardatzean jartzen da, eta bigarrena OY ardatzean. Frantsesezko eta ingelesezko noten adibidea adierazteko modua hau izango litzateke :Puntuak nola banatuta dauden ikusita adibide honetan bi aldagaiak erlazionaturik daudela esan daiteke, eta bat handitzen denean bestea ere handitzen dela. Puntuak mendekotasun motaren bat -lineala, parabolikoa, logaritmikoa edo besteren bat- iradokitzen dutenean bi aldagaien artean koerlazioa dagoela esaten da.Zenbaitetan puntuak zoriz banatzen dira, joerarik gabe.

Halakoetan, ez dago erlaziorik aldagaien artean.Horrelako diagrama batekin ezin adieraz daiteke puntu bati balio bat baino gehiago dagokionik. Sarrera bikoitzeko taula batekin, non bikote balioen maiztasuna askotan bat baino handiago den, puntuen ordez zirkuluak erabiltzen dira. Zirkulu horien gainaldea handiagoa edo txikiagoa da, maiztasunaren arabera. Edo ardatzak perspektiban jartzen dira eta bikote bakoitzaren gainean barra bat jartzen da ; barra horren garaierak maiztasuna adierazten du.

XI. Koerlazio neurria : kobariantza

Bi aldagai estatistikoren arteko koerlazioa neurtzeak adierazten du baten aldaketak, gorakadak edo beherakadak zein punturaino dauden lotuta bestearen aldaketekin. Gorakadak neurtzeko erreferentzia bat markatu behar da lehenbizi. Erreferentzia puntu onena (x,y) bikotea da, aldagai bakoitzaren batez bestekoekin osatua dena. Emaitzak adierazten dituen puntuz osatutako hodeian, puntu guztiak masa berdinekoak balira (x,y), bikoteak grabitate zentroaren koordenatuak emango lituzke ; horregatik, puntu horri multzoaren grabitate-zentroa esaten zaio estatistikan.Grabitate zentrotik puntu hodeira begiratuta, aldagaien artean koerlaziorik baldin badago, norabide batzuetan puntu gehiago bilduko dira besteetan baino. Erreferentzia ardatzarekiko bi ardatz paralelo marrazten badira grabitate zentroan, planoa lau koadranteetan banaturik dago. Bi aldagaiek batera handitzeko edo txikitzeko joera badute, puntuak 1. eta 3. koadranteetan pilatuko dira.

Hau da, koadrante horietan kendurek,eta, zeinu bera dute, + eta + Lan, edo - eta - I II.an. Hori dela eta, gehikuntzaren biderkadura positiboa izango da. Baina aldagai bat handitu egiten bada bestea txikitzen denean, puntuak 2. eta 4. koadranteetan pilatuko dira. Koadrante horietan kendurek zeinu desberdinak dituzte, eta gehikuntzen biderkadura negatiboa da. Ez badago inolako erlaziorik, gehinkuntzen biderkadurak konpentsatzen joango dira, eta puntu guztientzat batura zero izango da. Horretagatik, mendekotasunaren neurri bat hau izango da :non n emaitzen kopurua baiten. Eragiketa horren emaitzari kobariantza esaten zaio. Parentesien arteko biderkadurak egin eta formula sinplifikatuz gero, kobariantza honela idatz daiteke :Kobariantza positiboa bada, bi aldagaiak aldi berean handitu eta txikituko dira ; aldiz, negatiboa bada, bata handitzerakoan bestea txikitu egingo da. Kobariantza zerotik gertu badago, ez dago erlaziorik.Adibidez, sei ikasleren matematika, fisika eta gorputz heziketako notak jaso dira; matematika eta fisikako noten artean erlaziorik baden eta matematika eta gorputz heziketaren artean erlaziorik baden jakin nahi da. Emaitzak hauek dira:Eta dagokien puntu hodeiakMatematika-fisika bikotearen kobariantza kalkulatzeko batez bestekoak hauek dira :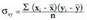formula erabiliz.Matematika-Gorputz heziketa bikotearen kobariantza kalkulatuz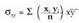formula laburtua erabiliz.Lehenengo bikotean mendekotasuna argiagoa da bigarrenean baino, kobariantza handiagoa baita. Gainera lehenengo kasuan positiboa da : matematikako nota handitzean fisikako notaren joera handitu egiten da. Bigarrengoan berriz negatiboa da, matematikako nota handitzen denean, gorputz heziketarena txikitu egiten da.Kobariantza horrela definituta arazo bat sortzen da : erabiltzen diren unitateek eragina dute azkeneko balioan. Adibidez, aldagaiak luzerak badira nahikoa da horiek zentrimetotan eman beharrean metrotan ematea, kobariantza 100 aldiz txikiago izan dadin.

Horregatik, eta datuen barreiadura kontuan hartzeko, koerlazio koefizientea erabiltzen da. Koerlazio koefizientea kobariantzaren desbideratze tipikoen biderkaduraren arteko zatidura da :Aurreko adibidean matematikarako x=5,667 eta, fisikarako y=5 eta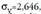inserted text. Emaitza yhoriekin koerlazio koefizienteak biribilduta hauek dira :Koerlazio koefizientea -1 eta 1 artean dago beti ; zerotik hurbil dauden balioek adierazten dute aldagaien artean ez dagoela koerlaziorik.

1 edo-1 balioak koerlazio lineala adierazten dute.

- Ariketak

17. Futbol txapelketa batean lehenengo 8 taldeak 32 par- tidu jolastu ondoren ondoko emaitzak izan dituzte.a) Postua-irabazitakoak, postua-berdindutakoak, postua- galdutakoak bikoteei dagozkien hodei puntuak marraz itzazu.b) Aldagai bikote hauentzat koerlazio kofizientea kalku- latu. Zer esan daiteke bere mendekotasunari buruz?c) Bilatu koerlazio koefizientea irabazitakoak-galdutakoak, irabazitakoak-berdindutakoak eta galdutakoak-berdin- dutakoa. Atera daiteke ondoriorik emaitza horietatik?18. Espainiara gehien esportatzen duten 6 lurraldeek, inportatzaile bezala ondoko lekua betetzen dute :Bilatu koerlazio koefizientea.19. Elkartu 1, -0,9 eta -0,5 koerlazio koefizienteak ondoko puntu hodeiekin.

XII. Erregresioa

Puntu hodeiari hobeki dagokion kurbari erregresio lerroa esaten zaio. Hurbiltasuna neurtzeko ordenatu keduraren karratuen batura erabili ohi da. y = f(x) funtzioa puntu hodei bati ondo dagokion jakiteko ondoko pausuak ematen dira :1.; aldagaiak hartzen duen balio bakoitzeko, y funtzioaren balioa eta; aldagaien arteko kendura kalkulatzen da.2. Kendura hauen karratuak kalkulatzen dira, eta ondoren batzen dira.3. Batura hau minimoa egiten duen funtzioa da ondoen doakiona.Bestalde, komeni da puntu hodeiari lotzen zaion kurba ahalik eta sinpleena izatea. Kurba sinpleena lerro zuzena da, eta hori da hain zuzen aztertuko dena, nahiz eta posible izan puntu hodeiari beste funtzioa batzuk elkartzea. Puntu hodeiari hobeki doakion lerro zuzena nola bilatu aztertzen duen estatistikaren partea erregresio lineala da.Lerro zuzen baten ekuazioa y= ax + b da. Hortaz, lerro zuzenaren ekuazioa bilatzea, a eta b-ren balioak bilatzea da. Horretarakominimoa izatea du baldintza.Froga daiteke baldintza hau erabiliz gero ondorio hauek lortzen direla.1. Lerro zuzenakgrabitate-zentrotik pasa behar du.

2. Zuzenaren maldada ; zuzenaren erregresio koefizientea esaten zaio horri. Erregresio lerro zuzenaren ekuazioa hortaz,da.Adibidez, lehen ikusitako noten kasuan erregresio lerro zuzenak hauek izango lirateke :a) Matematika aldagai librea eta fisika mendeko aldagaia izanikera laburreanb) Matematika-gorputz heziketaera laburreanErregresio lerro zuzena definitu daiteke baita ere y-tik adieraziden aldagaia, aldagai askea bezala hartuz eta x mendekoa, kasuhonetangeldituko zen ; kontuan izan behar da6 xy= (Yy x dela koerlazioa definitu zen era simetrikotik.Aztertutako kasuetan :a) Fisika-matematikaLaburtuz eta y aldagai mendekoarentzat eta x askearentzat erabiliz.b) Gorputz heziketa-matematikaLaburtuz eta x eta y aldagaiak ohi den bezala erabiliz :Kontuan izan erregresio lerro zuzenak ez datozela bat funtzio inbertsoarekin. Matematika-fisika lerro zuzenean x bakanduzgelditzen da, hau da :Matematika gorputz heziketa

- Ariketak

20. Postuari, irabazitako partiduei, berdindutakoei eta galdutakoei dagozkien datuak hauek badira :Bilatu ondoko bikoteei dagozkien erregresio lerro zuzenak : postua-irabazitako partiduak, postua-berdindutako partiduak eta postua-galdutako partiduak.Marraztu lerro zuzen hauek 17. ariketan egindako puntu hodeien gainean.21. 8 korrikalariei denbora minututan neurtu zaie, maratoi erdian eta karrera bukaeran, eta ondoko datuak lortu dira :

Emaitzak

4. A lehenengoa, B bigarrena eta C hirugarrena5. Me=6 ; batez besteko desbideratzea = 2.6. Me=3,5 ; batez testeko desbideratzea = 1,43757. Me=9,5 ; proportzionalki egiten bada 9,810. Kalkualuak egin aurretik tarteko markak jarri(biribilduz) Me=800 [724,46 zehatz] Mo=80011. 1. koartila= 3 [2,5] ; 2. koartila = mediana = 6 ; 3. koartila = 7 [6,5] ; ibiltartea : 10 - 1 =9 12. Unitateetara biribilduz medianaera berean 1. dezila = 163 ; 2. dezila=166 ; 3. dezila=169 ; 4. dezila=171 ; 6. dezila=175 ; 7.dezila=178 ; 8. dezila=180 ; 9. dezila=185Ibiltartea 210-155=5513. a)c) Me = 3 ; batez besteko desbideratzea=0'73 d) Mo = 314. a) Batez besteko istripuaren ordua. Ez da interesgarria.b) Modako tartea [ 18-21 ] da. Istripu gehienak ordu horietan izaten dira. Interesgarria da gidarientzat.c)d) Eguneko istripuen erdia 15.20etan izan da.e) Istripuen %42,7 ordu horietan gertatzen dira, eguneko laurden bat dela bakarrik.15. a) 12 gutxiegi B gelan, 4 gutxiegi A gelanb) A gelan nota gehiago daude 5 eta 7-ren artean.b) [185,54, 202,74] tartean 10 jokalari (hau da, %71,4a)c) [176,94 , 211,34] tartean daude guztiak. Beraz,d) esaten dena.17. a)Postua igotzerakoan irabazitako partidu kopuruen joera jaisten da, berdindutako eta galduen arteko koerlazioa ez da hain argia, baina postuak behera egiterakoan handitu egiten da.Koerlazio gutxi eta beti negatiboa.Grafikoak :b) Maratoi erdia 90 minututan egin badu guztira

- FORMULARIO

Batez beste aritmetikoaBariantza eta desbideratze tipikoaKobariantzaKorrelazioa koefizienteaZuzenaren erregresio

Pierre Simon de Laplace

(1749-1827)Laplace Normandian jaio zen burges familia batean. Gazte-gazterik Parisa joan zen matematikan aritzeko ; hasieran D'Alemberten babesa izan zuen. Luis XVI.aren erregealdian, Frantziar Iraultzan, Napoleonen Inperioaldian eta borbondarren berrezarpenean bizi izan zen. Denboraldi horretan, matematikek maila handia lortu zuten Frantzian, izan ere, matematikari handiak suertatu baitziren tartean, hala nola, Monge, Condorcet, Legendre, Lagrange, Carnot eta Laplace. Bestalde, hezkuntza erakundeetan errotiko aldaketak izan ziren, eta horrek liburu berri asko idaztera behartu zuen. Urte horietan sortu ziren Ecole Polytechnique eta Ecole Normale eta Pisu eta Neurrien Batzordean ere lan egin zuen, lehenik sistema metriko hamartarra Frantzia errepublikarrean ezarriz eta ondoren Europa osoan zabalduz.Matematika arloan, kalkulu infinitesimala eta integrala, geometria analitikoa eta mekanika arrazionala landu ziren aroaren amaiera izan zen alde batetik, baina beste aro baten hasiera ere izan zen bestetik, kalkulu infinitesimalean zorroztasuna eta doitasuna aurkitzen saiatu ziren eta adar berriak garatzen, hala nola aljebra abstraktua, probabilitatea, estatistika edota geometria deskribatzailea.Laplacek mekanika analitikoan, astronomian eta probabilitateen arloan lan egin zuen batez ere.

1799-1825 bitartean Mrcanique Celeste argitaratu zuen zenbait liburukitan. Lan horretan Newtonen teoria osatu eta sakondu zuen. Bestalde, fisikan potentzial ideia sartu zuen indarrak eta lanak ondorioztatzeko, eta matematikan, berriz, "Laplaceren" eragilea.Ulertzeko zaila da liburua. Gehiegitan azaltzen dira "erraz ikusten den moduan" eta gisakoak berez batere errazak ez diren urratsak egiteko.

Garapen urrats asko ditu bere-bereak, baina ez ditu aipatzen emaitzen iturriak; bestalde oso zaila da berak aurkitua, zalatzarik gabe ugaria, eta beste matematikariek aurkitua elkarrengandik bereiztea, Langrageri hartuetatik bereiztea batez ere.

Laplacek landu zuen beste arlo bat probabilitateen teoria izan zen. Harena da 1812an argitaratutako TheorieAnalytique des Probabilitrs izenekoa. Liburu horretan, "Laplaceren arau" ezaguna azaltzen da gertakari baten probabilitatea kalkulatzeko.

Liburu horretan ere beste matematikarien emaitzak, T. Bayes-enak eta Buffon-enak esaterako, eta bereak nahastu egiten ditu inolako bereizkuntzarik egin gabe. Horrek, lana osatu egiten badu ere, Laplaceren ekarpenak zeintzuk diren epaitzea zaildu egiten du. Liburu horretan, "Laplaceren transformazioak" sartzen ditu,ekuazio diferentzialen ebazketan erabiltzen direnak, hain zuzen ere.Laplacek, Pisu eta Neurrien Batzordean, sistema hamartarraren ezarpenean eta neurri berrien definizioetan esku hartu zuen. Ecole Normale-ko irakasle izan zen eta geroago berriz Ecole Polytecnique-ko azterketen arduradun. Kargu horretatik, geometria analitiko, kalkulu eta mekanika arrazionalerantz bideratutako egitaraua prestatu zuen eskola horretarako. Egitarau horretan Laplacek garrantzi gutxiago aitortu zion Mongek lehen urteetan bultzatutako geometria deskribatzaileari.Beste matematikari batzuek ez bezala, F,cole Polytechnique-n eta zientzia politikako agintaritza zeramaten beste hainbat erakundeetan hil arte iraunzuen Laplacek, alderdi politikoz aldatzeko izan zuen trebetasunari esker. Errepublika garaian, Laplacek, Lagrangek eta Legendrek ez zuten politika ihardunean esku hartu. Condorcetek, berriz, estatistikan ihardun zuen batez ere ; jatorriz noblea zen, baina errepublikazalea eta girondarra, eta kartzelan hil zen Izu Handiaren garaian. Monge, geometria deskribatzailea landu zuena, jatorri xumekoa zen eta jakobinoen Elkarteko kidea. Ia7are Carnotek, berriz, geometrian lan egin zuen, eta kalkulu infinitesimalaren oinarriak ezarri zituen ; burges militarra zen. Carnot izan zen denetan biziena.

Gudaroste errepublikarraren antolat zai le eta jeneral garaile, jakobinoen eta girondarren tartean irauten jakin zuen, eta horrexegatik gorrotatzen zuen Robespierrek; hala ere, Robespierre ez zen ausartu "garaipenaren antolatzailea' gillotinara bidaltzen.Napoleonek aginpidea hartu zuenean, Monge haren alde atera zen inolako zuhurtziarik gabe.

Carnotek kritikatu egin zuen eta erbesteratu egin zuten. Laplacek, berriz, Napoleon defendatu zuen eta Napoleonek barne ministro izendatu zuen. Halere, gutxi iraun zuen karguan. Napoleonek bere oroitidaztietan dioenez, "erdipurdikoa baino okerragoa zen administratzaile gisa" eta gobernu gaietan "infinitesimalen izpiritua" erabiltzen zuen. Lagrangek (1813an hila) eta Legendrek politikan sartu gabe jarraitu zuten.Borbondarrak Frantziara itzultzean, Laplacek berriro aldatu zituen bere irizpide politikoak eta markes izendatu eta kargu guztietan irautea lortu zuen. Mongek, aldiz, kargu guztiak galdu zituen eta berehala hil zen. Carnot Napoleonen aurkakoa zen eta argi eta garbi errepublikaren alde zegoenez atzerrira joan behar izan zuen. Legendrek ez zuen iharduera politikoetan esku hartu, baina Academie des Sciences-etik kanpora bota zuten borbondarrek, berriro erregetzara bihurturik, hartutako erabakien aurka egiteagatik.

Gobernu mota guztietara moldatzeko gaitasuna izan zuen bakarra Laplace izan zen. Bere liburuen hurrenez hurreneko argitarapenetan azaltzen diren eskaintzek argi eta garbi azaltzen dute politikan ez zela, ez matemakitan agertzen den bezain zorrotza eta ezta hartan zen bezain zehatza ere.