Matematika»Aljebra
Aljebra
XI. Polinomioaren deskonposaketa ruffiniren araua erabiliz. Faktorketa.
Maiz, polinomio bat polinomioen arteko biderkaketa moduan
idatzi beharra izango da, aljebrako zatikiak sinplifikatzeko adibidez.P(x) polinomioa deskonposagarria edota faktoretan zatigarria
dela esaten da, baldin eta 1. mailako edo goragoko mailako bi polinomio
g(x) eta h(x), edozein x zenbaki errealentzat honako hau
betetzen dutenak baldin badaude : ? Adibidea:
? Adibidea: polinomioa, deskonposagarria da, izan ere, bai baitira bi polinomio,
polinomioa, deskonposagarria da, izan ere, bai baitira bi polinomio, baldintza hau betetzen dutenak :
baldintza hau betetzen dutenak : Polinomio bat faktoretan deskonposatzen bada eta faktore horietako bat
Polinomio bat faktoretan deskonposatzen bada eta faktore horietako bat bada, orduan, a, polinomioaren emaitzetako edo erroetako bat da.Polinomio batek emaitza edo erro anitz baldin baditu :
bada, orduan, a, polinomioaren emaitzetako edo erroetako bat da.Polinomio batek emaitza edo erro anitz baldin baditu :
 orduan, polinomioa, faktore arteko biderkaketa moduan idatz daiteke.
orduan, polinomioa, faktore arteko biderkaketa moduan idatz daiteke. ? Adibidea:Bedi
? Adibidea:Bedi polinomioa.Ruffiniren araua erabiliz, x-en gai askearen zatitzaileen artean
erroak edo emaitzak aurkitzen dira, hots, 6 zenbakiarenak kasu
honetan.Izan daitezkeen erroak:
polinomioa.Ruffiniren araua erabiliz, x-en gai askearen zatitzaileen artean
erroak edo emaitzak aurkitzen dira, hots, 6 zenbakiarenak kasu
honetan.Izan daitezkeen erroak: x = 2, erro edo emaitzetako bat dax = 3, erro edo emaitzetako bat da
x = 2, erro edo emaitzetako bat dax = 3, erro edo emaitzetako bat da
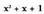 polinomioa ezin daiteke gehiago deskonposatu.Bedi
polinomioa ezin daiteke gehiago deskonposatu.Bedi polinomioa.Erro edo emaitza ahalak honako hauek dira:
polinomioa.Erro edo emaitza ahalak honako hauek dira:


- Proposatutako ariketak
25. Deskonposa itzazu polinomio hauek.
XII. Aljebrako zatikiak. Aljebrako zatikiekin eragiketak.
XII.1. Aljebrako zatikiak.
Aljebrako zatikia, zatikiaren gai deitutako bi polinomioren arteko zatidura da ;
bi polinomioren arteko zatidura da ; polinomioa zenbakitzailea da eta
polinomioa zenbakitzailea da eta izendatzailea. Izendatzailea ezin daiteke zero izan, horregatik, izen= datzailea zero eginarazten duten ezezagunaren balio guztiak kanpoan geldituko dira.? Adibideak :
izendatzailea. Izendatzailea ezin daiteke zero izan, horregatik, izen= datzailea zero eginarazten duten ezezagunaren balio guztiak kanpoan geldituko dira.? Adibideak : Bi aljebrako zatiki baliokideak dira, baldin eta beren letrei
emandako edozein baliorekin zenbakizko balio berbera lortzen
baldin badute, baina beti ere, izendatzaileak hutsal edo
gero bihurtzen ez diren bitartean.
Bi aljebrako zatiki baliokideak dira, baldin eta beren letrei
emandako edozein baliorekin zenbakizko balio berbera lortzen
baldin badute, baina beti ere, izendatzaileak hutsal edo
gero bihurtzen ez diren bitartean. Bi zatiki baliokideak diren jakiteko, biderkaketa gurutzatuak
:gin daitezke eta bat datozela ikus daiteke. Bitez honako zatiki
)aliokide hauek:
Bi zatiki baliokideak diren jakiteko, biderkaketa gurutzatuak
:gin daitezke eta bat datozela ikus daiteke. Bitez honako zatiki
)aliokide hauek: orduan honako hau beteko da :
orduan honako hau beteko da :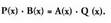
XII.2. Zatitzaile komun handiena (Z.k.h.) eta multiplo komun txikiena (m.k.t.).
Denok ere entzuna dugu Eratostenesek egindako "garbiketa"
famatua. Eratostenesek, zenbaki lehenak bakarrik utzi zituen, zenbaki
bikoitiak, hiruaren multiploak, bostaren multiploak, etab.. ulatu eta kentzen aritu ondoren. Zerrenda horretan gelditutakoak
beraz, honako hauek dira : 1,2,3,5,7,11,13,Zatigarritasun arauetan oinarrituta, zenbaki bat bere faktore
lehenetan zati daiteke. Adibidez : Bi zenbaki edo gehiago beren faktore lehenen biderkaketa
adieraziz idatzita daudenean, bien arteko Zatitzaile komun
handiena (Z.k.h.) kalkula daiteke ; bestela esanda, biek
komunki (batera) duten zatitzaile handiena. Multiplo
komun txikiena (m.k.t.) ere, era sistema beretsuaz baliatuz kalkula
daiteke eta zenbaki horiek elkarrekin duten multiplorik
txikiena izango da.Bi zenbaki edo gehiagoren Zatitzaile komun handiena
(Z.k.h.), bakoitzak dituen faktore komunak berretzailerik
txikienarekin hartuta biderkatuz kalkulatzen
da.Bi zenbaki edo gehiagoren multiplo komun txikiena
(m.k.t.), bakoitzak dituen faktore komunak eta komunak
ez direnak berretzailerik handienarekin hartuta
biderkatuz kalkulatzen da.? Adibideak :
12 eta 18 zenbakien
Bi zenbaki edo gehiago beren faktore lehenen biderkaketa
adieraziz idatzita daudenean, bien arteko Zatitzaile komun
handiena (Z.k.h.) kalkula daiteke ; bestela esanda, biek
komunki (batera) duten zatitzaile handiena. Multiplo
komun txikiena (m.k.t.) ere, era sistema beretsuaz baliatuz kalkula
daiteke eta zenbaki horiek elkarrekin duten multiplorik
txikiena izango da.Bi zenbaki edo gehiagoren Zatitzaile komun handiena
(Z.k.h.), bakoitzak dituen faktore komunak berretzailerik
txikienarekin hartuta biderkatuz kalkulatzen
da.Bi zenbaki edo gehiagoren multiplo komun txikiena
(m.k.t.), bakoitzak dituen faktore komunak eta komunak
ez direnak berretzailerik handienarekin hartuta
biderkatuz kalkulatzen da.? Adibideak :
12 eta 18 zenbakien da.12 eta 18 zenbakien
da.12 eta 18 zenbakien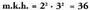 da.10 eta 18 zenbakien
da.10 eta 18 zenbakien da.10 eta 18 zenbakien
da.10 eta 18 zenbakien
XII.3. Aljebrako zatikien Zatitzaile komun handiena (Z.k.h.) eta multiplo komun txikiena (m.k.t.).
Zenbaki osoen kasuan bezalaxe, P(x) polinomioa, faktore lehenetan
deskonposa dezakegu. Nola ordea? XI. atalean ikusi dugunaren
arabera, polinomioa, beti ez bada ere, faktoretan deskonposa
daiteke :? Faktore komunak ateraz.? Maisutasunezko formulen edo formula nagusien bitartez :
karratuen diferentzia, binomioaren karratua, etab.? Ruffiniren araua erabiliz.Bi polinomio edo gehiagoren Z.k.h. kalkulatzeko, polinomioak
faktoretan zatitzen dira eta ondoren, faktore
komunak biderkatzen dira beti ere berretzailerik txikienarekin
hartuta.Ebatzitako ariketak.21. Kalkulatu adierazpen hauen Z.k.h.-ak. Emaitzak :
Emaitzak : Bi polinomio edo gehiagoren m.k.t. kalkulatzeko, polinomioak
faktoretan zatitzen dira eta ondoren, faktore
komunak eta komunak ez direnak biderkatzen dira beti
ere berretzailerik handienarekin hartuta.Ebatzitako ariketak.
Bi polinomio edo gehiagoren m.k.t. kalkulatzeko, polinomioak
faktoretan zatitzen dira eta ondoren, faktore
komunak eta komunak ez direnak biderkatzen dira beti
ere berretzailerik handienarekin hartuta.Ebatzitako ariketak.
22. Kalkulatu adierazpen hauen m.k.t. Emaitzak :
Emaitzak :
- Proposatutako ariketak
26. Kalkulatu adierazpen hauen Z.k.h.-ak.
- Proposatutako ariketak
27. Kalkulatu adierazpen hauen m.k.t.-ak. 28. Kalkulatu adierazpen hauen Z.k.h. eta m.k.t.
28. Kalkulatu adierazpen hauen Z.k.h. eta m.k.t.
XII.4. Aljebrako zatikien sinplifikazioa.
XII. 1. atalean ikusia dugu jada, zatikien oinarrizko propietatearen arabera, zatiki bateko bi gaiak, zero balio ez duen aljebrako adierazpen edo gai berberaz zatitzen edo biderkatzen baditugu, lortutako zatikia hasierakoaren berdina dela. Horren arabera, hasierako zatikiaren baliokidea izanik gai soilagoak dituen beste bat lortzeko, nahikoa da zatiki horren zenbakitzailea eta izendatzailea adierazpen edo gai berberaz zatitzea.Aljebrako zatikiak sinplifikatzeko egin beharreko eragiketak hauek dira:? Zenbakitzailea eta izendatzailea faktoretan deskonposatu.? Bi gaiak, bien arteko Z.k.h.-az zatitu.Ebatzitako ariketak.23. Sinplifikatu zatiki hauek.
- Proposatutako ariketak
29. Sinplifikatu zatiki hauek.
XII.5. Ipini zatikiak izendatzaile komunarekin.
Zatikiak izendatzaile komunarekin jartzeko, eragiketa hauek egin behar dira :? Lehenik, ahal bada, sinplifikatu.? Kalkulatu izendatzaileen arteko m.k.t.? Zatiki bakoitzeko bi gaiak, m.k.t. zatiki horren izendatzaileaz zatituta ateratzen den kopuruaz biderkatu behar da.
XII.6. Zatikien aljebrako batura.
Aljebrako zatikien batuketa egiteko, eragiketa hauek
egin behar dira :? Lehenik eta behin, ahal izanez gero, sinplifikatu.? Izendatzaile komunera laburtu.? Zenbakitzaileak batu izendatzaile komuna gordez.? Ahal izanez gero, azken emaitza sinplifikatu.Ebatzitako ariketak.24. Egizu zatiki hauen batura. Emaitzak:
Emaitzak:
- Proposatutako ariketak
30. Batu zatiki hauek.
XII.7. Aljebrako zatikien biderkaketa.
Aljebrako zatikiak biderkatzeko, eragiketa hauek egin behar dira:? Lehenik eta behin, ahal izanez gero, sinplifikatu.Biderkatu zenbakitzaileak beren artean zenbakitzailea lortzeko eta izendatzaileak halaber beren artean, izendatzailea lortzeko.? Ahal bada, emaitza sinplifikatu.Ebatzitako ariketak.25. Biderkatu zatiki hauek.
- Proposatutako ariketak
31. Biderkatu zatiki hauek.
XII.8. Aljebrako zatikien zatiketa.
Aljebrako bi zatiki zatitzeko, eragiketa hauek egin
behar dira :Biderkatu lehenengo zatikia bigarrenaren alderantzizkoaz.? Ahal izanez gero, sinplifikatu emaitza.Ebatzitako ariketak.26. Zatitu zatiki hauek. Emaitza :
Emaitza : Emaitza:
Emaitza: Emaitza:
Emaitza:
- Proposatutako ariketak
32. Zatitu zatiki hauek.
XII.9. Aljebrako zatikien berreketa.
Aljebrako zatikien berreketa egiteko, eragiketa hauek
egin behar dira :? Gai bakoitzaren berreketa egin.? Ahal izanez gero, emaitza sinplikatu.Ebatzitako ariketak.27. Kalkulatu adierazitako berreketak. Emaitza :
Emaitza : Emaitza :
Emaitza : Emaitza :
Emaitza :
- Proposatutako ariketak
33. Kalkulatu adierazitako berreketak.
Emaitzen eranskina
1. a) Razional osoab) Zatiki irrazionalac) Zatiki razionalad) Zatiki irrazionala 12. Zatiduraren maila 4.a da, eta hondarrarena 3.a edo hori
baino txikiagoa.
12. Zatiduraren maila 4.a da, eta hondarrarena 3.a edo hori
baino txikiagoa. 24. a) Ez, hondarra 134 da. b) Ez, hondarra 26 da.
24. a) Ez, hondarra 134 da. b) Ez, hondarra 26 da.
EUKLIDES (K.a. 111. mendean hila)
Elementuak lanak matematikaren historian izan
duen garrantzia dela-eta, egilea, Euklides, bigarren
mailan geratu da; ez da haren bizitzaz ia ezer ezagutzen,
eta Elementuak, berriz, gehien argitaratu den
matematika liburua da.Euklidesen biografiari buruz zeharkako iturbururik
baino ez dago. Horien arabera, K.a IV mendearen
bigarren erdian jaio zen Euklides. Matematika
Atenasen landu zuen, eta Platonen eskolako
kideak izan zituen irakasle. Alexandriara jo zuen
gero, eta han Ptolomeo Lak sorturiko Museoan eta
Liburutegian aritu zen lanean. Matematikak irakastea
eta jakintza horri buruzko liburuak idaztea izan
zen bere eginkizuna. Matematikako eskola bat sortu
zuen, mende bete geroago, Arkimedesen garaian,
oraindik ere garrantzitsua zena. K.a. 111. mendearen
lehen erdian hil zen.Euklidesek geometria, astronomia, optika, musika
eta mekanikako liburuak idatzi zituen. Horietatik
guztietatik, zati fidagarriak Elementuak lan famatukoak
besterik ez dira gorde, eta Elementuakgaratzen dituen problema liburu batenak, Datuak
liburuarenak hain zuzen. Gainerako liburuetatik,
zenbaiten laburpenak, iruzkinak eta fidagarritasun
handirik gabeko bertsioak ezagutzen dira. Beste
obra zenbaitez, ondorengo egileen iruzkinengatik
dakigu existitu zirela.Elementuak (stoiceiwn)Euklidesen Elementuak lana hamabi liburuz dago
osatua. Liburu horien helburua geometriaren elementuak
adieraztea da, hau da, geometrian jakin
beharreko auzi errazenak batetik, eta, bestetik, geometria
eraikitzeko abiapuntu diren oinarrizko elementuak.Elementuak liburuaren hasiera gisa, definizio,
axioma eta postulatu batzuk ematen ditu Euklidesek,
eta, horietatik abiaturik, lanaren parte nagusian,
proposizio, teorema edo problemak frogatzen
ditu gero. Definizioek matematika objektuen tasunak
adierazten dituzte (zuzen, hiruki, zirkuluenak,
etab.). Axiomak zientzia guztiei dagozkien hastapen
sail bat dira, Euklidesek agerikotzat jotzen dituenak.
Postulatuak matematikari soilik dagozkion hastapenak
dira, eta horiek ere frogatu beharrik gabe onartzen
dira. Ez da sistema axiomatiko bat, gaur ulertzen
den bezala, espezifikatu gabeko objektuen
tasun asko erabiltzen baitira definizioetan, eta hai
baitira zehazki adierazten ez diren axiomak ere ;
baina geometria sistematizatzeko erak, emaitzetara
dedukzioz iristeak, eta arrazoibideen zehaztasunak,
metodo axiomatiko modernoen aitzindari zuzena
egiten dute Euklides.Edukiari dagokionez, I. liburuak planoaren geometria
lantzen du, eta besteak beste hirukien berdintasuna,
paraleloak eta Pitagorasen teorema lantzen
ditu. Liburu horretan daude definizio
gehienak, eta postulatu eta axioma guztiak. Bertan
ageri da halaber bosgarren postulatu famatua : "5.Eta zuzen batek bi zuzen ebakitzen dituenean, alde
bereko barneko angeluak bi angelu zuzen baino nikiago
egiten baditu, bi zuzen haiek, mugagabe luzatuz
gero, elkartu egingo dira bi angelu zuzen baino
txikiago diren angelu horiek dauden aldean". 11.. iburuak zuzenkien batuketa edo kenketen gainean
egin daitezkeen lauki eta lauki zuzenak lantzen ditu.
111. liburua zirkunferentziari buruzkoa da, eta IV
liburua poligonoak zirkunferentzia batean inskribatzeari
eta zirkunskribatzeari buruzkoa. V liburua
zuzenkien arrazoiaren gainekoa da, eta edozein
zuzenki motatara zabaltzen du liburu horretan zatikien
teoria. VI. liburuak planoaren teoriari aplikatzen
dio V liburuko proportzioaren teoria, irudi eta
areen antzekotasuna aztertzen du, eta hiruki angeluzuzenen
tasunak orokortzen. VII-IX liburuek
aritmetika lantzen dute, multiploen eta zatitzaileen
tasunak, zenbaki osoen zatikiak eta zenbaki lehenak
aztertzen dituzte. X. liburua zenbaki irrazionalei
buruzkoa da, eta horixe da zailena. XI eta XII. liburuek
planoak, zuzenak eta espazioko irudiak aztertzen
dituzte, eta paralelepido, prisma, piramide,
kono, zilindro eta esferen bolumenak adierazten.
XIII. liburuak bost irudi gotor erregularrak lantzen
ditu : tetraedroa, kuboa, oktaedroa, dodekaedroa
eta ikosaedroa.Elementuak antzinako matematikari hoberenen
bilduma da, Euklidesek hobetua eta osatua. Parte
gehienak orijinalak ez badira ere, V liburua Eudoxorena
da, V1I-IX liburuak pitagorikoenak, eta
badira zenbait teorema eta froga Euldidesenak berarenak;
zehatzago, berea da, egile guztien arabera,
paraleloen postulatu ospetsuaren adierazpena.Bolyai eta Lobatchevskiren idatzien ondoren,
XIX. mendaren hasieraz geroztik, gauza jakina da
izan daitezkeela Euklidesena ez bezalako beste geometriak
ere. Baina oraindik ere berrargitaratzen eta
ikasten dira Euklidesen Elementuak.
Ekuazioak eta inekuazioak
I.1. Berdintzak.
Bi alde (=) zeinuaz berezita daudenean, berdintza bat dugu. Berdintzak,
zenbakizkoak izan daitezke zenbakiz adieraziak badira eta
letrazkoak edo literalak letra bidez adieraziak badatoz.? Adibideak:zenbakizko berdintza letrazko berdintza
letrazko berdintza
I.2. Identitatea.
Identitatea, partaide diren letrei egotz dakiekeen edozein baliorentzat
ere balio duen berdintza da. Identitateak, aljebrako adierazpen
bat, erabilerrazagoa den beste baliokide bat bilatzeko zerbitzen
du.? Adibidea :
I.3. Aljebrako ekuazioa.
Aljebrako ekuazioa, duen/dituen letraren/letren balio batzuentzat
bakarrik betetzen den berdintza da. Aljebrako ekuazioan
azaltzen diren letrei ezezagun deritze. Ekuazioaren lehen aldea,
berdin zeinuaren ezkerraldean idatzitako adierazpena da.Bigarren aldea, berdin zeinuaren eskuinaldean idatzitako adierazpena
da.Berdintza betetzen duen ezezagunaren balioari, ekuazioaren
emaitza cdo erro deritzo.Ekuazioa ebaztea, bere emaitzak edo erroak kalkulatzea da.
1. adibidea: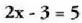 Lehen aldea :
Lehen aldea : Bigarren aldea : 5Emaitza edo erroa : 4, izan ere,
Bigarren aldea : 5Emaitza edo erroa : 4, izan ere, baita.2. adibidea :
baita.2. adibidea : Lehen aldea :
Lehen aldea : Bigarren aldea : 16Emaitzak edo erroak : 6 eta - 6Izan ere,
Bigarren aldea : 16Emaitzak edo erroak : 6 eta - 6Izan ere, baita eta baita
baita eta baita
I.4. Ekuazioaren gaiak
Ekuazioaren gaiak zera dira, osagai dituen lehen eta bigarren aldeetako monomioetako bakoitza. Ezezagun bat duten gaiei, "x" adibidez, x-en gai deitzen zaie eta ezezagunik ez duten gaiei berriz "gai aske". Horrela, ekuazioan,
ekuazioan,
I.5. Inekuazioa
Inekuazioa, desberdintza da, aljebrako bi adierazpenen artean (>)
"handiago.... (baino)", (<) "txikiago... (baino)", (>) "handiago
edo berdin" (<_) "txikiago edo berdin".Inekuazioaren lehen aldea, desberdintza adierazten duen zeinuaren
ezkerraldean idatzitako adierazpena da. Inekuazioaren bigarren
aldea, desberdintza adierazten duen zeinuaren eskuinaldean idatzitako
adierazpena da.1. adibidea: Lehen aldea : x - 3Bigarren aldea : 5x + 42. adibidea:
Lehen aldea : x - 3Bigarren aldea : 5x + 42. adibidea: Lehen aldea :
Lehen aldea : Bigarren aldea : 03. adibidea :
Bigarren aldea : 03. adibidea : 4. adibidea :
4. adibidea :
I.6. Ezezagun bateko ekuazioaren (edo inekuazioaren) maila.
Ezezagun bateko ekuazioaren (edo inekuazioaren) maila, ezezagunak
duen berretzailerik handiena da.? Adibideak:x - 5 = 8lehen mailako ekuazioa bigarren mailako ekuazioa
bigarren mailako ekuazioa hirugarren mailako ekuazioa
hirugarren mailako ekuazioa lehen mailako inekuazioa
lehen mailako inekuazioa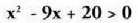
I.7. Ezezagun bat baino gehiagoko ekuazioaren (edo inekuazioaren) maila.
Ezezagun bat baino gehiagoko ekuazioaren (edo inekuazioaren)
maila, ezezagunek dituzten berretzaileetatik handiena da.? Adibidea: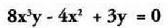 laugarren mailakoa da
laugarren mailakoa da
I.8. Ekuazio (edo inekuazio) baliokideak.
Ekuazio (edo inekuazio) baliokideak, emaitza edo erro berdinak
dituztenak dira.Bi ekuazio (edo inekuazio) baliokideak direla frogatzeko, lehenengoaren
edozein emaitza bigarrenarena ere badela frogatu behar
da eta baita alderantzizkoa ere. Ekuazio (edo inekuazio) baten
emaitza, harik eta emaitzak bistan jarriko dituen ekuazioa (edo inekuazioa)
lortu arte bera baliokide diren beste batzuetan bihurtzen
joanez lortzen da.? Adibideak : eta
eta baliokideak dira, izan ere, aurrerago ikusiko denez, emaitza berbera baitute : 7.
baliokideak dira, izan ere, aurrerago ikusiko denez, emaitza berbera baitute : 7.
.
I.9. Batuketa bidezko ekuazio (edo inekuazio) baliokideak.
Batuketa bidez ekuazio (edo inekuazio) baliokideak lortzeko,
printzipio hau hartu behar da kontuan :Ekuazio (edo inekuazio) bateko bi aldeei edozein zenbaki
batzen edo kentzen bazaie, lehenengoaren baliokidea
den ekuazioa (edo inekuazioa) lortzen da.Adibidea :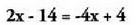 Ekuazio honen emaitza 3 da.
Ekuazio honen emaitza 3 da. Ekuazio honen emaitza ere 3 da.
Ekuazio honen emaitza ere 3 da. ekuazio baliokideak dira.
ekuazio baliokideak dira.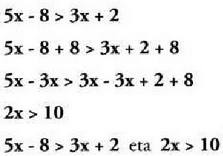 inekuazioak baliokideak dira.Lehenengo printzipio horren ondorioz :? Edozein gai ekuazioaren (edo inekuazioaren) aldez alda daiteke,
baina beti ere zeinua aldatu beharko du. Aldez aldatzeko
eragiketari gai iraulketa deritzo.
inekuazioak baliokideak dira.Lehenengo printzipio horren ondorioz :? Edozein gai ekuazioaren (edo inekuazioaren) aldez alda daiteke,
baina beti ere zeinua aldatu beharko du. Aldez aldatzeko
eragiketari gai iraulketa deritzo. , ekuaziotik,
, ekuaziotik, ekuaziora pasa daiteke.? Bigarren aldea beti labur daiteke zerora bertan dauden gai
guztiak lehen aldera irauliz edo pasaz.Bedi
ekuaziora pasa daiteke.? Bigarren aldea beti labur daiteke zerora bertan dauden gai
guztiak lehen aldera irauliz edo pasaz.Bedi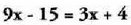 ekuazioa ; beste era honetan ere idatz daiteke :
ekuazioa ; beste era honetan ere idatz daiteke :
I.10. Biderkaketa edo zatiketa bidez baliokideak diren ekuazioak. Ekuazio honen emaitza ere 3 da.
Biderkaketa edo zatiketa bidez baliokideak diren ekuazioak lortzeko,
printzipio hau hartu behar da kontuan :Ekuazio baten bi aldeak, zero balio ez duen zenbaki
berberaz biderkatzen edo zatitzen badira, lehenengoaren
baliokidea den beste ekuazio bat lortzen da.? Adibideak : Ekuazio honen emaitza 3 da.
Ekuazio honen emaitza 3 da. Ekuazio honen emaitza ere 3 da.Beraz,
Ekuazio honen emaitza ere 3 da.Beraz,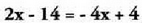 ekuazioa eta
ekuazioa eta ekuazioa elkarren baliokideak dira, izan ere, biek baitute emaitza berbera.Bedi 5x = 30 ekuazioa Ekuazio honen emaitza 6 da.Bi aldeak 5ez zatitzen badira, hondoko hau geldituko da :
ekuazioa elkarren baliokideak dira, izan ere, biek baitute emaitza berbera.Bedi 5x = 30 ekuazioa Ekuazio honen emaitza 6 da.Bi aldeak 5ez zatitzen badira, hondoko hau geldituko da : ; hau da
; hau da Printzipio horren ondorioz :? Ekuazio bateko izendatzaileak kendu egin daitezke, gai
guztiak izendatzaileen multiplo komun batez biderkatuta.Honako ekuazio honetatik,
Printzipio horren ondorioz :? Ekuazio bateko izendatzaileak kendu egin daitezke, gai
guztiak izendatzaileen multiplo komun batez biderkatuta.Honako ekuazio honetatik, beste hau ateratzen da
beste hau ateratzen da Gai bakoitza sinplifikatzen bada, hondoko hau ateratzen da :
Gai bakoitza sinplifikatzen bada, hondoko hau ateratzen da :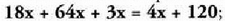 eta ekuazio honetan jada ez dira izendatzaileak azaltzen ; baina lehenengoaren baliokidea da, hala ere.? Ekuazio bateko gai guztiak, zero balio ez duen zenbaki berberaz
zati daitezke, hain zuzen ere, koefiziente osoen zatitzaile
komun handienaz. Ekuazioa sinplifikatuta gelditzen
da.? Adibidea :
eta ekuazio honetan jada ez dira izendatzaileak azaltzen ; baina lehenengoaren baliokidea da, hala ere.? Ekuazio bateko gai guztiak, zero balio ez duen zenbaki berberaz
zati daitezke, hain zuzen ere, koefiziente osoen zatitzaile
komun handienaz. Ekuazioa sinplifikatuta gelditzen
da.? Adibidea : Ekuazio horren emaitza 4 da.Ekuazioaren gai guztiak 8z zatitzen badira, honako hau ateratzen
da :
Ekuazio horren emaitza 4 da.Ekuazioaren gai guztiak 8z zatitzen badira, honako hau ateratzen
da : eta hori berori
eta hori berori ekuazioaren baliokidea da. Azken ekuazio honen emaitza ere 4 da. Beraz,
ekuazioaren baliokidea da. Azken ekuazio honen emaitza ere 4 da. Beraz, ekuazioa eta
ekuazioa eta
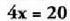
I.11. Biderkaketa edo zatiketa bidez berdinak diren inekuazioak
Inekuazio bat zero balio ez duen zenbaki batez biderkatzen
edo zatitzen bada, bi gauza gerta daitezke :? Zenbakia positiboa izatea ; kasu horretan, desberdintzaren
norantza mantendu egiten da.? Zenbakia negatiboa izatea ; kasu horretan, desberdintzaren
norantza aldatu egiten da. inekuazioa emanda :
inekuazioa emanda : baino bada,
baino bada, .
. baino bada,
baino bada, ? Adibideak :
? Adibideak :
II. Ekuazio motak.
Ekuazioak, era honetan sailka daitezke :? Ezezagun-kopuruaren arabera, ezezagun bat, bi ezezagun,
hiru ezezagun,..., n ezezagunekotan sailka daitezke.? Adibideak : ezezagun bateko ekuazioa da.
ezezagun bateko ekuazioa da. bi ezezaguneko ekuazioa da.Datuak adierazita dauden moduaren arabera, letrazko edo
zenbakizko ekuazioak izan daitezke, ezezagunei dagozkien letrez
gainera, beste letra batzuek badituzten ala ez kontuan hartuta.? Adibideak :
bi ezezaguneko ekuazioa da.Datuak adierazita dauden moduaren arabera, letrazko edo
zenbakizko ekuazioak izan daitezke, ezezagunei dagozkien letrez
gainera, beste letra batzuek badituzten ala ez kontuan hartuta.? Adibideak : 4x + 7 = 12x - 5 zenbakizko ekuazioa da eta ezezagun bakarra du.
4x + 7 = 12x - 5 zenbakizko ekuazioa da eta ezezagun bakarra du.
Aldiz, y = mx + b letrazko ekuazioa da eta bi ezezagun ditu.? Ekuazio osoak edo zatikidun ekuazioak ere izan daitezke.
Ekuazio osoak, izendatzailean ezezagunik ez dutenak eta berretzaile
negatiborik ere ez dutenak dira. Zatikidun ekuazioak
aldiz, horietakoak dituztenak.? Adibideak : zatikidun ekuazioa da eta bi ezezagunekoa gainera.
zatikidun ekuazioa da eta bi ezezagunekoa gainera. 4x + 7 = 12x - 5 ekuazio osoa (zenbaki osoduna) da.? Ekuazio razionaletan, ezezagunetako ezein ere erro-ikurpean ez
dagoenean eta zatikidun berretzailerik ere ez duenean edo ekuazio
irrazionaletan horietakoak dituenean.? Adibideak :
4x + 7 = 12x - 5 ekuazio osoa (zenbaki osoduna) da.? Ekuazio razionaletan, ezezagunetako ezein ere erro-ikurpean ez
dagoenean eta zatikidun berretzailerik ere ez duenean edo ekuazio
irrazionaletan horietakoak dituenean.? Adibideak : ekuazio irrazionala eta ezezagun bakarrekoa da.
ekuazio irrazionala eta ezezagun bakarrekoa da.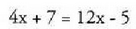 ekuazio razionala da.
ekuazio razionala da. ekuazio irrazionala da.? Ezezagunak duen berretzailearen arabera, lehen mailakoak
edo linealak, bigarren mailakoak edo koadratikoak, hirugarren
mailakoak edo kubikoak, laugarren mailakoak eta orokorki
n-garren mailakoak izan daitezke baldin eta beren maila
n baldin bada.Adibideak :
ekuazio irrazionala da.? Ezezagunak duen berretzailearen arabera, lehen mailakoak
edo linealak, bigarren mailakoak edo koadratikoak, hirugarren
mailakoak edo kubikoak, laugarren mailakoak eta orokorki
n-garren mailakoak izan daitezke baldin eta beren maila
n baldin bada.Adibideak :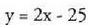 lehen mailako ekuazioa da, hots, ekuazio lineala.
lehen mailako ekuazioa da, hots, ekuazio lineala. bigarren mailako akuazioa edo ekuazio koadratikoa da.
bigarren mailako akuazioa edo ekuazio koadratikoa da.
III. Ekuazioen ebazpena
Ekuazioak ebazteko, lehendabizi, zein motatakoak diren hartu
behar da kontuan, izan ere, jarraitu beharreko bideak eta eman
beharreko urratsak oso desberdinak baitira era batekoak izan ala
bestekoak izan. Ez da bide berdina lehen mailako ekuazioak ezezagun
batekin jarraitzea eskatzen duena, bigarren mailakoak ezezagun
batekin behar duena edota bigarren mailatik gorako ezezagunak
eskatzen duena.Edozein kalkulu egiten hasi aurretik, ekuazioaren eremua zehaztu
behar da, hots, ekuazioaren lehenengo eta bigarren aldeak izan
ahal izateko (existitzeko) x-ek izan behar dituen balioen multzoa
zehaztu behar da.hain zuzen ere :? Ezezaguna zatiki baten izendatzailean baldin badago, izendatzailea
zero bihurtzen duten x-en balioak eremu horretatik
kendu beharra dago.? Adibideak :
Bedi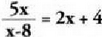 ; hori,
; hori, 0 baldin bada bakarrik ebatzi ahal izango da, hots,
0 baldin bada bakarrik ebatzi ahal izango da, hots, bada.? Ezezaguna erro-ikurpean baldin badago, errokizuna negatibo bihurtzen duten balioak kendu beharra dago eremutik.? Adibideak :
Bedi
bada.? Ezezaguna erro-ikurpean baldin badago, errokizuna negatibo bihurtzen duten balioak kendu beharra dago eremutik.? Adibideak :
Bedi ekuazioa;
ekuazioa; bada bakarrik ebatzi ahal izango da, hau da,
bada bakarrik ebatzi ahal izango da, hau da,
IV. Ezezagun bateko ekuazioak.
I V A.1. Lehen mailako ekuazioak.
Lehen mailakoa eta ezezagun batekoa den ekuazioa ebazteko arauak:- Baldin badaude, izendatzaileak kontzen dira. Horretarako, gai bakoitza, izendatzaileen arteko multiplo komun txikienaz biderkatu behar da.
- Baldin badaude, parentesiak (makoak) kentzen dira, horretarako lege banakorra erabiliz.
- Gaiak lekuz aldatu egiten dira harik eta x-dunak alde batean eta gabeak edo gai askeak bestean kokatzen diren arte.? Antzeko gaien artean laburpena egiten da.? Azkenik, ekuazioaren emaitza edo erroa lortzeko, gai
askea, ezezagunaren koefizienteaz zatitzen da.Edozein modutan aurkeztuta ere, ezezagun bat duen lehen mailako
ekuazioa, aurreko puntuetan esandakoaren arabera, baliokidea
den beste batera eralda daiteke. Beste horrek, itxura hau izango du : ? Baldin eta
? Baldin eta eta
eta badira ekuazioak,emaitza bakarraizango du eta emaitza horrek,
badira ekuazioak,emaitza bakarraizango du eta emaitza horrek,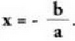 Ekuazioa, bateragarria eta zehatza da.a-k eta b-k zeinu berbera badute, erroa edo emaitza negatiboa da,
baina a-k eta b-k zeinu desberdinak badituzte, emaitza positiboa
izango da.? a = 0 eta
Ekuazioa, bateragarria eta zehatza da.a-k eta b-k zeinu berbera badute, erroa edo emaitza negatiboa da,
baina a-k eta b-k zeinu desberdinak badituzte, emaitza positiboa
izango da.? a = 0 eta badira, ekuazioak ez du emaitzarik. Ekuazioa bateraezina da.? a = 0 eta b = 0 badira, ekuazioak emaitza-kopuru infinitua du.
badira, ekuazioak ez du emaitzarik. Ekuazioa bateraezina da.? a = 0 eta b = 0 badira, ekuazioak emaitza-kopuru infinitua du.
Ekuazioa bateragarria eta zehazgabea da.Ebatzitako adibideak :1. Ebatzi ekuazio hauek. Egiaztapena :
Egiaztapena : Eremua : RIzendatzaileen multiplo komun txikiena 4 da.
Eremua : RIzendatzaileen multiplo komun txikiena 4 da. Egiaztapena :
Egiaztapena : Eremua : RIzendatzaileen multiplo komun txikiena 60 da.
Eremua : RIzendatzaileen multiplo komun txikiena 60 da. Egiaztapena:
Egiaztapena: Lehen aldea definituta dago, baldin eta
Lehen aldea definituta dago, baldin eta eta
eta baldin badira eta egon ere hala izanda bakarrik egongo da. Beraz, eremua,
baldin badira eta egon ere hala izanda bakarrik egongo da. Beraz, eremua, da.
da. Ekuazioa sinplifikatu egiten da
Ekuazioa sinplifikatu egiten da Egiaztapena :
Egiaztapena : Lehen aldea definituta dago, baldin eta
Lehen aldea definituta dago, baldin eta bada eta egon ere hala izanda bakarrik egongo da. Eremua,
bada eta egon ere hala izanda bakarrik egongo da. Eremua, Ekuazioa sinplifikatu egiten da
Ekuazioa sinplifikatu egiten da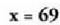 Egiaztapena:
Egiaztapena:
- Proposatutako ariketak
1. Ebatzi ekuazio hauek.
IV.A.2. Lehen mailako buruketak ezezagun batekin.
Buruketa edo problema bat aljebrako metodo bidez ebaztea,
buruketak ematen dituen datuak aljebrako hizkuntzara itzultzea
edo eraldatzea da. Buruketaren ebazpena, hiru zatitan bana daiteke :? Planteatzea? Ebaztea? EgiaztatzeaLehenengo atalean, aurkitu nahi dugun kopurua ezezaguntzat
hartzen da eta hori x letraz adierazten da ; beste edozein letraz ere
adieraz daiteke, nahi izanez gero. Problema, bere datuak erlazionatzen
dituen ekuazioa idatziz planteatzen da.Bigarren atalean, ezezagun bateko lehen mailako ekuaziora iritsi
behar da eta gero hori askatu behar da.Azkenik, lortutako emaitza/emaitzak egiaztatu egin behar da/dira
problemak edo buruketak planteatutako egoerari erantzuten
dion/dioten ala ez ikusteko.Ebatzitako adibideak.2. Ebatzi ondoren adierazten diren buruketak :a) 50 batuta, zein zenbakik ematen du 218?Planteamendua: Aurkitu nahi dugun zenbakiari x deituko diogu eta ekuazio hau idatziko dugu : Ebazpena:
Ebazpena: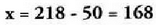 Egiaztapena : Kalkulatutako zenbakiari 50 batuta, 218 ematen digu.
Egiaztapena : Kalkulatutako zenbakiari 50 batuta, 218 ematen digu. b) Aurkitu hiru zenbaki bakoiti jarrai, hiruen batura 459
dutenak.Planteamendua : aurkitu nahi ditugun zenbakietako lehenengoari
x deituko diogu, hurrengoari x+2 eta hirugarrenari x+4. Ondoren,
ekuazio. hau idatziko dugu : x + x + 2 + x + 4 = 459.Ebazpena: 3x + 6 = 4593x=459-6=453
b) Aurkitu hiru zenbaki bakoiti jarrai, hiruen batura 459
dutenak.Planteamendua : aurkitu nahi ditugun zenbakietako lehenengoari
x deituko diogu, hurrengoari x+2 eta hirugarrenari x+4. Ondoren,
ekuazio. hau idatziko dugu : x + x + 2 + x + 4 = 459.Ebazpena: 3x + 6 = 4593x=459-6=453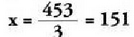 Egiaztapena. Kalkulatutako zenbakiak batuta, 459 lortzen da.151 + 153 + 155 = 459c) Pedrok, bere aitak baino 28 urte gutxiago ditu. Hemendik
hamabost urtera, Pedrok halako bi urte izango ditu aitak.
Egiaztapena. Kalkulatutako zenbakiak batuta, 459 lortzen da.151 + 153 + 155 = 459c) Pedrok, bere aitak baino 28 urte gutxiago ditu. Hemendik
hamabost urtera, Pedrok halako bi urte izango ditu aitak.
Zein da une honetan bakoitzak duen adina?Planteamendua: Ebazpena :
Ebazpena : Egiaztapena :
Egiaztapena : Aitaren adina hain zuzen ere, semearenaren bikoitza izango da.d) Laukizuzen baten altuera, oina baino 4 m txikiagoa da.
Aitaren adina hain zuzen ere, semearenaren bikoitza izango da.d) Laukizuzen baten altuera, oina baino 4 m txikiagoa da.
Altura 8 m handitu eta oina 3 m txikituz gero, laukizuzen berri bat ateratzen da eta azken honen azalera, hasierakoaren azalera baino handiagoa da. kalkulatu hasierako laukizuzenaren neurriak.
handiagoa da. kalkulatu hasierako laukizuzenaren neurriak. Ebazpena:
Ebazpena: Laukizuzenaren neurriak : oina = 10 eta altura = 6Egiaztapena.Lehenengo laukizuzenaren azalera :
Laukizuzenaren neurriak : oina = 10 eta altura = 6Egiaztapena.Lehenengo laukizuzenaren azalera : Bigarren laukizuzenaren azalera :
Bigarren laukizuzenaren azalera : Azaleren aldea edo diferentzia :
Azaleren aldea edo diferentzia : e) Beren artean 500 km-ko distantzia duten bi hiritatik, une
berean irten dira bi tren norabide berean eta aurkako
norantzetan, elkarrekin topo egiteko asmoz. Lehenengoa,
batez besteko 75 km/h lastertasunez doa eta bigarrena
berriz batez besteko 50 km/h lastertasunez. Non elkartuko
dira? Zenbat denboran ibiliak izango dira?Planteamendua :
e) Beren artean 500 km-ko distantzia duten bi hiritatik, une
berean irten dira bi tren norabide berean eta aurkako
norantzetan, elkarrekin topo egiteko asmoz. Lehenengoa,
batez besteko 75 km/h lastertasunez doa eta bigarrena
berriz batez besteko 50 km/h lastertasunez. Non elkartuko
dira? Zenbat denboran ibiliak izango dira?Planteamendua : Ibilbidea guztira = A-k egindako ibilbidea + B-k egindakoaHigidura zuzen uniformean (berdinbanatuan), ibilbidea edo
espazioa = abiadura. denbora.Ibilbideko zati desberdinentzat hori erabilita, hau ateratzen da :
Ibilbidea guztira = A-k egindako ibilbidea + B-k egindakoaHigidura zuzen uniformean (berdinbanatuan), ibilbidea edo
espazioa = abiadura. denbora.Ibilbideko zati desberdinentzat hori erabilita, hau ateratzen da : Ebazpena:
Ebazpena: Beraz, abiatu direnetik 4 ordura eta A trena irten den hiritik
300 km-ra elkartuko dira, izan ere, tren horrek ibilitako bidea 75
km/h. 4 h = 300 km baita.Egiaztapena :A trenak egindako bidea =
Beraz, abiatu direnetik 4 ordura eta A trena irten den hiritik
300 km-ra elkartuko dira, izan ere, tren horrek ibilitako bidea 75
km/h. 4 h = 300 km baita.Egiaztapena :A trenak egindako bidea =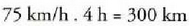 B trenak egindako bidea = 50 km/h. 4 h = 200 km
B trenak egindako bidea = 50 km/h. 4 h = 200 km Ibilbidea (espazioa) guztira = 200 km + 300 km = 500 km
Ibilbidea (espazioa) guztira = 200 km + 300 km = 500 km
- Proposatutako ariketak
2. Ebatzi ondoren adierazten diren buruketa hauek.. ) Josuk, Dabidek baino 18 urte gehiago ditu eta orain
hiru urte hark halako bi zituen. Kalkulatu gaur egun
biek dituzten adinak.. ) Zatiki baten izendatzailea, zenbakitzailea baino 5 unitate
handiagoa da. Zatiki horretan zenbakitzaileari 20
unitate batzen bazaizkio eta izendatzaileari 7, hasierako
zatikiaren alderantzizkoa ateratzen da.c) Mendizale talde batek, Cares errekaren ibilbidea (21
km) egitea erabaki du eta ibilbidearen bi muturretatik
abiatzen dira bi taldetan. Elkarrekin topo egitean, autoen
giltzak trukatzeko asmoa dute. Lehenengo taldea,
goizeko Betan iritsi da Poncebos-a (abiapuntuetako
batera) eta berehala abiatu da 4 km/h batez besteko lastertasunez.
Bigarren taldea ordea, goizeko 9etan hasi da
ibilbidean ibiltzen 4,5 km/h lastertasunez. Non elkartuko
dira? Zenbat denbora egina izango dute ibilian
elkartu arte?d) Lapur batek bitxitegi bati eraso ondoren, harrapakinak
zakuratu eta 80 km/h lastertasunez ihes egin du. Bitxijabeak,
telefonoz dei egin du hurbileneko polizitegira
eta lapurra baino 10 minutu geroago, polizi talde bat
abiatu da ibilbidearen norabide berean eta dirudienez
norantza berberean. Lapurra 50 km-ra atxilotu nahi
badute, zein izan behar du poliziek eraman beharreko
batez besteko lastertasuna?e) Migelen aitak, semea baino hiru aldiz zaharragoa da,
baina hemendik 14 urtera, Migel baino bi bider zaharrago
baizik ez da izango. Zer adin du gaur egun bietako
bakoitzak?f) Aita batek bere testamentua egin du eta bere kapitalaren
laurdena utzi dio seme zaharrenari. Bigarrenari, gainerakoaren
erdia utzi dio eta hirugarrenak berriz, banatutako
kopuruaren herena jaso du. Gainerako
hondarra, Gobernuz Kanpoko Erakunde (GKE) bati
utzi dio ; azken honek 600.000 pta. jaso ditu. Kalkulatu
banatu duen kapitalaren kopurua eta seme bakoitzari
utzitakoa.
IV B.1. Bigarren mailako ekuazioa.
Bere gaiak laburtu ondoren itxuran azaltzen den ezezagun bateko bigarren mailako ekuazio deritzo ; x da ezezaguna eta a, b eta c berriz zenbaki errealak
itxuran azaltzen den ezezagun bateko bigarren mailako ekuazio deritzo ; x da ezezaguna eta a, b eta c berriz zenbaki errealak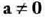 dela.
dela.
IVB.2. Bigarren mailako ekuazio-motak.
Bigarren mailako ekuazioak, era hauetakoak izan daitezke :? Osoak, eta
eta badira.? Ezosoak
badira.? Ezosoak
IV B.3. Bigarren mailako ekuazio osoen ebazpena.
Ezezagun bateko bigarren mailako ekuazio osoaren ebazpena
ematen duen formula ezartzeko, ondoren aipatzen diren eragiketak
egingo dira hurrenez hurren, harik eta lehenengo aldean binomioaren
karratua izatea lortzen den arte.Bedi bigarren mailako ekuazio hau : ? Lehendabizi, bi aldeak 4a-z biderkatzen dira eta hau ematen du :
? Lehendabizi, bi aldeak 4a-z biderkatzen dira eta hau ematen du : ? Ondoren, gai askea aldez aldatzen da eta honako hau ateratzen
da :
? Ondoren, gai askea aldez aldatzen da eta honako hau ateratzen
da : ? Segidan,
? Segidan, gehitzen zaie bi aldeei :
gehitzen zaie bi aldeei : Lortutako berdintzan, lehenengo aldea,
Lortutako berdintzan, lehenengo aldea, binomioaren karratua da, beraz, honela idatz daiteke :
binomioaren karratua da, beraz, honela idatz daiteke : Bi aldeen erro karratua eginda, hau ateratzen da :
Bi aldeen erro karratua eginda, hau ateratzen da : Hau da,
Hau da, eta x askatuz, aurkitu nahian gabiltzan formula orokorra lortzen da :
eta x askatuz, aurkitu nahian gabiltzan formula orokorra lortzen da : Emaitza honek adierazten digunez, bigarren mailako ekuazio
batek, bi erro edo emaitza izan ditzake, honako formula hauek emanak
:
Emaitza honek adierazten digunez, bigarren mailako ekuazio
batek, bi erro edo emaitza izan ditzake, honako formula hauek emanak
: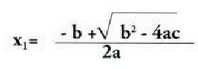 eta
eta
IV B.4. Bigarren mailako ekuazioen emaitzen izaera
 zenbaki erreala, D letraz (delta greziar letra larriz) irudikatzen da eta ekuazio edo trinomioaren diskriminatzaile edo bereizle deitzen zaio.?
zenbaki erreala, D letraz (delta greziar letra larriz) irudikatzen da eta ekuazio edo trinomioaren diskriminatzaile edo bereizle deitzen zaio.? baino bada, ax 2 + bx + c = 0 ekuazioak, bi emaitza erreal eta desberdin izan ditzake :
baino bada, ax 2 + bx + c = 0 ekuazioak, bi emaitza erreal eta desberdin izan ditzake : ekuazioak, bi emaitza erreal eta desberdin izan ditzake :
ekuazioak, bi emaitza erreal eta desberdin izan ditzake : eta
eta Emaitzak kalkulatu ondoren, lehen ikusi den moduan, bigarren
mailako ekuazioa bi faktoreen biderkaketa moduan deskonposa
daiteke :
Emaitzak kalkulatu ondoren, lehen ikusi den moduan, bigarren
mailako ekuazioa bi faktoreen biderkaketa moduan deskonposa
daiteke : ?
?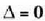 bada,
bada, ekuazioak, bi emaitza erreal eta berdin izan ditzake:
ekuazioak, bi emaitza erreal eta berdin izan ditzake: Kasu honetan, bigarren mailako ekuazioa, binomioaren karratuaz
ordezka daiteke :
Kasu honetan, bigarren mailako ekuazioa, binomioaren karratuaz
ordezka daiteke : ?
? baino bada, ekuazioak ez du emaitza errealik. Erroakzenbaki irudikariak dira.Ebatzitako ariketak.3. Aztertu ebatzi gabe ondoren ematen diren ekuazioen
emaitzen izaera.
baino bada, ekuazioak ez du emaitza errealik. Erroakzenbaki irudikariak dira.Ebatzitako ariketak.3. Aztertu ebatzi gabe ondoren ematen diren ekuazioen
emaitzen izaera. Diskriminatzailearen edo bereizlearen balioa kalkulatzen da :
Diskriminatzailearen edo bereizlearen balioa kalkulatzen da : Kasu honetan,
Kasu honetan, da. Diskriminatzailea negatiboa denez, ez dago ebazpen errealik. Emaitzak irudikariak dira.
da. Diskriminatzailea negatiboa denez, ez dago ebazpen errealik. Emaitzak irudikariak dira. Kasu honetan,
Kasu honetan, diskriminatzailearen balioa,
diskriminatzailearen balioa, da.
da.
Diskriminatzailea positiboa denez, bi emaitza erreal eta desberdin ditu. Kasu honetan,
Kasu honetan,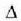 diskriminatzailearen balioa, 100-100=0 da.
diskriminatzailearen balioa, 100-100=0 da.
Diskriminatzailea zero denez, bi emaitza erreal eta berdin ditu.Ebatzitako ariketak.4. Aztertu ondoren ematen diren ekuazioen emaitzen edo
erroen izaera eta errealak badira kalkulatu. Diskriminatzailearen balioa kalkulatzen da :Kasu honeta, ,
Diskriminatzailearen balioa kalkulatzen da :Kasu honeta, , Diskriminatzailea edo bereizlea
positiboa delako, bi emaitza erreal eta desberdin ditu.Ondoren, emaitza horiek kalkulatu egin daitezke (I) formula
orokorra erabiliz :
Diskriminatzailea edo bereizlea
positiboa delako, bi emaitza erreal eta desberdin ditu.Ondoren, emaitza horiek kalkulatu egin daitezke (I) formula
orokorra erabiliz : eta
eta Diskriminatzailearen balioa kalkulatzen da :
Diskriminatzailearen balioa kalkulatzen da : Kasu honetan,
Kasu honetan, Diskriminatzailea edo bereizlea positiboa delako, bi emaitza erreal eta desberdin ditu.Jarraian, emaitza horiek, (I) formula orokorraren bitartez kalkula
daitezke :
Diskriminatzailea edo bereizlea positiboa delako, bi emaitza erreal eta desberdin ditu.Jarraian, emaitza horiek, (I) formula orokorraren bitartez kalkula
daitezke :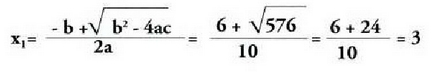 eta
eta Diskriminatzailea edo bereizlea zero denez, bi emaitza erreal eta
berdin ditu. Honako hauek dira :
Diskriminatzailea edo bereizlea zero denez, bi emaitza erreal eta
berdin ditu. Honako hauek dira : Lehendabizi, ekuazioa laburtu eta ordenatu egiten da, gai koadratikoa
koefiziente positiboarekin ipiniz eta gaiak laburtuz :
Lehendabizi, ekuazioa laburtu eta ordenatu egiten da, gai koadratikoa
koefiziente positiboarekin ipiniz eta gaiak laburtuz : Ondoren, diskriminatzaile edo bereizlearen balioa kalkulatzen da :
Ondoren, diskriminatzaile edo bereizlearen balioa kalkulatzen da :
- Proposatutako ariketak
3. Aztertu ebatzi gabe ondoren ematen diren ekuazioen emaitzen izaera.
- Proposatutako ariketak
4. Ebatzi ekuazio hauek.
IV B.5. Bigarren mailako ekuazio ezosoen ebazpena.
Ekuazioa ezosoak, aurreko atalean jada ikusia dugun formula
orokorra erabiliz ebatz daitezke, baina eragiketak oro har soilagoak
dira ondoren adierazten den moduan zuzenean ebazten badira.A) erako ekuazioak.Ekuazio-mota hau ebazteko, urrats hauek jarraitzen dira :? Lehendabizi x faktore komuna ateratzen da :
erako ekuazioak.Ekuazio-mota hau ebazteko, urrats hauek jarraitzen dira :? Lehendabizi x faktore komuna ateratzen da : ? Bigarren, biderkadura zero izan dadin, biderkatzaileetako batek
zero izan behar du, hau da, :x = 0 edota ax + b = 0. Emaitzak beraz,
? Bigarren, biderkadura zero izan dadin, biderkatzaileetako batek
zero izan behar du, hau da, :x = 0 edota ax + b = 0. Emaitzak beraz, dira.B)
dira.B) erako ekuazioak.Ekuazio mota hau ebazteko,? Lehenik,
erako ekuazioak.Ekuazio mota hau ebazteko,? Lehenik,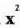 askatuz hasten da ; orduan, honako hau lortzen da :
askatuz hasten da ; orduan, honako hau lortzen da : ? Ondoren, bi aldeen erro karratua egiten da eta hau gelditzen da:
? Ondoren, bi aldeen erro karratua egiten da eta hau gelditzen da: Emaitzak, honako hauek dira :
Emaitzak, honako hauek dira : eta
eta Emaitza horiek errealak izando dira, baldin eta a-k eta c-k alderantzizko zeinuak badituzte, izan ere, beren zeinuak berdinak badira, emaitzak, irudikariak izango baitira.Ebatzitako ariketak.5. Ebatzi bigarren mailako ekuazio hauek :
Emaitza horiek errealak izando dira, baldin eta a-k eta c-k alderantzizko zeinuak badituzte, izan ere, beren zeinuak berdinak badira, emaitzak, irudikariak izango baitira.Ebatzitako ariketak.5. Ebatzi bigarren mailako ekuazio hauek : Emaitzak honako hauek dira :
Emaitzak honako hauek dira : Emaitzak honako hauek dira :
Emaitzak honako hauek dira : Emaitzak honako hauek dira :
Emaitzak honako hauek dira : eta
eta Emaitzak honako hauek dira :
Emaitzak honako hauek dira :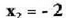 eta
eta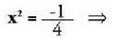
- Proposatutako ariketak
5. Ebatzi bigarren mailako ekuazio hauek.
IV. B.6 Bigarren mailako ekuazioen erroen eta koefizienteen arteko erlazioa.
Formula orokorraren emaitzak eragiketa soil batzuen menpe jartzen
direnean zer gertatzen den ikusiko dugu.? Lehendabizi, emaitzen batura kalkulatuko dugu : Bigarren mailako ekuazio baten emaitzen batura, letrazko gaiaren
eta gai koadratikoaren zatidura da zeinuz aldatuta.? Orain, emaitzen biderkadura kalkulatuko dugu :
Bigarren mailako ekuazio baten emaitzen batura, letrazko gaiaren
eta gai koadratikoaren zatidura da zeinuz aldatuta.? Orain, emaitzen biderkadura kalkulatuko dugu : Bigarren mailako ekuazio baten emaitzen biderkadura, gai askearen
eta gai koadratikoaren zatidura da.Ebatzitako ariketak.6. Kalkulatu ondoren ematen diren ekuazioen emaitzen baturak eta biderkadurak.. )
Bigarren mailako ekuazio baten emaitzen biderkadura, gai askearen
eta gai koadratikoaren zatidura da.Ebatzitako ariketak.6. Kalkulatu ondoren ematen diren ekuazioen emaitzen baturak eta biderkadurak.. ) Batura
Batura Biderkadura
Biderkadura b)
b) Batura
Batura Biderkadura
Biderkadura
- Proposatutako ariketak
6. Kalkulatu ondoren ematen diren ekuazioen emaitzen baturak eta biderkadurak.
I V.C. Bigarren mailako ekuazioetara labur daitezkeen ekuazioak
I V. C.1. Ekuazio bikoadratikoak edo bikoadratuak.
Ekuazio bikoadratikoak edo bikoadratuak, laugarren mailako ekuazioak dira, baina ez dute maila bakoitiko gairik. Honako itxura honekin azaltzen dira : Ebazteko, bigarren mailako ekuazio bihurtzen dira ordezkapen hauek eginda :
Ebazteko, bigarren mailako ekuazio bihurtzen dira ordezkapen hauek eginda : Orduan, ebatzi behar den ekuazioa,
Orduan, ebatzi behar den ekuazioa, da.Ekuazio horrek, lehen ikusi denaren arabera, bi emaitza ditu :
da.Ekuazio horrek, lehen ikusi denaren arabera, bi emaitza ditu : Aurkitu nahi ditugun x-en balioak lortzeko, z-rentzat kalkulatutako
balioen erro karratua egingo dugu. Hau da :
Aurkitu nahi ditugun x-en balioak lortzeko, z-rentzat kalkulatutako
balioen erro karratua egingo dugu. Hau da :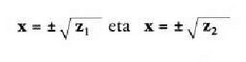 Ekuazio bikoadratikoak beti ere lau emaitza ditu eta
horietatik batzuek edota denak irudikariak izan daitezke.Ebatzitako ariketak.7. Kalkulatu ondoren ematen diren ekuazioen emaitzak.. )
Ekuazio bikoadratikoak beti ere lau emaitza ditu eta
horietatik batzuek edota denak irudikariak izan daitezke.Ebatzitako ariketak.7. Kalkulatu ondoren ematen diren ekuazioen emaitzak.. ) .
. eta
eta ordezkapenak egiten dira. Ateratzen den ekuazioa honako hau da:
ordezkapenak egiten dira. Ateratzen den ekuazioa honako hau da: ; hor, a=4, b = -5 eta c=1 dira.Diskriminatzaile edo bereizlearen balioa kalkulatuko dugu :
; hor, a=4, b = -5 eta c=1 dira.Diskriminatzaile edo bereizlearen balioa kalkulatuko dugu : Kasu honetan,
Kasu honetan, Diskriminatzailea positiboa denez, emaitzak, honako hauek dira :
Diskriminatzailea positiboa denez, emaitzak, honako hauek dira : x-en balioak honako hauek dira :
x-en balioak honako hauek dira : b)
b) .
. eta
eta ordezkapenak egiten dira. Ateratzen den ekuazioa honako hau da :
ordezkapenak egiten dira. Ateratzen den ekuazioa honako hau da : , hor, a=1, b=13 eta c=36 dira.Diskriminatzaile edo bereizlearen balioa kalkulatuko dugu :
, hor, a=1, b=13 eta c=36 dira.Diskriminatzaile edo bereizlearen balioa kalkulatuko dugu : Kasu honetan,
Kasu honetan, . Diskriminatzailea positiboa denez, emaitzak, honako hauek dira :
. Diskriminatzailea positiboa denez, emaitzak, honako hauek dira : x-en balioak honako hauek dira :
x-en balioak honako hauek dira :
- Proposatutako ariketak
7. Kalkulatu hondoko ekuazio hauen emaitzak.
IV C.2. Ekuazio irrazionalak.
Lehenago ikusi den moduan, ekuazio irrazionalak, ezezaguna
erro-ikurpean dutenak dira.Gauza jakina da noski, ekuazio baliokideak, emaitza berberak
dituztenak direla. Ikusi ere ikusia dugu, ekuazio baliokideak lortzeko,
nahikoa dela ekuazioaren bi aldeei adierazpen berbera batzea
edo kentzea. Era berean ekuazioaren bi aldeak ere adierazpen
berberaz biderka edo zati daitezke emaitzak deusik ere aldatu
gabe.Baina, zer gertatzen da ekuazio baten bi aldeen karratua
jartzen denean? Ekuazio berriak, emaitza berberak al ditu?
Erantzuna: ez beti. Ekuazio baten bi aldeen karratua idazten
denean, beste ekuazio bat lortzen da eta oro har ez da izan ohi
lehenengoaren baliokidea; halere ordea, lehenengo ekuazioko
emaitza oro, bigarrenekoa ere izaten da. Aldiz, bigarreneko
emaitza oro ez da beti lehenengoaren emaitza. Ekuazioaren bi
aldeen karratua egitean sartzen diren emaitza berri horiei, emaitza
arrotz deritze.Ondoren, adibide bat ebatzitako da esandakoa argitzeko.Bedi 3x = 12 ekuazioa. Ekuazio horren emaitza x = 4 da.Egin ditzagun orain ekuazioaren bi aldeen karratuak : Azken ekuazio hori ebatziz gero, emaitza hauek ateratzen dira :
Azken ekuazio hori ebatziz gero, emaitza hauek ateratzen dira :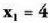 eta
eta - 4 zenbakia,
- 4 zenbakia, ekuazioaren emaitza da, baina ez da 3x =
12 ekuazioarena. Kasu horretan, -4, karratua kalkulatzean sartutako
emaitza arrotza dela esaten da.Aurrez esanarekin, kontuan hartu behar da, alegia, ekuazio
bat ebaztean ekuazioaren bi aldeen karratua kalkulatu
beharra baldin badago, gero, ematen dituen emaitzak
egiaztatu beharra dagoela, hasierako ekuazioa betetzen ez
duten emaitza arrotzak baztertzeko.Ekuazio razionalak ebazteko, ondoren adierazten den
moduan jokatu behar da :1. Aldeetako batean, errokizuna duen gaia bereizi egin
behar da.2. Ekuazioaren bi aldeen karratuak kalkulatu eta idazten
dira.3. Lortutako ekuazioa ebazten da.4. Ateratako emaitzek hasierako ekuazioa betetzen
duten ikusi behar da. Betetzen ez dutenak baztertu
egin behar dira.5. Aurrez esandakoaren arabera jokatzean, ekuazioa
errokizunik gabe gelditzen ez bada, berriro ere era
berean jokatzen da letik 4rako urratsak errokizunak
desagertu arte behar adina aldiz errepikatuz.Ebatzitako ariketak.8. Ebatzi ekuazio irrazional hauek. Adierazi emaitza arrotzik
dagoen ala ez.
ekuazioaren emaitza da, baina ez da 3x =
12 ekuazioarena. Kasu horretan, -4, karratua kalkulatzean sartutako
emaitza arrotza dela esaten da.Aurrez esanarekin, kontuan hartu behar da, alegia, ekuazio
bat ebaztean ekuazioaren bi aldeen karratua kalkulatu
beharra baldin badago, gero, ematen dituen emaitzak
egiaztatu beharra dagoela, hasierako ekuazioa betetzen ez
duten emaitza arrotzak baztertzeko.Ekuazio razionalak ebazteko, ondoren adierazten den
moduan jokatu behar da :1. Aldeetako batean, errokizuna duen gaia bereizi egin
behar da.2. Ekuazioaren bi aldeen karratuak kalkulatu eta idazten
dira.3. Lortutako ekuazioa ebazten da.4. Ateratako emaitzek hasierako ekuazioa betetzen
duten ikusi behar da. Betetzen ez dutenak baztertu
egin behar dira.5. Aurrez esandakoaren arabera jokatzean, ekuazioa
errokizunik gabe gelditzen ez bada, berriro ere era
berean jokatzen da letik 4rako urratsak errokizunak
desagertu arte behar adina aldiz errepikatuz.Ebatzitako ariketak.8. Ebatzi ekuazio irrazional hauek. Adierazi emaitza arrotzik
dagoen ala ez. Azken ekuazio honen emaitzak, honako formula honen bidez kalkulatzen dira :
Azken ekuazio honen emaitzak, honako formula honen bidez kalkulatzen dira : beraz,
beraz, Hasierako ekuazioa egiaztatzean,
Hasierako ekuazioa egiaztatzean, emaitza arrotza dela ikusten da. Proposatutako ekuazio razionalaren emaitza,
emaitza arrotza dela ikusten da. Proposatutako ekuazio razionalaren emaitza,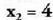 dela ikusten da, izan ere,
dela ikusten da, izan ere,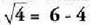 baita.
baita. Azken ekuazio honen emaitzak, formula honen bitartez kalkulatuko
ditugu :
Azken ekuazio honen emaitzak, formula honen bitartez kalkulatuko
ditugu : beraz,
beraz,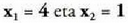 Hasierako ekuazioan egiaztatzean,
Hasierako ekuazioan egiaztatzean, proposatutako ekuazioaren emaitza dela egiaztatzen da. Emaitza arrotza, kasu honetan,
proposatutako ekuazioaren emaitza dela egiaztatzen da. Emaitza arrotza, kasu honetan, da, izan ere,
da, izan ere,
- Proposatutako ariketak
8. Ebatzi ekuazio irrazional hauek. Adierazi erro arrotzik dagoen ala ez.
V. Bigarrena baino maila handiagoa duten ekuazioak.
Bigarrena baino maila handiagoa duten ekuazioak baina bikoadratikoak
ez direnak ebazteko, liburu honek helburua baino harago
dauden prozedurak eta metodoak erabiltzen dira, beraz, aljebrako
testu berezituak kontsultatu beharko dira horretarako.Hala ere ordea, badaude ekuazioak, emaitza osoak dituztenak eta
Ruffiniren araua erabiltzeko aukera ematen dutenak, beraz, polinomioa
faktoreetan deskonposatzea, ekuazio ebazpenerako sistema
gisa ere erabil daiteke.Hala bada, bedi P(x) = 0 ekuazioa.Ekuazioaren lehen aldea osatzen duen P(x) polinomioa, faktoretan deskonposatzen bada, honako hau izango dugu  :
: edota gauza bera dena:
edota gauza bera dena: 
 dela.Jada ikusia denez, ekuazioaren bigarren aldea zero izan dadin, nahikoa da faktore horietako edozeinek zero balio izatea. Beraz,
dela.Jada ikusia denez, ekuazioaren bigarren aldea zero izan dadin, nahikoa da faktore horietako edozeinek zero balio izatea. Beraz,
 ekuazioaren emaitzak izango dira, izan ere,
ekuazioaren emaitzak izango dira, izan ere,
 balioek polinomioari zero balioa ematen baitiote.Ebatzitako ariketak.9. Ebatzi ekuazio hauek.
balioek polinomioari zero balioa ematen baitiote.Ebatzitako ariketak.9. Ebatzi ekuazio hauek.
a)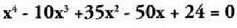 Ebazpena: Polinomioa Ruffini-ren araua erabiliz deskonposatzen da XI. atalean ikusi den moduan eta honako hau lortzen da :
Ebazpena: Polinomioa Ruffini-ren araua erabiliz deskonposatzen da XI. atalean ikusi den moduan eta honako hau lortzen da : . Emaitzak, honako hauek dira :
. Emaitzak, honako hauek dira :
 .. )
.. ) Ebazpena: Polinomioa Ruffiniren araua erabiliz deskonposatzen da eta hau lortzen da:
Ebazpena: Polinomioa Ruffiniren araua erabiliz deskonposatzen da eta hau lortzen da: Beraz, emaitzak hauek dira:
Beraz, emaitzak hauek dira: 
- Proposatutako ariketak
9. Ebatzi ekuazio hauek.
V. Bi ezezaguneko ekuazioak
vA.1. bi ezezaguneko lehen mailako ekuazioak
Bi ezezaguneko lehen mailako ekuazio bat berdintza bat da.
Ekuazio horrek bi ezezagun ditu, x eta y gehienetan, eta terminoak,
gehienez ere, lehen mailakoak ditu.Horrela adierazten da : , esate baterako
, esate baterako Bi ezezaguneko lehen mailako ekuazio batean, berdintza betetzen
duten balio pare guztiak (x,y) izan daitezke ekuazio horren emaitza.
Bi ezezaguneko lehen mailako ekuazio batean, berdintza betetzen
duten balio pare guztiak (x,y) izan daitezke ekuazio horren emaitza. adibidean ondoren azaltzen diren pareek berdintza egiaztatzen dute, beraz, ekuazioaren emaitza dira :
adibidean ondoren azaltzen diren pareek berdintza egiaztatzen dute, beraz, ekuazioaren emaitza dira :
V. A. 2 bi ezezaguneko lehen mailako ekuazio sistemak
Bi ekuaziok edo gehiagok sistema bat osatzen dutela esaten da,
baldin eta ekuazio horiek emaitza komuna badute. Emaitza
komun horiek dira sistemaren emaitza.Sistema bat ebaztea sistema horren emaitzak aurkitzea da. Eragiketa
hori egitean gerta daiteke :Sistemak emaitzarik ez izatea ; hala denean sistema bateraezina
dela esaten da.? Sistemak emaitza izatea; sistema bateragarria dela esaten da.
Baina sistema horrek edo emaitza bakarra du, eta sistemari
bateragarri mugatu esaten zaio halakotan, edo emaitza infinituak
ditu, eta orduan bateragarri mugagabe esaten zaio sistemari
.
















































































