Matematika»Aritmetika

2. Atala

Erroak eta berreketak.

Zenbaki erreala

I. Berreketak

Aurreko atalean, batuketa baten errepikatzeak biderkaketa definitzera eraman gaitu. Era berean, berreketaren ideia ekarriko digu biderkaketaren errepikatzeak. Zenbaki bat hartzen badugu, 2 adibidez, eta zenbaki horrez berorrez bost aldiz biderkatu nahi badugu,, eragiketa hori, laburturik, 25 idazten da, eta esaten da bi oinarriko eta bost berretzaileko berreketa dela, edo, besterik gabe, bi ber bost esaten da. Oinarria 2 izateak biderkatu behar den zenbakia 2 dela adierazten du, eta berretzailea 5 izateak, bost aldiz biderkatu behar dela oinarri hori. Berretzailea oinarriaren ondoren idazten da, goraxeago eta txikixeago. Hala adibidez :Definizio honek edozein eratako zenbakientzat balio du, natural, oso, arrazional, erreal nahiz konplexuentzat. Adibide baterako :Zenbaki errealak eta konplexuak alde batera utzirik, oraindik ez baitira definitu, hau da berretzaile naturaleko berreketaren definizio orokorra :Baldin badituguzenbaki bat eta beste bat,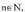, a oinarriko eta n berretzaileko berreketa dena, eta an adierazten eta ber n irakurtzen dena, hau izango da ondorengo biderkaketa :Bereziki,hartzen da.Berreketen zeinuaBaldin eta berreketaren oinarria positiboa bada, emaitza positiboa izango da beti. Oinarria negatiboa bada, emaitza negatiboa izango da berretzailea bakoitia denean, eta positiboa berretzailea bikoitia denean. Biderkaketaren zeinuen erregelaren ondorioa da hori, + bider + plus baita, + bider -, minus, eta - bider -, plus.• Adibidez:Hitzarmenez, berreketaren eragiketa zeinu aldaketarena baino lehenago egiten da; alegia,badago idatzirik, hau izango da emaitza :baina,badago idatzia, beste hau izango da :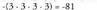Adierazpen idatzietan, berretzaileak azpian duen zenbakiari bakarrik eragiten dio. Zenbaki negatiboa hartu nahi bada oinarritzat, parentesi artean ipini behar da.• Adibidez:Garrantzitsua da hori berretzaile bikoitientzat, ezen emaitza zeinuz aldatzen baita. Berretzaileak bakoitiak direnean, emaitza negatiboa izango bi kasuetan. Hala adibidez :

Berretzaile naturaleko berreketen ezaugarriak

Definiziotik beretik, ondorengo tasun edo ezaugarri hauek ateratzen dira :Oinarri bereko berreketak biderkatzeko, berretzaileak batu egiten dira.

Izan ere,Hortaz,9 Adibidez :Izan ere,Berreketa bat beste batez berretzeko, berretzaileak biderkatu egiten dira.

Izan ere,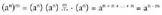Berreketaren definizioak justifikatzen du lehen urratsa, eta bigarren urratsean behin eta berriz aplikatzen da aurreko ezaugarria.• Adibidez: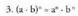Izan ere,Aurreneko berdintza berreketaren definiziotik ondorioztatzen da, eta biderkaketaren trukakortasun legetik bigarrena.• Adibidez :Berdintza hau, zenbaitetan, kontrako zentzuan ere aplikatzen da, alegia, zenbait berreketaren biderkaketa berreketa bakarra bihurtzeko, berreketa horren oinarria oinarrien biderkaketa dela, honela adibidez:Ezaugarri hau hirugarrenaren kasu berezitzat har daiteke, b-ren ordez 1/b jartzen baldin bada.• Adibidez :

Berretzaile negatiboa

Berretzaile negatiboekin ere erabil daiteke berretzaile naturaleko berreketa, berreketek zatiketan nola jokatzen duten azterturik.

Hau gertatzen da:Bestalde, berretzaileen arteko diferentzia 2 da : 5 - 3 = 2Emaitza ez da oinarriaren araberakoa :eta 5 - 2 = 3.Oro har, oinarria berbera baldin bada, eta zenbakitzailearen berretzailea izendatzailearena baino handiagoa baldin bada, zenbakitzailearen eta izendatzailearen biderkagaiek elkar sinplifikatzen dute, eta oinarria berretzaileen arteko kendurak berreturik geratzen da. Oinarria zenbaki arrazionala denean, edozein, (a), baina ez zero, eta m>n delarik, hau betetzen da :Izendatzailearen berretzailea zenbakitzailearena baino handiagoa baldin bada, orduan orobat sinplifika daiteke, baina berretzaile bat geratuko da izendatzailean :Halakoetan,Oro har, baldin n>m bada, biderkagaiak sinplifikatu egiten dira, eta hau betetzen da :Aurrekoa ikusirik, hau proposa daiteke berretzaile negatiboentzat :Baina kasu horretan,behar du izan• Adibidez:Oinarriaren zeinuek berretzaile positiboek bezala eragiten diote emaitzari :

Berretzaile nulua

Zenbakitzaileko eta izendatzaileko berretzaileak berberak badira, zatiketaren emaitza bat izango da beti :Berreketa edozein izanik ere, beti betetzen da berdintza hau :Horregatik, aurreko definizioak zabaldu eta berretzailea zero den kasua ere kontuan hartzen da, honela :• Adibideak:Berretzaileak negatiboak edo nuluak direnean ere, beste kasuetan bezala, adierazpen idatzietan, zeinu aldaketa baino lehen egiten da berreketa, eta, hortaz :Baina,Laburtuz, a-ren enegarren berreketa definitzen da, etaidazten,etadirelarik, hemen bezala: baldin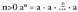bada,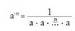Baldin n=0 bada, aO = 1Hortaz, baita berretzaileak negatiboak eta nuluak direnean ere, berreketen ezaugarriak, edozein berretzaile oso izanik ere, berretzaile naturalak dituzten berreketenak berberak dira; nolanahi ere, aurrenekoaribeste bat eranstea komeni da, zatiketarako baliokide dena:• Adibidez :Tasun horiek baliatuz, berreketa arteko eragiketak sinplifika daitezke . Adibidez :Biderkaketa eta zatiketetan, oinarri bera eduki beharra dago, sinplifikatu ahal izateko ; izan ere,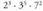adierazpenak ez du sinplifikazio argirik. Berreketen batuketak edo kenketak direnean, askoz ere urriagoak dira sinplifikatzeko aukerak, nahiz eta batzuetan biderkagai komuna kalkula daitekeen, eta era horretan adierazpen bakunagoa lortu. Adibidez :ez da sinplifikatzenBatuketa denean, edo kenketa, berretzen dena, lehenbizi batuketa egitea izaten da errazena :Batuketa, edo kenketa, aljebrako partean ikusiko den bezala, ezin egin denean, Newtonen binomioarena deritzan formula aplikatu behar da. Batuketa baten koadroarentzat, hau da emaitza :Kenketa batentzat:Banatze legea aplikatuz oso erraz froga daitekeen bezala. Hauxe da berdintza honen azalpen geometrikoa :Hau da a+b aldearen koadroa : a aldeko koadroa gehi b aldea duen lauki bat, gehi axb bi lauki zuzen.

II. Erroak

Erro koadroa aurkitzea berreketaren alderantzizko eragiketa da.

Hala, baldin etabadaukagu, 4-ren erro koadroa bi dela esaten da, eta honela idazten da :.

.etadirenez gero, orobat esaten da 2 8ren erro kuboa dela, edo 32ren erro bosgarrena, eta honela idazten da :Oro har, a zenbaki baten n errotzaileko erro (etaizanik) esaten zaio (izanik, aurrerago ikusiko diren salbuespen zenbaitekin), x-ek n-z berreturik a emango duen x kopuru bati.Erroketa egiten zaion zenbakiari errokizun esaten zaio ; eta errotzaile, errokizuna lortzeko emaitza zenbat aldiz berretu behar den adierazten duen n zenbakiari. x kopurua erroketaren emaitza da, hau da, erroa. Erro koadroetan 2 errotzailea ez da adierazi beharrik izaten. 3 errotzaileko erroketei kubo deritzaie, eta gainerakoei n-garren ; kasu horietan, 3 bat edo n bat idazten da erroketaren ikurrean errotzailea zehazteko.• Adibidea:Kalkula itzazu erro hauek :

Errokizunaren eta erroen zeinuak

Edozein delarik ere errotzailearen balioa, bi kasu bereizi behar dira. n bakoitia bada,izango da ; kasu horretan, n-tar erroa duenororentzat, erro hori bakarra izango da. Baldin eta a positiboa bada, erroa ere positiboa izango da, eta a negatiboa bada, negatiboa.• Adibidez :Zeren berreketa bakoiti baten emaitzak bere oinarriak duen zeinu bera baitu.n bikoitia bada, n-z berreturiko edozein kopuruk emaitza positiboa izango du. Izan ere, edozein izanik ere x oinarriaren zeinua, zenbaki bikoitiz berretzen bada,gertatzen baita. Zenbaki ororen koadroa positiboa da, zeren eta + bider +, edota- bider-, beti ere + izango baita. Horren ondorioz, zenbaki negatibo baten errotzaile bikoitiko erroa eskatzen bada, ez dago soluzio izan daitekeen den zenbaki arrazionalik, alegia, n errotzailea bikoitia baldin bada, zenbaki positiboko erroketak bakarrik egin ahal izango dira.Zenbaki negatiboen erro bikoitiak zenbakien multzoaren beste zabaltze baten abiapuntu izango dira, zenbaki konplexuena hain zuzen ere. Hurrengo atalean aztertuko dira zenbaki horiek.Bestalde, baldin Va = x, n bikoitiarekin, n = 2k bada, orduanbeteko da.Baina, era berean, egia izan behar du honek ereizan ere-ren zeinua gorabehera,haren koadroa egitean, emaitza positiboa izango da. Hortaz, erroakerrotzaile bikoitia baldin badu, bi emaitza izango dira, kontrako zeinukoak. Baldinorobat idatz daiteke. Gauza bera gertatzen da beste edozein errotzaile bikoitirekin:eta orobatNormalean, erroaren aurretik ipintzen da hartu nahi den emaitzaren zeinua :, baina problemak ebazterakoan kontuan hartu behar dira soluzioak izan ditzakeen bi zeinuak. Hala adibidez, koadroa 4 izango duten zenbaki arrazionalak eskatzen baldin badira, +2 eta -2 izango da erantzuna, ez +2 bakarrik. Hori, batzuetan,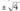edo

Notazio esponentziala eta erroketen ezaugarriak

n-garren erroaren definiziotik, hau ondorioztatzen da:Bestalde, berreketetan ikusi denez :Hortaz, erro bat berretzaile gisa adierazi nahi baldin bada, halako x kopurua izan beharko du, non; hortazeta horren ondorioz :Alegia, honela adierazten da erroketa :Erroketak egiterakoan notazio hau erabiliz, zatikizko berretzailea duten berreketak balira bezala har daitezke erroak. Baliokidetasun hori erroen ezaugarriak aztertzean egiaztatzen da.Hauek dira erroketen ezaugarri nagusiak :1.izan ere, baldinbada, honengatik gertatzen da:. Bestalde, baldinbada, honengatik gertatzen da :, etabada, honengatik:. Balioak ordezkatuz,eta hortik x=z.Berdintza horiek guztiak erroketan zeinu bera dutelakoan hartzen dira, baldin errotzailea bikoitia bada, eta erroketak bi emaitza baditu .• Adibidez :2.Honen ondorio da :• Adibidez :Ezaugarri horretatik, hau ondorioztatzen da :• Adibidez :Hori frogatzeko, aski da bigarren ezaugarria behar adina aldiz aplikatzea. Baldin eta a-ren ene-garren erroa, a oinarria eta 1 /n berretzailea dituen berreketa gisa hartzen bada, ezaugarri hauek guztiak berreketetan aurkitu diren ezaugarrien orokortzeak izango dira :

Erroketen sinplifikatzea eta beste eragiketak

Zenbait erroren adierazpena sinplifikatu daiteke errotzailea txikituz, baldin eta errokizuna errotzailearen zatitzaile den berretzaileko berreketa baten gisara ipini badaiteke. Izan ere,idatz badaiteke, hau lortuko dugu :, erroen lehenengo ezaugarria eta erroaren definizioa apli atuz.• Adibidea:Bereziki, errokizunaren biderkagaiak atera daitezke, komeni baldin bada :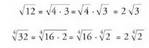Gauza bera da zatikizko berretzaile moduan adierazitako erro bat eta berretzailearen zatikia sinplifikatzea :Erroketen tasunek errazago bihurtzen dituzte euren arteko biderkaketak eta zatiketak. Batuketak eta kenketak, berreketen kasuan bezalaxe, zailagoak dira sinplifikatzen.Errotzaile bereko erroen biderkaketak edo zatiketak izan ezkero, errokizunak biderkatuz edo zatituz burutzen da eragiketa :Zatiketetan ere gisako propietate bat betetzen da.• Adibidea :Aldiz,ezin da burutu, ezberdinak baitira errotzaileak.

Burutu ahal izateko errotzaile bereko erro gisa jarri beharko lirateke biderkagaiak. Bada hori egiteko modu erraz bat, kontuan hartuz ezen,Berdintza hori aplikatuz berretzaile komun bat bila daiteke erroen edozein biderkaketarentzat :Eragiketa hauek orobat egin daitezke zatikizko berretzaileak erabiliz :• Adibidea :Erroen batuketan edo biderkaketan, ordea, ezin dira bat egin erroak, ezta errotzaile bera izanik ere, ez baitute berdin balio baturaren erroak eta erroen baturak :Erroaren definiziotik eta binomio baten berreduraren garapenetik ateratzen da hori :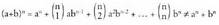Soilik baldin a edo b 0 bada da (a+O)n = an + OnBatez ere ez ahaztu ezen,Berbiduren batura eta baturaren berbidura berdinak balira Pitagorasen teorema ez litzateke beteko.Baturak bakunagoak egin daitezke baldin eta batugaietan erro bera azaltzen bada zenbait aldiz, hau da, berretzaile bera eta errokizun bera azaltzen badira. Esaterako :

Arrazionalizatzea

Erroa ateratzen denean lortzen diren balioak ez dira beti zehatzak, eta halakoetan gutxi gorabeherako kopuruak erabilitzen dira eragiketen emaitza gisa zenbakizko balio bat lortzeko. Zatiketetan, adibidez, baldin zatitzailea hurbilketazko kopuru bat bada, zifra asko hartu behar dira zehaztasunik galduko ez bada. Baina zifra asko dituen kopuru batez zatitzea eragiketa luzea eta aspergarria da, eta horregatik, halakoetan, hobe da erro guztiak zenbakitzailera pasa eta izendatzaile oso bat uztea.• Adibidez,Erroen zatiketa batean izendatzailetik erroak kentzea eragiketa arrazionalizatzea da. Gaur egun, baina, diren zatiketa zailenak ere istant batean ebatz daitezke kalkulagailuaz, eta arrazionalizatzen ibiltzeak ez du zentzurik. Nolanahi ere, oso jakingarria da zertan datzan.Izendatzailean dagoen adierazpenaren arabera egiten da arrazionalizatzea. Erro bakarra baldin badago, izendatzaileangisako adierazpena lortzeko behar den erroaz biderkatu behar dira zenbakitzailea eta izendatzailea.• Adibidea:Baldin izendatzailean bigarren erroen batuketa edo kenketa bada, formula hau baliatuz ken daiteke :• Adibidea:Ariketaka) Saia zaitez erroa bakuntzen ahalik biderkagai gehienak atereaz.8 zati berretzaile 3a ez baita zenbaki osoa, ezin bakundu gehiago.b) Ebatzi eta bakunduErrotzaile desberdinak dituzten biderkagaien biderkaketa errazago egiten da biderkagaiak bakunduz gero. Azkeneko kasuan, adibidez, honela egin beharko litzateke :Errotzaileak elkarrekin biderkatuz lortzen da zuzenean errotzaile komuna, baina adierazpenak errazagoak dira errotzaileen multiplo komunetan txikiena hartuz gero, azkeneko kasuan egin den bezala, non 12 hartu baita, eta ez 24, errotzaile komuntzat.Batuketa hau ezin da bakundu : errokizunak, 3, berretzaile ezberdinak baititu, eta erroek errotzaile ezberdinak.c) Arrazionalizatu

Berredurak eta erroak kalkulagailuz

Edozein kalkulagailuk, den sinpleenak ere, berredurak eta erroak kalkulatzeko aukera eskaintzen du.Erroa kalkulatzeko sakatu beharreko giltza edo teklanikurra azaltzen da.Lehenbizi zenbakia idazten da eta gero erroaren giltza sakatzen Adibidez, sakatu, eta 4 azalduko da pantailan.

Berrizjoz gero 2 azalduko da. Errotzailetzat 2ren berredurak dituzten erroak kalkulatzen dira horrela. Kalkulagailu batzuetan [=] giltza sakatu behar da emaitza azalduko bada.Zenbaki bat ber bi egiteko, lehenbizi zenbakia idatzi behar da, etaadierazten duen giltza sakatu gero. Ordea,funtzioa giltzaren bigarren aukera gisa azaltzen bada, edo [Shik] edo [Inv] sakatu beharko dasakatu baino lehen. Adibidez, 11 ber bi kalkulatzeko, honela egin beharko da :, eta 121 azalduko da pantailan. Berrizsakatu, eta 14641 aterako da, hau da,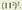. Bada ordea berreketak kalkulatzeko beste bide bat :sakatzen bada berriro, 14641 azalduko da, etab.Edozein errotzaileko berredura bat kalkulatzeko, xy giltza erabili behar da. Alegia,kalkulatu nahi bada, giltza hauek sakatu beharko dira hurrenez hurren :. Ordea, giltzaren bigarren funtzioa badaberredura, hauek sakatu beharko dira :.Hau da, lehenbizi oinarria sakatzen da, gero, eta azkenik berretzailea.

Ondoren, saka [=] giltza eta emaitza azalduko da : 177147.Edozein errotzaileko erro bat ateratzekogiltza erabili behar da. Alegia, 6.561 en zortzigarren erroa atera nahi bada, giltza hauek sakatu behar dira hurrenez hurren :, eta pantailatxoan 3 azalduko da. Hau da, lehenbizi errokizuna sakatu behar da, gero-giltzaren bigarren funtzio gisa azaltzen da normalean-, eta azkenik errotzailea.dela kontuan hartuz edozein erro kalkula daiteke xy giltza erabiliz :. Bestaldeetagiltzak bakoitzari dagokion giltzaren bigarren aukera izaten dira kalkulagailu askotan, eta horregatik [Shift] giltza sakatu behar izaten da aurretik.Bestalde, berredurak eta erroak kalkulatzeko, algoritmo bat erabiltzen dute kalkulagailuek, eta zifra hurbilekoekin egiten dituzte kalkuluak.

Beraz, edozein berretzaile onartzen du, baina arazoak izan daitezke oinarria negatiboa bada. Bestalde,-ren balio bat ere lor daiteke, giltza hauek sakatuz:, betiere kontuan hartuzedogiltzaren bigarren funtzio gisa azaltzen badira, [Shift] edo [Inv] sakatu beharko dela aurretik. Emaitza, gutxi gorabehera, 22, 459... da.ere berdin lortzen da ;, ordea, errore ematen du, ez baita zenbaki negatiboen errotzaile bikoitiko errorik, eta orobat ematen du erroreere, zeren berretzailea eta, beraz, errotzaile bikoitiko erroa da hau ere.

I I I. Hurbilketak

Problema bateanedota 787/131 bezalako kopuruak erabili behar direnean ez da erraza horrelako eragiketak burutzea. Zer maginitude ordena adierazten duten jakitea ere zail da askotan.

Ordea,ren lekuan 15 jarriko balitz eragiket a askoz errazagoa litzateke eta balioa argi legoke. Eta izan ere,kalkulatzean 15,06651917... ateratzen da ; bistan denez, 15 ez dago erroaren balio errealetik oso aldenduta, eta horregatik, problema askotan, 15 erabiltzen da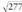ren ordez, errazago egiten baitira kalkuluak eta emaitzak ez baitira oso-oso desberdinak. Gauza bera gertatuko litzateke problema batean 787/131 jarri ordez 6 zenbaki osoa jarriko balitz, zeren 787/131 = 6,007633588...Matematika abstraktuetako eragiketaren bat ez bada behintzat, matematikak zientziaren batean aplikatzea baizik, zilegi da gisa horretako ordezkapenak egitea, neurrien zehazgabetasuna dela eta.

Izan ere, 1 m-ko karratu baten aldeak zentimetrotan zatiturik dagoen erregela batekin neurtu badira, ez dirudi egokia diagonalaren baliotzat 1,4142156 ematea ; izan ere, diagonolaizango da baldin eta aldeak 1 m badu justu-justu, eta zentimetrotan zatiturikdagoen erregela batekin neurtuta baliteke aldeak 1,004 metro izatea, eta hartara, diagonalak 1,41987... balio izatea. Hau da, maginitude ordenaz jabetzeko eta kalkuluak egiteko eragozpenak izateaz aparte, aplikazio praktikoetan hamarren askorekin lan egitea okerrago izan daiteke, errealitatearekin zerikusirik ez duen zehazgabetasun baten zehazgabetasuna gertatzen baita.Kopuru bati hurbilketa bat baino gehiago egin dakioke.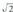ren lekuan, adibidez, 1 edo 1,5 edo 1,414 har daitezke ; denak diraren balio hurbilekoak, baina batzuk hurbilago daude balio errealetik beste batzuk baino. Balioaren eta hurbilketaren arteko diferentziaren balio absolutuari hurbilketaren errore absolutu esaten zaio. Aipatu berri diren kasuei dagokienez :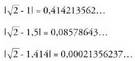Erabiltzen den balioa banakoetaraino hurbildu bada ez du zentzurik erroreak milioirenetan ematea. Beraz, errorearentzat ere magnitude ordena bat ematen da. Hala, aurreko adibideei dagokienez, hobe hartzea...Hau da, ez da errore zehatza erabiltzen, errorearen kota bat baizik.Oro har esaten da ezen, A-ren ordez a hartzean E(a) dela errore absolutua, baldin eta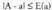izatea betetzen bada.Egindako errorearen magnitudea hurbilketa egin nahi zaion magnitudearen araberakoa izango da. Ez baita gauza bera banako erdi bateko errorea onartzea pertsona baten garaiera metrotan kalkulatzean edota errore bera egitea zentimetrotan kalkulatzen denean.

Hori dela eta, honela definitzen da hurbilketaren errore erlatiboa :Hurbilketak dagokion kopuruaren balio errealari hurbiltzeko eta kalkuluak bakuntzeko asmoz egiten direnez, hau hartzen da errore erlatibotzat :Zeren, zehatz-mehatz ez bada ere, nahikoa hurbiltzen baita errorera .Adibidez, baldin 1 hartzen bada, hau izango litzateke errore erlatiboa :Baina 1,414 hartzen bada hurbilketatzat :

Hurbilketa hamartarrak

Behar den baino zehaztasun handiagoz ezagutzen den balio batera hurbiltzeko modurik errazena, haren adierazpen hamartarretik hurrengo kalkuluetan zehaztasuna ez galtzeko gehien komeni diren zifrak hartzea da. Balio erreala baino balio txikiagoa hartuz edo handiagoa hartuz egin daiteke hurbilketa hori : lehenengo kasuan gutxiagoz hurbiltzea esaten zaio, eta bigarrenean, berriz, gehiagoz hurbiltzea .adibidearen kasuan, adibidez, hurbiltze hauek egin daitezke :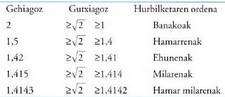Hurbilketaren ordenak egin den errorearen kota bat ematen du.

Baldin zenbakia milarenetara hurbildu bada errorea milarena baino txikiagoa da ; baldin banakotara hurbildu bada, banakoa izango da kota.Errore erlatiboa ezagutzeko dauden zifra zehatzen kopuruari erreparatu behar zaio. 1,4142 zenbakiak, adibidez, bost zifra zehatz ditu, eta, beraz, bere errore erlatiboabaino txikiagoa da. Hala beraz : 0,0001 errore absolutuko kota da eta1998 zenbakiaren hurbilketa egin nahi bada :

Biribiltzea

Banako hamartar jakin baten gehiagozko edo gutxiagozko hurbiltze hamartarrenetatik bada bat besteak baino zehatzagoa. Hala,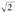ren hurbiltze hamartarretatik, baldin hamarrenetara egin nahi bada hurbilketa, hobe 1,4 hartzea 1,5 hartzea baino, txikiagoa baita errorea. Baldin 1989 hamarrenenetara hurbildu nahi bada, txikiagoa da errorera 2000 hartuta 1990 hartuta baino. Ordena baten hurbilketa hoberena delako kopurua ordena horretara biribiltzea da. Hala beraz, 1,4 da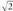ren biribiltzea eta 2000 da 1998rena.Biribiltze batean egiten den errorea ontzat hartu den hurbilketaren banako erdi batekoa baino ez da. Aurreko adibideei dagokienez, 1,4ren errorea,

Eragiketak eta errorea

Eragiketa bateko emaitzaren errorea delako eragiketa horretan parte hartzen duten zenbakien errorearen eta eragiketa motaren araberakoa da.Batuketa eta kenketetan, adibidez, batugaien edo kentzaileen batura da emaitzaren errore absolutua.Adibidez, 115,21 + 14,183 + 21,4 = 150,793 egin nahi bada.Batugai guztien zifra guztiak zehatzak direla jakinik, batugaien erroreen batura da baturaren errore absolutua : 0,0005 + 0,0005 + 0,05 = 0,0555. Beraz, emaitzatzat 150,8 ateratzea arrazoizkoa litzateke, baina azkeneko zifra zalantzazkoa litzateke, batugaien erroreak direla eta ezin baita 150,8485 eta 150,7375 artean dagoela baizik esan. 151 izango litzateke biribiltze seguru bat banakoetara, edota 150,8 ± 0,06 adieraztea, bestela.Emaitzak ez dira batere onak oso balio hurbilen kenketetan. Adibidez :Baldin bi balioak biribiltzeak badira, errore absolutua hau baino txikiagoa litzateke: 0,0005 + 0,0005 = 0,001. Baina errore erlatiboa dagoen balioaren heren bat da: E = 0,001/0,003 = 0,33333, alegia, %33,4.Biderkaketa eta zatiketetan errore erlatiboa errore erlatiboen batura da.n-garren berreduretan, emaitzaren errore erlatiboa n aldiz oinarriaren errore erlatiboa izango da.Oro har, f(a) funtzioan aldagaiaren errore erlatiboa txikia bada, funtzioaren diferentziala ateratzea da E(f(a))ren errorearen balio hurbila aurkitzeko modu erraz bat :E(f(a)) = df, eta da = E(a) ordezkatzen da.• Adibideak:1. Kalkulatubiderkaketaren errore erlatiboa, bi zenbakiak biribildutzat emanik.Lehenengoaren errore erlatiboa 0,005/4 = 00,00125 baino txikiagoa da eta bigarrenarena 0,05/25 = 0,002 baino txikiagoa. Beraz, biderkaduraren errore erlatiboa 0,00125 + 0,002 = 0,00325 da.Horrek esan nahi du emaitzaren errore absolutua 0,00325.104 = 0,338 dela, 0,3 ordenakoa. Emaitzak hiru zifra bakarrik ditu

I V. Zientzia notazioa

Oso zenbaki handiak edo oso txikiak erabiltzeko zientzia notazio deituriko adierazpide laburtua erabiltzen da.Lurraren masa 5.983.000.000.000.000.000.000.00 0 kilokoa da.

Kopuru hori irakurtzen zaila denez, eta kopuru hori harturik eragiketak egitea zaila denez,eran adierazi ohi da, eragiketak errazago egin ahal izateko eta kopuru horren magnitudearen ordena zein den ezagutzeko. Beste era batzutara ere adieraz daiteke, adibidez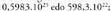; horrek ere erraztuko luke bidea, baina lehenengo adierazpena hartu ohi zientzia notaziotzat.Zientzia notazioan 1-10 arteko zenbaki baten eta hamarren berredura baten arteko biderkadura gisa adierazten dira zenbakiak.• Adibideak:Atsedenean dagoen elektroiaren masa 0,000000000000000000000000000000911 kilokoa da. Zientzia notazioankilo idazten da.

Ilargiaren masakilokoa da.Hidrogeno atomo baten erradioametrokoa da.Lurretik Eguzkira dagoen distantziada.Uranio 238aren semidesintegrazio epeasegundokoa da.Magnitude bat zientzia notazioan adierazteko, ezagutzen diren zifra esangarri guztiak sartu ohi dira 1 eta 10 arteko zenbakian. Hau da,zenbakiek, nahiz eta balio bera duten, ez dute emaitza bera. Izan ere, lehenak bi zifra zehatz bakarrik ditu, eta bigarrenak, berriz lau. Hau da, lehena magnitude baten neurri ez zehatzaren emaitza da, doitasun handiagoko tresna eta baliabideekinizan zitekeen emaitza hori ; eta bigarrena, berriz, gauza ziurra da

Ordena eta eragiketak zientzia notazioan

Zientzia notazioaren bidez adierazitako zenbakiak ordenatzeko 10-en berreduraren berretzailea hartzen da kontuan ; berretzaile handiena duena izango da handiena. Adibidez,Bi berretzaile berdin agertzen direnean bakarrik hartuko dira kontuan 1 eta 10 arteko zenbakiak ordena zehazteko orduan. Adibidez :Batuketa eta kenketa egiteko bi batugaietan 10-en berredura bera hartuko da, batugaiak batuko dira gero eta emaitza zientzia notazioaren arabera emango da berriro. Adibidez:Emaitzaren errorea erroreen batura izango da, beraz, 6,50 ez da izango emaitza biribildua, errorea 0,0 1 delako. Beste kasu batzuetan garrantzi gehiago izan dezake arazo honek, adibidez

Berredura eta zatiketa

Zientzia notazioko bi zenbakiren berreketa egiteko 1 eta 10 arteko zenbakiak biderkatzen dira zenbakia lortzeko, eta berretzaileak batzen berretzailea lortzeko. Azkenik, beharrezkoa izanez gero, zientzia notazioaren arabera ematen da emaitza. Adibidez :Berredura baten errore erlatiboa errore erlatiboen batura da, beraz aski da emaitzadela esatea.Bi zenbaki zatitzeko zatikiak zatitzen dira eta bider 10 ber berretzaileen arteko kendura egiten da. Azkenik, zientzia notazioan ematen da emaitza.• Adibidez :Ariketak:1. Ordena itzazu :Berretzaile handienak lehenarenak eta azkenarenak dira, hau da 7. Eta 8 > 2,8 denez, ordena honela gelditzen da :Aurkitu eragiketa hauen emaitza :Kentzailea askoz ere txikiagoa da kenkizuna baino eta honen errorea harena baino askoz handiagoa da.3. Egin eragiketak hauek :

Zientzia notazioa eta kalkulagailua

Kalkulagailu askok automatikoki egiten dute zientzia notaziorako aldaketa zenbakia oso txikia edo oso handia denean. Adibidez, milioi bat bider milioi bat egitean,agertzen da pantaila batzuetan.horrek esan nahi dudela. Kalkulagailuak zuzenean egiten du batetik besterako aldaketa pantailan lekurik ez galtzeko ; pantailak ez du idazten oinarriari dagokion 10 zenbakia eta atzean agertzen den zenbaki txikia 10 zenbakiaren berreduraren berretzailea izango da zientzia notazioan.-0,000001 zati milioi bat egiten bada,emaitza agertuko da pantailan ; kasu honetan, batekoaren aurretik agertzen den minus zeinuak emaitza negatiboa dela ematen du aditzera, eta 10aren berretzailea adierazten duten zenbaki txikien aurreko minus zeinuak 10en berretzailea negatiboa dela esan nahi du. Hau da, zenbaki hamartarra da.Kalkulagailuan zenbaki bat zientzia notazioan adierazi nahi bada, zuzenean egin daiteke [EXP] tekla sakatuz ; tekla horrek zenbakia eta 10arenberretzailea bereizten ditu. Adibidez, Lurretik Eguzkira dagoen distantzia sartu nahi bada (gutxi gorabeheradela esaten da) honela egingo da :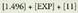Ez da idazten berreduraren oinarria, hau da 10 zenbakia.sartzen bada, kalkulagailuakautomatikoki idatziko du

Kalkulagailuen biribilketak eta borneak

Kalkulagailuek zenbaki kopuru jakin bat onartzen dute pantailan, zor±tzi edo hamar, eta beste bi zenbaki dituzte emaitzak kalkulatu eta biribiltzeko . Zenbaki bat pantailan satzen ez denean, zientzia notazioan adierazten du kalkulagailuak. Onartzen duen zenbaki positibo handiena 9,9999.... 10" da. Eragiketa baten emaitza 10 100 edo handiagoa bada, errorea ematen du, inolako errore matematikorik egin ez arren. Baldin eta emaitzaren balioa 1 • 10- 1D0 baino txikiagoa bada, kalkulagailuak zero ematen du.da. Eragiketa baten emaitzaedo handiagoa bada, errorea ematen du, inolako errore matematikorik egin ez arren. Baldin eta emaitzaren balioa

V Zenbaki arrazionalen multzoa zabaldu beharra

Zenbaki arrazionalen berredura osoen emaitzak zenbaki arrazionalak dira beti. Erroketetan, ordea, ez da beti hala izaten, hau da zenbaki arrazionalen hainbat erro aurki daitezke arrazionalak ez direnak. Hori dela eta zenbaki arrazionalen multzoa zabaldu eta zenbaki errealak definitu ohi dira.Zenbaki arrazional batzuen zenbait erro ez arrazionalak direla frogatzeko,ezin dela zatiki moduan adierazi frogatu behar da.

Horretarako erabiliko den metodoa beste erroketa askotan ere erabil daiteke, eta beraz, erroketa bat ez dela arrazionala frogatzeko erabiltzen da.Adierazpena absurdura murriztean datzan metodoaren kasu partikular bat da froga hau. Metodo horren arabera, frogatu nahi denaren kontrako egoera hartuko da oinarri, kasu honetan, beraz,arrazionala dela esango da. Ondoren, egiazko proposizioak erabiliz jarraituko da harik eta ziur faltsua den ondorio bat ateratzen den arte. Baldin eta ondorioa faltsua bada, arrazoiketaren bat okerra zelako izan daiteke hori, edo agian hipotesi faltsu bat hartu delako abiapuntutzat. Emandako urratsak zuzenak dira eta frogatu ezin i zan den hipotesi bakarrak dio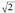arrazionala dela. Beraz, baieztapen hau faltsua izango da eta kontrakoa egia. Horrela,ez da arrazionala. Zehatzago adierazita : Eman dezagunarrazionala dela.

Hortaznon r zenbaki arrazional bat den eta a/b, berriz, zenbaki arrazionala zatiki murriztezin gisa adierazteko era.Berdintza ber bi eginez :Ondoren izendatzaileak kentzen dira :Beraz,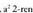anizkoitza da. Baina 2 zenbaki lehena denez, 2-ren anizkoitza behar du izan a-k. Hau da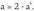. Ber bi eginez :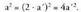Hortaz :Hortik, bi atalak zati bi eginez,ateratzen da.Beraz, arrazoinamendu bera erabiliz "b" 2-ren anizkoitza izango da.

Baina ezinezkoa da hori, hasieran esan baita "a/b" zatikia zenbaki arrazionalaren forma murriztezina zelako eta a eta b ezin izan daitezkeelako 2-ren bi anizkoitz, izan ere horrela zatikia murrizgarria litzateke.

Ikusten denez, kontraesan bat dago. Arrazoinamendua zuzena da, eta horrek esan nahi du hipotesi faltsua erabili dela, eta horrenbestez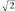ez da arrazionala.Horren antzeko frogak erabil daitezkekasuetan eta zenbaki lehen guztien erroentzat. Aldaketa txiki batzuk eginez aplika daitezke, halaber, erro zehatzik ez duten zenbaki oso elkartuetan. Izendatzaileak arrazionalizatuz edozein zatikiren erro koadroaren emaitza zenbaki oso bat da, beraz, zatikien erroak ere, zehatzak ez badira, ez dira izango arrazionalak. Prozedura horrek froga dezake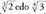edo maila garaiagoko errotzaileekiko erroketak ez direla arrazionalak. Laburbilduz, hainbat eta hainbat erro ez arrazional daude.Erro irrazional hauek interpretazio geometriko soila dute gainera.

Baldin eta laukiaren aldeak banako neurria badu, laukiaren diagonalak

Irrazionalen aurkikuntza

Iamblikok dioenez (K.a. III-IV m.) Pitagoras jabetu omen zen lehenengoerroketa ezin dela zatiki gisa adierazi, eta "neurgarritasunaren eta neurgaiztasunaren berri halako ezagueren duin ez zirenei eman ziena" elkarte pitagorikotik egotzi zutela eta hilobia eraiki ziotela, elkarte hartako kideentzat hila zela adierazteko. Beste batzuek diotenez gertaera haren berri eman zuena itsasontzi bat hondoratzean ito zen bere adiskideen mendekutik ihesi zihoala. Beste batzuek, aldiz, uste dute elkarte pitagorikoko kideek traizio egin izanagatik bidali zuten itsasontziaren kareletik bota zutela.Gaur egun, adituek diote aurkikuntza hori ez dela Pitagorasena, baizik eta haren jarraitzaile batena; Hipaso Metapontokoak (K.a. VI. mende amaieran edo V mende hasieran) aurkitu bide zituen irrazionalak pentagonoaren aldeen eta diagonalen arteko arrazoia ikertzen ari zela. Iamblikok, ordea, Hipasok plagio egin zuela dio, Pitagorasena zen aurkikuntza bat berak egin izan balu bezala aurkeztu zuela. Baina, Pitagorasen jarraitzaileen artean, matematikarien belaunaldi haren hasieran, joera zegoen guztia Pitagorasek aurkitu izan balu bezala aurkezteko, eta alde horretatik ez du indar handirik Iamblikoren baieztapenak.Egia dirudi, hala ere, arrazionalen eta irrazionalen arteko diferentziaren arazoa greziarren garaian gelditu zela agerian. Antzin Aroan matematikaren alorrean ezaguera handia izan zuten beste zibilizazio batzuek, txinatarrek edo indiarrek adibidez, matematikaren alde praktikoagoak eta kalkuluarekin zerikusia zutenak landu zituzten batez ere. Aski zuten erroetara ahal bezain hurbilketa zehatzak egitea, ez zuten eztabaidatzen zein eratako zenbakiak behar ziren.

VI. Zenbaki erreala

Zenbaki arrazionalen multzoabalio duten elementuez osatu behar da. Multzoan falta diren osagai hauek guztiak eta osagai horien arteko eragiketen emaitzak lortzeko modu bat bilatzean ikus daitekeenez, zenbaki arrazionalak ax + b = 0 motako ekuazioen emaitzak dira, ekuazio horietan koefizienteadela.

Horrela, biren erroa,ekuazioaren ebazpena daeta 3 erroketaekuazioarena. Zenbaki arrazionalen multzoa beste multzo batera orokor daiteke, ekuazio aljebraiko posible guztien emaitzak hartuko dituen multzo batera, hau da, ondoko tankerako ekuazio guztien soluzioak hartuko dituen multzora :non n zenbaki arrunta den etakoefizienteak arrazionalak diren.Zenbaki hauei zenbaki aljebraiko esaten zaie eta kasu partikulartzat dituzte zenbaki arrazionalak, hau daekuazioren ebazpenak, etaekuazioaren soluzio diren edozein mailako erroketak.Zoritxarrez, zenbaki arrazionalen zabaltze hau ez da aski ; izan ere, matematikan garrantzi handia duten zenbait zenbaki, adibidezedo e zenbakiak, zenbaki ez aljebraikoak direla frogatu ahal izan da.

Zenbaki irrazional ez aljebraiko hauei zenbaki transzendente esaten zaie, "aljebra metodoen ahalmena gainditzen baitute", Eulerrek zioen bezala.Transzendenteaketa "e" zenbaki ezagunak baizik ez balira, ez legoke arazo handirik, baina Cantorrek azaldu zuen XIX. mendean infinitu zenbaki transzendente daudela eta, are gehiago, zenbaki aljebraikoak baino ugariagoak direla. Esaterako,ere zenbaki transzendentea da, baina ugari izanda ere zenbaki transzendente interesgarriak ez dira asko.Hortaz, zenbaki arrazionalen multzoa zabaltzeko ezin har daitezke ekuazio aljebraikoak, oso multzo txikia baitlitzateke hori.Praktikan, zenbaki irrazionalak erabili ordez, zenbaki horiez egin nahi den kalkulua beste era batera egiten utziko duen hurbilketa hamartarra erabiltzen da. Gutxi gorabeherako hurbilketa horrek ematen du bidea zenbaki errealaren lehenengo definizio bat emateko .Zenbaki errealak dira zifra hamartarren kopuru infinitu edo finitu bat duten zenbakiak. Infinitu zifra hamartar dituztenak periodikoak ala ez periodikoak izan daitezke.• Adibidez:Zenbaki osoak dira, aldiz, zifra hamartarrik ez duten zenbakiak.

Zatikian zifra hamartarren kopuru finitua duten zenbakiak dira, edo zifra hamartar infinitu izan arren, errepikatzen den periodo bat dutenak. Infinitu zifra hamartar ez periodiko duten zenbakiak zenbaki irrazionalak dira.Definizio hau, ordea, ez da zuzena, ezin baita idatzi infinitu zifra hamartarreko zenbakirik, baina badaude ongi definituriko zenbaki irrazional baten nahi adina hamartar ateratzen uzten duten algoritmoak. Adibidez, erroaren algoritmoak aukera ematen du esatekodela, etaedo e zenbaki transzendenteentzat ere aurki daitezke nahi adina zifra hamartar lortzeko aukera ematen duten algoritmoak :edo e = 2,718281828.Zenbaki horiekin eragiketak egiteko zenbaki hamartar finituen arteko eragiketak hartzen dira oinarri. Eta ordena finkatzeko, berriz, zenbaki hamartarren ordena erabiliko da.Hamartar infinituen multzo horretan limitea izango luke edozein segida konbergentek. Aski litzateke segidaren ondoz ondoko terminoetan egonkor irauten diren zifra hamartarrak hartzea. Adibidez,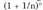segidaren limitearentzat zera ikusiko litzateke : segidaren gai guztiak 2 zenbakiaz hasten dira, 100. gaitik aurrerakoak 2,7-z, 1000.tik aurrerakoak 2,71-z, 1000000-etik aurrerakoak 2,7182-z, etab.Zenbaki errealak definitzeko metodo praktikoa da, baina ez da zorrotza. Fisikan edo beste zientzia alor batzuetan aplikatzeko erabilgarria da, izan ere, praktikan erabiltzen diren zenbakiek ez dute lanerako erabiltzen diren neurri esperimentalek baino doitasun handiagoa behar. Hau da, aski da infinitu hamartar defini daitezkeela jakitea. Ez da zertan hamartar infiniturekin jardunik.Baina halako zorroztasun matematikoa nahi denean infinitu hamartarreko zenbakiak alde batera utzi eta esapide horren oinarrian dagoen limitearen ideia zehaztu beharra izaten da. Horretarako definizio hauek erabil daitezke : Zenbaki arrazionalen segida bat,segida konbergentea da baldin eta edozeinzenbaki arrazionalentzat, zenbaki arrazional hori denik eta txikiena izanda ere, aurki badaitekebat p etaizanik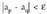dena. Konbergentzia horri Cauchyren konbergentzia esaten zaio.

Zenbaki arrazionalen segida hauek konbergenteak dira, baina ez zaie eskatzen limiterik izaterik. Adibidez, 1, 1/2, 1/3, 1/4,...,1/n segida arrazionala eta konbergentea da eta "0" du limitea. Aldiz 2 ; 2,25 ; 2,370 ; 2,44140625... ;segida segida arrazional konbergentea da, baina ez du limiterik. Bere limitea e zenbakia da, eta zenbaki hori ez da arrazionala.Zenbaki arrazionalen segida konbergente bakoitzari zenbaki erreal bat dagokio. Baldin eta bi segidak,, kopuru berera jotzen badute, hau dabat baldin badago nonizango den, orduan zenbaki erreal berak definitzen dutela esaten da.

Bi definizio horiekin ongi definiturik gelditzen da zenbaki errealen multzoa. Ikusten denez, Qmultzoko elementuak R multzoaren barnean daude.Zailagoa da, hala ere, eragiketak definitzea, horrela definituriko zenbaki errealen multzoaren ordena zehaztea eta zenbaki multzoen propietateak betetzen dituztela ikustea.

Era honetako segiden kasu partikularrak dira lehenengo gutxi gorabeherako definizioko infinitu zifra hamartarreko zenbakiak.

Horrela, e zenbakiarentzat :Definizio honen arabera e zenbakira irits gaitezke beste segida batzuekin ere :Zenbaki errealen definiziora heltzeko beste bide bat zuzen bateko puntuen eta zenbaki errealen artean ezar daitekeen korrespondentzia da. Zuzen jakin batean 0 zenbakiari dagokion O puntu bat jatorritzat harturik, eta beste puntu bat 1 unitatea definitzeko, zenbaki positibo osoak, +n, unitate zuzenkia n aldiz eskuinean hartuta adierazten dira, eta negatiboak, -n, n unitate ezkerretara hartuta.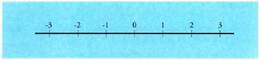Zatikiei berriz, m/n, Thalesen teorema erabiliz lortzen den puntu bana dagokie : m unitate hartzen dira zuzen errealean eta n unitate ardatz laguntzailean. m eta n puntuei dagozkien muturrak batzen dira gero. Zuzen laguntzaileko 1 puntutik pasatuz, m eta n batzen dituen zuzenaren paraleloa marrazten da. Paralelo horrek zuzen errealean zehazten duen puntua da m/n zatikiari dagokiona.Erroentzat Pitagorasen teorema erabil daiteke :Gero, unitatearen ainean perpendikularki, 1 luzeko zuzenki bat marrazten da, etadugu hasiera muturrarekin batzen duen zuzenean. Zuzenki hori jaisten da zuzenaren gainera konpasaren laguntzaz, etalortua dago.en gainean nahi bada, zuzenki unitatea igotzen da perpendikularki eta hipotenusa berriakneurtuko du. Unitate bat igotzen bada perpendikularki 2ren gainera ;lortzen da.Horrela jarrai daiteke gainerako erro koadroekin, eta beste eragiketaren bat eginda zenbaki irrazionalak lor daitezke erro koadroekin, hala nola urrezko zenbakia.Prozedura hau asko korapilatzen da erro kuboetan, eta zenbaki traszendenteetan berriz -esate baterako- ezin daiteke erabili.

Hurbilpena egin beharko litzateke, zenbakiaren adierazpen hamartarra erabiliz, eta geroz eta hurbilagoko zuzenkiak hartuz. Adibidez : 3 ; 3,1 ; 3,14 ; 3,141,...Horrela, zuzeneko puntu bakoitzari zenbaki erreal bat dagokio, eta alderantziz. Zenbaki errealak, zuzeneko puntu guztiek jatorrira duten distantziaren luzeraren arabera defini daitezke.Zenbaki errealak definitzeko modu hau, geometrikoa da, funtsean, eta bera erabili izan da, joan den mendea arte, kopuru irrazionalak baliatu ahal izateko. Eman liezaioke forma doiagoa eta aritmetikoagoa, tarte ahokatuen segidaren nozioa erabiliz.Ideia zera da, tarteak deitzen zaizkien geroz eta zuzenki txikiagoak hartzea, zuzenki bakoitza aurrekoaren parte dela. Zuzenki bakoitzean aurrekoan baino puntu gutxiago egongo da eta pentsa daiteke infinitua arte jarraituta puntu bakarra egongo litzatekeela azkenean. Puntu hori baliteke arrazionala ez izatea. Adibidez, ondorengo tarte hauek hartzen badira :Eta horrela hurrenez hurren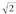ren hamartarrak doituz, ez da egongo zenbaki arrazional bati dagokion punturik,ez delako arrazionala. Elkarren segidan bata bestearen barruan ahokatutako tarte guztiei -tarte guztietan dagoen puntua bat bakarra dela- zenbaki bat egokitzen bazaie, definituta geratuko da zenbaki errealen multzoa.Ideia hau zehaztuz :Ondorengo legeak betetzen dituentarte segidari : - segidaren muturrak zenbaki arrazionalak izateaeta- tarte bakoitza aurrekoaren parte izatea :- tarteen luzerak,, zerora jotzeatarte ahokatuen segida deitzen zaio.Mota horretako tarte ahokatuen segida batek zenbaki erreal bat definitzen du.Zuzenki ahokatuen segiden artean, baliokidetasun erlazio bat ere definitzen da, puntu bera duten segida desberdinek definitutako zenbakiak berdintzeko.Puntua izan daiteke osoa -adibidez :segidak 1 zenbakia definitzen du-, zatikiarra -adibidez :segidakdefinitzen duedo irrazionala, hala nolasegida,definitzen duena.Zenbaki errealak definitzeko modu hau erlazionatu daiteke aurrekoarekin segida konbergenteetatik abiatuta. Baldin etatarte segidak zenbaki erreal bat definitzen badu, segida horretatik abiatuta defini daitezke bi segida konbergente,, zenbaki erreal bera definitzen dutenak.Aurreko definizioan bezala, zenbaki arrazionalek dituztenetatik abiaturik definitu behar dira zenbaki erreal hauen eragiketak eta ordena.Zenbaki errealak definitzeko modu errazena Dedekind-en epaiak deitu izan zaienak dira. Ondorengo ideia honetatik abiatzen da : zuzeneko puntu bakoitzari zenbaki erreal bat dagokio, beraz, zuzena edozein puntutatik ebakitzen dela ere, epai puntu horri dagokion zenbaki erreal bat dago. Epaien metodo hau Dedekind-ek proposatu zuen (1831-1916) joan zen mendearen hondarrean.

Zehatzago esanda :Zenbaki arrazionalen Q multzoan,deitu diegun bi azpimultzo ez baliogabe definitzen dira ondorengo legeak betetzen dituztenak :egiaztatzen dadela.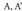azpimultzo pare bakoitzari zenbaki erreal bat dagokio.Baliteke A-ko zenbaki bat izatea denetan txikiena eta-ko zenbaki bat denetan handiena. Orduan esaten da epaiak definitzen duela zenbaki arrazional hori.Baliteke, orobat, A-k zenbaki txikiena ez izatea, ez eta-k ere handiena. Orduan esaten da epaiak zenbaki irrazional bat definitzen duela.Ezin daiteke gertatu A-k txikiena izatea eta-k handiena, zeren, hala balitz, emanik m eta M zenbakiak, m>M, "m" A multzokoa delako, (m+M)/2 zenbaki arrazionala m baino txikiagoa eta M baino handiagoa izango litzateke, eta beraz, bi multzoen artean egongo litzateke eta ezingo litzateke izan ez batekoa eta ez bestekoa, zeren bietakoren batekoa balitz, edo m ez zen A-ko txikiena, edota M ez zen-ko handiena. Baina hori epaiaren definizioaren aurka dago, eta ondorioz, ezinezkoa da txikiena eta handiena batera egotea.Hortik aurrera, zenbaki erreal guztiak definituta daude. Aurreko kasuetan bezala zenbaki berri hauen arteko eragiketak eta ordenak ere definitu beharra dago, beti ere, Q arrazionalen eragiketak eta ordena gorde beharko direlarik kasu berezi gisa.Definizio axiomatikoa da denetan errazena. Zenbaki errealak ez dira arrazionaletatik abiatuta osatzen baizik eta, alde batetik, postulatutzat ematen da badirela, eta bestetik, R multzoak ondorengoa bete behar du :

Eragiketak :

- Multzoak batuketa bat du definituta trukatze eta elkartze legeak betetzen dituena. Eragiketa honetan bada elementu neutro bat ere -zeroa- eta elementu bakoitzak aurkako bat du -harekin batuta zero ematen duena-. Alegia (R,+) talde trukakorra da.- Multzoak biderkaketa bat du definituta trukatze eta elkartze legeak betetzen dituena eta unitate elementu batekin. Elementu guztiek dute alderantzizkoa, zeroak ezik, honek ez baitu.Biderkadura banakorra da baturarekiko, hau da.

Ordena :

Zenbaki errealen multzoa erabat ordenatua dago, alegia, baldin etabada a>b edo b>a izango da.a > b erlazioak ordena erlazio baten legeak betetzen ditu : 1º)2º) baldinetabada a = b izango da.

3º) baldinetabadaizango daBestalde, ordena bateragarria da eragiketekin :Baldin a > b bada, a + c > b + c ;izango da.

Baldin a>b eta c>0,inserted textizango da.Gainera, multzoa trinkoa da, alegia, a eta b izeneko bi zenbakiren artean, a > b baldin bada, beti dago c zenbaki bat, a > b > c betetzen duena.R multzoa Arkimedesen araberakoa da, alegia, 0 > x > y baldin bada, badago zenbaki natural bat, n,

VII. Zenbaki erreal multzo baten borneak eta muturrak. tarte irekiak eta itxiak

Zenbaki errealen arteko -edo zuzen errealeko puntuen artekohurbiltasun edo urruntasun ideia zuzenaren topologian aztertzen da. Atal honetan azalduko diren definizio batzuk nahiko maiz erabiltzen dira analisien frogantzetan eta funtzioen azterketan.

Borneak

Izan bedi A zenbaki erreal multzo ez huts bat. Esaten da k zenbaki bat A-ren goiko bornea dela ondorengoa egiaztatzen denean :inserted textororentzatOrobat esaten da A-k goiko bornea duela• Adibidez :multzoaren goiko bornea 1 da, edo, 10 edo 1000000. Zenbaki erreal multzo batek goiko borne bat duenean (k), infinituak ditu, zerenoro ere goiko bornea da, desberdintasunen iragankortasun legea dela medio.Esaten da B zenbaki erreal multzo batek beheko bornea duela (k) ondoko hau egiaztatzen bada :ororentzatGoiko eta beheko borneak dituen multzo bati, bornetua dela esaten zaio.• Adibidez :multzoaren goiko bornea 1 da eta behekoa 0, beraz A bornetuta dago.multzoaren beheko bornea 0 da, baina ez du goiko bornerik, zeren zenbaki naturaletan, edozein kopuru dela ere, beti egin daiteke zenbaki handiagoren bat.

Goiko eta beheko muturrak

Goiko borneetan txikienari deitzen zaio multzo baten goiko borne txikiena, goiko muturra edo gorena. Emanik goiko bornea duen A zenbaki erreal multzo bat, "s" baldin bada goiko borne bat, beste goiko borne oro "z" bera baino handiagoa dela betetzen duena, z > s, orduan s da multzoaren goiko muturra edo gorena.

Adibidez,multzoan, 1 da goiko muturra.Era berean, B zenbaki erreal multzo batean, m baldin bada beheko borne bat, beste beheko borne oro -i- bera baino txikiagoa dela betetzen duena,, orduan m-ri deitzen zaio multzoaren beheko borneetan handiena, beheko muturra edo txikiena.

Adibidez,multzoaren beheko borneak 0, -1, eta beste zenbaki erreal batzuk dira. Horietatik 0 da handiena, eta beraz, 0 dela esaten da B-ren beheko muturra.Beheko muturra multzokoa denean, multzoko txikiena deitzen zaio, eta goiko muturra multzokoa denean, handiena. Aurreko adibideetan, 1 zen A-ren handiena eta 0 B-ren txikiena.Baina A-ren beheko muturra 0 da eta 0 ez da A multzokoa, eta beraz A-k ez du txikienik.Ondorengo definizioen bidez beste modu batean eman daiteke zenbaki errealen jarraitasun legea :A baldin bada zenbaki erreal multzo ez huts bat, goiko bornea duena, orduan A-k goiko muturra du.

Kontuan har bedi zenbaki arrazionalek ez dutela lege hori betetzen . Adibidez, har bedi2}. Multzo honen goiko bornea 1'5 da, baina ez du goiko muturrik, zeren 1'42 ere goiko bornea da eta txikiagoa da, eta baita 1'415, 1'4143, eta abar ere. Multzo hau R-n definitu izan balitz, izango luke goiko muturra,, baina Q-n definitua egonik, posible da zenbaki arrazionalak diren goiko borneen segida bat,

Tarte irekiak eta itxiak

Izan bitez "a" eta "b" bi zenbaki erreal, a < b betetzen dutenak. a < x < b betetzen duen x zenbakien multzoari irekia deitzen zaio eta honela adierazten da : ( a, b ), Frantzian izan ezik :Hau dahonelalb-al balioari tartearen zabaltasuna deitzen zaio.Adibidez, (2,4), 2 zabaltasuna duen tarte irekia da.betetzen duen zenbaki erreal multzoari tarte itxia deitzen zaio etaadierazten da. Alegiahonela adierazten daAdibidez, (2,5), 3 zabaltasuna duen tarte itxia da.a eta b zenbakiei tartearen muturrak deitzen zaie. Tarte irekian muturrak ez dira tartearen partaide, baina itxian bai.Emanik zenbaki erreal bat a, orobat tarte irekia deitzen zaie a < x betetzen duten x zenbakien multzoari,adierazten da, eta a > x betetzen duten zenbaki errealen multzoari,adierazten da.betetzen duten x balioen multzoaitxia da, etabetetzen duten x-ena berriz,itxia. Nola infinitua ez den zenbaki erreala, hobe da mutur horretan ) jartzea,ez dela multzokoa adierazteko. Adibidez,tarte irekia honela adierazten daetaberriz, honelaTarte erdi irekiak ere defini daitezke. Adibidez, bi zenbaki erreal emanik, a eta b-,betetzen duten x zenbakien multzoa [a,b) izango da, edo [a, b[, etabetetzen dutenena, berriz, (a,b], edo ]a,b].

Adibidez, ( 0 , 3 ] eta [ -1, 2) tarteak tarte erdiirekiak dira.

Ingurua

inguru esaten zaiopuntu bat duen edozein (a,b) tarte irekiri. Bainazentroa eta e erradioa duten inguruak dira erabili ohi direnak, horiek baitirairekiak.Adibidez, (1,3) tartea 2-ren inguru bat da. Tarte hori 5/2-ren inguru bat ere izan daiteke, baina kasu honetan ez da inguru zentratu bat, eta 2-ren kasuan, aldiz, bai.Zenbaki errealen A multzoa emanik,puntu bat barneko puntua dela esaten da baldin eta E(x) inguru bat baldin badago non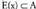betetzen den.Esaterako, 3 puntua [2,4] tartearen barneko puntu bat da.Eta, aldiz, x puntua A multzoko puntu bakan bat dela esaten da baldin eta E(x) bat badago zeinetan x puntua baita A-ko puntu bakarra.

Adibidez,multzoa harturik, 1 balioa multzo horretako puntu bakan bat dela esaten da 1/3, (2/3, 4/3) erradio zentratua duen inguru batek ez duelako A-ko beste punturik.x puntua A-ko metatze puntu bat dela esaten da, baldin eta x-en inguru murritz batean A- ko punturen bat badago. Metatze puntuak A-koak izan daitezke ala ez.(2,3) tartean tarte horri ez dagokion metatze puntu bat da 2 puntua, eta [-1,3] tarte itxian tarte horretakoa da 3 metatze puntua.

Baldin eta x puntua A multzoko metatze puntu bat bada, orduan A-ko infinitu puntu daude x-en inguruan. Izan ere, zenbaki finitu bat balego, aski litzateke hurbileneko puntura dagoen distantziaren erdia hartzea A-ko punturik ez duen inguru zentratu baten erradioa lortzeko.Multzo ireki esaten zaio puntu guztiak barnekoak dituenari.

Definizio honekin, tarte irekiak, partikularki, irekiak dira.Multzo bat itxia dela esaten da, baldin eta multzoaren metatze puntu guztiak multzo horretakoak badira. Tarte itxiak, partikularki, mutzo itxiak dira. Multzo irekien zein itxien propietateak dira :Multzo irekien bildura finitu zein infinituak multzo irekiak dira.- Multzo irekien ebakidura multzo ireki bat da.- Multzo ireki baten osagarria multzo itxi bat da, eta itxi batena ireki bat.- Multzo itxien bildura finitua multzo itxi bat da.Funtzioen teoriaren frogetan aurrez azaldu diren definizioetatik eta zenbaki errealen ezaugarrietatik ondorioztaturiko teorema hau erabiltzen da :Bolzano-Weierstrassen teoremaZenbaki errealen A multzo bornatu eta infinitu orok metatze puntu bat du.Soluzioak :

PITAGORAS

(Samos, K.a. 560, Metaponto, K.a. 480 ing.)Pitagoras Samosen jaio zen, K.a. 560. urtean.

Gazte zelarik bidaian ibili zen Egipton eta Babilonian, matematika eta astronomia ikasten. Samosa itzuli zen, baina uharteko agintari Polikrares tiranoarekin haserretu, eta Krotonako hiri grekoan bizi izan behar izan zuen K.a. 530-520 urteetan, Italiako hegoaldean. Erlijio eta filosofia elkarte bat sortu zuen han. Pitagorasen dotrinek ordenaren eta hierarkiaren alde egiten zuten, Krotona mendean zuten aristokraten alde beraz, eta, hala, haien babesa izan zuen hasieran. Baina denborarekin pitagorikoak indartsuegi egin ziren, eta haien kontra jarri ziren aristokratak, gogor gainera. Pitagorasek ihes egin behar izan zuen Metapontora K.a.

500 urtean. Bere sekta zabaltzen jarraitu zuen han, eta K.a. 480an hil zen.Pitagorasek unibertsoaren harmonian oinarritzen zituen bere filosofia eta erlijioa ; harmonia hori zenbakiek gidatzen zuten. Perfektotasun pertsonala eta gauzen ezagutza iristeko bide bakarra iniziazio berezi bat zen ; iniziazio horretan hasberriak beharrezko matematikak ikasten zituen.

Dizipuluek bi gradu zituzten : akoustmatikoi, "akustikoak" edo entzuleak, bileretan galderak egiteko eskubiderik ez zutenak, eta Pitagorasen irakaspenak buruz ikasi behar zituztenak, ulertu beharrik gabe, eta maqhmatikoi, "matamatikariak" edo ezagutzaileak, galdetu, ulertu eta iritziak emateko eskubidea zutenak.Izaki jainkozko eta argiduntzat hartzen zuten Pitagoras bere dizipuluek. Urte askoan, Pitagorasek berak eginak balira bezala aurkeztu ziren pitagorikoek matematikan egin zituzten aurkikuntzak. K.a.400 urtea arte ez ziren zabaltzen hasi matematikari pitagoriko banuen izenak, Arkitas Tarentokoarena adibidez.K.a. 450. urtean Italiako hegoaldeko hiri grekoetako tiranoen kontra matxinatu ziren hiritarrak, eta pitagorikoen etxeak ere birrindu egin zituzten, tirania grekoen aliatuak baitziren haiek ; iniziatuak sakabanatu beharra izan zuten. Beste alde batetik, akustikoen eta matematikoen arteko desberdintasunek bi taldeen banaketa ekarri zuten. Akustikoek errituei, ezkutukoei eta ezagutzen errepikapenari ematen zioten garrantzia ; matematikariak berriz erlijio partea baztertzen hasi ziren, matematikak garatu eta gizarte grekoari erakutsi ahal izateko. Izan ere, Pitagorasen garaian dizipuluek zin egin behar zuten ez zutela beren jakintza ezagutaraziko. Aldaketa horiekin denekin, pitagorikoek utzi egin zioten talde hermetiko eta sektazalea izateari.Pitagorasen dotrinak lau jakintza alor bereizten zituen: aritmetika, geometria, musika eta astronomia .Musikan, akordeak eratzen zituzten soinuak zenbaki arrazoi bakunei dagozkiela aurkitu zuen Pitagorasek. Era horretan, hari batek tonua ematen badu, hari erdi batek oktaba ematen du, hari baten 3/4ak laugarrena eta 2/3ek bosgarrena.Astronomian, planeten mugimenduaren aldizkakotasuna ezagutzen zuten, eta planetan orbita zirkularretan zebiltzala uste zuten, simetria eta edertasunezko arrazoiengatik. Azken pitagorikoek eguzkia hartzen zuten munduaren ardaztzat.

Izarrek eta planetek zenbaki bana zuten -haien iritzian-, eta mugitzerakoan musika zerutiarra sortzen zuten. Zoritxarrez, ordea, Pitagoras ezpada, beste inor ez da izan musika hori entzuteko gauza. Pitagorikoen unibertsoa beti itzultzen da, eta beti errepikatzen. Izaki bakoitzak zenbaki bana duela, diren zenbaki guztien multiplo komunetako txikiena igarotzen denean, dena etortzen da berriz lehengora, eta gertatu zen guztia berriro hasten da gertatzen.Aritmetikan, zenbaki osoen oinarrizko auzi asko ezagutu zituzten pitagorikoek. Multiploen eta zatitzaileen tasunak aztertu zituzten, eta zatitzaile komunetan handiena lortzeko algoritmoa ere ezagutzen zuten. Ezagutzen zituzten halaber, eta erabiltzen ere, zenbaki osoen arteko arrazoiak eta batez besteko aritmetikoa, geometrikoa eta harmonikoa. Horrekin batera, garrantzi handiaematen zioten zenbakien sailkapenari. Bakoiti eta bikoitiez gainera, zenbaki triangeluarrak ere ezagutzen zituzten, hala 3, 6 edo 10, karratuak, hala 4, 9 edo 16, pentagonalak, hala 5, 12 edo 22, etab. Perfekto deitzen zituzten, 6a bezala, bere zatitzaileen baturaren berdinak diren zenbakiak, zenbakia bera kontuan izan gabe [6 = 1 + 2 + 3].Zenbakien teoriarekin loturik daude, baina matematikatik oso urrun, pertsona, gauza edo kualitateen eta zenbakien artean ezartzen zituzten egokitasunak. Hala adibidez, 2 zenbakia emea zen, eta 3a arra. Zenbaki ideala 1 Oa zen, Tectratis deitzen zutena, lehen 4 osoen batura delako eta haien tasun eta perfektotasunen multzoa izateagatik.Geometrian, ezagutzen zituzten poligono erregularrak eta poliedro bakunenak. Zuzenkiak eta paralelogramoak ere bazekizkiten erabiltzen areak kalkulatzeko. Hain zuzen ere, Pitagorasen teorema ezagutzen zuten, nahiz eta, berez, hiruki angelu-zuzenen tasun hori ez zuen Pitagorasek berak aurkitu, ezaguna baitzen lehendik ere Egipton eta Babilonian. Pitagorikoen irudi ideala pentagonoa zen, eta huraxe hartu zuten, beste batzuekin batera, ikurtzat. Dirudienez, pentagonotik abiatuta egin zuten eskola pitagorikoaren aurkikuntzarik handiena, zenbaki irrazionalen existentzia, alegia, hainbat zuzenki, hala adibidez pentagono baten aldea eta diagonala, aldi berean neurtzeko banako komun bat aurkitzeko ezintasuna. Tradizioak dioenez, Hipaso Metapontokoak aurkitu zuen, K.a 500. urte inguruan, ezintasun hori. Hipaso eliza pitagorikoko heretiko bat izan zen, bere aurkikuntzaren berri eman baitzien sinesgabeei ; izaki bakoitzari zenbaki oso bat, edo bi zenbaki osoren arrazoi bat ezin zitzaiola egokitu frogatu zuen, eta uste horixe zen, hain zuzen ere, pitagorikoen sinesteen oinarria. Tradizioak dioenez, pitagorikoen jainkoak zigortu egin zuen Hipaso, eta itsasoan itota hil zen.Beste inoren aurretik, Pitagorasek eraman zituen Greziara Babilonia eta Egiptoko matematika ezagupenak. Erlijio pitagorikotik ezer gutxi geratu da. Haren matematika aurkikuntzak, berreginik, matematika grekoan txertatu ziren, eta Euklidesen Elementuak obraren 11, IV, VII, VIII eta IX liburuetan ageri dira adibidez. Baina harmonia eta edertasun ideiak munduaren azalpen ororen oinarri direla, eta unibertsoa matematikak erabiliz baizik ezin dela ulertu, ideia horiek bizi-bizirik diraute.