Fisika-Kimika»Fisika - Kimika

Kuantika

1. Plancken postulatua

1.1 Sarrera

Quantumen mekanika materiaren eta argiaren jokaeraren deskribapen zehatza da, eskala atomikoan gertatzen diren gertaera fisikoena, batez ere. Oso eskala txikian, maila mikroskopikoan, gure intuizioak eta esperientziak ezer gutxirako balio dute, objektuak ez baitira ez zatikiak ez uhinak. Newtonek argia zatikiz osatua zela uste bazuen ere, geroago interferentzia esperimentuek argiak uhin izaera zuela erakutsi zuten eta XX. mendearen hasieran argiaren jokaera bikoitza frogatzeko lehenengo urratsak egin ziren. Elektroiak, ordea, hasieran zatikitzat hartzen ziren arren, gaur egun argi eta garbi frogatu ahal izan da haien jokaerak zenbateraino ziren esperimentuetan erabili zen metodoaren mendeko. Quantumen teoriaren lehenengo urratsak nahikoa korapilotsuak izan arren, quantumen teoriaren ondorioak bateratzaileak dira: objektu guztiek (elektroiek, protoiek, neutroiek, fotoiek, e.a.) berdin jokatzen dute, jokaera hori azaltzen korapilatsua bada ere. XIX. mendearen bukaeran, teoria elektromagnetikoaren garapenarekin, munduko teoria fisiko osoa burutzeko gutxi falta zela uste zuten fisikariek. Ordura arte ikusi ziren gertaera gehienei azalpen teorikoa eman zekiekeen eta iragarpen klasikoaren eta esperimentuen emaitzen arteko aldeak kontuan ere ez hartzekoak ziren. Hala ere, bazen gertaera fisiko bat, mekanikaren eta elektromagnetismoaren formalismoa berriro aztertzera behartu zuena: gorputzek orekan igortzen duten erradiazioa.

1900. urtean Max Planckek «Espektru arruntaren energi banaketaren legearen teoria» izeneko lana aurkeztu zuen Alemaniako Fisika Elkartean. Lan horrek oso arreta gutxi sortarazi zuen, baina lan horrekin hasi zen, zinez, quantumen fisika eta zeharo aldatu zuen gure munduaren ikuspegia. Mende laurdenaren buruan, beste batzuen artean, Schrödingerrek quantumen mekanikaren formalismoa garatu zuen, eta era horretara, gaur egungo fisikako ezagutza behin betiko oinarritu.

XX. mendearen hasieran beste teoria bat sortu zen: Einsteinen er - latibitate bereziarena; kontzeptuei dagokienez, nabaria da erlatibitatearen eta quantumen teoriaren arteko antzekotasuna. Bi teoria hauek fisika klasikoa orokortu egiten dute, era horretara fisika klasikoa teoria orokorrago baten kasu berezi bezala geratzen delarik. Aztertu nahi ditugun zatikien lastertasunak oso handiak direnean, erlatibitate bereziaren teoria fisikako teoria klasikoaren ordezko bihurtzen da. Era berean, quantumen fisika baliagarria da mundu mikroskopikoan, atomo barruan gertatzen dena ulertu ahal izateko. Fisika klasikoa erabili beharrean, erlatibitate berezia zein kasutan baliatu behar den jakiteko konstante fisiko garrantzitsu batek, c konstanteak, argiaren lastertasunari dagokionak, laguntzen du. Era berean, fisika klasikoaren eta quantumen fisikaren arteko muga non dagoen jakiteko beste oinarrizko konstante bat aurkituko dugu, h, Plancken konstantea, hain zuzen.

Lehenengo lau ataletan fisika klasikoaren ezintasunak gainditzeko egin ziren lehenengo ahaleginak, quantumen mekanika zaharra deritzon teoria, alegia, aztertuko dugu eta bosgarren ataletik aurrera, quantumen mekanika modernoaren azterketa sistematikoa egingo dugu.

1.2 Gorputz beltzaren erradiazioa

Edozein gorputzek erradiazioa igorri eta zurgatu egiten du. Gorputzaren tenperatura ingurunearena baino beroagoa denean, zurgatu baino gehiago, igorri egingo du eta gorputzaren tenperatura jaitsi egingo da inguruarekiko bero oreka eratzen den arte. Oreka horretan gorputzak segunduko igortzen eta zurgatzen dituen energiak berdinak dira. Solidoek eta likidoek espektru jarraien bidez igortzen dute eta espektruaren maiztasun banaketak tenperaturarekiko aldakuntza nabariak jasaten ditu. Ohiko tenperaturetan gorputzek igortzen duten erradiazioa ikuskorra ez denez, gorputzen gainazaletan islatzen den erradiazioa besterik ezin dugu ikusi. Hala ere, edozein gorputz ilunbetan jarri eta tenperatura jasotzen balitz (1000K baino gehiago), aipatutako erradiazio termiko hori ikusiko genuke. Erradiazioaren kolorea tenperaturaren araberakoa da, hasieran gorria, eta tenperatura zenbat eta beroagoa izan, orduan eta zuriagoa izango litzateke ikusiko litzatekeen argia. Horrek esan nahi du igorritako erradiazioaren espektrua tenperaturaren araberakoa dela.

Oro har, konposizio desberdineko objektuek erradiazio termiko desberdinak igortzen dituzte, baina badago gorputz-mota berezi bat, gorputz beltza deritzona, bere erradiazio termikoa unibertsala duena. Gorputz beltzen gainazaletan ez da erradiaziorik islatzen, eta beltz ikusten dira, jasotzen duten erradiazio osoa zurgatzen dutelako. Tenperatura berean gorputz beltz guztiek, beren konposizio kimikoak axola ez diola, erradiazio espektru berdinak igortzen dituzte; horretan ez dago gorputzaren osagai kimikoen mendekotasunik.

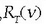Gorputz beltzen erradiazioaren espektru banaketa edo maiztasun banaketa erradiantzia espektralaren bidez adierazten da, magnitudea T tenperaturan eta v eta v + dv maiztasunen artean segunduko eta azalera unitateko bidalitako energia izanik. Gorputz beltzaren erradiantzia espektralaren lehenengo neurketa zehatzak Lummerrek eta Pringsheimek egin zituzten 1899an. Erradiantzia espektralaren integralari, hau da, T tenperaturan gorputz beltzek denbora eta azalera unitateko igorritako energiari erradiantzia deitzen zaio:

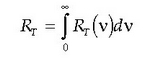
Erradiantzia espektralaren jokaera esperimentalaren (1.1 irudia) analisitik bi ondorio nagusi atera daitezke:

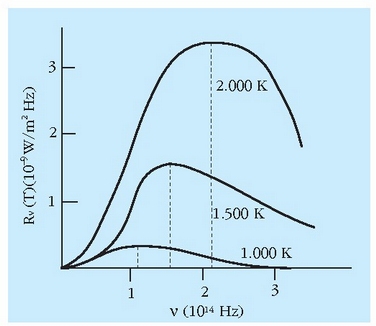
1.1. irudia: Gorputz beltzaren erradiantzia espektrala, erradiazioaren maiztasunaren funtzioan. Irudian ikus daitekeenez, tenperatura igotzen den neurrian, erradiazioaren maximoak goi-maiztasunetara jotzen du eta kurben azpiko azala, erradiantzia, azkar hazten da.

1. Tenperatura igo ahala, espektrua goi-maiztasunetarantz aldatzen da; espektruaren gehieneko puntuaren kokaera Wienen desplazamendu legeak azaltzen du:

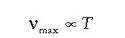
2. Erradiantzia tenperaturaren funtzio gorakorra da, Stefan-Boltzmann izeneko legea jarraituz:

non 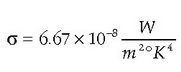konstante bat den.

Baina, nolakoak dira gorputz beltzak? Aipatu ditugun emaitza esperimentalak neurtzeko, gorputz beltzen eredu oso sinple bat erabili ohi da. Objektu baten barruan barrunbe bat egin behar da, barneko eta kanpoko ingurunearen artean oso zulo txiki bat utziz (1.2 irudia). Zuloan zehar sartzen den erradiazioa barrunbearenhormetan islatzen da, eta zuloa behar den bezain txikia bada, sar - tu den erradiazio hori hormek zurgatuko dute eta ez da berriro kanpora irtengo.

1.2. irudia: Gorputz beltzaren eredua. Zulotik sartzen den erradiazioa, isla batzuren ondoren zurgatu egiten da

Horrelako gorputz beltzak dira laborategietan erabiltzen direnak, barrunbeak eta zuloak gorputz beltza osatuz. Beraz, zulotxotik ateratzen den erradiazioaren espektrua eta barne-tenperatura neurtuz, ezagutu daiteke gorputz beltzaren irradiantzia espektrala.

Jo dezagun barrunbe kubiko bat dela eta hormak metalikoak dituela. Eremu elektrikoak zeharkako eremuak direnez eta gainazal metalikoetan eremua nulua denez (Ikus elektromagnetismoari buruzko atala), dimentsio bakoitzean barrunbean egon daitezkeen eremu elektriko bakarrak uhin geldikorrak dira, eta hau da horien adierazpena:

non 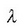uhin-luzera baita, v maiztasuna, eta 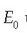uhinaren gehieneko anplitudea. Uhin-luzera eta maiztasuna c argiaren lastertasunaren bidez elkarrekin erlazionatuta daude:

Esan den bezala, hormetan eremuak nulua izan behar du, eta barrunbearen luzera a bada, 1.3 irudian ikus daitekeenez, maiztasunetarako onartutako balio bakarrak 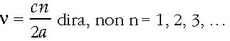den.

N( v) dv ikurraz v eta v + dv maiztasunen artean dagoen maiztasun kopurua adierazten badugu eta uhin elektromagnetikoek bi polarizazio onartzen dituztela (Ikus elektromagnetismoari buruzko atala) kontuan hartuz, ondoko hau ateratzen da:

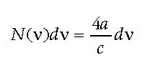
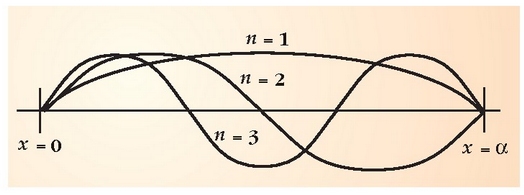
1.3. irudia: n=1,2 eta 3 balioei dagozkien uhin geldikorrak a luzerako barrunbe dimentsio-baklarrerako

Hiru dimentsiotako emaitzak aurreko emaitzaren berredura kubikoa izan behar duela badirudi ere, kalkuluak ez dira hain errazak, eta emaitza besterik ez dugu aipatuko:

non 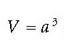gorputz beltzaren bolumena baita.

Formula honen bidez badaukagu uhin geldikorren kopurua kalkulatzea, uhin kopuruaren eta uhin bakoitzaren energiaren biderkadura sistemaren energia osoa izanik. Mekanika klasikoaren arabera uhin baten amplitudeak edozein balio har dezake, eta ikusiko dugunez, horretan datza mekanika klasikoaren hutsa. Askatasun gradu asko dituen sistema baten oreka termikoa aztertzeko mekanika estatistikoak emandako banaketa legeak erabili behar dira (Ikus termodinamikari buruzko atala). Boltzmannen banaketaren arabera, uhin bakoitzaren batez besteko energia < E > = KT da, non 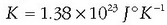Boltzmannen konstantea baita. Mekanika estatistikoak dioenez, uhin guztien batez besteko energia berdina da,maiztasuna edozein delarik ere. Horregatik, ( v, v + dv) tarteko maiztasunen energia bolumen unitateko edo energia dentsitatea ondoko hau da:

Goiko ekuazioari gorputz beltzaren Rayleigh-Jeans formula deitzen zaio, eta, 1.4 irudian ikus daitekeenez, bat dator behe-maiztasunetarako emaitza esperimentalekin. Rayleigh-Jeans formula klasikoa maiztasunaren funtzio gorakorra da, esperimentuetan, berriz, energia gehieneko dentsitatetik igaro ondoren beherantz doa. Goi-maiztasunetarako iragarpen oker horri hondamendi ultramorea deitzen zaio.

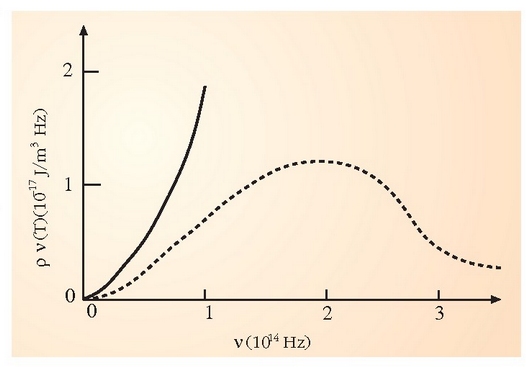
1.4. irudia: Rayleigh-Jeans formula klasikoak eta esperimentuek emandako emaitzen arteko konparaketa. Goi-maiztasunetarako desadostasunari hondamendi deitzen zaio.

1.3 Plancken teoria eta haren ondorioak

Boltzmannen banaketa estatistikoa mantenduz, mekanika klasikoaren emaitzak hobetzeko ondoko proposamen hau egin zuen Planckek: uhin bakoitzaren intentsitatea jarraia izan beharrean diskretizatua izatea. Beste era batean esanda, v maiztasuneko uhin batek izan dezakeen emendiorik txikiena da, non h doitu beharreko konstante bat baita. Teoriaren eta esperimentuaren akordioa lortzeko, h konstantearean balioa doitu zuen, era honetara:

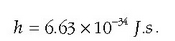
Aldaketa hori kontuan harturik, uhin geldikor bakoitzaren batez besteko energia da eta energia dentsitatearen adierazpena honako hau da:

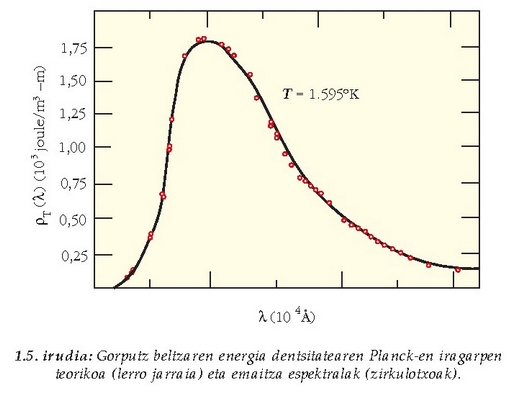
Formula horren emaitza 1.5 irudian ageri da, eta esperimentuekin erabat ados dago neurtutako tenperatura guztietarako. Planckek ez zuen Boltzmannen lege estatistikoa aldatu, uhin elektromagnetiko geldikorren energia aldakuntza diskretizatu baizik.

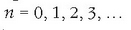Plancken teoria askoz orokorragoa da, esan baitaiteke n maiztasuneko edozein askatasun gradu harmonikori dagokion energia osoa ondoko era honetan adieraz daitekeela: non den. Beraz, energia aldaketarik txikiena da.

Hori egia bada, ohiko behaketetan zergatik ez da antzematen energiaren kuantizazioa? Esate baterako, pendulu baten oszilazioen anplitudea txikia denean sistema harmonikoa denez, Plancken postulatua aplika dakioke. Azter dezagun l =1m-ko luzerako eta m =1kg-ko masako pendulu baten kasua. Horrelako pendulu baten maiztasuna -koa izango litzateke eta Plancken postulatuaren arabera 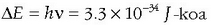izango litzateke energia aldaketarik txikiena. Penduluaren anplitudea 0.1 rad-ekoa dela hartuta, hau da penduluaren gehieneko energia potentziala:

Beraz, energiaren kuantizazioa neurtu ahal izateko 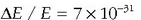balioko zehaztasuna behar da. Jakina, ezin da horren balio zehatza neurty eta ondorioa argi dago: h konstantea hain txikia denez, sistema klasikoetan energiaren kuantizazioa ez da begi bistan ageri edo, beste era batean esanda, fisika klasikoaren emaitzak berreskuratzeko h konstantearen balioa zerorantz eraman behar da.neurtu eta ondorioa argi dago: h konstantea hain txikia denez, sistema klasikoetan energiaren kuantizazioa ez da begi bistan ageri edo, beste era batean esanda, fisika klasikoaren emaitzak berreskuratzeko h konstantearen balioa zerorantz eraman behar da.

2. Erradiazioaren gorpuzki izaera

2.1 Efektu fotoelektrikoa

XIX. mendearen bukaeran Hertzek Maxwellen teoriak egiaztatzeaz gainera, efektu fotoelektrikoa deitu ohi dena ikusi zuen. Efektu fotoelektrikoa argiaren eta materiaren arteko elkarrekiko eraginean datza. Metal baten gainazala argi ultramorez argiztatzen bada, elektroiak ateratzen dira metal horretatik. Efektu fotoelektrikoa neurtzeko erabiltzen diren tresnen eskema 2.1 irudian ageri da. Ezkerretik bidalitako argi sorta monokromatikoa C katodora iristen denean, katodoak A anodorantz fotoelektroiak izeneko elektroiak igortzen ditu. Katodoaren eta anodoaren arteko elektroi jarioa korronte elektrikoa denez, galbanometroaren bidez (G) neur daiteke. Korronte horren intentsitateak nola jokatzen duen aztertzeko, katodoaren eta anodoaren arteko potentzial beherakada (V) eta argi intzidentearen intentsitatea aldatzen dira. Horrela egindako neurketen emaitzak 2.2 irudian ikus daitezke. Korronte fotoelektrikoa nulua izateko 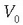balazta potentzial negatiboa jarri behar da, era horretara katodoak bidalitako elektroi guztiak balaztatuak dira eta ezin dira anodoraino iritsi. 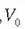Beraz, balazta potentziala elektroiaren gehieneko energia zinetikoarekin lotuta dago:

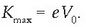
Balazta potentziala argi intzidentearen maiztasunaren funtzioan irudikatuz, (2.3 irudia) maiztasun minimo bat, 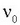ebakidura maiztasuna, dagoela ikus daitezke. Erabilitako argiaren maiztasuna ebakidura maiztasuna baino txikiagoa denean korronte fotoelektrikoa desagertu egiten da.

Efektu fotoelektrikoaren ezaugarri horiek ezin dira azaldu uhin teoria klasikoa erabiliz:

1. Uhin teoriaren arabera, intentsitatea emendatuz argi sortari dagokion eremu elektrikoa ere handitu egiten da. Horren arabera, elektroien energia zinetikoak handiagoa izan beharko luke, baina neurtutako gehieneko energia zinetikoa (2.2 irudia) ez dago argiaren intentsitatearen mende.

2.1 Irudia: Efektu fotoelektrikoaren azterketarako tresnaren eskema. A anodoa eta K katodoa metalezkoak dira eta hutsean daude.

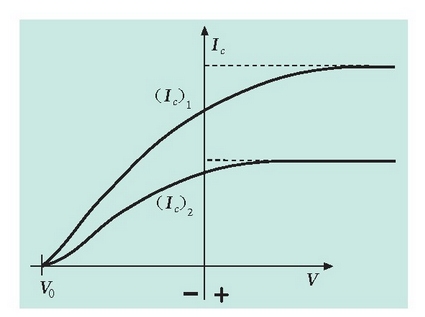
2.2. Irudia: Korronte fotoelektrikoaren intentsitatea V potentzialaren funtzioan eta argi intzidentearen bi intentsitatetarako.

2. Teoria klasikoei jarraituz, edozein argi erabilita ikus daiteke efektu fotoelektrikoa, elektroiak kitzikatzeko behar den energiarekin lotura duen parametro bakarra argiaren intentsitatea baita. Ostera, esperimentuetan maiztasun minimo bat dagoela ikusi da eta ebakidura maiztasun honen azpian dauden maiztasunek ez zutela efektu fotoelektrikorik sortzen.

Aipatutako arazo teorikoak direla eta, teoria klasikoa aldatu beharra zegoela uste izan zuen Einsteinek, eta bere teoria berria proposatu zuen. Plancken postulatua orokorragotzat hartu zuen, erradiazio energia multzotan biltzen zela esanez, fotoietan, hain zuzen ere. Planckek bere postulatua gorputz beltzaren barrunbean gertatzen denera mugatu zuen, uhin elektromagnetiko askeak kuantizatu gabe hedatzen direla uste baitzuen. Dena den, uhinen arteko interferentziak eta difrakzio esperimentuak ezin dira azaldu fotoien teoriaren bidez. Einsteinek oztopo guztiak gainditu zituen garai hartan egindako esperimentuen baldintzak aztertuz. Fotoi kopurua oso handia denean fotoi bakoitzaren jokaera ezin da aztertu, fotoi guztien batez besteko balioak baizik, eta batez besteko jokaera horren eraginez difrakzioa eta interferentziak sortzen dira.

Einsteinen teorian fotoiak lokalizatuta daude eta fotoi baten ener - giak badu lotura argiaren maiztasunarekin, era honetan:

Abiapuntutzat efektu fotoelektrikoan elektroiek fotoi bana zurgatzen dutela hartuz, ondoko dormula honen araberakoa izango litzateke metaletik ateratzen den elektroiaren energia zinetikoa:

non elektroiak metaletik ateratzeko egin behar den lana den.

W energia metal bakoitzaren ezaugarri bat da, eta W0 baldin bada metalaren elektroien lotura energia txikiena, elektroien gehieneko energia zinetikoa ondoko formula honen araberakoa da:

Aurreko formularen arabera, argiaren intentsitatea handiagotuz, fotoi kopurua ere handitu egiten da. Orduan, metalaren kontra fotoi gehiago bidaltzen direnez, elektroi gehiago ateratzen dira metaletik, baina beraien gehieneko energia aldatu gabe. Bestalde, elektroiaren energia zinetikoa nulua denean maiztasun txikiena zein den atera daiteke:

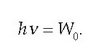
Argiaren maiztasuna n0 baino txikiagoa denean, fotoiak ez dira gai elektroiak ateratzeko, eta efektu fotoelektrikoa desagertu egiten da.

Beraz, laburtuz, argiaren kuantizazioaren bidez teoria sinple hau esperimentuen emaitza guztiak azaltzeko gai izan zen.

Efektu fotoelektrikoaren interpretazio honengatik 1921. urtean Albert Einsteinek Nobel saria jaso zuen.

2.2 Compton efektua

1923. urtean Comptonek argiaren gorpuzki izaeraren beste baieztapen garrantzitsu bat lortu zuen. Bere esperimentuan, X izpiz osatutako argi sorta bat igorri zuen grafitozko xafla baten kontra. Argi sorta intzidentearen uhin luzera inserted textbazen, bi uhin luzera ezberdin baizik ez zuen aurkitu sakabanatutako X izpietan: bata jatorrizko uhin luzera, bestea non intzidentzia angeluaren funtzioa zen. Uhin teoria klasikoan uhin luzeraren aldaketa honek ez du nola azaldurik. X izpi intzidenteen maiztasuna ? bada, elektroien karga elektrikoa dela eta, elektroiak dardar egiten hasiko dira, eta, horren ondorioz, maiztasun bereko eremu elektromagnetikoa igorri beharko dute, eta ez du zertan gertaturik topatzen den maiztasun lerraketa horrek.

Comptonek eta Debyek gertaera berri horri azalpena eman nahiz argiaren gorpuzki izaera erabili zuten. Berriro ere, fotoiek zatikiak balira bezala jokatzen dute, fotoien eta elektroien arteko eragina talka arrunt bat balitz bezala. Fotoiek eta elektroiek elkar jo dutenean (2.4 irudia) fotoiaren energia eta momentu apur bat elektroira igarotzen da, sakabanatutako fotoiaren energia eta momentua intzidentearena baino txikiagoa direlarik.

Elektroiak oso lastertasun handia hartzen duenez, ekuazio erlatibistak erabili behar dira Compton efektua azaltzeko. Lastertasun handiz higitzen den zatiki baten energia erlatibista era honetara adieraz daiteke:

2.4 Irudia: Fotoiaren eta elektroiaren arteko talka.

non c argiaren lastertasuna baita, p momentu lineala, eta zatikiaren geldiuneko masa. Fotoiari dagokionean, bere masa nuluaduenez, bigarren gaia zero da eta dugu, non h. Plancken konstantea baita, eta ? fotoiaren uhin luzera. 2.4 irudiko notazioa jarraituz, momentu linealaren kontserbazioa honela adierazten da:

Energia erlatibistaren kontserbazioak konako ekuazio hau ematen du:

non 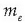elektroiaren geldiuneko masa baita, eta K elektroiaren energia zinetiko erlatibista.

Goiko ekuazioak burutuz, honako ekuazio hau ateratzen da:

eta h Plancken konstanteaz biderkatuz:

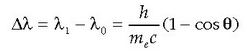
Aurreko hori da Comptonek atera zuen ekuazioa, eta neurketa esperimentalekin bat dator erabat.

Aipatu beharrekoa da efektu fotoelektrikoaren eta Compton efektuaren arteko ezberdintasuna ere. Lehenengo kasuan zurgapen prozesu bat aztertzen da, fotoien zurgapenarengatik elektroiak igortzen dira. Compton efektuan, ordea, sakabanaketa elastikoa gertatzen da fotoiak eta elektroiak pilotak balira bezala.

Albert Einstein (1879-1955)

Alemaniar-suitzar-amerikarra, erlatibitatearen teoriaren sortzailea da.

Einsteinen aita ingeniaria zen, eta, arazoak zituelarik negozioetan, familiak sarritan mugitu behar izan zuen herri batetik bestera. Ulmen jaio zen Einstein. Matematiketan larri zebilela-eta, behar baino beranduago, 17 urterekin, sartu zen Zuricheko Teknologia Institutu Federalean; graduatu zenean, Suitzako hiritar bihurtu zen, eta lan bila hasi zen unibertsitatean, eta baita eskoletan ere. Aurkitu ezinda, Suitzar Patente Bulegoan hasi zen lanean, Bernan. Ondo atera zitzaion: patente aztertzaile ona zen, eta aski denbora libre geratzen zitzaion bere ikerketak egiteko. 1903an, lankide bat, Mileva Maric fisikaria, esposatu zuen. Alaba bat izan zuten, eta bi seme gero. 1919an ordea dibortziatu egin ziren, eta Einstein bere lehengusu Elsarekin ezkondu zen; Elsak bi haur zituen bere aurreko senarrarengandik. Patente bulegoan zela, 1905ean, hiru artikulu argitaratu zituen, oso garrantzitsuak hirurak: Brownen higidura, efektu fotoelektrikoa eta erlatibitate berezia lantzen zituzten, hurrenez hurren.

Unibertsitateko aurreneko postua 1909an hartu zuen, Zuricheko Unibertsitateko irakasle laguntzaile gisa; ondoren, irakasle osoa izan zen Pragan (1910) eta Zurichen (1912).1913an, Berlinen, Fisikako Institutuko Zuzendari izendatu zuten, Gilen Kaiser Institutuan. Lehen Mundu gerraren urteetan osatu zuen erlatibitatearen teoria orokorra, eta argitaratu zuenean (1915), Fisikako Nobel saria eman zioten (1921), 1905ean egindako lanagatik.

Mundu guztian hitzaldiak ematen hasi zen, eta Kalifornian zen Hitler agintera iritsi zenean, 1933an. Ez zen Alemaniara itzuli; Berlinen dimisioa eman ondoren, Princentonen hasi zen lanean. Einstein gogor saiatu zen grabitazio indarra eta indar elektromagnetikoa eta nuklearra ekuazio sail batean bateratzen, baina ez zuen lortu. Garai hartan politikan ere aritu zen, lehen atomo bonba prestatzen lagundu baitzien aliatuei (Manhattan proiektua), eta, 1939an, Roosvelt lehendakariari jakinarazi zion, gutun baten bidez, horretan ari zirela alemaniarrak. 1952an Israelgo lehendakaritza eskaini zioten, baina ez zuen onartu. Bigarren Mundu gerraren ondoren, lan handia egin zuen arma nuklearren kontra. Bizimodu soila egiten zuen, eta arrantza eta musika zituen lanaz kanpoko zaletasun nagusiak.

1905eko lehen artikuluan, partikula txiki eskegien zorizko mugimendua aztertu zuen (Brownen higidura, 1828an aurkitua). Jariakari batean dagoen partikula txiki-txiki bat molekula inguratzaileez bonbardatzen baldin bada, norabide gabe mugitzen hasten da, eta Einsteinen kalkuluek molekulen existentziaren froga zuzenak eman zituen, Perrinek esperimentu bidez baieztu zuenean (1908).

Einsteinen hurrengo artikuluak efektu fotoektrikoa lantzen zuen, irrada fotoelektrikoa aztertuz, Maxwellen ekuazioen arabera normalean uhin gisara ulertzen zena. Einsteinen aburuz, argiaren energia sortetan bakarrik igor daiteke, alegia, Planckek erabilitako quantum direlakoetan. Einstein orduan gai izan zen Lenarden teoria (1902) esplikatzeko: haren arabera, gainalde metaliko batetik egotzitako elektroien energia, hura jotzen duen argiaren uhin luzeraren araberakoa da, baina ez intentsitatearen araberakoa. Horren emaitza quantumen teoriaren oinarriak jartzea izan zen, eta Plancken quantumak fisikako interpretazio batez osatzea.

Azkenik, erlatibitatearen teoria berezia osatu zuen Einsteinek (elkarri buruz lastertasun uniformez mugitzen diren gorputzetara mugatua), hirugarren artikuluan. Maxwellen uhin elektromagnetikoaren argiaren teoriak adierazten zuen argi uhin baten lastertasuna ez dela iturburuaren edo behatzailearen lastertasunaren araberakoa, eta, era horretan, kontra egiten zion mekanika klasikoari. Lorentz, Fitzgerald eta Poincarék transformazio bat aurkitu zuten Maxwellen ekuazioko mugimendu uniformeko parte batean, zeinak argiaren lastertasuna bere horretan uzten baitzuen, espazioaren eta behatzailearen lastertasun erlatiboak aldatu gabe alegia (Lorentz transformazioa).

Einsteinek proposatu zuen, zuzen proposatu ere, argiaren lastertasuna berbera dela elkarri buruz mugitzen diren parametro guztietan; berakjakin gabe, Michelson-Morley esperimentuak agertu zuen hori (1881, 1887); erlatibitatearen printzipioa aurreratu zuen, hau da, lege fisiko guztiak berdinak direla elkarri buruz mugimendu uniformea duten parametro guztietan. Einsteinek ateratako beste ondorio bat da, ezen gorputz baten energia E kopuru batez aldatzen baldin bada, orduan haren masak E/c2 aldatu behar du (c argiaren lastertasuna izanik).

1907tik aurrera, erlatibitatearen teoria elkarri buruz azeleratzen ari diren parametroetara zabaltzen saiatu zen Einstein. Grabitazio azelerazioa eta mugimendutik datorrena, azeleratzen ari den parametro batean behatuz gero, guztiz baliokide direla zen hastapen nagusia (baliokidetasunaren hastapena). Hortik, iragarri zuen grabitazio erakarpenak argi izpiak makurraraziko zituela.

1911n iragarpen zehatz bat egin zuen: Eguzkia doi-doi ukitzen duen izar baten argiak arkuko 1,7" desbideratu behar du. 1919. urtean eguzki eklipse oso bat izan zenean, Eddingtonek neurtu zuen fenomeno hori Afrika Mendebalean, Principén, eta aurkitu zuen arkuko 1.6" zela. Froga ikusgarri horrek berehala famatu zuen Einstein mundu osoan, eta argi utzi zuen fisikaren oinarriak mugiarazi zituela. 1915ean osorik argitaratu zuen erlatibitatearen teoria, Riemannen geometria eta matematikako beste ideia batzuk erabiliz, hala H. Minkowski (1864-1909) (1907an), Riemann (1854) eta C. Riccirenak (1853-1925) (1887an). Masa hartu zuen espazio-denboraren ‘lautasuna’ itxuraldatzeko, eta espazioan elkarri buruzko bide makurretan zehar mugitzen diren gorputzak sorrarazteko. Hortik sortzen den ‘grabitazio’ erakarmena Newtonen legeak iragarritakoaren oso antzekoa bada ere, badira zuzenketa txiki batzuk. Einsteinek eta M. Grossmannek (1878-1936) egindako kalkuluen arabera, Merkuriok Eguzkiaren inguruan egindako elipseak arkuko 43" errotazio handiagoa behar zuen izan gizaldiko, Newtonen teoriak zioena baino. Hori behatu zelarik, hain zuzen ere 43" gehiago da balioa. Hala esan zuen orduan Einsteinek: ‘Nire onetatik aterea nengoen, estasiaren estasiz, garai hartan’.

Erlatibitate orokorrak beste iragarpen harrigarri asko ekarri zituen, hala adibidez grabitazio eremu batetik bestera igarotzen den argiak aldaketa bat izango zuela bere uhin luzeran. Ortzian, 1925an aztertu zen hori, eta Lurrean, R. Pound eta G. Rebkak ikusi zuten, 23 metroko dorre batekin, Mossbauer efektua erabiliz, 1959an. Uhin luzera handiagoa zutela aurkitu zen dorreko behealdetik goraino mugitzen ziren gamma izpiek.

Era berean, munduaren eredu kosmologikoak erabat aldatu zituen erlatibitate orokorrak; hala, Friedmannek (1922), espantsioan ari den unibertso bat irudikatzen duen eredu bat proposatu zuen, Einsteinen ekuazioen araberakoa.

1920 eta 1930 ondoko hamarraldietan, quantumen teoriari buruzko eztabaidetan jardun zuen Einsteinek, Bornen probalitatearen kontzeptuari uko eginez (‘Jainkoa izan daiteke burutsua, baina maltzurra ez da’). Era berean, saiatu zen eremu elektromagnetiko eta grabitazio eremuen teoria bateratu bat aurkitzen, baina ez zuen lortu. Hala esan zuen 1921ean: ‘Munta handiko aurkikuntzak gazteen gauza dira…, eta, hortaz, horiek iraganeko kontuak dira niretzat’.

3. Zatikien uhin jokaera

3.1 Materia uhinak

Aurreko atalean erradiazioaren zatiki jokaerari buruzko lehenengo esperimentu eta teoriak aipatu ondoren, atal honetan zatikien uhin ezaugarriak aztertuko ditugu.

Louis de Brogliek, unibertsoa materiaz eta erradiazioaz osatua denez, bi osagai hauen arteko asimetria ez zuen gustoko. Egindako esperimentuaren arabera argiak uhin (difrakzioa, interferentziak,…) edo zatiki (efektu fotoelektrikoa, Compton efektua) bezala jokatzen duenez, zergatik ez baliatu teoria hori bera zatikietarako? 1924. urtean de Brogliek E =hv ekuazioak bai uhinetarako, bai zatikietarako balio zuela proposatu zuen. Momentu eta uhin luzeraren arteko 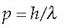erlazioa erabiliz de Broglieren formula ondoko eran idatz daiteke:

Erlazio hau orokorra bada, zergatik ez dugu behatzen edozein zatikiri dagokion uhin luzera? Kalkulu erraz batek lagunduko digu ulertzen. 10 m/s-ko lastertasuna eta 1kg-ko masa dituen pilota baten uhin luzera kalkulatzen badugu, balioa ateratzen da, eta penduluaren energiaren kasuan bezala ezinezkoa da hain balio txikia neurtzea. 100eV-ko energia duen elektroi bat hartuta, berriz, bere uhin luzera 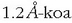du. Oso balio txikia badirudi ere, materiaren atomoen arteko distantzia batzuetakoa denez, badago difrakzio efektuak ikustea elektroiak material baten kontra bidaliz. Esperimentu hori egin zuten, hain zuzen ere, Davisson eta Germerek, eta elektroien uhin jokaera erakutsi zuten.

De Broglieek asmatutako teoriari esker, uhinen eta zatikien arteko simetria berria ondo oinarrituta geratu zen. Unibertsoaren osagai guztiek berdin jokatzen dute eta Plancken konstantearen eta zatikiaren edo uhinaren momentuaren arteko erlazioak zehazten du ikus dezakegun jokaera.

3.2 Heisenbergen ziurgabetasunaren printzipioa

Mekanika klasikoan zatiki baten ibilbidea jakin ahal izateko bere gaineko indarrak eta hasierako baldintzak, hau da, hasierako posizioa eta lastertasuna ezagutzea aski litzateke. Hala ere, neurketa prozesuetan behatzaileak sistemaren baldintzak aldatu egiten ditu. Zatikiaren masa oso handia denean behatzailearen eta sistemaren arteko eragina kontuan ez hartzeko modukoa da, mundu makroskopikoan gertatzen den bezala, baina masa txikiko zatikiak azter - tzean, behatzailearen eragina aintzat hartu beharrekoa da.

Heisenbergek zehaztasun osoa lortzeko ezintasuna ondoko formula honetan adierazi zuen:

non momentuaren eta posizioaren x koordenatuen ziurgabetasunak diren, hurrenez hurren. Formula horrek ez du esan nahi zatikiaren posizioa edo zatikiaren momentua zehazki jakiterik ez dagoenik, horiek biak batera zehaztasun osoz ezagutzea ezinezkoa dela baizik. Bi osagaien gaineko ziurgabetasunen biderkadura da magnitude garrantzitsua. Jakina, momentuaren eta posizio bektorearen y eta z osagaiei erlazio bera aplikatzen zaie baina ekuazioak arintzeko asmoz, batez ere, sistema unidimentsionalak aztertuko ditugu.

Badago ziurgabetasunaren printzipioaren bigarren zatia, neurtutako energiari eta neurketa egiteko behar den denbora tarteari dagokiena:

Aipagarria da h Plancken konstantea berriro agertzea. h konstantearen balioa oso txikia denez, fisika klasikoan eta mundu makroskopikoan ziurgabetasunaren printzipioaren aztarnarik ezin dugu ikusi. Ziurgabetasuna dela eta, ezin ditugu zatikiaren hasierako baldintza mekanikoak ezagutu eta, horren ondorioz, sistema batek jarraituko duen ibilbidea ezin da zehaztasun osoz jakin. Beraz, quantumen munduan iragarpen deterministak egin ordez, gertaerak suertatzeko probilitate erlatiboak behar dira kalkulatu.

Ziurgabetasunaren printzipioa hobeto ulertzeko Bohrek proposatutako arbel esperimentua aztertuko dugu. Jo dezagun elektroi baten posizioa ezagutzeko mikroskopio bat erabili nahi dugula, 3.1 irudian ageri den bezala. Elektroia ikusi ahal izateko fotoiak bidali behar zaizkio, baina Compton efektua dela eta, elektroiaren eta fotoiaren momentuak aldatu egingo dira. Beraz, behaketa egin aurretik elektroiak zeukan egoera mekanikoa aldatu behar dugu eta neurketa prozesuak berak elektroiaren egoeraren gainean eragiten du. Gainera, behatzailearen eta behatutakoaren arteko eragina beti gertatzen da, beharrezkoa baita neurketa egiteko. Demagun elektroi bakar batek elektroiaren aurka talka egiten duela. Sakabanatutako fotoiak 3.2 irudiko tarte angeluarraren barruan irten behar du mikroskopioaren objektiboan sartzeko. Horrek esan nahi du sakabanaturiko fotoiaren momentuaren x osagaiak tik + -rako tartean egon behar duela, non p fotoiaren hasierako momentu lineala den. Beraz, talka egin eta gero era honetakoa da fotoiaren momentuaren gaineko ziurgabetasuna:

Momentuaren kontserbatzioak elektroiaren momentuaren aldaketa fotoiarenaren aurkakoa izatera behartzen duenez, elektroiaren momentuaren gaineko ziurgabetasuna fotoiarenaren berdina da. Baina, fotoiaren posizioari buruz, zer dakigu? Mikroskopioaren bidez lor daitekeen fotoi baten irudia ez da puntuala, disko bat baizik. Difrakzioarengatik bereizmen ahalmena mugatua da (Ikusoptikari dagokion atala) eta posizioaren x osagaiaren gaineko ziurgabetasunerako diskoaren erradioa hartzen bada, honako emaitza hau ateratzen da:

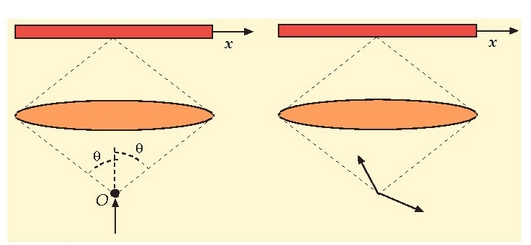
3.1. Irudia: Ziurgabetasunaren printzipioaren oinarria azaltzeko Bohr-ek proposatutako arbel-esperimentuaren eskema.

eta elektroiaren ziurgabetasunak biderkatuz:

Emaitza hau ziurgabetasunaren printzipioak emandako limitearekin ados dago. Ez da pentsatu behar emaitza hau misteriozkoa denik, erradiazioaren kuantizazioaren ondorioa besterik ez da eta, berriro ere, fisika klasikoaren eta quantumen fisikaren arteko mugaren giltza Plancken konstatean datza.

3.3 Zatiki uhinen ezaugarriak

De Broglieren printzipioa erabiliz, hau da, zatikien uhin jokaera kontuan hartuz, badago Heisenbergen printzipioa frogatzea, atal honetan ikusiko dugunez.

Uhin baten 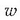hedapen lastertasuna ondoko formularen bidez adieraz daiteke, 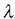uhin luzeraren eta n maiztasunaren funtzioan: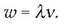

De Broglieren printzipioaren arabera 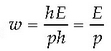da zatikiaren ph p lastertasuna. Energia potentziala nulua bada, energia osoa energia zinetikoa besterik ez da:

Beraz, zatiki uhinaren lastertasuna w da eta zatiki uhinak adierazten duen zatikiaren lastertasuna da. Itxurazko kontraesan hau erraz azal daiteke materia uhinei interpretazio fisikoa emanez. Ikusiko denez, zatikia espazioko puntu batean egoteko probabilitatea uhinaren anplitudeak adierazten du eta ziurgabetasunaren printzipioaren arabera elektroiaren posizioa erabat zehaztuta ez dagoenez, materia uhinaren anplitudea ez da zero izango espazioko tarte batean. Demagun uhinaren anplitudea neurtzeko gai den tresna bat badela, eta tresna horren bidez elektroi bati dagokion anplitudea neurtu dugula. Adibidez, unean neurtutako uhina 3.2 irudiko uhina izan daiteke. Denbora pasa ahala, irudiko uhina, uhin taldea deritzona, eskuinera mugituko da zatikiaren higidurari dagokion lastertasunaz. Puntu horretan agertzen da uhinaren lastertasunari interpretazioa eman beharra: uhin taldebaten higiduraren barruan bi lastertasun mota bereizi behar dira, w fase lastertasuna eta g talde lastertasuna, alegia.

3.2. irudia: t = 0 unean zatiki bat adierazten duen uhina.

3.3. irudia: Bi uhin sinusoidalen batura, bi uhinen maiztasunak eta uhinzenbakiak antzekoak direla. Puntuzko lerroak uhinaren inguratzailea adierazten du

Bi lastertasun horien arteko desberdintasuna aztertzeko, kasurik errazenetik hasiko gara, uhin sinusoidalarenetik.

Uhin sinusoidal edo harmoniko baten adierazpena honela da:

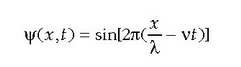
non 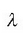uhin luzera baita, v maiztasuna, eta uhinaren lastertasuna da, honetan 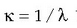uhin zenbakia dela. Uhin sinusoidalek ez dute adierazten 3.2 irudiko funtzioa bezalako uhin talderik. Uhin sinusoidalen anplitudea espazioko toki guztietan konstante denez zatikiaren posizioaren ziurgabetasuna erabatekoa da, zatikia edonon egon liteke.

Uhinaren anplitudea modulatu egin behar da uhin talde bat lortzeko. Anplitude modulazioari esker, zatikia aurkitzeko probabilitatea eremu finitu batera mugatuko da eta lokalizatutako zatikiak adieraz daitezke. Matematikoki, maiztasun desberdineko funtzio harmonikoen kopuru infinitua batuz egiten da, baina metodoaren oinarria ulertu ahal izateko aski da ondoko bi uhinen batura kalkulatzea:

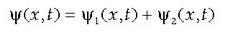
non

eta

baitira, eta direla aukeratu diren.

Formula trigonomotrikoen bidez garatuz, era honetara idatz daiteke bi uhinen batura:

3.3 irudian ikus daitekeenez, uhin osoaren anplitudea modulatua da eta uhin taldez osatuta agertzen da. Bi uhin bakarrik batu beharrean kopuru infinitua batuz gero, uhin talde bakarra agertuko litzateke.

Irudian azkar aldatzen den osagaiaren lastertasuna berriro da baina modulazioarena (3.3 irudian puntuzko lerroa), hau da, uhinaren inguratzailearen lastertasuna (talde lastertasuna) hau da:

Einsteinen eta de Broglieren erlazioak erabiliz talde lastertasuna eta zatikiaren lastertasun berdinak direla frogatzen da, hasierako kontraesanari azalpena emanez.

Uhin taldeen talde lastertasuna kalkulatu eta gero, ziurgabetasun erlazioak beste era batean azter daitezke. Zatikia bat adierazten duen uhin funtzioa sinusoidala bada, uhin luzera finkoa da eta momentuan ez dago inolako ziurgabetasunik. Posizioari dagokionez, ordea, guztiz ezezaguna da, uhinaren anplitudea berdina baita espazioko edozein puntutan. Anplitudea posizioaren eta denboraren funtzioa izateko uhin batzuk gainezarri behar dira, bakoitzak maiztasun eta uhin luzera desberdinak dituela. Era honetan eraikitako uhin taldeek bi ziurgabetasunak erakusten dituzte, espazioan eta momentu linealean.

3.4 Ziurgabetasunaren printzipioaren ondorioak

Ziurgabetasunaren printzipioari esker erraz uler daiteke uhinen eta zatikien bikoiztasuna. Uhinaren eta zatikiaren kontzeptuak ez dira kontrajarriak quantumen fisikan, egindako esperimentuaren baldintzek behartuak baizik. Adibidetzat Youngen esperimetua aztertuko dugu.

Youngen esperimentua optika arloan erabili ohi da argiaren uhin izaera frogatzeko. Uhin sinusoidal bat elkarren hurbil dauden bi zirrikituetan zehar igaro ondoren, zirrikituen atzean kokatutako pantaila batean intentsitatea jasotzen da. Pantailan jasotako irudia uhin intzidentearen intentsitatearen arabera aldatzen da, eta ondoko gertaeraak ageri dira:

1. Argi sorta intzidentearen intentsitatea handia denean, edota esposizio denbora oso luzea denean, fotoi askok hartzen dute parte esperimentuan. Bi zirrikituetatik igarotako uhinen arteko interferentziarengatik, pantailan gune argitsu eta ilun azaltzen dira. Argiaren uhin jokaeraren egiaztapena denez, erradiazioa erabat gorpuzkizkoa delako teoria ezin da onartu.

2. Zirrikituetan zehar fotoi gutxi igarotzen direnean, ez da interferentzia irudirik ikusten, inpaktu lokalizatuak baizik. Honen arabera erradiazioaren uhin deskribapen hutsak ezin du neurtutakoa azaldu.

3. Azken kasu honetan fotoien momentuaren ziurgabetasuna dela eta, pantailako inpaktu banaketa zorizkoa da. Hala ere, inpaktu dentsitatea interferentzia irudiaren proportzionala da. Horregatik zenbat eta fotoi gehiago erabiltzen diren irudiaren itxura orduan eta gehiago hurbiltzen da interferentzia irudira.

Beraz, Einsteinek uste izan zuen bezala, uhin efektuetan batez besteko balio estatistikoek eragiten dute. Fotoi bakar baten jokaera aztertzean, ordea, zatikiek bezala jokatzen duela ikusten da.

3.4. Irudia: Young-en zirrikitu bikoitzaren esperimentua. a) Zirrikitu bakoitzak sortutako difrakzio-irudiaren intentsitatea beste zirrikitua estalita dagoenean. Puntuzko lerroa intentsitateen batura da. b) Interferentzia irudiaren intentsitatea bi zirrikituak irekita daudenean. Intentsitatearen aldaketak argiaren uhin-izaera egiaztatzen du.

Broglie, Louis-Victor Pierre Raymond, dukea, printzea

(1892-1987)

Frantses fisikaria. Berak aurkitu zuen zatikien uhin portaera.

Louis de Broglieren familia piamontetarra zen jatorriz. 1740an, Luis XIV.ak duke titulu jaraunsgarria eman zion familiako buruari. Hala, 1960an, bere anaia Maurice (fisikaria hau ere) hil zenean, Louisek jarauntsi zuen duke titulua. Printze titulua berriz (alemaniarra), Austriarrentzat Zazpi Urteko Gerran (1756tik 63ra) familiak egindako zerbitzuengatik zuen. Broglie, ikasketaz, historialaria zen, eta Lehen Mundu Gerran, Eiffel dorreko irrati estazioan ari zela piztu zitzaion zientzietarako interesa. Sorbonan egin zuen fisikako doktoretza (1924) eta fisikaren teoriako irakasle izan zen orduan sortu berria zen Henri Poincaré institutuan (1928-62).

Argiaren bi teoria matematikoak uztartzeko ahaleginetan –korpuskularra eta uhin teoria–, bere doktoretza tesian uhin mekanika izenekoa sortu zuen. Teoria horren arabera, mugitzen diren zatikiek uhinen portaerak eta tasunak dituzte. Teoria hori egiaztatuta geratu zen hurrengo urtean, Davissonek eta Germerrek, kristal xafla bat erabiliz, elektroi sorta bat difraktatzea lortu zutenean. Fisikako Nobel Saria irabazi zuen Brogliek 1929an.

4.Bohren eredu atomikoa

4.1 Thompson eta Rutheforden eredua

1910. urtean atomoetan elektroiak zirela ezaguna zen. Elektroiaren karga elektrikoa negatiboa dela eta atomoen karga osoa nulua dela kontuan hartuz, fisikariek eta kimikariek bazekiten beste osagai batek egon behar zuela. Hala ere, atomoaren barruan elektroien eta karga positiboaren arteko banaketari buruz ezer gutxi zekiten. Thompsonek karga positiboaren dentsitatea 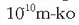esfera batean konstante zela eta elektroiak uniformeki banatuta zeudela proposatu zuen. Bere ereduaren arabera, egoera atomiko arruntean, orekan, elektroiak geldirik daude, sistema osoko energia ahalik eta txikiena izateko. Atomoaren egoera kitzikatuetan, berriz, elektroiak bibratzen ari ziren eta bibrazio horiek sortarazten zituzten atomoaren igorpen espektruak. Hala ere, eredu hau onartuz gero, oinarrizko kalkuluek erakusten dute Hidrogenoaren kasuan marra espektral bakar bat legokeela, esperimentalki neurtutakoarekin desadostasun osoa erakutsiz.

1911. urtean Rutherfordek xafla metaliko baten kontra helio atomoak jaurtiz, eta hartatik barreiatzen ziren zatikien banaketa aztertuz, Thompsonen eredua okerra zela egiaztatu zuen. Emaitza esperimentaletatik lortutako ereduan, karga positiboa eta harekin batera atomoaren masa gehiena eremu txiki batean, nukleoan, bilduta dago, eta eremu horren erradioa 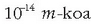da. Gaur egun dakigunez, Rutherforden eredua benetako atomoetatik oso hurbil dago.

4.2 Atomoaren egonkortasuna

Rutherforden eredua ezin da ulertu teoria klasikoaren bidez. Planetek eguzkiaren inguruan bezala, elektroiak nukleoaren inguruan biraka dabiltzala irudika daiteke. Hala ere, elektroiak kargatuak dira eta teoria elektromagnetiko klasikoaren arabera, azeleraturiko zatiki kargatuek erradiazio elektromagnetikoa igorri behar dute. Demagun elektroien ibilbideak zirkularrak direla. Orduan, azelerazio tangentziala nulua bada ere, azelerazio normala badago eta elektroiak uhin elektromagnetikoak igortzen ditu. Igorritako energia elektroiaren energia mekanikoari kendu behar zaio, elektroiaren energia mekanikoa gero eta txikiago delarik. Ondorioa argi dago: elektroiaren ibilbideak ezin dira zirkularrak izan, espiral itxurakoak baizik, eta aldi baten buruan nukleora erori behar du. Gainera, hala balitz, igorritako uhin elektromagnetikoaren espektrua jarraia izango litzateke eta hurrengo atalean ikusiko denez, esperimentuetan ikusi diren espektruak diskretuak dira. Arazo honek bultzatu zuen Bohr bere eredu atomikoa proposatzera.

4.3 Espektru atomikoak

Gas monoatomikoaz betetako hodi batean zehar korronte elektrikoa igarotzen denean, gas horretako atomoek elkar jotzen dute,eta kitzika egoerak sortzen. Alditxo baten ondoren kitzikatutako atomoek egoera normalera itzuli behar dute, soberako energia uhin elektromagnetikoaren bidez igorriz. Esperimentuek erakusten dute atomo askeak igorritako erradiazioaren espektrua ez dela jarraia, soilik uhin luzera diskretu batzuetarako gertatzen dela. Uhin luzera bakoitzari marra espektrala deitzen zaio eta uhin luzeren multzoari segida espektrala (4.1 irudia). Segida espektralak atomoaren ezaugarri zehatzak dira, beraz, marra espektralak neurtuz hodian dagoen atomo mota zein den jakin daiteke. Nahiz eta espektru atomikoak oso korapilotsuak izan daitezkeen, atomo sinpleetarako formula enpiriko errazen bidez adieraz daitezke. Hidrogeno atomoaren segida espektralerako lehenengo formula Balmerrek proposatu zuen 1885. urtean, eta Rydbergek 1890.ean beste elementu kimiko batzuetarako orokortu zuen marra espektralaren adierazpena ondoko formula honen bidez:

4.1. Irudia: Balmer-en segidari dagozkion hidrogenoaren marra espektralak (Å-etan).

non Rydbergen konstantea, eta a eta b espektru bakoitzeko konstanteak baitira. m zenbaki oso finkoa da eta n zenbaki oso aldakorra da.

Esaterako, hidrogeno atomoaren kasuan Balmerren formula lortzeko a =b=0, eta m = 2 egin behar da, eta honako formula hau geratzen da:

4.4 Bohren postulatuak eta eredua

Hidrogeno atomoaren marra espektralen egitura azaldu nahian, Bohrek eredu sinple bat proposatu zuen, ondoko puntu hauetan oinarrituz:

1. Elektroiak Coulomb erakarpen indarrari esker, nukleoaren inguruan ibilbide zirkularretan higitzen dira mekanika klasikoaren legeen arabera.

2. Mekanika klasikoan orbita kopurua infinitua bada ere, elektroien kasuan orbita guztiak ez dira onargarriak. Orbitaren L momentu angeluarrak 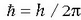konstantearen anizkoitza izan behar du: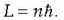

3. Nahiz eta aipatutako orbitetan elektroiaren azelerazio normala nulua ez izan, elektroiek ez dute erradiazio elektromagnetikorik igortzen eta elektroien energiak konstante dirau.

4. Elektroiak orbita batetik beste orbita batera igarotzen direnean erradiazioa elektromagnetikoa era ezjarraian igortzen dute, eta igorritako erradiazioaren maiztasuna ondoko formula honetan adierazten da:

non hasierako eta bukaerako orbiten energiak diren, hurrenez hurren.

Lehenengo postulatuak nukleoaren existentzia hartzen du kontuan. Bigarrenak orbiten kuantizazioa sortzen du. Plancken arabera kuantizaturiko magnitudea energia zen eta Bohrek momentu angeluarrari jarri zion kuantizazio baldintza. Hirugarren puntuaren bidez atomoaren egonkortasunaren arazoa konpondu egiten da eta azkenak marra espektralen egitura diskretua azaltzeko balio du.

Borhen postulatuen balioa aztertu nahi bada, horietan oinarrituta egiten diren iragazpenak emaitza esperimentalekin konparatu behar dira. Demagun +Ze kargako eta M masako nukleoaz eta -e kargako eta m masako elektroi bakarrez osatutako atomoa aztertu nahi dela. Elektroiaren egonkortasun mekanikoa lortzeko ondoko erlazioa bete behar da:

non v elektroiaren lastertasuna eta r orbitaren erradioa diren.

Ekuazioaren lehen atala Coulomb erakarpena da eta bigarrenak elektroiaren azelerazio normala adierazten du. Elektroiaren gaineko indarra erradiala denez, elektroiaren momentu angeluarra, L = mvr, higiduraren konstante bat da. L = nh = mvr kuantizaziorako baldintza aplikatuz, eta aurreko ekuazioan v ordezkatuz ondoko formula hauek atera daitezke:

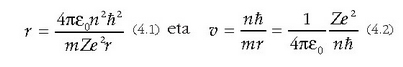
Orbitaren energia osoa era honetan kalkulatzen da:

Energia potentziala

Energia zinetikoa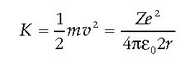

Energia osoa

(4.1) ekuazioa erabiliz energia osoa era honetan idatz daiteke:

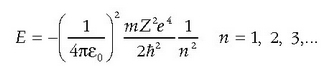
Beraz, momentu angeluarraren kuantizazioak energiaren kuantizazioa eragin du.

Bohren 4. postulatua erabiliz erraz kalkula daitezke elektroiek igorritako erradiazio elektromagnetikoaren maiztasun onartuak:

eta k uhin zenbakiaren funtzioan:

non

eginez eta R konstantearen balioa Rydbergen konstantearena dela konturatuz, (4.3) ekuazioa, Balmerren segida espektralarena, alegia, eskuratu dugu berriro.

Bohr, Niels (Henrik David)

Daniar fisikari teorikoa: atomoen egitura elektronikoaren quantum teoria aurreratu zuen.

Familia onetik zetorren Bohr: aita fisiologiako irakaslea zen Kopenhagenen, eta anaia gaztea, Harald, talentu handiko matematikaria. Niels eta Harald, biak, futbol jokalariak ziren, profesionalak, eta Nielesek eta bere semeak, Aagek (1922an jaio zen), biek irabazi zuten Fisikako Nobel saria, 1922an eta 1975ean hurrenez hurren.

Bohrrek, Kopenhagen doktoretza amaitu ondoren (1911), zortzi hilabete eman zituen Cambridgen, J.J. Thompsonekin; Thompson ez zuten erakarri atomoaren egiturari buruz Bohrrek zeuzkan ideiek, eta, hala, Ruthefordengana jo zuen, Manchesterra, eta lau urte eman zituen han. Rutheforden atomoaren ereduaren arabera (1911), nukleo zentral positibo baten inguruan daude elektroiak, baina, fisika klasikoaren arabera, sistema hori ez litzateke egonkorra izango. Bohrrek, arazo hori gainditzeko, adierazi zuen elektroiak orbita mugatuetan mugitzen direla nukleoaren inguruan, eta atomoak nola igortzen eta absorbatzen duen energia agertu zuen. Era horretan, quantumen teoria atomoaren egituraren kontzeptuarekin konbinatu zuen.

1916an Bohr Kopenhagera itzuli zen, eta bi urte geroago hango Fisika Teorikoko Institutuko lehen zuzendaria izendatu zen. Zentro hori izan zen belaunaldi batez fisika teorikoaren gune nagusia, eta hantxe jardun zuten mundu osoko fisikariak quantumen teoria osatzen. Lehen urte horretan, Bohrrek ‘korrespondentziaren printzipioa’ adierazizuen: fisika mikroskopikoko quantum bidezko deskribapen batek deskribapen klasikora jo behar du, dimentsio handigoetarako.

‘Osagarritasun printzipioa’ 1927an agertu zen: ez dago erabateko banaketarik objektu atomikoen eta haiek neurtzen dituzten tresnen elkarrekiko eraginaren artean. Bat dator hori Broglieren ideiarekin, alegia, baliokide direla materiaren uhin eta partikula deskribapena; Heisenbergen ziurgabetasunaren printzipioa eta Bornen uhinen probabilitatearen erabilera materia deskribatzeko, bat datoz orobat printzipio horrekin.

Rutheforden lanak fisika nuklearra garatu zuen; hala, 1930 inguruan, gai zen Bohr quantumen teoria nukleoari ere aplikatzeko. Horren arabera, nukleoan neutroiak eta protoiak estu-estu daude lotuak, molekulak isurkari tanta batean bezala (1936). Nukleoen erantzunak, energia desberdineko neutroiak jotzen dituztenean era askotakoak direlarik, ‘isurkari tanta’ horren egoera kitzikatu posibleak kontuan izanik ager daitezke. 1939rako, bazuten Bohrrek eta J.A. Wheelerrek (1911- 15) fisio nuklearraren teoria egoki bat, eta gai ziren aurrez esateko uranio-235a isotopo egokiagoa izango zela fisiorako (eta, Einsteinek seinalatu zuen bezala, atomo bonbarako), uranio-238a baino.

1943ko udazkenean arriskuan zegoen Bohr Danimarka okupatuan (ama judua zuen), eta Suediara ihes egitea erabaki zuen, arrantza ontzi batean. Ingalaterrara eraman zuten gero, Mosquito hegazkin baten bonba gordelekuan. Danimarkatik alde egin baino lehen, azidoan disolbatu zuen bere Nobel sariko urrezko domina astuna; alemanek ez zioten itxura txarrik hartu disoluzio itxura inuzenteko hari; gero, metalera erreduzitu, eta domina berregin zuen. Ihes egin ondoren, atomo bonbaren plangintzan sartu zen. 1944an atomo bonbek zuten arriskuaren berri eman zien Roosvelt eta Chruchilli, eta Mendebalaren eta Sobiet Batasunaren arteko akordioak egiteko beharraz ere mintzatu zitzaien. Ondoren, 1955an, Bakerako Atomoen lehen Konferentzia antolatu zuen Geneban.

Hil zenean, 1962an, mundu osoan onartu zen Bohr munduko fisikari teoriko nagusitzat, Einsteinen ondoren. Bohrren atomoaren eredua behatu diren espektroetan atomo soilenen kasuan bakarrik adosten da ondo (hidrogenoa eta helioa), eta asko aldatu zuten gero, baina kontzeptua mugarria gertatu zen fisikan nahiz kimikan. Era berean, nukleoaren isurkari tantaren eredua ere asko garatuko zuten gero, Aage Bohrrek bereziki.

4.5 Kuantizazio baldintzen interpretazioa

Bohren ereduak arrakasta izugarria izan zuen fisikari eta kimikarien artean baina Plancken energiaren kuantizazioaren eta Bohren momentu angeluarraren kuantizazioaren arteko erlazioak misteriozkoa zirudien. 1916. urtean Wilson eta Sommerfeldek bai Plancken bai Bohren kuantizaziorako aplikagarriak diren arau orokorrak postulatu zituzten.

Emandako arauak honela adieraz daitezke:

Edozein sistema fisikotan denboraren funtzio periodikoa den koordenatu bakoitzerako badago ondoko kuantizazio baldintza hau:

integral berezia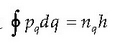

non q koordenatu periodikoa baita, eta q koordenatuari dagokion momentua 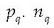zenbaki osoa da eta «integral berezia» ikurrak periodo batean egindako integrazioa adierazten du.

Kuantizazio arau hauen esangura ulerterrazagoa egingo zaigu orain arte ikusi ditugunetako bi adibide aztertuz.

1.Osziladore harmonikoa

Osziladore unidimentsionalaren energia osoa, zinetikoa gehi potentziala, ondoko hau da:

edota

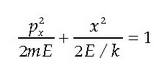
non k osziladorearen konstante elastikoa baita.

Bigarren ekuazioa elipse bati dagokio, eta elipsearen ardatz nagusiak dira. Osziladorearen periodo batean elipseari bira oso bat ematen zaio eta integralaren balioa elipsearen azalera da:

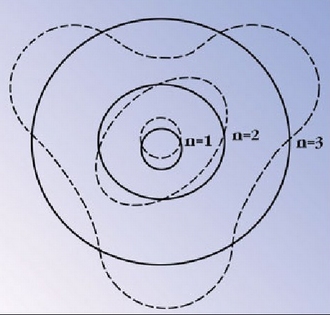
4.2. irudia: Orbiten kuantizaziorako da Broglie-ren interpretazioa. Irudian, egon daitezkeen lehenengo hiru orbitak.

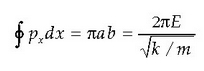
dela kontuan hartuz Wilson-Somerfelden kuantiza- 2 zio arauak Planken energiaren kuantizazioa ematen du.

integral berezia

2. Elektroiaren momentu angeluarraren kuantizazioa

Elektroiaren orbitaren kasuan kuantizazio arauak ondoko forma hauhartzen du:

non 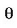koordenatu angeluarra baita.

Momentu angeluarra konstante denez oso erraz lor daiteke Bohren kuantizazioa:

1924. urtean de Brogliek beste interpretazio bat eman zion Bohren kuantizazioari. Elektroiaren momentu angeluarra momentu linealaren funtzioan idatziz eta de Broglieren erlazioa erabiliz ondokoerlazio hau daukagu:

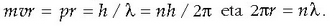
Hau da, orbita onartuetan orbitaren zirkunferentziaren luzera de Broglieren uhin luzeraren kopurua zenbaki osoa da. Grafikoki 4.2 irudian emaitza honen interpretazioa ikus daiteke. Uhin luzeraren kopurua zenbaki osoa ez denean bira batetik hurrengora uhinak desfasatuta daude eta denbora pasa ahala ateratzen den batez besteko anplitudea nulua da. Bohren kuantizazio baldintza betetzen denean, berriz, anplitudeak fasean daude eta anplitudeen batura ez da nulua egiten. Anplitudearen karratua elektroia aurkitzeko probabilitatearekin lotuta dagoenez, Borhen kuantizazio baldintza beharrezkoa da uhinek elektroiaren benetako ibilbideak adieraz ditzaten. Ikuspuntu honetatik elektroiaren higiduraren deskribapena ez litzateke izango zatiki arrunt batena. Soka baten kasuan ge-r tatzen den bezala, uhin geldikorren bidez adierazi behar da elektroiaren dinamika

4.6 Korrespondentzia printzipioa

Korrespondentzia printzipioa Bohrek 1923. proposatu zuen eta honela dio:

Quantumen zenbakiak oso handiak direnean teoria kuantikoaren iragarpenek eta fisika klasikoarenek bat etorri behar dute.

Korrespondentzia printzipioa aplikatu ahal izateko lehendabizi jakin beharra dago non dagoen fisika klasikoaren eta kuantikaren arteko muga. Bohren arabera muga horretara quantum zenbaki handiak direnean iristen da. Kasu batzuetan korrespondentziaprintzipioa lagungarria da quantumen teoria interpretatzeko eta, batez ere, quantumen teoriaren eta klasikoaren arteko bateragarritasuna egiaztatzeko.

4.7 Quantumen teoria zaharra

Orain arte aztertu ditugun teoriak quantumen mekanikaren lehenengo urratsak baino ez dira. Gaur egungo ikuspuntutik kritikagarria da, ondoko puntuetan adierazitako gaietan, batez ere:

Wilson-Sommerfelden teoriak sistema periodikoetarako baizik ez du balio.

Sistema baten energia mailak eta energia mailen arteko trantsizioak kalkula daitezke, baina trantsizioak gertatzeko probabilitatea zein den ez dakigu.

Bohren ereduak ez du balio atomoen elektroi kopurua handia denean.

Oro har hartuta, quantumen teoria zaharra errezetaz osaturik dago eta haren koherentzia eza kritikagarria da.

Hurrengo ataletan, Schrödingerren teoria abiapuntutzat hartuta, gaur egun erabiltzen den mekanika kuantikoa azaltzen ahaleginduko gara, Schrödingerren teorian baitago fisika kuantiko modernoaren oinarria.

Heisenberg, Werner Karl

(1901-1976)

Alemaniar fisikaria. Quantumen mekanika garatu, eta ziurgabetasunaren printzipioa aurkitu zuen.

Heisenberg Municheko Unibertsitateko grekoko irakasle baten semea zen, eta Munichen eta Göttingenen egin zituen ikasketak. Bornekin aritu zen lanean Göttingenen, eta Bohrrekin Kopenhagenen. 1927an irakasle lanetara itzuli zen Alemaniara, Leipzigera.

Quantumen teoriaren bidez, fisika erabat aldatu zuen Heisenbergek. 24 urte zituela quantumen mekanikaren forma ez erlatibista adierazi zuen, era berean matrizen mekanikaren bertsioa sortuz, eta, hori zelaeta, 1932ko Fisikako Nobel saria jaso zuen. Horren teoria baliokide bat, uhin mekanika deritzana, Schröridengerrek eman zuen aditzera 1925ean; Von Neumannek frogatu zuen baliokidetasun hori.

Heisenbergek baztertu egin zuen atomoaren ikusmenezko kontzeptua, eta era horretan saihestu egin zituen arazo batzuk, uhin-partikula itxurazko bikoiztasuna adibidez, atomoaren kopuru behagarriak bakarrik kontuan hartuz ‘erreal’ gisa. Banatu egin zituen, teorian, aztertu beharreko sistema eta sistema horren gaineko eragiketak, kopuru behagarri bat eskuratzeko. Matriz gisa eta matrizaren gaineko eragiketa matematiko gisa hurrenez hurren, adierazi ziren horiek. Arrakastaz baliatu zuen teoria espektro lerro atomiko eta molekularren maiztasun eta intentsitate behatuak aurreikusteko. Ondorio gisa, adierazi zuen badirela hidrogeno molekularreko bi forma, orto- eta para-hidrogeno izenekoak: aurrenekoak lerrokatuak dauzka spin nuklearrak, eta elkarren aurrez aurre jarriak bigarrenak.

1927an Heisenbergek quantumen mekanikaren beste alderdi bat aurkitu zuen, ziurgabetasunaren printzipioa; horren arabera, ezin dira aldi berean zehaztasunez finkatu partikula baten posizioa eta momentua. x posizioaren eta p momentuan honela gertatzen da ziurgabetasuna: x p h /4, non h Plancken konstantea den. Printzipio horrek, aurreneko aldiz fisikan, erabateko determinazioa, hau da, kausa-efektu erlazioa, ezabatu zuen, eta probabilitate estatistikoa ipini zuen horren lekuan. Aurkikuntza horrek biziki asaldatu zituen Einstein eta beste batzuk, baina orain, oro har, fisikari guztiek onartzen dute. Laplaceren ideia hura –partikula guztien posizio eta lastertasunetik, une batean emanez gero, ondoriozta zitekeela funtsean unibertsoaren etorkizuna–, baztertua geratu zen. Adibide baterako: elektroi baten posizio zehatza finkatzeko, uhin luzera laburreko irradak (gamma izpiak adibidez), igorri dakizkioke. Alabaina, energia izpi horiek erabat aldatuko dute izpiek jo duten elektroiaren momentua, eta, era horretan, posizioaren ziurtasuna ere aldatu egiten da, momentuaren ziurtasunaren kontura. 1932an, Chadwickek neutroia aurkitu ondoren, Heisenbergek nukleo eredu berri bat, protoi eta neutroikoa, proposatu zuen protoi eta elektroikoa baino hobea zelakoan, ordu arte uste ez bezala. Nukleoaren osagaiek elkarri loturik beharko lukete egon truke mekanikoko quantum indarren bidez; hori, geroago, Yukawaren elkarrekintza nuklear gogorraren teoriak, zeinaren bidez pi-mesoiak trukatzen diren, baietsi zuen. Geroago, oinarrizko partikulen teoria bateratu bat proposatu zuen Heisenbergek (1966), oro har harrera onik izan ez zuena.

Nazien garaian, nazien aldeko ez bazen ere, Alemanian geratzea erabaki zuen Heisenbergek, eta alemaniar zientzia tradizioari eutsi. Arazoak izan zituen naziekin, ez ziolako inola ere Einsteinen teoriari kontra egin nahi izan. Horren ondorioz, Sommerfeldek Municheko Unibertsitatean utzitako postua betetzeko aukera galdu zuen. Gerra garaian, energia eta arma atomikoen plangintzaren buru izateko deitu zuten, eta Berlingo Gilen Kaiser Institutuko zuzendari egin zuten 1941ean. Gerra amaituta, Göttingengo Max Planck Institutua antolatzen lagundu zuen, eta erakundea Munichera eraman zutenean (1955), hara joan zen bera ere, zuzendari gisa.

Ez dago argi nola jokatu zuen Heisenbergek gerra garaian. Berak zioenez, ez zuen asmorik atomo bonba Hitlerren eskuetara irits zedin uzteko, eta hain postu garrantzitsua zeukanez gero, plangintza aldatuko omen zuen arrakastarik izan balu; esan omen zion hori Bohrri 1941ean, baina Bohrrek adierazi zuen ez zituela ondo ulertu Heisenbergek esandakoak. Arma hura Alemaniak egin ez bazuen, lehentasuna hegazkin eta bonba hegalariei eman zitzaielako izan zen seguraski.

5. Schrödingerren teoria

5.1 Sarrera

Schrödingerren teoriak de Broglieren postulatua orokortzen du, eta bere barruan Newtonen ekuazio klasikoak ditu kasu berezitzat. Newtonen ekuazioek zatiki klasikoen ezaugarri mekanikoen arteko loturak zehazten dituzte eta Newtonen ekuazioak ebatzita zatikiaren ibilbide klasikoa ezagutu daiteke. Schrödingerren ekuazioa, berriz, uhin ekuazioa da, baina zatikien uhin jokaera dela eta, Schrödingerren ekuazioaren bidez zatikiari dagokion uhin funtzioaren bilakaerak (denboran eta espazioan) atera daitezke, eta, horrekin batera, zatikien ibilbideei buruzko informazioa.

Baina, nolakoa izan behar du uhin ekuazioak? Zer baldintza eskatu behar zaio? Schrödingerren ekuazioa postulatutakoa izan arren, badaude argudio sinple batzuk, ekuazioaren ezaugarriak baldintzatzen dituztenak:

1. De Broglie eta Einsteinen postulatuekin bat etortzea:

2. Mekanika klasikoko energiaren ekuazioarekin ados egotea:

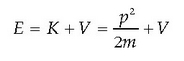
Hau da, zatikiaren energia osoa energia zinetikoaren eta potentzialaren batura izatea.

3. Schrödingerren ekuazioak lineala izan behar du. eta ekuazioaren ebazpenak, eta zenbaki konplexuak badira, hau da, ebazpenen edozein konbinazio lineal ebazpena da. Linealtasunari esker uhin funtzioen arteko interferentziak sor daitezke.

4. Oro har, energia potentziala denboraren eta espazioaren funtzioa da, baina energia potentziala aldaketarik gabea denean 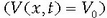zatiki aske bat daukagu. Newtonen bigarren ekuazioaren arabera zatikiaren gaineko indarra baliogabea da:

eta zatikiaren momentu lineala eta energia osoa aldaketarik gabeak dira. Hirugarren atalean ikusitakoaren arabera, badakigu uhin sinusoidalek momentu lineala eta energia konstanteko zatikiak adierazten dituztela. Horregatik, bada, zatiki askearen Schrödingerren ekuazioaren ebazpenak itxura sinusoidala izango du.

De Broglieren eta Einsteinen erlazioak erabiliz, energiaren ekuazioa honako hau da:

magnitudeak definituz hauxe da energiaren adierazpena:

non k uhin bektorea baita, eta maiztasun angeluarra.

Lau baldintza horiek eta fisikako beste arrazoibide batzuk kontuan hartuz, Schrödingerrek, dimentsio bakar batean, ondorengo ekuazio diferentzial hau proposatu zuen:

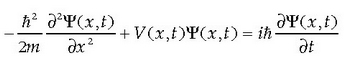
non

Ekuazio hau ateratzeko Schrödingerrek erabili zituen metodoak ezagutzeak ez du garrantzi handirik, gehien interesatzen zaiguna ekuazio honetatik atera daitezkeen ondorioak dira eta. Horregatik, ez dugu gehiago argituko Schrödingerren ekuazioaren oinarria eta ondoren ekuazio horren barruan gordeta dagoen fisika aztertzeari ekingo diogu

5.2 Uhin funtzioen interpretazioa

Schrödingerren ekuazio diferentzialaren ebazpenei uhin funtzioak deitzen zaie eta ekuazioan i zenbaki irudikaria ageri denez, uhin funtzio horiek konplexuak izango dira. Beraz, hurrengo garapenak ulertu ahal izateko beharrezkoa da zenbaki konplexuen oinarrizko erlazio matematikoak ezagutzea, ondoko formula hau batez ere:

Uhin funtzioak konplexuak izateak ez du esan nahi errealitatearekin lotuta ez daudenik, haien interpretazio fisikoa zuzena ez dela baizik. Horregatik, uhin funtzioetan dagoen zatikiari buruzko informazioa aztertuko dugu atal honetan.

Zatikiaren jokaeraren eta uhin funtzioen arteko loturarik garrantzitsuena P(x,t) probabilitate dentsitatean datza. P(x,t) probabilitate dentsitateak x puntuan eta t unean zatikia aurkitzeko probabilitatea adierazten du, eta era honetan kalkulatzen da:

non 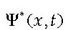ikurraz, 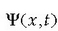uhin funtzioaren konjokatu konplexua adierazi baita. Era honetan definitutako probabilitatea positiboa da beti. Baina, zein da probabilitate horren esangura? t unean zatikiaren kokalekua kalkulatzeko neurketa bat egiten bada, zatikia ( x, x + dx) tartean aurkitzeko dagoen probabilitatea 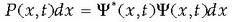da. Horregatik P(x,t) magnitudeari probabilitate dentsitatea deitzen zaio.

Uhin funtzioen interpretazioa guztiz ados dago ziurgabetasunaren printzipioarekin. Uhin funtzioak zatikia aurkitzeko probabilitatea besterik ematen ez duenez, ezin dugu zatikia non dagoen zehatz esan. Hala ere, probabilitate dentsitateari dagokionez, mekanika k uantikoaren bidez informazio zehatza jaso dezakegu. Bohrek esan zuen bezala: "zatikiak probabilitatearen legeen arabera higitzen dira, baina probabilitatea bera kausalitatearen arabera hedatzen da". Kausalitate lege hori da Schrödingerren ekuazioak ematen duena.

Schrödingerren ekuazioa lineala denez, ebazpen bat edozein faktorez biderkatuta, ebazpena izaten jarraitzen du. Horregatik uhin funtzioei honako normalizazio baldintza hau betetzea eskatu ohi zaie:

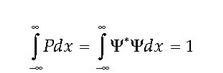
Era honetan, zatiki bat espazioko punturen batean aurkitzeko probabilitatea unitatea da, hau da, espazio osoa arakatuz ger o zatikia ziurtasun osoz aurkituko genuke.

5.3 Magnitude fisikoen batez besteko balioak

Badakigu zer informazio lor daitekeen zatikiaren kokalekuari buruz, baina energia, momentu lineala eta bestelako magnitude fisikoak nola kalkulatu?

Demagun sistema berdinetan neurketa bera behin baino gehiagotan errepikatzen dugula. Neurtutako zatikiaren kokalekua, esaterako, desberdina izango da neurketa bakoitzean, eta neurketa kopurua infinitura doanean emaitzen banaketa P(x,t) probabilitate dentsitatea izango da. Beraz, lortutako emaitzen batez besteko balioak edota zatikiaren batez besteko kokalekua hauxe da:

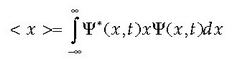
Ekuazio hau kontu handiz interpretatu behar da. Integralaren bidez kalkulatutako balioa neurtutako emaitzen batez besteko balioa da. Zatikia aurkitzeko probabilitate handiena duen espazioko puntua, berriz, probabilitate dentsitatearen gehienekoa da.

Kokalekuarekin erabili dugun metodoa edozein magnitudetarako balia daiteke:

non f(x) ikurrak, momentu linealaren, kokalekuaren edo denboraren funtzioa den edozein magnitude mekaniko adierazten baitu.

Baina, zein da momentu linealaren adierazpena kokalekuaren eta denboraren funtzioan? Schrödingerren arrazoibideak erabiliz, Schrödingerren ekuazioan agertzen den lehenengo eta hirugarren gaiak energia zinetikoa eta energia osoa badira, hurrenez hurren, ondoko baliokidetasunak egin ditzakegu:

eta momentu lineala eta energia eragile diferentzialaren bidez adieraziz, momentuaren eta energiaren definizio kuantikoak ondoko hauek dira:

Erlazio hauek uhin askearen kasuan balio dutela erraz egiazta daiteke eta badago frogatzea guztiz orokorrak direla, hau da, edozein sistematan aplika daitezkeela.

Beraz, momentu linealaren eta energiaren batez besteko balioak ondoren adierazten den moduan kalkula daitezke:

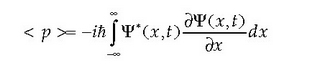
Oro har, kokalekua, momentu eta denboraren funtzioa den magnitude dinamikoen batez besteko balioa, ondokoa hau da:

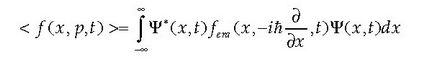
non 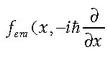, t) lortzeko f( x, p, t) funtzioaren adierazpenean

p momentu lineala jarri beharrean ipini behar baita.

Aurreko formulek mekanika kuantikoaren ezaugarri garrantzitsu bat utzi dute agerian: magnitude dinamikoak ez dira zenbakiak, uhin funtzioei aplikatzen zaizkien eragileak baizik. Mekanika klasikoaren ohiko magnitudeak neurketen bidez lortu behar ditugu. Neurketa horien emaitzen baliokide kuantikoak batez besteko balioak dira.

5.4 Denboraren mendekoa ez den Shrödingerren ekuazioa

Schrödingerren ekuazioa ekuazio diferentziala denez, ekuazio diferentzialak ebazteko erabiltzen diren metodo orokorrak aplikatu behar zaizkio. Energia potentziala denboraren mende ez badago (V(x,t) =V(x)), askotan gertatzen den bezala, aldagai banaketa izeneko metodoa erabiliz, forma errazagoa hartzen du Schrödingerren ekuazioak.

Aldagai banaketaren metodoa bi funtzioren arteko biderkaduraz osaturiko uhin funtzioak eraikitzean datza, espazioaren eta denboraren mendekotasunak bi funtzioetan banatuta daudela:

Horrela eraikitako uhin funtzioa jatorrizko Schrödingerren ekuazioan ordezkatuta, ondoko bi ekuazio hauek geratzen dira:

Espazio mendekotasuna eta denbora mendekotasuna banatuta geratu dira, eta G integrazio konstante bat da.

Bigarren ekuazioaren ebazpena zuzena da:

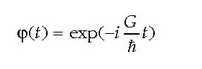
beraz funtzioa denboraren funtzio oszilakorra eta konplexua da, oszilazioen maiztasuna v = G / h delarik. De Broglie eta Einsteinen postulatuen arabera, uhinaren maiztasuna v = E / h da, non E zatikiaren energia osoa den. Beraz, G konstantea eta E zatikiaren energia osoa berdinak dira, eta uhin funtzioaren denborazko atala 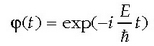da. E energia osoa sartu eta gero, espazio men- h dekotasuna daraman ekuazio diferentziala hauxe da:

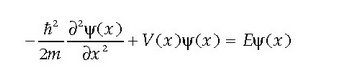
Ekuazio horri «denboraren mende ez dagoen Schrödinger ekuazioa» edo, laburrago, «Schrödingerren ekuazioa» deitzen zaio. Guk, besterik aipatzen ez bada, hemendik aurrera Schrödingerren ekuazioa deituko diogu eta bere ebazpenei berriz autofuntzioak edota egoera geldikorrak.

Schrödingerren ekuazioa bigarren ordenako ekuazio diferentziala denez, autofuntzioak adierazteko bi konstante agertuko dira. Bi konstante hauek kasu bakoitzerako problema fisikoaren itxidura baldintzak emandakoak dira. Autofuntzioen interpretazio fisikoa onargarria izateko propietate batzuk eskatzen zaizkie. Esaterako, funtzioek eta berorien deribatuek finituak eta jarraiak izan behar dute uhin funtzioen jokaera ona izateko

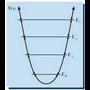
5.5 Energiaren kuantizazioa Shrödingerren teorian

Argudio kualitatibo edo teorikoaren bidez, badago jakitea zein baldintzatan gertatzen den energiaren kuantizazioa. Oro har, ondoko hau esan daiteke: Zatikiaren energia osoaren eta energia potentzialaren arteko erlazioa dela eta, klasikoki zatikiak espazioko eremu finitu batean egon beharko balu, Schrödingerren teoriaren arabera, energia osoa kuantizatuta dago. Klasikoki zatikia edozein tokitan egon badaiteke, hau da, eremu debekaturik ez badago, energia osoak edozein balio har dezake.

Schrödinger, Erwin

(1887-1961)

Austriar fisikaria, uhin mekanikaren sortzailea.

Schrödinger familia aberats bateko semea zen. Tutore pribatu batek eta aitak hezi zuten, Vienako Unibertsitatera joan aurretik. 1910ean eskuratu zuen doktoretza, eta ondoren unibertsitatean hasi zen lanean. Lehen Mundu gerran, artilleriako ofizial postuan egon zen gotorleku urruneko batean, eta fisika irakurtzen aritzen zen han. 1920tik aurrera, adli laburrak eman zituen Jena, Stuttgart, Breslau eta Zurichen ikasten. Lanean hasita, artikulu sail bat argitaratu zuen 1926an, uhin mekanikaren fundatzaile izan zirenak. Horren ondorioz, Plancken lekua hartu zuen fisika teorikoko irakasle postuan Berlinen (1927), baina nahiago izan zuen lanpostu hori utzi Hitlerrek aginpidea hartu zuenean, 1933an. Oxfordera joan zen, baina, aberri minez, Grazera itzuli zen 1936an. Alemanak Austrian sartu zirenean (1938), heriotzaren mehatxupean, ihes egin behar izan zuen; Dublinen hartu zituen bizilekua eta lanpostua, De Valera irlandar lehen ministroak, oso matematika zalea baitzen, berarentzat sortu zuen Ikasketa Aurreratuetako Institutuan. Eiren hamazazpi urte zorionez beteak eman ondoren, Vienako Unibertsitatera joan zen irakasle, uko egin baitzion hara itzultzeari, harik eta sobietarrek alde egin arte. Baina iritsi eta berehala gaixotu egin zen, eta ez zen inoiz erabat sendatu.

Schrödinger Broglieren ideien ondorioak lantzen hasi zen, 1924an argitaratu zirenak. Broglieren arabera, zatiki orok badu uhin bat berarekin lotua, eta zatiki eta uhin izate bikoitzaren ondorio dira zatiki horren ezaugarriak. Schrödinger eta Broglie, biak, konturatu ziren ekuazio diferentzial partzial batek –ehun ekuazio izenekoak–, deskriba zezakeela zatiki baten mugimendua, eta mota horretako ekuazio bat prestatu zuten. Uhin funtzioa bakarrik kontuan hartze horrek Bohrren quantum teoria zaharraren arazoak saihesten zituen, baina zaila zen praktikan aplikatzen. Schrödingerrek orduan zatikien mugimendua deskribatzen zuen Hamiltonen metodoa baliatu zuen, eta uhin moduan berridatzi zuen ‘Schrödingerren ekuazioa’ sortuz. Aurreko ekuazioek ez bezala, honek ez ditu kontuan hartzen erlatibitatearen ondorioak, baina askoz errazagoa da ikusten (nukloaren inguruan dauden uhin moduan), eta orobat benetako egoeretan aplikatzen. Hidrogenoaren atomoari aplikatzen zaionean, ekuazioak atomo bateko elektroi baten energia maila zuzenak ematen ditu, Bohrren atomoaren ereduaren ad hoc suposizioak gabe. Energia maila horiek esperimentalki neurtu ziren, hidrogenoaren espektroan ikusiriko lerroak erabiliz horretarako. Lorpen horrengatik, 1933an, Fisikako Nobel saria jaso zuen, Diracekin batera.

Schrödingerren teoriari uhinen mekanika deitu zitzaion (1926), eta, Diracek frogatu zuenez, matrizen mekanikaren baliokide zen, zeina 1925ean Born, Jordan eta Heisenbergek formulatu zuten. Teoria osatu hori, Pauliren esklusio hastapenarekin batera, erabili zuen Diracek quantumen mekanika urte bukaerarako ia osorik prestatzeko.

Quantumen mekanikak aurreikuspen ahalmen handia zuen, eta egoki deskribatzen zituen ordu arte ezin azaldu izan ziren puntu batzuk, baina Schrödingerrek arazo zail bat ikusten zion. Uhin funtzioa zatikiari (adibidez, elektroiari) lotzea, zaila da. Bornek azalpen bat eman zuen aditzera, gaur egun onartua: zatikia puntu horretan aurkitzeko probabilitatea deskribatzen duela uhinaren anplitudeak. Schrödinger, Broglie eta Einstein bezala, ez zegoen horrekin ados, eta elkarrekin aritu ziren argudioak lantzen probabilitateen quantum mekanika baten kontra. Bornen ikusmoldeak gertaera bat bestearen atzetik etortzeko probabilitate hutsa deskribatzera kondenatzen du fisika, eta, beraz, fisika ez litzateke gai izango kausa eta ondorioaren aurreikuspen zehatza egiteko, teoria klasikoek egin behar duten bezala.

Schrödinger oso gizon irekia eta lasaia zen, eta, hori zela-eta, bere lankide eta ikasleek asko estimatzen zuen; bizitza osoan bidaiatu zen mendiko botak jantzita eta motxilarekin, eta arazoak izaten zituen horregatik Nobel saridunen Solvay bileretan sartzeko.

6. Schrödingerren ekuazioaren ebazpen lotu gabeak dimentsio batean

6.1 Potentzial baliogabea

Atal honetan Shrodingerren ekuazioaren zenbait adibide sinple landuko dugu, egoera lotu gabeak sortzen dituzten potentzialetarako, hain zuzen ere.

Potentzial sinpleena aldaketarik gabea eta baliogabea da. V(x) =0 potentzialari dagokion indarra da, hau da, zatikia aske dago eta zatikiaren momentua zein energia aldaketarik gabeak dira. Shrödingerren ekuazioak ondoko eite hau hartzen du:

eta autofuntzioa eta uhin funtzioa hauexek dira:

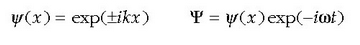
non diren.

Plus eta minus zeinuak eskuinera eta ezkerrera hedatzen diren uhin lauekin daude lotuta, hurrenez hurren. Schrödingerren ekuazioa lineala denez, bi autofuntzio horien edozein gainezarmen Schrödingerren ekuazioaren ebazpena da eta hauxe da uhin funtzio orokorra:

non A eta B konstante konplexuak diren.

Azter ditzagun uhin funtzio horien ezaugarriak, esaterako, eskuinera hedatzen denarenak:

Momentu linealaren balioa hauxe da:

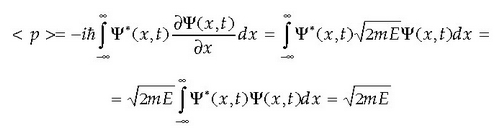
non azken pausuan uhin funtzioari normalizazio baldintza aplikatu diogun.

Ezkerrera hedatzen den uhinaren momentua, ordea, Ondorioz, lortutako uhin lauak, eta uhinek beraiek adierazten dituzten zatikien higidura norabide berean hedatzen dira. Gainera,zatikiaren energiaren eta momentu linealen arteko erlazioa, mekanika klasikoak emandako emaitzarekin ados dago:

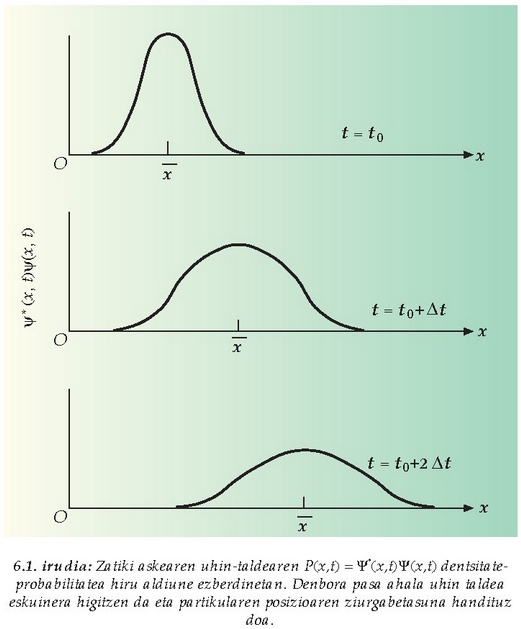
Uhin lauak uhin funtzio idealizatuak dira, zatikia eskuinera zein ezkerrera higitzen da baina espazioko edozein tokitan egon daiteke. Probabilitate dentsitatea aldaketarik gabea denez, Dx=infinitua da. Aurreko atalean ikusi den bezala, energia eta momentu desberdinetako uhin harmoniko asko elkarrengainkatuz, hedatzen diren uhin taldeak eraiki daitezke. Schrödingerren ekuazioaren linealtasuna dela eta, gainezarmena ebazpena izango da, baina uhin talde hauen probabilitate dentsitateak ez dira aldaketarik gabeak ez eta beraien momentu lineala ere guztiz definitua. Era honetan eratutako uhin talde baten probabilitate dentsitatea –hiru aldiunetan– 6.1 irudian ageri da.

Uhin taldearen gehienekoaren kokalekuak zatikiaren batez besteko kokalekua adierazten du, eta gehieneko horren lastertasuna talde lastertasuna da, hau da, zatikiaren lastertasuna, talde lastertasuna eta fase lastertasunak desberdinak dira. Horregatik, uhin taldearen eitea aldatu egiten da. Probabilitate dentsitatea baliogabea ez den eremua gero eta zabalagoa denez, zatikiaren kokalekuaren ziurgabetasuna ere gero eta handiagoa da.

V(x) potentziala aldaketarik gabea ez den arren, bere aldaketak zatikiaren de Broglieren uhin luzerarekin alderatuta oso txikiak badira, zatikiaren bilakaera irudikoaren antzekoa da. Baina badago desberdintasun txiki bat, potentzialaren aldaketen eraginagatik talde lastertasuna poliki-poliki aldatu egiten baita. Schrödingerren ekuaziotik abiatuta, badago talde lastertasunaren eta potentzialaren aldakuntzak erlazionatzea:

non g talde-abiadura den.

Aurreko ekuazioa garatzeko egin beharreko kalkuluak korapilotsuak dira, baina interpretazio fisikoa adierazgarria da. Dena den, goiko ekuazioa Newtonen bigarren legea da.

Batez besteko higiduraren gaineko gorabeherak ziurgabetasunaren printzipioaren bidez azaldu behar dira eta oso garrantzitsuak dira ikuspuntu mikroskopikotik. Mundu makroskopikoan ordea, gorabeherak oso txikiak dira eta behatutako magnitudeak batez besteko balioak dira. Beraz, sistema makroskopikoetarako Newtonen legea Schrödingerren ekuazioaren kasu berezia dela ondoriozta daiteke.

6.2 Maila itxurako potentziala, mailaren energia zatikiarena baino handiagoa denean

Hurrengo ataletan energia potentzialak balio desberdinak hartuko ditu espazioko bi eremutan. Benetako sistemetan ez dago potentzial aldaketa jarraitasun gabekorik, baina baliagarriak dira benetako potentzialen hurbilketa gisa.

Kasurik errazena 6.2 irudian ageri da. Jatorritik ezkerrera potentzialabaliogabea da, eta eskuinera 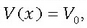, non aldaketarik gabea den. Zatikia eskuinetik mailarantz abiatzen da, eta zatikiaren energia mailarena baino txikiagoa denean, mekanika klasikoaren arabera zatikia ezin da eskuineko eremuan sartu:

Eskuineko eremuan energia zinetikoak negatiboa izan behar du, momentu lineala irudikaria delarik. Mekanika klasikoan, zatikia eskuinera joango litzateke mailarekin topo egin arte, eta hortik aurrera ezkerrera abiatuko litzateke hasierako noranzkoaren aurka eta lastertasunaren magnitudea aldatu gabe.

Mekanika kuantikoan Schrödingerren ekuazioak adierazten du zatikiaren dentsitatearen higidura, eta ekuazio diferentziala erraz ebazteko bi zatitan bana daiteke:

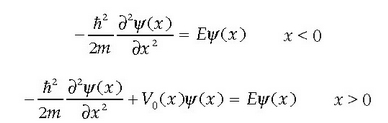
Bi ekuazio hauek banaka ebatzi behar dira eta lortutako bi ebazpenak x=0 puntuan lotu behar dira ebazpen osoa lortzeko. Ezkerreko eremuan potentziala baliogabea denez, egoera geldikorrak aurreko atalean aurkitutakoak dira:

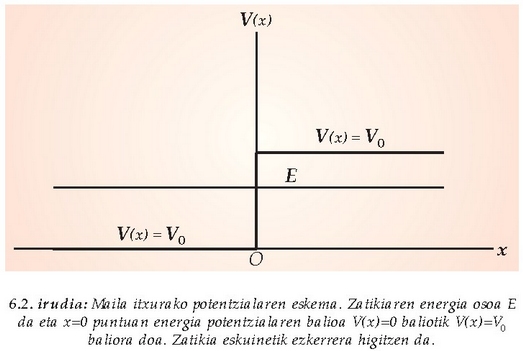
no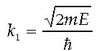n den.

Emaitza honek ez du balio eskuineko eremurako eta beste funtzio mota bat aukeratu behar da, esaterako:

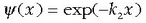
Bigarren ekuazioa ordezkatuz eta deribatuak eginez, ondoko baldintza lortzen da:

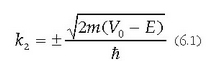
Beti bezala, lortutako ekuazioen edozein gainezarmen lineal Schrödingerren ekuazioaren ebazpena denez, eskuineko eremurako ondoko hau ateratzen da:

no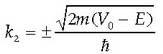n den

Orain, A, B, C eta D konstanteak aukeratu behar ditugu uhin funtzio osoa eta bere deribatuak finituak eta jarraiak izan daitezen. Argi eta garbi C = 0 egin behar dugu, bestela x koordenatua infinitura doanean uhin funtzioaren balioa infinitua izango litzateke. Uhin funtzioaren jarraitasun baldintzak ondoko ekuazioa ematen du: D=A+B eta deribatuen jarraitasun baldintza x=0 puntuan hau da:

Bi ekuazioetatik A eta B koefizienteak D koefizientearen funtzioan ipiniz, era honetara geratzen da autofuntzio osoa:

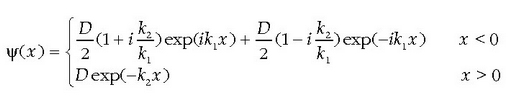
non D konstantearen balioa atera nahi izanez gero, normalizazio baldintza aplikatu beharko genukeen.

Denboraren mendekotasuna kontuan hartuz, uhin funtzioaren adierazpena ondoko hau da:

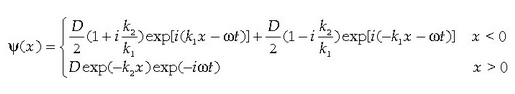
Ezkerreko eremuan bi gai daude; lehenengoak eskuinera hedatzen den uhina adierazten du, eta bigarrenak ezkerrera hedatzen dena. Interpretazio fisikoa erraza da: lehenengo gaiak uhin intzidentea adierazten du eta bigarrenak mailan islatutako uhina. Horren arabera, isla gertatzeko probabilitatea, isla koefizientea deritzonaren bidez kalkula daiteke. Jakina, isla koefizienteak B/A erlazioaren funtzioa izan behar du, hau da, uhin intzidentearen eta uhin islatuaren anplitudeen arteko erlazioaren funtzioa. Hala ere, mekanika kuantikoan probabilitateak uhinen anplitudeen karratuek adierazten dituzte eta isla koefizientearen definizioa hau da:

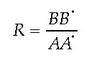
Eta gure kasuan lortutako koefizienteak ordezkatuta, hau da:

Honen ondorioz, zatikia islatua izateko probabilitatea osoa da, mailaren garaiera zatikiaren energia baino handiagoa denez zatikia beti islatuko da, mekanika klasikoan gertatzen den bezala.

Lortutako autofuntzioen esponentzial irudikariak garatuz, era honetara idatz daiteke uhin funtzioa:

Beraz, gure uhin funtzioa ezkerreko eremuan uhin geldikor bat da, gehieneko, gutxieneko eta zeroen kokalekuak ez dira aldatzen denboran zehar.

Baina zer gertatzen da eskuineko eremuan? D koefizientea baliogabea ez denez, klasikoki debekatutako eremuan zatikia aurkitzeko probabilitatea ez da baliogabea:

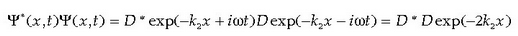
6.3 irudian ikus daitekeenez, x=0 puntutik eskuinera joanez, probabilitatea zerorantz oso azkar jaisten da, baina eskuineko aldean eta bi eremuen arteko mugatik hurbil, zatikia egon daiteke, aurresan * klasikoak kontrakoa esan arren.

Eskuineko eremuan probabilitate dentsitatea baliogabea ez den gunearen zabalera era honetan adieraz daiteke:

Zatikiaren masa eta energia diferentzia 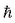konstantearen balioarekin alderatu eta oso handia denean, gune horren sakonera ez da kontuan hartu behar. Sistema makroskopikoetan hori gertatzen denez, fisika kuantikoaren eta klasikoaren iragarpenak bat datoz.

6.3. irudia: a) Maila-itxurako potentzial baten kontra jotzen duen zatikiaren autofuntzioa. Aipagarria da zatikia klasikoki debekatutako eremuaren barruan sartzen dela. b) Aurreko autofuntzioari dagokion dentsitate probabilitatea.

6.3 Maila itxurako potentziala, mailaren energia zatikiarena baino txikiagoa denean

Aurreko atalean bezala, zatikia ezkerretik maila itxurako potentzial baterantz abiatzen da, baina atal honetan mailaren garaiera zatikiaren energia baino txikiagoa da (6.4 irudia). Schrödingerren ekuazioa bi eremuetan banaturik ondoko hau da:

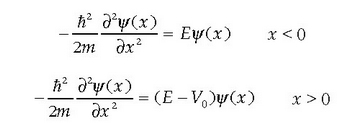
Kasu honetan 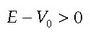denez, eskuineko eremuan esponentzial irudikariak ebazpen onargarriak dira, bi eremutarako ebazpenak hauexek izanik:

non 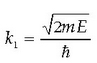eta diren.

Berriro ere, uhin funtzioa eta bere deribatuak jarraiak izateko baldintza erabilita, bi konstante desagertu egingo dira. Zatikia mailara ezkerretik hurbiltzen denez, eskuineko eremuan ezin dugu izan ezkerrerantz higitzen den uhinik eta D koefizienteak baliogabea izan behar du. Kalkulu guztiak egin ondoren ondoko hau da lortutako egoera geldikorra:

Ezkerreko eremuko ebazpenak garatu eta gero, berriz ere, uhin geldikor bat geratzen da. Mekanika klasikoak zatikia beti eskuineko eremura igarotzen dela esaten badu ere, gure emaitzak ezkerrerantz hedatzen den uhin bat dagoela erakusten du eta zatikia islatua izateko probabilitatea ez da baliogabea. Kasu honetan islatze faktorea ondoko hau da:

E zatikiaren energia mailaren garaiera baino txikiagoa denean R <1 daukagu. Beste aldetik, zatikiak maila zeharkatzeko probabilitatea transmisio koefizientea izeneko magnitudearen bidez adierazten da:

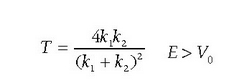
R+T=1 erlazioa betetzen dela erraz egiazta daiteke. Jario intzidentea jario transmitituaren eta islatuaren batura da eta zatikia espazio osoan aurkitzeko probabilitateak aldaketarik gabe dirau. Mailara hurbiltzen den zatikiak bide bat edo bestea hartuko du eta ahalegin asko eginez gero, edo zatiki kopuru asko erabiliz gero, transmisio eta islatze koefizienteek emango lukete zatikia transmititua edo islatua izateko probabilitatea, hurrenez hurren. 0.0 ekuazioetan

6.5 irudian islatze eta transmisio faktoreak ageri dira, erlazioaren funtzioan ondoko formulen arabera:

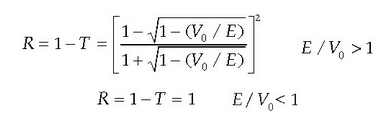
6.4 Potentzial langa

6.6 irudiko potentziala, potentzial langa deritzona, aztertuko dugu atal honetan. Matematikaren bidez ondoko eran adieraz daiteke:

Kalkulu kuantikoak hasi baino lehen, mekanika klasikoaren iragarpen kualitatiboak aipatuko ditugu. Ezkerretik langara hurbiltzen den zatiki intzidentearen energia langarena baino txikiagoa baldinbada, zatikiak ezin du langa gainditu eta islatu ondoren berriro ezkerrera abiatuko da. Zatikiaren energia langarena baino handiagoa denean, zatikiak langa gaindituko du eta mekanika klasikoak dio beti transmitituko dela.

Ikus ditzagun mekanika kuantikoaren emaitzak zeintzuk diren. Aurreko ataletan ikusi dugunaren arabera, langatik eskuinera eta ezkerrera uhin lauek adierazitako ebazpenak onargarriak dira:

non den.

Langan bertan ebazpen desberdinak erabili behar dira erlazioaren arabera. Hortaz, zatikiaren energia osoa langaren garaiera baino txikiagoa denean,

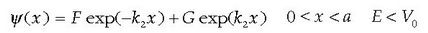
dugu, non den.

Zatikiaren energia langaren garaiera baino handiagoa denean autofuntzioak hauexek izango dira:

non 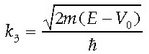den.

Zatiki intzidentea langara ezkerretik hurbiltzen denez D koefizientea baliogabea da. Kasu honetan ezin dugu G = 0 egin langaren bigarren jarraitasun gabeko puntuan islatu daitekeelako.

Ikus dezagun nolakoak diren Schrödingerren ekuazioaren ebazpenak, aipatutako bi kasuetarako:

Zatikiaren energia langarena baino txikiagoa denean 0.0 ekuazioak adierazten du ebazpenen eitea. x=a eta x = 0 puntuetan ohiko jarraitasun baldintzak jarriz, lau ekuazio sortzen dira. Beraz, hasierako bost konstanteetatik bat bakarrik geratzen zaigu.

6.7 irudian probabilitate dentsitatea ageri da. x>a eremuko probabilitatea ia aldaketarik gabea denez eskuinera hedatzen den uhin lau bat daukagu. x < 0 eremuan probabilitatearen eiteak, ordea, uhin geldikor baten antza du. Hala ere, uhinaren gutxienekoak ez dira baliogabeak eta honek esan nahi du islatutako uhinaren anplitudea uhin intzidentearena baino txikixeagoa dela eta badagoela eskuinera hedatzen den osagai txiki bat. 0 < x < a eremuko probabilitate dentsitatea exponentzial beherakorra da. Emaitzarik interesgarriena T transmisio koefizienteari dagokiona da, langan zehartransmititutako jarioarena, alegia. Transmisio koefizientea ondokoa da:

6.7 irudia: Probabilitate dentsitatearen adierazpena, non zatikiak langa zeharkatzeko duen probabilitatea ez den nuloa.

non 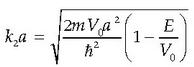den.

deneko kasuan, transmisio faktorea ondoko formula honen bidez adieraz daiteke:

0.0 ekuazioaren esangura oso garrantzitsua da, potentzial langaren garaiera zatikiaren energia baino handiagoa izan arren, langa zeharkatzeko probabilitatea ez baita baliogabea. Gertaera horri tunel efektua deitzen zaio eta bere jatorria guztiz kuantikoa da.

Kasu honetan hiru eremuetako autofuntzioa oszilakorra da eta transmisio faktoreak ondoko forma hartzen du:

no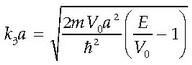n den.

Transmisio eta islatze koefizienteak erlazioaren funtzioan irudikatzea oso adierazgarria da eta 6.8 irudian ageri da. denean transmisio koefizientea oso txikia da eta zatikia ia beti islatuko da. E zatikiaren energia langaren garaieraren baliora hurbiltzen denean, transmisio koefizientea onargarria da. denean transmisio faktorea handia, baina bat baino txikiagoa da. Horren arabera, zatikia transmititzeko probabilitatea handia den arren, badago zatikia islatua izateko probabilitate txiki bat ere. erlazioaren balio batzuetarako T=1 dugu eta isla ez da gertatzen. 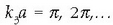Transmisio oso hau erlazioa betetzen denean gertatzen da. Beste ikuspuntu batetik, transmisio osoa gertatzeko a langaren zabalerak zatikiaren de Broglieren uhin luzeraren kopuru osoa edo erdi osoa izan behar du, ondoko erlazioa betetzen delarik:

Dirac, Paul Adrien

(Bristol, 1902 - Tallahassee, 1984)

Fisikari ingelesa. Ingeniaritza elektriko eta matematikako ikasketak egin zituen Bristol eta Cambridgeko unibertsitateetan. Gero, Estatu Batuetan, Japonian eta Siberian irakasle ibili ondoren, 1932an matematikako katedradun izendatu zuten Cambridgen, eta han aritu zen 1969 arte. 1971an, Estatu Batuetako lau unibertsitatetan hitzaldiak ematen ibili ondoren, fisikako irakasle izendatu zuten Floridako unibertsitatean.

Oso ezaguna da fisika teorikoan (quantumen mekanikan batez ere) egin zituen lanengatik. 1928an erlatibitatearen teoria ezarri zuen quantumen mekanikan, elektroiaren propietateak deskribatuz eta elektroiaren spina azaltzeko teorian Schrödingerrek egindako hutsa zuzenduz.

1930ean proposatu zuenez, elektroiarentzat teorian posible diren energia soluzio negatiboak egoera moduan esistitzen dira, baina egoera horiek energia negatiboz beterik daude, eta sarrera eragozten diete gainerako elektroiei. Aztertu zuenaren arabera, fotoi batek, behar adina kargatua, elektroi-positroi pare bat sor dezake, ezerezetik itxura batean, energia egoera negatibo horietako batetik kanpora bidaliz elektroia. Geratzen den hutsune karga positibokoa positroi deritzan elektroi baten antizatikia litzateke. Bestalde, elektroi bat eta positroi bat elkarrekin topatzean, elkar suntsituko dute, eta energia askatuko dute, fotoi gisa (argia). Diracen iragarpen horiek guztiak esperimentu bidez frogatu zituen Andersonek 1932an. Diracen arrazoiketa ez dagokio elektroiari bakarrik, zatiki mota guztiei baizik. Horren arabera, beraz, zatiki guztiei dagokie antizatiki bat.

1930ean Quantumen Mekanikaren Oinarriak liburua argitaratu zuen. Fisikari askoren iritzian, liburu horrek —klasiko bat haien artean— XX. mendeko Newton baten mailara goratzen du Dirac. 1933an Fisikako nobel saria jaso zuen, Schrödingerrekin batera.

7. Schrödingerren ekuazioaren ebazpen lotuak

7.1 Sarrera

Orain arte ikusitako potentzialek zatikiari edonon egoten uzten diote, ez dira zatikia espazioko eremu batera lotzeko gai, eta horregatik 5.5 atalean esan dugun bezala, ez dute energiaren kuantizaziorik sortu. Izadian ugari dira potentzial estekatzaileen adibideak: atomoetan elektroiek jasaten dutena eta solidoetan atomoak elkarrekin egotera behartzen dituztenak dira garrantzitsuenak. Atomoetako potentzial estekatzaileak hurrengo atalean jorratu baino lehen, atal honetan energia kuantizatuaren zenbait adibide errazago aztertuko dugu.

7.2 Potentzial osin karratua

Benetako potentzialaren hurbilketa den arren, potentzial osin karratuak badu atal honetan interesatzen zaigun ezaugarri bat: egoera lotuak sortzen ditu, hain zuzen ere. Potentzial osin karratuaren egitura 7.1 irudian ageri da, eta, matematika bidez adierazita, hau da:

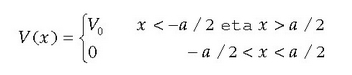
Zatikiaren energia osoa 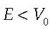denean, mekanika klasikoaren arabera zatikiak osinaren barruan egon behar du. Zatikiaren energiaren balioei dagokienez, mekanika klasikoak ez du baldintzarik jartzen, 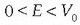tarteko edozein balio har dezake zatikiaren energiak. Mekanika kuantikoan, ostera, onartutako energiaren balioak diskretizatuak direla ikusiko dugu.

Aurreko atalean egin dugun bezala, Schrödingerren ekuazioaren hiru eremuetarako ebazpenak kalkulatu behar ditugu, osinaren ezkerrean, osinean bertan eta osinaren eskuinean, alegia. Osinaren barruan ondoko hau da ebazpen orokorra:

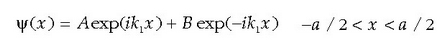
non 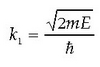den.

Lehenengo eta bigarren gaiek, ezkerrerantz eta eskuinerantz hedatzen diren uhin lauak adierazten dituzte, hurrenez hurren. Esponentzial irudikariak garatuz, proposaturiko ebazpena beste era batean idatz daiteke:

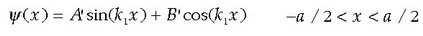
Osinetik kanpoko ebazpenak ondokoak izan daitezke:

no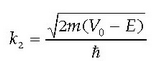n den.

Berriz ere, D eta F koefizienteek baliogabeak izan behar dute eta ebazpenei jarraitasun baldintzak aplikatuz, lau ekuazio eta lau konstante geratzen zaizkigu. Honek esan nahi du uhin funtzioaren anplitudea aukeratzerik ez dagoela. Konstante guztien balioak finkatzen baditugu, ezin dugu uhin funtzioa normalizatu eta gure ekuazio sistemak ez bide dauka ebazpen onargarririk. Itxurazko ezintasun hau energia parametro doigarri bihurtuz konpon daiteke. Metodo honen bidez energiaren kuantizazioa lortzen da, eta energiak balio diskretu batzuk baizik ez ditu hartzen, 7.1 irudian ageri den bezala.

Aipatutako metodoak eskatzen dituen kalkuluak ez dira errazak, batez ere, ekuazio transzendentalak agertzen direlako. Beraz, energiaren kuantizazioa potentzial errazago baterako kalkulatuko dugu, osinaren sakonera infinitua denean, hain zuzen ere. Esan beharra dago zatikiaren energia osinaren sakonera baino handiagoa denean energia mailak jarraiak direla eta aipatutako energiaren kuantizazioa desagertu egiten dela

7.3 Potentzial osin karratu infinitua

Potentzial osin karratu infinituaren adierazpen matematikoa ondoko hau da:

Berriro ere, Schrödingerren ekuazioaren ebazpen orokorra –osinean bertan– uhin geldikorren bidez idatz daiteke:

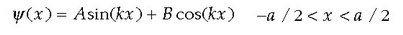
no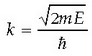n den.

Kasu honetan osinetik kanpoko ebazpena oso erraza da. Eremu horietan energia potentzialaren balioa infinitua denez, zatikia egoteko probabilitateak baliogabea izan behar du. Beraz, jarraitasunekuazioa puntuan, hau da 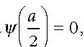, eta ondoko hau ematen du:

eta puntuan:

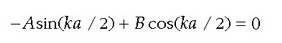
Aurreko bi ekuazioek adierazten dute osinaren barruko autofuntzioak baliogabeak direla osineko hormetan, eta bi motatako ebazpenak daude:

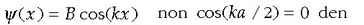
eta

Bi ebazpen mota hauen gaineko baldintzek momentuaren balio onargarriak mugatzen dituzte:

eta

n zenbaki osoari zenbaki kuantikoa deitzen zaio energiaren kuantizazioarekin lotuta dagoelako. 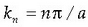erlazioa aintzat hartzen, energiaren kuantizazioa ondoko formularen bidez adieraz daiteke:

Osin finituaren eta infinituaren artean desberdintasun kualitatibo gutxi daude. Aipagarriena uhin funtzioaren eitea da, 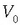sakonera finitua denean uhin funtzioen balioak ez baitira baliogabeak osinetik kanpo, baizik eta zerorantz doazen funtzio beherakorrak.

n = 1 denean, energia apaleneko egoera kuantikoak garrantzi berezia du, eta zero puntuko energia deitzen zaio:

Osinean dagoen zatiki batek izan dezakeen gutxieneko energia zero puntuko energia da. Mekanika klasikoaren arabera, zatiki baten gutxieneko energia zero bada ere, gure emaitzak dio baliogabea ez den energiaren balio minimo bat beti dagoela. Ondorio hau ziurgabetasunaren printzipioarekin lotuta dago. Zatikiak osinaren barruan egon behar baldin badu, kokaerari buruzko ziurgabetasuna, 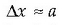izango da, osinaren zabalera, alegia. Ziurgabetasunaren printzipioa erabiliz, zatikiaren momentu linealaren ziurgabetasuna izango da. Momentuaren ziurgabetasuna baliogabea ez izateak energiaren ziurgabetasuna ere baliogabea ez. izatera behartzen du, eta energia negatiboa ez denez ezin da energia baliogabeko egoerarik egon. Bestalde, zero puntuko energia zero ez bada, esan dezakegu zero puntuko higidura bat ere badagoela. Fisika klasikoan zero tenperaturan zatikiak geldi egon daitezke, baina gure kalkuluen arabera, beti geratzen da zero puntuko hondar higidura bat. Emaitza hau tenperatura apaletan gertatzen diren gertaera batzuetan egiaztatu da.

7. 2 irudian potentzial osin karratu infinituaren lehenengo hiru auikus daitezke, non n zenbaki kuantikodun uhinak n - 1zero dituen. Irakurleak musika tresnen bidez sortutako uhin geldikorrak ezagutzen baditu, berehala nabarituko du soinu uhinen eta 7.2 irudiko egoera kuantikoen arteko antza. Dena dela, bi sistemen itxidura baldintzak berdinak dira eta ebazpenen eiteak ere bai. Hala ere, ekuazio diferentzialak desberdinak direnez, energiaren balio onartuak desberdinak dira bi kasuetan.

7.2. irudia: Potentzial osin karratu infinituaren lehenengo hiru egoera geldikorrak.

7.4 Osziladore harmoniko sinplea. Potentzial osin parabolikoa

Orain arte ikusitako potentzialak jarraitasun gabeak izateaz gain, espazioko gune gehienetan aldaketarik gabeak izan dira. Atal honetan errealitatera hurbilduko gara. Oso potentzial gutxi daude Schrödingerren ekuazioaren ebazpenak analitikoak dituztenak eta gehienetan zenbakizko metodoak erabili behar dira. Zorionez, Coulomben potentzialak, –hurrengo atalean aztertuko dugu– eta osziladore sinple baten potentzialak ebazpen analitikoak onartzen dituzte. Osziladore harmonikoak garrantzi izugarria du Fisikako arlo gehienetan. Benetako potentziala korapilotsuegia denean eta oszilazioak sortzen dituenean, egin ohi den lehenengo hurbilketa osziladore sinpleari dagokiona da, hurbilketa harmonikoa deritzona. Potentzial baten eraginpean zatiki bat oreka egonkorrean badago, potentzialak gutxieneko bat eduki behar du eta zatikiak gutxieneko horren inguruan oszilazioak egin ditzake. Eman dezagun potentzial korapilotsu bat analitikoa dela, eta zatikiak egiten dituen dardaren anplitudeak txikiak direla, kasu horretan potentzial osin harmoniko batez ordezka daiteke, 7.3 irudian ageri den bezala. x koordenatuaren eta energiaren jatorriak gutxienekoaren posiziora eramanez, ondoko hau da potentzialaren hurbilketa harmonikoa:

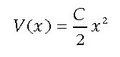
non C konstantea osinaren kurbadura erradioarekin lotuta dagoen.

Potentzial honetan higitzen den zatikiaknon C konstantea osinaren kurbadura erradioarekin lotuta dagoen.

Potentzial honetan higitzen den zatikiak 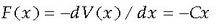indarra jasaten du. Oreka posiziotik lekur aldatzen bada, zatikia higidura harmoniko sinplearen arabera oszilatuko da, eta oszilatofuntzioak zioen maiztasuna ondoko hau izango da:indarra jasaten du. Oreka posiziotik lekur aldatzen bada, zatikia higidura harmoniko sinplearen arabera oszilatuko da, eta oszilatofuntzioak zioen maiztasuna ondoko hau izango da:

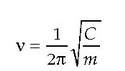
Mekanika klasikoak ez du energiaren balioa mugatzen, baina, mekanika kuantikoaren formalismoa erabiliz, energiaren balioak diskretuak direla ondorioztatzen da. 1.3 atalean Plancken postulatua aipatu dugu eta postulatu horrek osziladore harmoniko baten energiaren balioak ondokoak izatera behartzen du:

non n = 0, 1, 2, 3,..... izan daitekeen.

Zeintzuk dira Schrödingerren ekuazioaren bidez kalkulatutako energiaren balioak? Osziladore harmonikoaren Schrödingerren ekuazioa ebazteko erabili behar diren metodoak ekuazio diferentzialei buruzko edozein liburutan agertzen dira. Metodo hauek oso korapilotsuak ez diren arren, garapen osoa luze samarra da. Horregatik atal honetan emaitzak baino ez dugu aipatuko.

Plancken postulatua ez zen erabat zuzena, energiaren onartutako balioak ondoko hauek baitira: 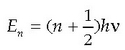non n = 0,1,2,3,..... den.

Beraz, egoera kuantikoen arteko energia diferentzia hn da, Planckek proposatu zuen bezala, baina energiaren jatorria aldatuta dago. Osin harmoniko batean dagoen zatikiaren gutxieneko energia ezda baliogabea, baizik. Berriro ere, gutxieneko energia baliogabea ez izatea ziurgabetasunaren printzipioaren ondorioa da eta zatikia ezin da geldirik egon. Lehenengo energia mailen kokalekua 7.4 irudian ikus daitezke, non energia mailen arteko tartea finkoa dela egiaztatzen den.

Plancken teoriaren eta benetako emaitzaren arteko aldea kasu gehienetan ez da oso nabaria. Askotan, zurgapen eta igorpen prozesuak neurtzen direnez, mailen arteko energia tarteak neurtzen dira eta horretan Plancken postulatua eta kalkulu zehatzak bat datoz.

7.4. irudia: Potentzial parabolikoaren lehenengo lau energia mailak. Elkarren segidako edozein mailaren arteko aldea, h?, berdina da

Osziladore harmonikoaren lehenengo lau egoerak 7.5 irudian ikus daitezke, non egoeraren energiaren arabera, klasikoki mugatutako higiduraren eremua marra zutez adierazita dagoen.

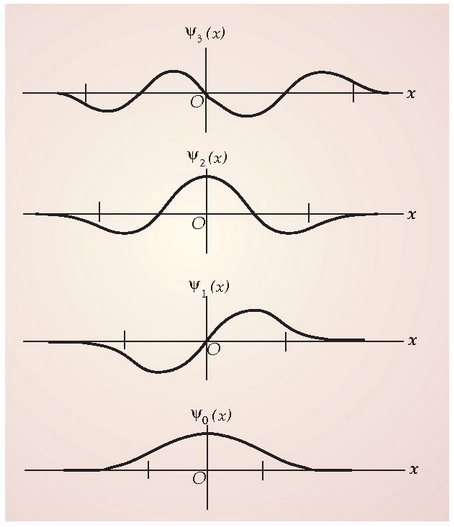
7.5. irudia: Osziladore harmoniko sinplearen lehenengo lau egoera geldikorrak. Marra bertikalek mekanika klasikoak oszilazioen anplitudeei jarritako mugak adierazen dituzte.