Fisika-Kimika»Fisika - Kimika
Optikari dagokion atal hau, lau kapitulutan banatua da; lehenengo, ikuspegi historikoa aztertuko da, argiaren gainean proposatu diren teoriak eta egin diren esperimentu nagusiak. Ondoren, isla, errefrakzioa eta polarizazioa azalduko dira; fenomeno horiek behar bezala azaltzeko argiaren hedatze lerrozuzena deskribatzeko izpiak erabiltzen dira, eta hurbilketa horren mugak ere izango dira aztergai. Geroago, islari eta errefrakzioari buruzko emaitzak aztertuko dira, ispilu eta lenteek irudiak nola eratzen dituzten azaltzeko, hots, optika geometrikoari buruzko azalpenak emango dira. Aplikazio modura, zenbait tresna optiko ikertuko dira, hala nola, begia, lupa, argazki kamera, mikroskopioa etabar. Azkenik, argiaren interferentzia eta difrakzioa landuko dira.
1. Argia
Argia edo argi ikuskorra ez da aurreko atalean aztertutako espektro elektromagnetikoaren zati bat baizik, gure begiek `ikus' dezaketena hain zuzen ere. Tarte horrek 400 eta 700 nm arteko uhin luzerak izaten ditu gutxi gorabehera. Argiak betidanik liluratu izan du gizakia, eta azken hamarraldietan aurrerapen handiak egin badira ere, ikerlari multzo handi bat ari da oraindik ere argiaren teoria eta bere aplikazioak aztertzen.
Uhinak ala zatikiak?
Argiaren nolakotasunak mendez mende sortu izan duen eztabaida izan da zientziaren historiak izan duen eztabaida interesgarrienetako bat. Antzinako teorien arabera, argia iturri batek igorritako zatiki jario bat zen. Zatiki horiek ikusmen sentipena eragiten zuten begietan. Newton izan zen gorpuzkien teoria horren bultzatzaile nagusia, eta haren bidez eman zituen islaren eta errefrakzioaren legeak.
Argia bi ingurune garden -airea eta ura edo airea eta beira, adibidez- banatzen dituen muga batera heltzen denean, argiaren energiaren zati bat islatu egiten da, eta bestea igorri. Izpi islatuak muga gainaldearen normalarekiko eratzen duen angelua eta izpi intzidenteak eratzen duena berdinak dira, aurrerago ikusiko denez (ikus 1. irudia). Izpi igorria, ordea, normalerantz hurbiltzen da
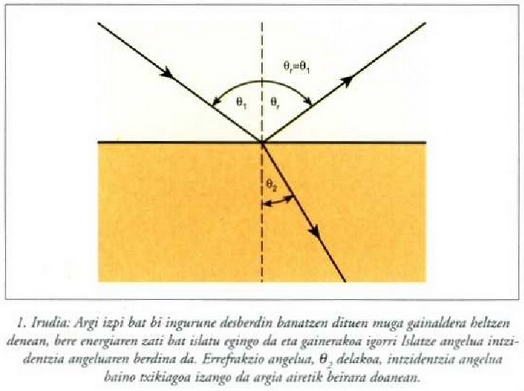
(argia uretatik edo beiratik airera igarotzen baldin bada, izpi igorria normaletik urruntzen da). Izpiaren desbideratze horri errefrakzioa esaten zaio.
Muga gainalde lau bati dagokion argiaren islatzearen legea gorpuzkien teoriaren bitartez azaltzen da; pilota batek inolako marruskadurarik ez duen gainalde gogor eta lau batean bote egiten badu, pilotaren momentu linealaren osagai paraleloak (gainaldeari buruz paraleloa, alegia) ez du aldaketarik izaten talkaren ondorioz, baina hari buruz elkarzuta den osagaia alderantzizkoa izango da (baldin eta onartzen bada hormaren masa pilotarena baino askoz handiagoa dela, eta talka, berriz, elastikoa). Islatze angelua eta intzidentzia angelua berdinak dira, beraz, ispilu lauan islatzen diren argi izpietan ikusten den bezala.
Errefrakzioa azaltzeko, Newtonek hau uste izan zuen: argi zatikiak airetik uretara edo beirara joaten zirela, urak edo beirak indar handiz erakartzen zituela zatiki horiek, eta, muga gainaldetik gertu zeudenean, une bateko bultzada izaten zutela. Horren ondorioz, zatikien momentu linealaren osagai elkarzuta gehitu egiten zen. Beraz, argi zatikien momentu linealaren norabidea aldatu egiten zen, eta argi izpiak gainaldearekiko normalerantz desbideratu behar izaten zuen, esperimentu bidez ikus daitekeen bezala. Teoria horrek badu ezaugarri garrantzitsu bat: desbideratze hori azaldu ahal izateko, argiaren lastertasunak balio handiagoa izan behar zuen beiran edo uretan airean baino. Argiaren lastertasunak uretan duen balioa ez zen esperimentu bidez 1850 inguru arte neurtu, 200 urte geroago arte, alegia.
Gorpuzkien teoriak alde batera utzita, Christian Huygens eta Robert Hooke izan ziren argiaren hedatzearen uhin teoriaren bultzatzaile nagusiak. Huygensek argiaren islatzea eta errefrakzioa azaldu zituen; oinarrizko uhinen metodo bat asmatu eta erabili zuen horretarako, haina aldez aurretik onartu behar izan zuen argia geldiago dabilela beiran edo uretan barrena airean harrena baino. Newtonek aintzat hartu zituen uhin teoria haren alderdi batzuk, berak sakon ikertuak zituen geruza meheek sortzen zituzten koloreak azaltzen zituztenak batez ere. Uko egin zion, hala ere, uhin teoriari, argia beti zuzen hedatzen zela esanez, ordu arte egin ziren esperimentu guztietan garbi ikusi ahal izan zen bezala. Garai hartan difrakzioa ez zegoen oraindik aztertua. Newtonen iritzian, uhinen higidura eta izpien hedatze zuzena ez ziren inondik inora bateragarriak.
Newtonen ospearen eraginez, haren jarraitzaile guztiek ere zalantzarik gabe ukatu zuten argiaren uhin teoria. Izan ere, argiaren difrakzioa frogatu ondoren ere, Newtonen teoriaren jarraitzaileek zatikien barreiatzearen bidez azaldu nahi izan zituzten arestian aipatu diren behaketa horiek. Gorpuzkien teoriak mende bete baino gehiago iraun zuen indarrean zientzialarien artean.
1801ean, Thomas Youngek bultzada handia eman zion argiaren uhin teoriari. Hura izan zen interferentzia kontzeptua uhinekin lotu zuen lehena. Argiaren bidez interferentziak ikusi zituen, eta hala frogatu zuen argiak uhinezkoa zuela nolakotasuna. Baina garai hartako zientzialariak hamar urtez egon ziren Youngen lanaren berri izan gabe. Augustin jean Fresnel frantses fisikariaren (1788-1827) lanari esker onartu zuten azkenik zientzialariek argiaren uhin teoria. Ikerlari horrek interferentziari eta difrakzioari buruzko hainbat esperimentu egin zituen, eta oinarri matematiko sendoa eman zion uhin teoriari. Hau frogatu zuen, besteak beste: argiak bidean oztoporik aurkitzen ez duen bitartean egiten duen ibilbide zuzena argi ikuskorraren uhin luzera txikiagatik dela. Garai hartan, Poissonek esperimentu bat iradoki zion Fresneli, uhin teoria zalantzan jartzeko. Esperimentu hau egin zuen Poissonek: disko opako baten ardatzeko argi iturri batek disko hori argitzen badu, Fresnelen uhin teoriaren arabera, argi uhinak tolestu egiten dira diskoaren ertzaren inguruan, ardatzeko puntu batera biltzen dira, eta interferentzia rail:iv.,iilea sortu beharko clute; diskoaren itzalaren erdian puntuargitsu bat agertu beharko da, beraz. Poissoni onclorio hori kontraesan barregarria iruditu zitzaion, baina harri eta zur geratu zen Fresnelek puntu hori agertu egiten zela berehala frogatu zuenean. Saio horri esker, zalantzan zeuden azken zientzialariek uhin teoria onartu zuten azkenik (ikus 2. irudia).

2. Irudia: Disko opako batek eragindako difrakzioa. Itzalaren erdigunean puntu distiratsua kus daiteke.
1850ean Foucaultek argiak uretan zuen lastertasuna neurtu zuen, eta airean baino
gelcliago zebilela frogatu zuen, era horretara Newtonen gorpuzkien teoria ezeztatuz.
1860ean James Clerk Maxwellek elektromagnetismoaren teoria matematikoa argitaratu zuen;
teoria h orretan iragarri zuen bazirela argiaren lastertasunez
 hedatzen ziren uhin elektromagnetikoak. Haren ustez, ez zen kasualitate hutsa hori,
aitzitik, argia uhin elektromagnetikoa zela frogatzen zuen.
1887an Hertzek Maxwellen teoria egiaztatu zuen, bitarteko elektriko soilen bidez sortutako
uhinak ikusi baitzituen laboratorioan. Hertzek sistema bat eratu zuen erresonantzia
zirkuitu katean txinpartak sortzeko, eta horren bidez uhinak sortu ahal izan zituen.
Uhin horiek atzemateko, antzeko heste zirkuitu bat erabiltzen zuen. 1850etik aurrera,
Kirchoffek eta beste ikerlari batzuek Maxwellen ekuazioak aplikatu zituzten argiaren
eta beste uhin elektromagnetikoen interferentzia eta difrakzioa azaltzeko, eta,
horrez gainera, oinarri matematikoa eman zieten Huygensek uhinak sortzeko erabili
zituen metodo enpirikoei.Argia uhina ala gorpuzkia ote den eztabaidari buruzko ikuspegia
osatzeko ezin da aipatu gabe utzi XX. mendeko aurkikuntza bat.
hedatzen ziren uhin elektromagnetikoak. Haren ustez, ez zen kasualitate hutsa hori,
aitzitik, argia uhin elektromagnetikoa zela frogatzen zuen.
1887an Hertzek Maxwellen teoria egiaztatu zuen, bitarteko elektriko soilen bidez sortutako
uhinak ikusi baitzituen laboratorioan. Hertzek sistema bat eratu zuen erresonantzia
zirkuitu katean txinpartak sortzeko, eta horren bidez uhinak sortu ahal izan zituen.
Uhin horiek atzemateko, antzeko heste zirkuitu bat erabiltzen zuen. 1850etik aurrera,
Kirchoffek eta beste ikerlari batzuek Maxwellen ekuazioak aplikatu zituzten argiaren
eta beste uhin elektromagnetikoen interferentzia eta difrakzioa azaltzeko, eta,
horrez gainera, oinarri matematikoa eman zieten Huygensek uhinak sortzeko erabili
zituen metodo enpirikoei.Argia uhina ala gorpuzkia ote den eztabaidari buruzko ikuspegia
osatzeko ezin da aipatu gabe utzi XX. mendeko aurkikuntza bat.
Argia eta beste uhin elektromagnetikoak deskribatzeko erabiltzen den uhin teoriak ezin ditu, hain zuzen ere, esperimentazio bidez ikus daitezkeen tasun guztiak azaldu. Hona zientziaren historiako egoera bitxienetako bat: arestian esan dugu nola Hertzek Maxwellen teoria egiaztatu ahal izan zuen, 1887an egin zuen esperimentuaren bidez; baina horrez gainera, efektu fotoelektrrkoa ere aurkitu zuen. Fenomeno hori azaldu ahal izateko nahitaez hartu behar da aintzat argiaren gorpuzki eredua, Einsteinek handik urte batzura frogatu zuenez. Saio haietan, Hertz konturatu zen txinpartak errazago igarotzen zirela erabiltzen ari zen hargailuko gune hutsetik, baldin eta hargailu hura argitzen bazuen.
1900ean, gertaera hori bera ikertzen ari zela, Lenard ohartu zen argi izpi batek,
metalezko gainalde bat joz gero, elektroiak askatzen zituela. Eta gainera elektroi horien
energiak ez zuen zerikusirik argiaren intentsitatearekin. Aurkikuntza horrek ezuste handia
sortu zuen, argiaren intentsitatea eta metalezko gainalde bat jotzen duen argi izpiak
eremu unitate bakoitzeko eta denbora unitate bakoitzeko sortzen duen energia, gauza bera baitira.
1905ean Einsteinek frogatu zuen emaitza hori hipotesi hau onartuz azal zitekeela:
argi uhinaren energia kuantizaturik dago, fotorctk esaten zaien multzo txikitan hain zuzen ere.
Fotoien energia proportzionala da uhinaren maiztasunarekiko. Einsteinen arabera,
fotoi baten energia E = h v formulaz adierazten da ( 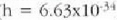 J s, Plancken konstantea da, eta v, argi uhinaren maiztasuna).
J s, Plancken konstantea da, eta v, argi uhinaren maiztasuna).
Metalezko gainalde argitutik askatzen den elektroiak fotoi bakar katen energia jasotzen du.
Maiztasun jakin bateko argiaren intentsitatea gehituz gero, fotoi gehiago helcluko clira gainaldera,
eta, beraz, fotoi horiek elektroi gehiago askatuko clituzte, baina elektroi bakoitzaren energia ez
da aldatuko. Metodo horri jarraituz, Einsteinek hau iragarri zuen: efektu fotoelektrikoak askatu duen
elektroi baten energia argi intzidentearen maiztasunaren proportzioan gehitzen da, eta argiaren
maiztasun hori 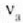 jakin baten atari maiztasun bat (metal mota nolako, atari maiztasuna
halako) baino txikiagoa balitz, ez litzateke efektu fotoelektrikorik
izango, argiaren intentsitatea edozein izanda ere, fotoi intzidente
batek ere ez bailuke izango elektroia askatzeko behar adina energiarik.
Iragarpen horiek bete-betean egiaztatu ziren handik
hamar urtera, Estatu Batuetako R. A. Millikan fisikariaren esperimentu
korapilatsuen bielez. Horrela hartu zuen herriz ere indarra
argia gorpuzkiz eratua dagoelako teoriak.
jakin baten atari maiztasun bat (metal mota nolako, atari maiztasuna
halako) baino txikiagoa balitz, ez litzateke efektu fotoelektrikorik
izango, argiaren intentsitatea edozein izanda ere, fotoi intzidente
batek ere ez bailuke izango elektroia askatzeko behar adina energiarik.
Iragarpen horiek bete-betean egiaztatu ziren handik
hamar urtera, Estatu Batuetako R. A. Millikan fisikariaren esperimentu
korapilatsuen bielez. Horrela hartu zuen herriz ere indarra
argia gorpuzkiz eratua dagoelako teoriak.
Argia gorpuzkiz eratua zegoela ez zen 1920ko hamarraldia arte erabat ulertu ahal izan. C. J. Davison, L. Germer eta G. P Thomson ikerlariek garai hartan egin zituzten esperimentuek argi eta garbi azaldu zuten elektroiak (eta beste `zatiki' batzuk ere bai) izatez bikunak zirela: batzuetan uhinei dagozkien interferentziazko eta difrakziozko tasunak zituzten, eta beste batzuetan, berriz, gorpuzkiei dagozkien tasunak zituzten. Mekanika kuantikoaren teoriak deskribatzen du oinarrizko magnitude horien funtzionamendua -argia, elektroia eta heste zatiki azpiatomikoak-. E. Schrficlinger, W Heisenherg, P A. M. Dirac eta beste zientzialari batzuek landu zuten teoria hori; teoria kuantikoa, bestalde, eta uhin teoria klasikoa eta gorpuzkien teoria klasikoa elkarren oso bestelakoak elira. Nolanahi ere, batzuetan teoria kuantikoa uhin teoria klasikoaren antzekoa izaten da, eta beste batzuetan, berriz, gorpuzkien teoria klasikoaren antzekoa. Adibidez, arestian aipatu diren oinarrizko zatiki horiek nola hedatzen diren deskribatzeko, uhin arrunten interferentzia eta difrakzio efektuetako uhin hedatzea erabili behar izaten da beti. Eta oinarrizko zatiki horien arteko energia trukatzeak -efektu fotoelektrikoan, esate baterako- hobe argitzen ditu zatikien mekanikak. Uhinak aztertzean ondorio hau ateratzen da, besteak beste: eclozein uhinek, bere uhin luzera bidean izan clitzakeen oztopoak eta irekiuneak baino askoz laburragoa ciuenean, ontzat eman daiteke izpien hurbilketa, eta lerrozuzen batean harrena hedatuko da uhin hori. Hori dela eta, ez da batere erraza izaten elektroien eta 'zatiki' esaten zaien heste gorputz batzuen uhinezko nolakotasunari erreparatzea, oso uhin luzera laburrak izaten baitituzte. Newtonek ere arrazoi berberagatik ezin izan zion argiaren uhinezko nolakotasunari erreparatu. Argiari dagokion energia trukatzearen gorpuzkiko nolakotasunari erreparatzea ere zaila da, oso fotoi kopuru handia izaten duelako tartean, eta fotoi bakoitzak oso energia gutxi izaten duelako. Era berean da zaila ontzi baten barruko gasak ontziko hormen kontra egiten duen presioa aztertzerakoan as horren molekulen gorpuzkizko nortasunari erreparatzea.
Argiaren lastertasuna
Argiak hedatzean duen lastertasuna neurtzeko lehen saioa Galileok egin zuen. Muino baten tontorrera igo zen, eta beste behatzaile bat heste tontor batera igo zen. Kilometro inguruko aldea zegoen bien artean. Linterna bana zeramaten neurketak egiteko, eta obturadoreak linternetako argiari argitzen ez uzteko. Bi behatzaile horien arteko distantzia bi aldiz egiteko argiak behar zuen denbora neurtu nahi zuen Galileok. A behatzaileak estalkia kenduko zion bere linternari, eta A-ren argia ikusterakoan B behatzaileak gauza hera egin behar zuen. A-ren linterna argitzen hasiko zen unetik B-tik zetorkion argia ikusiko zuen unerainoko bitartea izango zen bi behatzaile horien arteko joan-etorria egiteko argiak behar zuen denbora. Metodo hori teorian behintzat zuzena da, baina argiaren lastertasuna hain handia da, non neurtu beharreko bitartea gizakiaren erantzunaren gorabeherak baino askoz txikiagoa baita. Hortaz, Galileok ez zuen argiaren lastertasuna behar hezala neurtzerik izan.
Argiaren lastertasunaren lehenengo neurketa zehatzak astronomia behaketei esker egin ziren. Jupiterren ilargietako baten periodoa neurtu zuten. Ilargiaren bi eklipseen (ilargia Jupiterren atzean ezkutatzen den aldia) arteko denbora neurtuz jakin zuten periodo horrek zenbat neurtzen zuen. Eklipsearen periodoa 42.5 ordukoa da gutxi gorabehera, baina neurketak Lurra Jupiterretik urruntzen ari denean egiten direnean, 3. irudiko A eta C puntuen artean gertatzen den bezala, Lurra Jupiterrerantz hurbiltzen ari denean egiten direnean baino luzeagoak izaten dira denboraren neurketa horiek (irudiko C puntutik A punturako tartea). Neurketa horiek 15 segunduko aldea dute gutxi gorabehera batez besteko balioarekiko, eta heraz alde horiek beroriek ere nekez neurtuko zituzten zehatz. 1675ean Ole Roemer astronomoak hauxe esan zuen: argiaren lastertasuna infinitua ez izateak sortzen ditu eklipseen periodoen neurketan ageri ziren aldeak. Jupiterren ilargiaren bi eklipseen artean dauden 42.5 ordu horietan Jupiterren eta Lurraren arteko distantzia aldatu egiten da, eta argiak egin beharreko ibilbidea luzeagoa edo laburragoa izango da beraz. Lastertasun horrek zenbateko balioa zuen jakiteko, Roemerrek neurketa metodo hau asmatu zuen: Jupiterren higidura kontuan hartzen ez bada durrarena baino askoz txikiagoa baita), ilargiaren periodoa lehenik Lurra A puntuan dagoenean neurtu behar da. Urte erdi geroago gertatuko den durra C puntuan dagoenean) heste eklipse baten egun eta ordu zehatza kalkulatu behar da gero. Eklipsea aurrez iragarri baino 16 minutu beranduago izaten da gutxi gorabehera. Horixe da, hain zuzen ere, argiak Lurraren orbitaren diametroa zeharkatzeko behar cluen denbora.
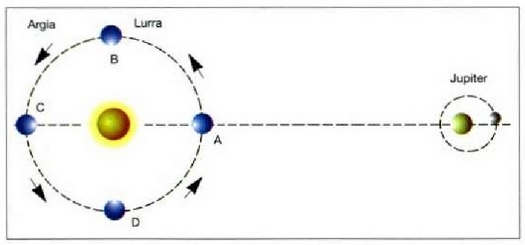
3. Irudia: Argiaren abiadura neurtzeko Roemerrek asmaturiko metodoa. Jupiterren ilargiaren eklipseen arteko denbora tartea handiagoa da Lurra A-tik C-ra higitzen denean, C-tik A-ra doanean baino. Ageri den alde hori, ilargiak periodo bat osatu duen bitartean, argiak Lurrak ibilitako distantzia egiteko behar duen denborari zor zaio.
Fizeau frantses fisikariak 1849an neurtu zuen lehendabizikoz argiaren lastertasuna metodo astronomikoetan oinarritu gabe. 4. irudian ikusten da haren metodoa. Foucaultek metodo hori hobetu zuen, ispilu biratzaile bat erabiliz gurpil koskadunaren ordez. Foucaultek 1850 inguruan neurtu zituen argiak uretan eta airean dituen lastertasunak, eta uretakoa airekoa baino geldiagoa zela frogatu zuen. 1880tik 1930era A. A. Michelson Estatu Batuetako fisikariak oso zehatz neurtu zuen argiaren lastertasuna, arestian aipatu den metodoa erabiliz funtsean.

4. Irudia: Argiaren lastertasuna neurtzeko Fizeauk erabilitako tresnaren eskema. Iturritik datorren argia B ispiluan islatuko da, eta gurpil koskadunaren zuloetariko batean zehar transmitituko da A ispiluraino heldu arte. Gurpilaren lastertasuna angeluarrak balio egokia duenean, A ispiluan islaturiko argiak gurpil koskadunaren hurrengo zuloa zeharkatuko du eta behatzaileak iturriaren irudia ikusi ahal izango du. Gurpilaren abiadura angeluarra eta datu geometrikoak jakinez, argiaren lastertasuna lor daiteke.
Beste neurketa metodo bat badago, argiaz baliatzen ez dena. Maxwellen teoria elektromagnetikoa baliatzen du metodo horrek. Teorian, argiaren lastertasunak c = 1/J ejt,, formula du. e,, konstantea, kondentsadore lau baten kapazitatea zehatzmehatz neurtuz ateratzen da, eta µ,, konstante magnetikoa, bi burdin hari eroaleren arteko indarra neurtuz. Argiaren lastertasunaren lehen neurketa elektrodinamiko zehatzak Rosa eta Dorsey ikerlariek egin zituzten 1906an U. S. Bureau of Standards laboratorioan.
Metodo asko daude argiaren lastertasuna neurtzeko, baina metodo horien guztien emaitza guztiak berdinak dira, balio bera dute, alegia. c-ren balioa bezain zehatza da gaur egun 3x10s m/s-ko balioa kalkulu gehienetan.
Islatzea
Edozein motatako uhinek oztopo lau bat jotzen tiutenean, uhin berriak sortzen dira, eta oztopo horretatik urruntzen dira. Esperimentazioz ikusten da nola uhin intzidenteei eta uhin islatuei dagozkien izpiek angelu bera eratzen duten muga gainaldearen normalarekiko, eta, gainera, izpi islatua izpi intzidenteak eta normalak eratzen duten intzidentzia planoan dagoen. Islatzearen lege hori honela adierazten da: izpi islatua intzidentzia planoan dago beti, eta islatze angelua eta intzidentzia angelua berdinak dira. Islatzearen legeak uhin mota guztietarako balio du: uretan dauden uhinak, soinu uhina, eta uhin elektromagnetikoak. Islatzearen legea bide desberdinetatik ateratzen da. Huygensen printzipioaren arabera, uhin fronte jakin bateko puntu bakoitza bigarren mailako uhinak sortzen dituen iturri puntual da. Beraz, denbora puska baten ondoren, uhin fronte berria iturri puntual horiek guztiek igorri dituzten eta tarte horretan hedatuz joan diren oinarrizko uhin esferikoen inguratzaileari dagokion gainaldea da. 5. iruclian oztoporik gahe hedatzen diren uhin lauak eta esferikoak aztertzeko Huygensek egin zuen tresna ageri da. Uhin fronteak bere ibilbidean oztopo bat edo irekiune bat aurkitzen badu, uhin diagrama honela ateratzen da: oztoporik izan ez duen uhin frontearen zatian dauden iturri puntualen interferentzia diagrama kalkulatzea. Oztopoekin eta irekinueekin zerikusia duten egoerak aurrerago aztertuko dira.

5. Irudia: Huygensen eraikuntza metodoa ondoko bi kasuetarako: (a) eskuin alderantz hedatzen ari diren uhin lauak, eta (b) uhin dibergente esferiko edo zirkularrak.

6 Irudia: Oztopo lau batean islatzen ari den uhin laua. Izpi intzidentearen eta oztopoarekiko norabide normalaren arteko qi angelua, eraso angelua da. Uhin intzidentearen eta oztopoak eratzen duten angeluaren berdina da.
Huygensen metodoaren bidez aterako dugu islatzearen legea.
6. irudian muga gainalde bateko A puntuan jotzen duen AA' uhin fronte laua dago adierazita.
Muga gainaldearen normalak eta uhin fronte horri dagokion izpiak eratzen duten
 angeluari intzidentzia angelua esaten zaio.
Irudian ageri denez,
angeluari intzidentzia angelua esaten zaio.
Irudian ageri denez,  intzidentzia angelua
eta muga gainaldeak eta uhin intzidentearen fronteak eratzen duten
intzidentzia angelua
eta muga gainaldeak eta uhin intzidentearen fronteak eratzen duten
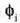 , angeluak berdinak dira.
, angeluak berdinak dira.
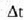 bitartearen ondoren
uhin frontea non kokatua egongo den jakiteko, aintzat hartu behar dira AA uhin fronteko
puntuek sortzen dituzten bigarren mailako uhinak.
Hau da,
bitartearen ondoren
uhin frontea non kokatua egongo den jakiteko, aintzat hartu behar dira AA uhin fronteko
puntuek sortzen dituzten bigarren mailako uhinak.
Hau da, 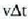 erradioko uhin
esferikoak eratu behar dira, eta esferen zentroak lehen aipatu diren puntu horietan daude.
Muga gainaldea jotzen ez duten bigarren mailako uhinek uhin fronte berriaren BB' zatia eratzen dute.
Muga gainaldea jotzen dutenak, ordea, islatu egiten dira eta BB" zatia eratzen dute.
Antzeko prozesua erabiliz, B'BB" uhin frontetik sortu diren bigarren mailako uhinek eratuko duten C"CC'
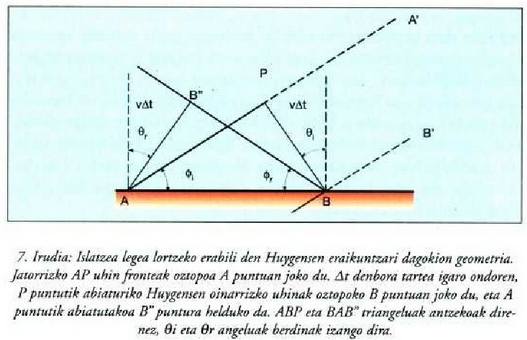
uhin frontea ateratzen da. 7. irudian, aurreko irudiaren zati bat handituta dago. vAt bitartearen muga
gainaldea jotzen duen uhin frontearen AP zatia ikusten da irudi horretan. Bitarte horretan,
P puntuan sortu den bigarren mailako uhinak B puntuan jotzen du gainaldea, eta A puntuan sortu denak,
berriz, B" p untuan. B B " uhin fronte islatuak eta muga gainaldeak
erradioko uhin
esferikoak eratu behar dira, eta esferen zentroak lehen aipatu diren puntu horietan daude.
Muga gainaldea jotzen ez duten bigarren mailako uhinek uhin fronte berriaren BB' zatia eratzen dute.
Muga gainaldea jotzen dutenak, ordea, islatu egiten dira eta BB" zatia eratzen dute.
Antzeko prozesua erabiliz, B'BB" uhin frontetik sortu diren bigarren mailako uhinek eratuko duten C"CC'
uhin frontea ateratzen da. 7. irudian, aurreko irudiaren zati bat handituta dago. vAt bitartearen muga
gainaldea jotzen duen uhin frontearen AP zatia ikusten da irudi horretan. Bitarte horretan,
P puntuan sortu den bigarren mailako uhinak B puntuan jotzen du gainaldea, eta A puntuan sortu denak,
berriz, B" p untuan. B B " uhin fronte islatuak eta muga gainaldeak
 angelua eratzen dute,
eta angelu hori eta izpi islatuak eta gainaldearen normalak eratzen duten
angelua eratzen dute,
eta angelu hori eta izpi islatuak eta gainaldearen normalak eratzen duten
 berdinak dira.
ABP eta BAB" triangeluak angeluzuzenakdira, AB hipotenusa komuna dute, eta katetoak berdinak:
berdinak dira.
ABP eta BAB" triangeluak angeluzuzenakdira, AB hipotenusa komuna dute, eta katetoak berdinak:

Beraz, triangelu horiek antzekoak dira,
eta 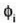 eta
eta  , angeluak ere berdinak dira.
Beraz,
, angeluak ere berdinak dira.
Beraz,  isla angelua
eta
isla angelua
eta  intzidentzia angelua berdinak dira.
Horra islatzearen legea. Lege hori ateratzeko, uhin frontearen hedatzea eta Huygensen printzipioa hartu dira kontuan,
haina aurrerantzean, errazagoa izango da uhin fronteen ordez, fronte horiei buruz elkarzut diren izpiak baizik ez hartzea kontuan.
intzidentzia angelua berdinak dira.
Horra islatzearen legea. Lege hori ateratzeko, uhin frontearen hedatzea eta Huygensen printzipioa hartu dira kontuan,
haina aurrerantzean, errazagoa izango da uhin fronteen ordez, fronte horiei buruz elkarzut diren izpiak baizik ez hartzea kontuan.
Bada beste bide bat islatzearen legea ateratzeko, XVII. mendean Pierre de Fermat frantses matematikariak enuntziatutako printzipioan oinarritua. Printzipio hori honela adierazten da:
Argiak puntu batetik beste batera higitzean egiten duen ibilbideak baldintza hau betetzen du: denbora gutxiago beharko du ibilbide hori egiteko haren inguruan nahi bezain hurbil dagoen beste edozein ibilbide egiteko baino.
8. irudian, eman dezagun argia A puntutik atera dela, gainalde laua jo du gero (ispilutzat har daiteke gainalde hori) eta B punturainoiritsi da azkenik. Islatzearen problema honela enuntziatu behar da Fermaten printzipioa aplikatu ahal izateko: Irudi horretako ispiluko zein P puntutan jo behar du argiak, A puntutik B puntura ahalik eta denbora gutxienean igaro dadin? Kasu honetan argia gutxienekoa ingurune material bakarrean ari denez higitzen, denbora izango da distantzia ere gutxienekoa denean. Irudi horretako APB eta APB distantziak berdinak dira, A puntua A iturriaren irudia baita. Alegia, AA lerroa ispiluari buruz elkarzut dago, eta A eta A puntuak ispilutik distantzia berera daude. P puntua aldatuz gero, APB distantzia gutxienekoa izango da, baldin eta A, P eta B puntuak lerro zuzen batean baldin badaude. Irudi horretan ikusten denez, baldintza hori betetzen denean, intzidentzia angelua eta islatze angelua berdinak dira.

8. Irudia: Islatzea legea Fermaten printzipiotik abiatuta lortzeko aintzat hartu beharreko geometria
Bi eratara aztertu da islatzearen legea, baina oraindik ez da islatzea bera zer den azaldu; ez da aztertu atomoek argia zergatik eta nola islatzen duten, eta ezta ere argi islatuaren eta argi igorriaren intentsitate erlatiboa zein den. Islatzea zehatz eta osorik aztertu nahi izanez gero, kontuan hartu beharra dago argia oso maiztasun handiko uhin elektromagnetikoa dela, eta elektrizitatearen eta magnetismoaren legeak aplikatu behar dira gero. Baina hori ez da hemen egingo, azterketa hau oinarrizkoa baita. Aipatuko ditugu ordea azterketa zehatz eta oso horien emaitza nagusiak: emaitzak bat datoz esperimentuetan atera diren ondorioekin.
Bi inguruneen arteko muga gainaldean islatzen den energiaren frakzioa faktore hauek baldintzatzen clute: intzidentzia angeluak, inguruneen errefrakzio indizeak eta argi uhin intzidentearen polarizazioak. Ingurune baten n errefrakzio indizea uhinek ingurune horretan izango tiuten v lastertasunarekin loturik dago, formula honen bidez:

non c argiak hutsean duen lastertasuna den. Energia islatuaren frakzioari dagokion adierazpen orokorra oso korapilatsua da. Argiak elkarzut jotzen duenean hauxe da intentsitate islatua:
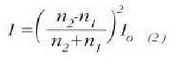
non  intentsitate intzidentea den,
eta
intentsitate intzidentea den,
eta  eta
eta
 , bi inguruneen errefrakzio indizeak.
, bi inguruneen errefrakzio indizeak.
Adibidez, airea eta beira hartzen badira,  eta
eta  izango da.
Hortaz, azken ekuazio horrek
izango da.
Hortaz, azken ekuazio horrek  ,
emango du; energiaren gutxi gorabehera %4 baino ez da islatuko argiak elkarzut jotzen duenean,
gainerakoa igorri egingo da. Argiak beste intzidentzia angelu
bat duenean, haren balioak ere ordena horretakoak izango dira
,
emango du; energiaren gutxi gorabehera %4 baino ez da islatuko argiak elkarzut jotzen duenean,
gainerakoa igorri egingo da. Argiak beste intzidentzia angelu
bat duenean, haren balioak ere ordena horretakoak izango dira
Errefrakzioa
Arestian esana dago argia edo beste edozein uhin bi inguruneen arteko muga gainaldera
iristen denean zati bat islatu egiten dela, eta bestea igorri. Izpi igorriak eta gainaldearen
normalak eratzen duten  angelua, errefrakzio angelua esaten zaiona,
angelua, errefrakzio angelua esaten zaiona,  intzidentzia angeluarekin formula honen bitartez dago lotua:
intzidentzia angeluarekin formula honen bitartez dago lotua:
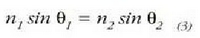
non  eta
eta
 , lehenengo eta bigarren
ingurunearen errefrakzio indizeak diren hurrenez hurren. Emaitza hori W Snellek aurkitu zuen
esperimentu bidez 1621ean, eta errefrakzioaren Snellen legea esaten zaio. Islatzearen legearen
kasuan bezala, ekuazioaren emaitza hori Huygensen printzipioa zein Fermatenena oinarritzat harturik
atera daiteke. 9. irudian Huygensen printzipioa erabili da uhin igorriaren uhin frontea zein den jakiteko.
Horretarako erabili den metodoa islatzearen legean erabili denaren antzekoa da.
, lehenengo eta bigarren
ingurunearen errefrakzio indizeak diren hurrenez hurren. Emaitza hori W Snellek aurkitu zuen
esperimentu bidez 1621ean, eta errefrakzioaren Snellen legea esaten zaio. Islatzearen legearen
kasuan bezala, ekuazioaren emaitza hori Huygensen printzipioa zein Fermatenena oinarritzat harturik
atera daiteke. 9. irudian Huygensen printzipioa erabili da uhin igorriaren uhin frontea zein den jakiteko.
Horretarako erabili den metodoa islatzearen legean erabili denaren antzekoa da.
 ingurunean dagoen
uhin frontearen zati bat da; irudian ikus daitekeenez,
ingurunean dagoen
uhin frontearen zati bat da; irudian ikus daitekeenez, 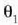 angelua ciagokio uhin fronte horri, eta A puntuan ebakitzen du muga gainaldea.
angelua ciagokio uhin fronte horri, eta A puntuan ebakitzen du muga gainaldea.

 bitartean,
P puntuan sortzen den bigarren mailako uhinak
bitartean,
P puntuan sortzen den bigarren mailako uhinak  distantzia egiten clu, eta muga gainalcleean dagoen B punturaino iristen da. A puntuan sortzen den uhinak, ostera,
distantzia egiten clu, eta muga gainalcleean dagoen B punturaino iristen da. A puntuan sortzen den uhinak, ostera,
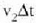 distantzia egiten du bigarren
ingurunean barrena. BB' uhin fronte herri hori ez da paraleloa AP jatorrizko uhin fronteari buruz,
distantzia egiten du bigarren
ingurunean barrena. BB' uhin fronte herri hori ez da paraleloa AP jatorrizko uhin fronteari buruz,
 eta
eta
 lastertasunak desberdinak baitira.
APB triangeluarekin formula hau eratzen da:
lastertasunak desberdinak baitira.
APB triangeluarekin formula hau eratzen da:

 angelua eta
angelua eta  intzidentzia angelua
berdinak direla kontutan harturik. Era berean, AB'B triangeluarekin formula hau eratzen da:
intzidentzia angelua
berdinak direla kontutan harturik. Era berean, AB'B triangeluarekin formula hau eratzen da:

non  izpi errefraktatuak
eta gainaldearen normalak eratzen duten angelua baita. AB tartearen balio biak berdinduz formula
hau ateratzen da:
izpi errefraktatuak
eta gainaldearen normalak eratzen duten angelua baita. AB tartearen balio biak berdinduz formula
hau ateratzen da:

 eta
eta
 uhin lastertasunak
errefrakzio indizeen funtzioan idatziz gero (n = c/v) Snellen legea ateratzen da.
uhin lastertasunak
errefrakzio indizeen funtzioan idatziz gero (n = c/v) Snellen legea ateratzen da.
 lastertasuna
lastertasuna
 baino txikiagoa denean,
baino txikiagoa denean,
 indizea
indizea
 baino handiagoa da, eta, beraz,
baino handiagoa da, eta, beraz,
 errefrakzio angelua
errefrakzio angelua
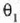 intzidentzia angelua baino
txikiagoa da. Kasu horretan izpia normalerantz hurbilduz desbideratzen da. Adibidez, argia airetik
beirara igarotzen denean, izpia normalerantz hurbiltzen da; beiratik airera igarotzen denean, ordea,
izpi hori normaletik urruntzen da.
intzidentzia angelua baino
txikiagoa da. Kasu horretan izpia normalerantz hurbilduz desbideratzen da. Adibidez, argia airetik
beirara igarotzen denean, izpia normalerantz hurbiltzen da; beiratik airera igarotzen denean, ordea,
izpi hori normaletik urruntzen da.
Uhin igorrien (eta islatuen) maiztasuna eta uhin intzidenteena berdinak dira. Hori ulertzeko, Huygensen metodoa erabili behar da. Izan ere, metodo hori aplikaturik, uhin intzidentea muga gainaldera iristen denean hura hartzen da uhin igorriaren iturritzat. Uhin igorriaren eta uhin intzidentearen lastertasunak desberdinak direnez, uhin horien uhin luzerak ere desberdinak dira.
Errefrakzioaren legea Fermaten printzipioaren bitartez ematea askoz korapilatsuagoa da, eta ez da hemen aztertuko.
(3) ekuazioan
 elementua bakanduz gero,
elementua bakanduz gero,
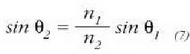
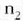 indizea
indizea 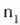 baino handiagoa
baldin bada (argia airetik uretara edo beirara igarotzen denean bezala), ekuazio horren bidez
beti ebatzi ahal izango da
baino handiagoa
baldin bada (argia airetik uretara edo beirara igarotzen denean bezala), ekuazio horren bidez
beti ebatzi ahal izango da  angelua, edozein delarik ere
angelua, edozein delarik ere  intzidentzia angelua. Hala ere,
intzidentzia angelua. Hala ere, 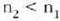 baldin bada (argia uretatik edo beiratik airera igarotzen denean bezala), (7) ekuazioan,
baldin bada (argia uretatik edo beiratik airera igarotzen denean bezala), (7) ekuazioan,
 elementuak dituen balioak
banakoa baino handiagoak izango dira, baldin eta intzidentzia angeluak
elementuak dituen balioak
banakoa baino handiagoak izango dira, baldin eta intzidentzia angeluak
 angelu kritikoa gainditzen badu.
Baldintza honek definitzen du angelu kritiko hori:
angelu kritikoa gainditzen badu.
Baldintza honek definitzen du angelu kritiko hori:

Edozein angeluren sinuak banakoa baino txikiagoa izan behar duenez beti, (7) ekuazio hori ezingo da ebatzi
intzidentzia angelua  baino handiagoa
baldin bada. 10. irudian ikusten da argiak beira/ura gainaldea jotzen duenean zer gertatzen den:
baino handiagoa
baldin bada. 10. irudian ikusten da argiak beira/ura gainaldea jotzen duenean zer gertatzen den:
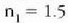 eta
eta
 izanez gero,
hau izango da angelu kritikoa:
izanez gero,
hau izango da angelu kritikoa: 

Intzidentzia angeluak angelu kritiko hori gainclitzen cluenean, bigarren ingurunean ez dago uhin errefraktaturik. Energia osoa islatu egiten da. Fenomeno horri islatze osoa deritzo. Islatze osoa beira zuntzetan da oso erabilia. Argi sorta hasieran zuntzaren ardatzari buruz paraleloa baldin bada, argiak angelu kritikoa baino handiagoz joko ditu beti zuntzaren hormak, eta zuntzaren mutur batetik bestera joango da, eta ez du batere energiarik galduko hormetan zehar.
Argiaren errefrakzioaren azterketa zehatzak elektrizitarearen eta magnetismoaren legeak ditu oinarri, haina azterketa hori ez da lan honetan egingo. Dena den, argi igorriaren intentsitatea zein den jakiteko, energiaren kontserbazioaren legea aplika daiteke, argi islatuaren intentsitatea zein den jakinez gero. Izan ere, energia igorriaren eta energia islatuaren baturak eta energia intzidenteak berdinak izan behar dute beti.
11. irudian agertzen ola nola beira baten errefrakzio indizea uhin luzeraren arabera aldatzen den. I handitzean, n indizea txikitu egiten da; alegia, uhin lastertasunak ingurune batean duen balioa argiarenuhin luzeraren edo maiztasunaren araberakoa da.

Fenomeno horri dispertsioa esaten zaio. Argi sorta batek beira baten gainaldea angelu jakin bat eratuz jotzen duenean, uhin luzera laburrenei (espektro ikuskorreko mutur urdinaren inguruan daudenei) dagokien errefrakzio angelua uhin luzera luzeenei (espektroko mutur gorrian daudenei) dagokiena baino txikixeagoa da. Hortaz, argi sorta zuria oinarrian dituen kolore edo uhin luzeretan deskonposatuko da (12. irudia). Ostadarra ez da dispertsioaren adibide bat baizik, eguzkiaren argia ur tantetan errefraktatzen denean sortzen baita.

Polarizazioa
Zeharkako edozein uhinen dardara elkarzut dago uhina hedatzen den norabideari buruz; beraz, dardara hori aise deskonposa daiteke uhina hedatzen den norabideari buruz elkarzut dagoen planoaren osagai angelu zuzenetan. Esate baterako, x norabidean barrena hedatzen ari den uhin elektromagnetikoan (uhin elektromagnetikoak zeharkako uhinak dira), eremu elektrikoa eta magnetikoa yz planoari buruz paraleloa den planoan daude, eta y eta z osagaietan deskonposa daitezke. Eremu elektrikoa espazioko lerro zuzen bati buruz paralelo mantentzen bada, uhina lerroan olago polarizatua (polarizazio laua duela ere esaten da). Kasu horretan, eremu magnetikoak ere etengabe iraungo du espazioko lerro bati buruz paralelo, uhin elektromagnetikoetan bi eremuek elkarzutak izan behar baitute beti. Uhin elektromagnetikoak ikertzeko, aski da beraz bi eremuetatik bat aztertzea. Eremu elektrikoa aukeratzen da normalean, detektagailu gehienek, giza begiak ere bai, hobeto sumatzen baitute E B baino.
Zeharkako uhinak zirkuluan edo elipsean ere egon daitezke polarizatuta. Zirkuluan edo elipsean polarizatuta dauden uhin elektromagnetikoetan, eremu elektrikoa biraka aritzen da zirkulu bat edo elipse bat eginez. Adibidez, x norabidean hedatzen ari den uhinean, honela adierazten dira eremu elektrikoaren y eta z osagaiak:

eta

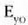 eta
eta  anplitudeak berdinak badira, uhina zirkuluan dago polarizatuta, polarizazioa
eliptikoa izango da bestela.
anplitudeak berdinak badira, uhina zirkuluan dago polarizatuta, polarizazioa
eliptikoa izango da bestela.
Zeharkako uhinen polarizazio motak erraz ikus daitezke soketan sortzen diren uhin mekanikoen bidez. Soka luze baten muturra lerro batean zehar gora eta behera mugituz gero, sortzen diren uhinak lerroan egongo dira polarizaturik, eta sokaren elementu bakoitza lerro batean barrena ariko da dardaraka. Bestalde, sokaren muturra lastertasun konstantez zirkulu bat eginez mugituz gero, zirkuluan polarizaturiko uhina sokan barrena hedatuko da, eta sokaren elementu bakoitzak zirkulu bat egingo du. Era berean, sokahori ibilbide eliptikoa eginez mugituz gero, sortzen den uhina elipsean polarizatuta egongo da.
Iturri bakar batek sortzen dituen uhin gehienak polarizaturik daude,
adibidez, sokaren mutur baten dardarak sortzen dituen uhin mekanikoak, edo atomo bakarrak
edo antena bakarrak sortzen dituen uhin elektromagnetikoak. Iturri askok sortzen dituzten uhinak,
ordea, polarizatu gabe egoten dira. Esaterako, argi uhin arrunta bakoitzak bere aldetik eragiten
duten milioika atomok sortua da. x ardatzean barrena hedatzen ari clen argi uhinaren eremu
elektrikoa y eta z osagaietan deskonposa daiteke aldi oro, baina osagai horien arteko
 fase diferentzia zoriaren arabera aldatzen da, ez
baitago inolako korrelaziorik atomoek sortzen duten eremu elektrikoen
artean. Mota horretako argi uhina ez dago beraz polarizatuta.
fase diferentzia zoriaren arabera aldatzen da, ez
baitago inolako korrelaziorik atomoek sortzen duten eremu elektrikoen
artean. Mota horretako argi uhina ez dago beraz polarizatuta.
Badago argi polarizatu gabetik argi polarizatua sortzea. Horretarako metodoak gertaera hauetan daude oinarrituta: xurgatzea, islatzea, barreiatzea eta birrefringentzia. Azter ditzagun, labur bada ere, banan-banan metodo horiek.
Xurgatzea
Polarizazioa lortzeko bide arrunt batek polaroide izeneko material komertzial batez egindako xaflen xurgatzea du oinarri. Material hori 1938an asmatu zuen E. H. Landek, eta hau du ezaugarri nagusia: katea luzeko hidrokarburo molekulak ditu, eta molekula horiek lerrokatu egiten dira, fabrikazio prozesua bitartean xafla norabide batean deformatu ahala. Kate horiek eroale bilakatzen dira (maiztasun optikoetarako) xafla iodo disoluzio batean sartzen denean. Argiak materiala jotzen duenean, argiaren E bektorea-eremu elektrikoaren adierazlea- material horretako kateei buruz paraleloa izanik, korronte elektrikoak sortzen dira kateetan barrena eta argiaren energia xurgatu egiten da. Eremu elektrikoa kate horiei buruz elkarzuta baldin bada, ostera, argiak materiala zeharkatzen du. Kateei buruz elkarzuta den norabideari transmisio ardatza deritzo. Onar dezagun hipotesi hau: E bektorea transmisio ardatzari buruz paraleloa denean argia oso-osorik igortzen da (materiala zeharkatuko du), eta E bektorea transmisio ardatzari buruz elkarzuta denean, erabat xurgatuko clu argia, ez da argirik igorriko, alegia.
Demagun z ardatzean barrena hedatzen ari den argi sorta polarizatu gabeak transmisio ardatza y norabideari buruz paralelo daukan polaroide batean jotzen duela. Polaroide horretan jotzen duen argiaren erdiak y norabidean du E bektorea, eta beste erdiak, berriz, x norabidean. Xaflan jo duen argi horren intentsitatearen erdia igorriko da beraz, eta argi igorri hori lerroan polarizaturik egongo da, eta E bektorea y norabidean zuzen egongo da.
Demagun beste polaroide bat; haren transmisio ardatzak 9 angelua eratzen du lehen polaroidearen ardatzarekin, 13. irudian ikustenden bezala.

Bi polaroide horien artean dagoen argiaren E bektorea bi osagaitan deskonposatzen da; osagai bat bigarren polaroidearen transmisio ardatzari buruz paraleloa da, eta bestea, berriz, ardatz horri buruz elkarzuta. Bigarren polaroidearen transmisio ardatzaren norabideari y' esaten bazaio, hauxe izango da formula:

Bigarren polaroideak  osagaia baino ez du igorriko.
Intentsitate igorri hori anplitude igorriaren karratuaren proportzionala da.
Horrela bada, bi polaroideen artean dagoen intentsitatea
osagaia baino ez du igorriko.
Intentsitate igorri hori anplitude igorriaren karratuaren proportzionala da.
Horrela bada, bi polaroideen artean dagoen intentsitatea
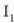 baldin bada,
bi polaroide horiek igortzen duen intentsitatea hau izango da:
baldin bada,
bi polaroide horiek igortzen duen intentsitatea hau izango da:
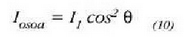
(Kontuan har bedi bigarren polaroidean jotzen duen argiaren intentsitatea lehenengoan jotzen duenaren erdia dela). Elkarren segidan polarizazioa sortzen duten bi xafla argi sorta baten ibilbidean jartzen direnean, lehenengoari polarizatzailea esaten zaio, eta bigarrenari, analizatzailea. Polarizatzailea eta analizatzailea gurutzatuta baldin badaude, transmisio ardatzak elkarzutak badira, alegia, ez da argirik igorriko, xaflak idealak badira. Baina, praktikan, gurutzatuta dauden bi polaroideetan zehar argi motel gorri edo urdinen bat ikusten da, espektro ikuskor osoan argia erabat xurgatzen ez den seinale. (10) ekuazioari Malusen legea deritzo, lege hori aurkitu zuen E. L. Malus (1775-1812) zientzialariaren ohoretan
Islatzea
Argi polarizatu gabea gainalde lau batean islatzen denean -airea eta beira, edo airea eta ura bereizten dituzten gainaldeak, adibidez-, argi islatu hori, aldez bederen, polarizatuta egoten da. Polarizazio maila intzidentzia angeluaren eta bi inguruneen errefrakzio indizeen araberakoa da. Intzidentzia angeluari balio jakin bat emanez gero, izpi islatuak eta errefraktatuak elkarzutak izango dira, eta kasu horretan argi islatua erabat polarizaturik egongo da. Emaitza hori D. Brewsterrek esperimentazio bidez aurkitu zuen 1812. urtean.
14. irudian ageri den argi intzidenteak normalarekiko eratzen duen
 angelua,
argi islatua erabat polarizatuta ateratzen den kasuari dagokio.
angelua,
argi islatua erabat polarizatuta ateratzen den kasuari dagokio.

Horregatik, polarizazio angelua deritzo 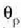 angeluari. Argi intzidentearen E eremu elektrikoa bi osagaitan deskonposa daiteke;
bata intzidentzia planoari buruz paraleloa da, bestea, berriz, elkarzuta. Argi islatua,
arestian esan den bezala, erabat polarizaturik dago, eta haren E eremu elektrikoa elkarzuta da intzidentzia planoari buruz.
angeluari. Argi intzidentearen E eremu elektrikoa bi osagaitan deskonposa daiteke;
bata intzidentzia planoari buruz paraleloa da, bestea, berriz, elkarzuta. Argi islatua,
arestian esan den bezala, erabat polarizaturik dago, eta haren E eremu elektrikoa elkarzuta da intzidentzia planoari buruz.
 polarizazio angeluaren eta inguruneen
errefrakzio indizeen arteko lotura zein den Snellen legearen bidez jakin daiteke.
Lehen ingurunearen errefrakzio indizea
polarizazio angeluaren eta inguruneen
errefrakzio indizeen arteko lotura zein den Snellen legearen bidez jakin daiteke.
Lehen ingurunearen errefrakzio indizea  baldin bada, eta
baldin bada, eta  baldin bada bigarrenarena, hau beteko da:
baldin bada bigarrenarena, hau beteko da:
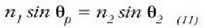
non 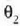 errefrakzio angelua den.
14. irudian ikusten den bezala, islatze angeluaren eta errefrakzio angeluaren arteko batura 90 °koa da.
Baina islatze angelua eta intzidentzia angeluak berdinak direnez, ekuazio hau ateratzen da:
errefrakzio angelua den.
14. irudian ikusten den bezala, islatze angeluaren eta errefrakzio angeluaren arteko batura 90 °koa da.
Baina islatze angelua eta intzidentzia angeluak berdinak direnez, ekuazio hau ateratzen da:
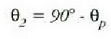
Orduan,

Hau da,

(12) formulari Brewsterren legea esaten zaio. Intzidentzia angelua
 denean argi errefraktatua
aldez baizik ez da polarizatuta egongo, nahiz argi islatua erabat polarizatua egon, argi
intzidentearen zati txiki bat baizik ez baita islatzen. Gainaldean jotzen duen argia bera polarizaturik
baldin badago, eta eremu elektrikoa intzidentzia planoan baldin badu, intzidentzia angelua
denean argi errefraktatua
aldez baizik ez da polarizatuta egongo, nahiz argi islatua erabat polarizatua egon, argi
intzidentearen zati txiki bat baizik ez baita islatzen. Gainaldean jotzen duen argia bera polarizaturik
baldin badago, eta eremu elektrikoa intzidentzia planoan baldin badu, intzidentzia angelua
 denean ez da argi islaturik
egongo (ikus 15. irudia). Bestalde, Brewsterren legearen ondorioak ezin dira modu erraz batean adierazi; a
rgiaren teoria elektromagnetikoaz baliatu beharra dago horretarako. Emaitza horren nolakotasuna 15. irudiari begiratuz ulertzen da.
denean ez da argi islaturik
egongo (ikus 15. irudia). Bestalde, Brewsterren legearen ondorioak ezin dira modu erraz batean adierazi; a
rgiaren teoria elektromagnetikoaz baliatu beharra dago horretarako. Emaitza horren nolakotasuna 15. irudiari begiratuz ulertzen da.

Demagun bigarren inguruneko molekulak izpi errefraktatuaren eremu elektrikoaren norabidean ari direla oszilatzen. Molekula horiek ezingo dute orduan energiarik igorri oszilazio norabidean -balizko izpi islatuari legokiokeen norabidean, alegia-
Argi islatuaren polarizazioa dela eta, eguzkitarako betaurrekoen kristalak material polarizatzailez eginak izan behar dute itsutuko ez badute. Argia gainalde horizontal batean islatzen bada -aintzira batean edo elurretan, adibidez-, intzidentzia planoa bertikala izango da, eta argi islatuaren eremu elektrikoa horizontala izango da gehienbat. Eguzkitarako betaurrekoen kristaletako transmisio ardatz bertikalek itsutzeko arriskua gutxitzen dute, xurgatu egiten baitute gainalde horizontalean islatzen den argi gehiena.
Barreiatzea
Argia lehenik xurgatu eta gero irradatu egiten denean barreiatzea esaten zaio horri. Argiaren isla ez da, oinarrian, uhin luzeraren aldean elkarrengandik oso gertu dauden hainbat barreiatze gunek sorrarazten tiuten barreiatzea baizik. Errefrakzioa ere barreiatzearen antzeko fenomenoa da, baina interferentzia izaten du argi barreiatuaren eta gainaldean jotzen duen argiaren artean. Hala eta guztiz ere, barreiatze hitza erabiltzen denean, uhin luzeraren aldean barreiatze guneen arteko clistantziak txikiak ez diren kasua aipatzen da. Hauxe da argiaren barreiatzearen adibide ezagunena: aire molekulek multzoak eratzen dituzte, airearen dentsitateak izaten dituen gorabeheren eraginez, eta multzo horiek gehiago barreiatzen dituzte uhin luzera laburrak uhin luzera luzeak baino; beraz, zerua kolore urdinekoa da.
Hona barreiatzearen beste adibide bat: ontzi urez bete batean esne hauts apur bat bota; esne zatikiek argia xurgatzen dute lehenengo, eta irradiatu egiten dute gero, irradatzaile dipolarrak balira bezala. Demagun z norabidean doan argi sorta bat (ikus 16. iruclia). Sorta horri dagokion E eremu elektrikoa x eta y norabideetan egongo da.

16 Irudia: Barreiatzea bidezko polarizazioa. z norabidean barrena hedatzen ari den polarizaturik gabeko argiak, ardatzen jatorrian kokaturiko barreiatze gune batean egingo du eraso. Orduan, x ardatzean barreiaturiko argia polarizaturik dago, bere E bektorea y ardatzaren paraleloa izanik; y ardatzean barreiaturiko argia, berriz, x ardatzean dago polarizatuta
Zatiki barreiatzaileek uhin intzidentearen E eremuari buruz paralelo oszilatuko dute, x eta y norabideetan, alegia, baina ez z norabidean. Sorta hori elkarzut aztertuz gero -x ardatzean esate baterako-, barreiatze guneetan dauden eta y norabidean oszilatzen ari diren kargek irradatzen duten argia ikusten da, ezingo da ordea x norabidean duten oszilazioari zor zaion irradiazioa sumatu, dipoloari dagokion lerroan barrena ez baita inolako energiarik irradatzen
Bestalde, z norabideko irrada ere ez da ikusiko, zatiki barreiatzaileek ez baitute norabide horretan oszilatzen. Hortaz, x ardatzean barrena irradatzen den argia lerroan polarizatuta egongo da, E eremua y ardatzari buruz paraleloa baita. Hori erraz egiazta daiteke sorta intzidentea polaroide baten bidez polarizatuz. Argi intzidentea x norabidean polarizatuta badago, x ardatzean barrena ez da argi barreiaturik ikusiko, y ardatzean bai ordea. Polaroidea 90' biratuz alderantziz gertatzen da: y ardatzean ez da argi barreiaturik agertuko; argi hori x ardatzean agertuko da
Birrefringentzia
Material anisotropiko batzuek birrefringentzia izaten dute. Gisa horretako materialek norabide nagusi bat dute; kaltzitak adibidez. Nahiz eta material gehienak isotropoak izan (norabide guztiak berdinak elira), haien barnean norabide desberdinetan higitzen diren argi sortek tasun optiko desberdinak izaten dituzte, kristal jakin hatzuek duten egitura atomikoaren eraginez. Argiaren lastertasunak ez du norabide guztietan balio hera izaten, kaltzitan eta beste zenbait materialetan. Horrelako materialei errefrakzio bikoitzekoak edo birrefringenteak deritze. Argi izpi batek kaltzitazko kristal bat jotzen duenean bi izpi bereizten dira; bakoitzak bere lastertasuna du, eta polarizaturik daude elkarzutak eliren norabideetan. Izpi horietako bati dagozkion Huygensen oinarrizko uhinak esferikoak dira, edozein material isotropo arruntetan gertatzen den bezala, eta izpi horri arrunta esaten zaio. Izpi hereziaren kasuan Huygensen oinarrizko uhinak biratze elipsoideak dira, eta, beraz, hedatze lastertasuna norabidearen funtzioa izango da. Bi izpiak lastertasun berberaz hedatzen dira elipsoidearen biratze ardatzean harrena. Huygensen oinarrizko uhinak elkarren ukitzaileak dira norabide horretan, ardatz opokoa deritzon norabidean hain zuen. Ardatz optikoaren norabide elkarzutetan gehieneko aldea izango da bi izpien lastertasunaren artean. Kaltzitan, izpi berezia arrunta baino bizkorrago mugitzen da ardatz optikoaren norabide elkarzutetan. Kaltzitaren izpi arruntari dagokion errefrakzio indizeak 1.66 balio du gutxi gorabehera. Izpi bereziaren errefrakzio indizea 1.66 balioaren (ardatz optikoan zehar) eta 1.49 balioaren artekoa da (nor abi- de elkarzutetan).
Kristal birrefringente batean zehar izpi arrunta eta berezia nola hedatzen eliren jakiteko, Huygensen metodo grafikoa erabiltzen da. Kristalak edozein orientazio izan dezakeenean prozedura hori osokorapilatsua izaten da. Badira bi kasu erraz azter daitezkeenak: kristalaren ardatz optikoa intzidentzia planoan dagoenean, eta ardatz optikoa intzidentzia planoari buruz elkarzuta denean. Bi kasu horietan izpi arrunta nahiz berezia intzidentzia planoan egongo dira, eta orduan ez da zaila izaten izpien polarizazioa lortzea. Izpi arrunta lerroan polarizatuta egongo da, haren eremu elektrikoa elkarzuta denean ardatz optikoak eta hedatze norabideak eratzen duten planoari buruz. Izpi berezia ere lerroan polarizatuta egongo da, baina haren eremu elektrikoa ardatz optikoak eta hedatze norabideak eratzen duten plano berean egongo da (ikus 17. iruclia). Dena den, emaitza horiek guztiak ateratzeko bidea ez da hemen aztertuko.
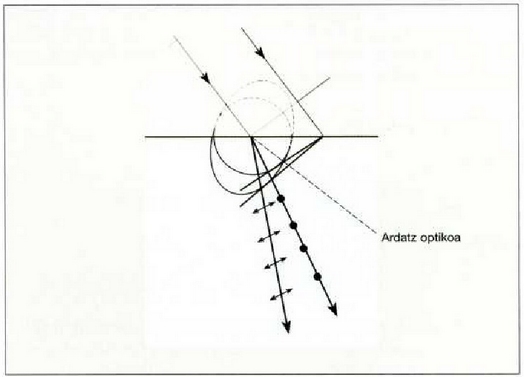
17. Irudia: Huygensen oinarrizko uhinak izpi arrunt eta berezirako, argiak kristal birrefingente batean egiten duenean eraso (kristalaren ardatz optikoa eraso planoan dago). Izpi berezia polarizaturik dago, bere E eremua intzidentzia planoan dagoelarik; izpi arruntaren polarizazio bektorea, ordea, intzidentzia planoaren perpendikularra izango da. Izpi arruntak Snellen legea betetzen du eta izpi bereziak, aldiz, ez.
Amaitzeko, esan behar da errefrakzio bikoitzak badituela erabilera interesgarri batzuk. Nicolen prisma da horietako bat, polarizatzaile gisa erabiltzen den tresna, alegia. Birrefringentziaren bidez orobat biraraz daiteke lerroan polarizaturiko argi baten polarizazio planoa, edo zirkuluan polarizaturiko argia sorraraz daiteke, lerroan polarizatutako argia harturik abiapuntutzat.
2. Optika geometrikoa
Argiaren uhin luzera oso laburra izaten da bidean aurkitzen dituan oztopo edo irekiuneen tamainaren aldean, difrakzio efektuak ez dira, heraz, oro har kontuan hartu behar. Kasu horietan izpien hurbilketa onar daiteke, argia lerro zuzenetan hedatzen dela, alegia, eta horrelako gertakizunak aztertzea du hain zuzen ere optika geonretrrkoak zeregin nagusia. Aurreko kapituluan landu diren islatzearen eta errefi -akzioaren legeak kapitulu honetan aplikatuko dira, ispiluek eta lenteek eratzen dituzten irudiak aztertzeko.
Ispilu lauak
P puntu bakarreko iturri jakin batetik ateratzen den ar.gi izpi sorta estu bat ispilu lau batean nola islatzen olen agertzen clu l. irudiak. Izpi horiek, islatu ondoren, elkarrengandik urruntzen dira, etaurruntze hori eta ispiluaren planoaren atzealdeko P' puntutik Zetorkeen izpi sorta baten urruntzea berdinak dira.

1. Irudia: Ispilu lau batek eraturako irudia. P puntutik datozen izpiak, ispiluan islatu ondoren begira sartzen dira. Izpi horiek, ispiluaren atzealdean dagoen P' irudi puntutik datozela ematen du. P puntuaren irudia rkusteko, begiak, irudian bertan adierazitako eremuaren barnean egon beharko du.
P' puntuari P objektuaren irudia esaten zaio. Begiak ezin ditu bereizi izpi horiek eta P' puntutik zuzenean (ispilurik gabe) helduko liratekeenak. Irudi horri alegazko irudia esaten zaio beraz, argia ez delako benetan puntu horretatik ateratzen, hala badirudi ere. Puntu horretan pantaila bat jarriz gero, ez litzateke ezer ikusiko. Islatzearen legearen bidez sortu clen irudi geometrikoak hauxe erakusten du: irudi puntua (P') objektutik igarotzen den eta ispiluari buruz elkarzut dagoen lerroan dago, eta P' eta P puntuek distantzia bera dute ispilutik. Irudi hori ikusi ahal izateko, begiak 1. irudian agertzen den eremuan egon behar du; P' puntuak eta ispiluaren muturrak lotzen dituzten bi lerroek mugatzen clute eremu hori. Irudia ikusi ahal izateko, objektuak eta ispiluak ez clute zertan aurrez aurre egonik; aski da objektua ispiluarenplanoa baino gorago egotea.
2. irudiak puntu bakarrekoa ez den objektu baten irudia ispiluan nola eratzen den erakusten clu. Irudia eta objektua tamaina berekoak dira beti.

2. Irudia: Ispilu lau baten aurrealdean kokaturik dagoen eta objektu puntua ez den objektu baten rrudia. Irudiaren eta objektuaren neurria berdinak dira.
3. irudian, berriz, angelu bat eratzen duten bi ispilu lauk sortzen dituzten irudi anizkunak ageri elira.
1. ispiluan islatzen olen argiak 2. ispiluan jotzen du, 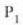 puntutik etorriko balitz bezala.
puntutik etorriko balitz bezala. 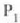 irudiari
2. ispiluko objektu puntua esaten zaio, eta
irudiari
2. ispiluko objektu puntua esaten zaio, eta  puntuan du irudia.
puntuan du irudia.

3. Irudia: Bi ispilu lauk eraturiko irudia. PI delakoa, P objektuak 1 ispiluan izango duen irudia da, eta P2, behiz, 2 ispiluan izango duena. P12 puntua, PI delakoak 2 ispiluan izango duen irudia da, objektutik abiaturiko izpiak Lehenik 1 ispiluan eta ondoren 2 ispiluan islatzen direnean ikusten dena hain justu. P2 irudiak ez du 1 ispiluan irudirik izango, hots, ez dugu P21 punturik izango, P2 puntua 1 ispiluaren atzealdean baitago.
 objektu puntua 2. ispiluaren
planoaren aurrealdean baldin badago, irudi hori beti hedatuko da. Objektutik atera eta 2.
ispiluan zuzenean islatzen diren izpiek sortzen dute
objektu puntua 2. ispiluaren
planoaren aurrealdean baldin badago, irudi hori beti hedatuko da. Objektutik atera eta 2.
ispiluan zuzenean islatzen diren izpiek sortzen dute 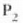 puntuaren irudia.
puntuaren irudia.  puntua 1. ispiluaren planoaren atzealdean dago, eta
ezin du heraz 1. ispiluan beste irudi bat sor lezakeen objektu
puntua izan. Ispiluen arteko angeluak eta objektuaren kokalekuak
baldintzatzen dute ispiluek sortzen dituzten irudi anizkunen
kopurua
puntua 1. ispiluaren planoaren atzealdean dago, eta
ezin du heraz 1. ispiluan beste irudi bat sor lezakeen objektu
puntua izan. Ispiluen arteko angeluak eta objektuaren kokalekuak
baldintzatzen dute ispiluek sortzen dituzten irudi anizkunen
kopurua
Ispilu esferikoak
Demagun ispilu esferiko ahur bat. (ikus 4. irudia). Ispiluaren ardatzeko P puntutik ateratzen diren izpiak ispiluan islatzen dira, eta P' puntura biltzen dira gero. Izpi horiek puntu horretatik urrunduko dira beraz, puntu horretan objektu bat balego bezala. Irudi horrierreala esaten zaio, argia puntu horretatik sortzen delako. Ispiluaren ezkerraldetik ispilurantz begiratzen duen begiak irudi hori ikus dezake. Era berean, pantaila bat jartzen bada P' puntuan, puntu argitsu bat ikusten da. Alegiazko irudi bat ezin da irudi puntuan jarritako pantaila batean ikusi, puntu horretan ez baitago argirik. Irudi errealen eta alegiazkoen artean alde hori dagoen arren, berdin-berdinak dira irudi erreal batetik urruntzen diren izpiak eta alegiazko irudi batetik urruntzen ari direla diruditenak; hala bada, begiak ez du inolako bereizkuntzarik egiten mota bateko zein besteko irucliak begiratzean.

4. Irudia: Ispilu esferiko ahurraren AO ardatzean kokaturiko P objektu puntual batetik datozen izpiek P'puntuan irudi bakarra eratuko dute, baldin eta izpiek ardatzetik gertu jotzen badute ispilua. Ispilua ardatzetik urrunago joka duten izpiak, hots, paraxialak ez direnak, islatu ondoren, ez dira P' irudi puntutik pasatuko.
Arestian aipatu den 4. irudiko izpien ibilbideak aztertuz gero, ondorio hau ateratzen da: P' puntutik ez dira igaroko AO ardatzetik gertu dauden puntuetan ispilua jo eta islatzen diren izpiak baizik. Mota horretako izpiei izpi paraxial esaten zaie. Ardatzetik urrunago dauden puntuetan ispilua jotzen duten beste izpi batzuk P' irudiko puntutik hurbil dauden beste puntu batzuetara bilduko dira, eta iruclia lausoturik agertuko da; aberrazio esferikoa esaten zaio horri. Ispilua tamainaz txikitzen baldin bada, irudia garbiagoa izango da, paraxial ez diren izpiek ezin baitute orcluan ispiluan jo. Hori eginez gero irudia garbiagoa izango da, baina irudiaren distira apalagoa, argiaren intentsitatea apalago islatuko da eta.
Islatzearen legea eta oinarrizko geometria erabiliz, parametro hauen arteko lotura egiten da: O puntutik irudirainoko distantzia (s'), O puntutik objekturainoko distantzia (s), eta ispiluaren bihurdura erradioa (r). 5. irudian dago adierazita eskema geometrikoa. Azken emaitza hauxe da:

Ekuazio hori egingo bada, izpi intzidenteak eta izpi islatuak ardatzarekin eratzen dituzten angeluek txikiak beharko dute izan; izpi paraxialen hipotesiak esaten duen gauza bera, alegia.

Objektuari dagokion s distantzia ispiluaren bihurdura erradioa baino askoz handiagoa denean, (1) ekuazioko 1/s elementua ez da kontuan hartzen, eta irudiari dagokion distantzia s' = r/2 da beraz. Distantzia horri ispiluaren foku distantzia (o esaten zaio, eta irudi puntuarifokua edo foku puntua (F). Hortaz,
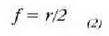
f foku distantziaren funtzioan hau da ispiluaren ekuazioa:

Infinitutik datozen uhin lauei dagozkien izpi paraleloak biltzen dituen puntua da fokua, 6. irudian ikus daitekeenez. Berriz ere esanbeharra dago puntu horretara ez direla izpi paraxial baizik bilduko. 7. irudian fokuan kokatutako puntu bakarreko iturri jakin batetikateratzen diren izpiak adierazi dira.

6. Irudia: Ispilu ahur batean eraso egiten duten izpi paralelo paraxialak. Islatu ondoren, ispiluaren puntu fokaletik pasatuko dira denak.

7. Irudia: Itzulgarritasunaren adibidea. Ispilu ahur baten fokuan kokaturiko iturri puntual batetik abiaturiko izpiak, islatu ondoren, ardatzaren paraleloak diren izpi modura irtengo dira. Irudikaturiko izpiak, 6 irudiko berak dira, baina aurkako norantza dute
Izpi horiek ispiluan jotzen clute, eta ardatzari buruz paraleloan islatzen dira gero. Uhinen tasun orokor bat adierazten du horrek: itzulgarritasuna. Izpi islatu bat kontrako noranzkoan jartzen bada, izpi islatu berria jatorrizko izpi intzidentearen toki berean egongo da, eta aurkako noranzkoa izango du, islatzearen legearen arabera. Itzulgarritasunak balio berdina du izpi errefraktatuen kasuan ere. Gainalde errefraktatzaile edo islatzaile batek iturri baten irudi erreala ematen duenean, jartzen baldin bada irudiaren puntu horretan beste iturri bat, jatorrizko iturriak zuen kokaleku berean eratuko da irudi berria.
Optikan bada magnitude bat maiz erabilia eta
foku distantziari lotua: sistema optikoaren ahalmen optikoa
 .
Honela definitzen da:
.
Honela definitzen da:

Horrek esan nahi du sistemaren ahalmen optikoak foku distantziaren alderantzizko balioa duela definizioz.
Ispilu esferikoak  du ahalmen optikoa.
Magnitude horrek edozein sistema optikotarako balio du, aurrerago aztertuko eliren lenteetarako,
adibidez. f metrotan neurtzen da, eta
du ahalmen optikoa.
Magnitude horrek edozein sistema optikotarako balio du, aurrerago aztertuko eliren lenteetarako,
adibidez. f metrotan neurtzen da, eta  magnitudea dioptria
magnitudea dioptria 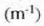 izeneko banakotan
adierazten da.
izeneko banakotan
adierazten da.
Ispiluek eratzen dituzten irucliak sortzeko metodo egokia izpi diagrama geometriko bat egitea da. 8. irudian giza irucli bat dago irudikatuta, ardatzari buruz elkarzut. Giza irucli horren burutik ateratzen diren zenbait izpi berezi behar bezala aukeratuz gero, berehala sortzen da objektuari cagokion irudia. Orain aipatuko dira horietako bi izpi berezi. Burutik ateratzen den izpi bat ardatzari buruz paraleloa baldin bada, izpi horrek foku puntutik igaro beharko du islatzen denean (ikus irudia). Ispiluaren bihurdura gunetik igarotzen den beste izpi batek (irudiko C puntua) ispiluari buruz elkarzut joko du ispiluan, eta ibilbide bera izango du ispiluan jo aurretik eta ispiluan jo ondoren. Bi izpi horiek elkar ebakitzen Gluten lekua da buruaren irudiari dagokion puntua. Hirugarren izpia F foku puntutik igarotzen da, islatu egiten da, eta ardatzari buruz paralelo ateratzen da.
8. irudia alderantziz dago, eta ez du objektuaren neurri bera. Eclozein sistema optikoren
handitzea honela definitzen da: irudiaren eta objektuaren neurrien arteko zatidura:
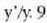 . irudiko triangeluak alderatzen hadira,
ispilu esferikoaren handitzea eta s' eta s distantzien arteko zatidura berdinak dira.
. irudiko triangeluak alderatzen hadira,
ispilu esferikoaren handitzea eta s' eta s distantzien arteko zatidura berdinak dira.

8. Irudia: Objektu baten irudia, eraikuntza geometrikoaren bitartez lortzeko erabili ohi den izpi diagrama

Objektua ispiluaren eta foku puntuaren artean dagoenean, ispiluan islatzen den izpiak ez dira puntu batera bilduko; ispiluaren atzealdean dagoen puntu hatetik urruntzen direla emango du (ikus 10. irudia). Izpi islatu horien luzapenek puntu horretan ebakiko dute elkar.

10. Irudia:Objektua fokuaren eta ispiluaren artean dagoenean, irudia alegiazkoa da eta ispiluaren atzeko aldean dago. Irudi hori non dagoen jakiteko, honako bi izpi hauek erabili dira: lehena, fokutik abiatuta, burutik pasatzen den eta ispilura heltzen den izpia, islatu ondoren paraleloki irtengo dena. Bigarren izpia, kurbadura zentrutik abiatuta, burutik pasatzen dena izango da; islatu ondoren bide beretik itzuliko da. Dakigunez, ardatzaren paraleloa den beste izpi bat ere erabil daiteke (ez da irudian adierazi)
Kasu horretan, irudia alegiazkoa eta zuzena da (alderantziz ez dagoena). (1) ekuazioan s distantzia r/2 baino txikiagoa bada, s' irudirainoko distantzia negatiboa izango da. Hortaz, (1) eta (3) ekuazioak ispilu ahurren zein ganbilen kasuetan aplikatu ahal izango dira, hitzarmenez zeinuak behar bezala hautatuz gero. Ispilua ganbila edo ahurra baldin bada, benetako irudiak ez dira objektua dagoen aldean baizik eratuko, eta alegiazko irudiak, berriz, ispiluaren beste aldean, benetako argi izpiak ez dauden tokian eratuko dira. Ispiluaren alde errealean dauden puntuei dagozkien zeinuak positiboak dira, eta alegiazko aldean daudenak, berriz, zeinu negatiboak. Beraz, ispilu ahurra denean, s eta r positiboak dira, eta irudia erreala edo alegiazkoa izan, hala izango da s' distantzia positiboa edo negatiboa. Ispilu ganbilean (ikus 11. irudia), bihurdura gunea alegiazko aldean dago, eta r magnitudea negatiboa da beraz. Foku distantzia ere negatiboa da. Bestalde, s distantzia zein den jakin ondoren, (1) ekuazioaren bidez jakin ahal izango da s' distantzia zein den, eta horrek argituko clu zein den irudi distantziaren zeinua.

11. Irudia: Ispilu ganbil bati dagokion izpi diagrama. Ardatzaren paraleloa den izpia, ispiluaren eskuin aldean dagoen fokutik baletor bezala islatuko da, eta makurdura zentrotik pasatzen den izpia, islatu ondoren, bide beretik itzuliko da. Islaturiko izpi horien luzapenak eginez lortuko dugu irudia. Oraingoan ere, irudian adierazi gabe dagoen beste izpi bat ere erabil daiteke, ispiluaren fokurantz zuzendutakoa hain zuzen ere.

Ispilu ganbilak angelu handiak behatu ahal izateko erabilgarriak dira, baina ematen duten irudiaren distortsioa ere handia da.
Hitzarmenez aukeraturiko zeinu hori gogoan izanik eta 9. irudiko triangeluak kontuan hartuz, honela definituko da irudiaren m alho handitzea:

Objektuen eta irudien garaieraren zeinuei dagokienez, ardatzetik gorakoak positiboak dira, eta beherakoak, berriz, negatiboak. Hori dela eta, handitzea negatiboa baldin bada, s eta s' distantziak positiboak direnean agertzen dena, alegia, horrela eratzen den irudia alderantziz dago. Ekuazio horiek eta hitzarmenezko zeinuak erabil errazak izaten dira optikan egiten den lan praktikoan, baina hala ere aski izaten da jakitea irudia erreala edo alegiazkoa den, eta irudi hori gutxi gorabehera non dagoen. Eta horretarako, izpi diagrama geometrikoa egiten da. Izpi diagramak oso garrantzitsuak dira optika geometrikoan. Lente batek edo lente multzo batek eratzen duen irudia aztertzeko, erabilgarriagoa da metodo grafikoa irudiaren eta objektuaren kokalekuak lotzen dituen ekuazio multzoa baino, aurrerago ikusiko den bezala.
Errefrakzioz eratzen diren irudiak
Bi ingurune banatzen dituen gainalde esferiko baten errefrakzioak eratzen
dituen irudiak aztertuko dira orain. Demagun inguruneek
 eta
eta
 errefrakzio indizeak dituztela.
12. irudian ikus daitekeenez, objektua lehenengo ingurunean dago, eta handik ateratzen diren izpiak
errefraktatu egiten dira, eta bigarren inguruneko P' puntura biltzen dira gero.
errefrakzio indizeak dituztela.
12. irudian ikus daitekeenez, objektua lehenengo ingurunean dago, eta handik ateratzen diren izpiak
errefraktatu egiten dira, eta bigarren inguruneko P' puntura biltzen dira gero.

12. Irudia: Gainalde esferiko batean gertatutako errefrakzioaren bidez eraturiko irudia.
Kasu horretan izpi paraxialek baino ez dute puntu hakar horretan elkar ebakiko.
Objektuen eta irudien distantziak, bihurdura erradioa, eta errefrakzio indizeak lotuko
dituen ekuazioa egiteko, Snell-en legea hartu behar da kontuan eta angelu txikien hurbiltzea
aplikatu behar da. 13. irudiko geometriaren arabera eta angeluak txikiak direla kontuan hartuz,
Snellen leea honela idazten da:  .
.

13. Irudia: (6) ekuazioa erdiesteko kontutan izan beharreko geometria
Bestalde, hau da ACP' triangeluen emaitza:

Eta PAC triangeluak berdintza hau du: 0, = a + R.
Bi ekuazio horietatik  ezabatzen bada,
ezabatzen bada,  (3 da emaitza.
Baina angelu txikien hurbiltzea aplika daitekeenez, angelu horiek era honetara idatzi behar dira:
(3 da emaitza.
Baina angelu txikien hurbiltzea aplika daitekeenez, angelu horiek era honetara idatzi behar dira:
 eta
eta
 Hortaz, egin nahi zen ekuazioa honela adierazten da:
Hortaz, egin nahi zen ekuazioa honela adierazten da:

Ekuazio hori egiteko, arestian hitzarmenez erabili diren zeinu berberak erabil daitezke, baina kontuan hartu beharra dago errefrakzioa izaten denean irudi errealak gainaldearen eskuinaldean eratzen direla (objektua ezkerraldean baldin barlago, jakina), eta alegiazkoak, berriz, ezkerraldean. Beraz, irudia eta bihurdura gunea gainaldearen eskuinaldean daudenean, s' eta r positiboak dira.
Adibidez, urpean dagoen objektu hati gainaldeari buruz elkarzut begiratzen bazaio, (6) ekuazioaren bidez jakin daiteke objektu horrek itxuraz zer sakonera duen. Kasu honetan gainaldea laua dit, eta, beraz, bihurdura erradioa infinitua da. Hortaz, objektuaren eta irudi distantziak honela erlazionatuta daude:
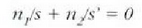
beraz,

Formula horretako minus zeinuak irudi hori alegiazkoa clela esan nahi du, eta errefrakzio
gainaldeko objektua dagoen alde berean dagoela esan nahi du. Egoera horri dagokion izpi diagrama 14.
irudian dago adierazita. (7) ekuazioan
 eta
eta  balioak jartzen badira,
hauxe da emaitza: s'/s = -3/4. Beraz, itxurazko sakonera benetako sakoneraren hiru laurdena da.
balioak jartzen badira,
hauxe da emaitza: s'/s = -3/4. Beraz, itxurazko sakonera benetako sakoneraren hiru laurdena da.

14. Irudia: P' irudia s'sakmeeran agertuko da, P objektuaren benetako s sakonera baino txikiagoa izango dena. Goitik perpendikularki begiratzen dugunean, itxurazko sakonera, benetako sakoneraren eta uraren errefrakzio indizearen arteko zatidura izango da
Lenteak
Arestian aipatu den (6) ekuazioak lente batek eratzen ehien irudia zehaztea
du aplikazio garrantzitsuena. Irudi hori zehazteko, lentearen gainalde bakoitzak
izaten duen errefrakzioa hartu behar da kontuan. Demagun lente bat: airean dago
eta n du errefrakzio indizea. Lente horren gainalcleen bihurdura erradioak
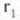 eta
eta  dira.
Objektu bat lehenengo gainaldeetik s distantziara balclin badago,
lehenengogainalde horretako errefrakzioak sortuko duen irudia (6) ekuazioren bidez kalkulatzen da, honela:
dira.
Objektu bat lehenengo gainaldeetik s distantziara balclin badago,
lehenengogainalde horretako errefrakzioak sortuko duen irudia (6) ekuazioren bidez kalkulatzen da, honela:

Irudi hori ez da, oro har, eratuko dentea oso lodia ez bada behinik behin),
argia bigarren gainaldean errefraktatuko baita irudi hori eratu aurretik.
Demagun, esate baterako, 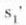 irudi distantzia negatiboa dela, lehenengo gainaldearen ezkerraldean dagoen alegiazko
irudi bat dela, alegia. Gainalde horretatik ateratzen den argia alegiazko iruclia dagoen tokian
kokatutako objektu batetik datorrela dirudi orduan. Lentearen lodiera t baldin barla, objektua
legokeen puntu horretatik bigarren gainalderainoko distantziaren balioa
irudi distantzia negatiboa dela, lehenengo gainaldearen ezkerraldean dagoen alegiazko
irudi bat dela, alegia. Gainalde horretatik ateratzen den argia alegiazko iruclia dagoen tokian
kokatutako objektu batetik datorrela dirudi orduan. Lentearen lodiera t baldin barla, objektua
legokeen puntu horretatik bigarren gainalderainoko distantziaren balioa
 izango da (kasu honetan,
izango da (kasu honetan,
 elementua positiboa izango da,
elementua positiboa izango da,
 negatiboa baita).
Bi errefrakzio horien eraginez sortzen den azken irudia non kokatua dagoen jakiteko, arestian aipatu
den distantzia hori bera bigarren gainaldeari dagokion (6) ekuaziora eraman behar da
(
negatiboa baita).
Bi errefrakzio horien eraginez sortzen den azken irudia non kokatua dagoen jakiteko, arestian aipatu
den distantzia hori bera bigarren gainaldeari dagokion (6) ekuaziora eraman behar da
(  da orduan objektu distantzia berria).
Bestalde,
da orduan objektu distantzia berria).
Bestalde,  positiboa baldin bada, irudi erreala lehenengo gainaldearen eskuinaldean baldin badago,
alegia, irudi puntua bigarren gainaldetik eskuinalclera egongo da,
positiboa baldin bada, irudi erreala lehenengo gainaldearen eskuinaldean baldin badago,
alegia, irudi puntua bigarren gainaldetik eskuinalclera egongo da,
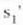
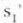 baino handiagoa denean.
Edozein kasutan ere, bigarren gainaldetik puntu horretarainoko distantzia
baino handiagoa denean.
Edozein kasutan ere, bigarren gainaldetik puntu horretarainoko distantzia
 da.
Nahiz irudi hori bigarren gainaldetik eskuinaldera egon, distantzia hori bera erabil daiteke (6)
ekuazioan ere, azken irudiari dagokion irudi distantzia zein den jakiteko.
Kasu horretan, bigarren errefrakzioari dagokion objektu distantzia negatiboa izango da,
hau da, alegiazko objektua agertuko da gainaldearen eskuinaldean
Beran,
da.
Nahiz irudi hori bigarren gainaldetik eskuinaldera egon, distantzia hori bera erabil daiteke (6)
ekuazioan ere, azken irudiari dagokion irudi distantzia zein den jakiteko.
Kasu horretan, bigarren errefrakzioari dagokion objektu distantzia negatiboa izango da,
hau da, alegiazko objektua agertuko da gainaldearen eskuinaldean
Beran,  lehenengo irudi distantziak izan ditzakeen balio guztietan, bigarren gainalceko errefrakzioak
eratuko duen irudia formula honen araberako
lehenengo irudi distantziak izan ditzakeen balio guztietan, bigarren gainalceko errefrakzioak
eratuko duen irudia formula honen araberako  distantziara egongo da bigarren gainalde horretatik:
distantziara egongo da bigarren gainalde horretatik:

Bigarren errefrakzio horretan, argia n errefrakzio indizea duen ingurunetik 1 errefrakzio indizea duen airera joaten da.
Edozein t lodiera duen lentean hau egin behar da: lehenik, (8) ekuazioaren bidez
 distantziaren zenbakizko balioa zein den jakin behar da, eta balio hori (9) ekuazioan sartu behar da gero,
distantziaren zenbakizko balioa zein den jakin behar da, eta balio hori (9) ekuazioan sartu behar da gero,
 distantzia zein den jakiteko.
(8) eta (9) ekuazioen
distantzia zein den jakiteko.
(8) eta (9) ekuazioen 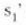 ezaba daiteke baina ez da erraza. Hala ere, lentearen t lodiera heste distantzia guztiak baino askoz ere
txikiagoa izaten da kasu askotan. Horrelako lente mehetan, ez dago t lodiera (9) ekuazioan zertan
kontuan harturik, eta, beraz, erraza da lantzen ari garen bi ekuazioen artean
ezaba daiteke baina ez da erraza. Hala ere, lentearen t lodiera heste distantzia guztiak baino askoz ere
txikiagoa izaten da kasu askotan. Horrelako lente mehetan, ez dago t lodiera (9) ekuazioan zertan
kontuan harturik, eta, beraz, erraza da lantzen ari garen bi ekuazioen artean
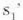 ezabatzea. Hori eginez gero, hauxe da emaitza:
ezabatzea. Hori eginez gero, hauxe da emaitza:

edo

(10) ekuazioari esker jakin ahal izango da s objektu distantziaren funtzioan 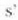 irudiak duen distantzia. Parametro horien arteko lotura lenteak bere baitan dituen ezaugarriek
egiten dute; lentearen
irudiak duen distantzia. Parametro horien arteko lotura lenteak bere baitan dituen ezaugarriek
egiten dute; lentearen  eta
eta  , erradioak eta
lentearen n errefrakzio indizea ezagutu behar dira beraz (10) ekuazio hori erabili ahal izateko.
Ispiluekin gertatzen den bezala, lente mehe baten foku distantzia objektu cistantzia infinitu denean
lente horri dagokion irudi distantziaren berdina da. (10) ekuazioan s eta infinitua berdintzen badira,
eta s' parametroaren ordez f idazten bada, hauxe da emaitza:
, erradioak eta
lentearen n errefrakzio indizea ezagutu behar dira beraz (10) ekuazio hori erabili ahal izateko.
Ispiluekin gertatzen den bezala, lente mehe baten foku distantzia objektu cistantzia infinitu denean
lente horri dagokion irudi distantziaren berdina da. (10) ekuazioan s eta infinitua berdintzen badira,
eta s' parametroaren ordez f idazten bada, hauxe da emaitza:

eta

(11) ekuazioari lente fabrikatzailearen ekuazioa esaten zaio batzuetan, lente mehe baten foku
distantzia bere tasunen arabera ematen duelako. Errepara bedi hitzarmenez zer zeinu aukeratu
diren, hala izango direla lentearen erradio bat edo biak negatiboak.
Adibidez, 15. irudiko bi ganbileko lentearen  lehen erradioa positiboa da, bihurdura erradioa gainaldearen eskuinaldean (alde errealean) dagoelako,
baina
lehen erradioa positiboa da, bihurdura erradioa gainaldearen eskuinaldean (alde errealean) dagoelako,
baina 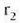 negatiboa da,
bigarren gainaldearen bihurdura erradioa gainaldearen ezderraldean (alegiazko aldean) dagoelako.
negatiboa da,
bigarren gainaldearen bihurdura erradioa gainaldearen ezderraldean (alegiazko aldean) dagoelako.

Kasu horretan, argi izpiak ardatzerantz bideratzeko joera izango dute bi gainaldeek, eta,
beraz, lente konbergentea esaten zaio. (11) formulako 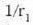 nahiz
nahiz  elementuak positiboak direnez,
eta n - 1 ere positiboa denez, lentearen foku distantzia ere positiboa izango da; hortaz,
ezkerraldetik datozen izpi paraleloek lentea zeharkatzen dute, eta lentearen eskuinaldean (
alde errealean) fokatuko dira gero. Lente konbergenteek foku distantzia positiboak dituzte beti,
eta horregatik lente positiboak deritze.
elementuak positiboak direnez,
eta n - 1 ere positiboa denez, lentearen foku distantzia ere positiboa izango da; hortaz,
ezkerraldetik datozen izpi paraleloek lentea zeharkatzen dute, eta lentearen eskuinaldean (
alde errealean) fokatuko dira gero. Lente konbergenteek foku distantzia positiboak dituzte beti,
eta horregatik lente positiboak deritze.
16. irudiak bi ahurreko lentea irudikatzen du.
Lentearen bi gainaldeek dute izpiak ardatzetik urruneratzeko joera. Kasu horretan,
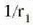 zein
zein
 elementuak negatiboak dira, eta,
beraz, foku distantzia ere bai. Hortaz, ezkerraldetik datozen argi izpi paraleloek lentea zeharkatzen dute,
eta dibergente bihurtzen dira, lentearen ezkerraldeko puntu batetik etorriko balira bezala.
elementuak negatiboak dira, eta,
beraz, foku distantzia ere bai. Hortaz, ezkerraldetik datozen argi izpi paraleloek lentea zeharkatzen dute,
eta dibergente bihurtzen dira, lentearen ezkerraldeko puntu batetik etorriko balira bezala.


Ezker aldetik datozen eta ardatzaren paraleloak diren argi izpiek lente ganbilbiko batean egin dute eraso. Errefraktaturiko izpiak, lentearen irudi fokura bilduko dira. Halaber, lehenengo gainaldeak ispilu ganbil gisa jokatuko du, islaturiko izpi dibergenteak emango dituelarik. Bigarren gainaldeak, ordea, ispilu ahur modura jokatuko du, eta ondorioz, islaturiko izpi konbergenteak emango ditu.

Ezker aldetik datozen eta ardatzaren paraleloak diren argi izpiek lente ahurbiko bat joko dute. Errefraktaturiko izpiak, ardatzetik urrundu egingo dira, lentearen ezker aldean dagoen irudi fokutik baletoz bezala. Aurreko argazkian bezala, oraingoan ere, lentearen bi gainaldeetan islaturiko izpiak ere ikus daitezke. Kasu honetan, lehenengo gainaldea ispilu ahurgisa jokatuko du eta islaturiko izpi konbergenteak emango ditu. Bigarren gainaldea, berriz, ispilu ganbil modura jokatuko du, eta ondorioz, islaturiko izpi dibergenteak emango ditu.
Lente dibergenteek foku distantzia negatiboak dituzte, eta lente negatiboak esaten zaie.
Bestelako lenteetan,  eta
eta  positiboak edo negatiboak
diren kasuetan, bihurdura erradioaren balioa handiagoa edo txikiagoa izan,
hala izango da lentea konbergentea edo dibergentea. Edozein lente alderantziz jartzean,
positiboak edo negatiboak
diren kasuetan, bihurdura erradioaren balioa handiagoa edo txikiagoa izan,
hala izango da lentea konbergentea edo dibergentea. Edozein lente alderantziz jartzean,
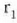 eta
eta
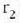 trukatu egiten dira,
etazeinuak aldatu behar zaizkie; alderantziz jarritako lente bati dagozkion bihurdura erradio berriak
honela adierazi behar dira beraz jatorrizkoen funtzioan:
trukatu egiten dira,
etazeinuak aldatu behar zaizkie; alderantziz jarritako lente bati dagozkion bihurdura erradio berriak
honela adierazi behar dira beraz jatorrizkoen funtzioan:
 eta
eta  .
( 11) ekuazioan f' foku distantzia berriak jatorrizkoaren balio eta zeinu berak ditu.
Hala bada, bi ganbileko lente batera izpi paraleloz osaturiko sorta bat heltzen bada
eskuinaldetik, sorta hori lente horren ezkerraldean fokatuko da, f distantziara dagoen puntu batean.
Edozein lente meheren ezkerraldean eta eskuinaldean f distantziara dauden bi puntuak
lentearen foku puntuak dira; ezkerraldean dagoenari objektuaren foku puntua deritzo
eta F sinboloaz adierazten da, eskuinaldekoari, berriz, irudiaren foku puntua esaten
zaio eta F sinboloa dagokio. Argi izpien itzulgarritasunaren bidez aise iragar daiteke
edozein foku puntutatik ateratzen diren izpiei zer gertatuko zaien; izpi horiek lentea
zeharkatzen dute, eta izpi paralelo gisa ateratzen dira. (11) ekuazioan ere fenomeno hori
ikus daiteke, izan ere, s distantziaren ordez f foku distantzia jarriz gero,
.
( 11) ekuazioan f' foku distantzia berriak jatorrizkoaren balio eta zeinu berak ditu.
Hala bada, bi ganbileko lente batera izpi paraleloz osaturiko sorta bat heltzen bada
eskuinaldetik, sorta hori lente horren ezkerraldean fokatuko da, f distantziara dagoen puntu batean.
Edozein lente meheren ezkerraldean eta eskuinaldean f distantziara dauden bi puntuak
lentearen foku puntuak dira; ezkerraldean dagoenari objektuaren foku puntua deritzo
eta F sinboloaz adierazten da, eskuinaldekoari, berriz, irudiaren foku puntua esaten
zaio eta F sinboloa dagokio. Argi izpien itzulgarritasunaren bidez aise iragar daiteke
edozein foku puntutatik ateratzen diren izpiei zer gertatuko zaien; izpi horiek lentea
zeharkatzen dute, eta izpi paralelo gisa ateratzen dira. (11) ekuazioan ere fenomeno hori
ikus daiteke, izan ere, s distantziaren ordez f foku distantzia jarriz gero,
 ateratzen da;
izpi sorta ez da inon fokatzen, izpi paralelo gisa ateratzen da, alegia.
ateratzen da;
izpi sorta ez da inon fokatzen, izpi paralelo gisa ateratzen da, alegia.
Bi lente mehe mota horiek 17. irudian ageri den bezala adierazi ohi dira, modu sinbolikoan.
Lente bakarraren ordez lente multzo bat dagoenean, sistema optiko horrek eratzen duen azken irudia prozedura honen bidez irudikatzen da:

17. Irudia: Lente meheen adierazpen sinbolikoa. (a) Lente konbergentea. (b) Lente dibergentea
lehenengo lenteari dagokion irudi distantzia kalkulatzen da lehendabizi, eta gero bigarren lenteari dagokion objektu distantzia zein den jakin behar da, lehenengo eta bigarren lenteen arteko distantzia kontuan harturik horretarako. Urrats horiek behin eta berriro errepikatu behar dira lente guztietan. Alegia, lente bakoitzaren irudia (eratu ala ez eratu) hurrengo lentearen objektu puntutzat hartu behar da.
Ispiluek eratzen dituzten irudiak bezala, lenteek eratzen dituzten irudiak ere grafikoen bidez ulertu behar dira. 18. irudian lente konbergenteari dagokion grafikoa ikus daiteke.
Irudi horretan giza irudia da objektua, eta ispiluetan bezala, irudi horretako buruari zer irudi puntu dagokion jakin behar da. Irudika daitezkeen izpi guztien artean, badira hiru lenteak zer irudi eratzen duen jakiten laguntzen dutenak: (a) ardatzari buruz paraleloa den izpia, lentea zeharkatzen du, eta irudiaren foku puntutik igarotzen da; (b) lentearen erdigunetik igarotzen den izpia, izpi hori ez da desbideratzen; (c) lentearen objektuaren foku puntutik igarotzen den izpia, lentea zeharkatzen du eta ardatzari buruz paraleloan ateratzen da. Hiru izpi horiek irudi puntuan elkar ebakitzen dute, irudian ikus daitekeen bezala. Irudi hori zein den jakiteko, aski cta hiru izpi horietatik bi erabiltzea.
Aurrera egin baino lehen, arestian aipatu den (b) izpi hori hobeto aztertu beharra dago. Izpi hori zergatik ez da desbideratzen? Kontuan hartu behar da izpi horrek lentearen erdigunearen inguruneetan zeharkatuko dituen bi gainaldeak elkarri buruz ia-ia paraleloak direla. Hortaz, izpiak xafla lau bat zeharkatzen duela esan daiteke (ikus 19. irudia). Lentea mehea denez, izpi horrek berez egingo lukeen ibilbidearekiko izango duen desbideratzea ez da kontuan hartzekoa.
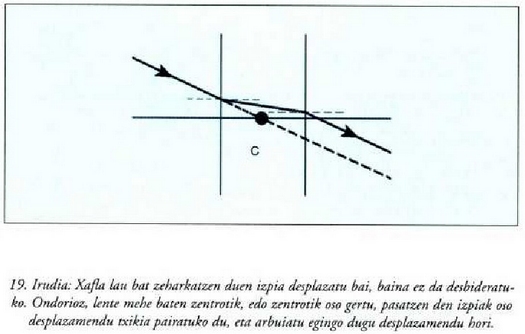
18. irudian ageri diren triangeluetan  betetzen da.
Beraz, da:
betetzen da.
Beraz, da:

Formula hori eta ispiluena berdinak dira. Oraingoan ere, handipena negatiboa bada, irudia alderantziz egongo da.
Orain zenbakizko bi adibide aztertuko dira. Demagun lente mehe bat bi ganbilekoa, n = 1.5 duena eta lentearen bi bihurdura erradioak balio berekoak dituena (20 zentimetro). 2 zentimetro luze den objektu bat lentearen ezkerraldean, 10 zentimetrora, jartzen da; objektu horren irudiaren ezaugarriak asmatu behar dira.
Lehendabizi, (11) ekuazioaren bidez lentearen foku distantzia kalkulatu behar da. Hitzarmenez aukeratu diren zeinuen arabera, r, = 20 zentimetro eta rz = -20 zentimetro direla kontuan harturik, hau da f foku distantzia:

20. irudian lentetik 10 zentimetrora dagoen objektu txiki bati dagokion izpi diagrama dago adierazita. Ardatzari buruz paraleloa den izpia irudi fokurantz (F puntua) desbideratzen da. Lentearen erdigunetik igarotzen den izpia ez da desbideratzen. Zer irudi eratzen duen jakiteko, izpi irudikatu horiek atzerantz luzatu behar dira, elkargunera iritsi arte. Arestian aipatu den hirugarren izpia ere erabil daiteke, nahi izanez gero, eragiketa hori ondo egina dagoela egiaztatzeko. Hirugarren izpi horrek objektutik atera behar du, F objektu fokutik igarotzenden lerro bati jarraituz. Izpi hori ardatzari buruz paralelo aterako ola lentetik. Grafikoari begiratze hutsarekin jakin daiteke ea irudi hori alegiazkoa den, ea zuzena den, eta ea objektua baino handiagoa den. Irudi hori lentearen ezkerraldean olago, lentetik 20 zentimetrora.

Edonola ere, emaitza horiek guztiak algebraren bidez ere atera daitezke, (12) ekuazioaz baliatuz:
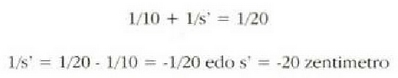
Irudi distantzia negatiboa denez, irudia alegiazkoa da. Albo handitzea honela kalkulatuko da:
 .
Irudi hori, heraz, objektua halako bi da. Objektu horren garaiera 2 zentimetrokoa denez,
irudiarena 4 zentimetrokoa da.
.
Irudi hori, heraz, objektua halako bi da. Objektu horren garaiera 2 zentimetrokoa denez,
irudiarena 4 zentimetrokoa da.
Bigarren adibidea lehengoaren jarraipen gisa har daiteke. Foku distantzia + 10 zentimetrokoa duen lente bat jarriko da orain, aurreko adibideko lentearen eskuinaldean, 20 zentimetrora. Bi lente horiek osatzen duten sistema optikoak zer irudi sortzen duen jakin behar da.
Adibide horri dagokion izpi diagrama 21. irudian ageri ola.
hehenengo lenteak eratzen duen irudia ezaguna denez, horixe izango da higarren
lenterako kontuan hartu beharreko objektua. Hortaz, izpiak berriz irudikatu behar dira,
eta objektu hori eta bigarren lentea hartu behar dira kontuan. Bi izpi adierazi dira grafikoan;
bata, ardatzari buruz paraleloa, eta  fokutik igarotzen olena, eta hestea, lentearen erdigunetik igarotzen dena batere desbideratu gabe.
Azken irudia bi izpi horien arteko elkargunean eratuko da. Azkenirudi hori erreala ola,
alderantziz dago, eta bigarren lentearen irudi
fokua baino haruntzago olago. Irudi hori zehatz-mehatz kokatu nahi
bada, (12) ekuazioa erabili behar ola herriz ere. Oraingoan, s = 40
zentimetro eta f = 10 zentimetro ola, beraz
fokutik igarotzen olena, eta hestea, lentearen erdigunetik igarotzen dena batere desbideratu gabe.
Azken irudia bi izpi horien arteko elkargunean eratuko da. Azkenirudi hori erreala ola,
alderantziz dago, eta bigarren lentearen irudi
fokua baino haruntzago olago. Irudi hori zehatz-mehatz kokatu nahi
bada, (12) ekuazioa erabili behar ola herriz ere. Oraingoan, s = 40
zentimetro eta f = 10 zentimetro ola, beraz


21. Irudia: Bigarren adibidearen izpi diagrama. Lehenengo lenteak emandako irudia, bigarren lentearen objektutzat hartu behar da. Azken irudiaren kokapena, lehen iruditik abiaturiko izpiak marraztuz lortu behar da. Kasu honetan, lehen irudiaren posizioa deterninatzeko erabili diren izpietako bat ez da desbideratuko bigarren lentea zeharkatzean. Lehen iruditik abiaturiko beste izpi bat, ardatzaren paraleloa dena, aski da aurrekoarekin batera, azken irudimen kokapena zehazteko.
Aberrazioak
Objektuaren puntu batetik ateratzen diren izpi guztiak irudiaren puntu bakar hatera hiltzen ez direnean, irudia lausoturik agertzen ola; gertaera horri aberrazio esaten zaio. Sistema optikoetan era askotako aberrazioak ager daitezke. Adibidez, ispilu esferiko batek edo lente batek bere ardatzean duen objektu jakin baten irudia eratzen duenean, ardatzetik urrun dauden puntuetan jotzen Gluten izpiek ere eratzen badute irudi hori, irudi hori ez ola guztiz garbia izango. Efektu horri aberrazio esferakoa esaten zaio. Bestalde, ardatzez kanpo dagoen objektu jakin baten irudia eratzen denean, irudiak kometa itxura izango du, lentearen edo ispiluaren zati desberdinek desberdin handitzen baitute; efektu horri koma esaten zaio. Badaude beste bi aberrazio ere, ustrgmatisrnoa eta distortsioa. Ispiluetan eta lenteetan agertzen diren aberrazio horiek guztiak islatzearen eta errefrakzioaren legeak gainalde esferikoetan aplikatzearen ondorio hutsa dira. Hemen agertzen diren ekuazio errazetan aberrazio horiek ez dira inondik inora agertzen, angelu txikien hurbiltzea (izpi paraxilak) erabili baita ekuazio horiek ebazteko. Aberrazio horietako batzuk ezabatu edo zertxobait zuzendu daitezke, ispilua edo lentea egitean esferikoak ez diren gainaldeak erabiliz gero. Halere, hori egitea zaila izaten da gehienetan, eta gainalde esferikoak egitea baino askoz garestiagoa orobat. 22. irudiko ispilu parabolikoa esferikoak ez diren gainalde islatzaileen adibide bat da. Gainalde parabolikora heltzen diren izpi paraleloak islatu egiten dira, eta puntu bakarrera biltzen dira guztiak, edozein dela ere izpiaren eta ardatzaren arteko distantzia. Mota horretako gainalde islatzaile parabolikoek garrantzi handia clute teleskopio astronomiko handietan, ahalik eta gainalde islatzaile handiena behar izaten baitute irudiaren intentsitatea ere ahalik eta handiena izan dadin. Gainalde parabolikoa hedadura handiko argi sorta paraleloak sortzeko ere erabil daiteke, eta horretarako argi iturri txiki bat jarri behar da gainaldearen fokuan.

22. Irudia: Aberrazio esferikoa, gainalde paraboliko bat erabiliz ezaba daiteke. Gainalde horretan, ardatzaren paraleloak diren izpi guztiak, foku bakar batetik pasatuko dira islatu ondoren
Bada beste aberrazio bat, lenteetan baizik agertzen ez dena, aberrazio kromatikoa. Aberrazio horren jatorria argiari dagokion kapituluan dago aztertuta, eta beiraren errefrakzio indizeak uhin luzeraren mende egoteak sortua da. Ispiluek ez dute aberrazio hori izaten, ispiluetan izpiak islatu baizik ez baitira egiten. (11) ekuazioaren arabera, nahiz eta izpi paraxialak baizik ez kontuan hartu, lentearen foku distantzia errefrakzio indizearen mendean egongo da eta, beraz, uhin luzerak nolakoak (kolore desberdinak) f-ren balioak ere halakoak izango dira (hala ere ez dute alde handirik izaten). Lente bakarraren ordez lente sistema bat erabiliz zuzendu daitezke aberrazio kromatikoak. Adibidez, lente positibo bat eta foku distantzia handiagoko lente negatibo bat elkarrekin erabil daitezke sistema konbergente bat eratzeko, eta sistema horren aberrazio kromatikoa sistemaren foku distantzia berbera duen lente bakarrarena baino askoz txikiagoa izango da


















