Fisika-Kimika»Fisika - Kimika
3. Estatika

3.1. Sarrera
Aurreko atalean zatikien mugimendua aztertu da, mugimendu horren arrazoiak kontuan hartu gabe. Gai honetan, berriz, indarren eragina jasaten duten gorputzen oreka egoerak izango dira aztergai, mekanikan estatika deritzon alorra hain zuzen ere. Oreka egoerak gorputz baten atseden egoera adierazten du, gorputz batek beste gorputz batzuei buruz duen atseden egoera.
Esperientziak erakusten duenez, gorputzek oso portaera berezia dute indarrek eragiten dietenean. Gorputz gotor zurrunak direnean, altzairuzko barra batean adibidez, gorputz horren bi punturen arteko distantzia ez da aldatuko nahiz eta gorputzak indar baten eragina jasan. Baina, aldiz, malguki tankerako gorputz gotorrei forma aldatzen zaie indarren eraginarekin eta hasieran zuten forma hartzen dute berriro indarraren eraginpetik kanpo gelditzean; gorputz hauei gorputz elastiko deritze. Indarrak eragiten dienean nola jokatzen duten, gorputz plastikoak ere bereizten dira –buztina adibidez–, hau da, indarraren eraginez forma aldatu eta indarraren eraginpetik atera ondoren lehengoratzen ez direnak, eta baita isurkari eta gasak ere, indarraren zuzeneko eragina jasan gabe forma aldaketak izan ditzaketenak; isukariei dagokienean, aipagarria da forma aldatu arren, bolumenak bere horretan irauten duela.
3.2. Indarra
Gorputz bat oreka egoeran ala mugimenduan dagoen, gorputz horren eta beste gorputz batzuen arteko elkar eraginak esango du hori. Izan ere, beste gorputz batzuekiko elkar eraginen ondorioz forma aldaketak, erakartze indarrak edo aldaratze indarrak jasaten dituzte gorputzek. Gorputzen arteko eragin mekanikoa neurtzen duen magnitudea da indarra.
Indarra magnitude bektoriala da. Gorputz jakin batean duen eragina ezagutzeko indarraren aplikazio puntua, hau da indarrak gorputza zein puntutan jotzen duen; modulua, hau da, aztertu nahi den indarraren eta banako gisa hartzen den beste indar baten arteko erlazioa; norabidea, indarraren eragina soilik jasaten duenean zein lerro zuzen egiten duen gorputzak, eta azkenik, indarraren noranzkoa, hau da, indarra bideratzen den zuzenaren burua zein aldetan dagoen.
Indarra neurtzeko erabiltzen diren banako ezagunenak Newton (N) eta indar kiloa (kg) dira. Hau da bi banako horien arteko erlazioa:
indar kilo bat = 9,81 Newton.
Aurrerantzean indar sistema esapidea erabiliko da gorputz jakin bati eragiten dioten indarren multzoa adierazteko, eta gorputz gotor aske esango zaie beste inolako gorputzekin loturarik gabe espazioan nahierara lekualda daitezkeen gorputzei.
3.3. Estatikaren printzipioak
Gorputzen orekari eta mugimenduei buruz egindako esperientzia eta azterketa askoren ondorio dira estatikaren printzipioak, eta esperientziak behin eta berriz egiaztatzen ditu.
a) Transmitigarritasun printzipioa
Eman dezagun gorputz gotor aske bati
 indarrek eragiten diotela A puntuan. Gorputz hori orekan egon dadin,
bi indarrek norabide bera izan behar dute, baina elkarren kontrako noranzkoa (3.1. a irudia).
Baldin eta
indarrek eragiten diotela A puntuan. Gorputz hori orekan egon dadin,
bi indarrek norabide bera izan behar dute, baina elkarren kontrako noranzkoa (3.1. a irudia).
Baldin eta  indarraren aplikazio puntua A puntua izan ordez B puntua balitz (3.1. b irudia),
kasu horretan ere oreka egoeran egongo litzateke gorputza.
Beraz, indar jakin batek gorputz zurrun batean duen eragina ez da aldatuko baldin eta indarrak norabide bera badu,
nahiz eta aplikazio puntua aldatu eta gorputz gotorraren beste edozein puntutan finkatu.
Adierazpen honi transmisibilitate printzipio esaten zaio, eta indarrak bektore lerrakorrak direla adierazten du.
Adibide horretan aipatu dena, ordea, gorputz zurrunentzat bakarrik betetzen da.
Adibidez, 3.2. irudiko barra orekan egongo da baldin eta
indarraren aplikazio puntua A puntua izan ordez B puntua balitz (3.1. b irudia),
kasu horretan ere oreka egoeran egongo litzateke gorputza.
Beraz, indar jakin batek gorputz zurrun batean duen eragina ez da aldatuko baldin eta indarrak norabide bera badu,
nahiz eta aplikazio puntua aldatu eta gorputz gotorraren beste edozein puntutan finkatu.
Adierazpen honi transmisibilitate printzipio esaten zaio, eta indarrak bektore lerrakorrak direla adierazten du.
Adibide horretan aipatu dena, ordea, gorputz zurrunentzat bakarrik betetzen da.
Adibidez, 3.2. irudiko barra orekan egongo da baldin eta
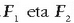 indarrak neurri berekoak badira.
Eta indar horien aplikazio puntuak puntu arbitrario batera aldatzen badira, barraren C puntura esaterako, edo
indarrak neurri berekoak badira.
Eta indar horien aplikazio puntuak puntu arbitrario batera aldatzen badira, barraren C puntura esaterako, edo
 indarraren aplikazio puntua B
puntura aldatzen bada eta
indarraren aplikazio puntua B
puntura aldatzen bada eta 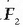 indarrarena A puntura (3.2. c irudia), barra oreka egoeran egongo da. Baina, gorputza oreka egoeran egon arren,
ez du portaera mekaniko bera izango hiru kasuetan: lehen kasuan barra luzatu egingo da, indarren eraginez;
bigarren kasuan, barrari ez zaio inolako aldaketa mekanikorik gertatuko, eta hirugarren kasuan, azkenik,
barra konprimatu egingo da.
indarrarena A puntura (3.2. c irudia), barra oreka egoeran egongo da. Baina, gorputza oreka egoeran egon arren,
ez du portaera mekaniko bera izango hiru kasuetan: lehen kasuan barra luzatu egingo da, indarren eraginez;
bigarren kasuan, barrari ez zaio inolako aldaketa mekanikorik gertatuko, eta hirugarren kasuan, azkenik,
barra konprimatu egingo da.

3.1. irudia. Indar batek gorputz zurrun bati egiten dion eragina ez da aldatzen indarraren aplikazio puntua indarrak gorputzean duen eragin lerroaren beste edozein puntutan jarriz gero ere.

b) Indar paralelogramoaren printzipioa
Printzipio honen arabera, gorputz bati O aplikazio puntuan eragiten zaizkion
 indarrak ordezka ditzake puntu horretanbertan eragindako F indar bakarrak, hau da,
indar horien batura geometriko edo bektorialaren balio bera duen F indarrak (3.3. irudia).
F indarrari ondoriozko indar edo emaitza bektore esaten zaio kasu horretan, eta
indarrak ordezka ditzake puntu horretanbertan eragindako F indar bakarrak, hau da,
indar horien batura geometriko edo bektorialaren balio bera duen F indarrak (3.3. irudia).
F indarrari ondoriozko indar edo emaitza bektore esaten zaio kasu horretan, eta
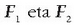 indarrak F indarraren indar osagaiak dira. Beraz,
indarrak F indarraren indar osagaiak dira. Beraz,

Ikusten denez, ondoriozko indarraren magnitudeak ez du bi indar osagaien magnitudeen baturaren balio bera, beste balio hau baizik:


3.3. irudia. Gorputz bati puntu batean aplikaturiko bi indarren ondoriozko indarra puntu horretan bertan aplikaturiko indar bat da, eta bi indarrak alde gisa harturik osatzen diren paralelogramoaren diagonalak adierazten du indar hori grafikoki.
c) Akzio-erreakzioaren berdintasunaren printzipioa
Indarrak sekula ez dira bakarturik agertzen. Gorputz batek beste gorputz bati nolabaiteko indarra eragiten badio (akzioa), indarra jasaten duen gorputzak neurri eta norabide bereko baina kontrako noranzkoko beste indar bat eragiten dio lehenengo gorputzari (erreakzioa). Printzipio honen arabera, baldin eta A gorputzak B gorputzari F indarra egiten badio, B gorputzak F' indarra egiten dio A gorputzari. Beraz,

Adibide horretan F eta F' indarrek ez dute osatzen orekan dauden indarren sistema bat, ez baitira gorputz berari eragiten zaizkion bi indar (3.4 irudia).

3.4. irudia. Gorputz batek beste baten gainean indar bat egiten duenean, indarra jasaten duen gorputzak indar bera eragiten dio lehenengoari
3.4 Indar baten deskonposaketa
Indar bat deskonposatzeak indar jakin bat ondoriozko indar gisa hasieran emandako indarra izango duen indar sistema bat eskatzen du. 3.5 irudian F indarra F1, F2 eta F3 indar elkarzutetan deskonposatu da. Horrenbestez,

Problema hau ebazteko, beraz, aski da hasieran emandako indarra diagonaltzat eta indar osagaiak erpin gisa dituen paralelepipedo bat irudikatzea.

3.5. irudia. F indarra elkarri buruz zut diren hiru indarretan deskonposatu da. Paralelepipedoaren diagonalak hasierako indarra adierazten du eta erpinek indar horren indar osagaiak.
3.5 Indar konkurrenteen osaera

3.6. irudia. Indar konkurrenteen osaerarako metodo analitikoa. Ondoriozko indarra ardatz batean proiektatuz lortzen den emaitza indar osagaien proiekzioak ardatz horretan bertan proiektatzean lortzen den batura aljebraikoaren berdina da
Eman dezagun n indarrez osaturiko 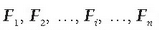 indar sistema,
bere indarrek O puntu jakin batean eragiten dutena (3.6 irudia).
Sistema horren ondoriozko F indarra aurkitzeko, koordenatu laukizuzenez osaturiko sistema bat hartzen da,
sorburua O puntuan duena. n indar bakoitzaren osagaiak,
indar sistema,
bere indarrek O puntu jakin batean eragiten dutena (3.6 irudia).
Sistema horren ondoriozko F indarra aurkitzeko, koordenatu laukizuzenez osaturiko sistema bat hartzen da,
sorburua O puntuan duena. n indar bakoitzaren osagaiak,  indarraren osagaiak esaterako, hauek dira:
indarraren osagaiak esaterako, hauek dira:

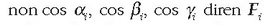 indarraren kosinu zuzentzaileak. Bektore batuketaren erregelaren arabera,
n indarren F ondoriozko indarraren balioa hau izango da:
indarraren kosinu zuzentzaileak. Bektore batuketaren erregelaren arabera,
n indarren F ondoriozko indarraren balioa hau izango da:

Bektore ekuazio hori ondoko hiru ekuazio eskalarren baliokidea da:
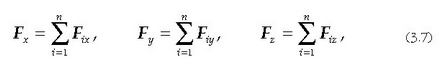
Ekuazio eskalar horiek hasieran emandako indarren osagai eskalarren batura gisa azaltzen dituzte ondoriozko indarraren osagaiak. Ondoriozko indarrari dagokion modulua kalkulatzeko berdintza hau erabiltzen da:

Eta ondoriozko indarraren kosinu zuzentzaileak hauek izango dira:

INDAR SISTEMAK ESPAZIOAN
Espazioan zoriaren arabera kokaturiko indar sistema bat ebazteko oinarrizko zenbait kontzeptu azaldu behar dira lehenik.
3.6. Indar baten momentua
Eman dezagun F indar batek P zatiki bati eragiten diola eta indar hori
 zuzenaren gainean mugitzen dela.
F indarrak espazioko O puntu finkoari buruz duen momentua
zuzenaren gainean mugitzen dela.
F indarrak espazioko O puntu finkoari buruz duen momentua
 ondoko bektore biderketa honen bidez adierazten da:
ondoko bektore biderketa honen bidez adierazten da:

non P zatikiak O puntuari buruz duen posizio bektorea baita r (3.7. irudia).
F indarrak zatikia  momentuaren eragin lerroaren inguruan birarazteko duen joera neurtzen du
momentuaren eragin lerroaren inguruan birarazteko duen joera neurtzen du
 momentuak.
momentuak.

Bektore biderketaren definizioaren arabera,  bektorea zuta da r bektoreak eta F indarrak eratzen duten planoari buruz; bektorehorren
noranzkoa torlojuaren legeak zehazten du, eta modulua, berriz, formula honek:
bektorea zuta da r bektoreak eta F indarrak eratzen duten planoari buruz; bektorehorren
noranzkoa torlojuaren legeak zehazten du, eta modulua, berriz, formula honek:

non r eta F bektoreek osaturiko angelua baita f, eta d, berriz, indarraren eragin lerrotik O momentu zentrora (r = 0), hau da momentuak neurtzeko oinarri hartzen den zentrora, dagoen distantzia.
Baldin eta r eta F bektoreak beren osagai laukizuzenen arabera adierazten badira, adierazpen hau lortzen da:

Indar baten momentua puntu jakin bati buruz m-kg-tan edo cmkg-tan adierazten da.
Ikusten denez, F indar baten  momentuak ez du adierazten F indarraren aplikazio puntua zein den.
Baina, hala ere,
momentuak ez du adierazten F indarraren aplikazio puntua zein den.
Baina, hala ere,  momentua eta F indarra ezagututa F indarraren eragin lerroa, hau da
momentua eta F indarra ezagututa F indarraren eragin lerroa, hau da
 zuzena,
zehaztuta gelditzen da. Zuzen horrek O puntutik igarotzen den
zuzena,
zehaztuta gelditzen da. Zuzen horrek O puntutik igarotzen den
 momentuaren planoari buruz zuta izan behar du;
momentuaren planoari buruz zuta izan behar du;
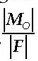 zatikiak O puntura dagoen d distantzia ematen du,
eta
zatikiak O puntura dagoen d distantzia ematen du,
eta  momentuaren noranzkoak esaten du zuzena O puntuaren zein aldetan
irudikatu behar den
momentuaren noranzkoak esaten du zuzena O puntuaren zein aldetan
irudikatu behar den
3.7. Indar baten momentuaren ezaugarriak
Indar baten momentuaren definizioaren arabera, hauek dira momentuaren ezaugarriak:
a) Indar baten momentua puntu jakin bati buruz ez da aldatzen F bektorea bere eragin lerroan zehar lekualdatu arren (3.8. irudia).
F bektorearen lerratzeak posizio bektorea aldarazten du, r izan ordez
 izango da, eta kontuan harturik
izango da, eta kontuan harturik
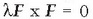 dela, orduan:
dela, orduan:


3.8. irudia. F indarraren momentua O puntuari buruz ez da aldatzen indarra bere eragin lerroan zehar lekualdatu arren
Era berean, r bektorea O sorburutik F bektorearen edozein puntura irudikatzen dela ere, indarraren momentua ez da aldatzen. Hori dela eta, ez du zentzurik bektore aske baten O puntuari buruzko momentuaz aritzeak, bektore lerrakor baten O puntuari buruzko momentua da kalkulatu behar dena.
b) Modulu bera eta elkarren kontrako noranzkoa duten bi bektore lerrokide direnean,
edozein punturi buruzko momentuen bektore batura zero izango da. Bedi
 zuzena P eta O puntuetan,
hurrenez hurren, aplikaturiko F eta - F indarren eragin lerroa, eta O puntu bat, edozein (3.9. irudia).
Bi indar horien momentua O puntuari buruz honela kalkulatzen da:
zuzena P eta O puntuetan,
hurrenez hurren, aplikaturiko F eta - F indarren eragin lerroa, eta O puntu bat, edozein (3.9. irudia).
Bi indar horien momentua O puntuari buruz honela kalkulatzen da:

Baina 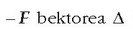 zuzenean zehar mugitzen bada,
bere sorburua P puntuan kokatu arte, bektorearen momentuak aldagabe irauten du.
Beraz, aurreko adierazpenaren ordez beste hau ere erabil daiteke:
zuzenean zehar mugitzen bada,
bere sorburua P puntuan kokatu arte, bektorearen momentuak aldagabe irauten du.
Beraz, aurreko adierazpenaren ordez beste hau ere erabil daiteke:


3.9. irudia. Modulu bera eta elkarren kontrako noranzkoa duten bi indar lerrokideren momentua edozein punturi buruz zero da.
c)  momentuak O sorburuari buruz duen balioaren eta F indarraren berdina den beste indar batek,
O sorburu horri berorri buruz baina O' puntua aplikatzen delarik, duen momentuaren balioaren arteko diferentziaren
balio bera du F indar batek edozein O' punturi buruz duen
momentuak O sorburuari buruz duen balioaren eta F indarraren berdina den beste indar batek,
O sorburu horri berorri buruz baina O' puntua aplikatzen delarik, duen momentuaren balioaren arteko diferentziaren
balio bera du F indar batek edozein O' punturi buruz duen 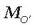 momentuak. Beraz, O puntuaren ordez O' puntua hartuz gero (3.10. irudia):
momentuak. Beraz, O puntuaren ordez O' puntua hartuz gero (3.10. irudia):

Eta horrenbestez,

Horrela, F indarra eta O puntu bati buruzko
 ezagututa, beste edozein O' punturi buruzko
momentua ere kalkula daiteke.
ezagututa, beste edozein O' punturi buruzko
momentua ere kalkula daiteke.

3.10. irudia. Indar batek O' puntu bati buruz duen momentua O puntuari buruz duen momentuaren eta emandako indarraren berdina den beste indar batek, O' puntuan aplikatzen denak, O puntu horri berari buruz duen momenduaren arteko diferentzia da.
d) F eta (3.17) ekuazioa arteko biderkaketa eskalarra egiten bada, adierazpen hau ateratzen da:

izan ere, 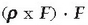 bidekarketa baliogabea da bi bektore berdin dituelako, eta
bidekarketa baliogabea da bi bektore berdin dituelako, eta
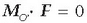 berdintza betetzen da bi bektore
horiek elkarzutak direlako. Beraz, F bektorea beti da puntu jakin bati buruz bektore horrek duen momentuari buruz perpendikularra.
berdintza betetzen da bi bektore
horiek elkarzutak direlako. Beraz, F bektorea beti da puntu jakin bati buruz bektore horrek duen momentuari buruz perpendikularra.
e) (3.10) ekuazioaren arabera,  bektoreak momentu baliogabe bat du,
bektoreak momentu baliogabe bat du,  bektorea baliogabea izan gabe momentua baliogabea izan dadin, baldintza beharrezko eta nahikoa da O puntua
F bektorearen eragin lerroan egotea.
bektorea baliogabea izan gabe momentua baliogabea izan dadin, baldintza beharrezko eta nahikoa da O puntua
F bektorearen eragin lerroan egotea.
f) Indar bektorearen koordenatuak. Jakina da bektore aske batek hiru osagai dituela.
Hala ere, indar bat, F bektore askeak eta  momentuak definitua denean,
momentuak definitua denean,  sei parametro arbitrariok ezaugarritu behar lukete, baina beti betetzen denez
sei parametro arbitrariok ezaugarritu behar lukete, baina beti betetzen denez

berdintza, bost parametro arbitrarioren arabera definitzen da indar bat.
3.8 Indar baten momentua ardatz bati buruz
Bedi  momentua A puntuan aplikaturiko F indar baten momentua O puntuari buruz, eta
momentua A puntuan aplikaturiko F indar baten momentua O puntuari buruz, eta
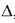 , berriz, O puntutik igarotzen den ardatz bat,
zeinu positiboa e unitate bektoreak definitua duena (3.12 irudia). Definizioz,
, berriz, O puntutik igarotzen den ardatz bat,
zeinu positiboa e unitate bektoreak definitua duena (3.12 irudia). Definizioz,

biderkaketa eskalarrari ? ardatzari buruzko F bektorearen momentua esaten zaio. Indar batek ardatz bati buruz duen momentua momentu bektoreak ardatz horretan duen proiekzio ortogonalaren neurri aljebraikoa da.
Hala, e, r, F bektoreen osagaien arabera:

non  ardatzaren kosinu
zuzendariak baitira, (x y z) F indarraren aplikazio puntuaren koordenatuak, eta
ardatzaren kosinu
zuzendariak baitira, (x y z) F indarraren aplikazio puntuaren koordenatuak, eta
 , berriz, F bektorearen osagaiak.
, berriz, F bektorearen osagaiak.
Hain zuzen ere, baldin eta  ardatza x ardatzarekin, y ardatzarekin edo z ardatzarekin bat badator, orduan
ardatza x ardatzarekin, y ardatzarekin edo z ardatzarekin bat badator, orduan
 momentuaren osagaiak,
horietako edozein norabidetan, eta koordenatuen ardatzei buruzko
momentuaren osagaiak,
horietako edozein norabidetan, eta koordenatuen ardatzei buruzko
 momentua berdinak izango dira.
momentua berdinak izango dira.
Indar baten momentua ardatz bati buruz ez dago ardatzean harturiko O puntuaren mende.
Ardatzeko beste O' puntu batek ere momentu bera emango luke,
 , e bektorearen paraleloa denez,
adierazpen hau ateratzen baita:
, e bektorearen paraleloa denez,
adierazpen hau ateratzen baita:

Beraz, indar baten momentua ardatz bati buruz baliogabea izango bada, baldintza beharrezkoa da,
eta nahikoa, ardatza eta indarra planokideak izatea, orduan bakarrik izango baita baliogabea
 .
(Hiru bektore horiek eratzen duten paralelepipedoaren bolumena baliogabea da).
.
(Hiru bektore horiek eratzen duten paralelepipedoaren bolumena baliogabea da).

3.11. irudia. Indar batek ardatz bati buruz duen momentua magnitude eskalarra da, eta momentu bektoreak ardatzaren gainean duen proiekzio ortogonalaren neurri aljebraikoa ematen du.
3.9 Indar bikotea
Indar bikote esaten zaio modulu eta norabide bera, elkarren kontrako noranzkoa eta eragin lerro desberdina duten bi indarrez osaturiko sistemari. Eta sistemako bi indarren eragin lerroak hartzen dituen planoa bikotearen planoa da.
Bitez  puntuetatik igarotzen den indar bikotearen osagaiak eta
puntuetatik igarotzen den indar bikotearen osagaiak eta
 bektoreak O puntuari buruz
(edozein puntu harturik) indar horiek hurrenez hurren dituzten posizio bektoreak (3.12. irud.).
Indar bikotea osatzen duten bi indarren O puntuari buruzko momentuen batura bikotearen momentua da. Beraz:
bektoreak O puntuari buruz
(edozein puntu harturik) indar horiek hurrenez hurren dituzten posizio bektoreak (3.12. irud.).
Indar bikotea osatzen duten bi indarren O puntuari buruzko momentuen batura bikotearen momentua da. Beraz:

edo, bestela:

non  puntuak
puntuak
 puntuari buruz duen posizio bektorea baita r.
(3.25) ekuazioak erakusten duenez, indar bikote baten, edo, besterik gabe, bikote baten,
momentua ez dago aukeratzen den momentu zentroaren mende. Bektore hori bektore askea da beraz,
hau da, ez dago eragin lerro jakin bati lotuta, indarretan gertatzen zen moduan, eta ez dago
sorburu jakin baten mende ere. [Horregatik kendu da O azpi indizea (3.25) ekuaziotik.]
Bektore horren modulua kalkulatzeko indarretako baten magnitudearen eta bi indarren eragin
lerroen artean dagoen distantzia perpendikularraren arteko biderkadura egiten da; eragin lerroen
arteko distantzia adierazteko Fd erabiltzen da, eta d letrari indar bikotearen beso deitzen zaio.
Bektorearen norabidea bikotearen planoari buruz zuta da, eta noranzkoa torlojuaren legeak ematen du.
Indar bikote baten momentuan neurtzeko erabiltzen diren banakoak indar baten momentua neurtzeko
erabiltzen diren berberak dira.
puntuari buruz duen posizio bektorea baita r.
(3.25) ekuazioak erakusten duenez, indar bikote baten, edo, besterik gabe, bikote baten,
momentua ez dago aukeratzen den momentu zentroaren mende. Bektore hori bektore askea da beraz,
hau da, ez dago eragin lerro jakin bati lotuta, indarretan gertatzen zen moduan, eta ez dago
sorburu jakin baten mende ere. [Horregatik kendu da O azpi indizea (3.25) ekuaziotik.]
Bektore horren modulua kalkulatzeko indarretako baten magnitudearen eta bi indarren eragin
lerroen artean dagoen distantzia perpendikularraren arteko biderkadura egiten da; eragin lerroen
arteko distantzia adierazteko Fd erabiltzen da, eta d letrari indar bikotearen beso deitzen zaio.
Bektorearen norabidea bikotearen planoari buruz zuta da, eta noranzkoa torlojuaren legeak ematen du.
Indar bikote baten momentuan neurtzeko erabiltzen diren banakoak indar baten momentua neurtzeko
erabiltzen diren berberak dira.
Noski, r eta F bektoreen banakako balioak alda daitezke, bikotearen momentua aldatzen ez dela, ondoko baldintza hauek betez gero: a) Fd biderkaketak konstante irauten badu; b) r eta F bektoreak bere baitan hartzen dituen planoaren orientazioak aldagabe irauten badu, edo c) bikotearen noranzkoa aldatzen ez bada. Bikote baten momentua bektore magnitude bat denez (paralelogramoaren
legea betetzen duela egiazta daiteke), bektoreekin egin daitezkeen eragiketa baliozko guztiak aplika dakizkioke hari ere.
Bikote bat gorputz gotor zurrun bati eragiten zaionean, biratzeko joera du gorputz horrek, baina ez da aldatuko lekuz, ondoriozko indarra zero delako.

3.12. irudia. Indar bikote baten momentuaren bektore adierazpena. Bektore hori edozein puntutan aplika daiteke (bektore askea da).
3.10 Indar-bikote sistema
Eman dezagun A puntuari F indar batek eragiten diola (3.13 a). Indar horren ordez haren paraleloa den beste
indar bat aplikatuko balitz O puntu batean, edozeinetan, (3.13 b), indarrak gorputzean duen eragina aldatuko litzateke,
izan ere, transmisibilitate printzipioari jarraituz, indar bat beren eragin lerroan zehar bakarrik mugi daiteke.
Dena dela, F eta – F indarrak ere aplika daitezke O puntuan, bi indar horiek elkarri buruz orekan baitaude beti.
Horrela, ez da aldatuko hasierako indarraren eragina. Hala ere, aldaketa horren ondorioz,
hiru indarrez osatua izango da sistema: O puntuan eragindako F indarra, eta indar bikote bat, zeinaren
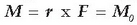 momentua hasierako indarrak O
puntuari buruz zuen momentuaren baliokidea, eta beraz, F indarraren perpendikularra baita.
momentua hasierako indarrak O
puntuari buruz zuen momentuaren baliokidea, eta beraz, F indarraren perpendikularra baita.

3.13. irudia. Gorputz gotor zurrun bati aplikaturiko indar bat bere buruari buruz paraleloan alda daiteke lekuz, gorputzaren gaineko eragina aldatzen ez dela, baldin eta aldi berean bikote bat eransten bazaio hasierako indarrak aplikazio puntu berriari buruz duen momentuaren momentu bera duena.
Hitzarmenez, M bektorea F bektorearekin batera aplikatzen da O puntuan, eta bi bektore horiek osaturiko
konbinazioari indar-bikote sistema esaten zaio (3.13 c irudia). Beraz, gorputz gotor zurrun bati eragiten
dion edozein F indar edozein O puntu arbitrariotara aldatu ahal izango da, baldin eta emandako indarrak O
puntuari buruz duen  momentuaren M momentu baliokidea dagokion bikote bat eransten bada.
momentuaren M momentu baliokidea dagokion bikote bat eransten bada.
3.11 Edozein indarren sistema
Lehen lortutako emaitzei esker, edozein indarrez osatutako sistema bat ordezka,
edo murriz daiteke lehenengo sistemaren baliokide den beste sistema soilago batez.
Demagun, gorputz gotor bati  edozein indarrez osatutako sistema batek eragiten diola, eta indar horiek
edozein indarrez osatutako sistema batek eragiten diola, eta indar horiek
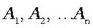 puntuetan aplikatuak direla,
hurrenez hurren (3.14. irudia). Gorputz horretako O puntu bat, edozein, hartzen bada -murrizketa zentroa-,
eta aurrez emandako indarren ekipolente diren indarrak marrazten badira puntu horretatik abiatuta,
gorputz horri indar sistema batek eta indar bikote sistema batek eragingo diote.
O puntuari aplikatutako indar sistema ondoriozko indar orokorra izeneko F indar bakar batez ordezka daiteke,
eta indar hori indar guztien batuketa geometrikoaren berdina izango da:
puntuetan aplikatuak direla,
hurrenez hurren (3.14. irudia). Gorputz horretako O puntu bat, edozein, hartzen bada -murrizketa zentroa-,
eta aurrez emandako indarren ekipolente diren indarrak marrazten badira puntu horretatik abiatuta,
gorputz horri indar sistema batek eta indar bikote sistema batek eragingo diote.
O puntuari aplikatutako indar sistema ondoriozko indar orokorra izeneko F indar bakar batez ordezka daiteke,
eta indar hori indar guztien batuketa geometrikoaren berdina izango da:

Indar bikoteen sistemaren ordez, berriz, ondoriozko momentua izeneko
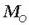 momentua har daiteke.
Momentu hori indar bakoitzak O puntuari buruz duen momentuen batuketa geometrikoaren berdina izango da:
momentua har daiteke.
Momentu hori indar bakoitzak O puntuari buruz duen momentuen batuketa geometrikoaren berdina izango da:
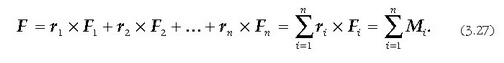
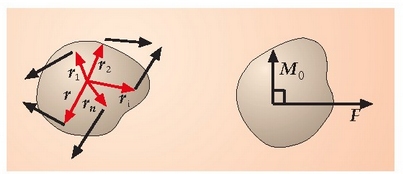
3.14. irudia. Gorputz gotor zurrun bai eragiten dion edozein indar sistemar en ordezkoa izan daiteke edozein O puntu batean aplikatutako indar bat eta bikote bat; bikote horren momentua eta sistemaren ondoriozko momentua O puntu horri buruz, berdinak dira.
Beraz, O murrizte zentroari aplikatutako F indar batek eta O puntuari buruzko
 momentuko indar bikote
batek ordezkatu ahal izango dute gorputz zurrun batean eragiten duen edozein indar sistema.
F indarra ez dago O puntuaren mende (bektore askea); baina
momentuko indar bikote
batek ordezkatu ahal izango dute gorputz zurrun batean eragiten duen edozein indar sistema.
F indarra ez dago O puntuaren mende (bektore askea); baina  bektorearen modulua, norabidea eta noranzkoa aldatu egiten dira O puntua aldatzen denean (bektore finkoa).
Emaitza horretatik ondorio hau atera daiteke: sistema baliokideak dira F ondoriozko indar orokorra eta
bektorearen modulua, norabidea eta noranzkoa aldatu egiten dira O puntua aldatzen denean (bektore finkoa).
Emaitza horretatik ondorio hau atera daiteke: sistema baliokideak dira F ondoriozko indar orokorra eta
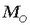 ondoriozko momentu berdinak
dituzten bi sistema
ondoriozko momentu berdinak
dituzten bi sistema
3.12 Varignon-en teorema
Demagun sistemako indar guztiek A sorburu bera dutela.
Bedi O puntuari buruzko A sorburu puntuaren r kokaera bektorea, eta

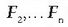 indarren eragin lerroetako puntuen
indarren eragin lerroetako puntuen  kokaera bektoreak.
kokaera bektoreak.


3.15. irudia. Indarrek sorburu bera dutenean, ondoriozko indarraren momentua indar osagaien momentuen baturaren berdina izango da.
Bektore berdintza horretako osagai guztien eta r bektorearen arteko bektore biderkaketa eginez gero, eta bektore biderkaketaren banaketa legea aplikatuz gero, emaitza hau ateratzen da:

Beraz:

hau da, edozein punturi buruz sorburu bera duten indarrez osatutako sistema baten ondoriozko indarraren momentuak eta puntu horri buruzko indar osagaien momentuen baturak balio bera dute. Baieztapen horrek osatzen du Varignonen teorema. Teorema horri esker, F indar baten momentua kalkula daiteke sorburu bera duten bi indarren edo gehiagoren momentuetatik abiatuta.
3.13 Indar sistema baten murriztea
Indar sistema bat murriztean ondoko kasu hauek gerta daitezke:
a)  Sistema zeroren baliokide da (sistema baliogabea).
Kasu honi buruzko azalpenak aurrerago emango dira.
Sistema zeroren baliokide da (sistema baliogabea).
Kasu honi buruzko azalpenak aurrerago emango dira.
b) 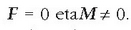 Bikote bakar batera murrizten da. Kasu honetan ondoriozko momentua ez dago murrizketa zentroaren mende. [ikus 3.17. ekuazioa]
Bikote bakar batera murrizten da. Kasu honetan ondoriozko momentua ez dago murrizketa zentroaren mende. [ikus 3.17. ekuazioa]
c)  murrizketa zentrotik igarotzen den F ondoriozko indar orokorrera murrizten da sistema hori.
murrizketa zentrotik igarotzen den F ondoriozko indar orokorrera murrizten da sistema hori.
d)  bektoreari buruz zuta (3.16a eta b irudiak). F ondoriozko indar orokorrera murrizten da sistema,
baina murrizketa era honetan ondoriozko indar hori ez da O murrizketa zentrotik igarotzen.
bektoreari buruz zuta (3.16a eta b irudiak). F ondoriozko indar orokorrera murrizten da sistema,
baina murrizketa era honetan ondoriozko indar hori ez da O murrizketa zentrotik igarotzen.
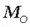 eta F elkarzutak direnez gero, plano berean daude batetik, bikotea,
eta F elkarzutak direnez gero, plano berean daude batetik, bikotea,
 momentuak adierazia, eta bestetik, F ondoriozko indar orokorra.
momentuak adierazia, eta bestetik, F ondoriozko indar orokorra.
 indar bikoteko
indarrak hartzen badira halako eran non horien moduluak eta F ondoriozko indar orrokorraren
moduluak bat egiten duten, eta indar bikote hori 1.16c irudiak adierazten duen bezala jatzen bada,
or - duan F eta F'' indarrek oreka galtzen dute eta ondoriozko sistema O' puntutik igarotzen den F' = F
indar bakar batera murrizten da (3.16d irud.).
indar bikoteko
indarrak hartzen badira halako eran non horien moduluak eta F ondoriozko indar orrokorraren
moduluak bat egiten duten, eta indar bikote hori 1.16c irudiak adierazten duen bezala jatzen bada,
or - duan F eta F'' indarrek oreka galtzen dute eta ondoriozko sistema O' puntutik igarotzen den F' = F
indar bakar batera murrizten da (3.16d irud.).  berdintzaren araberakoa da. Indar paraleloz osatutako sistema batean, edo indar planokidez osatutako batean,
berdintza hori beteko da baldin eta
berdintzaren araberakoa da. Indar paraleloz osatutako sistema batean, edo indar planokidez osatutako batean,
berdintza hori beteko da baldin eta 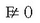 betetzen bada.
betetzen bada.

3.16. irudia. Indar planokidez osaturiko sistema bat, baldin eta bere ondoriozko indar orokorra eta ondoriozko momentua baliogabeak badira, 0 murrizketa zentrotik igarotzen ez den indar bakar batera murrizten da.
e)  bektoreari buruz paralelo (3.17a Irud.).
F indarrera eta indarrari buruz zuta den planoan dagoen F', F" indar bikotera murrizten da sistema (3.17b irud.).
F indarraren eragin lerroari ardatz zentral esaten zaio.
bektoreari buruz paralelo (3.17a Irud.).
F indarrera eta indarrari buruz zuta den planoan dagoen F', F" indar bikotera murrizten da sistema (3.17b irud.).
F indarraren eragin lerroari ardatz zentral esaten zaio.

3.17. irudia. Ondoriozko indar orokorra eta ondoriozko momentua paraleloak badira, indar batera eta pare batera murrizten da sistema. F indarraren eragin lerroari ardatz zentrala esaten zaio.
f)  bektoreak ez dira ez elkarren paralelo eta ez elkarzut (3.18a Irud.). Kasu honetan,
indar sistema indar eta bikote batera murrizten da, baina ardatz zentrala ez da igaroko O murrizketa puntutik.
Izan ere,
bektoreak ez dira ez elkarren paralelo eta ez elkarzut (3.18a Irud.). Kasu honetan,
indar sistema indar eta bikote batera murrizten da, baina ardatz zentrala ez da igaroko O murrizketa puntutik.
Izan ere,  bektorea F indarraren paralelo den
bektorea F indarraren paralelo den  bektorean eta F indarrari buruz zuta den
bektorean eta F indarrari buruz zuta den  bektorean deskonposatzen bada (3.18 b irudia), orduan,
bektorean deskonposatzen bada (3.18 b irudia), orduan,  bektoreak eta F indarrak adierazten duten bikotea (ikus 3.16 irudia) ordezkatu ahal izango da, eta horren ordez O'
puntuan aplikaturiko F' indarra erabili ahal izango da (3.18 c irudia).
Beraz, hasieran emandako indar sistemaren ordez F' = F indarra eta bikote bat,
bektoreak eta F indarrak adierazten duten bikotea (ikus 3.16 irudia) ordezkatu ahal izango da, eta horren ordez O'
puntuan aplikaturiko F' indarra erabili ahal izango da (3.18 c irudia).
Beraz, hasieran emandako indar sistemaren ordez F' = F indarra eta bikote bat,
 momentua duen eta F' indarraren paraleloa den bikotea hain zuzen, erabil daiteke (3.18 d irudia).
momentua duen eta F' indarraren paraleloa den bikotea hain zuzen, erabil daiteke (3.18 d irudia).

3.18 irudia. Sistema batean ondoriozko indar orokorra eta ondoriozko momentuak ez badira elkarren paraleloak eta elkarzutak, sistema hori indar bat eta bikote batera murrizten da; murrizketa horretan, bikotearen ardatz zentrala ez da igarotzen O murrizte zentrotik
3.14 Indar paraleloen sistema
 puntuei eragiten dien
puntuei eragiten dien
 indar paraleloen sistema batean,
indar horien posizio bektoreak
indar paraleloen sistema batean,
indar horien posizio bektoreak  posizio bektorea eta koordenatu sistema bat dira; koordenatu sistema hori "Z" ardatza indar guztien
norabideari buruz paralelo dela aukeratu dira. Bedi O' puntu baten r posizio bektorea;
O' puntua aukeratzeko kontuan hartu da
posizio bektorea eta koordenatu sistema bat dira; koordenatu sistema hori "Z" ardatza indar guztien
norabideari buruz paralelo dela aukeratu dira. Bedi O' puntu baten r posizio bektorea;
O' puntua aukeratzeko kontuan hartu da  ondoriozko indar orokorra puntu horretan aplikatuz gero, puntu horrek koordenatuen sorburuari buruz duen
momentuaren balioa eta sistemako F i indar guztiek O puntu berari buruz duten momentuen batura berdinak izan behar dutela. Beraz:
ondoriozko indar orokorra puntu horretan aplikatuz gero, puntu horrek koordenatuen sorburuari buruz duen
momentuaren balioa eta sistemako F i indar guztiek O puntu berari buruz duten momentuen batura berdinak izan behar dutela. Beraz:

eta

betetzen denez:

lortuko da. Horrenbestez:

edo bestela, O' puntuak, k bektorearen norabidea edozein dela ere, azken ekuazio hori egiaztatzen duenez gero, ondoko adierazpen hau erabil daiteke:


3.19. irudia. Indar paraleloz osatutako sistema bat O' puntu batean eragindako F indar bakar baten baliokide da.
Eta jakina,

adierazpenak, non 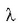 den zorizko eskalarra, (3.34) ekuazioa betetzen du. Azken ekuazio horrek lerro zuzen bat adierazten du,
eta F indarra lerro horretako edozein puntutan aplikatzen bada, O sorburuari buruzko bere momentua
den zorizko eskalarra, (3.34) ekuazioa betetzen du. Azken ekuazio horrek lerro zuzen bat adierazten du,
eta F indarra lerro horretako edozein puntutan aplikatzen bada, O sorburuari buruzko bere momentua
 indar sistemaren ondoriozko momentuaren berdina izango du.
indar sistemaren ondoriozko momentuaren berdina izango du.
(3.35) ekuazioa beste bi ekuazio eskalar hauen baliokidea da:

MASA ZENTROA
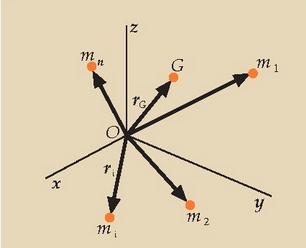
3.15 Zatiki diskretuez osaturiko sistema baten masa zentroa
Har dezagun sistema bat masa  duten n zatikiz osatua (ikus 3.20 irudia). Sistemaren masa osoak, m, honenbeste balioko du:
duten n zatikiz osatua (ikus 3.20 irudia). Sistemaren masa osoak, m, honenbeste balioko du:

Bitez  zatiki baten -edozeinen- koordenatuak;
bedi mi zatiki horren masa eta ri posizio bektorea. Orduan:
zatiki baten -edozeinen- koordenatuak;
bedi mi zatiki horren masa eta ri posizio bektorea. Orduan:

Horra, beraz, 3n eskalarreko multzo bat, zatikien koordenatuak adieraziz. Hurrengo bektore ekuazio honek definitzen duen G puntuari, berriz, sistemaren masa zentroa esaten zaio:
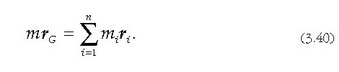
non
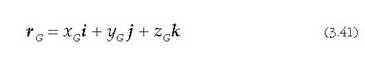
ekuazioak O puntutik G masa zentrora doan posizio bektorea adierazten baitu.
Masa zentroak ez du zertan O puntua izanik. Nolanahi ere, masa zentroa hartuz gero O puntutzat (96) dela ateratzen da, non
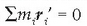 baita
baita
 masaren posizio bektorea G puntuari buruz.
masaren posizio bektorea G puntuari buruz.
3.20. irudia. n zatiki diskretuz osaturiko sistema bateko masa zentroa.
Eta (3.40) ekuazioan  eta
eta
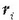 bektoreen ordez bektore
horiei dagozkioen balioak jarriz gero:
bektoreen ordez bektore
horiei dagozkioen balioak jarriz gero:

Hau da:

Ekuazio horretako lehenengo atalaren bektorea bigarren atalaren berdina denez:

3.16 Gorputz gotor baten grabitate zentroa
Lur azaletik gertu dagoen gorputz bateko zatikiak Lurraren erdigunerantz zuzen-zuzen erakartzen dituen indar baten mende daude. Indar horri grabitate indarra esaten zaio (ikus 3.21 irudia). Lurraren erradioarekin alderaturik oso dimentsio txikiak dituzten gorputzentzat, haiek osatzen dituzten zatikietan eragiten duten grabitate indarrak elkarren paraleloak direla eta modulu konstantea dutela onartzen da.
Baldin W esaten bazaio gorputz horren zatikietan eragina duten grabitate indarren emaitzari, orduan

ekuazioak gorputzaren pisua adierazten du. Gorputz horretako zatikietan eragina duten grabitate indar guztien ondoriozko indarraren eragin lerroa igarotzen den puntua, berriz, gorputz horren grabitate zentroa da, gorputz horrek bertikalari buruz duen kokalekua gorabehera. Grabitate zentroaren koordenatuak, indar paraleloen erdigune gisa, 3.37 formulen bidez ateratzen dira:
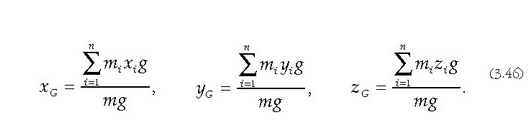
Edo honela, bestela:
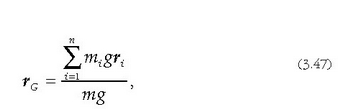
non  zatikiaren koordenatuak baitira;
zatikiaren koordenatuak baitira;
 , berriz, gorputzaren masa osoa baita;
eta
, berriz, gorputzaren masa osoa baita;
eta 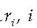 zatikiaren posizio bektorea.
Kontuan hartu (3.37) ekuazioei
zatikiaren posizio bektorea.
Kontuan hartu (3.37) ekuazioei  koordenatuari dagokion ekuazioa gehitu diegula. Gorputza eta gorputzarekin batera koordenatu ardatzak x edo y
ardatzak bertikal jarri arte - grabitate indarraren paralelo jarri arte, beraz - biratuz frogatzen da hori. ( 3. 37 )
ekuazioak deduzitzeko erabili den arrazoibideak berak antzeko ekuazioa ematen digu
koordenatuari dagokion ekuazioa gehitu diegula. Gorputza eta gorputzarekin batera koordenatu ardatzak x edo y
ardatzak bertikal jarri arte - grabitate indarraren paralelo jarri arte, beraz - biratuz frogatzen da hori. ( 3. 37 )
ekuazioak deduzitzeko erabili den arrazoibideak berak antzeko ekuazioa ematen digu
 koordenatuarentzat.
koordenatuarentzat.

3.21. irudia. Gorputz gotor baten grabitate zentroa delako gorputz horren zatikien grabitate indarren ondoriozko indarra igarotzen den puntua da.
Grabitate indarrak paraleloak direla eta modulu konstantea dutela onartu denez, grabitate zentroa ere bat etorriko da masen zentroarekin
3.17 Masa jarraitu baten grabitate zentroa
Baldin zatiki sistemak masa jarraitu bat osatzen badu integral mugatu bihurtzen dira (3.40) ekuazioko batuketak. mi masa bakoitza n handitzen den neurrian txikitzen da; nolanahi ere, infinitu ematen du beti batura horrek. Gero, mi ordez dm idatziz gero, eta batukari zeinuen ordez integrazio zeinuak jarriz gero, zera gertatzen da

non O sorburutik dm masako gorputzaren elementura doan posizio bektorea baita r,
elementu horren dentsiatea baita 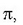 eta bolumena, berriz, dV. Hauek dira (3.48) bektore ekuazioari dagozkion ekuazio eskalarrak:
eta bolumena, berriz, dV. Hauek dira (3.48) bektore ekuazioari dagozkion ekuazio eskalarrak:

non gorputz osora hedatzen baita integrazioa. Gorputz errealak, baina, ezin dira matematikan jarraitutzat hartu; hala ere, aplikazio gehienentzat aski hurbiltze zehatza ematen du banaketa jarraitu ideal horrek.
Baldin gorputz hori xafla mehe bat bada, dentsitate uniformekoa, paperezko orri bat bezala, aski da grabitate zentroaren bi koordenatu finkatzea; gainalde baten grabitate zentro esaten zaio halakoetan. Ordea, makilatxo baten itxurakoa bada gorputza, dentsitate uniformekoa ez izanda ere, aski da koordenatu bat finkatzea; lerro baten grabitate zentro esaten zaio halakoetan. Makilatxo zuzen eta dentsitate uniformeko baten grabitate zentroa, baina, erdi-erdian dago, noski.
a) Lerro baten grabitate zentroa. Gorputz baten dentsitate lineala honela adierazten da definizioz,

non dm baita gorputzaren masa eta dL, berriz, luzera. Eta, beraz:

b) Gainalde baten grabitate zentroa. Gorputz baten gainaldearen dentsitatea honela adierazten da definizioz,

non dm baita gorputzaren masa eta dA, berriz, gainaldea. Eta, beraz:

b) Bolumen baten grabitate zentroa. Gorputz baten bolumen dentsitatea honela adierazten da definizioz,

non dm baita elementuaren masa eta dV, berriz, bolumena. Eta, beraz:

ADIBIDEA
Zehaztu L luze den makilatxo mehe baten grabitate zentroa. Hartzen den puntuaren eta makilatxoaren muturraren (0) artean dagoen distantzia makilatxoaren dentsitate linealaren proportzionala dela onartzen da haren edozein puntutan.
Ebazpena. Har dezagun dx luze den elementu bat, 0 muturretik x distantziara kokatua (ikus 3.22 irudia). Orduan,
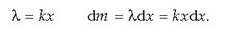
Beraz,

Hala, beraz,


Ikusten denez, grabitate zentroa ez dago proporzionaltasun faktorearen mende.
3.18 Zatiki baten oreka
Bitez  zatiki bakartu batean eragiten duten indarrak.
Zatiki hori orekan egongo bada, baldintza beharrezkoa da eta nahikoa,
haren gainean eragiten duten kanpo indarren batura zero izatea. Hau da,
zatiki bakartu batean eragiten duten indarrak.
Zatiki hori orekan egongo bada, baldintza beharrezkoa da eta nahikoa,
haren gainean eragiten duten kanpo indarren batura zero izatea. Hau da,

Ekuazio bektorial hori beste hiru ekuazio eskalar hauen baliokide da:
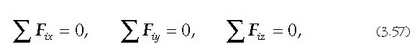
Ekuazio horiek zera adierazten dute: alegia, koordenatu ardatzetako bakoitzean eragiten duten indar guztien osagaien batura zer o izan ezean ez dela zatikia orekan egongo.
3.19 Gorputz gotor baten oreka espazioan
Espazioan, indar sistema arbitrario baten mende dagoen gorputz gotor, zurrun, aske bat orekan egoteko baldintza beharrezkoa eta nahikoa da kanpoko indarren batura zero izatea eta edozein punturi buruz kanpo momentuen batura zero izatea (sistema baliogabea). Hau da:

Aurreko bi bektore ekuazio horiek eta beste sei ekuazio eskalar hauek balio bera dute:

eta hauxe adierazten dute ekuaziook: alegia, espazioan, indar sistema arbitrario baten eraginpean dagoen gorputz gotor, zurrun, aske bat orekan egongo bada, koordenatu ardatzetako bakoitzaren gaineko indar guztien osagaien baturak eta ardatz horiekiko momentuen baturak zero izan behar dutela.
Ikusten denez, gorputza koordenatu ardatzetan zehar higi ez dadin bete beharreko baldintzei dagozkie lehenengo hiru ekuazioak, eta ardatz horien inguruan biratu ez dezan bete beharr ekoei, berriz, gainerako hirurak.
MARRUSKADURA
3.20 Erreakzioa gainalde baten gainean
Imajina dezagun gorputz bat gainalde horizontal batean geldi (ikus 3.23 irudia). Gorputz hori orekan dago bi indarren eraginpean:
alegia, batetik, W pisua, zuta eta beheranzkoa, eta, bestetik, gainaldearen beraren R erreakzioa. Gorputza bakarrik bi indarren mende baitago orekan, indar horiek lerro zuzen berean egon behar dute, eta modulu bera, norabide bera eta kontrako norazkoa izan behar dute. Beraz:


3.23. irudia. Gorputza orekan dago, bi indarren eraginpean: batetik, beheranzko indar zut bat, bere pisua (W), eta, bestetik, gainaldearen erreakzioa (R).
Gainalde horizontalak, beraz, gorputzari eusteko adinako erreakzio indarra besterik ez du egiten (non eta ez den gainaldearentzat astunegia gertatzen gorputza).
3.21 Marruskadura
Imajina dezagun beste indar bat, P indar horizontala, egiten dugula orain gorputz horretan, eta indar horren modulua mailaz maila handitzen dela zerotik hasita (ikus 3.24 irudia). P oso handia ez bada gorputza ez da mugituko, geldi segituko du, baina hiru indarren eraginpean orain: P, W eta R indarren eraginpean, alegia. W pisua lehengo bera izango da, noski; gainalde horizontalaren R erreakzioa ordea ez da orain berari buruz zuta edo normala izango, eta angelu jakin bat, ø, eratuko du. Erreakzio indar horrek bi osagai ditu: alegia, batetik N indarra, gainaldeari buruz zuta, osagai normala deitua, eta bestetik Fr indarra, gainaldeari buruz paraleloa, erreakzioaren marruskadura osagaia deitua. Eta jakina, orekan dagoenez gorputza:


3.24. irudia. Gorputzari P indar horizontal batek eragiten dionean, P> Fr izan ezean ez da gorputza mugituko.
Edo:

Beraz:

eta

P magnitudeak mailaz maila handitzen segitzen badu, ø angelua ere handitu egingo da, gehieneko balioa hartzeraino (e bidez adierazten da balio hori); baina balio horretaz harago handitzen bada P indarra, mugitzen hasiko da gorputza, eta oreka desegingo da. Gainaldearen erreakzioak berari buruzko normalarekin eratzen duen e angelu horri (gehieneko angelua) marruskadura angelu esaten zaio.
Esperimentu bidez froga daitekeen bezala, elkar ukitzen dauden sustantzien ezaugarrien mende baizik ez dago marruskadura angelua, eta ez, neurri batean behintzat, elkar ukitzen dauden gainaldeen eta presio normalen mende.
Baldin (3.66) ekuazioaren bidez definitzen bada marruskadura angelua, orduan, gainalde batean orekaren mugan dagoen gorputz batentzat, edozeinentzat, (3.67) dela beteko da.
Berdintza horretan, gainaldeari buruz paralelo den marruskadura indarraren modulua da Fr, eta hari buruz zuta den indarraren modulua, berriz, N. Bestalde, marruskadura koefizientea esaten zaio m magnitudeari.
Elkar ukitzen duten gainaldeak erabat leunak ez direlako gertatzen da marruskadura; guztiz leunak balira –matematikaren zentzuan leun– ez litzateke marruskadurarik izango. Marruskadura behar-beharrezkoa da batzuetan. Marruskadurarik ez balitz ezingo genuke ibili, eta auto batek ezingo luke aurrera egin; marruskadurarik gabe iltzeek ez lukete ezertarako balioko. Beste batzuetan, aldiz, ardatzaren inguruan biratzen duen bolantearen kasuan edo zilindro batean dagoen pistoiaren mugimenduaren kasuan, esate baterako, nahiago izango litzateke marruskadurarik ez balitz.
Gainalde leun batean gainaldeari buruz normala da beti erreakzioa.
ADIBIDEA
W pisatzen duen gorputz bat gainalde zimur horizontal baten gainean dago. Gorputzari P indarrak eragiten dio, f angelua osatzen duela horizontalarekin. Baldin gorputza orekaren mugan badago, zer modulu izango du P-k? Gorputzaren eta planoaren arteko marruskadura koefizientea m da.
Ebazpena. Hauek dira gorputzari eragiten dioten indarrak: P indarra, gorputzaren W pisua eta planoaren R erreakzioa (ikus 3.25 irudia). Azkeneko indar horrek bi osagai ditu: N, planoari buruz zut, eta Fr, planoari buruz paralelo. Eta gorputza orekan dagoenez:
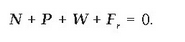
Alegia,

Beraz,

Eta hau lortuko dugu:


Baina gorputza orekaren mugan aurkitzen bada, orduan,
 eta, beraz:
eta, beraz:

Eta hau ateratzen da adierazpen horretatik:

3.22 Oreka plano makurtu batean
Gorputz bat plano makurtu batean geldi egongo bada, planoaren eta horizontalaren arteko f angeluak marruskadura angelua baino txikiagoa izan behar du, edota berdina gehienez ere (ikus 3.26 marrazkia).

3.26. irudia. R erreakzioak gainaldearen normalarekin eratzen duen gehieneko angeluari marruskadura angelu esaten zaio.
Nola gorputzari grabitate indarrak eta planoaren erreakzioak besterik ez dioten eragiten,
biek ala biek lerro zuzen berean egon behar dute eta moduluek berdinak izan behar dute.
R erreakzioak, beraz, angelu bat osatzen du normalarekin, eta angelu hori ere
 izango da.
Eta hala, R erreakzioak normalarekin osatzen duen angelua marruskadura angelua bezalakoa edo hura
baino handiagoa izan ezean gorputza ez da mugituko; hau da,
izango da.
Eta hala, R erreakzioak normalarekin osatzen duen angelua marruskadura angelua bezalakoa edo hura
baino handiagoa izan ezean gorputza ez da mugituko; hau da,
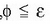 izatean
baizik ez da gorputza geldirik egongo.
izatean
baizik ez da gorputza geldirik egongo.
